
Emergency Medical Services Modelling
Paul Harper, Jonathan Gillard, Vincent Knight, Leanne Smith, Julie Vile and Janet Williams
School of Mathematics, Cardiff University, Cardiff, U.K.
Keywords: Healthcare Modelling, Forecasting, Priority Queueing Theory, Discrete Event Simulation, Ambulance
Allocation.
Abstract: Emergency Medical Services (EMS) are facing increasing pressures in many nations given that demands on
the service are rising. This paper focuses on the operations of the Welsh Ambulance Service Trust (WAST),
which provides urgent care services on a day-to-day basis across the whole of Wales. Facing ever-
increasing pressures to provide rapid responses, the Trust is keen to develop new initiatives to meet the
response time targets set by the government. This article describes work performed at Cardiff University in
collaboration with WAST, investigating a range of Operational Research (OR) methods, including computer
simulation, to assist the Trust with capacity planning issues and deployment of emergency vehicles and
crews.
1 INTRODUCTION
The Welsh Ambulance Service Trust (WAST)
provides urgent care services on a day-to-day basis
across the whole of Wales. Facing ever increasing
pressures to provide rapid responses that satisfy the
targets set by the government in the midst of a
challenging two decades over which the ambulance
service has seen demand levels rise threefold,
WAST has been scrutinised in respect of
performance issues (Lightfoot Solutions, 2009;
Welsh Government 2011).
As WAST furthers its
ambitions to provide high quality healthcare, it has
become keen to work with partner organisations to
address the issues it faces across the health service
and develop new initiatives to improve its
performance, resulting in a successful working
relationship being established between the
Operational Research (OR) department at Cardiff
University and WAST. A comprehensive database
was provided by the Trust consting of 2,500,000
data records from April 2005 to December 2009,
corresponding to either a submission of request for
WAST assistance, the dispatch of a response
vehicle, or both.
The main challenges envisioned by the Trust for
the future may be classified into two distinct fields:
(i) capacity planning; and (ii) location analysis. The
issues are accordingly summarised within this paper.
The first involves the development of a workforce
capacity planning tool which integrates forecasting,
priority queueing theory and scheduling models into
a single spreadsheet model to optimise resource
allocation in terms of capacity. The second reveals
insights in improvements that can be gained from
positioning resources in different locations with the
development and use of a discrete event simulation.
2 RESPONSE TIME TARGETS
AND DEMAND
The Welsh Government requires the service to
achieve a set of national standards and targets,
designed to illustrate the quality of service they
provide; and their performance is analysed on a
monthly basis. Emergency 999 calls received are
immediately categorised into three classes of
urgency by the calltaker, using a triage system
known as the Advanced Medical Priority Dispatch
System (AMPDS) (see Lightfoot Solutions, 2009):
Category A: Immediately life threatening
condition/injury.
Category B: Serious but not life threatening
condition/injury.
Category C: Neither life threatening or serious
condition/injury.
The coinciding targets, reported by the Welsh
Government (2011), applied at the time and
549
Harper P., Gillard J., Knight V., Smith L., Vile J. and Williams J..
Emergency Medical Services Modelling.
DOI: 10.5220/0004538705490555
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (HA-2013), pages
549-555
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

considered in this research may further be
summarised as:
Target 1: To attain and maintain a month on
month performance of at least 60% of first
responses to Category A calls arriving within 8
minutes in each region (local Health Board);
and to follow up with a fully equipped
emergency ambulance to a level of 95% within
14, 18 or 21 minutes respectively in urban, rural
or sparsely populated areas.
Target 2: To send a fully equipped emergency
ambulance to all other emergency calls
(Category B and Category C) to a level of 95%
within 14, 18 or 21 minutes respectively in
urban, rural or sparsely populated areas.
The primary vehicles used are Rapid Response
Vehicles (RRVs) and fully equipped Emergency
Ambulances (EAs). RRVs cannot be used to
transport patients as they are typically small vehicles
operated by a single health worker; however they
offer the advantage that they can rapidly reach the
scene of the incident. EAs can be used to transport
patients and are typically manned by a two crew
members (at least one of whom must be a fully
trained paramedic). Typically a single EA is sent to
all emergency calls, and an additional RRV is
required to attend every Category A incident.
Over the 56 month period of data provided by
WAST (2005-2009), an average of 1011 incidents
(999 calls) (standard deviation 68.43) were reported
each day, although the number reported fluctuated
from 697 to 1485, as highlighted in Figure 1.
Figure 1: WAST daily demand (01/04/2005 – 31/12/2009).
Preliminary analysis of the data reveals daily,
weekly and yearly periodicities; special-day effects;
autocorrelations and a positive trend. Linear
regression analysis applied to daily demand against
time yields a significant slope coefficient of 0.045.
All four high extreme values occur on January 1st,
representing the repeating pattern of extreme
demand for the service following annual New Year's
Eve celebrations. The notable troughs occur on 21st
March 2006, 31st October 2007 and 18th May 2009.
There is no obvious reason for these low counts.
Figure 2 displays box plots of daily demand
volumes for each month of the year and day of the
week. December is the busiest month with a median
of 1063 incidents requiring WAST mobilisation a
day. Higher demand is generally demonstrated
during the winter months of November, February
and October, although the lowest median demand
occurs in January (984) despite the extreme peak
each New Year's Day. Clear weekday effects are
notable with larger volumes of incidents observed on
Fridays and Saturdays. All such observations will
become of key importance when designing
schedules for ambulance crews.
Figure 2: Box plots of demand volumes by month and
weekday.
In light of the information contained above revealing
that demand for WAST assistance is heavily time
dependent (both upon the day of week and time of
day), and further prioritised as either a life-
threatening or a less serious injury; the techniques
that are described to optimise WAST resources in
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
550

the following sections are accordingly designed to
aptly deal with both non-stationary and prioritised
demand.
3 WORKFORCE PLANNING
The process of optimising resources by means of
rostering of employees using low-costs shifts that
match stochastic demand levels requires the
investigation of several inter-related procedures. The
process traditionally begins with the consideration of
methods to generate accurate forecasts of demand,
followed by techniques to convert the demand
profiles to coverage requirements, and generate
optimised shift schedules. The resulting shift
schedule can be ultimately used as input to a
rostering system, detailing the work to be performed
over a specified time period by each member of the
workforce in a way to minimise labour costs. Most
current practice to optimise personnel scheduling
follows the general approach originally presented in
Buffa et al. (1976), which recommends that the
following steps be taken to roster employees: (i)
forecast demand; (ii) convert demand forecasts into
staffing requirements; (iii) schedule shifts optimally;
and (iv) assign employees to shifts.
The research reported in this paper however
integrates the processes into a single spreadsheet
tool, designed to find minimum staffing
requirements that allow the government response
time targets to be met, as illustrated in Figure 3.
Figure 3: Integration of techniques in the workforce
capacity planning tool.
3.1 Demand Forecasts
To aid with the decision of the number of
ambulances and paramedics to be deployed,
intensive OR has been conducted in the fields of
optimal fleet size and vehicle deployment strategies;
yet for these deployment schemes to be effective, the
values used to forecast future demand levels for
service must obviously be accurate (Setzler et al.,
2009). This research begins by responding to the
need to produce accurate forecasts of demand,
investigating methods that adequately account for
non-stationarities. A technique known as Singular
Spectrum Analysis (SSA) has been used for this
purpose as Table 1 illustrates that SSA is able to
generate superior forecasts to traditional methods.
The table evaluates the quality of rolling forecasts
generated for December 2009 by SSA and two well-
known conventional methods, using the Root Mean
Square Error (RMSE) and standard deviation
(reported in brackets). By decomposing a time series
into various elements, and separating the trend and
periodic components from structureless noise (i.e.
random fluctuations), SSA is able to adequately
account for the seasonal and stochastic variations in
the data when reconstructing the time series and
produce forecasts that simultaneously account for
several factors affecting demand. Further details
regarding the underpinnings of the SSA technique
and its ability to produce forecasts of WAST
demand are contained in Vile et al. (2012).
Table 1: Comparison of model forecast for daily demand
(December 2009).
In further investigations, SSA has been consistently
found to generate accurate forecasts for various
months and forecasting horizons, especially for
longer-term forecasts which are desired by WAST to
set staffing schedules and rosters. In addition to
producing high quality forecasts, SSA further
benefits from its ability to be easily embedded into a
spreadsheet tool, and flexibly adjusted to produce
forecasts at various levels of granularity, including
distinct forecasts for Category A, B and C demands.
3.2 Time-dependent Priority Queues
With the demand forecasts estimated, the next part
of the resource allocation optimisation process
involves converting these into minimum staffing
requirements. This task has been approached using
queueing theory and modelling WAST as a priority
queue (recognising that Category A incidents are
treated with precedence). Using the expected arrival
rates as output from SSA, and distributions
surrounding service times, mathematical expressions
EmergencyMedicalServicesModelling
551

can be used to evaluate summary measures under
various scenarios, such as the probability of an
excessive wait as is relevant for our research, to
construct minimum coverage requirements.
However, the non-stationary nature of
demand for WAST assistance renders the queueing
model analytically intractable, i.e. there are no
closed-form expressions by which one can evaluate
various performance metrics over time, so both
quick approximation techniques and more
computationally expensive numerical methods have
been developed to adequately deal with time-
dependent and priority demand, and ultimately
produce minimum hourly coverage requirements
that satisfy the response time targets. The most basic
type of analysis can be achieved using a SIPP
(Stationary Independent Period by Period)
approximation (see for example Green et al, 2001).
SIPP estimates the time-dependent behaviour by
first segmenting the operation period into distinct
shifts, and finding the average arrival rate in each
shift. Then treating each shift independently and
assuming the system settles down to steady-state
(operates at a consistent level) within each period,
closed-form formulae can be used to calculate the
number of staff required for each shift and match the
coverage requirements to the demand levels.
Recognising that the approximation method
requires many assumptions and fails to account for
the dependency that exists between periods, we have
also investigated a numerical method which
produces accurate estimates at the expense of
computation speed by accurately tracking the
movement of customers through the service system
using a set of differential-difference equations to
predict the number of patients awaiting and
receiving assistance at all time points. Balancing the
ability of the approximation method to provide
rough solutions rapidly, and the advantage of the
numerical method to produce accurate predictions at
the expense of computation speed, the ultimate
methodology we have proposed to WAST is a novel
hybrid method which employs both methods to
produce coverage requirements (Vile et al, 2013).
3.3 Scheduling and Rostering
Finally, with the minimum hourly coverage
requirements produced, we have investigated shift
scheduling and rostering techniques that can be used
to optimise the shift pattern and assign staff to shifts.
Both problems have been formulated in terms of
integer linear programs, which may be incorporated
as part of the capacity planning tool, and solved
using exact methods and heuristic search techniques
(using random descent and simulated annealing).
The heuristic method is helpful for inclusion in the
developed spreadsheet tool in case no commercial IP
solvers are available, such as in use by WAST.
Various objectives can be chosen to construct
optimised functions, such as minimising the total
labour hours used or crew size, and any number of
constraints can be added to the model to develop
potential schedules. Whilst the shift schedule may be
optimised prior to the application of a rostering
model, our research has acknowledged the benefit in
simultaneously constructing the shift schedule and
roster, due to complex working time directives
which can prevent crews from working certain shift
patterns of the optimised shift schedule.
The workforce capacity planning and
scheduling tool which amalgamates all of the above
techniques into a single integrated model, has been
designed with a user-friendly interface with
parameters that may be flexibly adjusted by the user
to provide staffing recommendations for various
scenarios that satisfy the response time targets.
While taking into account the importance of
accurately estimating future demand, the need to
develop OR methodology to evaluate service quality
in time-dependent priority multi-server systems, and
generate efficient shift schedules, the tool:
a) Incorporates time-series methods that
adequately account for the stochastic nature of
demand to produce accurate forecasts of future
demand;
b) Provides both accurate and approximate
evaluations of system performance over time;
c) Permits a certain service quality to be met as
inexpensively as possible by generating an
efficient staffing function that accurately
matches resources to fluctuating demand levels;
d) Assigns staff to shifts in an efficient manner,
whilst adhering to governmental regulations and
working time directives;
e) Is user-friendly and practical; so it could be
used to inform WAST staffing decisions and
readily adopted by planners to optimise
resources independently.
4 AMBULANCE LOCATION
AND DEPLOYMENT
We now turn our attention to location and
deployment of the vehicles. An EMS system can be
thought of as a priority queueing system with arrival
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
552
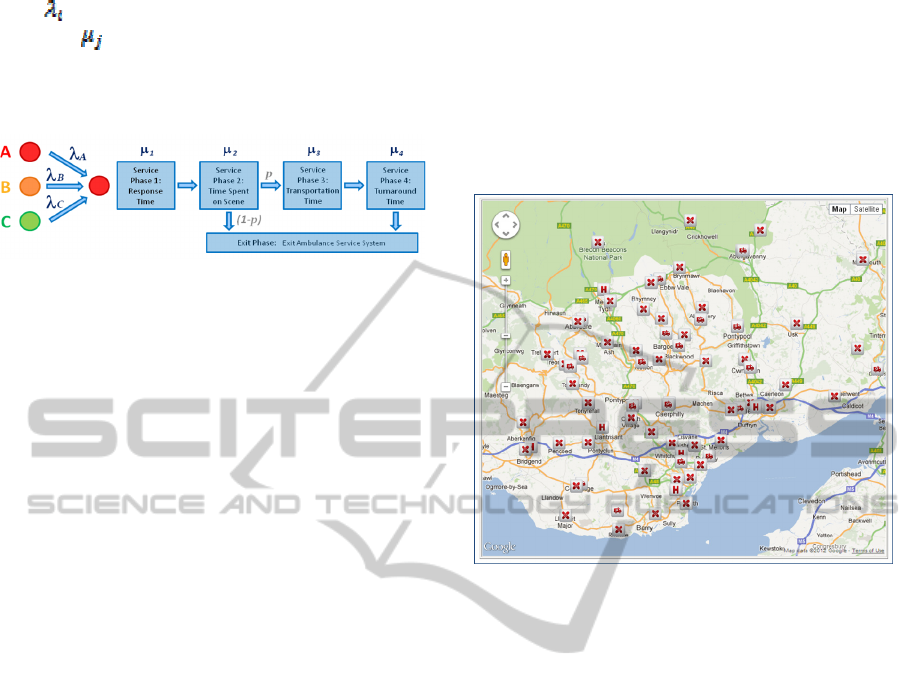
rates
(i =1,..,n for n priority types), service phase
durations
(j =1,..,4), probability p that the patient
requires transportation to hospital and (1-p) that the
patient exits the system after treatment on scene (see
Figure 4).
Figure 4: Welsh EMS system represented as a queueing
system.
Using this modelling design, the problem is
decomposed into two components. Firstly, location
analysis is used to obtain initial allocations of
ambulance vehicles to stations. Secondly, these
allocations are fed into a developed discrete event
simulation model to investigate in greater detail the
time-dependent demand placed upon the service and
the movement of emergency vehicles across the
network
4.1 Regional Parameters
From the data provided by WAST, there were
approximately 175,000 unique ambulance call
records covering South East Wales for 2009.
Category A (life-threatening) and B (serious) each
make up a third of the overall demand; category C
and Urgent calls contribute around 15% and 18% of
the demand respectively. Distributional analysis has
been conducted for the four service components
described in Figure 4, as well as analysis capturing
the time-dependent demand of the region for
different emergency categories. These findings are
provided as input parameters to the simulation
model, allowing scenario testing in a representative
environment.
4.2 Travel Time Estimation
Since travel time information is vital for such EMS
studies, a Travel Time Matrix Generator has been
designed using the Google Maps API (Figure 5).
This allows travel time and/or distance matrices to
be obtained and utilised in both the location analysis
and simulation modelling processes. Journey times
provided by Google Maps do not accurately
represent the speed of an EMS vehicle; therefore,
travel times have been estimated from Google
distances via regression techniques.
Assume Y is travel time, X is the travel distance
obtained from the Google Maps API, then journey
time is modelled as:
Y ~ Lognormal(μ,σ
2
) (1)
where μ = a + bX + ε and ε is normally distributed
with mean and variance of the regression residuals;
σ² is the variance given by the data (Smith, 2013).
Figure 5: Google Maps API interface inbuilt to Travel
Time Matrix Generator Tool, displaying demand nodes,
vehicle bases and hospitals in the South East Wales region.
Many ambulance services across the UK, including
WAST, are moving towards clinical outcome based
performance measures as opposed to hard response
times. This reflects patient condition, particularly
where the chance of survival depends greatly on
response time (Pell et al. 2001; Persse et al. 2003).
The Maximal Expected Survival Model for
Heterogeneous Patients (MESLMHP) has been
developed (Knight et al., 2012) to show how
survival functions manage the variation in urgency
and patient outcome compared with current EMS
planning methods, potentially saving lives. The
model builds on work by Erkut et al. (2008) and
aims to maximise the overall survival probability of
patients whereby categories can be defined
according to medical condition with a corresponding
survival function (e.g. probability s(t) of survival
after a cardiac arrest given a vehicle arrives within t
minutes). The resulting allocation of vehicles is used
as input to the simulation model. Graphically, the
allocations of all vehicles across regional stations
can be viewed and altered within the simulation
model for different shift patterns (Figure 6).
EmergencyMedicalServicesModelling
553

Figure 6: Station allocations per shift over a week as input
to the simulation model.
4.3 Simulation Framework
A discrete event simulation model has been built in
the C# programming language (seen in Figure 7)
using a priority calendar queueing system to
represent all arrival and all service processes of
emergency calls to WAST in a typical week. The
intention of the model is to evaluate potential
allocations and fleet capacities in order to help
WAST provide a more efficient and effective service
to the population. The model allows demonstration
of the impact some operational factors – such as
volume of demand, number of available vehicles,
locations and turnaround times – have on response
and performance.
Fixed allocations of vehicles over the network
are unknown, and many other aspects of an EMS
system cannot be easily captured through analytical
modelling. The simulation tool is able to give a
broader insight to operational procedures and can
demonstrate how decisions regarding dispatching
rules and allocation of vehicles to stations
stochastically affects other phases of service and
fleet utilisation.
Figure 7: Example of the simulation tool interface.
4.4 Illustrative Results
The simulation is run under various conditions of
interest to WAST in order to suggest operational and
strategic solutions that will help meet government
set targets and provide the best response to the
medical emergencies of the Welsh population.
Optimal vehicle allocation and fleet capacity as
given by the location model can be fed into the
simulation tool in order to explore impact of location
on response and as support for WAST’s current
move towards clinical performance measures.
Reduction of turnaround time can also be explored
to see its effect on utilisation, availability and
subsequently, response. Figure 8 demonstrates how
as demand on a particular weekday has an effect on
the average response time witnessed within the
region.
Figure 8: Average demand and response time for South
East Wales region from a simulation experiment.
5 DISCUSSION
This paper illustrates the ways in which OR can
assist with EMS planning. Using a range of
modelling tools, this paper describes the interactions
with the Welsh Ambulance Service, assisting them
with forecasting demand, scheduling crews and
decisions on locations and deployment of vehicles.
The work has recently gained the attention of Welsh
Government, and working with alongside WAST we
will pilot the tools to hopefully assist them and
improve patient outcomes and make more efficient
use of existing resources.
ACKNOWLEDGEMENTS
The authors wish to thank staff at WAST who
provided the data used here and shared their many
helpful insights allowing us to progress this
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
554

research. The research was funded by an EPSRC
grant EP/F03338 as part of the LANCS Initiative
(www.lancs-initiative.ac.uk)
REFERENCES
Buffa, E., Cosgrove, M. and Luce, B. (1976). An
integrated work shift scheduling system,
Decision Sciences 7: 620–630.
Erkut, E. et al. (2008). Ambulance location for maximum
survival. Naval Research Logistics 55(1), pp. 42-58.
Green, L., Kolesar, P. and Soares, J. (2001). Improving the
SIPP approach for staffing service systems that have
cyclic demands. Operations Research 49: 549–564.
Knight, V. A., Harper P. R. and Smith L. (2012).
Ambulance allocation for maximal survival with
heterogeneous outcome measures. OMEGA 40(6):
919-926.
Lightfoot Solutions (2009). Time to make a difference:
Transforming ambulance services in Wales. A
modernisation plan for ambulance services and NHS
Direct Wales, Technical report.
Pell, J. P. et al. (2001). Effect of reducing ambulance
response times on deaths from out of hospital cardiac
arrest: Cohort study. British Medical Journal 322:
1385-1388.
Persse, D. E. et al. (2003). Cardiac arrest survival as a
function of ambulance deployment strategy in a large
urban Emergency Medical Services system.
Resuscitation 59: 97-104.
Setzler, H., Park, S. and Saydam, C. (2009). EMS call
volume predictions: A comparative study, Computers
& Operations Research 36: 1843–1851.
Smith, L. (2013), Modeling emergency medical services.
PhD Thesis, Cardiff University, Cardiff, UK.
Vile, J., Gillard, J., Harper, P. and Knight, V. (2012).
Predicting ambulance demand using singular spectrum
analysis. Journal of the Operational Research Society
63(11): 1556–1565.
Vile, J., Gillard, J., Harper, P. and Knight, V. (2013). A
comparison of approximate and numerical methods to
analyse priority queues with time-varying demand.
Working paper, Cardiff School of Mathematics,
Cardiff University, Cardiff, UK.
Welsh Government (2011). Ambulance Services in Wales:
February 2011, Technical Report SDR 59/2011.
EmergencyMedicalServicesModelling
555
