
Chaotic Quantum-behaved Particle Swarm Optimization Approach
Applied to Inverse Heat Transfer Problem
Leandro dos Santos Coelho
1
, Fabio A. Guerra
2
, Bruno Pasquim
3
and Viviana Cocco Mariani
4
1
Pontifical Catholic University of Parana, Industrial and Systems Engineering Graduate Program (PPGEPS)
and Federal University of Parana (UFPR), Department of Electrical Engineering (DEE/PPGEE), Curitiba, PR, Brazil
2
Electricity Department, DPEL/DVSE/LACTEC, Institute of Technology for Development, Curitiba, PR, Brazil
3
Pontifical Catholic University of Parana, Mechanical Engineering Graduate Program (PPGEM), Curitiba, PR, Brazil
4
Pontifical Catholic University of Parana, Mechanical Engineering Graduate Program (PPGEM)
and Federal University Of Parana (UFPR), Department of Electrical Engineering (DEE), Curitiba, PR, Brazil
Keywords: Particle Swarm Optimization, Quantum Mechanics, Chaos Theory, Heat Transfer.
Abstract: Particle swarm optimization (PSO) algorithms are attracting attentions in recent years, due to their ability of
keeping good balance between convergence and diversity maintenance. Several attempts have been made to
improve the performance of the original PSO algorithm. Inspired by trajectory analysis of the PSO and
quantum mechanics, a quantum-behaved particle swarm optimization (QPSO) algorithm was recently
proposed. QPSO has shown some important advantages by providing high speed of convergence in specific
problems, but it has a tendency to get stuck in a near optimal solution and one may find it difficult to
improve solution accuracy by fine tuning. In this paper, a modified and efficient version of the QPSO
combined with chaotic sequences (CQPSO) is proposed and evaluated. We conduct simulations to estimate
the unknown variables of an inverse heat transfer problem to verify the performance of the proposed
CQPSO method and show that the method can be competitive when compared with the classical QPSO.
1 INTRODUCTION
The particle swarm optimization (PSO) has been
introduced in the middle of 90’s (Kennedy and
Eberhart, 1995); (Eberhart and Kennedy, 1995) and
it is based on a ”social interaction” metaphor in
which the parameter space is searched by controlling
the trajectories of a set of particles according to a
swarm- or flock-like set of rules.
PSO is a fertile research paradigm and its simple
structure has encouraged the exploration of
algorithmic variations. Furthermore, PSO
approaches are well known for their ability to deal
with nonlinear and complex optimization problems.
Details of different PSO approaches are presented in
Parsopoulos and Vrahatis (2002), Eslami et al.,
(2012), and Khare and Rangnekar (2013).
One of the recent developments in PSO is the
application of quantum laws of mechanics to
observe the behavior of PSO. Inspired by quantum
mechanics, Sun et al. (2004a, 2004b) proposed
quantum-behaved particle swarm optimization
(QPSO) which the state of a particle is depicted by
wavefunction, instead of position and velocity. A
wavefunction is a probability amplitude in quantum
mechanics describing the quantum state of a particle
and how it behaves.
The success of the search in QPSO is dependent
on a good balance between two processes:
exploration and exploitation. Exploration allows
searching the entire search space by ensuring the
redirection of the search toward new regions, while
exploitation favors a quick convergence toward the
optimum. Several studies (Coelho and Mariani,
2008); (Sun and Lu, 2010); (Sun et al., 2012)
propose modifications in the QPSO algorithm to
improve its performance in continuous optimization.
A review of QPSO is presented in Fang et al. (2010).
On the other hand, due to its certainty, ergodicity
and stochastic properties, chaotic sequences have
been used to replace random numbers and to
enhance the performance of metaheuristic
optimization algorithms (Coelho and Pessôa, 2011);
(Coelho and Mariani, 2012); (Peitgen et al., 2004).
In this paper, a novel version of QPSO namely
CQPSO is proposed in which QPSO is combined
with chaotic sequences generated by a Hénon’s map
97
dos Santos Coelho L., A. Guerra F., Pasquim B. and Cocco Mariani V..
Chaotic Quantum-behaved Particle Swarm Optimization Approach Applied to Inverse Heat Transfer Problem.
DOI: 10.5220/0004538900970102
In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 97-102
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

(Peitgen et al., 2004) to modify the local attractor
strategy. The idea behind the inclusion of chaotic
sequences is to facilitate the CQPSO to enhance the
global search performance in preventing premature
convergence to local minima when compared with
the classical PSO and QPSO algorithms.
The goal of this study is to explore and analyze
the performance of CQPSO when compared with
classical PSO and QPSO estimating accurately the
time-varying temperature field. The enthalpy
formulation of the heat conduction process utilizes
two dependent variables, enthalpy and temperature.
This paper is structured as follows: Basics of
PSO approaches are presented in Section 2. Details
of the inverse heat transfer problem and its
formulation are explained in Section 3. The
numerical results and discussions are presented in
Section 4. Finally, the conclusions are given in
Section 5.
2 PSO APPROACHES
In the next subsections first, a brief overview of the
classical PSO and QPSO are provided; and finally,
the proposed CQPSO is explained.
2.1 Classical PSO Algorithm
The PSO algorithm consists of changing the velocity
that accelerates each particle (potential solutions)
toward its pbest (personal best) and gbest (global
best) locations. The procedure for implementing the
global version of classical PSO is given by the
following steps:
Step 1: Initialization of Swarm Positions and
Velocities: Initialize a population (array) of particles
with random positions and velocities in the n
dimensional problem space using uniform
probability distribution function.
Step 2: Evaluation of Particle’s Fitness: Evaluate
each particle’s fitness value.
Step 3: Comparison to pbest (personal best):
Compare each particle’s fitness with the particle’s
pbest. If the current value is better than pbest, then
set the pbest value equal to the current value and the
pbest location equal to the current location in n-
dimensional space.
Step 4: Comparison to gbest (global best): Compare
the fitness with the population’s overall previous
best. If the current value is better than gbest, then
reset gbest to the current particle’s array index and
value.
Step 5: Updating of each Particle’s Velocity and
Position: Change the velocity, v
i
, and position of the
particle, x
i
, according to equations (1) and (2):
)]()([
2
)]()([
1
)()1(
t
i
xt
g
pUdc
t
i
xt
i
pud ct
i
vwt
i
v
(1)
)1)()1(
(t
i
vtt
i
xt
i
x
(2)
where i=1,2,…,N indicates the number of particles
of population (swarm); t=1,2,…t
max
, indicates the
generations (iterations);
T
,...,
2
,
1
in
v
i
v
i
v
i
v
stands
for the velocity of the i-th
particle,
T
,...,
2
,
1
in
x
i
x
i
x
i
x
stands for the position
of the i-th particle of population, and
T
,...,
2
,
1
in
p
i
p
i
p
i
p
represents the best previous
position of the i-th particle. The inertia weight w
plays the role of balancing the global and local
searches. Parameter c
1
represents the “self-
cognition” that pulls the particle to its own historical
best position, helping explore local niches and
maintaining the diversity of the swarm. Parameter c
2
represents the “social influence” that pushes the
swarm to converge to the current globally best
region, helping with fast convergence. In other
words, positive constants c
1
and c
2
are the cognitive
and social components, respectively (Ratnaweera et
al., 2004). Index g represents the index of the best
particle among all the particles in the swarm.
Variables ud and Ud are two random numbers
generated in the range [0,1]. Equation (2) represents
the position update, according to its previous
position and its velocity, considering
1t .
Step 6: Repeating the evolutionary cycle: Return to
Step 2 until a stop criterion is met, usually a
sufficiently good fitness or a maximum number of
generations.
2.2 QPSO Algorithm
In the quantum model of a PSO called here QPSO,
the state of a particle is depicted by wavefunction
(x, t) (Schrödinger equation), instead of position
and velocity of classical PSO. The probability of the
particle’s appearing in position x
i
from probability
density function |
(x,t)|
2
, the form of which depends
on the potential field the particle lies. Employing the
Monte Carlo method, the particles move according
to the following iterative equation (Sun et al., 2004a;
2004b):
i,j i j i,j
i,j i j i,j
x(t 1) p(t) β Mbest (t) x (t) ln(1/ u), if k 0.5
x(t 1) p(t) β Mbest (t) x (t) ln(1/ u), if k 0.5
(3)
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
98

where x
i,j
(t+1) is the position for the j-th dimension
of i-th particle in t-th generation (iteration); Mbest
j
(t)
is the global point called Mainstream Thought or
Mean Best (Mbest) for the j-th dimension;
is a
design parameter called contraction-expansion
coefficient; u and k are values generated according
to a uniform probability distribution in range [0,1];
and p
i
(t) is local point (local attractor) defined in
(Clerc and Kennedy, 2002). The Mainstream
Thought or Mean Best (Mbest) is defined as the
mean of the pbest positions of all particles and it
given by
N
j
t
jg
p
N
(t)
j
Mbest
1
)(
,
1
,
(4)
where g represents the index of the best particle
among all the particles’ swarm in j-th dimension. In
this case, it is adopted
21
,2,1
)(
cc
ig
pc
ik
pc
t
i
p
,
(5)
where p
k,i
(pbest) represents the best previous i-th
position of the k-th particle and p
g,i
(gbest)
represents the i-th position of the best particle of the
population. In the same form that the classical PSO,
constants c
1
and c
2
are the cognitive and social
components, respectively. The procedure for
implementing the QPSO is given by the following
steps (Sun et al., 2004a, 2004b):
Step 1: Initialization of Swarm Positions: Initialize a
population (array) of particles with random positions
in the n dimensional problem space using a uniform
probability distribution function.
Step 2: Evaluation of Particle’s Fitness: Evaluate
the fitness value of each particle.
Step 3: Comparison of each Particle’s Fitness with
its Pbest (personal Best): Compare each particle’s
fitness with the particle’s pbest. If the current value
is better than pbest, then set a novel pbest value
equals to the current value and the pbest location
equals to the current location in n-dimensional
space.
Step 4: Comparison of each Particle’s Fitness with
its Gbest (global best): Compare the fitness with the
population’s overall previous best. If the current
value is better than gbest, then reset gbest to the
current particle’s array index and value.
Step 5: Updating of Global Point: Calculate the
Mbest using equation (4).
Step 6: Updating of Particles’ Position: Change the
position of the particles using equations (3) and (5).
Step 7: Repeating the Evolutionary Cycle: Loop to
Step 2 until a stopping criterion is met. In this paper,
it is adopted a maximum number of iterations
(generations).
2.3 The Proposed CQPSO Algorithm
Recently, some applications of chaotic sequences in
PSO and its variations have been investigated by the
literature (Chuang et al., 2011; Mukhopadhyay and
Banerjee, 2012; Yang et al., 2012; Wang et al.,
2011; Coelho and Lee, 2008; Acharjee and
Goswami, 2010; Araujo and Coelho, 2008).
Numerous examples and statistical results show that
some chaotic sequences applied to PSO are able to
increase the algorithm-exploitation capability in the
search space and enhance its convergence rate.
An interesting dynamic system evidencing
chaotic behavior is the Hénon’s map. Hénon (1976)
introduced this map as a simplified version of the
Poincaré map of the Lorenz system (Lorenz, 1963),
whose equation is given by:
)1(
2
2
)1(
1
1)(
1
tytyaty
(6)
)1(
1
)(
2
tybty
(7)
where t is the iteration number. The map depends on
two parameters, a and b. The Hénon’s map is used
in this work for a=1.4 and b=0.3. The adopted
values for a and b for which the Hénon’s map has a
strange attractor (details in Cao and Kirik, 2000).
This work proposes the CQPSO, a combination
of classical QPSO and the Hénon’s map sequences
are represented by modification of c
1
and c
2
values.
Furthermore, in CQPSO design, another Hénon’s
map using the same equations (6) and (7) where
]3819.0,3854.0[
2
y
are used to generate the
variables h
1
(t) and h
2
(t) normalized in the range
[0.001, 1]. The initial value of
)(
2
ty and )1(
2
ty
are given by random numbers generated in the range
[0,1] in each run of CQPSO.
In the CQPSO approach, the parameters c
1
and c
2
used in the equation (5) are substituted by h
1
(t) and
h
2
(t), respectively, and equation (8) is employed in
Step 6. In this case, it is adopted
)(
2
)(
1
,
)(
2,
)(
1
)(
thth
ig
pth
ik
pth
t
i
p
,
(8)
3 PHYSICAL PROBLEM
To solve inverse heat transfer problem (IHTP) there
are several optimization techniques, allowing the
determination of more than one thermo-physical
ChaoticQuantum-behavedParticleSwarmOptimizationApproachAppliedtoInverseHeatTransferProblem
99

property and the understanding of complex materials
(Da Silva et al., 2009). Unlike the conventional
techniques, the resolution of the IHTP permits the
determination of more than one thermo-physical
property and the understanding of complex
materials.
Nonlinear heat conduction problem, involving
phase change, without internal heat generation, can
be described by
TTk
ti
H
)(.
,
(9)
where k (W/m
o
C) is the apparent thermal
conductivity, T (
o
C) is the temperature, and ti (s) is
the time (Scheerlinck et al., 2001). The present work
considers one-dimensional geometry in rectangular
coordinates, simulating a product slab. The initial
condition associate to equation (9) is given by
T(xc, ti) = T
0
(xc); ti = t
0
, xc [0, L],
(10)
where T
0
(
o
C) is known temperature in initial time
obtained through of experiment, t
0
(s) is initial time.
In the surface (xc=0) the convective condition is
considered,
)()(
TTh
x
T
Tk
; x = 0, ti 0,
(11)
where T
(
o
C) is the ambient temperature, h
(W/m
2o
C) is the surface heat transfer coefficient, and
L is the half length in x direction. The boundary
condition used in the center of the product slab
(xc=L) was the classical zero flux, which is
expressed by
0)(
xc
T
Tk
; xc = L, ti 0.
(12)
Due to the characteristics of the mathematical
problem, the simpler finite difference technique can
be used for the solution of that partial differential
equation. Knowing the food geometry and physical
properties, as the boundary and initial conditions,
enables one to solve the equations (9)-(12), thus
determining the transient temperature distribution in
the food. This kind of problem is called a direct
problem. If any of these magnitudes or a
combination of them is unknown, but experimental
data are available on the temperature measured
inside and/or on the external surface of the food, one
has an inverse problem that allows one to determine
the unknown magnitudes, provided those data
contain sufficient information.
For the inverse problem of interest here, the
apparent thermal conductivity is regarded as
unknown quantity. For the estimation of such
parameters, we consider known transient
temperature measurements
n
(
o
C) taken at the
center node of the food. Thus, in this work is desired
to minimize the difference between experimental
and predicted temperatures. Mathematically
optimization problem to solve is:
Min f(k) (13)
where the objective function f (fitness function) is
given by
N
Ns
t
k
t
n
T
t
n
kf
1
2
)]([
)(
,
(14)
where T
n
(
o
C) is the temperature of the product at
node central calculated numerically by finite
difference method and Ns is the number of samples.
It was proposed the use of a nonlinear function
dependent of temperature to thermal conductivity,
. -1,
32
-1,),/1exp(
1
TATA
TTA
k
(15)
The proposed approach was analyzed for the case in
which three parameters, A
j
, were treated as
unknowns where the lower and upper boundaries
constraints used for them were
]05.0,
10
10[
1
A
,
]1,1[
2
A
and
]1,0[
3
A
.
4 RESULTS AND DISCUSSION
In the next subsections first, we applied the PSO
approaches to two algebraic test functions. In a next
stage, we utilized the PSO approaches for the
solution of IHTP.
4.1 Benchmark Functions
To validate the effectiveness of PSO approaches,
two well-known benchmark functions of
unconstrained minimization problems with 30
dimensions are used.
Rastrigin function has many local minima and
maxima, making it difficult to find the global
optimum. Rastrigin function is a fairly difficult
problem for optimization algorithms due to the large
search space and large number of local minima. The
Rastrigin function is given by
n
i
i
x
i
xxf
1
)2cos(10
2
10)(
1
(16)
with upper and lower bounds given by [-5.12, 5.12]
for each dimension.
Rosenbrock’s valley or Rosenbrock function
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
100
(Rosenbrock, 1960) is a classic optimization
problem, also known as Banana function. The
Rosenbrock function [31] is given
1
1
2
)1(
2
)
1
2
(100)(
2
n
i
i
x
i
x
i
xxf
(17)
with upper and lower bounds given by [-30,30] for
each dimension. It is important mention here that the
Rosenbrock function can be treated as a multimodal
problem (Shang and Qiu, 2006). It has a narrow
parabolic-shaped deep valley from the perceived
local optima to the global optimum. To find the
valley is trivial, but to achieve convergence to the
global minimum is a difficult task.
The settings adopted in the tested PSO
approaches for the benchmarks functions is the
swarm size (population size) equal to 50 particles,
30 runs and the stopping criterion is 10,000
generations. In terms of classical PSO, c
1
= c
2
= 2.05
and the inertia factor linear decreasing of 0.9 to 0.4
during the iterations is adopted. QPSO and CQPSO
use a linearly decreasing contraction-expansion
coefficient (
) is used which starts at 1 and ends at
0.2.
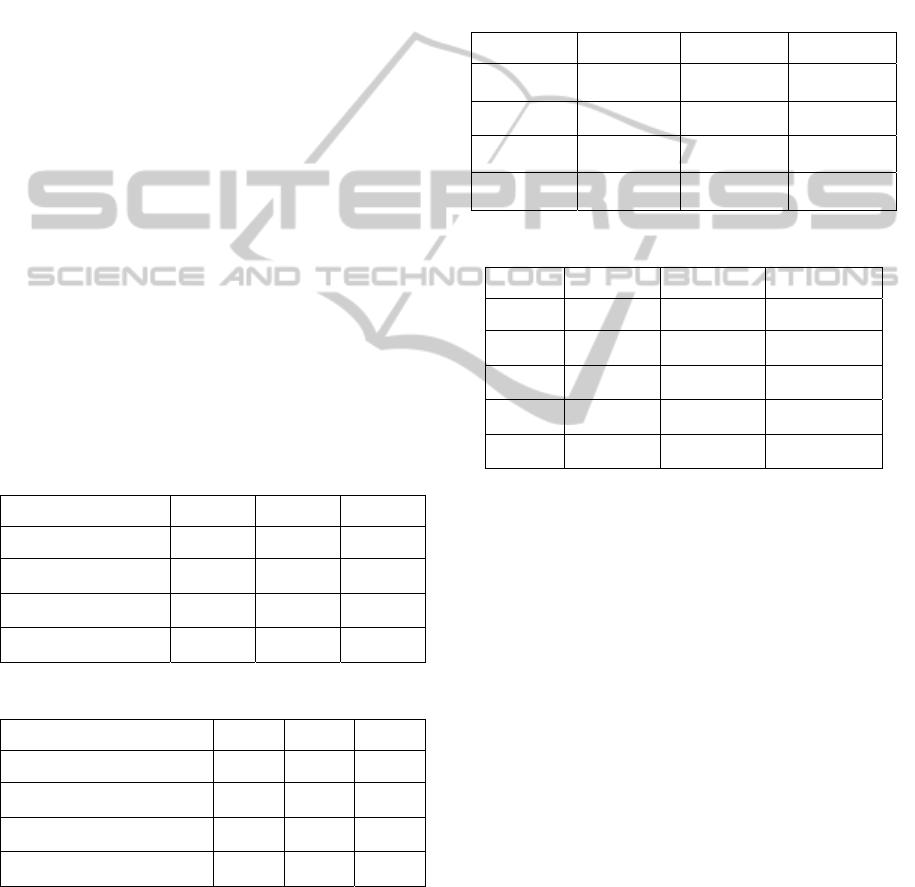
Simulation results presented in Tables 1 and 2
showed that the CQPSO outperform the adopted
PSO and QPSO on the basis of mean and standard
deviation of the best objective function value of the
total runs for the two benchmark functions.
Table 1: Optimization results of f
1
(x) in 30 runs.
Index PSO QPSO CQPSO
Maximum (Worst) 0.9803 0.9723 0.8914
Mean 0.2105 0.1603 0.1297
Minimum (Best) 0.19×10
-8
0.23×10
-15
0.89×10
-12
Standard Deviation 0.3272 0.7218 0.0632
Table 2: Optimization results of f
2
(x) in 30 runs.
Index PSO QPSO CQPSO
Maximum (Worst) 23.7934 22.1930 22.1185
Mean 42.7117 31.3839 25.0847
Minimum (Best) 23.1006 21.0594 19.0059
Standard Deviation 1.5973 0.6301 0.3421
4.2 IHTP Case
The setup adopted in IHTP for the PSO approaches
is the swarm size (population size) equal to 20
particles and the stopping criterion is 100
generations. Optimization results are presented in
Table 3. The CQPSO found the best convergence
(mean) and best solution (minimum f) with f =
0.4213. The best parameters obtained by tested
optimization methods are presented in Table 4 where
can be observed that the CQPSO presented a
promising R
2
in comparison to the classical PSO.
Best result using CQPSO is illustrated by
temperature profiles shown in Figure 1.
Table 3: Optimization results of f(k) in 30 runs.
Index PSO QPSO CQPSO
Maximum
(Worst)
30.9319 29.3703 29.3252
Mean 18.0494 18.0468 17.9352
Minimum
(Best)
0.4889 0.4669 0.4213
Standard
Deviation
9.4806 9.4842 8.9836
Table 4: Best parameters obtained by methods.
Index PSO QPSO CQPSO
A
1
0.02610 0.02605 0.02602
A
2
-0.00091 -0.00111 -0.00116
A
3
0.6545 0.6531 0.6637
R
2
0.9885 0.9898 0.9912
f(k) 0.4658 0.4469 0.4213
5 CONCLUSIONS
Simulation results demonstrate the feasibility and
validity of the proposed CQPSO in terms of solution
quality when compared with the classical PSO and
QPSO algorithms in the IHTP and also two well-
know benchmark functions.
CQPSO may be a promising and viable tool to
deal with complex inverse heat problems. The future
work includes the studies on how to improve the
proposed CQPSO in terms of the self-tuning of
control parameters. Furthermore, more extensive
experimentation, hypothesis tests and statistical
significance tests to compare different optimization
approaches with CQPSO will be carried out to
different case studies.
REFERENCES
Acharjee, P. and Goswami, S. K. (2010). Chaotic particle
ChaoticQuantum-behavedParticleSwarmOptimizationApproachAppliedtoInverseHeatTransferProblem
101

swarm optimization based robust load flow.
International Journal of Electrical Power & Energy
Systems
32(2): 141-146.
Araujo, E. and Coelho, L. S. (2008). Particle swarm
approaches using Lozi map chaotic sequences to fuzzy
modelling of an experimental thermal-vacuum system.
Applied Soft Computing 8(4): 1354-1364.
Cao, Y. and Kirik, S. (2000). The basin of the strange
attractors of some Hénon maps. Chaos, Solitons &
Fractals
11(5): 729-734.
Chuang, L. -Y., Tsai, S. -W., and Yang, C. -H. (2011).
Chaotic catfish particle swarm optimization for
solving global numerical optimization problems.
Applied Mathematics and Computation 217(16): 6900-
6916.
Clerc, M. and Kennedy, J. F. (2002). The particle swarm:
explosion, stability and convergence in a multi-
dimensional complex space. IEEE Transactions on
Evolutionary Computation
6(1): 58-73.
Coelho, L. S. and Lee, C. -S. (2008). Solving economic
load dispatch problems in power systems using chaotic
and gaussian particle swarm optimization approaches.
International Journal of Electrical Power & Energy
Systems
30(5): 297-307.
Coelho, L. S. and Mariani, V. C. (2008). Particle swarm
approach based on quantum mechanics and harmonic
oscillator potential well for economic load dispatch
with valve-point effects. Energy Conversion and
Management
49(11): 3080-3085.
Coelho, L. S. and Mariani, V. C. (2012). Firefly algorithm
approach based on chaotic Tinkerbell map applied to
multivariable PID controller tuning.
Computers &
Mathematics with Applications
64(8): 2371-2382.
Coelho, L. S. and Pessôa, M. W. (2011). A tuning strategy
for multivariable PI and PID controllers using
differential evolution combined with chaotic
Zaslavskii map. Expert Systems with Applications
38(11): 13694-13701.
Da Silva, C. K. F., Da Silva, Z.E., and Mariani, V.C.
(2009). Determination of the diffusion coefficient of
dry mushrooms using the inverse method.
Journal of
Food Engineering
95(1): 1-10.
Eberhart, R. C. and Kennedy, J. F. (1995). A new
optimizer using particle swarm optimization. In
Proceedings of the International Symposium on Micro
Machine and Human Science
, Japan, 39-45.
Eslami, M., Sharref, H., Khajehzadeh, M. and Mohamed,
A. (2012). A survey of the state of the art in particle
swarm optimization.
Research Journal of Applied
Sciences, Engineering and Technology
4(9): 1181-
1197.
Fang, W., Sun, J., Ding, Y., Wu, X., and Xu, W. (2010). A
review of quantum-behaved particle swarm
optimization. IETE Technical Review 27(4): 336-348.
Hénon, M. (1976). A two-dimensional mapping with a
strange attractor. Communications in Mathematical
Physics
50(1): 69-77.
Kennedy, J. F. and Eberhart, R. C. (1995). Particle swarm
optimization. In Proceedings of the IEEE Conference
on Neural Networks
, Perth, Australia, 1942-1948.
Khare, A. and Rangnekar, S. (2013). Particle swarm
optimization: a review.
Applied Soft Computing (in
press).
Lorenz, E. N. (1963). Deterministic nonperiodic flow.
Journal of the Atmospheric Sciences 20(2): 130-141.
Mukhopadhyay, S. and Banerjee, S. (2012). Global
optimization of an optical chaotic system by chaotic
multi swarm particle swarm optimization.
Expert
Systems with Applications
39(1) 917-924.
Parsopoulos, K. E. and Vrahatis, M. H. (2002). Recent
approaches to global optimization problems through
particle swarm optimization.
Natural Computing 1(2-
3): 235-306.
Peitgen, H. -O., Jürgens, H., and Saupe, D. (2004).
Chaos
and fractals: new frontiers of science
, 2nd edition,
Springer, New York, NY, USA.
Ratnaweera, A., Halgamuge, S., and Watson, H. (2004).
Self-organizing hierarchical particle swarm optimizer
with time-varying acceleration coefficients. IEEE
Transactions on Evolutionary Computation
8(3): 240-
255.
Rosenbrock, H. H. (1960). An automatic method for
finding the greatest or least value of a function.
The
Computer Journal
3: 175-184.
Scheerlinck, N., Verboven, P., Fikiin, K. A., de
Baerdemacker, J., and Nicolaï, B. M. (2001). Finite
element computation of unsteady phase change heat
transfer during freezing or thawing of food using a
combined enthalpy and Kirchhoff transform method.
Transactions of the ASAE, 44(2): 429-438.
Shang, Y. W. and Qiu, Y. H. (2006). A note on the
extended Rosenbrock function, Evolutionary
Computation
14(1): 119-126.
Sun, J., Xu, W. B., and Feng, B. (2004a). A global search
strategy of quantum-behaved particle swarm
optimization. In
Proceedings of IEEE Conference on
Cybernetics and Intelligent Systems
, Singapore, 111-
116.
Sun, C. and Lu, S. (2010). Short-term combined economic
emission hydrothermal scheduling using improved
quantum-behaved particle swarm optimization.
Expert
Systems with Applications
37(6): 4232-4241.
Sun, J., Feng, B., and Xu, W. B. (2004b). Particle swarm
optimization with particles having quantum behavior.
In
Proceedings of Congress on Evolutionary
Computation
, Portland, Oregon, USA, 325-331.
Sun, J., Wu, X., Palade, V., Fang, W., Lai, C. -H. and Xu,
W. (2012). Convergence analysis and improvements
of quantum-behaved particle swarm optimization.
Information Sciences 193: 81-103.
Wang, Y., Zhou, J., Lu, Y., Qin, H., and Wang, Y. (2011).
Chaotic self-adaptive particle swarm optimization
algorithm for dynamic economic dispatch problem
with valve-point effects. Expert Systems with
Applications
38(11): 14231-14237.
Yang, C. -H., Tsai, S. -W., Chuang, L. -Y., and Yang, C. -
H. (2012). An improved particle swarm optimization
with double-bottom chaotic maps for numerical
optimization. Applied Mathematics and Computation
219(1): 260-279.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
102
