Semi-supervised Clustering with Example Clusters

Celine Vens

, Bart Verstrynge

and Hendrik Blockeel

1,2

Department of Computer Science, KU Leuven, Leuven, Belgium

Leiden Institute of Advanced Computer Science, Universiteit Leiden, Leiden, The Netherlands

Keywords:

Clustering, Semi-supervised Clustering, Constraint-based Clustering, Metric Learning.

Abstract:

We consider the following problem: Given a set of data and one or more examples of clusters, ﬁnd a clustering

of the whole data set that is consistent with the given clusters. This is essentially a semi-supervised clustering

problem, but different from those that have been studied until now. We argue that it occurs frequently in

practice, but despite this, none of the existing methods can handle it well. We present a new method that

speciﬁcally targets this type of problem. We show that the method works better than standard methods and

identify opportunities for further improvement.

1 INTRODUCTION

We consider the task of (non-hierarchical) clustering:

given a dataset D, partition D into clusters such that

instances within the same cluster tend to be similar,

and instances in different clusters dissimilar.

This task is usually considered unsupervised. Re-

cently, however, some research has focused on semi-

supervised clustering. Here, some information is

given about which elements belong to the same clus-

ter, usually in the form of pairwise constraints: two

particular instances should be in the same cluster

(must-link constraint), or should not be (cannot-link

constraint). Such background information helps the

system ﬁnd a clustering that meets the user’s criteria.

There are multiple reasons why a user might want

to provide partial supervision. They all boil down

to the fact that clustering is essentially undercon-

strained: there may be many “good” clusterings in a

data set. For instance, hierarchical clustering methods

yield clusterings at many different levels of granular-

ity, and it is up to the user to select the desired level.

Also, in high-dimensional spaces, a different cluster

structure may occur in different subspaces, and the

clustering system cannot know which subspace is the

most relevant one for the user (Agrawal et al., 2005).

In this paper, we introduce a new type of semi-

supervised clustering. Supervision here consists of

providing one or more example clusters. This type

of supervision is often quite natural. Consider entity

resolution in a database of authors: the task is to clus-

ter occurrences of author names on papers such that

occurrences are in the same cluster if they refer to the

same actual person.

If one person indicates all the

papers she authored, that set of papers is an example

cluster. Knowing one, or a few, such clusters may

help the system determine what kinds of clusters are

good, so it can better cluster the other instances.

Example clusters can be translated to pairwise

constraints, but that induces many of those, dis-

tributed unevenly over the instance space. Most ex-

isting systems expect the pairwise constraints to be

distributed more evenly, and have been evaluated un-

der this condition. It is therefore not obvious that they

will work well in the new setting.

This paper is a ﬁrst study of this new type of semi-

supervised clustering task. We ﬁrst brieﬂy survey the

work on semi-supervised clustering (Section 2). We

next discuss the new setting, relate it to existing set-

tings, and argue that none of the existing methods are

very suitable for this task (Section 3). We propose

a novel method that focuses speciﬁcally on this task

(Section 4), and experimentally evaluate it in Sec-

tion 5. We conclude in Section 6.

2 SEMI-SUPERVISED

CLUSTERING

Most research on semi-supervised clustering has fo-

This task is not trivial because different persons may

have the same name, and the same person may be referred

to in different ways, e.g., “John Smith”, “J.L. Smith”.

Vens C., Verstrynge B. and Blockeel H..

Semi-supervised Clustering with Example Clusters.

DOI: 10.5220/0004547300450051

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval and the International Conference on Knowledge

Management and Information Sharing (KDIR-2013), pages 45-51

ISBN: 978-989-8565-75-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

cused on providing pairwise constraints to the clus-

tering algorithm. Wagstaff et al. (2000, 2001) deﬁne

must-link and cannot-link constraints, respectively,

for specifying that two instances should, or should

not, be in the same cluster.

One way of dealing with these pairwise con-

straints is adapting existing clustering algorithms to

take them into account. Wagstaff et al. (2001) adapt

K-Means to this effect, treating must-link and cannot-

link as hard constraints.

Alternatively, one can use a standard algorithm,

but adapt the distance metric. Xing et al. (2002) pro-

pose to learn a Mahalanobis matrix M (Mahalanobis,

1936), which deﬁnes a corresponding Mahalanobis

distance

(x,y) =

(x −y)

M(x −y) (1)

They ﬁnd the M that minimizes the sum of squared

distances between instances that must link, under the

constraint that d

(x,y) ≥ 1 for all x and y that can-

not link. M can be restricted to be a diagonal matrix,

or can be full. The idea of learning such a distance

function is generally referred to as metric-based or

similarity-adapting methods (Grira et al., 2004).

Combining algorithm and similarity adaptation,

Bilenko et al. (2004) introduced the MPCK-Means

algorithm. A ﬁrst difference with Wagstaff et al. is

that constraints are now handled in a soft-constrained

manner by deﬁning costs for unsatisﬁed constraints.

Furthermore, the k means are initialised using a seed-

ing procedure proposed by Basu et al. (2002). For the

metric-based part of MPCK-Means, a separate Maha-

lanobis metric can be learned for each tentative cluster

in every iteration of the algorithm, allowing clusters

of different shapes in the ﬁnal partition.

Alternatively to pairwise constraints, Bar Hillel et

al. (2005) use chunklets, groups of instances that are

known to belong to the same cluster. Their Relevant

Component Analysis (RCA) algorithm takes chun-

klets as input and learns a Mahalanobis matrix. This

approach is shown to work better than Xing et al.’s in

high dimensional data. A downside is that only must-

link information is taken into account. There is no

information about which instances cannot link: dif-

ferent chunklets may belong to the same cluster, or

they may not. RCA minimizes the same function as

Xing et al.’s method, but under different constraints

(Bar-Hillel et al., 2005).

Yeung and Chang (2006) have extended RCA to

include cannot-link information. They treat each pair-

wise constraint as a chunklet, and compute a sepa-

rate matrix for the must-link constraints, A

, and

for the cannot-link constraints, A

. The data are

then transformed by A

1/2

·A

−1/2

. This “pushes apart”

cannot-link instances in the same way that must-link

instances are drawn together.

3 CLUSTERS AS EXAMPLES

3.1 Task Deﬁnition

We deﬁne the task of semi-supervised clustering with

example clusters as follows (where P (···) denotes the

power set):

Given: An instance space X, a set of instances D ⊆X,

a set of disjoint example clusters E ⊆ P (D), and a

quality measure Q : P (D) ×P (D) → R.

Find: A partition C = {C

,...,C

} over D that

maximizes Q(C,E).

Q typically measures to what extent C is consis-

tent with E (ideally, E ⊆C), but may also take general

clustering quality into account. Note that the number

of clusters to be found, or the distance metric to be

used, are not part of the input. Also, the requirement

that E ⊆ C is not strict; this allows for noise in the

data.

The task just deﬁned has many applications. We

mentioned, earlier on, entity resolution. A simi-

lar task is face recognition, in a context where all

(or most) occurrences of the face of a few persons

have been labeled. This application is typically high-

dimensional. Clustering in high-dimensional spaces

is difﬁcult because multiple natural clusterings may

occur in different subspaces (Agrawal et al., 2005).

For instance, one might want to cluster faces accord-

ing to identity, poses, emotions shown, etc. An ex-

ample cluster can help the system determine the most

relevant subspace.

3.2 Translation to Pairwise Constraints

Example clusters can easily be translated into pair-

wise constraints. Let ML(x, y) denote a must-link

constraint between x and y, and CL(x,y) a cannot-

link constraint. Providing an example cluster C corre-

sponds to stating ML(x,y) for all x,y ∈C and CL(x,y)

for all x ∈C,y 6∈C. If C has n elements (call them x

. . . , x

), and the complete dataset has N elements (x

to x

), this generates n(n−1)/2 must-link constraints

and n(N −n) cannot-link constraints

. Clearly, this

set of constraints can be large (O(nN)), potentially

By applying two inference rules: ∀x,y, z : ML(x, y) ∧

ML(y,z) ⇒ ML(x,z) and ∀x, y,z : CL(x,y) ∧ ML(y,z) ⇒

CL(x, z), it sufﬁces to list a minimal set of n −1 must-

link constraints and N −n cannot-link constraints. How-

ever, the existing metric learning methods that use pairwise

constraints do not automatically apply these rules.

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

making existing methods slow, and the constraints

are distributed unevenly, making these methods un-

informed about large parts of the instance space.

Cluster examples can also be seen as “complete”

chunklets. RCA could therefore be applied without

any translation, but then the information about the

maximality of the chunklets is lost; RCA allows sep-

arate chunklets to end up in the same cluster, which

is not wanted when chunklets are known to be com-

plete. Yeung and Chang’s extension allows for nega-

tive information, which solves this problem; but this

negative information is again expressed by means of

pairwise constraints. Thus, although the chunklet

based methods provide a concise representation for

the must-link constraints, they do not provide one for

cannot-link constraints, so they, too, suffer from the

problem of generating many constraints.

4 CLUSTERING USING

EXAMPLES: CLUE

We now present CLUE (Clustering Using Example

clusters). Given some example clusters, CLUE tries

to ﬁnd a good overall clustering consistent with them.

The proposed solution does not require the number of

clusters as input.

Algorithm 1: The CLUE algorithm.

Input:

D: a data set

E: a set of example clusters {E

}

i=1

with E

⊆ D

Output: a partition P of D

Algorithm:

1. Rescale all attributes linearly to [0,1]

2. Learn a Mahalanobis distance d

that is maximally

consistent with the constraints

3. Construct a dendrogram ∆ by applying a bottom-

up hierarchical clustering procedure with d

4. Find the range of partitions in ∆ for which the ex-

amples clusters are reconstructed optimally

5. Within that range, ﬁnd the best partition P

The high-level algorithm is shown as Algorithm 1.

We next explain all steps in detail.

Step 1: Rescaling. Attributes are rescaled to [0,1] to

avoid the effects of incomparable ranges.

Step 2: Metric Learning. This step computes a dis-

tance metric over the instance space that best corre-

sponds to the example clusters given. Our approach

is based on Yeung and Chang (2006). We compute

two matrices, A

and A

, as follows:

∑

∈E

∑

x∈E

(x −

)(x −

)

(2)

∑

∈E

∑

x /∈E

(x −

)(x −

)

(3)

with N

∑

∈E

and N

−

∑

∈E

Thus, while Yeung and Chang use as chunklets

the pairwise constraints, we use as “positive” chun-

klets the example clusters, and as negative chunklets,

pairs (x,

) with x 6∈E

and

the mean of the cluster.

This makes the computation of A

O(n) (with n the

number of instances in all example clusters together),

and that of A

O(kN), with N the total number of in-

stances and k the number of example clusters. A

−1/2

transforms the space so that examples in a cluster are

drawn closer to its center (in other words, intra-cluster

variance is reduced) and A

1/2

transforms it such that

examples outside a cluster are pushed farther from its

center (inter-cluster variance is increased). The Ma-

halanobis matrix corresponding to this transformation

is M = A

−1/2

·A

−1/2

Step 3: Hierarchical Clustering. A standard

bottom-up hierarchical clustering method is used, us-

ing d

as distance metric, and using single or com-

plete linkage. This gives a dendrogram that represents

N partitional clusterings, from N singletons at the bot-

tom to a single cluster at the top.

Step 4: Filtering the Partitions. After the bottom-

up clustering procedure, we investigate all resulting

partitions P

and select those where the example clus-

ters have been reconstructed optimally. For this, we

propose the COnstraint based Rand Index (CORI). It

is based on the Rand index measure (Rand, 1971),

which is used to compare a predicted clustering to a

target clustering.

Let S

and S

respectively denote the set of

all must-link and cannot-link constraints induced by

the example clusters. The CORI for a clustering

C = {C

,...,C

} is deﬁned as follows:

CORI(C) =

correct



correct



/2 (4)

correct

{

ML(x, y) ∈ S

| ∃i : x ∈C

∧y ∈C

}

correct



CL(x,y) ∈ S

| ∃i, j 6= i : x ∈C

∧y ∈C



The CORI equals 0.5 at the start and the end of

the agglomerative clustering procedure. Initially, all

cannot-link constraints and none of the must-link con-

straints are fulﬁlled, as the instances each belong to a

singleton cluster. As the clustering process advances,

Semi-supervisedClusteringwithExampleClusters

the cannot-link component in the CORI deﬁnition de-

creases, and the must-link component increases. Fi-

nally, all must-link constraints and none of the cannot-

link constraints are fulﬁlled when only a single clus-

ter remains. Note that the must-link and cannot-link

components of the CORI are weighted independently,

in contrast to the Rand index. This is because usually

|  |S

The result of this step is a range of clusterings with

maximal CORI.

Step 5: Final Partition. In the previous step, clus-

terings were evaluated based on the reconstruction

of the example clusters, resulting in a range of op-

timal clusterings. We now select from that range the

clustering that yields the best overall cluster quality.

Category utility (Fisher, 1987) is an evaluation met-

ric that judges cluster quality in terms of intra- and

inter-cluster dissimilarity. Witten et al. (2011) pro-

vide a deﬁnition for numeric data, by assuming nor-

mally distributed data:

CU(C) =

∑

∈C

Pr(C

)

√

∑

i=1



−



, (5)

where k is the number of clusters, d is the number

of attributes, σ

denotes the standard deviation of at-

tribute i, and σ

the standard deviation of attribute i

for instances in cluster l.

Category utility gives an equal importance to all

attributes. However, as the clusters were constructed

using supervised information, we want to return the

best clustering according to the learned distance mea-

sure. By deﬁning a weighted variant of the category

utility, we can interpret the dissimilarities using the

Mahalanobis matrix M:

WCU(C) =

∑

∈C

Pr(C

)

√

∑

i=1

1/2

(l)

(6)

(l)



−



...



−



where M

1/2

denotes the i-th row of M

1/2

5 EVALUATION

In this section, we empirically evaluate our approach

towards learning from example clusters on synthetic

and real world datasets. We compare our method -

both with a single (SL) and complete linkage (CL) for

the agglomerative clustering step - with K-MEANS

and MPCK-MEANS (Bilenko et al., 2004) (see Sec-

tion 2). Since MPCK-MEANS can learn either one

global or multiple local distance metrics, we tested

both cases. K-MEANS and MPCK-MEANS are pro-

vided with the exact number of clusters as input.

5.1 Datasets

5.1.1 Synthetic Data

A synthetic dataset was created with 200 instances

and 6 numeric dimensions with different domain

sizes, see Figure 1. Three dimensions were randomly

generated, one dimension contains ﬁve bar-shaped

clusters, and two dimensions together form 16 circle-

shaped clusters. These are the two target clusterings

that we try to discover using an example cluster.

0 2 4 6 8 10

circ

0 20 40 60

bar

rand

0 10 20 30 40 50

rand

Figure 1: The 6 dimensions of the synthetic dataset.

5.1.2 Real-world Data

We used three UCI datasets (Frank and Asuncion,

2010). CMU Face Images contains 640 pictures of

20 different persons

, each shown with 4 poses, 4

emotions, and with or without sunglasses. This is a

nice example of a dataset that can naturally be clus-

tered in several ways. We used the “identity” and

“pose” as target clusterings. Principal Component

Analysis was applied to the original data to repre-

sent the images as linear combinations of eigenfaces

(Turk and Pentland, 1991). Only the ﬁrst 100 eigen-

faces were kept; this allowed us to represent the data

in a more compact way, while presevering 97% of the

original variance in the data. Libras Movement con-

tains 15 classes of 24 instances each. Each class ref-

erences to a hand movement type in Brazilian signal

language. Seeds contains measurements of seven ge-

ometrical properties of kernels belonging to three dif-

ferent varieties of wheat. It has 210 instances.

5.2 Evaluation Measures

In our evaluation, we wish to compare the returned

clustering to a target clustering. We now discuss

the measures we will use for this. In the following,

= {C

,...,C

} denotes the predicted cluster-

ing, and C

= {C

,...,C

} the target clustering.

The function p : X → {1,...,k} returns the predicted

Due to a corrupted image ﬁle, the identity “karyadi”

was left out, resulting in 19 identities.

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

cluster for an instance, and similarly, t : X →{1,...,l}

returns the target cluster. The notations p(x) = i and

t(x) = j are abbreviated as p

(x) and t

(x).

Rand Index. The Rand Index (RI) is a popular

measure for comparing clusterings. It expresses the

proportion of instance pairs for which both cluster-

ings agree on whether they are in the same clus-

ter or not. When there are many clusters, RI can

be dominated by instances correctly predicted not

to be in the same cluster. For instance, if C

{{a,b}, {c,d}, {e, f },{g,h},{i, j}}and C

= {{j,a},

{b,c},{d, e}, {f , g}, {h, i}}, we obtain RI =

0+35

, a high score for a very bad predicted clustering.

Normalized Mutual Information. Normalized Nor-

malized mutual information (NMI) (Manning et al.,

2008) measures the amount of information that is

shared by two clusterings, and penalizes large clus-

terings. It is deﬁned as follows:

NMI(C

) =

MI(C

)

(H(C

) + H(C

))/2

(7)

MI(C

) =

∑

i=1

∑

j=1

Pr(p

(x),t

(x))·log



Pr(p

(x),t

(x))

Pr(p

(x)) ·Pr(t

(x))



H(C

) = −

∑

i=1

Pr(p

(x)) ·log (Pr(p

(x)))

However, this measure can give unexpected results if

the individual cluster cardinalities differ substantially.

For instance, consider C

= {{a}, {b}, {c}, {d,e, f }}

and C

= {{a,b,c}, {d,e, f }}. If we add more and

more instances to the last cluster in both C

and C

then H(C

) and H(C

) will get closer to zero, making

a better clustering, although it still only correctly

ﬁnds one of the four clusters.

Complemented Entropy. To deal with the above

shortcomings, we propose a new clustering evalua-

tion measure, called complemented entropy (CE). It

scores the entropy of the target labels in the predicted

clusters (H

), as well as the entropy of the predicted

labels in the target clusters (H

). These entropies are

in a sense complementary: predicting too few clusters

will increase H

, while predicting too many clusters

will increase H

. A formal deﬁnition is given below:

= −

∑

i=1

∑

j=1

Pr(t

(x) | p

(x)) ·log (Pr(t

(x) | p

(x)))

= −

∑

j=1

∑

i=1

Pr(p

(x) |t

(x))·log (Pr(p

(x) | t

(x)))

CE = 1 −



maxH



/2 (8)

In this deﬁnition, maxH

denotes the maximally pos-

sible value for H

and is reached when all pre-

dicted clusters contain an equal number of tar-

get labels, and analogously for maxH

. Consider

again the previous example. If we increase the

number of instances in the last clusters, leading

to C

= {{a},{b},{c},{d,e, f ,g,h,i, j}} and C

{{a,b, c}, {d,e, f , g,h,i, j}}, then the CE score re-

mains unchanged (while NMI went up). The CE can

only become one when the predicted clustering per-

fectly matches the target clustering.

NMI vs. CE. NMI and CE evaluate different aspects

of the predicted clustering. Roughly, NMI gives more

weight to clusters with high cardinality, while CE

treats all clusters equally. Figure 2 illustrates the dif-

ference for two clusterings over the same dataset.

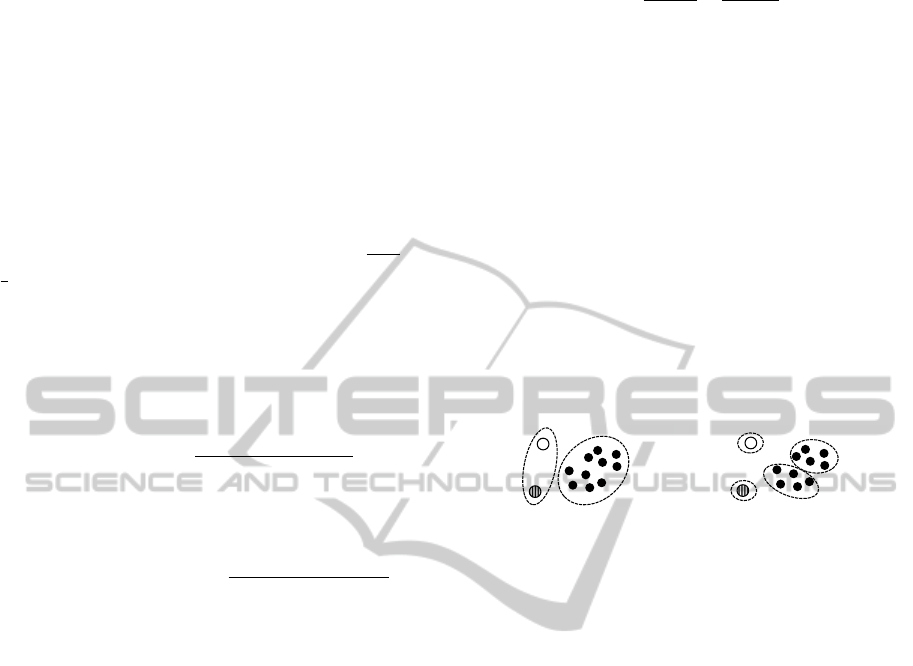
(a) NMI=0.89, CE=0.84 (b) NMI=0.66, CE=0.91

Figure 2: NMI prefers the clustering where more instance

pairs are labeled consistently (left), CE prefers the one

where more target clusters are reconstructed (right).

5.3 Experimental Results

The experiments are set up as follows. In each run, we

use one target cluster as an example cluster, run the

clustering method, and compute the RI, NMI and CE

for the part of the clustering that excludes the example

cluster. For each dataset, we repeat this procedure for

each target cluster and report the average and standard

deviation of the results. For MPCK-MEANS, the ex-

ample cluster is translated into a set of must-link and

cannot-link constraints. K-means consistently ignores

the constraints.

Table 1 presents the results for NMI, CE, and RI.

We observe that 18 out of 22 highlighted results are

in CLUE rows (9 for CLUE-CL, 9 for CLUE-SL);

MPCK-MEANS(global) scores 4, the others 0.

Surprisingly, MPCK-MEANS scores worse than

(unsupervised) K-MEANS in about half of the cases,

which suggests that using non-evenly spread con-

straints may actually hurt its performance. CLUE has

a similar issue on one dataset (Seeds).

We also observed (not shown here) that CLUE re-

turns too many clusters. (The other systems use the

number of clusters as an input, so they cannot go

wrong there.) This turns out to be a result of over-

ﬁtting: the learned Mahalanobis distance compresses

Semi-supervisedClusteringwithExampleClusters

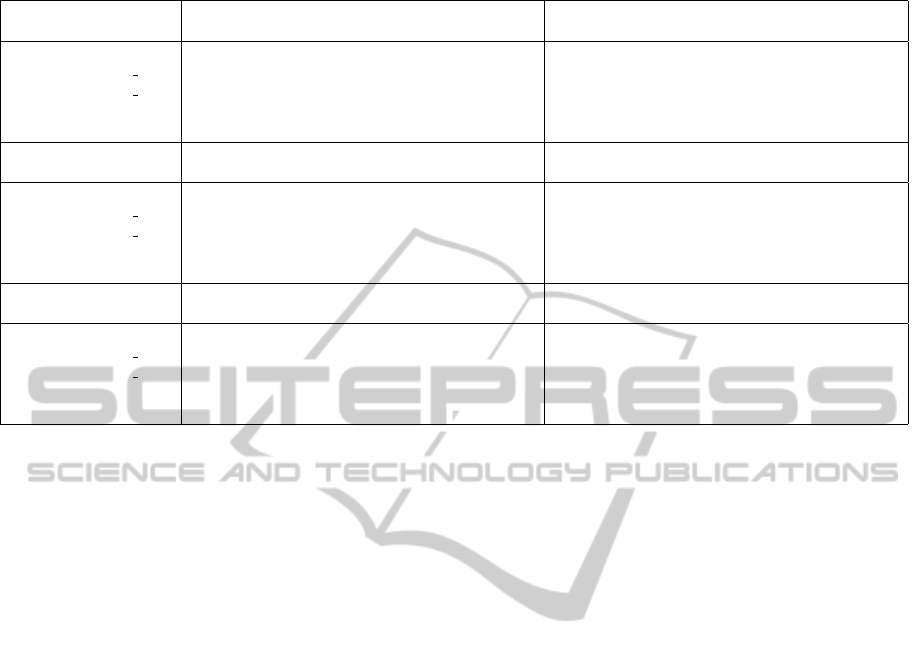
Table 1: Results.

Synthetic (Bars) Synthetic (Circles)

Method NMI CE RI NMI CE RI

K-MEANS 0.039 (0.005) 0.051 (0.005) 0.651 (0.003) 0.501 (0.006) 0.529 (0.008) 0.896 (0.001)

MPCK-MEANS glob 0.757 (0.247) 0.757 (0.246) 0.878 (0.125) 0.281 (0.033) 0.336 (0.031) 0.866 (0.005)

MPCK-MEANS loc 0.391 (0.206) 0.513 (0.121) 0.670 (0.206) 0.252 (0.050) 0.419 (0.086) 0.806 (0.129)

CLUE, SL 1.000 (0.000) 1.000 (0.000) 1.000 (0.000) 0.883 (0.115) 0.932 (0.079) 0.937 (0.061)

CLUE, CL 1.000 (0.000) 1.000 (0.000) 1.000 (0.000) 0.952 (0.084) 0.965 (0.062) 0.984 (0.022)

Faces (Identity) Faces (Pose)

Method NMI CE RI NMI CE RI

K-MEANS 0.717 (0.013) 0.768 (0.008) 0.930 (0.004) 0.039 (0.012) 0.133 (0.016) 0.561 (0.007)

MPCK-MEANS glob 0.797 (0.024) 0.829 (0.020) 0.944 (0.007) 0.035 (0.027) 0.074 (0.042) 0.555 (0.012)

MPCK-MEANS loc 0.673 (0.014) 0.711 (0.013) 0.924 (0.003) 0.026 (0.012) 0.054 (0.024) 0.554 (0.004)

CLUE, SL 0.725 (0.199) 0.892 (0.046) 0.845 (0.208) 0.357 (0.021) 0.637 (0.019) 0.681 (0.012)

CLUE, CL 0.706 (0.126) 0.780 (0.086) 0.911 (0.097) 0.357 (0.013) 0.619 (0.011) 0.675 (0.003)

Libras Seeds

Method NMI CE RI NMI CE RI

K-MEANS 0.559 (0.011) 0.615 (0.008) 0.899 (0.003) 0.641 (0.143) 0.704 (0.032) 0.853 (0.063)

MPCK-MEANS glob 0.535 (0.021) 0.558 (0.026) 0.888 (0.004) 0.750 (0.218) 0.760 (0.209) 0.899 (0.089)

MPCK-MEANS loc 0.433 (0.015) 0.534 (0.017) 0.857 (0.004) 0.748 (0.218) 0.764 (0.205) 0.891 (0.096)

CLUE, SL 0.641 (0.006) 0.746 (0.017) 0.931 (0.005) 0.380 (0.254) 0.768 (0.081) 0.659 (0.156)

CLUE, CL 0.645 (0.009) 0.744 (0.008) 0.933 (0.002) 0.453 (0.237) 0.631 (0.177) 0.679 (0.134)

the example cluster very well, but the other clusters

much less. As a result, the example cluster is recon-

structed well before other clusters are. This overﬁt-

ting seems inherent to the rescaling approach that also

earlier methods use, and may explain why the existing

methods can perform worse than unsupervised clus-

tering. We are still investigating this issue.

6 CONCLUSIONS

We introduced a novel type of supervision for semi-

supervised clustering. The supervision consists of one

or more complete example clusters. Whereas exist-

ing semi-supervised clustering methods assume lim-

ited knowledge over the complete instance space, this

setting assumes complete knowledge over a limited

part of the instance space.

We have proposed a novel method designed

speciﬁcally for this task. It learns a Mahalanobis dis-

tance that is maximally consistent with the given ex-

ample clusters. Then it performs agglomerative clus-

tering using this distance. Finally, it returns the parti-

tion for which the example clusters are reconstructed

optimally. Evaluating this method on six clustering

tasks, we have found that the novel method performs

better than existing methods in this setting. The eval-

uation also points to a problem of “overﬁtting the ex-

ample cluster” which is as yet unresolved.

ACKNOWLEDGEMENTS

Celine Vens is a Postdoctoral Fellow of the Re-

search Foundation - Flanders (FWO-Vlaanderen).

Work supported by the Research Foundation - Flan-

ders (G.0682.11) and the KU Leuven Research Fund

(GOA 13/010).

REFERENCES

Agrawal, R., Gehrke, J., Gunopulos, D., and Raghavan, P.

(2005). Automatic subspace clustering of high dimen-

sional data. Data Mining and Knowledge Discovery,

11(1):5–33.

Bar-Hillel, A., Hertz, T., Shental, N., and Weinshall, D.

(2005). Learning a mahalanobis metric from equiv-

alence constraints. Journal of Machine Learning Re-

search, 6:937–965.

Basu, S., Banerjee, A., and Mooney, R. (2002). Semi-

supervised clustering by seeding. In Proceedings of

19th International Conference on Machine Learning

(ICML-2002.

Bilenko, M., Basu, S., and Mooney, R. (2004). Integrat-

ing constraints and metric learning in semi-supervised

clustering. In ICML, pages 81–88.

Fisher, D. (1987). Knowledge acquisition via incremental

conceptual clustering. Machine learning, 2(2):139–

172.

Frank, A. and Asuncion, A. (2010). UCI machine learning

repository.

Grira, N., Crucianu, M., and Boujemaa, N. (2004). Unsu-

pervised and Semi-supervised Clustering: a Brief Sur-

vey. A Review of Machine Learning Techniques for

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

Processing Multimedia Content, Report of the MUS-

CLE European Network of Excellence (FP6).

Mahalanobis, P. C. (1936). On the generalised distance in

statistics. In Proceedings National Institute of Sci-

ence, India, pages 49–55.

Manning, C. D., Raghavan, P., and Schtze, H. (2008). In-

troduction to Information Retrieval. Cambridge Uni-

versity Press, New York, NY, USA.

Rand, W. M. (1971). Objective Criteria for the Evaluation

of Clustering Methods. Journal of the American Sta-

tistical Association, (336):846–850.

Turk, M. A. and Pentland, A. P. (1991). Face recognition

using eigenfaces. Proceedings 1991 IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition, 591(1):586–591.

Wagstaff, K. and Cardie, C. (2000). Clustering with

instance-level constraints. In Proceedings of the Sev-

enteenth International Conference on Machine Learn-

ing, pages 1103–1110.

Wagstaff, K., Cardie, C., Rogers, S., and Schroedl, S.

(2001). Constrained K-means clustering with back-

ground knowledge. In ICML, pages 577–584. Morgan

Kaufmann.

Witten, I., Frank, E., and Hall, M. (2011). Data Mining:

Practical Machine Learning Tools and Techniques.

Morgan Kaufmann.

Xing, E., Ng, A., Jordan, M., and Russell, S. (2002). Dis-

tance metric learning, with application to clustering

with side-information. In Advances in Neural Infor-

mation Processing Systems 15, pages 505–512. MIT

Press.

Yeung, D. and Chang, H. (2006). Extending the relevant

component analysis algorithm for metric learning us-

ing both positive and negative equivalence constraints.

Pattern Recognition, 39(5):1007 – 1010.

Semi-supervisedClusteringwithExampleClusters