Linguistic-variable Deﬁnition in OWL 2

A Prot

e Plugin

Silvia Calegari

, Davide Ciucci

and Matteo Mondini

DISCo, Universit

a di Milano–Bicocca, Milano, Italy

Istituto di Ricerche Farmacologiche ”Mario Negri”, IRCCS, Milano, Italy

Keywords:

Linguistic Variable, Fuzzy Ontology, Prot

e, OWL 2.

Abstract:

Linguistic Variables play a key role in the Computing with Words paradigm and in general in representing and

managing vague knowledge. They are strongly related to Fuzzy Set Theory since the semantic of linguistic

variables is given through fuzzy sets. In order to deal with structured vague information, it is thus fundamental

to integrate ontologies and related instruments with fuzzy capabilities. Several approaches are known in

literature that introduce fuzzy ontology languages, fuzzy reasoners and editor plug-ins to represent them.

However, none directly deals with the problem of representing linguistic variables. In the present paper, we

introduce a Prot

e Plugin developed to deﬁne linguistic variables in ontologies. The plug-in is based on

OWL2 and on a lite version of its fuzzy extension.

1 INTRODUCTION

In the last decade the need to represent and share

knowledge in several domain applications has given

rise to a growing interest in research on ontology.

An ontology is deﬁned as an explicit speciﬁcation of

a conceptualization (Gruber, 1993a; Gruber, 1993b)

and following this principle an ontology identiﬁes the

objects (both abstract and concrete things of the do-

main) and the relations that link them. Ontologies

are used in many research areas such as knowledge

engineering, database design, information retrieval

and extraction, context-aware, agent-based system,

etc. (Guarino, 1998); but its great notoriety can be

awarded to the key role in the Semantic Web.

In the Semantic Web a critical open issue is how

to deal with imprecise and vague knowledge that is

a typical factor in real world applications (Sanchez,

2006). It is well known that Fuzzy Set Theory is able

to describe vague concepts through a generalized no-

tion of set according to which an object may belong to

it with a certain degree (typically, a real number in the

range [0, 1]) (Klir and Yuan, 1996). Many researchers

have focused their research activities in order to inte-

grate the fuzzy logic formalism in the ontological one

with the aim of deﬁning the so called Fuzzy Ontology

(Sanchez and Yamanoi, 2006; Calegari and Ciucci,

2008; Calegari and Sanchez, 2008). To support the

fuzzy ontology formalism is a really hard topic that

mainly includes four aspects: (i) extend both the se-

mantic and syntax of Description Logics

(DLs) with

fuzziness, (ii) deﬁne a fuzzy extension of the OWL

language (OWL, 2005) (the well-known ontology lan-

guage that provides three increasingly expressive lan-

guages, i.e. “OWL Lite”, “OWL DL” and “OWL

Full”) based on the considered fuzzy DL, (iii) have

reasoners that can support the fuzzy OWL language,

and (iv) extend ontology editors with new plug-ins

able to deﬁne and represent fuzzy knowledge based

on the previous points.

In literature, there exist many papers related to the

deﬁnition of fuzzy DLs (Bobillo and Straccia, 2013;

Bobillo et al., 2013b; Mailis et al., 2010) or fuzzy

OWL (Calegari and Ciucci, 2007b; Gao and Liu,

2005; Stoilos et al., 2005), but none of these works

do tackle the problem of real situations where experts

by interacting with an ontology editor have to con-

cretely deﬁne knowledge based on the fuzzy ontol-

ogy formalism. Also to deﬁne fuzzy reasoners is not

a simple process due to the time complexity for the

execution of some reasoning tasks. Currently only

the fuzzyDL

reasoner for fuzzy S H I F with con-

crete fuzzy concepts has been presented. This rea-

Description Logics are a family of knowledge repre-

senting structured knowledge. Each logic is named through

a sequence of capital letters that identify the constructors of

the logic and then its complexity.

http://www.cs.man.ac.uk/∼sattler/reasoners.html

269

Calegari S., Ciucci D. and Mondini M..

Linguistic-variable Deﬁnition in OWL 2 - A Protégé Plugin.

DOI: 10.5220/0004548002690277

In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2013), pages 269-277

ISBN: 978-989-8565-81-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

soner supports the “OWL Lite” language which is

the less expressive OWL language as it is used only

for a classiﬁcation hierarchy and simple constraints

features. At this point, straightforward problems on

the use of scalable reasoning procedures to deal with

vague knowledge can arise too (Cimiano et al., 2008).

To overcome the scalability issue, a trend of research

deals with how to reduce fuzzy DLs to crisp DLs with

the aim of preserving the knowledge satisﬁability. In

this way, standard DL reasoners based on the crisp

OWL language can be used for reasoning with fuzzy

ontologies. For example, in (Bobillo et al., 2012; Bo-

billo et al., 2013b) the Pellet

(Sirin et al., 2007)) DL

reasoner that supports OWL 2

is adopted. OWL 2 is

the new standard ontology language for the Semantic

Web supported by the W3C

, and it is conformed to

the “OWL 2 DL” language.

The aim of this paper is to present the develop-

ment of a plug-in, called FuzzyOntologyView, that is

compliant with the fuzzy logic formalism.The Prot

4.2

ontology editor has been chosen to be integrated

with the FuzzyOntologyView plug-in as it supports

OWL API 3

(Horridge and Bechhofer, 2011), the lat-

est version of the OWL APIs. Our plug-in does not

use fuzzy (or crisp) reasoners but it allows to man-

age fuzzy knowledge by deﬁning fuzzy concepts that

are represented as linguistic variables in the sense of

Zadeh (Zadeh, 1975). A linguistic variable is a vari-

able whose values correspond to linguistic adjectives,

e.g. the variable Height with values “small, medium

and tall”. We propose a solution to extend the OWL 2

language by including fuzzy concepts deﬁned as lin-

guistic variables preserving the standard formalism of

OWL 2

. As previously stated, the works presented

in (Bobillo et al., 2012; Bobillo et al., 2013b) pro-

pose a solution to reduce the fuzzy ontology to the

corresponding crisp ontology using standard DL rea-

soners. To this aim, a plug-in in Prot

e 4.2 (Bo-

billo and Straccia, 2011) that allows to manage fuzzy

knowledge has been developed, but only by adding

such information as annotations simplifying the prob-

lem of representing the fuzzy knowledge in OWL 2.

On the other hand, the plug-ins deﬁned in (H. Ghorbel

and Bouaziz, 2009; Calegari and Ciucci, 2008; Cale-

http://clarkparsia.com/pellet

OWL 2 Web Ontology Language: http://www.w3.org/

TR/owl2-overview/

World Wide Web Consortium: http://www.w3.org/

http://protege.stanford.edu/download/

registered.html#p4.2

http://owlapi.sourceforge.net

Let us remark that we need some functionalities of

OWL2 not present in OWL, such as punning and extended

datatypes

gari and Ciucci, 2007a) are able to manage fuzzy lite

ontologies where only membership relations are con-

sidered, and they support old ontology languages, i.e.

RDFS and “OWL Lite”, respectively. The paper is

organized as follows: Section 2 introduces the fuzzy

notions used for the development of the plug-in, in

Section 3 the FuzzyOntologyView plugin is presented

and comparative evaluations with other solutions pro-

posed in literature are given. In Section 4 some con-

clusions and possible future trends are outlined.

2 FUZZY ONTOLOGY

2.1 Fuzzy Set Basics

Fuzzy sets on a universe U are a generalization of

standard sets deﬁned through a membership function

: U 7→ [0, 1] which associates with any element

x ∈ U its degree of membership to a set A. Fuzzy

set theory has almost ﬁfty years, the ﬁrst paper dates

back to 1965 (Zadeh, 1965), and it is now widely used

in all those situations where we need to represent and

manage vague information. Despite of this general

deﬁnition of a fuzzy set, where no restrictions are put

on the function f

, the membership function shape is

often chosen among a limited set of possibilities. The

most used ones are: singleton, triangular, trapezoidal,

gaussian and beta, whose deﬁnition reads as follows.

• Singleton: s : U 7→ [0, 1], there exists a particular

element x ∈ U such that s(x) = 1 and s(y) = 0 for

all y 6= x, that is the set s has only one element

with membership value equal to 1;

• Trapezoidal: Tr : U 7→ [0, 1], Tr(x) =

max(min(

x−a

b−a

d−x

d−c

, 1), 0) where a, b, c, d are

constants whose meaning is clear from ﬁgure 1;

• Triangular fuzzy sets are trapezoidal ones with

b = c;

• Gaussian: G : U 7→ [0, 1], G(x) = e

−

(c−x)

2σ

with c

the center of the curve and σ the width;

• Beta: B : U 7→ [0, 1], B(x) = x

(α−1)

(1−x)

(β−1)

for

α, β > 0 real-valued parameters.

a b

Figure 1: An example of trapezoidal fuzzy set.

KEOD2013-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

270

We now introduce linguistic variables (Zadeh,

1975) a central notion in so called Computing with

words paradigm (Zadeh, 1996). A linguistic variable

is a quintuple (L, T (L),U, G, M) where L is the name

of the variable, T (L) is the set of values for L, which

are called linguistic terms (also linguistic values or

linguistic labels), U is a universe of discourse; G is a

syntactic rule which generates the terms in T (L), and

M is a semantic rule which maps each linguistic term

A ∈ T (L) to its meaning, M(A), where M(A) denotes

a fuzzy subset of U.

Example 2.1. As an example let us consider to de-

ﬁne the concept of Height with its nuances. We have

that the linguistic variable is L = Height and its val-

ues are T(L) = {small, medium, tall }. The universe

is the interval U = [0, 200] expressing the height in

centimeters, the rule G just says that the only linguis-

tic terms are the ones in T (L) and the mapping M is

represented by the fuzzy subsets of Figure 2.

Figure 2: “Height”: an example of Linguistic Variable.

2.2 Combining Fuzzy Sets with

Ontologies

As said in the introduction, several approaches to use

fuzzy sets with ontologies can be found in literature.

Here, we are dealing with a simple situation, where

each concept is a fuzzy subset on the instance domain.

Deﬁnition 2.1. A Fuzzy Ontology is deﬁned as the tu-

ple O

= {I, C, R, F, A} where:

- I is the set of individuals, also called instances.

- C is the set of concepts. Each concept C ∈ C is a

fuzzy set on the domain of instances C : I 7→ [0, 1].

-A special role is held by the taxonomic relation T ⊆

which identiﬁes the subsumption relation among

the concepts.

-R is the set of non-taxonomic and crisp relations;

- F is the set of the fuzzy relations on the set of

entities E and a speciﬁc domain contained in D =

{integer, string, ...}. In detail, they are n-ary func-

tions such that each element F ∈ F is a relation F :

(n−1)

× P 7→ [0, 1] where P ∈ D.

- A is the set of axioms expressed in a proper logical

language, i.e., predicates that constrain the meaning

of concepts, individuals, relationships and functions.

This corresponds to a fragment of the more gen-

eral deﬁnition of fuzzy ontology (Calegari and Ciucci,

2008), where any relation can be fuzzy and more

freedom is given in the possibility to deﬁne axioms.

This issue becomes more clear when considering the

OWL/DL deﬁnition of fuzzy ontology. Indeed, from

a more formal standpoint we have to consider the

deﬁnition of a fuzzy ontology based on description

logic. Let us note that in literature several deﬁni-

tions of Fuzzy Description Logic can be found (Strac-

cia, 2006; Stoilos et al., 2005; Calegari and Ciucci,

2007b; Bobillo et al., 2012). We consider here a

fuzzy variant of SROIQ(D), since it is equivalent to

the OWL2, the W3C standard language. However, in

order to cope with linguistic variables only a fragment

of fuzzy S ROIQ(D) is needed. The only parts which

need to be fuzzyﬁed are concepts, concrete domains

and individual axioms. Indeed, in order to represent

the concept of Small_People, subconcept of People

(i.e., the set of people corresponding to the linguistic

term Small, relative to the linguistic variable Height),

we need to deﬁne the relation Height, the concrete

fuzzy concept Small as a fuzzy set on the universe

[0, 250] and then state that the concept Small-People

is equivalent to ∃Height.Small.

For further details about S ROIQ(D) we refer the read-

ers to (Bobillo et al., 2012).

3 FuzzyOntologyView: THE

PROT

E PLUGIN

This section presents the Prot

e plugin that inte-

grates the Fuzzy Set Theory notions (see Section 2)

into the ontology-knowledge; this goal is obtained by

deﬁning linguistic variables through fuzzy concepts.

The ﬁrst part of this section describes the main phases

of the FuzzyOntologyView plug-in that allow to create

the fuzzy concepts. The second part explains how the

fuzzy concepts deﬁnition can preserve the standard

formalism of OWL 2 and provides a simple example.

The third part gives a comparison of the FuzzyOntolo-

gyView plug-in with other approaches proposed in the

literature.

3.1 Deﬁning Fuzzy Knowledge in

Domain Ontologies

To interact with the plug-in, it must be previously in-

stalled in the usual way of Prot

e plug-ins. A new

tab called FuzzyOWLView will be added as a new

functionality of the standard element Classes in the

editor, i.e., beside the tabs Class hierarchy and Class

Linguistic-variableDefinitioninOWL2-AProtégéPlugin

271

hierarchy (inferred). The ﬁrst two phases for using

the FuzzyOWLView tab are: (1) create/import the non-

fuzzy domain Ontology, (2) select the concept from

the Class hierarchy tab that has to be fuzziﬁed. Now,

a user can select the FuzzyOWLView tab and choose

the membership function (see Section 2) that better

represents the semantic of the fuzziﬁed concept.

As an example we deﬁne inside the Travel domain

Ontology the linguistic variable Airport Distance, the

two terms Near Airport, Not so far Airport and ﬁnally,

the individuals Roma, Madrid, Washington will be as-

sociated to these terms.

Figure 3: Selection of a membership function.

Figure 3 shows the FuzzyOWLView tab where the

concept nearAirport has been selected and the list of

four membership functions that a user has to choose

among. In our example, we suppose that the Trape-

zoid function has been selected, and the related panel

is displayed. Figure 4 illustrates the Trapezoidal func-

tion deﬁned by typing the values of the constants in

the speciﬁc area called Trapezoid parameters. In de-

tail, the left-shoulder trapezoidal function has been

deﬁned as it better represents the notion of a near

airport. However, a user can draw and redraw in-

ﬁnite times the selected function by the button Re-

draw function, and only when she/he is convinced

can click-on the button Create membership function.

However, before it is mandatory to choose the Dat-

aProperty associated with the fuzzy concept, other-

wise an alert message will advice the user. In the ex-

ample, the DataProperty is AirportDistance and the

fuzzy concept is nearAirport.

Figure 4: Trapezoidal function for the concept nearAirport.

After that a membership function is associated

with a concept, whenever the same concept is chosen

by interacting with FuzzyOWLView then a new panel

will be displayed to the user (see Figure 5). Now,

there are three different operations on individuals of

a fuzzy concept: (1) create a new individual to asso-

ciate with the concept, (2) add an existing individual

in the ontology to the concept by selecting the indi-

vidual from a list and then write a suitable value, and

(3) view all the fuzzy concepts and individuals that

Figure 5: Management of individuals to a fuzzy concept.

KEOD2013-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

272

Figure 6: Management of individuals to a fuzzy concept.

have been assigned to the same DataProperty.

In Figure 6 a user is creating the individual Roma

belonging to the fuzzy concept not-so-farAirport with

a distance from the airport of 28km. As it happens

for the creation of a membership function, a user can

draw and re-draw an individual and only the selection

of the button Create individual establishes its deﬁni-

tion in the Ontology.

Figure 7: Management of individuals to a fuzzy concept.

In Figure 7 there is a more complete view of the

fuzzy concepts and individuals that have been de-

ﬁned. In this case, for the DataProperty AirportDis-

tance two fuzzy concepts have been deﬁned, i.e. near-

Airport and not-so-farAirport, and two individuals

have been assigned to them, i.e. Madrid and Washing-

ton cities with the meaning that Madrid is more near

to its airport than Washington (considering Dulles In-

ternational Airport).

3.2 Translation in OWL 2

The output of the FuzzyOntologyView plug-in is a

fuzzy ontology that can be directly encoded in the

OWL 2 language by the usage of the library OWL API

3. The crucial objective of adding fuzzy notions by

preserving the standard formalism of OWL 2 will be

reached by a suitable deﬁnition of linguistic variables.

In the following all the elements deﬁned to map the

notion of linguistic variable in OWL 2 are explained.

These elements act on Classes, ObjectProperties and

DataProperties. Classes:

• FuzzyTypeDefinition. This class can be con-

sidered one of the most important as its scope is

to deﬁne ternary relations among an individual, a

concept and its degree of membership. In OWL

2 it is not possible to directly create a ternary re-

lation among a concept, an individual and a de-

gree. The solution adopted in the ontology lan-

guages is to consider the standard notion of reiﬁ-

cation where a link between two individuals or an

individual and a value is deﬁned. This means to

duplicate the concept involved in the relation as an

individual and to link this last with each instance

assigned to the starting fuzzy concept (see Sec-

tion 3.1). By considering the example of Figure 7

and the notion of linguistic variable (see Section

2), we have four ternary relations between two in-

dividuals and their degree as each individual be-

longs to the two fuzzy concepts (NearAirport, not-

so-far-Airport) with a different degree. For ex-

ample, one of them is r1(Madrid, nearAir port +

code) = 1.0 with the assumption that the trans-

formation ’concept 7→individual’ for nearAirport

is applied. During the reiﬁcation process a code

is automatically added to the new instance by the

editor. Finally, the class FuzzyTypeDefinition

is deﬁned at the top level in the hierarchy, and

when this class is selected in the Usage tab all the

ternary relations between individuals are listed.

• Type of membership function. Several

classes related to the type of membership

function selected by the user are instanci-

ated. In the example of Section 3.1 the class

TrapezoidalMembershipFunction is deﬁned at

the top level in the hierarchy tree as the user has

always preferred the Trapezoidal function, and

thus only the class related to this function has to

be presented to the user. In case of selection of

other functions, the corresponding class will be

instanciated as GaussianMembershipFunction,

SingletonMembershipFunction, and BetaMem-

bershipFunction. In the considered example,

when the TrapezoidalMembershipFunction

class is selected all the Trapezoidal functions

are listed in the Usage tab. Moreover, at this

step, the deﬁnitions of the speciﬁc Trapezoidal

functions created in the ontology are shown.

By considering the example of Section 3.1, the

functions membershipFunctionOfnearAirport

and membershipFunctionOfnot-so-farAirport are

listed as individuals. This is due to the necessity

to manage and save the parameters inserted by

the user during the creation of the speciﬁc mem-

bership function (see the statement datatype in

DataProperties).

Linguistic-variableDefinitioninOWL2-AProtégéPlugin

273

• FuzzyConcept. This class is deﬁned to know all

the concepts that have been deﬁned as a member-

ship function in the ontology, and it is created at

the top level in the hierarchy. By considering the

example of Section 3.1, the two concepts nearAir-

port and not-so-farAirport deﬁned as individuals

(see FuzzyTypeDefinition) are listed.

ObjectProperties:

• fuzzyType. It represents the name of

the relation between an individual and the

FuzzyTypeDefinition class.

By analysing the previous example of

FuzzyTypeDefinition, we have that

r1(Madrid, nearAirport + code) = 1.0 7→

FuzzyType(Madrid, nearAirport + code) = 1.0.

• hasBaseType. It links a FuzzyTypeDefinition

to a concept in order to represent which individu-

als belong to the speciﬁc concept.

• hasMembershipFunction. It links a concept to

the related fuzzy membership function.

DataProperties:

• hasDegree. It indicates the degree between two

individuals in a ternary relation as deﬁned in the

FuzzyTypeDefinition class. The degree is de-

ﬁned in the range [0, 1]. This value is automati-

cally obtained as shown in the example of Figure

2 where the compatibility of Height 156cm with

Small might be 0.35.

• datatype. It allows to save the parameters for the

type of membership function selected by the user.

• DataProperty. It indicates the DataProperty

name used to group all the fuzzy concepts that

have a semantic association (i.e., the linguistic

variable name). Moreover, by selecting each in-

dividual it also stores the value that has been writ-

ten by the user during the creation of the individ-

ual for a speciﬁc fuzzy concept (see Section 3.1

where the user has inserted the value 12Km to in-

dicate the distance from the city of Madrid to its

airport).

3.2.1 From a Linguistic Variable to OWL 2

We now explain through an example how a linguistic

term has been represented in OWL 2.

First of all, a linguistic variable L, AirportDis-

tance in our case, is realized through a DataProp-

erty. Then, a term A ∈ T (L) is a concept, in our ex-

ample Not-so-farAirport is a subclass of the concept

City. In order to represent the semantic of a term,

that is the fuzzy set M(A), we reify the term A = Not-

so-farAirport (see FuzzyTypeDefinition) and ob-

tain the individual Not-so-farAirport which belongs

to the class FuzzyConcept and is linked through

the object property hasMembershipFunction to the

individual MembershipFunctionOfnot-so-farAirport.

This last individual, on its turn, is a member of

the class TrapezoidalMembershipFunction. The

four values a, b, c, d deﬁning the trapezoidal shape

of the fuzzy set M(Not − so − f arAirport) are set

using four datatype properties HasFirstParame-

ter, HasSecondParameter, HasThirdParameter, Has-

FourthParameter of MembershipFunctionOfnot-so-

farAirport.

Finally, we explain how to represent individu-

als. Let us consider the case of Madrid, whose air-

port is 12Km from the city and thus its member-

ship degree to not-so-farAirport is 0.0. The dis-

tance in kilometers, 12, is the value of the prop-

erty Airport Distance whereas 0.0 is the value of the

property hasDegree of the individual Fuzzynot-so-

far-Airport-921045970, linked to Madrid through the

fuzzyType property. Let us note that the individual

Fuzzynot-so-far-Airport-921045970 is automatically

created by the editor and generally is the value dis-

played during the reiﬁcation process where the code

921045970 is added as previously explained. In or-

der to make the semantic of each individual readable,

we have deﬁned a reiﬁed ternary relation between the

name of the individual and the individual having as-

signed the automatically generated code by the ob-

ject property fuzzyType. By considering the same

example, we have fuzzyType(madrid,Fuzzynot-so-far-

Airport-921045970).

Here below, a partial fuzziﬁed knowledge in OWL

2 of the Travel Ontology related to the example ex-

plained in the paper is reported. In particular, we con-

sider the deﬁnition of the city Madrid and its distance

to the airport by analysing the belongingness of the

fuzzy concept not-so-farAirport.

<!-- Individual: Madrid>

</Declaration>

</ClassAssertion>

</DataPropertyAssertion>

<!-- Individual: Fuzzynot-so-farAirport-921045970>

</ClassAssertion>

KEOD2013-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

274

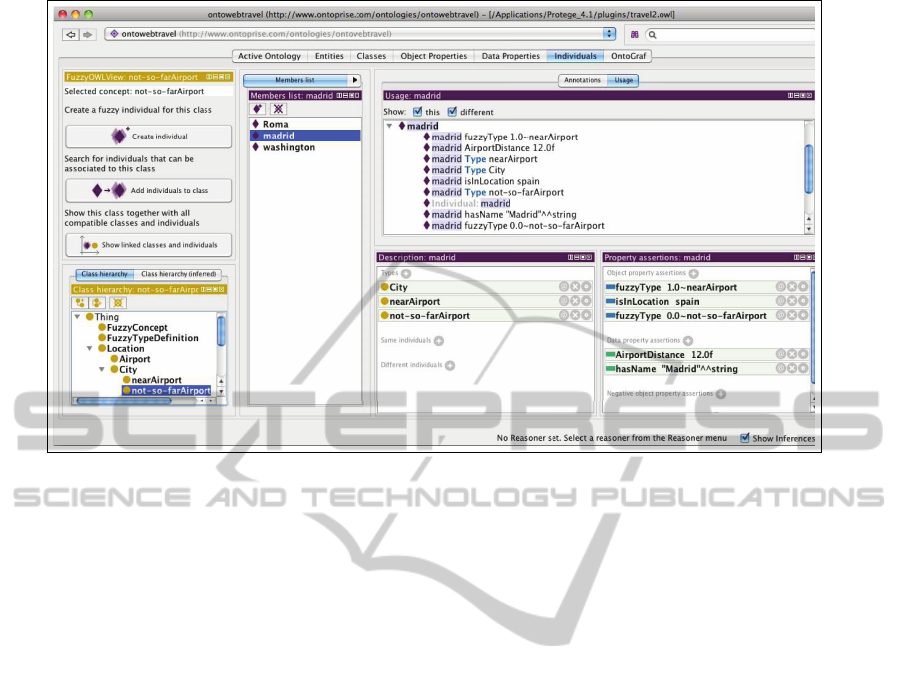
Figure 8: An overview of the fuzzy notions deﬁned in the Travel Ontology.

</ObjectPropertyAssertion>

</ObjectPropertyAssertion>

</DataPropertyAssertion>

<!-- Trapezoidal Function: TrapezoidalMembershipFunction>

</ClassAssertion>

</DataPropertyAssertion>

Figure 8 shows some of the fuzzy notions previ-

ously described by clicking-on the individual Madrid

after the selection of the concept not-so-farAirport.

As expected and depicted in Figure 7, two fuzzy-

Type are deﬁned, i.e. fuzzyType 1.0 nearAirport

and fuzzyType 0.0 not-so-farAirport. In the lower

right window of Figure 8 also the DataProperty in-

formation is reported where the name of the prop-

erty (AirportDistance) and the value wrote by the

user (12.0 f ) are stated (the value is stored as a ﬂoat

number). The same information is also reported

in the Usage tab for Individuals. At the bottom

left part of the ﬁgure, the concepts FuzzyConcept,

FuzzyTypeDefinition are located at the top level of

the hierarchy with the meaning explained previously.

Let us note that when the Individuals tab is focused on

the menu, then the FuzzyOWLView tab is displayed as

a plug-in and not as a tab beside the ones deﬁned for

the Classes tab as shown in Figure 5.

3.3 Other Solutions

The solution we adopted to represent a linguistic vari-

able, and speciﬁcally a fuzzy concept, is not the only

possible one in OWL2. Other possibilities are:

• Add a Datatype property to the fuzzy axioms in

order to represent the membership degree. How-

ever, in this case it would be impossible for an

object to belong to two different classes, since we

would have two “withDegree” tags for the same

object without knowing the linked property, as in

the following example:

<fowl:Thing rdf:about="a">

<rdf:type rdf:resource="A" >

<rdf:type rdf:resource="B" >

<fowl:withDegree>0.5</fowl:withDegree>

<fowl:withDegree>0.4</fowl:withDegree>

</fowl:Thing>

• Subclasses. Create a subclass of a fuzzy concept

C for any desired degree C

0.1

, C

0.2

, etc. This solu-

Linguistic-variableDefinitioninOWL2-AProtégéPlugin

275

tion requires either to parse the name of the con-

cept to know the membership degree or to add it as

a property to the concept C, a feature only present

in OWL full (which is not desirable to use for its

well-known undecidability).

• Annotations. With this solutions all the fuzzy part

is realized through the annotations. In this way

all the fuzzy constructs and axioms can be repre-

sented and standard editors and reasoners can use

the classical part. However, this is not compliant

with the scope of the annotations which, accord-

ing to the W3C, “should be used when the infor-

mation attached to entities should not be consid-

ered a part of the domain and when it should not

contribute to the logical consequences of an on-

tology”. Indeed, it is desirable that the fuzzy ele-

ments are at the same semantic level of the stan-

dard ones.

This last solution is the only one implemented in lit-

erature by (Bobillo and Straccia, 2011). It is part of a

complete suite with a Fuzzy Reasoner which enables

to represent and reason with a Fuzzy Ontology. Be-

sides the fact the we are moving towards a real fuzzy

ontology (not a one existing only in comments) as

described above, the main improvements to represent

fuzzy concepts introduced in our solution can be sum-

marized as follows:

Representation and Building of Linguistic Vari-

ables:

• The possibility to represent a linguistic variable,

with all the linguistic terms linked among them

(see Section 3.1);

• The simplicity to represent a linguistic term. In-

deed, in the approach (Bobillo and Straccia, 2011)

in order to create the concept “City not so far from

airport” we have to

– Create the DataProperty Has-Distance-to-

airport and set it as a superclass of the concept

City;

– Create the trapezoidal fuzzy datatype not-so-

far-airport;

– Add the concept City-no-far-airport with an an-

notation that it is a fuzzy concept, using a spec-

ify fuzzy logic (Zadeh or Łukasiewicz);

– State that City-no-far-airport is equivalent to a

city with Has-Distance-to-airport SOME not-

so-far-airport;

A list of operations which is deﬁnitely more com-

plex than in our plug-in.

Graphical Issues:

• the dynamical graphic representation, which is

absent in the Bobillo-Straccia approach. Indeed,

in our plug-in it is possible to draw and re-draw in-

ﬁnite time a function before to create it in the on-

tology; instead in the Bobillo-Straccia approach

only a static picture is displayed to help the user

recall the meaning of the parameters but a user

does not have the view of the membership func-

tion created. In addition, at any time it is possible

to have a complete overview of all the fuzzy con-

cepts and individuals associated with a speciﬁc

DataProperty. This functionality can improve the

usability of the system by supporting the user dur-

ing the deﬁnition of the domain Ontology.

• in the Bobillo-Straccia approach only a few mem-

bership functions can be deﬁned such as triangu-

lar, trapezoidal and linear.

• the ontology updates in realtime when some mod-

iﬁcations occur, whereas in the Bobillo-Straccia

approach it is necessary to save the ontology and

re-open it.

4 CONCLUSIONS AND FUTURE

WORK

This paper has presented the FuzzyOntologyView

plug-in, the ﬁrst that integrates the notion of linguistic

variable in ontologies. FuzzyOntologyView has been

deﬁned for the well known ontology editor Prot

In detail, the plug-in is compliant with the last ver-

sion of this editor that directly supports the OWL 2

language. To extend the ontology knowledge with

fuzzy notions that is directly supported in OWL 2 is

not an easy task. Indeed, in the literature a solution

(Bobillo et al., 2012; Bobillo et al., 2013b) that al-

lows to manage fuzzy knowledge has been presented,

but only by adding such information through the state-

ment annotation in OWL 2, thus simplifying the

problem of a direct representation in OWL 2.

In future works, we plan to integrate the DE-

LOREAN reasoner inside the FuzzyOntologyView

plug-in with the objective to directly use all the deﬁn-

able fuzzy notions to infer new knowledge inside the

OWL2 framework. Once this step will be complete,

the plug-in will be made available on-line.

REFERENCES

Bobillo, F., da Costa, P. C. G., d’Amato, C., Fanizzi, N.,

Laskey, K. B., Laskey, K. J., Lukasiewicz, T., Nickles,

M., and Pool, M., editors (2013a). Uncertainty Rea-

soning for the Semantic Web II, International Work-

shops URSW 2008-2010 Revised Selected Papers, vol-

ume 7123 of LNCS. Springer.

KEOD2013-InternationalConferenceonKnowledgeEngineeringandOntologyDevelopment

276

Bobillo, F., Delgado, M., and G

omez-Romero, J. (2012).

DeLorean: A reasoner for fuzzy owl 2. Expert Syst.

Appl., 39(1):258–272.

Bobillo, F., Delgado, M., and G

omez-Romero, J. (2013b).

Reasoning in fuzzy OWL2 with DeLorean. In (Bo-

billo et al., 2013a), pages 119–138.

Bobillo, F. and Straccia, U. (2011). Fuzzy ontology rep-

resentation using owl 2. Int. J. Approx. Reasoning,

52(7):1073–1094.

Bobillo, F. and Straccia, U. (2013). Finite fuzzy descrip-

tion logics and crisp representations. In (Bobillo et al.,

2013a), pages 99–118.

Calegari, S. and Ciucci, D. (2007a). Fuzzy Ontology and

Fuzzy-OWL in the KAON Project. In Proceedings of

Fuzz IEEE-07, pages 1415–1420.

Calegari, S. and Ciucci, D. (2007b). Fuzzy Ontology, Fuzzy

Description Logics and Fuzzy-OWL. In Proceedings

of WILF 2007, volume 4578 of LNCS, pages 118–126.

Calegari, S. and Ciucci, D. (2008). Towards a Fuzzy On-

tology Deﬁnition and a Fuzzy-Extension of an Ontol-

ogy Editor. In Manolopoulos, Y., Filipe, J., Constan-

topoulos, P., and Cordeiro, J., editors, ICEIS (Selected

Papers), volume 3 of Lecture Notes in Business Infor-

mation Processing, pages 147–158. Springer.

Calegari, S. and Sanchez, E. (2008). Object-fuzzy concept

network: An enrichment of ontologies in semantic in-

formation retrieval. JASIST, 59(13):2171–2185.

Cimiano, P., Haase, P., Ji, Q., Mailis, T., Stamou, G., Stoi-

los, G., Tran, D. T., and Tzouvaras, V. (2008). Rea-

soning with large a-boxes in fuzzy description logics

using dl reasoners: An experimental evaluation. Pro-

ceedings of the ESWC Workshop on Advancing Rea-

soning on the Web: Scalability and Commonsense,

pages 1–15.

Gao, M. and Liu, C. (2005). Extending owl by fuzzy de-

scription logic. In 17th IEEE International Confer-

ence ICTAI 05, pages 562–567.

Gruber, T. (1993a). A Translation Approach to Portable On-

tology Speciﬁcations. Knowledge Acquisition, 5:199–

220.

Gruber, T. (1993b). Towards Principles for the Design of

Ontologies Used for Knowledge Sharing. Technical

report, Knowledge System Laboratory, Stanford Uni-

versity.

Guarino, N. (1998). Formal Ontology and Information Sys-

tems. In Guarino, N., editor, Proceedings of FOIS’98,

pages 3– 15.

H. Ghorbel, A. B. and Bouaziz, R. (2009). Fuzzy prot

for fuzzy ontology models. In Proc. of 11th Interna-

tional Prot

e Conference IPC’2009, pages 1–4, Uni-

versity of Amsterdam, Amsterdam, Netherlands.

Horridge, M. and Bechhofer, S. (2011). The owl api: A java

api for owl ontologies. Semant. web, 2(1):11–21.

Klir, G. and Yuan, B. (1996). Fuzzy Sets and Fuzzy Logic:

Theory and Applications. Prentice Hall, New Jersey.

Mailis, T. P., Stoilos, G., and Stamou, G. B. (2010). Expres-

sive reasoning with horn rules and fuzzy description

logics. Knowl. Inf. Syst., 25(1):105–136.

OWL (2005). Ontology Web Language (OWL).

http://www.w3.org/2004/OWL/.

Sanchez, E. (2006). Fuzzy Logic and the Semantic Web.

Capturing Intelligence. Elsevier.

Sanchez, E. and Yamanoi, T. (2006). Fuzzy ontologies for

the semantic web. In Larsen, H. L., Pasi, G., Arroyo,

D. O., Andreasen, T., and Christiansen, H., editors,

FQAS, LNCS 4027, pages 691–699. Springer.

Sirin, E., Parsia, B., Grau, B. C., Kalyanpur, A., and Katz,

Y. (2007). Pellet: A practical owl-dl reasoner. Web

Semantics, 5(2):51–53.

Stoilos, G., Stamou, G., Tzouvaras, V., Pan, J. Z., and Hor-

rocks, I. (2005). Fuzzy owl: Uncertainty and the se-

mantic web. In In Proc. of the International Workshop

on OWL: Experiences and Directions.

Straccia, U. (2006). A fuzzy description logic for the se-

mantic web. In Sanchez, E., editor, Fuzzy Logic and

the Semantic Web, Capturing Intelligence, chapter 4,

pages 73–90. Elsevier.

Zadeh, L. A. (1965). Fuzzy sets. Inform. and Control,

8:338–353.

Zadeh, L. A. (1975). The concept of a linguistic variable

and its application to approximate reasining — part I,

II and III. Information Sciences, 8–9:199–251, 301–

357, 43–80.

Zadeh, L. A. (1996). Fuzzy logic = computing with words.

Fuzzy Systems, IEEE Transactions on, 4(2):103–111.

Linguistic-variableDefinitioninOWL2-AProtégéPlugin

277