Recommending the Right Activities based on the Needs of each Student

Elias de Oliveira

∗

, Márcia Gonçalves Oliveira and Patrick Marques Ciarelli

Programa de Pós-Graduação em Informática, Universidade Federal do Espírito Santo, Vitória, Brazil

Keywords:

Activities Recommendation, Computers Programming, e-Learning, kNN Algorithm.

Abstract:

Today more than ever, personalization is the most important feature that a system needs to exhibit. The

goal of many online systems, which are available in many areas, is to address the needs or desires of each

individual user. To achieve this goal, these systems need to rely on a good recommendation system. Hence,

recommendation systems must work under the assumption that an individual’s need could also be applied to

someone else who has similar desires, tastes, and/or necessities. In this paper, we took this assumption into

account and applied it to the context of learning computer programming. As a result, we present a system that

recommends additional activities to students according to their individual needs. An additional assumption

that is used is that a prompt reply and tailored guidance at each step of the learning process improves an

individual’s chances of success. We propose the use of the kNN algorithm to recommend activities that are as

similar as possible to those that an expert would assign. The results are promising because we were able to

mimic the human assessment decisions 90.0% of the time.

1 INTRODUCTION

We are overwhelmed by the amount of information

that we need to process on a daily basis (Bawden and

Robinson, 2009) to select the information that is rele-

vant. Currently, one can ﬁnd, either physically or on-

line, a large number of items in numerous areas that

might be of interest. Browsing all of these items and

choosing one or some of these is sometimes stress-

ful. To mitigate this difﬁcult problem, an increasing

number of studies have been conducted in the area of

recommendation systems to help the user select those

items that may be suitable.

A recommendation system is a program that anal-

yses the behaviors and characteristics of users and

attempts to recommend actions or items that could

be useful to those users (Koren et al., 2009). Rec-

ommendation systems can be used in many differ-

ent areas of knowledge to learn what users’ interests

are and to make recommendations accordingly (Her-

locker et al., 1999). For instance, in e-commerce, rec-

ommendation systems can recognize customer pro-

ﬁles from their preferences or their buying habits and

recommend products according to their interests (Lin-

∗

The ﬁrst author would like to thanks CAPES for the

research grant 56128-12-2. And the second author would

like as well to thank the FAPES/FUNCITEC foundation for

their ﬁnancial support for the development of this research

under the project number 001/2009.

den et al., 2003). In medical systems, patient proﬁles

can be associated with the presence of different symp-

toms, and medications can be recommended based on

the symptom combinations (Meisamshabanpoor and

Mahdavi, 2012; Chen et al., 2012). Similarly, in the

area of e-learning, recommendation systems can map

proﬁles based on the performances of students in dif-

ferent evaluation variables and offer them personal-

ized instruction (Baylari and Montazer, 2009).

In the e-learning area, teaching computer pro-

gramming is one of the modules that are considered

to be difﬁcult by many,particularly the students them-

selves. This type of knowledge is considered complex

because it requires the combination of a set of cogni-

tive skills and extensivepractice of certain activitiesto

achieve mastery (Pea and Kurland, 1984). To be suc-

cessful and to encourage learning, the students must

be well monitored on their practice of programming.

Therefore, the goal of our recommendation system is

to recommend the most appropriate activities for stu-

dents such that they can improve their performances

and reduce their difﬁculty as they learn programming.

To identify and automatically recommend activi-

ties in accordance with the evaluation variables that

need improvement, we use a kNN (nearest neighbor)

strategy (Soucy and Mineau, 2001). This is a baseline

type of algorithm for recommendation systems (Tsai

and Hung, 2012).

The kNN algorithm is a typical technique of col-

183

de Oliveira E., Gonçalves Oliveira M. and Marques Ciarelli P..

Recommending the Right Activities based on the Needs of each Student.

DOI: 10.5220/0004549501830190

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval and the International Conference on Knowledge

Management and Information Sharing (KDIR-2013), pages 183-190

ISBN: 978-989-8565-75-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

laborative ﬁltering recommendation systems because

it makes recommendations based on the following

three steps: building user proﬁles from user prefer-

ences, discovering user behaviors similar to the pro-

ﬁle, and recommending the top-N preferred items

from the nearest neighbors (Park et al., 2012).

When the implementation of our strategy was ap-

plied to our dataset, which is composed of 1,784 sam-

ples, the results showed that our strategy is effective

for the recommendation of the most appropriate ac-

tivities for different student proﬁles. The experiments

indicated that our algorithm can mimic the instruc-

tor’s assessment decisions most of the time.

This work is organized as follows. We present

the problem and its context in Section 2. In Section

3, some related works are brieﬂy reviewed. We dis-

cuss the results of an analogous problem tackled by

a very simple strategy (kNN, when k = 1) in Section

4. This simple strategy will be compared against the

more general kNN approach (kNN, when k > 1), and

the ﬁrst technique will be used as a lower bound in

this work. In Section 5, we describe how the experi-

ments were performed and the results obtained in the

activities recommendation task. The conclusions are

then presented in Section 6.

2 THE PROBLEM DESCRIPTION

In a learning environment, a recommendation system

will be of great use if it can constantly monitor the

coursework performances of the students. By analyz-

ing their performances, this system could then rec-

ommend a tailored set of activities for the improve-

ment of the learning performance of each individual

student. Typically, a recommendation system uses in-

formation from other neighboring users to predict the

choices that an active user would make. In the learn-

ing context, this strategy is analogous to the use of

a set of neighboring students’ proﬁles to suggest a

range of activities to the target student, i.e., activities

that could change the target student’s performance in

terms of his/her learning progress. In other words, in

this paper, we discuss the recommendation portion of

the system (see Section 5) using our dataset, which

structural features are similar to those of MovieLens,

which is a traditional dataset used for movie recom-

mendations (Herlocker et al., 1999), as discussed in

Section 4.

In a more formal manner, consider D the domain

of proﬁles and Ω = {d

, d

, . . . , d

|D|

} an initial cor-

pus of proﬁles to which extra activities were previ-

ously manually assigned by an expert. A proﬁle d

, x

, ..., x

)(∀ j = 1, 2, 3, . . . |Ω|) is composed

of a set of |d

| assessment variables v

≥ 0 (∀q =

1, 2, 3, . . . , |d

|). Each proﬁle d

of Ω is previously

associated with a subset of activities c

∈ C (∀i =

1, 2, . . . , |C|). A recommendation system of activi-

ties implements a function f : D × C → R that re-

turns a value for each pair (d

, c

) ∈ D × C, which

indicates that the test proﬁle d

should be assigned

activity c

∈ A

, where ∪

p=1

⊆ C. The function

of the actual value f (., .) can be transformed into a

ranking function r(., .), which is a one-to-one map-

ping onto 1, 2, . . . , |C| such that f(d

, c

) > f (d

, c

This results in r(d

, c

) < r(d

, c

). If A

is the set of

appropriate activities for test proﬁle d

, a good recom-

mendation system should organize the activities for d

within A

over those that are not in A

In this work, a formalization of the problem was

applied as follows: D is the domain of proﬁles that

are obtained from the programming activities of the

students at

. The activities c

∈ C are assumed to be related to

more than one type of programming language module

contents. Within proﬁle d

, each value v

is the per-

formance of a student on a cognitive q item within a

programming activity. For example, item q can rep-

resent an understanding indicator of a programming

concept or the proper use of an arithmetic, logical, or

relational operator.

3 RELATED WORKS

Recommendation systems can be categorized accord-

ing to their goal. For instance, in the e-commerce

ﬁeld, the goal is to ﬁnalize the business transactions,

assist consumers in purchasing even more products,

encourage consumers to buy other products, and/or

conquer the loyalty of consumers (Drachsler et al.,

2009). A slightly different goal is found in the ed-

ucational context. In this case, the goal of recom-

mendation systems for Technology Enhanced Learn-

ing (TEL) is to assist the students on their learning

activities either by providing tips or actually suggest-

ing a variety of activities to help them improve their

learning experience. In these cases, the objective of

the system was to support the development of the stu-

dent’s skills (Drachsler et al., 2009).

Other systems tackle the problem of ﬁnding al-

ternative paths through learning sources (Manouselis

et al., 2011). The Protus system is a proposed hybrid

recommendation model that was developed to recom-

mend a sequence or a path to be followed by selected

sources of learning (Klašnja-Mili

cevi

c et al., 2011).

Protus recognizes student proﬁles through their habits

and learning styles. From these proﬁles, the system

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

184

identiﬁes clusters of students, discovers patterns, and

recommends a sequence of activities based on fre-

quent sequences of learning and perceived patterns in

accordance with the proﬁles of the learners (Klašnja-

Mili

cevi

c et al., 2011). In this recommendation strat-

egy, the sequence of suggested activities is based on

a browsing history of the learner through the contents

of a course. As a result, the system can ﬁnd the habits

and preferences of the learner but might not necessar-

ily help their in the learning process. Thus, the Protus

system could also assess whether the sequence of ac-

tivities that is recommended to the learner does repre-

sent the most necessary activities that could improve

the student’s learning.

With respect to the algorithms used in this area,

the kNN algorithm is a typical technique of collab-

orative ﬁltering recommendation systems because it

makes recommendations based on the following three

steps: building user proﬁles from user preferences,

discovering user behaviors similar to a proﬁle, and

recommending the top-N preferred items from the

nearest neighbors (Park et al., 2012). The neighbor-

hood selection consists of three main tasks: proﬁle

selection, proﬁle matching, and best proﬁle collec-

tion (Ujjin and Bentley, 2002). After proﬁle selection,

the proﬁle matching process computes the distance or

similarity between the selected proﬁles and the active

user’s proﬁle using a distance function (Sarwar et al.,

2001; Ujjin and Bentley, 2002).

Following these steps, as described by (Baylari

and Montazer, 2009), we used the performance of stu-

dents to compose multidimensional proﬁles in order

to recognize learning difﬁculties that are character-

ized by the students’ performances on different eval-

uation variables. We can then predict the evaluation

variables of a student’s performance proﬁle based on

the performances of other students on the same vari-

ables (Sarwar et al., 2001). This prediction may be

based on the similarities between the students’ pro-

ﬁles (Manouselis et al., 2010) or on the similarities

between items, i.e., between the values of the assess-

ment variables (Sarwar et al., 2001; Lops et al., 2011).

In this paper, we used the user similarity approach

based on proﬁles. To develop a student’s skills, as

was noted by (Drachsler et al., 2009), we then recom-

mend the most appropriate activities according to the

values of the performance evaluation variables associ-

ated with the target student’s proﬁle (Tsai and Hung,

2012).

In the next section, we show some of the results of

our strategy using the MovieLens dataset to compare

and discuss the similarities of both problems.

4 RECOMMENDATION OF

MOVIES

In general, a recommendation system considers that

one’s choices could also be applied to someone else

with similar tastes. Therefore, one basic approach is

to use a set of users’ choices to make recommenda-

tions to the target user, which is also named the ac-

tive user. The set of users with similar tastes will be

called neighbors of the target user, and the neighbor-

hood is usually found by calculating a threshold simi-

larity value between the target user and the other users

in the dataset (Herlocker et al., 1999).

In the area of movie recommendations, a very

well-known dataset is included in MovieLens, which

is provided by the GroupLens research group

(Park

et al., 2012). Within this dataset, one can ﬁnd users’

proﬁles, their choices, and their actual ratings of

movies. It is not necessary to mention that choos-

ing movies is a very subjective type of decision mak-

ing. Thus, the challenge in this area is to devise a

system that recommends the right movies to a person

based on their characteristics, their previous choices,

and other knowledge available in their proﬁle. Usu-

ally, this is achieved through a comparison with the

proﬁles of similar users. In other words, the system

attempts to ﬁnd a user in the database who is very

similar to the target user by searching for another user

whose proﬁle exhibits the most similar choices (Ujjin

and Bentley, 2002).

The MovieLens dataset utilizes 17 features to char-

acterize movies genres: (1) action, (2) adventure,

(3) animation, (4) children, (5) comedy, (6) crime,

(7) documentary, (8) drama, (9) fantasy, (10) ﬁlm-

noir, (11) horror, (12) musical, (13) mystery, (14) ro-

mance, (15) sci-ﬁ, (16) thriller, (17) war, and western.

An additional 4 features are used to proﬁle the user:

(1) movie rating, (2) age, (3) gender, and (4) occupa-

tion

(Herlocker et al., 1999)extensivelyevaluated a va-

riety of features to analyze their effect on the accu-

racy of the system. One of their ﬁndings was that the

number of neighbors used to predict the active user’s

rate affects the results. Based on their work, we pro-

pose the use of the kNN algorithm (Hao et al., 2007),

and brieﬂy discuss two situations. In the ﬁrst situa-

tion, we choose only one neighbor (the nearest one),

i.e. k = 1, to predict the outcome of the active user.

This will be our lower-bound result for the additional

experiments. In the second case, we choose a better

neighborhood using more neighbors to improve the

results, i.e. k = 5.

http://www.movielens.umn.edu/

RecommendingtheRightActivitiesbasedontheNeedsofeachStudent

185

4.1 Recommending Movies based on the

Nearest Neighbor

In this ﬁrst approach, similarly to (Sarwar et al.,

2001), we are interested in analyzing the accuracy of

the results if we base our movie recommendations to

the target user solely on the nearest neighbor.

We want to investigate the degree of accu-

racy of the lower-bound result. In this case,

only the nearest neighbor user was used to deter-

mine the recommendation. Therefore, let T

, R

, . . . , R

} be the set of items rated

by the nearest neighbor and T

= {. . . , R

, . . .} be that

set of items rated by the active user. Note that each

user can give different rates to the same movie. How-

ever, we calculate the predicted rate only when both

the neighbor and the active user rated an item, e.g.

n,i

, and R

a,i

. In this case, the predicted rate that the

active user would use for this item is determined us-

ing the following equation:

= R

× φ, where, in

the case of the experiments included in Sections 4.1

and 4.2, we use the cosine similarity (Baeza-Yates and

Ribeiro-Neto, 2011) between the active user and the

nearest neighbor for the value of φ. The difference

between the actual rate and the predicted rate will be

computed as an error: MAE

= e

∑

i=1

−

In this equation, N is the total number of items that

both the nearest neighbor and the active user rated.

Thus, N is typically markedly less than the total num-

ber of items within the dataset. The results of this

approach are shown in Table 1.

These results show that the average error is

0.9161. As shown in Figure 1(a), half of the error

values are either above or below 0.91.

Table 1: Descriptive analysis of the error predictions.

Min. Median Mean Max. SD

0.0204 0.9041 0.9161 2.2631 0.2697

The ﬁrst column in Table 1 (Min.) shows the min-

imum MAE error value obtained using this strategy.

The second column (Median) shows the middle (me-

dian) value among the list of error values. The (Mean)

column show the calculated mean value of the set of

errors. The maximum error value is shown in the col-

umn titled (Max.), whereas the standard deviation is

shown in the last column (SD).

In this case, the standard deviation is high at

0.9161±0.2697. Due to this level of error, we may

conclude that, in the worst case, we are missing the

exact prediction match by, on average, 1 point over

the N items rated by the pair of users (active user and

nearest neighbor).

Table 2: Descriptive analysis of the error predictions.

Min. Median Mean Max. SD

0.0060 0.0316 0.0521 0.7343 0.0546

Based on the quadratic complexity nature of the

procedure used to ﬁnd the nearest neighbor, we argue

that this is the simplest and the fastest strategy for this

type of problem.

4.2 Recommending Movies based on the

Neighborhood

In this second approach, we exert a greater effort to

ﬁnd better results using the neighborhood to predict

the ratings of the active user. As mentioned previ-

ously, the size and the quality of the neighborhood

has a great impact on the predicted results (Herlocker

et al., 1999). However, in this section, we will show

only the results of a neighborhood constructed of the

ﬁve nearest neighbors to the active user.

As shown in Figure 2, the results were improved

by using a neighborhood for the prediction of the rat-

ings. From the descriptive statistics, we found that the

error decrease, on average, to 0.0521 compared with

the previous results. Moreover, the results in Figure

2(a) demonstrate the new median value is 0.031. In

summary, these results assert what was already noted

by other authors in the literature on simple strategies.

Although other strategies exist and have been pro-

posed by other researchers, the strategy that used a

combination of techniques yielded better results (Tsai

and Hung, 2012).

5 RECOMMENDING ACTIVITIES

In our recommendation system, we follow the same

strategy used with the MovieLens dataset to predict

the user’s ratings and recommend movies (Herlocker

et al., 1999). The user-based collaborative ﬁltering

recommendation system was used to suggest activ-

ities for the students of a programming course. In

this case, we predict the performance of a student in

an assessment variable based on the performances of

similar students in this same variable. After a value

has been predicted for the assessment variable, we as-

sessed whether this value is an indicator of learning

success or a deﬁciency. If this value indicates a learn-

ing deﬁciency, activities related to this variable are

recommended.

Through the prediction, we can anticipate a stu-

dent’s performance in different assessment variables

to recognize their skills and difﬁculties in program-

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

186

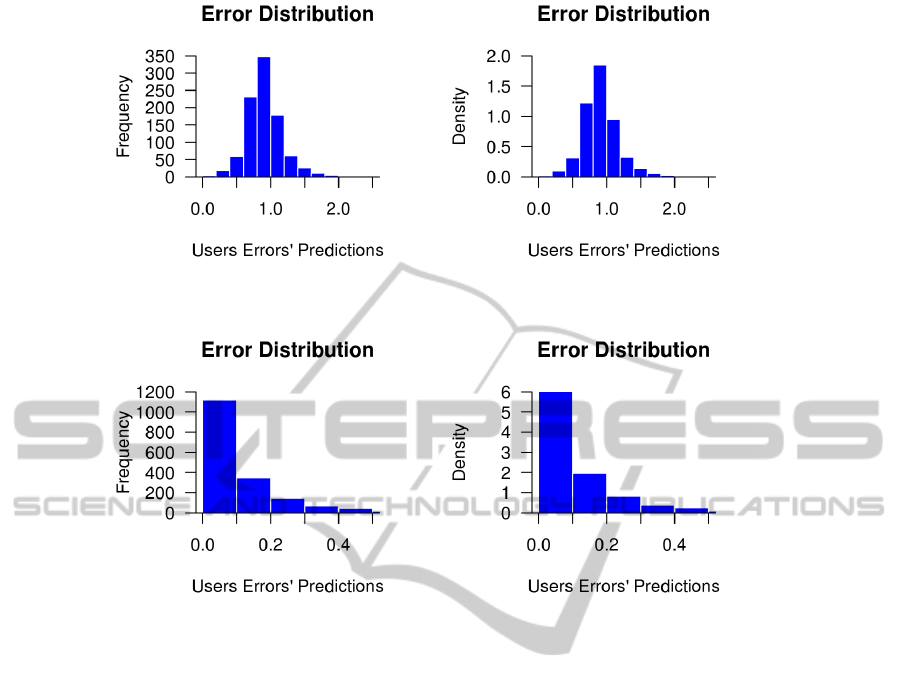
(a) (b)

Figure 1: Error distributions found using the nearest neighbor approach

(a) (b)

Figure 2: The neighborhood approach.

ming practice and to evaluate their learning condi-

tions for the development of new computer programs

with various levels of complexity. Using the system to

determine the learning states of the students through

their predicted performances, we can improve the

learning process of these students by providing them

recommendations of speciﬁc activities according to

their learning needs. The process of predicting the

performances and recommending activities proposed

in this paper uses the following steps (Herlocker et al.,

1999): 1. Generate a dataset representing the perfor-

mance of students through different evaluation vari-

ables; 2. Compute the similarity between the proﬁles

of different students; 3. Predict the values of the eval-

uation variables of a student based on the proﬁles of

the nearest students; 4. Recommend activities accord-

ing to the values of the predicted variables; 5. Evalu-

ate the results of the prediction. These steps are pre-

sented in detail in the following subsections.

5.1 The ds-FAR Dataset

For the prediction of a student’s performance and the

recommendation of activities, we generated a dataset

denoted the Formative Assessment Recommendation

(ds-FAR) that is composed of computer programs

written in the programming language that were de-

veloped by students in a programming course. These

programs were mapped to assessment variables repre-

senting the use of keywords, operations, commands,

symbols, and structures of the C programming lan-

guage.

The ds-FAR dataset consists of 1,784 samples of

programs in the C programming language mapped to

37 assessment variables. These programs were devel-

oped by approximately 50 students for 39 activities

proposedby an instructor. Unlike discrete ratings, i.e.,

the values of the MovieLens dataset were limited be-

tween the values 0 and 5, the values R

≥ 0. Mapped

from a proﬁle d

to the assessment variable v

are con-

tinuous.

The programming activities within ds-FAR were

divided into seven coursework activities and a ﬁnal

exam. Figure 4 shows an example of how three stu-

dent proﬁles were represented by these assessment

variables.

In Figure 4, the three proﬁle states A1, A2 and A3

are represented by the performances of students in a

programming activity that students solve by writing a

computer program in the C programming language.

RecommendingtheRightActivitiesbasedontheNeedsofeachStudent

187

Figure 3: Selection of predictors for the assessment vari-

ables.

Each written program is mapped to the assess-

ment variables, and each variable v

represents the

frequency of occurrence of a reserved word, an op-

erator in the C programming language, or an execu-

tion indicator of the compilation of the program and

its correct execution. The values for each assessment

variable v

of a student proﬁle were calculated by di-

viding the value of the variable by its corresponding

value in the model solution chosen by the instruc-

tor. The comments and strings found in the programs

written by the students were not considered in the as-

sessment.

If the performance of a student in an assessment

variable has a value less than 0.7, we assume that the

student has difﬁculties using the C programming con-

cept associated with the variable.

Similarly, if a student’s performance on any of the

assessment variables is above 1, s/he likely has some

difﬁcultiesassociated with the efﬁcient use of the con-

trols, structures, and operations of the C programming

language that are represented by these variables. In

other words, this particular student developed a com-

puter program using more structures and operations

than is required for resolving the given task.

In summary, the ds-FAR is a representative dataset

for the prediction of student performances and for ac-

tivities recommendations because it has many sam-

ples, it exhibits a great variability in the solutions de-

veloped by the students, and it contains a wide range

of values for the different assessment variables.

5.2 Procedures

To predict the student performances, we utilized

the traditional neighborhood-based recommendation

method (see Section 4) using three steps (Herlocker

et al., 1999): 1. Assign weights to the assessment vari-

ables of the student proﬁles based on their similarity

with the active user; 2. Select a subset of student pro-

ﬁles to be predictors of an active user; 3. Normalize

the values of the assessment variables and compute

the prediction of a weighted combination of the near-

est neighbors.

In Step 1, after we have represented the active user

and the other students using multidimensional vec-

tors, we calculated the similarity index between these

proﬁles using the cosine similarity and formed a sim-

ilarity matrix M

sim

, where each of this matrix is the

similarity between two proﬁles (d

and d

All of the variables of each student proﬁle are then

weighted by multiplying the similarity indexes be-

tween these proﬁles and d

the proﬁle of the active

user.

In Step 2, using the kNN algorithm (Soucy and

Mineau, 2001; Duda et al., 2001), we identiﬁed the k

nearest neighbors to the active user d

, i.e., those stu-

dents whose proﬁles exhibit higher rates of similari-

ties with the proﬁle of the active user. Thus, the neigh-

bors that are selected as predictors to determine the

value of assessment variable v

of the active user are

those with non-zero performance and those who have

obtained better performances on the particular assess-

ment variable of interest. In Figure 3, the hatched

student proﬁles represent the selected predictors that

will be used to predict the values and for variables R

and R

, respectively, of active user A1.

In Step 3, using a regression algorithm, we predict

the performance of in assessment variable for the ac-

tive user P

. i

6∈ I

is the assessment variable set

in which the active user has already obtained perfor-

mances. The prediction value is computed by the fol-

lowing equation: P

∑

k=1

d,k

∗R

k,i

)

∑

k=1

(|s

d,k

In this equation, N is the number of nearest neigh-

bors to the active user d

who have a value for assess-

ment variable i. The value s

a,k

is the similarity index

between the k neighborsand the active user. The value

of R

k,i

is the performance of neighbor k in assessment

variable i.

Finally, to analyze the predicted value for an as-

sessment variable, we indicate what types of activities

should be recommended to an active user.

When the predicted values in some assessment

variables have values of less than 0.7, speciﬁc ac-

tivities related to these concepts are recommended to

help the student improve his/her performance in these

assessment variables.

Similarly, if the predicted values in any of the as-

sessment variables is higher than 1, activities are rec-

ommended to help the student more efﬁciently use

the concepts of the programming language associated

with the variable.

To evaluate the accuracy of the predictions ob-

tained using our strategy with the ds-FAR dataset, we

used the metric MAE, which was presented in Section

4 in the evaluation of the rating prediction using the

MovieLens dataset.

5.3 Results

The results in Figure 5 demonstrate the efﬁcacy of

the user-based collaborativeﬁltering recommendation

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

188

Figure 4: Student proﬁles mapped to assessment variables that represent the student’s performances in different concepts of

the C programming language.

strategy using the neighborhood-basedmethod to pre-

dict student performances in programming activities.

Figure 5: Results of the prediction of student performances

using the ds-FAR dataset

As shown in Figure 5, the MAE values obtained

for the ds-FAR dataset increase as the number of

neighbors used in the evaluation is increased (Her-

locker et al., 1999). However, if 30 neighbors are used

for the prediction, the average MAE value for the ds-

FAR dataset does not exceed 0.2, which indicates that

the prediction results for the continuous assessment

variables are satisfactory.

The maximum values of MAE for the ds-FAR

dataset shown in Table 3 indicate poor predictions;

however, these values could be improved if the val-

ues that are greater than 1 are normalized to a unique

value, as performed in Step 2 of the experimental pro-

cedures, because any value greater than 1 represents

an inefﬁcient use of the programming instructions.

The results presented by (Herlocker et al., 1999),

who analyzed the MovieLens dataset using different

numbers of neighbors in the range of 0 to 100, re-

vealed that the MAE error slightly oscillated between

0.69 and 0.71. As shown in Table 3, the results ob-

tained for the ds-FAR dataset were well above those

obtained using the MovieLens dataset.

Table 3: Descriptive analysis of the error predictions ob-

tained with the ds-FAR dataset.

k Min. Median Mean Max. SD

1 0.0000 0.0181 0.0945 7.2810 0.2692

30 0.0000 0.1146 0.1729 7.3600 0.2650

The superiority of the results obtained with the

ds-FAR dataset compared with the MovieLens dataset

might be the result of the difference in the level of

sparsity between these datasets. The non-null items in

the ds-FAR dataset constitute 38.8% of the total items,

whereas the non-null items in the MovieLens dataset

are 6.3%, which indicates that the ds-FAR dataset is

less sparse than the MovieLens dataset.

According to (Sarwar et al., 2001), the nearest

neighbor algorithms exhibit poor performance with

large and sparse datasets. However, for datasets that

are not as wide and sparse as the ds-FAR dataset,

these algorithms can exhibit good performance, as in-

dicated by our results.

6 CONCLUSIONS

In this paper, we proposed a strategy for proﬁling and

then recommending activities to students with learn-

ing difﬁculties in computer programming. The per-

sonalized recommendations give each individual stu-

dent speciﬁc suggestions to improve their learning ex-

perience by performing additional individualized ac-

tivities.

The comparison of the results obtained with the

recommendation system and that produced by an ex-

pert revealed that the system was able to imitate the

human expert up to 90.0% of the times. This ﬁnding

also showed that we can greatly reduce the effort of

the instructor through the use of this approach. More-

over, the students would beneﬁt the most because

they would have additional prompt support through-

out their learning process. In future work, we plan to

apply this strategy to a larger audience and to more

classes to further analyze the behavior and the quality

of the algorithm.

REFERENCES

Baeza-Yates, R. and Ribeiro-Neto, B. (2011). Modern In-

formation Retrieval. Addison-Wesley, New York, 2

edition.

Bawden, D. and Robinson, L. (2009). The Dark Side of

Information: Overload, Anxiety and other Paradoxes

and Pathologies. J. Inf. Sci., 35(2):180–191.

Baylari, A. and Montazer, G. (2009). Design a Personalized

e-Learning System Based on Item Response Theory

RecommendingtheRightActivitiesbasedontheNeedsofeachStudent

189

and Artiﬁcial Neural Network Approach. Expert Sys-

tems with Applications, 36(4):8013 – 8021.

Chen, R.-C., Huang, Y.-H., Bau, C.-T., and Chen, S.-M.

(2012). A Recommendation System Based on Domain

Ontology and SWRL for Anti-Diabetic Drugs Selec-

tion. Expert Systems with Applications, 39(4):3995 –

4006.

Drachsler, H., Hummel, H. G. K., and Koper, R. (2009).

Identifying the Goal, User Model and Conditions

of Recommender Systems for Formal and Informal

Learning. J. Digit. Inf., 10(2).

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pat-

tern Classiﬁcation. Wiley-Interscience, New York,

2nd edition.

Hao, X., Tao, X., Zhang, C., and Hu, Y. (2007). An Effec-

tive Method to Improve kNN Text Classiﬁer. In Eighth

ACIS International Conference on Software Engineer-

ing, Artiﬁcial Intelligence, Networking, and Paral-

lel/Distributed Computing, volume 1, pages 379–384.

Herlocker, J. L., Konstan, J. A., Borchers, A., and Riedl,

J. (1999). An Algorithmic Framework for Perform-

ing Collaborative Filtering. In 22nd International

ACM SIGIR Conference on Research and Develop-

ment in Information Retrieval, SIGIR ’99, pages 230–

237, Berkeley, California, USA. ACM.

Klašnja-Mili

cevi

c, A., Vesin, B., Ivanovi

c, M., and Budi-

mac, Z. (2011). E-Learning Personalization Based on

Hybrid Recommendation Strategy and Learning Style

Identiﬁcation. Computers & Education, 56(3):885 –

899.

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix Factor-

ization Techniques for Recommender Systems. Com-

puter, 42(8):30–37.

Linden, G., Smith, B., and York, J. (2003). Amazon.com

Recommendations: Item-To-Item Collaborative Fil-

tering. Internet Computing, IEEE, 7(1):76 – 80.

Lops, P., Gemmis, M., and Semeraro, G. (2011). Content-

based Recommender Systems: State of the Art and

Trends. In Ricci, F., Rokach, L., Shapira, B., and Kan-

tor, P. B., editors, Recommender Systems Handbook,

pages 73–105. Springer US.

Manouselis, N., Drachsler, H., Vuorikari, R., Hummel, H.,

and Koper, R. (2011). Recommender Systems in

Technology Enhanced Learning. In Ricci, F., Rokach,

L., Shapira, B., and Kantor, P. B., editors, Recom-

mender Systems Handbook, pages 387–415. Springer

US.

Manouselis, N., Vuorikari, R., and Van Assche, F. (2010).

Collaborative Recommendation of e-Learning Re-

sources: an Experimental Investigation. Journal of

Computer Assisted Learning, 26(4):227–242.

Meisamshabanpoor and Mahdavi, M. (2012). Imple-

mentation of a Recommender System on Medical

Recognition and Treatment. International Journal

of e-Education, e-Business, e-Management and e-

Learning, 2(4):315–318.

Park, D. H., Kim, H. K., Choi, I. Y., and Kim, J. K. (2012).

A Literature Review and Classiﬁcation of Recom-

mender Systems Research. Expert Systems with Ap-

plications, 39(11):10059–10072.

Pea, R. D. and Kurland, D. (1984). On the Cognitive Effects

of Learning Computer Programming. New Ideas in

Psychology, 2(2):137 – 168.

Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2001).

Item-Based Collaborative Filtering Recommendation

Algorithms. In Proceedings of the 10th international

conference on World Wide Web, WWW ’01, pages

285–295, New York, NY, USA. ACM.

Soucy, P. and Mineau, G. W. (2001). A Simple KNN Algo-

rithm for Text Categorization. In ICDM ’01: Proceed-

ings of the 2001 IEEE International Conference on

Data Mining, pages 647–648, Washington, DC, USA.

IEEE Computer Society.

Tsai, C.-F. and Hung, C. (2012). Cluster Ensembles in Col-

laborative Filtering Recommendation. Applied Soft

Computing, 12(4):1417–1425.

Ujjin, S. and Bentley, P. (2002). Learning User Preferences

Using Evolution. Proceedings of the 4th Asia-Paciﬁc

Conference on Simulated Evolution and Learning,

Singapore.

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

190