
Bayesian versus Neural Network Analysis of Algae Data Population
A New Method to Predict and Analyse Cause and Effect
Jen J. Lee
1
, Jorge A. Achcar
2
, Emílio A. C. Barros
3
and Carlos D. Maciel
1
1
Signal Processing Laboratory, University of São Paulo (USP), São Carlos, Brazil
2
Social Medicine Department, University of São Paulo (USP), Ribeirão Preto, Brazil
3
Statistics Department, Maringá State University (UEM), Maringá, Brazil
Keywords: Algae, Bayes, Neural Network, Population, Machine Learning.
Abstract: In biology, advanced modelling techniques are needed since there is a mixture of qualitative, linguistics and
numerical data on the environmental and biological relationships. Also, experiments and data collecting are
expensive and time consuming, so determine which variables are relevant and using inference models less
data demanding are highly desirable. In this work, from a set of 200 multivariate data samples of algae
population and environmental variables, we propose a Bayesian method to predict compositional population
distribution. This is a good application example, since measuring environmental variables are easier to
automate, faster and less expensive than population counting that usually involves the need of a large
amount of specialized human interaction. An additive log-ratio transformation and a regression model were
applied to the data and 255.000 Gibbs samples were simulated using the OPENBUGS software. Also an
Artificial Neural Network (ANN) was designed on Matlab to predict the distribution for benchmarking
purposes. Both models showed similar prediction performance, but on the Bayesian model an analysis of
credible interval of the variables corresponding to the each regression parameters is possible, showing that
most of the variables on this study are relevant, which is consistent to the expected results in this case.
1 INTRODUCTION
The geographic region, anthropomorphic impacts
but mainly hydrology, gives to aquatic environments
great heterogeneity, especially regarding to the
concentrations of nutrients and abundance of
organisms (López-Flores et al., 2011).
Currently, it's clear that subtle variations in
nutrient levels and chemical balance from farming
land run-off and waste from sewage treatment have
serious effects, even if indirect, in the state of rivers,
lakes and even the ocean. The summers of temperate
climates around the world are characterized by
numerous reports of seasonal algal overgrowth,
resulting in poor water clarity, massive deaths of fish
from reduced oxygen levels and the closure of
recreational water facilities because of toxic effects
from algae (Univesity of California - Irvine, 1999).
However, algae, when maintained in controlled
processes, can be used for carbon sequestration,
production of biomass, oils, compounds of interest
for the industry and act as biological indicators, such
as diatoms, that have a high sensitivity in small
changes in acidity of its environment.
The need to reduce human impact on our waters
and make use of algae on controllable processes has
stimulated numerous researches, mainly in the field
of biology with the goal of identifying the crucial
variables for chemical control in biological
processes. That said, the relationship between
chemical and biological characteristics is complex
and the need for advanced modeling techniques is
expected, especially when using data containing, in
addition to the great number of variables, the
mixture of qualitative (fuzzy), linguistic and
numerical information. It is important to note that, in
biological processes, conducting experiments and/or
collecting samples probably has a great cost of time
and resources to be made and samples are often
incomplete or inconsistent, therefore, little data may
be available, affecting inference methods and
analysis that are based solely on a large amount of
data.
Regardless of the approach one takes to statistics,
the process of statistics involves (1) formulating a
research question, (2) collecting data, (3) developing
a probability model for the data, (4) estimating the
482
J. Lee J., A. Achcar J., A. C. Barros E. and D. Maciel C..
Bayesian versus Neural Network Analysis of Algae Data Population - A New Method to Predict and Analyse Cause and Effect.
DOI: 10.5220/0004552304820488
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 482-488
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
model, and (5) summarizing the results in an
appropriate fashion to answer the research question
(a process often called “statistical inference”)
(Lynch, 2007).
At this work we suggest the use of a Bayesian
model for multivariate compositional processing of
data collected in European rivers to create a model
for inference of population distribution of algae that
have quantitative (concentrations of chemical
compounds, pH, etc.) and qualitative (season, etc.)
variables. We also propose a method to identify the
variables that cause the most significant effects on
this population distribution. The performance of
Bayesian inference model was also compared to an
Artificial Neural Network.
On section 2 we describe the data and the pre-
processing method used to prepare the variables and
the compositional data to analysis, on section 3 the
Bayesian model is described and the results of this
analysis are presented, on section 4 the Artificial
Neural Network design is described and on section 5
there is a comparison of performance between the
two prediction models, finally on section 6 the
conclusions are discussed.
2 DATA SAMPLES
The data used in this paper are the results of a
research on river water quality, where samples were
taken from different European rivers over a period
of approximately one year. These samples were
analyzed for several variables as nitrogen in the
form of nitrates, nitrites and ammonium, phosphates,
pH, oxygen, chloride. In parallel, algae population
distributions from these samples were determined.
Although chemical analysis is relatively inexpensive
and easily automated, biological analysis involves
the examination under a microscope, requiring
trained manpower and is usually expensive and very
slow.
The data set contains 200 samples, where the
first 11 values are: season of the year (winter,
spring, autumn or summer), river size (small,
medium or large), water speed (low, medium or
high) and 8 chemical concentrations (according to
Table 1). These variables are known to be relevant
to the algae species population distribution.
The last 7 columns represent the distribution of
different types of algae (according to Table 2), and
these do not represent the entire population of algae
in the medium, some of the species were omitted.
The data, kindly donated by prof. Jens Strackeljan
from Otto von Guericke University Magdeburg
(OVGU), do not indicate which components are
represented by each chemical concentration column
and neither which algae species are presented in the
distribution of population. Also, the location and
date of the samples were not disclosed for public as
well. For modeling purposes these characteristics do
not affect the result.
2.1 Data Pre-processing
The data were described as a representation of
population distribution (Univesity of California -
Irvine, 1999), therefore a restriction was added to
the analysis and data in one additional column was
created to represent the complement of the
population distribution, i.e. for each row of Table 2 a
field was added with the value of 100%
.01.02⋯.07, characterizing
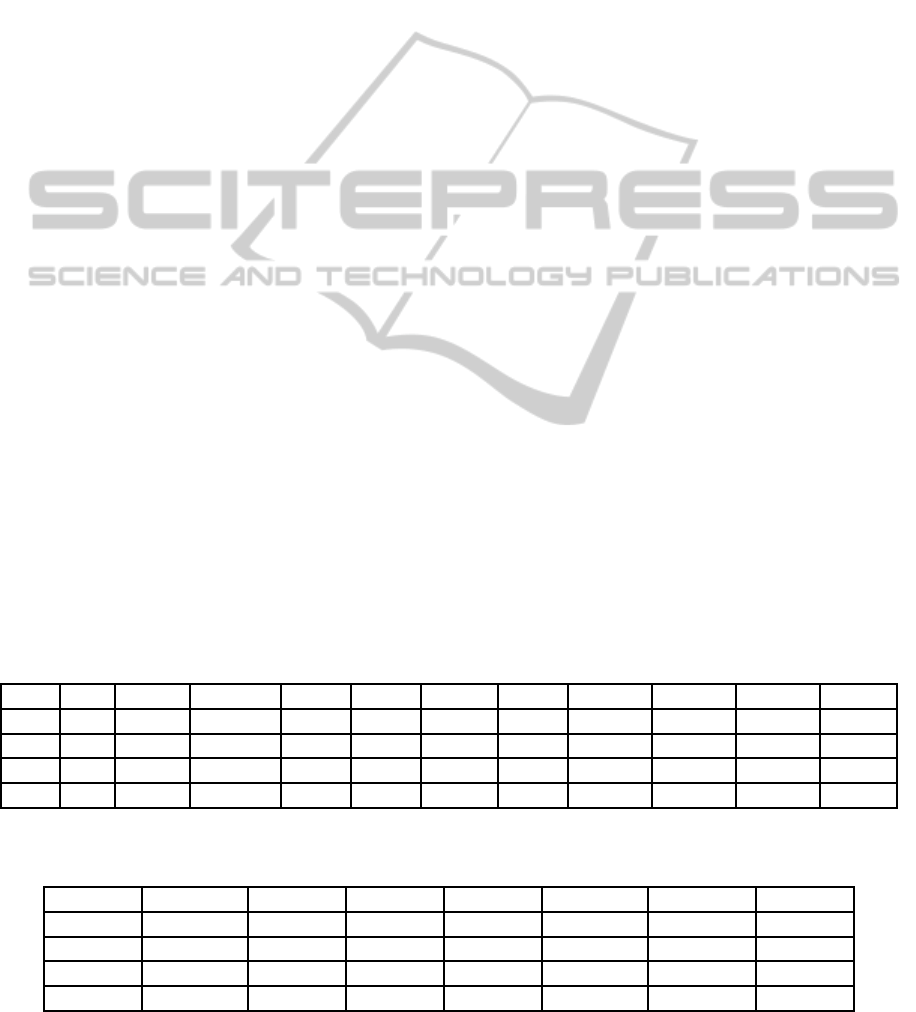
Table 1: Relevant variables related to algae population distribution; 3 of 200 samples shown by lines, 3 qualitative variables
(Season, River Size and Water Speed) and 8 numerical variables (Concentrations 1 to 8).
Sample Season River Size Water Speed Conc. 01 Conc. 02 Conc. 03 Conc. 04 Conc. 05 Conc. 06 Conc. 07 Conc. 08
1
winter small_ medium 8.000.000 9.800.000 60.800.000 6.238.000 578.000.000 105.000.000 170.000.000 50.000.000
2
spring small_ medium 8.350.000 8.000.000 57.750.000 1.288.000 370.000.000 428.750.000 558.750.000 1.300.000
...
... ... ... ... ... ... ... ... ... ... ...
200
winter small_ high__ 7.740.000 9.600.000 5.000.000 1.223.000 27.286.000 12.000.000 17.000.000 41.000.000
Table 2: Algae species population distribution is the target values for each set of variables related to Table 1; 3 of 200
samples shown by lines of 7 species each sample.
Amostra Pop. 01 Pop. 02 Pop. 03 Pop. 04 Pop. 05 Pop. 06 Pop. 07
1
0.000000 0.000000 0.000000 0.000000 34.200.000 8.300.000 0.000000
2
1.400.000 7.600.000 4.800.000 1.900.000 6.700.000 0.000000 2.100.000
...
... ... ... ... ... ... ...
200
43.500.000 0.000000 2.100.000 0.000000 1.200.000 0.000000 2.100.000
BayesianversusNeuralNetworkAnalysisofAlgaeDataPopulation-ANewMethodtoPredictandAnalyseCauseand
Effect
483

the database as compositional according to Table 3.
To simplify the model development, after pre-
processing the data, 16 samples were identified as
incomplete or inconsistent and were excluded from
the database. Therefore 167 samples were used in
this study. For the inclusion of qualitative variables
(Season, River Size and Water Speed) the linguistic
data were replaced by a binary (0 or 1) variable,
when all values in a category are 0, it represents the
item that has not a column for itself (Table 4).
Therefore we have in this system, for each
sample, 15 input variables and 8 target values.
3 COMPOSITIONAL DATA
BAYESIAN ANALYSIS
Compositional data are vectors of proportions
specifying fractions as a whole. Thus, for
,
,…,
’ to be a compositional vector, we
must have
0, for i 1,…,G and
…
1. Compositional data often result when
raw data are normalized or when data is obtained as
proportions of a certain heterogeneous quantity.
These conditions are usual in geology, economics
and biology. Standard existing methods to analyze
multivariate data under the usual assumption of
multivariate normal distribution (see for example,
Johnson and Wichern, 1998) are not appropriate to
analyze compositional data, since we have
compositional restrictions. Different modeling
systems have been considered to analyze
compositional data. A first model considered to
analyze this kind of data is given by the Dirichlet
distribution, but this model requires that the
correlation structure is wholly negative, a fact not
observed for compositional data where some
correlations are positive (see for example, Aitchison,
(1982); or Aitchison, (1986)).
Aitchison and Shen (1980) introduced the
lognormal distribution to analyze compositional
data, transforming the component vector to a
vector in
considering the additive log-ratio
(ALR) function. Rayens and Srinivasan (1991a)
(1991b) extended the ALR transformation
considering Box-Cox transformations as a
generalization of the log-ratio function. Usually we
could have some difficulties to get classical
inference results for these models, especially in the
presence of a vector of covariates. Alternatively, the
use of Bayesian methods (Gelfand et al., 1995) is a
good alternative to analyse compositional data (see
for example, Iyengar and Dey, (1996), (1998); or
Tjelmeland and Lund, (2003)), especially
considering Markov Chain Monte Carlo (MCMC)
methods (see for example, Gelfand and Smith,
(1990) or Roberts and Smith, (1993)) to simulate
samples of the joint posterior distribution of interest.
In our application we have eight compositions
(see Table 3), that is,
1, for i=1,...,167. Let
us assume an additive log-ratio (ALR)
transformation for the compositional data (see for
example, Aitchison (1982), (1986) and Iyengar &
Dey (1996) given by
(1)
where j1,2,...,7 and i1,2,...,167.
3.1 Model
To model the compositional data of Table 3 with
Table 4 and the additive log-ratio (ALR)
transformation
, let us assume the regression
models (see for example, Iyengar and Dey (1996)
Table 3: Complementary population data added to database as Pop. 08 and 16 inconsistent samples removed.
Sample Pop. 01 Pop. 02 Pop. 03 Pop. 04 Pop. 05 Pop. 06 Pop. 07 Pop. 08
1 0.000000 0.000000 0.000000 0.000000 34.200.000 8.300.000 0.000000 57.50
2 1.400.000 7.600.000 4.800.000 1.900.000 6.700.000 0.000000 2.100.000 75.50
... ... ... ... ... ... ... ... ...
167 43.500.000 0.000000 2.100.000 0.000000 1.200.000 0.000000 2.100.000 51.10
Table 4: Qualitative variables data conversion for numerical input in statistical the model.
Season of the year River size Water speed
Sample Winter Spring Autumn Medium Large Medium High Conc. 01 Conc. 02 ... Conc. 08
1
1 0 0 0 0 1 0 8.000.000 9.800.000 ... 50.000.000
2
0 1 0 0 0 1 0 8.350.000 8.000.000 ... 1.300.000
...
... ... ... ... ... ... ... ... ... ... ...
167
1 0 0 0 0 0 1 7.740.000 9.600.000 ... 41.000.000
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
484

and (1998)) given by:
α
α
∗winter
α
∗spring
α
∗autumn
α
∗medium.river
α
∗large.river
α
∗
medium.speed
α
∗high.speed
α
∗conc.01
α
∗conc.02
α
∗
conc.03
α
∗conc.04
α
∗
conc.05
α
∗conc.06
α
∗
conc.07
α
∗conc.08
Є
(2)
where j1,2,...,7 and i1,2,...,167; winter
i
,
spring
i
, autumn
i
, medium.river
i
, large.river
i
,
medium.speed
i
, high.speed
i
, conc.01
i
, conc.02
i
,
conc.03
i
, conc.04
i
, conc.05
i
, conc.06
i
, conc.07
i
and
conc.08
i
correspond to a vector of covariates
associated to the i-th sample and ε
ji
are random
errors assumed to be independent random variables
with a normal distribution N0,σ
.
For a Bayesian analysis of the model, we assume
the following prior distributions for the parameters:
α
~Na
,b
(3)
α
~Na
,b
ζ
~
,
where ζ
1 σ
⁄
, , denotes a gamma
distribution with mean / and variance /
; a
,
b
, a
, b
,
and
are known hyper parameters,
j 1,…,7.
Let us denote the model defined by (1), (2) and
(3) as “model 1”.
3.2 Bayesian Analysis for the Data of
Table 4
BUGS is an acronym for a class of software package
designed to perform Bayesian inference Using
Gibbs Sampling Algorithm. The user specifies a
statistical model by simply stating the relationships
between related variables. The software includes an
‘expert system’, which determines an appropriate
MCMC (Markov Chain Monte Carlo) scheme
(based on the Gibbs sampler) for analysing the
specified model. It woks assuming that the specified
model belongs to a class known as Directed Acyclic
Graphs (DAGs), for which there exists an elegant
underlying mathematical theory. This allows us to
break down the analysis of arbitrarily large and
complex structures into a sequence of relatively
simple computations. BUGS includes a range of
algorithms that its expert system can assign to each
such computational task. (OpenBUGS, 2009).
Usually, BUGS written software code have the
following components:
Model parameters;
Specification of the “likelihood function” (or
“sampling density”) of the data;
Specification of a “prior distribution” for the
model parameters;
Derivation of the “posterior distribution” for the
model parameters;
Samples variables inputs and outputs to use as
simulation parameters.
Assuming the additive log-ratio model defined by
(2) and the prior distributions (3), with hyper
parameter values; a
1
, b
=10
, a
1
,
b
10,
1 and
1, we simulated 255,000
Gibbs samples using the OpenBUGS software where
the first 5,000 simulated samples of the joint
posterior distribution of interest were discarded to
eliminate the effects of the initial values; after this
“burn-in-sample” period, we considered every 50
th
sample among the 250,000 simulated Gibbs
samples, which gives a final sample of size 5,000 to
get the posterior summaries of interest. Convergence
of the simulation algorithm was verified from trace
plots of the simulated Gibbs samples.
In Table 5, we have the posterior summaries for
the parameters of “model 1” based on these 5,000
final simulated Gibbs samples. The terms marked
with asterisks in Table 5 show the variables that do
not have a zero value included in their credible
intervals corresponding to their regression
parameters indicating the variables that have a
significant effect in determining the population
distribution.
Table 5: Posterior summaries of “model 1” after
simulation.
mean SD val2.5pc Median val97.5pc
α10 -0.69 5.18 -10.72 -0.82 9.70
α11 -0.04 0.75 -1.47 -0.04 1.47
α110 -0.01 0.01 -0.03 -0.01 0.00
α111 -0.13 0.15 -0.42 -0.13 0.17
α112 0.00 0.00 0.00 0.00 0.00
α113 -0.01 0.01 -0.02 -0.01 0.01
α114 -0.01 0.01 -0.02 -0.01 0.01
α115 (*) -0.03 0.02 -0.07 -0.03 0.00
α116 0.35 0.79 -1.20 0.35 1.84
α13 0.66 0.83 -1.00 0.66 2.29
α14 0.08 0.72 -1.32 0.09 1.45
α15 (*) -2.88 0.90 -4.64 -2.88 -1.12
α16 -1.10 0.85 -2.75 -1.09 0.57
α17 -1.45 0.98 -3.41 -1.44 0.45
α18 0.01 0.65 -1.25 0.02 1.26
α19 0.16 0.15 -0.14 0.17 0.46
α20 (*) -18.39 5.73 -29.72 -18.29 -7.25
α21 -0.08 0.79 -1.66 -0.08 1.43
α210 0.01 0.01 -0.01 0.01 0.02
α211 (*) 0.48 0.16 0.17 0.48 0.79
α212 (*) -0.01 0.00 -0.01 -0.01 0.00
α213 0.01 0.01 -0.01 0.01 0.03
α214 0.00 0.01 -0.02 0.00 0.01
α215(*) 0.04 0.02 0.01 0.04 0.08
BayesianversusNeuralNetworkAnalysisofAlgaeDataPopulation-ANewMethodtoPredictandAnalyseCauseand
Effect
485

Table 5: Posterior summaries of “model 1” after
simulation (cont.).
mean SD val2.5pc Median val97.5pc
α22 -0.43 0.84 -2.09 -0.42 1.20
α23 0.23 0.88 -1.50 0.24 1.98
α24 0.30 0.76 -1.17 0.30 1.82
α25 1.11 0.96 -0.79 1.10 2.96
α26 0.80 0.93 -1.04 0.79 2.59
α27 -0.38 1.07 -2.50 -0.38 1.71
α28 (*) 1.40 0.71 0.05 1.40 2.84
α29 -0.05 0.17 -0.38 -0.05 0.28
α30 -5.23 5.66 -15.70 -5.50 6.23
α31 -0.36 0.83 -1.96 -0.36 1.24
α310 -0.362 0.01 -0.02 -0.355 0.02
α311 0.25 0.16 -0.08 0.24 0.57
α312(*) -0.01 0.00 -0.01 -0.01 0.00
α313 -0.02 0.01 -0.04 -0.02 0.00
α314(*) 0.02 0.01 0.00 0.02 0.04
α315 -0.02 0.02 -0.06 -0.02 0.01
α32 0.22 0.87 -1.49 0.22 1.95
α33 0.46 0.93 -1.35 0.47 2.28
α34 0.77 0.79 -0.75 0.78 2.33
α35 0.95 0.99 -0.98 0.96 2.90
α36 1.03 0.94 -0.78 1.03 2.87
α37 2.03 1.10 -0.13 2.04 4.13
α38 0.19 0.70 -1.22 0.21 1.53
α39(*) -0.44 0.17 -0.78 -0.44 -0.11
α40 6.57 5.24 -3.44 6.48 16.77
α41(*) 1.45 0.72 0.03 1.46 2.87
α410 0.01 0.01 0.00 0.01 0.02
α411 -0.47 0.14 -0.75 -0.47 -0.20
α412(*) 0.01 0.00 0.00 0.01 0.01
α413(*) -0.03 0.01 -0.04 -0.03 -0.01
α414(*) 0.02 0.01 0.00 0.02 0.03
α415 -0.03 0.02 -0.06 -0.03 0.00
α42 0.95 0.75 -0.55 0.95 2.43
α43 0.65 0.80 -0.96 0.64 2.22
α44 0.67 0.67 -0.61 0.67 2.00
α45 -0.68 0.88 -2.38 -0.68 1.09
α46 1.38 0.82 -0.22 1.37 3.02
α47 1.73 0.95 -0.13 1.73 3.61
α48(*) -1.68 0.65 -2.94 -1.67 -0.40
α49(*) -0.30 0.15 -0.59 -0.31 0.00
α50 -8.65 5.28 -19.21 -8.65 1.82
α51 -0.75 0.79 -2.27 -0.75 0.79
α510 0.00 0.01 -0.01 0.00 0.02
α511(*) 0.50 0.16 0.19 0.49 0.81
α512 0.00 0.00 0.00 0.00 0.00
α513 -0.454 0.01 -0.02 -0.404 0.02
α514 0.01 0.01 -0.01 0.01 0.02
α515(*) -0.05 0.02 -0.08 -0.05 -0.01
α52 -0.55 0.84 -2.20 -0.56 1.09
α53 0.52 0.88 -1.29 0.52 2.22
α54(*) 1.93 0.76 0.49 1.94 3.44
α55 0.35 0.96 -1.50 0.34 2.24
α56 0.79 0.90 -0.98 0.80 2.53
α57 0.79 1.05 -1.30 0.80 2.86
α58 -0.21 0.66 -1.54 -0.21 1.12
α59 0.21 0.16 -0.12 0.21 0.51
α60 -7.50 5.83 -18.81 -7.50 3.97
α61 -1.46 0.85 -3.12 -1.45 0.20
α610 0.00 0.01 -0.02 0.00 0.01
α611(*) 0.53 0.17 0.21 0.53 0.87
α612 0.00 0.00 0.00 0.00 0.01
α613 -0.01 0.01 -0.03 -0.01 0.01
α614 0.01 0.01 -0.01 0.01 0.03
α615 0.00 0.02 -0.04 0.00 0.03
α62 -1.33 0.89 -3.04 -1.35 0.44
α63 0.04 0.96 -1.83 0.06 1.84
α64(*) 1.95 0.81 0.38 1.95 3.54
α65 1.95 1.03 -0.06 1.95 3.98
α66(*) 2.35 0.97 0.42 2.34 4.27
α67(*) 2.82 1.15 0.54 2.83 5.11
α68 -1.15 0.74 -2.60 -1.17 0.31
α69(*) 0.52 0.18 0.15 0.52 0.86
α70 2.43 5.95 -9.29 2.52 13.86
α71 -0.07 0.88 -1.80 -0.08 1.67
α710 -0.01 0.01 -0.03 -0.01 0.00
α711 0.17 0.17 -0.15 0.17 0.50
α712 0.994 0.00 0.00 0.00 0.00
α713 -0.01 0.01 -0.03 -0.01 0.01
α714 0.01 0.01 -0.01 0.01 0.03
Table 5: Posterior summaries of “model 1” after
simulation (cont.).
mean SD val2.5pc Median val97.5pc
α715(*) 0.05 0.02 0.02 0.05 0.09
α72 0.33 0.92 -1.45 0.31 2.15
α73 -0.11 0.97 -2.05 -0.10 1.80
α74 0.31 0.82 -1.29 0.31 1.93
α75 0.42 1.04 -1.62 0.41 2.48
α76 0.73 0.98 -1.22 0.73 2.68
α77 0.54 1.14 -1.65 0.53 2.74
α78 -1.43 0.74 -2.87 -1.43 0.10
α79 -0.02 0.18 -0.38 -0.02 0.33
The list of significant variables in Table 6 shows
that only variable Conc. 3 is low significant. The
seasons (Spring and Autumn), the size of the river
(small) and the speed of the river (low), despite
having the value 0 in the credible interval, have
terms that compose the variable without the term 0
in the credible interval (Summer, Winter, Large), so
they are also significant.
Table 6: Posterior summaries indicating significant
variables.
Term Related variable
α115 Conc. 8
α15 Size: Large
α20 Season: Summer
α211 Conc. 4
α212 Conc. 5
α215 Conc. 8
α28 Conc. 1
α312 Conc. 5
α314 Conc. 7
α39 Conc. 2
α41 Season: Winter
α411 Conc. 4
α412 Conc. 5
α413 Conc. 6
α414 Conc. 7
α48 Conc. 1
α49 Conc. 2
α511 Conc. 4
α515 Conc. 8
α54 Size: medium
α611 Conc. 4
α64 Size: medium
α66 Speed: medium
α67 Speed: High
α69 Conc. 2
α715 Conc. 8
4 ARTIFICIAL NEURAL
NETWORK
Like its counterpart in the biological nervous
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
486

system, a neural network can learn and therefore can
be trained to find solutions, recognize patterns,
classify data, and forecast future events. The
behavior of a neural network is defined by the way
its individual computing elements are connected and
by the strengths of those connections, or weights.
The weights are automatically adjusted by training
the network according to a specified learning rule
until it performs the desired task correctly (The
MathWorks, Inc., 1994-2013). According to da
Silva, et al. (2010) the Artificial Neural Networks
(ANN) is a popular choice to solve biological
problems and have works published over the
following topics:
Bat species identification from biosonar data;
Cancer prediction based on individuals genetic
profiles;
Analyse weather influence over the grow rate of
trees.
An ANN approach was applied to this problem
using a supervised network that was designed as a
two-layer feed-forward network with sigmoid
hidden neurons and linear output neurons. The
network was trained with Levenberg-Marquardt
backpropagation algorithm. The Neural Network
Toolbox (nnstart) from MatLab R2012b was used to
create the network with the topology presented in
Figure 1 as a Fitting problem.
Figure 1: Neural Network (n=15 inputs, n
1
=12 hidden
neurons and m=8 outputs). Adapted from: (da Silva et al.,
2010).
5 PERFORMANCE
COMPARISON
The inferred data were compared with the observed
data using the ratio:
|
|
, where
is the
population observed value and e
the output value
of the inference where 1,…,167.
Figure 2: Linear tendency lines of means of all 167 samples from |Expected - Inferred| from each population.
Table 7: Maximum, Mean and Standard Deviation values for each population of calculated ratios
|
|
,
where
is the
observed value and e
the output value of the parameterized Bayesian inference where
1,…,167.
Pop. 01 Pop. 02 Pop. 03 Pop. 04 Pop. 05 Pop. 06 Pop. 07
Max: 74.860000 70.501000 42.320600 38.680000 42.903000 50.782000 31.1506
Mean: 4.400000 2.940900 4.163577 0.084850 2.357600 0.996700 0.825800
SD: 13.847888 11.291766 6.209362 3.301484 7.728617 9.002339 5.766513
Table 8: Maximum, Mean and Standard Deviation values for each population of calculated ratios
|
|
, where
is the
observed value and e
the output value of the Neural Network where
1,…,167.
Pop. 01 Pop. 02 Pop. 03 Pop. 04 Pop. 05 Pop. 06 Pop. 07
Max:
58.54958 45.93419 39.78041 9.130595 33.92973 36.03939 27.6264
Mean:
10.08046 7.251721 4.794875 1.405569 4.301284 5.668362 3.439153
SD:
10.83919 6.984214 5.140308 1.474641 4.97424 5.378425 4.046496
0,00
2,00
4,00
6,00
8,00
10,00
12,00
012345678
Mean of ratio
Population
Bayesian
ANN
Linear (Bayesian)
Linear (ANN)
BayesianversusNeuralNetworkAnalysisofAlgaeDataPopulation-ANewMethodtoPredictandAnalyseCauseand
Effect
487

For each population ratio column the maximum
value, the mean and the standard deviation were
extracted and are presented in Table 7 and Table 8.
The prediction performance of the Bayesian
inference shows a slightly better performance when
we analyze the linear tendency lines of the means of
ratios of each population (Figure 2), since it is lower
in the graph and nearer from 0, although, comparing
Table 7 and Table 8, the Standard Deviation in the
ANN approach is lower. Overall, performance of
both methods is similar.
6 CONCLUSIONS
In this work we provided a complete statistical
analysis method of a complex biological database,
including a method to mixture qualitative and
quantitative data, which can be used in several
inference models. Also, the regression model
associated to the compositional data analysis is a
powerful statistical tool to understand several
biological population data.
The Bayesian method may be improved and
other prior distributions for the parameters and/or
other error distributions in (2) can be used for a
better prediction performance. The ability to
evaluate the significance of each variable is an
important tool to maximize experiments resources
and understand biological processes. It is expected
with the improvement of the Bayesian inference
method, that less data could be necessary to train the
algorithm to acquire good regression parameters. It
is important to notice that previously knowledge of
the problem can be very useful to model the problem
and determine the best distributions for the
problems.
REFERENCES
Aitchison, J., 1982. The statistical analysis of
compositional data. Journal of the Royal Statistical
Society, pp. p. 139-177.
Aitchison, J., 1986. The statistical analysis of
compositional data. Chapman and Hall.
Aitchison, J. & Shen, S. M., 1980. Logistic-normal
distributions: Some properties and uses. Biometrika,
Issue 67, pp. 261-272.
da Silva, I. N., Spatti, D. H. & Flauzino, R. A., 2010.
Redes Neurais Artificiais para engenharia e ciências
aplicadas. I ed. São Paulo: ArtLiber.
Gelfand, A. E., Carlin, J. B., Stern, H. S. & Rubin, D. B.,
1995. Bayesian Data Analysis. Issue 85, pp. 398-409.
Gelfand, A. E. & Smith, A. F. M., 1990. Sampling based
approaches to calculating marginal densities. Journal
of the American Statistical Association, Issue 85, pp.
398-409.
Iyengar, M. & Dey, D. K., 1996. Bayesian Analysis of
Compositional Data. Department of Statistics,
University of Connecticut, Storrs, CT.
Iyengar, M. & Dey, D. K., 1998. Box-Cox transformations
in Bayesian analysis of compositional data.
Environmetrics, Issue 9, pp. 657-671.
López-Flores, R., Romaní, A. M. & Quintana, X. D.,
2011. Phytoplankton composition in shallow water
ecosystems: influence of environmental gradients and
nutrient availability, In 4
th
international Workshop on
Compositional Data Analysis.
Lynch, S. M., 2007. Introduction to Applied Bayesian
Statistics and Estimation for Social Scientists.
s.l.:Springer .
OpenBUGS, 2009. OpenBUGS, accessed 10 Feb 2013,
<http://www.openbugs.info/w.cgi/FrontPage>.
Rayens, W. S. & Srinivasan, C., 1991a. Box-Cox
transformations in the analysis of compositional data.
Journal of Chemometrics, Issue 5, pp. 227-239.
Rayens, W. S. & Srinivasan, C., 1991b. Estimation in
compositional data. Journal of Chemometrics, Issue 5,
pp. 361-374.
Roberts, G. O. & Smith, A. F. M., 1993. Bayesian
methods via the Gibbs sampler and related Markov
Chain Monte Carlo methods. Journal of the Royal
Statistical Society, 55(1), pp. 3-23.
The MathWorks, Inc., 1994-2013. Neural Network
Toolbox, accessed 20 Jan 2013, <http://
www.mathworks.com/products/neural-network/descri
ption2.html>.
Tjelmeland, H. & Lund, K. V., 2003. Bayesian modelling
of spatial compositional data, preprint n.1. Journal of
Applied Statistics, Issue 30, pp. 87-100.
Univesity of California - Irvine, 1999. COIL 1999
Competition Data, accessed 10 Jul 2013,
<http://kdd.ics.uci.edu/databases/coil/coil.data.html>.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
488
