Multi-objective Scatter Search with External Archive for Portfolio

Optimization

Khin Lwin

, Rong Qu

and Jianhua Zheng

ASAP Research Group, School of Computer Science, University of Nottingham, NG8 1BB, Nottingham, U.K.

School of Computer Science, University of Nottingham, NG8 1BB, Nottingham, U.K.

Keywords:

Evolutionary Multi-objective Portfolio Optimization, Hybrid Metaheuristic, Multi-objective Scatter Search,

Cardinality Constrained Portfolio Selection Problem, Mean-Variance Portfolio Optimization.

Abstract:

The relevant literature showed that many heuristic techniques have been investigated for constrained portfolio

optimization problem but none of these studies presents multi-objective Scatter Search approach. In this work,

we present a hybrid multi-objective population-based evolutionary algorithm based on Scatter Search with

an external archive to solve the constrained portfolio selection problem. We considered the extended mean-

variance portfolio model with three practical constraints which limit the number of assets in a portfolio, restrict

the proportions of assets held in the portfolio and pre-assign speciﬁc assets in the portfolio. The proposed

hybrid metaheuristic algorithm follows the basic structure of the Scatter Search and deﬁnes the reference

set solutions based on Pareto dominance and crowding distance. New Subset generation and combination

methods are proposed to generate efﬁcient and diversiﬁed portfolios. Hill Climbing operation is integrated

to search for improved portfolios. The performance of the proposed multi-objective Scatter Search algorithm

is compared with the Non-dominated Sorting Genetic Algorithm (NSGA-II), Strength Pareto Evolutionary

Algorithm (SPEA-2) and Pareto Envelope-based Selection Algorithm (PESA-II). Experimental results indicate

that the proposed algorithm is a promising approach for solving the constrained portfolio selection problem.

Measurements by the performance metrics indicate that it outperforms NSGA-II, SPEA2 and PESA-II on the

solution quality within a shorter computational time.

1 INTRODUCTION

The portfolio selection problem is concerned with the

optimal allocation of a limited capital among avail-

able risky assets. The mean-variance (MV) model of

Markowitz (Markowitz, 1952) (Markowitz, 1959) is

a single period static portfolio model based on two

criteria: to maximize the reward of a portfolio (mea-

sured by the mean of return), and to minimize the risk

of the portfolio (measured by the variance of return).

It is considered to be the ﬁrst mathematical model that

formalizes the concept of diversiﬁcation and is widely

used in ﬁnance. It helps risk-averse investors to con-

struct desirable portfolios by taking into considera-

tion of the trade-off between risk and expected return.

With the above stated two conﬂicting objectives, the

portfolio selection problem could be considered as a

class of multi-objective optimization problems. As a

consequence, a single unique solution that optimizes

all the conﬂicting objectives hardly exists and instead

there exists a set of solutions which are optimal in

such a way that no other solutions in the search space

are superior to them when all objectives are consid-

ered simultaneously. This set of solutions is known as

non-dominated or Pareto optimal set.

Although Markowitz’s MV model is the funda-

mental theory of Modern Portfolio Theory, direct

application of this model is not of much practical

uses mainly due to the fact that it is simpliﬁed with

unrealistic assumptions. In many practical situa-

tions, constraints such as cardinality, quantity and

pre-assignment constraints are required. The cardi-

nality constraint imposes a limit on the number of as-

sets in the portfolio either to simplify the management

of the portfolio or to reduce transaction costs. The

quantity constraint restricts the proportion of each as-

set in the portfolio to lie between the lower and upper

bounds in order to avoid very small (or large) and un-

realistic holdings. The pre-assignment constraint re-

quires certain asset(s) to be included in the portfolio.

These constraints are hard in the sense that they have

to be satisﬁed at any time. In this work, Markowitz’s

MV model extended with cardinality, quantity and

pre-assignment constraints is studied.

When the basic model is extended with such prac-

tical constraints, the problem transforms to an NP-

Hard problem (Moral-Escudero et al., 2006) and ex-

111

Lwin K., Qu R. and Zheng J..

Multi-objective Scatter Search with External Archive for Portfolio Optimization.

DOI: 10.5220/0004552501110119

In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 111-119

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

act methods are inadequate to solve the problem in an

efﬁcient way. In recent years, several researches have

been conducted applying metaheuristics to the portfo-

lio selection problem with real-world constraints. Al-

though the portfolio selection problem involves two

conﬂicting objectives, many researches in the litera-

ture have been performed with single objective ap-

proaches with aggregating function (Chang et al.,

2000) (Lwin and Qu, 2013). Recently, there are an

increasing number of multi-objective evolutionary ap-

proaches that have been studied. The main advantage

of evolutionary multi-objective portfolio optimization

is that an estimation of the efﬁcient risk-return frontier

can be searched in a single run as opposed to the sin-

gle objective approaches with multiple runs. Several

researches have been conducted to solve the portfo-

lio optimization problem by adopting the evolutionary

multi-objective approach (Branke et al., 2009) (Skol-

padungket et al., 2007).

The aim of this paper is to apply the multi-

objective scatter search to the mean-variance portfo-

lio optimization problem. The rest of the paper is

organized as follows. Section 2 provides the mean-

variance model with cardinality, quantity and pre-

assignment constraints considered in this study. Sec-

tion 3 presents the multi-objective Scatter Search al-

gorithm with external archive and describes the de-

tails of its components. Section 4 is provided with nu-

merical results and conclusion remarks are presented

in Section 5.

2 MULTI-OBJECTIVE

CONSTRAINED PORTFOLIO

OPTIMIZATION

The portfolio optimization problem concerns the

choice of an optimal set of assets to include in the

portfolio and the distribution of investment among

them. In the multi-criteria variant of portfolio opti-

mization problem, the model is usually formalized as

follows:

min f

∑

i=1

∑

j=1

i j

(1)

max f

∑

i=1

(2)

sub ject to

∑

i=1

= 1 (3)

∑

i=1

≤ K, (4)

≤ w

≤ δ

, i = 1, ..., N, (5)

≥ z

, i = 1, ..., N (6)

∈

{

0,1

}

, i = 1, ..., N (7)

∈

{

0,1

}

, i = 1, ..., N (8)

where N is the number of available assets, µ

is the

expected return of asset i (i = 1...N), σ

i j

is the covari-

ance between assets i and j (i = 1...N; j = 1...N), and

(0 ≤ w

≤ 1) is the decision variable which repre-

sents the proportion held of asset i. Eq(3) deﬁnes the

budget constraint (all the money available should be

invested) for a feasible portfolio. K is the maximum

number of invested assets in the portfolio, s

denotes

whether asset i is invested or not, z

denotes a binary

value such that z

is set to one if asset i is included

in the pre-assigned set in the portfolio. If s

equals to

one, asset i is chosen to be invested and the proportion

of capital w

lies in [ε

, δ

], where 0 ≤ ε

≤ δ

≤ 1. Oth-

erwise, asset i is not invested and w

equals to zero.

3 MULTI-OBJECTIVE SCATTER

SEARCH WITH EXTERNAL

ARCHIVE (MOSSwA)

In this paper, a multi-objective Scatter Search with

external archive has been developed for constrained

portfolio selection problem. Scatter Search (SS)

(Glover et al., 2000) is a population based meta-

heuristic that uses sets of solutions called the refer-

ence sets to combine its solutions to construct others.

The method generates reference sets from a popula-

tion of solutions. Then a subset of solutions is se-

lected from the reference sets. The selected solutions

are combined to generate new solutions. The gener-

ated solutions are enhanced by an improvement pro-

cedure. The result of the improved solution can mo-

tivate the updating of the reference sets. The pro-

posed multi-objective Scatter Search with external

archive (MOSSwA) consists of procedures namely,

initial population creation, reference sets formation,

subset generation, solution combination, improve so-

lution, reference set update and archive update. The

detailed procedure of the MOSSwA is provided in

Figure 1.

3.1 Solution Representation

In our solution representation, two vectors of size N

are used to deﬁne a portfolio p: a binary vector s

i = 1,...,N denoting whether asset i is included in the

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

112

Let

NP = number of individuals in the population

M = number of portfolio(s) in the archive

X = number of portfolio(s) in the reference set

A = the archive maintaining the M

non-dominated portfolio(s) found so far

re f 1 = the reference set maintaining the X

non-dominated portfolio(s)

re f 2 = the reference set maintaining the X

least crowded portfolio(s)

Sub = the subset that is used for generating

new trial solutions

t pop = list of portfolios in the trial population

r[x,y] = uniform random real-value between x

and y inclusive

portfolio, and a real-value vector w

, i = 1,...,N rep-

resenting the proportions of the capital invested in the

assets.

3.2 Initial Population Generation

Method

To generate a trial initial population, maximum K

different indexes (including all assets in the pre-

assignment subset) are randomly selected and propor-

tions are assigned to those selected assets randomly.

If the generated portfolio violates the budget and/or

quantity constraints, such solution is corrected by the

constraint handling techniques provided in Section

3.9. Hence, all generated solutions in the trial pop-

ulation are feasible.

3.3 Reference Set Formation

The reference sets are initialized from an initial pop-

ulation composed of random solutions and they are

updated by the improved and diverse solutions. Two

reference sets are maintained: ref1 and ref2. The

ref1 and ref2 sets maintain the best solutions and the

least crowded solutions from the archive (A) and the

trial population(t pop) by Pareto optimal (Fonseca and

Fleming, 1995) and the crowding distance (Deb et al.,

2002) concepts respectively.

A solution a is efﬁcient (i.e., Pareto optimal) if

there does not exist any solution b such that b domi-

nates a. Solution a is considered to dominate solution

b if and only if:

(a) ≤ f

(b) AND f

(a) > f

(b)

(a) ≥ f

(b) AND f

(a) < f

(b)

Pseudocode: MOSSwA

BEGIN

INITIALIZATION:

for each portfolio p

, j := 1 to NP do

t pop ← randomly generate an individual with pre-

assigned asset(s) included; (if infeasible)

repair by constraint handling techniques

(see Section-3.9)

end for

Repeat until certain number of generations

ARCHIVE:

A ← update archive with M non-dominated

portfolio(s) found so far

REF SET:

re f 1 ← select the X non-dominated portfolio(s) from

archive A

re f 2 ← select the X non-redundant and least crowded

portfolio(s) from the remaining set of

portfolios in archive A and from t pop

(see Section-3.8)

for j := 1 to NP do

SUBSET:

Sub ← select random |Sub| portfolio(s) from

re f 1 and/or re f 2

COMBINE:

for i := 1 to |Sub| −1 do

randomly select three portfolios from Sub

← generate a new portfolio with combination

method (see Section-3.5); (if infeasible)

repair by constraint handling techniques

end for

IMPROVE:

new

← perform local search on p

for certain number of moves

if p

dominates p

new

t pop ← p

else if p

new

dominates p

t pop ← p

new

else

t pop ← p

new

; t pop ← p

end if

end for

END

Figure 1: Pseudocode of the proposed MOSSwA.

The crowding distance is used to measure the ap-

proximate density of solutions toward each other in a

population. The crowding distance of a portfolio p is

calculated by taking the average distance of the two

portfolios taken one from either side of p (Deb et al.,

2002).

Multi-objectiveScatterSearchwithExternalArchiveforPortfolioOptimization

113

3.4 Subset Generation Method

This method selects a subset of solutions from the ref-

erence set to create a subset (Sub). This generated

subset (Sub) will later be used in solution combina-

tion method to produce new solutions. Our approach

generates the subset by three different variants as fol-

lows:

1. randomly select X solutions from re f 1.

2. randomly select X solutions from re f 2.

3. randomly select arbitrary R solutions from re f 1

and X −R solutions from re f 2 where R ≤ X.

3.5 Solution Combination Method

This method uses the generated subset Sub (see Sec-

tion 3.4) and combines solutions from Sub and returns

one or more trial solutions. In ﬁnance literature, it is

considered to be a fundamental premise to utilize as-

sets that have low correlation with each other. Hence

the assets which are less correlated to each other are

preferable to the heavily correlated assets. It is also

commonly believed that it is beneﬁcial to reduce the

portfolio’s standard deviation of return. Intuitively,

investors prefer higher return assets with less risk.

By taking into accounts of the above stated intu-

itive appeal, in this work, we propose three problem-

speciﬁc combination mechanisms for the constrained

portfolio selection problem as follows: Three portfo-

lios (p1, p2 and p3) from subset Sub are selected to

use in the combination mechanism. The assets se-

lected in these three portfolios are observed and anal-

ysed. The set potential is constructed by inserting all

the indexes of assets which are selected in at least two

out of the three portfolios. A new portfolio is then

constructed by selecting random n indexes of assets

in potential set where n ≤ K. Like the DE offspring

generation scheme investigated in (Robi

c and Filipi

2005), the proportion w of those selected assets for

the new solution are assigned as follows:

:= w3

+ r[0, 1] × (w1

− w2

)

The remaining assets of the new portfolio are selected

by one of the following heuristic methods in selection

of asset:

HigherExpRet: K - n assets which have the highest

expected return values are selected in the new so-

lution and the proportions of those selected assets

are randomly assigned.

LessSTD: K - n assets which have the least standard

deviation values are selected in the new solution

and the proportions of those selected assets are

randomly assigned.

LeastCov: K - n assets which have the lowest corre-

lation values are selected in the new solution and

the proportions of those selected assets are ran-

domly assigned.

It may be noted that the combination mechanisms

construct solutions that may or may not be feasible.

Hence, the repair mechanism is employed if the newly

generated solution violates the constraints. (see Sec-

tion 3.9)

3.6 Improvement Method

The solutions obtained by the combination method

(see Section 3.5) are improved by a local search tech-

nique (i.e., hill climbing). It simply moves the current

solution to a better candidate solution by using muta-

tion operation. This is done by randomly altering a

proportion of an asset or a selection of the asset in the

portfolio until no improved solutions can be found in

a certain number of moves. Then the trial population

is updated by adding those non-dominated solutions.

3.7 Maintaining the External Archive

The main objective of the external archive (A) is

to keep all the non-dominated solutions encountered

along the search process. This approach is adopted

in order to save and update all well spread non-

dominated solutions generated by the algorithm dur-

ing the search.

In each generation, the archive (A) is updated with

the non-dominated solutions from the trial population.

The computational time of maintaining the archive in-

creases with the archive size. Hence, the size of the

archive is restricted to a prespeciﬁed value. When the

external archive has reached its maximum capacity

(M), the crowding distances of the solutions are cal-

culated to delete the most crowded archive members.

3.8 Reference Set Update Method

Once the archive (A) has been updated with non-

dominated solutions obtained from the trial popu-

lation (t pop), the reference sets are updated. For

our proposed algorithm for the portfolio optimization

problem, the reference set update method has been

devised as follows.

The non-dominated solutions obtained from the

archive (A) are sorted by using the Pareto dominance.

The X best non-dominated solutions obtained from

the archive (A) are updated to ref1. Similarly, the so-

lutions in the trial population are sorted by the crowd-

ing distance. The X least crowded solutions obtained

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

114

from the sorted archive (A) and trial (t pop) solutions

are updated to ref2.

3.9 Constraint Handling

During the population sampling, each constructed in-

dividual must be repaired if the representative port-

folio does not satisfy the constraints of the problem.

The budget constraint in Eq.(3) is satisﬁed by ﬁrstly

normalizing the weights: w

= w

∑

j=1

over those

assets selected. Moreover, the bounding constraint

in Eq.(5) requires the proportion of asset i to be in

the range [ε

, δ

]. If the proportion of asset after the

normalization violates the quantity constraints, then it

employs repair mechanism described in (Chang et al.,

2000).

4 EXPERIMENTAL RESULTS

In this work, we compared the performance of the

proposed algorithm with the Non-dominated Sort-

ing Genetic Algorithm (NSGA-II) (Deb et al., 2002),

the Strength Pareto Evolutionary Algorithm (SPEA2)

(Zitzler et al., 2001) and Pareto Envelope-based Se-

lection Algorithm (PESA-II) (Corne et al., 2001).

Twenty independent runs were performed for all

experiments and the same random seed is assigned to

each set of the sum so that the algorithms start with

the same initial population. In order to ensure a fair

comparison, we have used the same population size

and archive size (if applicable) for all the algorithms

tested in this work. We have chosen to run all the al-

gorithms for the same stopping criteria (i.e. the same

number of evaluations) to generate the Pareto front.

Each algorithm also uses the same encodings (see

Section 3.1) and repair mechanism (see Section 3.9)

when a newly constructed portfolio violates the con-

sidered constraints. NSGA-II uses binary tournament

selection based on the crowding distance. NSGA-II,

SPEA2 and PESA-II use simulated binary crossover

and polynomial mutation evolutionary operators.

Before the experiments were performed, param-

eters are tuned for all algorithms using the small-

est problem instance, i.e. Hang Seng. The param-

eter value of the compared algorithms are provided

in Table 1. For constraint values, we use K = 10,

= 0.01(i = 1,...,N), δ

= 1.0(i = 1,...,N) and z

1(i = 30).

Table 1: Parameter setting of for four algorithms.

Parameters MODEwAwL NSGA-II SPEA2 PESA-II

Number of Population (NP) 100 100 100 100

Number of Generation 10,000N 10,000N 10,000N 10,000N

Scaling Factor (F) 0.3 - - -

Crossover Probability (CR) 0.9 0.9 0.9 0.9

Crossover Distribution Index - 20 20 20

Mutation Probability - 1/N 1/N 1/N

Mutation Distribution Index - 20 20 20

Tournament Round - - 1 -

Number of Bisection - - - 5

Archive Size (M) 100 - 100 100

4.1 Dataset

A test data for the portfolio optimization problems

from the OR-library (Beasley, 1990) is used to

evaluate the performance of the algorithms described

above. These datasets contain the estimated returns

and the covariance matrix of ﬁve different stock

market indices: Hang Seng in Hong Kong, DAX

100 in Germany, FTSE 100 in UK, S&P 100 in

USA and Nikkei 225 in Japan. For each set of

the test data, the number of assets N is 31, 85, 89,

98 and 225, respectively. In the current literature

of portfolio selection problem, this set of dataset

has been widely tested, and is recognized as the

benchmark to evaluate computational algorithms.

All information of the dataset itself and their best

known solutions can be accessed online at the URL

http://people.brunel.ac.uk/

∼

mastjjb/jeb/orlib/portinfo

.html.

4.2 Performance Metric

To evaluate the performance of the proposed algo-

rithm for the constrained portfolio optimization prob-

lem, we use three criteria: Inverted Generational Dis-

tance, Generational Distance and Diversity metric

(∆).

4.2.1 Inverted Generational Distance (IGD)

The Inverted Generational Distance (Sierra and

Coello, 2005) uses the true Pareto front as a refer-

ence and measures the distance from the true Pareto

front to the Pareto front obtained by an algorithm. It

is mathematically deﬁned as:

IGD =

∑

i=1

where Q is the number of solutions in the true Pareto

front and d

is the Euclidean distance between each

of the solution and the nearest member from the set

of non-dominated solutions found by the algorithm.

Multi-objectiveScatterSearchwithExternalArchiveforPortfolioOptimization

115

Figure 2: Performance Comparisons of the algorithms in term of GD, IGD and ∆ metrics for Hang Seng.

Figure 3: Performance Comparisons of the algorithms in term of GD, IGD and ∆ metrics for DAX 100.

Figure 4: Performance Comparisons of the algorithms in term of GD, IGD and ∆ metrics for FTSE 100.

Figure 5: Performance Comparisons of the algorithms in term of GD, IGD and ∆ metrics for S&P 100.

This metric measures both the diversity and the con-

vergence of an obtained non-dominated solution set.

The smaller the value of this metric, the closer the ob-

tained front is to the true Pareto front.

4.2.2 Generational Distance (GD)

The Generational Distance (Van Veldhuizen and La-

mont, 1998) is a variant of the IGD. It measures

how far the solutions of the computed Pareto front

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

116

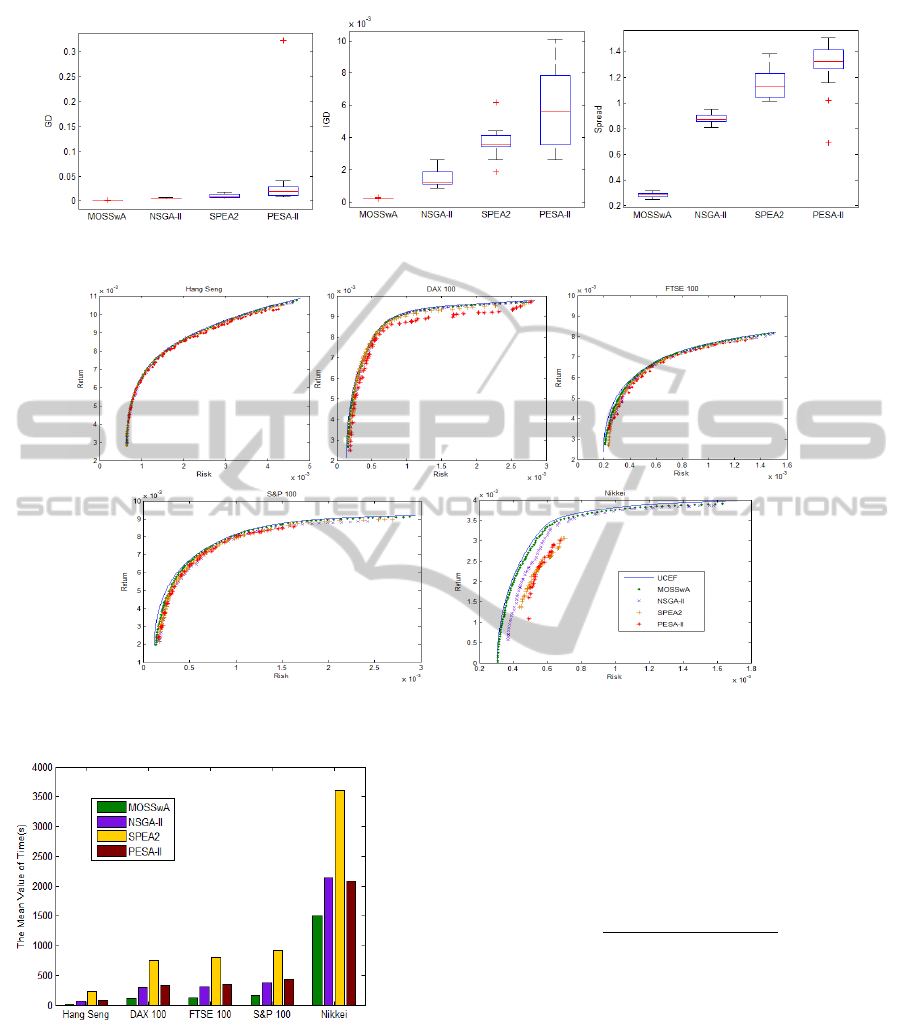
Figure 6: Performance Comparisons of the algorithms in term of GD, IGD and ∆ metrics for Nikkei.

Figure 8: Comparison of Obtained Efﬁcient Frontier of all the algorithms for Constrained Portfolio Optimization Probelm.

Figure 7: Running Time Measures of the algorithms for

Constrained Portfolio Optimization Problem.

obtained by an algorithm are from those at the true

Pareto front. The smaller value indicates that all the

generated solutions are on the true Pareto front.

4.2.3 Spread (∆)

The Diversity metric (∆) (Deb et al., 2002) mea-

sures the extent of spread achieved among the non-

dominated solutions as follows:

∆ =

+ d

|Q|−1

∑

i=1

−

+ d

+ (|Q| − 1)

where d

is the Euclidean distance in the objective

space between consecutive solutions in the obtained

non-dominated front Q, and

d is the average of these

distances. The parameters d

and d

are the Euclidean

distance between the extreme solutions of the Pareto

front P

∗

and the boundary solutions of the obtained

front Q. The lower value of the spread (∆) indicates a

better diversity.

4.2.4 Comparisons of the Algorithms

The experimental results of GD, IGD and ∆ of the

four algorithms performed on ﬁve datasets from OR-

Multi-objectiveScatterSearchwithExternalArchiveforPortfolioOptimization

117

Table 2: Student t-Test Results of Different Algorithms on ﬁve problem instances from OR-Library.

Algorithm1 ↔ Algorithm2 Hang Seng DAX 100 FTSE 100 S & P 100 Nikkei

MOSSwA ↔ NSGA-II + + + + +

MOSSwA ↔ SPEA2 + + + + +

MOSSwA ↔ PESA-II + + + + +

NSGA-II ↔ SPEA2 ∼ ∼ ∼ ∼ +

NSGA-II ↔ PESA-II + + + + +

SPEA2 ↔ PESA-II + + + + +

library (see Section 4.1) are shown in Figure 2, Fig-

ure 3, Figure 4, Figure 5 and Figure 6. The running

time of the algorithms are shown in Figure 7. The re-

sults showed that our proposed algorithm (MOSSwA)

is not only superior in performance measures but

also is efﬁcient in computational time compared with

NSGA-II, SPEA2 and PESA2.

For illustrative purpose, four obtained efﬁcient

frontiers of the algorithms from a single run for ﬁve

problem instances along with the true unconstrained

efﬁcient frontier (UCEF) are provided in Figure 8.

To further support our observation that MOSSwA

outperforms others, we compare the IGD values of

the ﬁve algorithms by using Student’s t-test (Walpole

et al., 1998). The statistical results obtained by a

two-tailed t-test with 38 degrees of freedom at a 0.05

level of signiﬁcance are given in Table 2. The re-

sult of Algorithm 1 ↔ Algorithm 2 is shown as ”+” ,

”−”, or ”∼” when Algorithm 1 is signiﬁcantly better

than, signiﬁcantly worse than, or statistically equiva-

lent to Algorithm 2, respectively. Results show that

MOSSwA outperforms other algorithms in all prob-

lem instances. We therefore can conclude that the

proposed MOSSwA has the best optimization per-

formance for the portfolio optimization problem with

considered constraints.

5 CONCLUSIONS

In this work, we presented a multi-objective evolu-

tionary algorithm based on Scatter Search with exter-

nal archive (MOSSwA) for solving the mean-variance

portfolio selection problem with cardinality, quantity

and pre-assignment constraints. Experimental results

indicate that the proposed adapted multi-objective

Scatter Search algorithm (MOSSwA) outperforms the

Non-dominated Sorting Genetic Algorithm (NSGA-

II), Strength Pareto Evolutionary Algorithm (SPEA-

2) and Pareto Envelope-based Selection Algorithm

(PESA-II) in all performance measures. The pro-

posed hybrid metaheuristic algorithm follows the ba-

sic structure of the Scatter Search and deﬁnes the

reference set solutions with the Pareto dominance

and crowding distance concepts. New subset gener-

ation and combination methods are proposed to con-

tribute to the literature in order to generate efﬁcient

and diversiﬁed portfolios. When cardinality and pre-

assignment constraints are considered, the proposed

three combination mechanisms enhance the solution

quality signiﬁcantly in terms of both the computa-

tional time and all the measures of solution quality.

REFERENCES

Beasley, J. (1990). Or-library: Distributing test problems by

electronic mail. Journal of the Operational Research

Society, 41(11):1069–1072.

Branke, J., Scheckenbach, B., Stein, M., Deb, K., and

Schmeck, H. (2009). Portfolio optimization with

an envelope-based multi-objective evolutionary algo-

rithm. European Journal of Operational Research,

199(3):684–693.

Chang, T., Meade, N., Beasley, J., and Sharaiha, Y. (2000).

Heuristics for cardinality constrained portfolio op-

timisation. Computers and Operations Research,

27(13):1271–1302.

Corne, D. W., Jerram, N. R., Knowles, J. D., Oates, M. J.,

et al. (2001). Pesa-ii: Region-based selection in evo-

lutionary multiobjective optimization. In Proceedings

of the Genetic and Evolutionary Computation Confer-

ence (GECCO2001. Citeseer.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

Nsga-ii. Evolutionary Computation, IEEE Transac-

tions on, 6(2):182–197.

Fonseca, C. and Fleming, P. (1995). An overview of evo-

lutionary algorithms in multiobjective optimization.

Evolutionary computation, 3(1):1–16.

Glover, F., Laguna, M., and Mart

ı, R. (2000). Fundamen-

tals of scatter search and path relinking. Control and

cybernetics, 39(3):653–684.

Lwin, K. and Qu, R. (2013). A hybrid algorithm for

constrained portfolio selection problems. Applied

Intelligence,DOI:10.1007/s10489-012-0411-7.

Markowitz, H. (1952). Portfolio selection. The Journal of

Finance, 7(1):pp. 77–91.

Markowitz, H. (1959). Portfolio selection: Efﬁcient diver-

siﬁcation of investments. John Wiley and Sons, New

York.

Moral-Escudero, R., Ruiz-Torrubiano, R., and Suarez, A.

(2006). Selection of optimal investment portfolios

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

118

with cardinality constraints. In Evolutionary Com-

putation, 2006. CEC 2006. IEEE Congress on, pages

2382–2388. IEEE.

Robi

c, T. and Filipi

c, B. (2005). Demo: Differential

evolution for multiobjective optimization. In Evolu-

tionary Multi-Criterion Optimization, pages 520–533.

Springer.

Sierra, M. R. and Coello, C. A. C. (2005). Improving

pso-based multi-objective optimization using crowd-

ing, mutation and epsilon-dominance. In EMO’05,

pages 505–519.

Skolpadungket, P., Dahal, K., and Harnpornchai, N. (2007).

Portfolio optimization using multi-obj ective genetic

algorithms. In Evolutionary Computation, 2007. CEC

2007. IEEE Congress on, pages 516–523. IEEE.

Van Veldhuizen, D. A. and Lamont, G. B. (1998). Multiob-

jective evolutionary algorithm research: A history and

analysis. Technical report, Citeseer.

Walpole, R. E., Myers, R. H., Myers, S. L., and Ye, K.

(1998). Probability and statistics for engineers and

scientists, volume 8. Prentice Hall Upper Saddle

River, NJ:.

Zitzler, E., Laumanns, M., Thiele, L., Zitzler, E., Zitzler, E.,

Thiele, L., and Thiele, L. (2001). Spea2: Improving

the strength pareto evolutionary algorithm.

Multi-objectiveScatterSearchwithExternalArchiveforPortfolioOptimization

119