
Improving a Fuzzy Discretization Process by Bagging
Jos
´
e Manuel Cadenas, Mar
´
ıa del Carmen Garrido and Raquel Mart
´
ınez
Dpt. Information Engineering and Communications, Computer Faculty, University of Murcia
30100-Campus of Espinardo, Murcia, Spain
Keywords:
Crisp/Fuzzy Discretization, Bagging, Numerical Attributes, Data Mining.
Abstract:
Classification problems in which the number of attributes is larger than the number of examples are increas-
ingly common with rapid technological advances in data collection. Also numerical data are predominant in
real world applications and many algorithms in supervised learning are restricted to discrete attributes. Focus-
ing on these issues, we proposed an improvement in a fuzzy discretization method by means of the introduction
of a bagging process in the different phases of the method. The bagging process tries to solve problems which
can appear with small size datasets. Also we show the benefits that bagging introduces in the method by means
of several experiments. The experiments have been validated by means of statistical tests.
1 INTRODUCTION
Successful decision-making, whether done by an in-
dividual or as a group relies on the presence of
many ingredients. Availability and quality of infor-
mation is an essential element of successful decisions,
(O’Reilly, 1982). On the one hand, with the advent of
key information technologies in recent decades, deci-
sion makers now have access to vast amount of his-
torical data. In this case, the information available
could be enough depending on its quality. On the
other hand, due to the highly competitive global mar-
ket, companies must meet the customer increasing de-
mands to rapidly and continually improve the stan-
dard of their products and services. In the real world,
there are many situations where organizations have to
work with small datasets. For instance, with the pi-
lot production of a new product in the early stages of
a system, dealing with a small number of VIP cus-
tomers, and some special cancers, such as bladder
cancer for which there are only a few medical records,
(Der-Chiang and Chiao-Wen, 2012).
The extraction of valuable information from these
small data sources requires purposeful application of
rigorous analysis techniques such as data mining, ma-
chine learning, and other statistical learning tech-
niques, (Unler and Murat, 2010).
Data mining methods are often employed to un-
derstand the patterns present in the data and derive
predictive models with the purpose of predicting fu-
ture behavior. While data mining encompasses a wide
range of data processing and manipulation steps (for-
matting, filtering, visualization,...), machine learning
algorithms are central to the data mining process. Ma-
chine learning algorithms are a collection of meth-
ods that are capable of learning to optimize a per-
formance criterion using example data or past expe-
rience. The classification problem, as a form of su-
pervised machine learning, aims to induce a model
with the purpose of predicting categorical class labels
for new samples given a training set of samples each
with a class label. Classification has found applica-
tions in various domains such as credit approval in
financial services, target marketing in retailing, med-
ical diagnosis in healthcare, and treatment effective-
ness analysis in healthcare. A typical implementa-
tion of the classification problem involves selecting
a training dataset with class labels, developing an ac-
curate description or a model for each class using the
attributes available in the data, and then evaluating the
prediction quality of the induced model.
This paper will focus on supervised classification
and models which have been obtained from datasets
with few examples in relation with the number of at-
tributes. From the computational learning viewpoint,
these datasets are very important in machine learning
problems, because the information contained can be
more difficult to extract. For instance, with a classi-
fier, it is hard to make accurate predictions because
these datasets do not only make the modeling pro-
cedure prone to overfitting, but also cause problems
in predicting specific correlations between the inputs
201
Manuel Cadenas J., del Carmen Garrido M. and Martínez R..
Improving a Fuzzy Discretization Process by Bagging.
DOI: 10.5220/0004553402010212
In Proceedings of the 5th International Joint Conference on Computational Intelligence (FCTA-2013), pages 201-212
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

and outputs, (Der-Chiang and Chiao-Wen, 2012). For
that reasons, this paper focus on these kind of datasets
because all of the commonly used classifiers can suf-
fer from the curse of dimensionality.
While an exact relationship between the probabil-
ity of misclassification, the number of training exam-
ples, the number of attributes and the true parame-
ters of the class-conditional densities is very difficult
to establish, some guidelines have been suggested re-
garding the ratio of the sample size to dimensionality,
(Jain, 2000).
As a general rule, a minimum number of 10 ·
|A| · |C| training examples is required for a |A|-
dimensionality classification problem of |C| classes,
(Jain, 2000). Following this rule, when datasets have
few examples (hereafter called small size datasets),
we should take into account in the learning algorithm
some measure in order to build better models to get
good accuracy in classification.
In this paper we focus on discretization of numer-
ical attributes in small size datasets. The discretiza-
tion of numerical attributes is a crucial step in ma-
chine learning problems since there are classifiers that
cannot deal with numerical attributes, and there are
other classifiers that exhibit better performance when
these attributes are discretized, since discretization re-
duces the number of numerical attribute values, en-
abling faster and more accurate learning (Antonelli
et al., 2011).
More specifically we propose the introduction of
a measure in the discretization method presented in
(Cadenas et al., 2012b), OFP CLASS, that allows it
to get good accuracy in classification when it deals
with small size datasets. This measure is based on the
use of bagging in order to improve the stability and
accuracy of the discretization process. Bagging is a
special case of the model averaging approach. We
have called the resulting method BAGOFP CLASS.
This paper is organized as follows. First, in Sec-
tion 2, we describe some of the different methods re-
ported in literature to discretize numerical attributes
highlighting the fulfilling degree of the rule. Next,
in Section 3, we describe the BAGOFP CLASS dis-
cretization method. Then, in Section 4, we present
some experimental results illustrating the perfor-
mance of BAGOFP CLASS method. Finally, in Sec-
tion 5 remarks and conclusions are presented.
2 RELATED WORKS
There are some classification algorithms which can
only take nominal data as inputs and some of them
need to discretize numerical data into nominal data
before the learning process. Therefore, discretization
is needed as a pre-processing step to partition each
numerical attribute into a finite set of adjacent dis-
tinct intervals/items. A good discretization algorithm
should not only characterize the original data to pro-
duce a concise summarization, but also help the clas-
sification performance (Zhu et al., 2011).
Discretization algorithms can be categorized from
different viewpoints depending on the measure that is
being focused on. If the class label is used to build
partitions, the discretization methods can be catego-
rized into two ways, namely unsupervised and su-
pervised. With the focus on the kind of logic, dis-
cretization algorithms can be categorized into fuzzy
discretization and crisp discretization. On the one
hand, when the fuzzy logic is used, we can create
fuzzy partitions where a value can belong to more
than one partition. On the other hand, when the clas-
sical logic is used, we create crisp partitions where a
value can only belong to one partition. Furthermore,
discretization methods can be classified taking into
account the kind of measure that it is used or the way
that the partitions are created.
In this section, we focus on how several discretiza-
tion methods consider the management of small size
datasets explicitly. From this viewpoint, there are
methods that build partitions taking into account the
possible problems that datasets with few examples
can induce in the discretization process and later in
loss of accuracy.
However, there are methods which are not specific
for small size datasets but get good precision for this
kind of datasets.
For instance, in (Armengol and Garc
´
ıa-Cerdana,
2012) a method, called ε-procedure, that constructs
crisp partitions on the range of an attribute taking nu-
merical values is proposed. These partitions can be
seen as refinements of the ones given by the expert
or the ones given by a standard discretization method.
Moreover, the method can be seen as “similar” to the
fuzzy discretization methods since the ε-procedure
takes into account the neighborhood of the thresholds
given by the crisp discretization methods.
Another method that does not specify anything
about managing small size datasets is proposed in
(Zhu et al., 2011), where a novel and effective su-
pervised discretization algorithm based on correlation
maximization is proposed by using multiple corre-
spondence analysis. For each numerical attribute, the
candidate cut point that maximizes the correlation be-
tween attribute intervals and classes is selected as the
first cut point, then this strategy is carried out in the
left and right intervals recursively to further partition
the intervals.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
202

As a last instance for discretization methods
which do not consider small size datasets, in (Wang
et al., 2012) the discretization quality is improved by
increasing the certainty degree of a decision table in
terms of deterministic attribute relationship, which is
revealed by the positive domain ratio in rough set the-
ory. Furthermore, they take into account both the
decrement of uncertainty level and increment of cer-
tainty degree to induce a Coupled Discretization al-
gorithm. This algorithm selects the best cut point ac-
cording to the importance function composed of the
information entropy and positive domain ratio in each
run. The algorithm builds crisp partitions because it
is focused on classical logic.
In contrast to the methods which do not consider
the problems of small size datasets, in literature there
are some methods that explicitly work with this kind
of datasets.
So, in (Qureshi and Zighed, 2009) a novel soft de-
cision tree method that uses soft of fuzzy discretiza-
tion instead of traditional crisp cuts is proposed. They
take into account the dataset size and use a resampling
based technique to generate soft discretization points.
They use a fuzzy decision tree and an ordinary boot-
strap as a method for resampling. Bootstrap allows
them to get global partitions and a better estimation
toward the entire population.
In (Der-Chiang et al., 2012), a trend-diffusion
and tree-structure based approach, which is called a
tree structure based trend diffusion (TTD) procedure,
specifically designed for small datasets in manufac-
turing problems has been proposed. In the first phase
of the proposed procedure, TTD is employed to es-
timate the possible value bounds, and then uses a
heuristic mechanism to fill values within the bounds
to form a new training set. In the second phase,
the M5’ model tree is adopted (Wang and Witten,
1997) as the modeling tool to concretely represent the
knowledge. In this second phase it is necessary to
discretize data for the tree. The discretization process
should be repeated whenever each branching process
of M5’ begins. This repetition is a special treatment
to deal with small datasets. In this case, the method
works with small datasets (microarrays), although,
they do not apply the technique for small datasets ex-
plicitly.
Typical datasets which have few examples are the
microarrays datasets. In (Kianmehr et al., 2010) this
kind of data is used. That paper presents a novel clas-
sification approach that integrates fuzzy class associa-
tion rules and support vector machines. Also, a fuzzy
discretization technique based on fuzzy c-means clus-
tering algorithm is employed to transform the training
set, particularly quantitative attributes, to a format ap-
propriate for association rule mining. A hill-climbing
procedure is adapted for automatic thresholds adjust-
ment and fuzzy class association rules are mined ac-
cordingly. The compatibility between the generated
rules and fuzzy patterns is considered to construct a
set of attribute vectors, which are used to generate a
classifier.
Another paper which deal with biology issue (mi-
croarray time series datasets) is presented in (Dim-
itrova and Vera-Licona, 2010). In that paper a new
algorithm, called SSD, is introduced. SSD is espe-
cially designed for short time series data and is capa-
ble of determining the optimal number of discretiza-
tion states. An important characteristic of such time
series is the relatively small number of data points
(typically no more than ten). A graph-theoretic clus-
tering method is employed to perform the discretiza-
tion and an information-theoretic technique to mini-
mize loss of information content. One of the most
useful characteristic of that method is the determina-
tion of an optimal number of discrete states that is
most appropriate for the data.
It is notable that some of the above methods
use some kind of repetitions to manage small size
datasets. This approach is also used in other types
of machine learning algorithms to manage small size
datasets such as in (Liu et al., 2004) to attribute selec-
tion or in (Zararsiz et al., 2012) to classify. Following
this line, a bagging method is used, in order to emu-
late the repetitions that others methods use.
Bagging was proposed by Breiman in (Breiman,
1996a), and is based on bootstrapping and aggregat-
ing concepts, so it incorporates the benefits of both
approaches. Bagging uses the same training set mul-
tiple times, and has been shown to outperform a sin-
gle classifier trained from the training set (Breiman,
1996a).
In bagging, the training set is randomly sampled
k times with replacement, producing k training sets
with sizes equal to the original training set. Since the
original set is sampled with replacement, some train-
ing instances are repeated in the new training sets,
and some are not present at all. Bagging has several
advantages. First, because different classifiers make
different errors, combining multiple classifiers gener-
ally leads to superior performance when compared to
a single classifier, and thus it is more noise tolerant.
Second, bagging can be computationally efficient in
training because it can be implemented in a parallel
or distributed way. Finally, bagging is able to main-
tain the class distribution of the training set.
In the next section, we are going to describe the
BAGOFP CLASS method which also obtains good
results when discretizing numerical attributes of small
ImprovingaFuzzyDiscretizationProcessbyBagging
203

size datasets.
3 BAGOFP CLASS:
DISCRETIZING BY BAGGING
In this section we are going to present the
BAGOFP CLASS method so that this method gets
better fuzzy partition than OFP CLASS method (Ca-
denas et al., 2012b) when it works with datasets which
do not verify the rule commented in Section 1. This
rule states that datasets should have more examples
than 10 ·|A|·|C|, where |A| is the number of attributes
that describe each example and |C| is the number of
different values of the class attribute.
Following the methodology of OFP CLASS (Ca-
denas et al., 2012b), BAGOFP CLASS is composed
of two phases. The former uses a fuzzy decision tree
in order to find possible cut points to create the par-
titions. The latter takes as input the cut points of the
first phase to optimize and to build the final fuzzy par-
titions by means of a genetic algorithm. It should be
noted that if the second phase is not carry out, with
the cut points it could be possible to construct inter-
vals and crisp partitions would be obtained for the at-
tributes instead of fuzzy partitions.
The use of bagging in OFP CLASS method is mo-
tivated by the fact that bagging can give substantial
gains in accuracy when the classification method used
is unstable. If perturbing the learning set can cause
significant changes in the classifier constructed, the
bagging can improve accuracy (Breiman, 1996a). In-
stability was studied in (Breiman, 1996b) where it
was pointed out that neural nets, classification and re-
gression trees, and subset selection in linear regres-
sion were unstable. The result, both experimental and
theoretical, is that bagging can push a good but unsta-
ble procedure a significant step towards optimality.
In addition, instability of decision trees can be in-
creased by using small size datasets because in a de-
cision tree when a node is split, the attribute with
higher information gain is selected. When the num-
ber of examples is small relative to the number of
the attributes, the probability that redundant attributes
exist is increased. In this way, there will be several
attributes that have the same information gain and
the selection of one of them is random. With a cer-
tain probability, the unselected attributes are not par-
titioned and, therefore, these attributes might not be
part of the final partition generated by the decision
tree. When a bagging process is introduced, the prob-
ability that these attributes can be part of the final par-
tition is increased. In this situation, the method will
work with different bagging of the dataset. By re-
peating the process, the selection of other attributes is
allowed.
Therefore, since the first phase of the algorithm
is based on decision trees, can be improved with the
use of bagging obtaining a better partitioning from
the set of decision trees generated and enabling that
a greater number of attributes to be part of the parti-
tion when the information gain of various attributes
is the same. The second phase of the algorithm is re-
sponsible for selecting the most relevant attributes for
classification.
On the other hand, the genetic algorithm in the
second phase of the OFP CLASS method, uses a fit-
ness function which tries to find the best set of parti-
tions to divide the examples with respect to the class
attribute. Again, the second phase of OFP CLASS
method can be improved with a bagging process with
the motivation of reducing variability in the partition-
ing results via averaging. The fitness function is mod-
ified in order to obtain a better value for those par-
titions (individuals) with better average performance
when we using a bagging of the dataset. Also with
bagging the genetic algorithm studies different region
of the searching space and it can get more global
fuzzy partitions.
Therefore, we will introduce a bagging process
into the two phases of BAGOFP CLASS method: 1)
in the construction of the decision tree which gen-
erates the cut points of the first phase, and 2) in the
fitness function that will be used in the genetic algo-
rithm of the second phase.
The fuzzy partitions created with
BAGOFP CLASS have the same characteristics
as the fuzzy partitions created with the OFP CLASS
method. This means that the domain of each numer-
ical attribute is partitioned in trapezoidal fuzzy sets
and the partitions are:
• Completeness (no point in the domain is outside
the fuzzy partition), and
• Strong (it verifies that ∀x ∈ Ω
i
,
∑
F
i
f =1
µ
B
f
(x) = 1
where B
1
,..,B
F
i
are the F
i
fuzzy sets for the par-
tition of the i numerical attribute with Ω
i
domain
and µ
B
f
(x) are its functions membership).
The domain of each i numerical attribute is parti-
tioned in trapezoidal fuzzy sets and the membership
functions B
1
,B
2
..,B
F
i
are calculated in the following
way:
µ
B
1
(x) =
1 b
11
≤ x ≤ b
12
(b
13
−x)
(b
13
−b
12
)
b
12
≤ x ≤ b
13
0 b
13
≤ x
;
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
204
µ
B
2
(x) =
0 x ≤ b
12
(x−b
12
)
(b
13
−b
12
)
b
12
≤ x ≤ b
13
1 b
13
≤ x ≤ b
23
(b
24
−x)
(b
24
−b
23
)
b
23
≤ x ≤ b
24
0 b
24
≤ x
;
·· ·;
µ
B
F
i
(x) =
0 x ≤ b
(F
i
−1)3
(x−b
(F
i
−1)3
)
(b
(F
i
−1)4
−b
(F
i
−1)3
)
b
(F
i
−1)3
≤ x ≤ b
(F
i
−1)4
1 b
F
i
3
≤ x
In the next subsection, we are going to detail
the two phases of the BAGOFP CLASS method
and we are going to highlight the more important
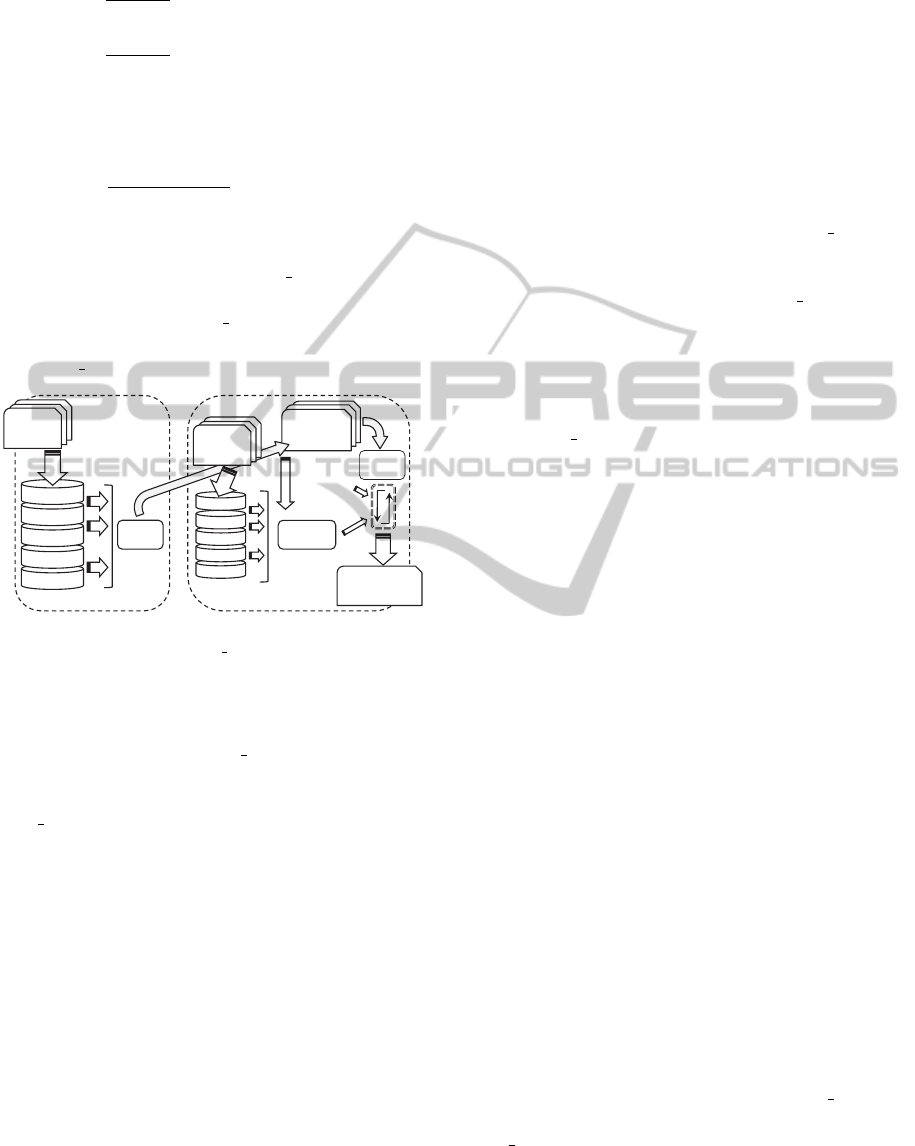
changes regarding the OFP CLASS method. Figure
1 shows, in an illustrative way, the whole process of
BAGOFP CLASS method.
cut points
of attributes
selection
crossing
mutation
Bagging d
·······
Bagging 3
Bagging 2
FIRST PHASE SECOND PHASE
GA
FDTs
Bagging 1
Initial
Dataset
Fuzzy partition
of attributes
Initial
Dataset
Bagging b
·······
Bagging 3
Bagging 2
Bagging 1
Fitness
function
Figure 1: BAGOFP CLASS method.
3.1 First Phase: Cut Points
The first phase of BAGOFP CLASS uses a fuzzy
decision tree as base method to search the possible
cut points to build the fuzzy partitions, but unlike of
OFP CLASS method, the input dataset to this fuzzy
decision tree is each dataset obtained by performing a
bagging process over the original dataset.
The kind of values, with which this fuzzy decision
tree can work, are nominal attributes, numerical dis-
cretized attributes by means of a fuzzy partition, non-
discretized numerical attributes described with crisp
values, interval and fuzzy values and furthermore it
allows the existence of missing values in all of them.
The fuzzy decision tree behavior changes depending
on the kind of attribute that is analyzed by the tree in
order to find the best of them to divide a node.
On the one hand, when the attribute is numerical
and does not have partitions available, the process to
follow is similar to the decision tree C4.5 process.
The thresholds selected in each node of the tree for
these attributes will be the cut points that delimit the
intervals. On the other hand, for the other kind of
attributes, the methodology followed is the same as
the fuzzy decision tree presented in (Cadenas et al.,
2012b). During the rest of the process the method be-
havior is the same for both discretize attributes and
non-discretized attributes. The procedure of building
the fuzzy decision tree has a priority tail which is used
to arrange tree nodes depending on the number of ex-
amples each one has. The reason for incorporating
the priority tail is that the nodes with more examples
are analized first because these nodes will have more
information than those with less examples.
Comparing the new method with the OFP CLASS
method, the main difference between them is that for
datasets which do not have 10 · |A| · |C| training ex-
amples, the cut points obtained by OFP CLASS are
not rich enough in information to provide a good par-
tition, because these cut points are too specific and
partitions obtained are not global. In order to pre-
vent getting cut points so specific and more attributed
can be discretized, the input to the fuzzy decision tree
in BAGOFP CLASS is a bagging obtained from the
whole dataset.
It must be remembered that in the bagging pro-
cess, it is possible that a cut point may appear several
times. In this case the cut point will be included once.
Algorithm 1 describes all the process to get all
possible cut points.
All the cut points obtained after the first phase are
introduced as input in the second phase in order to
build optimal fuzzy partitions.
3.2 Second Phase: Building Fuzzy
Partitions
In the second phase of the method, we are going to
use a genetic algorithm to get the fuzzy sets that make
up the partitioning of non-discretized attributes. We
have decided to use a genetic algorithm, because these
algorithms are very powerful and robust, as in most
cases they can successfully deal with an infinity of
problems from very diverse areas and specifically in
Data Mining. These algorithms are normally used in
problems without specialized techniques or even in
those problems where a technique does exist, but is
combined with a genetic algorithm to obtain hybrid
algorithms that improve results (Cox, 2005).
In this section we briefly describe the several
elements which compose the algorithm. We focus
on those that characterizing the BAGOFP CLASS
method. For remaining elements originating from the
OFP CLASS method a more detailed description can
be found in (Cadenas et al., 2012b).
ImprovingaFuzzyDiscretizationProcessbyBagging
205

Algorithm 1: Getting Cut points.
FindingCutPoints(in : E; out : Cut points)
begin
• Initialize the set of cut points to each numerical
attribute k to empty: CPS
k
=
/
0
• Initialize bagging size δ.
• For j=1 to δ
1. Obtain the dataset BA
j
consisting of |E| ex-
amples selected from E randomly and with re-
placement.
2. Obtain a fuzzy decision tree from BA
j
:
– Start at the root node, which is placed in the
initially empty priority tail. Initially, in the
root node the set of examples BA
j
with an ini-
tial weight are found.
– Extract the first node from the priority tail.
– Select the best attribute to split this node using
information gain, which is explained in detail
in (Cadenas et al., 2012b), as the criterion.
– Having selected the attribute to expand node,
all the descendants generated are introduced
in the tail. If the selected attribute is nomi-
nal, a descendant is generated to each possible
value of that attribute. If the selected attribute
(SA) is numerical it is necessary to obtain the
corresponding cut point and two descendants
are generated. In this case, CPS
SA
is updated
as follows:
CPS
SA
= CPS
SA
∪
{cut point}
– Go back to step two to continue constructing
the tree until no nodes remain in the priority
tail or until another stopping condition occurs,
such as reaching nodes with a minimum num-
ber of examples allowed by the algorithm.
• Return CPS
k
sets for each numerical attribute k.
end
The genetic algorithm takes as input the cut points
which have been obtained in the first phase, but it is
important to mention that the genetic algorithm will
decide what cut points are more important to con-
struct the fuzzy partitions, so it is possible that many
cut points are not used to obtain the optimal fuzzy
partitions. If the first phase gets F cut points for the
attribute i, the genetic algorithm can make up F
i
+ 1
fuzzy partitions for the attribute i at the most. How-
ever, if the genetic algorithm considers that the at-
tribute i will not have a lot of relevance in the dataset,
this attribute will not be partitioned.
The different elements which compose this ge-
netic algorithm are as follows:
Encoding. An individual has a real coding and its
size will be the sum of the number of cut points that
the fuzzy decision tree will have provided for each
attribute in the first phase. Each gene represents the
quantity to be added to and subtracted from each at-
tribute’s split point to form the fuzzy partition. Also,
each gene is associated with a boolean value which in-
dicates whether this gene or cut point has to be taken
into account or not, in other words, if this gene or
cut point is active or not. We must consider that if a
gene is not active the domain of the adjacent gene can
change. The domain of each gene is an interval de-
fined by [0,min(
p
r
−p
r−1
2
,
p
r+1
−p
r
2
)] where p
r
is the r-th
cut point of attribute i represented by this gene except
in the first (p
1
) and last (p
u
) cut point of each attribute
whose domains are, respectively:
[
0
,
min
(
p
1
,
p
2
−p
1
2
]
and [0, min(
p
u
−p
u−1
2
,1 − p
u
].
When F
i
= 2, the domain of the single cut point is
defined by [0,min(p
1
,1 − p
1
].
Initialization. Firstly, it is determined if each gene
is active or not. We must consider that at least one
gene from each individual must be active because if
all genes were inactive, any attribute would be dis-
cretized. Once the boolean value of each gene of the
individual has been initialized, the domain of each
gene is calculated, considering which cut points are
active and which are not. After calculating the do-
main of each gene, each gene is randomly initialized
generating a value within its domain.
Fitness Function. The fitness function of each indi-
vidual is defined according to the information gain de-
fined in (Au et al., 2006). In this case, in the same way
as in the first phase of the method BAGOFP CLASS,
to calculate the fitness for each individual a bagging
process is applied. In this case, the fitness of the in-
dividual is an average fitness using different bagging
of the input dataset. In this way, the algorithm obtains
a more robust fitness for each individual because the
average fitness gives a more general vision over dif-
ferent data subsets and is a more reliable measure. Al-
gorithm 2 implements the fitness function.
In the algorithm µ
i f
(·) is the membership func-
tion corresponding to fuzzy set f of attribute i. This
fitness function, based on the information gain, indi-
cates how dependent the attributes are with regard to
class, i.e., how discriminatory each attribute’s parti-
tions are. If the fitness obtained for each individual
is close to zero, it indicates that the attributes are to-
tally independent of the classes, which means that the
fuzzy sets obtained do not discriminate classes. On
the other hand, as the fitness value moves further away
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
206

from zero, it indicates that the partitions obtained are
more than acceptable and may discriminate classes
with good accuracy.
Algorithm 2: Fitness Function.
Fitness(in : E, out : FinalFitness)
begin
• Initialize bagging size β
• Initialize ValueFitness = 0
• For j=1 to β
1. Obtain the dataset BA
j
consisting of |E| ex-
amples selected from E randomly and with re-
placement.
2. For each attribute i = 1, ...,|A|:
2.1 For each set f = 1, ...,F
i
of attribute i
For each class k = 1,...,|C| calculate the prob-
ability
P
i f k
=
∑
e∈BA
jk
µ
i f
(e)
∑
e∈BA
j
µ
i f
(e)
2.2 For each class k = 1,...,|C| calculate the prob-
ability P
ik
=
∑
F
i
f =1
P
i f k
2.3 For each f = 1, ...,F
i
calculate the probability
P
i f
=
∑
|C|
k=1
P
i f k
2.4 For each f = 1,...,F
i
calculate the information
gain of attribute i and set f
I
i f
=
|C|
∑
k=1
P
i f k
· log
2
P
i f k
P
ik
· P
i f
2.5 For each f = 1, ...,F
i
calculate the entropy
H
i f
= −
|C|
∑
k=1
P
i f k
· log
2
P
i f k
2.6 Calculate the I and H total of attribute i
I
i
=
∑
F
i
f =1
I
i f
and H
i
=
∑
F
i
f =1
H
i f
3. Calculate the fitness as :
ValueFitness = ValueFitness +
∑
|A|
i=1
I
i
∑
|A|
i=1
H
i
• FinalFitness = ValueFitness/β
• Return FinalFitness
end
Selection. Individual selection is by means of tourna-
ment, taking subsets with size 2. It must be taken into
account that the best individual is always selected due
to the elitism that the method carries out.
Crossover. The crossover operator is applied with a
certain probability, crossing two individuals through
a single point, which may be any one of the positions
on the vector. Not all crossings are valid, since one
of the restrictions imposed on an individual is that the
individual must not have all its genes inactive. When
crossing two individuals and this situation occurs, the
crossing is invalid, and individuals remain in the pop-
ulation without interbreeding. If the crossing is valid,
the domain for each gene is updated in the individuals
generated. As in selection, the method applies elitism
in this operator, so the best individual is not crossed.
Mutation. Mutation is carried out according to a cer-
tain probability at interval [0.01,0.2].
Since each gene has a boolean associated value
which indicates whether the gene is active or not and
the gene value represents the amount to add and sub-
tract the cut point, the mutation operator is hybrid. In
BAGOFP CLASS method when a gene has to mutate
by chance, there are two options:
1. to activate or deactivate the gene and
2. to modify the amount to add and subtract to the
cut point.
The first option allows us to explore new search
spaces. When the second option is applied the slopes
of the partition are modified. This last option is in-
cluded in the method in order to adjust the slopes as
much as possible and in this way to get better accu-
racy.
The method applies the first option 50% of the
time and the second option 50% of the time.
When a gene is activated or deactivated, first, the
boolean value associated to the gene is modified and
then a check is made to make sure there are still active
genes. If there are still active genes, their domains and
the domains of adjacent genes must be updated. If
all the individual genes are deactivated, the mutation
process is not performed.
When the mutation have to modify the value to
add and subtract, a randomly calculated value within
its domain is generated.
Stopping. The stopping condition is determined by
the number of generations.
The genetic algorithm should find the best possi-
ble solution in order to achieve a more efficient clas-
sification.
In the next section we show some computational
experiments where we are going to compare us-
ing several datasets the accuracy in classification
of discretizing with OFP CLASS method and with
BAGOFP CLASS method. In these experiments, we
can see that the behavior of the BAGOFP CLASS
ImprovingaFuzzyDiscretizationProcessbyBagging
207

method with datasets with a few examples is better
than the previous method.
4 EXPERIMENTS
This section shows the details of the experimental
framework. We present the datasets employed and
we describe the experimental setup, the performance
measure and the statistical test employed to analyze
the results. Finally, we present and analyze the results
obtained.
4.1 The Datasets and the Experimental
Setup
The proposed approach is going to evaluate by means
of experiments on various datasets selected from UCI
machine learning repository (Frank and Asuncion,
2010). In addition, three high dimensional datasets
(ADE, PRO, SRB) available in (Diaz-Uriarte and
de Andr
´
es, 2006) have been added. These datasets
used to test the proposed approach are summarized in
Table 1.
Table 1: Datasets.
Dataset Abbr |E| |A| |C| rule
Australian credit AUS 690 14 2 YES
Breast Cancer W. BCW 699 9 2 YES
Statlog Heart HEA 270 13 2 YES
Iris Plant IRP 150 4 3 YES
Vehicle VEH 946 18 4 YES
Adenocarcinoma ADE 76 9868 2 NO
Apendicitis APE 106 7 2 NO
Glass GLA 214 9 7 NO
Ionosphere ION 351 34 2 NO
Prostate PRO 102 6033 2 NO
Sonar SON 208 60 2 NO
SPECTF SPE 267 44 2 NO
Srbct SRB 63 2308 4 NO
Wis. D. Breast C. WDB 569 31 2 NO
Wine WIN 178 13 3 NO
Table 1 shows the number of examples (|E|), the num-
ber of attributes (|A|) and the number of classes (|C|)
for each dataset. All the various dataset attributes are
numerical except AUS dataset having six numerical
attributes and eight nominal attributes. In addition,
the last column “rule” of the Table 1 shows whether
the dataset verifies the condition |E| ≥ 10 · |A| · |C|.
“Abbr” indicates the abbreviation of the dataset used
in the experiments.
In order to evaluate the partitions obtained both in
the OFP CLASS method and the BAGOFP CLASS
method, we use an ensemble classifier called Fuzzy
Random Forest (FRF) (Cadenas et al., 2012a). This
ensemble needs as input data a fuzzy partition for the
numerical attributes. FRF ensemble was originally
presented in (Bonissone et al., 2010), and then ex-
tended in (Cadenas et al., 2012a) to handle imprecise
and uncertain data. The ensemble is composed of a
set of fuzzy decision trees (FDTs).
The experimental parameters are as follows:
• Parameters of the FRF ensemble.
– Ensemble Size: 500 FDTs
– Random selection of attributes from the set of
available attributes:
√
|A|
• Parameters for GA in both methods (OFP CLASS
and BAGOFP CLASS).
◦ Individual Number: 100
◦ Generation Number: 250
◦ Crossover probability: 0.8
◦ Mutation probability: 0.1
4.2 Estimation of the Classification
Performance and Validating the
Experimental Results
To analyze the results obtained in the study, the fol-
lowing performance measure has been employed: to
compare the results in the experiments the accuracy
(number of successful hits relative to the total number
of classifications) is used. More specifically, the ac-
curacy medium obtained as the average accuracy of a
3×5-fold cross-validation is used.
To complete the experimental study, we perform
an analysis of them in each subsection using statistical
techniques. Following the methodology proposed by
Garc
´
ıa et al. in (Garc
´
ıa et al., 2009) we use a non-
parametric test.
We use the Wilcoxon signed-rank test to compare
two methods. This test is a non-parametric statisti-
cal procedure for performing pairwise comparison be-
tween two methods. This is analogous with the paired
t-test in non-parametric statistical procedures; there-
fore, it is a pairwise test that aims to detect significant
differences between two sample means, that is, the
behavior of two methods.
In order to carry out the statistical analysis R
packet (Ihaka and Gentleman, 1996) has been used.
4.3 BAGOFP CLASS Method and
Bagging Size Parameters
As we have commented in Sections 2 and 3, the use of
bagging is justified by the fact that bagging can give
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
208

substantial gains in accuracy when the classification
method used is unstable (in our case, fuzzy decision
trees). If perturbing the learning set can cause signifi-
cant changes in the classifier constructed, the bagging
can improve accuracy.
In this subsection we show computationally that
fact. As a result of these tests, we will select the val-
ues for δ and β in the method.
To this end, we will show the behavior of the
FRF classifier using different partitions obtained by
the BAGOFP CLASS method. We will change the
values of δ and β of the following way.
We will set the value of β = 1, and we will vary δ
from 1 to 20. Next, we will set δ = 20, we will vary β
from 2 to 30.
In Figures 2 and 3 the obtained results are shown
using GLAS and ION datasets. The horizontal axis
shows the different values (δ,β) and the vertical axis
the average accuracy of a 3×5-fold cross-validation.
68
70
72
74
76
0
4
8
12
16
20
24
28
32
36
40
44
48
52
Accuracy
(delta,beta)
68
0
4
8
12
16
20
24
28
32
36
40
44
48
52
(delta,beta)
(1,1)
(4,1)
(8,1)
(12,1)
(16,1)
(20,1)
(20,4)
(20,8)
(20,12)
(20,16)
(20,20)
(20,24)
(20,28)
(20,32)
(delta,beta)
Figure 2: Behavior of BAGOFP CLASS method with GLA
dataset when vary parameters δ and β.
28
beta
8
92,593 92,688
y = 0,258ln(x) + 92,09
MWF1
MWF1
Logarítmica (MWF1)
Exponencial (MWF1)
92,7
93,3
93,9
94,5
0 4 8 12 16 20 24 28 32 36 40 44 48 52
Accuracy
delta beta
4 8 12 16 20 24 28 32
0
4
8
12
16
20
de
lt
a
b
et
a
4 8
12 16 20 24 28 32
(1,1)
(4,1)
(8,1)
(12,1)
(16,1)
(20,1)
(20,4)
(20,8)
(20,12)
(20,16)
(20,20)
(20,24)
(20,28)
(20,32)
(delta,beta)
Figure 3: Behavior of BAGOFP CLASS method with ION
dataset when vary parameters δ and β.
As we can see in these figures, in the first changes
of δ, the accuracy presents the biggest changes. Next,
the behavior is stabilizing.
Values of δ = 20 and β = 30 have an acceptable
performance with all the datasets used in this work.
Therefore, we will use these values for experiments
of the next subsection:
• Parameters for BAGOFP CLASS method.
◦ In first phase - δ bagging size: 20
◦ In second phase - β bagging size: 30
4.4 Evaluation of the Classification
Performance
The experiments are designed to evaluate the per-
formance of the proposed approach. First, we com-
pare the OFP CLASS method (Cadenas et al., 2012b)
with the proposed method BAGOFP CLASS using
datasets which verify the condition |E| ≥ 10 · |A| · |C|.
The accuracy results are shown in Table 2. And sec-
ond, we compare these two discretization methods us-
ing the datasets that do not verify the condition. The
accuracy results are shown in Table 3.
In Tables 2 and 3, training and test are the per-
centages of classification average accuracy (mean and
standard deviation) for training and test datasets, re-
spectively. Moreover, the obtained p-values, when
comparing the results of the test phase using a
Wilcoxon signed-rank test are shown.
In Table 2 it is observed that the results obtained
by the new method seem to be similar to the results
obtained by OFP CLASS. Analyzing the different p-
values with α = 0.05, we can conclude:
• There are no significant differences between the
datasets.
• Globally, analyzing all the results obtained for dif-
ferent datasets, we can conclude that there are
no significant differences between evaluating with
the discretization of the method OFP CLASS
and evaluating with the discretization of the new
method BAGOFP CLASS.
Table 2: Results obtained by FRF after classifying the
datasets that verify |E| ≥ 10 · |A| · |C| using the discretiza-
tion obtained by OFP CLASS and BAGOFP CLASS.
OFP CLASS BAGOFP CLASS
training test training test p-value
AUS 99.85
0.15
86.42
2.94
100
0.00
86.81
3.12
0.1768
BCW 99.74
0.10
96.13
1.27
98.19
0.22
95.90
1.55
0.7772
HEA 97.84
0.54
79.01
5.34
98.92
0.41
79.26
6.56
0.5092
IRP 97.78
0.92
96.67
3.26
98.98
0.62
96.22
3.16
0.6578
VEH 93.60
0.47
71.16
3.48
99.99
0.02
71.55
4.80
0.4325
aver. 97.76
0.44
85.88
3.26
99.21
0.26
85.95
3.84
0.5805
In Table 3 it is observed that the results obtained
by the new method seem to be better than the results
obtained by OFP CLASS. Analyzing the different p-
values with α = 0.05, we can conclude:
ImprovingaFuzzyDiscretizationProcessbyBagging
209

• For all datasets, the analysis indicates that there
are significant differences between the two meth-
ods, where BAGOFP CLASS is the best method.
• Globally, analyzing all the results obtained for dif-
ferent datasets, we can conclude that there are
significant differences between evaluating with
the discretization of the method OFP CLASS
and evaluating with the discretization of the new
method. The method which gets the best average
accuracy is BAGOFP CLASS.
Table 3: Results obtained by FRF after classifying
the datasets that do not verify |E| ≥ 10 · |A| · |C| us-
ing the discretization obtained by OFP CLASS and
BAGOFP CLASS.
OFP CLASS BAGOFP CLASS
training test training test p-value
ADE 84.32
2.05
81.94
9.96
100
0.00
85.06
9.83
0.01102
APP 90.33
1.80
88.33
7.95
94.02
0.86
90.25
5.72
0.00529
GLA 85.82
1.03
69.80
5.60
100
0.00
73.38
6.68
0.01199
ION 95.89
0.41
93.07
2.38
100
0.00
94.11
2.05
0.00424
PRO 94.93
1.36
89.84
6.98
100
0.00
93.78
5.36
0.00464
SON 93.59
1.59
80.31
5.11
100
0.00
83.68
4.72
0.00105
SPE 79.81
0.97
79.41
4.12
100
0.00
81.78
4.58
0.00108
SRB 94.58
1.72
78.46
13.54
100
0.00
96.79
3.77
0.00109
WDB 93.99
0.41
93.79
2.23
100
0.00
95.49
1.66
0.00692
WIN 94.33
1.28
93.82
3.54
100
0.00
97.57
1.76
0.00253
aver. 90.76
1.26
84.88
6.14
99.40
0.09
89.19
4.61
2.2e-16
Figure 4 shows, in an illustrative way, the results
obtained using BAGOFP CLASS and OFP CLASS
methods with datasets containing enough examples.
84
86
88
90
92
94
96
98
100
Training
Test
Classification accuracy average
OFP_CLASS
BAGOFP_CLASS
Figure 4: Comparing results of datasets verifying |E| ≥ 10 ·
|A| · |C|.
Figure 5 shows in an illustrative way the results
obtained using BAGOFP CLASS and OFP CLASS
methods with datasets containing few examples.
In general, with the datasets used (which either
verify or do not verify |E| ≥ 10 · |A| · |C|) we can con-
84
86
88
90
92
94
96
98
100
Training
Test
Classification accuracy average
OFP_CLASS
BAGOFP_CLASS
Figure 5: Comparing results of datasets that do not verify
|E| ≥ 10 · |A| · |C|.
clude that the proposed method is useful. When the
datasets do not verify the condition, the fundamental
difference of the new method of discretization is the
partitioning of the attributes. The most important at-
tributes in the classification are partitioned possibly
into more parts and more precisely.
From the computational viewpoint, the introduc-
tion of bagging and therefore an iterative process
in both phases increases the runtime of the method.
However, as discussed in Section 2, bagging can be
computationally efficient because it can be imple-
mented in a parallel or distributed way.
5 CONCLUSIONS
In this study we have presented an improvement on
a discretization method, in order to get better parti-
tions and better accuracy in the classification task with
small size datasets.
The discretization method is divided into two
phases. On the one hand, in the first phase the method
uses a fuzzy decision tree to search possible cut points
to create partitions. On the other hand, in the sec-
ond phase a genetic algorithm is used to construct the
fuzzy partitions taking as input data, the cut points
obtained in the first phase.
The way to improve the discretization method is
using a bagging process into the two phases. The
capacity of bagging to improve the accuracy of un-
stable classifiers is exploited in the first phase of the
method based on fuzzy decision trees. In addition, the
use of the bagging procedure allows the discretization
of more attributes when datasets have a few training
examples compared with the number of attributes, in
other word, when the rule |E| ≥ 10 ·|A| ·|C| is not ver-
ified.
Also we have presented several experiments
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
210

where the new proposed method using bagging gets
better accuracy in classification with this kind of
datasets. These conclusions have been validated by
applying statistical techniques to analyze the behav-
ior of different methods in the experiments.
Improve the discretization of numerical attributes
in small size datasets is important like previous step to
carry out feature selection in microarrays data which
is a topic of current interest and we want to carry out
the feature selection using a fuzzy ensemble which
needs a partition of the numerical attributes.
ACKNOWLEDGEMENTS
Supported by the project TIN2011-27696-C02-02 of
the Ministry of Economy and Competitiveness of
Spain. Thanks also to “Fundaci
´
on S
´
eneca - Agen-
cia de Ciencia y Tecnolog
´
ıa de la Regi
´
on de Murcia”
(Spain) for the support given to Raquel Mart
´
ınez by
the scholarship program FPI.
REFERENCES
Antonelli, M., Ducange, P., Lazzerini, B., and Marcel-
loni, F. (2011). Learning knowledge bases of multi-
objective evolutionary fuzzy systems by simultane-
ously optimizing accuracy, complexity and partition
integrity. Soft Computing, 15:2335–2354.
Armengol, E. and Garc
´
ıa-Cerdana, A. (2012). Refining dis-
cretizations of continuous-valued attributes. In The
9th International Conference on Modeling Decisions
for Artificial Intelligence, pages 258–269.
Au, W. H., Chan, K. C., and Wong, A. (2006). A fuzzy ap-
proach to partitioning continuous attributes for classi-
fication. IEEE Tran, Knowledge and Data Engineer-
ing, 18(5):715–719.
Bonissone, P. P., Cadenas, J. M., Garrido, M. C., and
D
´
ıaz-Valladares, R. A. (2010). A fuzzy random for-
est. International Journal of Approximate Reasoning ,
51(7):729–747.
Breiman, L. (1996a). Bagging predictors. Maching Learn-
ing, 24(2):123–140.
Breiman, L. (1996b). Heuristics of instability and sta-
bilization in model selection. Annals of Statistics,
24(6):2350–2383.
Cadenas, J. M., Garrido, M. C., Mart
´
ınez, R., and Bonis-
sone, P. P. (2012a). Extending information processing
in a fuzzy random forest ensemble. Soft Computing,
16(5):845–861.
Cadenas, J. M., Garrido, M. C., Mart
´
ınez, R., and Bonis-
sone, P. P. (2012b). Ofp class: a hybrid method to
generate optimized fuzzy partitions for classification.
Soft Computing, 16:667–682.
Cox, E. (2005). Fuzzy Modeling and Genetic Algorithms
for Data Mining and Exploration. Morgan Kaufmann
Publishers, New York, USA.
Der-Chiang, L. and Chiao-Wen, L. (2012). Extending at-
tribute information for small data set classification.
IEEE Transactions on Knowledge and Data Engineer-
ing, 24:452–564.
Der-Chiang, L., Chien-Chih, C., Che-Jung, C., and Wu-
Kuo, L. (2012). A tree-based-trend-diffusion predic-
tion procedure for small sample sets in the early stages
of manufacturing systems. Expert Systems with Appli-
cations, 39:1575–1581.
Diaz-Uriarte, R. and de Andr
´
es, S. A. (2006). Gene selec-
tion and classification of microarray data using ran-
dom forest. BMC Bioinformatics, 7(3).
Dimitrova, E. S. and Vera-Licona, M. P. (2010). Discretiza-
tion of time series data. Journal in Computational Bi-
ology, 17(6):853–868.
Frank, A. and Asuncion, A. (2010). UCI Machine Learning
Repository. University of California, Irvine, School of
Information and Computer Sciences.
Garc
´
ıa, S., Fern
´
andez, A., Luengo, J., and Herrera, F.
(2009). A study statistical techniques and perfor-
mance measures for genetics-based machine learn-
ing: accuracy and interpretability. Soft Computing,
13(10):959–977.
Ihaka, R. and Gentleman, R. (1996). R: A language for data
analysis and graphics. Journal of Computational and
Graphical Statistics, 5(3):299–314.
Jain, A. K. (2000). Statistical pattern recognition: A review.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 22:4–37.
Kianmehr, K., Alshalalfa, M., and Alhajj, R. (2010). Fuzzy
clustering-based discretization for gene expression
classification. Knowledge and Information Systems,
24:441–465.
Liu, B., Cui, Q., Jiang, T., and Ma, S. (2004). A com-
binational feature selection and ensemble neuralnet-
work method for classification of gene expression
data. BMC Bioinformatics, 5(1).
O’Reilly, C. A. (1982). Variations in decision makers’ use
of information sources: the impact of quality and ac-
cessibility of information. Academy of Management
Journal, 25(4):756–771.
Qureshi, T. and Zighed, D. A. (2009). A soft discretization
technique for fuzzy decision trees using resampling.
Intelligent Data Engineering and Automated Learning
- IDEAL 2009, Lecture Notes in Computer Science,
5788:586–593.
Unler, A. and Murat, A. (2010). A discrete particle swarm
optimization method for feature selection in binary
classification problems. European Journal of Oper-
ational Research, 206:528–539.
Wang, C., Wang, M., She, Z., and Cao, L. (2012). Cd: A
coupled discretization algorithm. Advances in Knowl-
edge Discovery and Data Mining Lecture Notes in
Computer Science, 7302:407–418.
Wang, Y. and Witten, I. (1997). Inducing model trees for
continuous classes. In Proceedings of the poster pa-
ImprovingaFuzzyDiscretizationProcessbyBagging
211

pers of the european conference on machine learning,
pages 128–137, Prague.
Zararsiz, G., Elmali, F., and Ozturk, A. (2012). Bagging
support vector machines for leukemia classification.
IJCSI International Journal of Computer Science Is-
sues, 9(1):355–358.
Zhu, Q., Lin, L., Shyu, M. L., and Chen, S. C. (2011).
Effective supervised discretization for classification
based on correlation maximization. In IEEE Interna-
tional Conference on Information Reuse and Integra-
tion (IRI), pages 390–395.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
212
