Evaluating Neuromodulator-controlled Stochastic Plasticity for Learning

Recurrent Neural Control Networks

Christian W. Rempis, Hazem Toutounji and Frank Pasemann

Institute of Cognitive Science, AG Neurocybernetics, Osnabrueck University, 49076 Osnabrueck, Germany

Keywords:

Neuromodulation, Benchmark, Learning, Sensori-motor Loop, Neurorobotics.

Abstract:

Learning recurrent neural networks as behavior controllers for robots requires measures to guide the learn-

ing towards a desired behavior. Organisms in nature solve this problem with feedback signals to assess their

behavior and to reﬁne their actions. In line with this, a neural framework is developed where the synaptic

learning is controlled by artiﬁcial neuromodulators that are produced in response to (undesired) sensory sig-

nals. To test this framework and to get a base line to evaluate further approaches, we perform ﬁve classical

benchmark experiments with a simple random plasticity method. We show that even with this simple plasticity

method, behaviors can already be found for all experiments, even for comparably large networks with over

90 plastic synapses. The performance depends strongly on the complexity of the task and less on the chosen

network topology. This suggests that controlling learning with neuromodulators is a viable approach that is

promising to work also with more sophisticated plasticity methods in the future.

1 INTRODUCTION

One of the major challenges in the ﬁeld of neuro-

robotics is to enable a robot to autonomously learn

neural networks as behavior controllers in the sensori-

motor loop. In this domain, efﬁcient learning meth-

ods are rare due to the difﬁculties inherent to learn-

ing in recurrent neural networks. Although some ap-

proaches have been reported (Soltoggio and Stanley,

2012; Pitonakova, 2012; D

urr et al., 2008; Hoinville

and H

enaff, 2004; Floreano and Urzelai, 2001), the

learning usually takes place in very small networks or

with network topologies very speciﬁcally adapted to

the task. One problem is to provide a proper feedback

signal, preferably generated by the network itself, to

guide the learning towards the desired behavior. This

problem can be addressed by extending the neural net-

work with a neuromodulator (NM) layer (Buckley,

2008; Doya, 2002; Fellous and Linster, 1998) that

enables the modulation of the learning process as re-

action to the observed behavior. A second problem

is the difﬁculty to decide, whether a synaptic weight

should be increased or decreased. In contrast to clas-

sical feedforward training, neither the desired output,

nor the actual effect of a weight change is known. In-

creasing and decreasing a synapse in such a network

may have the same effect on the behavior, depending

on the other parts of the network. Hence, the direct-

edness of the learning is a problem, because there are

no convincing heuristics about the correct direction of

a weight change.

To systematically examine these problems, we

presented a ﬁrst framework for feedback driven learn-

ing with neuromodulator networks in (Rempis et al.,

2013). This framework (Sect. 2) allows the descrip-

tion of a desired behavior in terms of modulator sub-

networks, small network structures that monitor the

behavior of the robot and stimulate so-called neuro-

modulator cells (NMCs) in response to undesired or

beneﬁcial behavior. Stimulated NMCs produce neu-

romodulators to trigger or inhibit plastic changes.

In the previous work we could show, that even

with a trivial plasticity method – random weight

changes – simple behaviors like obstacle avoidance,

locomotion and tropisms can be learned successfully

from scratch. In accordance with Ashby’s ultrastable

systems (Ashby, 1960), such networks stabilize in a

desired behavior after a while and keep that behavior

until a failure triggers further plastic changes to ﬁnd a

better suited network conﬁguration.

In this contribution, we provide a further analysis

of the performance and the limitations of this simple

approach. For this, we deﬁne ﬁve benchmark exper-

iments and test the learning performance with differ-

ent topologies of plastic network structures. These

benchmarks, among others, will serve as a base for

489

W. Rempis C., Toutounji H. and Pasemann F..

Evaluating Neuromodulator-controlled Stochastic Plasticity for Learning Recurrent Neural Control Networks.

DOI: 10.5220/0004554504890496

In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 489-496

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

comparing more sophisticated learning approaches

currently under development. However, the bench-

marks may be of general interest for comparing dif-

ferent approaches against the simple random search

to ensure that the methods are, indeed, better.

In the next section we describe the modulator

network model with the simple random plasticity

method, followed by an introduction of the bench-

marks. Then, the results of the learning experiments

are discussed, in particular the limitations and charac-

teristics of this learning approach.

2 METHODS

A modulated neural network (MNN) can be based

on any kind of standard artiﬁcial neural network, ex-

tended by a neuromodulator layer (Buckley, 2008).

Some related approaches, though more specialized,

are e.g. GasNets (Husbands, 1998), Artiﬁcial En-

docrine Systems (Timmis et al., 2009) and Artiﬁcial

Hormone Systems (Moioli et al., 2009).

Our variant of a NM layer provides neuromodula-

tor cells (NMCs) that maintain spatial distributions of

NM concentrations as part of the network. NM pro-

duced by a NMC usually diffuses into the surround-

ing tissue and inﬂuences nearby network structures.

Each NMC represents a single source for a speciﬁc

NM type and maintains its own concentration level

and distribution within the network. The NM concen-

tration c(t, x, y) at each point in the network at time

t is the sum of all locally maintained concentration

levels c

(t, x, y) at that position.

NMCs are always in one of two modes: In produc-

tion mode the cell may increase its modulator concen-

tration, in reduction mode it may decrease it. To enter

the production mode, a NMC must be stimulated for

some time, whereas it falls back into reduction mode

when it was not stimulated for a while. Usually, the

concentration of the NM and its area of inﬂuence in-

crease and decrease depending on the current stimu-

lation and mode.

2.1 Linearly Modulated Neural

Networks (LMNN)

The speciﬁc variant of the modulated neural network

used for the ﬁrst presented experiments is based on

the standard discrete-time neuron model given by

(t + 1) = τ

(θ

∑

j=1

i j

(t))), i, j = 1, . . . , n (1)

where o

(t) is the output of the neuron i at a dis-

crete time step t, w

i j

is the weight of the synapse from

neuron j to neuron i, θ

is a bias term of neuron i and

a transfer function, for instance tanh.

The stimulation of NMCs follows a simple lin-

ear model. Each NMC is attached to a neuron and

is stimulated when the output of this neuron is within

a speciﬁed range [S

min

, S

max

]. At each time step t, in

which the NMC is stimulated, its stimulation level s

increases by a small amount given by parameter S

gain

If not stimulated, it decreases by S

drop

. If the stimula-

tion level exceeds a given threshold T

prod

, the NMC

enters the production mode. If the level decreases be-

low a second threshold T

red

, the NMC re-enters the

reduction mode. This allows the deﬁnition of various

delays and hysteresis effects between the two modes,

which is an important prerequisite for stable learning

(see Sect. 3).

(t + 1) =

(

min(1, s

(t) + S

gain

) if S

min

≤ o

(t) ≤ S

max

max(0, s

(t) − S

drop

) otherwise

(2)

In production mode the modulator concentration

c and the radius r of, here, a circular diffusion area

are increased from 0 to C

max

and R

max

respectively.

During reduction mode both decrease again. The rate

of change of the concentration is given by parameters

gain

and C

drop

, that of the radius similarly by R

gain

and R

drop

. Equation 3 shows this for the concentration

level c

; the area radius r

is deﬁned analogously.

(t +1) =











min(C

max

, c

(t) +C

gain

)

if production mode

and still stimulated

max(0, c

(t) −C

drop

)

if reduction mode

and not stimulated

(t) otherwise

(3)

The diffusion mode of each NMC can be chosen,

so that the NM concentration is either constant across

the diffusion area, or decays according to a linear or

nonlinear function of the distance to the NMC. The

inhomogeneous distributions are interesting for sce-

narios with local learning. However, in the shown ex-

amples, we will restrict the experiments to a homoge-

neous, global modulation to demonstrate that success-

ful controllers can develop even in this simple case.

2.2 Plasticity via Modulated Random

The synapses of the network react to NM exposure

with plastic changes. To demonstrate the viability of

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

490

Table 1: Parameters of a NMC in a LMNN.

Parameter Description

Type The NM type produced by this NMC

min

, S

max

Stimulating neuron activation range

gain

, S

drop

Rate of stimulation gain and drop

prod

, T

red

Pro- and reduction mode thresholds

max

Max. concentration level of this NMC

gain

drop

Rates of concentration gain and drop

max

Max. radius of the diffusion area

gain

, R

drop

Rates of diffusion area gain and drop

using neuromodulation to control the learning pro-

cess, we choose one of the most simple plasticity

methods available: Random weight changes. We

chose this stochastic plasticity method because it is

vastly unbiased and is capable of ﬁnding all kinds

of network topologies and weight distributions within

a given network substrate. Furthermore, the method

does not require any heuristics for the choice of the

network topology, except that solutions are possible

with the given structure.

For a synapse i, the probability of a weight change

at time t is the product of an intrinsic weight

change probability W

and the current NM concen-

tration c(t, x, y) at the position (x

, y

) of the synapse.

Hereby, each synapse may limit its sensitivity to NM

to a maximal concentration level M

to prevent too

rapid changes when large amounts of overlapping

NMs are present.

(t) = min(M

, c(t, x

, y

))W

, 0 < W

≪ 1 (4)

Stochastic weight changes may occur at any time

step, therefore W

must be very small. If a weight

change is triggered, a new weight w

is randomly cho-

sen from the interval [W

min

max

], given as parame-

ters of the synapse.

In addition to weight changes, synapses can also

disable and re-enable themselves following a similar

stochastic process. The probability p

for a transition

between the two states during each time step is the

product of the modulator concentration c(t, x, y) and

the disable probability D

(t) = min(M

, c(t, x

, y

))D

, 0 ≤ D

< W

(5)

If a transition is triggered, an enabled synapse be-

comes disabled and vice versa. A disabled synapse

is treated as a synapse with weight w

= 0, but its

actual weight is preserved until it is enabled again.

This mechanism allows for a simple topology search

within a given neural substrate.

Table 2: Parameters of a Modulated Random Search

synapse.

Parameter Description

Type The NM type the synapse is sensitive to

W Weight change probability

D Disable / enable probability

min

max

Min. and max. weight of the synapse

M Max. NM sensitivity limit of the synapse

3 EXPERIMENTS

3.1 Robots, Tasks and Environments

The experiments use robot systems typical for clas-

sical benchmark problems: a differential drive robot

(Fig. 1-e) and a simple pendulum (Fig. 1-f). In all

cases, motor neurons with an activation range [-1,1]

control the desired velocity of the motors. Negative

activations are interpreted as backwards rotation. The

differential drive robot is equipped with distance sen-

sors (DS) at the front, eight touch sensors (TS), three

ambient light sensors (ALS) to measure brightness

at three equally distributed positions on the robot,

and three directed light sensors (DLS) in the front of

the robot to sense the direction towards light sources

(with a maximal viewing angle of ±90 degrees). For

simplicity, light can penetrate obstacles freely. The

pendulum is equipped with an angular sensor for the

current angle of the pendulum. All experiments have

been simulated with the NERD Toolkit (Rempis et al.,

2010) and can be replicated with material from our

supplementary page.

The ﬁrst experiment (E1) is a positive light

tropism task (Fig. 1-a). Four light sources are dis-

tributed in some distance from the corners of a

quadratic arena. At any time, only one light source

is switched on. Each light source is bright enough to

cover the entire arena. When the robot arrives at that

light source, it is switched off and a randomly chosen

source is switched on.

The second experiment (E2) focuses on an obsta-

cle avoidance task (Fig. 1-b), where the robot has

to navigate in a quadratic environment riddled with

round objects and sharp corners. The arena also com-

prises a number of light sources each emitting a differ-

ent, homogeneous light that allow the robot to recog-

nize different locations and hence to monitor its own

exploration behavior.

As a combination of the previous experiments, E3

extends the ﬁrst experiment with four small obstacles

placed with a small asymmetric shift near the four

EvaluatingNeuromodulator-ControlledStochasticPlasticityforLearningRecurrentNeuralControlNetworks

491

a b

Figure 1: The differential drive robot (f) with three of the

environments (a-d) and the simulation of the pendulum (e).

The white spheres in (b,d) denote possible light source po-

sitions.

light sources (Fig. 1-c). Here, the robot has to ap-

proach the lights and simultaneously avoid the obsta-

cles next to the light sources.

A more difﬁcult variant is experiment E4. While

the task remains the same, there are now larger obsta-

cles in the middle of the arena and one of the corners

is more narrow (Fig. 1-d). Furthermore, a ﬁfth light

source was added in the center of the arena. All lights

are now also randomly moved away from their initial

positions every time they get switched on. In contrast

to E3 the robot now gets confronted with many more

different light-obstacle combinations, which makes

the task quite difﬁcult.

The pendulum experiment (E5, Fig. 1-e) requires

the controller to learn to swing with a speciﬁc ampli-

tude between the two target angles ±65

◦

with a toler-

ance of ±5

◦

. The difﬁculty is that the motors are too

weak to get to the target angles without swinging the

pendulum up ﬁrst.

3.2 Control Sub-Networks (CSN)

Each CSN includes the necessary sensory and motor

neurons, a number of intermediate processing neu-

rons and a bias neuron. The latter allows the bias of

neurons to be changed using the same technique as

used for other synapses. The network substrates vary

over the different experiments, ranging from trivial

feed-forward networks over a layered network with

4 hidden neurons, to fully connected, recurrent net-

works with 2, 4 and 6 intermediate neurons. The net-

Table 3: Experiment setups. τ

exp

is the experiment time in

simulated minutes, τ

temp

is the duration in minutes with-

out neuromodulation production to consider a behavior a

successful temporary solution. See text for further descrip-

tions.

Exp. τ

exp

temp

Sensors NMC Modules

E1 120 0.5 2 DLS Light

E2 240 5 3 DS Obst, Drive, Explore

E3 720 0.75 2 DS, 2 DLS Light, Obst

E4 720 0.75 2 DS, 2 DLS Light, Obst

E5 240 5 1 AS 2 × TurningAngle

work conﬁgurations for the experiments are summa-

rized in Table 3.

3.3 Modulatory Sub-Networks (MSN)

Each MSN uses experiment-speciﬁc network struc-

tures to detect undesired behavior based on (sensor)

activations to produce NMs when needed. As a re-

action to the NMs, synapses of the CSN randomly

change and explore different topologies and weight

distributions. This has an effect on the behavior and,

accordingly, on the NM production in the MSN. Simi-

lar to the work by Ashby (Ashby, 1960), the system is

destabilized when an undesired behavior is detected,

leading to continuous changes until the system stabi-

lizes again in a new, valid conﬁguration. In this spirit,

six different NMCs are used in the experiments:

The Obst cell reacts on the activation of any of the

eight force sensors to detect undesired contact with

objects. The stimulation is quite rapid so that obstacle

contact immediately leads to NM production to alter

the behavior.

Drive gets stimulated when the two motor signals

are too low, the robot is moving backwards, or the dif-

ference of the motors becomes too large, i.e. the robot

is moving in narrow circles. Because the desired be-

havior also may include moving backwards and espe-

cially moving in circles, the stimulation is less rapid

and tolerates such movements as long as they do not

dominate the behavior.

Explore is stimulated when the robot is not enter-

ing the detectable locations frequently. Its associated

modulating network classiﬁes the signal of one of the

ambient light sensors into the nine detectable loca-

tions (inspired by place cells (O’Keefe and Dostro-

vsky, 1971)) and integrates these signals to deter-

mine the duration of each location not being visited.

Explore is stimulated if some locations have not been

visited for a long time. If a location is entered that has

not been visited for a long time, then all integrator

neurons for all locations are inhibited, so this poten-

tial behavior improvement already leads to a fast NM

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

492

CSN

MSN

CSN

MSN

ObstLight

ObstDrive

Explore

Disabled Synapse

NMC Neuron

Sensor Motor

Bias

Loc1

Loc2 Loc8 Loc9

...

E2 E3

Figure 2: Network for Pendulum, Network for Pole Bal-

ancer.

decrease to allow the new conﬁguration to be tested.

The Light cell also uses an auxiliary network that

interprets the ambient light sensors to detect whether

the robot is getting closer to the light. If not, the NMC

is stimulated.

TurningAngle gets persistently, but slowly stim-

ulated over time. However, if the pendulum changes

its swinging direction within the desired angle range,

then the NMC stimulation decreases rapidly. The de-

sired angular range can be adjusted independently for

each of the two NMCs in the pendulum networks.

Table 3 shows which NMCs, with their corre-

sponding auxiliary networks, are used in each ex-

periment. Figure 2 shows the structure of both the

CSN and the MSN for experiments E2 and E3, giv-

ing also the neural structures for the six auxiliary sub-

networks.

The experiments here are restricted to a global

modulator release with a uniform concentration lev-

els. For a discussion, see (Rempis et al., 2013). Table

4 summarizes the parameter choices for the NMCs

used across the experiments.

3.4 Experiments Setup

Each experiment has been run with ﬁve different net-

work substrates for the CSN: a layered network with

4 intermediate neurons (L4) and four fully, recurrently

connected networks with 0, 2, 4 and 6 intermedi-

ate processing neurons (N0-N6). Due to the differing

number of motors and sensors, the total number of

synapses varies. An overview can be found in table

5. All additional settings of the network, speciﬁcally

the settings for the plastic synapses and the NMC set-

tings, have been ﬁxed at the values given in tables 4.

Each such learning scenario (experiment + net-

work substrate) has been repeated 50 times with iden-

tical settings, each starting with a new CSN composed

of disabled synapses with zero weights. Thus, the en-

tire network topology and the synaptic weights had

to be learned from scratch within the given network

substrate.

4 RESULTS AND DISCUSSION

For all experiments and with all but one of the dif-

ferent network substrates, solutions have been found

within the given time windows. All behaviors dis-

covered in this way have been sufﬁciently effective

and comply with the desired and expected behaviors.

However, as can be seen in ﬁgure 3, by far not all

runs did ﬁnally end up with a proper behavior network

during the limited learning time. Consistent with in-

tuition, the easier the task is, the larger the percentage

of successful learning trials.

The simple light tropism task, therefore, led to

successful behaviors in almost all cases, despite its

comparably short learning time of up to only two

hours. Also, the ﬁnal solutions have been found very

fast (Fig. 4A-E1) without many intermediate temporal

solutions (Fig. 4C-E1).

In contrast, the almost similarly short duration of

the obstacle avoidance task with four hours seems to

be much too low to consistently ﬁnd solutions, con-

trary to our expectation. Therefore, only about half

of the experiments were successful. A reason for

this may be the relatively slow detection of insufﬁ-

cient exploration behavior with the Explore NMC.

This modulator has to react with a larger delay to give

the networks a chance to actually do exploration. So,

behaviors violating the exploration condition – while

still doing a ﬁne obstacle avoidance – are detected

only after a signiﬁcant delay. Also, such intermediate

solutions get destroyed quite easily when a bad ex-

ploration behavior is detected, leading to the destruc-

tion – not to a reﬁnement – of the temporary solu-

tion. This, obviously, is one of the major limitations

of the stochastic search: due to the missing directed-

ness of the learning, temporary solutions are usually

not improved, but rather destroyed and replaced by

very different networks. This can be seen in ﬁgure

4E that shows the average differences per synapse be-

tween two successive (temporary) solutions. Indepen-

dently of the chosen architecture and the experiment,

this difference is quite large with ≈ 0.5 per synapse

EvaluatingNeuromodulator-ControlledStochasticPlasticityforLearningRecurrentNeuralControlNetworks

493

Table 4: Parameter values for NMCs in the experiments.

Param. Obst Drive Explore Light TurningAngle Param. Synapses

min

, S

max

0.9,1.0 0.9,1.0 0.4,1.0 0.9,1.0 0.5,1.0 W 0.0001

gain

, S

drop

0.01,0.01 0.001,0.001 0.001,0.01 0.0002,0.0001 0.005,1 D 0.00002

prod

, T

red

0.95,0.95 0.95,0.95 0.95,0.95 0.99,0.99 0.95,0.95 W

min

−1.5

max

2 1 1 1 1 W

max

1.5

gain

drop

0.1,0.1 0.001,0.01 0.001,0.01 0.01,0.1 0.001,1 M 1.0

100

E1 E2 E3 E4 E5

L4N4

Figure 3: Percentage of successful experiments with stable

solutions. The gray tips indicate the number of temporary

solutions with a continuous modulator-free behavior during

at least 30 minutes, which would be interpreted as solutions

in short-term evaluations.

Table 5: Number of plastic synapses in each of the exper-

iments. L4 provides a layered network with 4 neurons, all

others are fully connected.

Number of Processing Neurons

N0 N2 N4 N6 L4

E1 14 32 60 96 46

E2 10 28 54 88 42

E3 14 32 60 96 42

E4 14 32 60 96 42

E5 4 15 35 63 32

weight, which indicates large differences between the

networks. For the obstacle avoidance behavior this

means that large parts of the experimental time are

spent with enabled learning (Fig. 4D-E2) or in tem-

porary behaviors that are too short-lived to be consid-

ered by us being a temporary solution (< 5 minutes

without modulation, see ﬁgure 3).

The results for the combination of the two tasks

(E3) reﬂect the increasing difﬁculty of the task. Even

tough the experiment was simulated 12 hours per try,

only ≈ 20% of the runs lead to a fully stable behav-

ior. First temporary solutions have been found quite

fast (Fig. 4B-E3), but most light tropism behaviors

with only a partial obstacle avoidance behavior are

easily destroyed due to hitting one of the small ob-

stacles close to the light sources. Because the light

sources are approached with slightly different angles,

at some point a situation is encountered where the ob-

stacle avoidance behavior brieﬂy fails and the obsta-

100

150

200

400

600

200

400

600

100

150

200

100

150

200

400

600

200

400

600

100

150

200

100

150

200

400

600

200

400

600

100

150

200

0.5

E1 E2 E3 E4 E5

L4N4

Figure 4: (A) Time to ﬁnal solution. (B) Time to ﬁrst (tem-

porary) solution. (C) Number of (temporary) solutions. (D)

Minutes spent in learning mode. (E) Average changes per

synapse between successive (temporary) solutions.

cle is hit. This leads to a strong production of NM

and the behavior is usually destroyed. This alterna-

tion between many temporary solutions (Fig. 4C-E3)

and the subsequent network destruction, and thus long

phases with enabled plasticity (Fig. 4D-E3), describes

the typical way how network conﬁgurations are ex-

plored with the stochastic search: only if all require-

ments of the behavior are fully met with a single mu-

tation burst, the behavior remains stable in the long

run. This all or nothing approach is another limiting

characteristics of the simple stochastic search.

This becomes even more severe in the aggravated

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

494

0.5

1.5

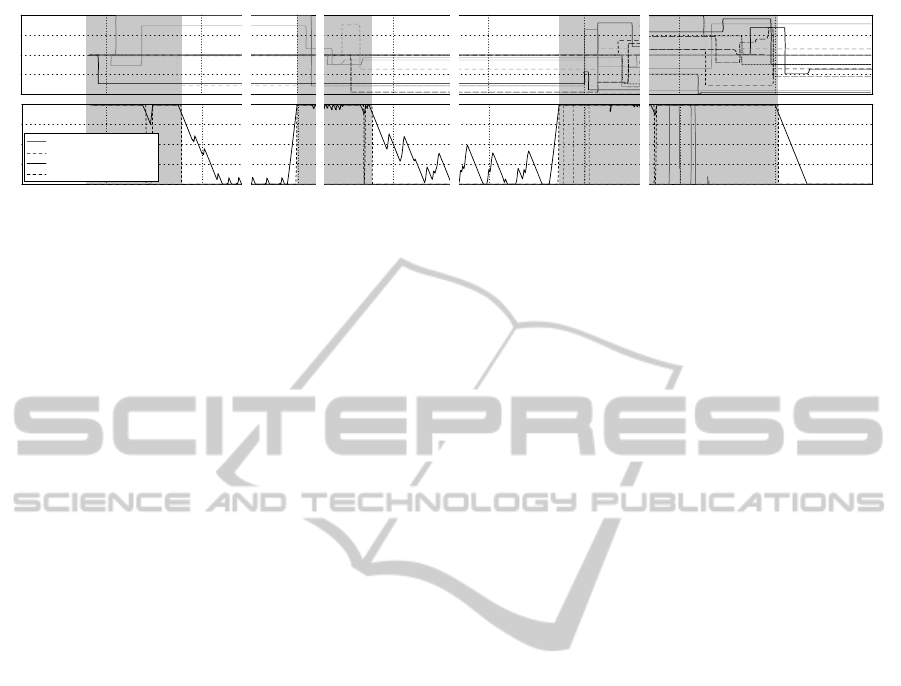
-1.5

Stimulation Obst

Concentration Obst

Stimulation Light

Concentration Light

Modulation Modulation Modulation

Stable Stable Final

Figure 5: Example run for the light tropism behavior, showing the alternation between stable and plastic states during the

behavior learning. The upper graph shows the individual weights over time, the lower graph the stimulation and concentration

level of the two NMCs.

variant of this experiment (E4), in which large and

more various obstacles enforce the robot to do sig-

niﬁcant detours against the desired direction towards

the light. Here, a proper behavior requires a ﬁne tun-

ing of weights, which makes it much more difﬁcult

to accidentally stumble upon a working network. The

percentage of ﬁnal solutions, therefore, is even lower

with only about 10%. However, the number of long-

term temporary solutions with a continuous runtime

of more than 30 minutes exceeds the number of stable

solutions by a factor of ≈ 2 (Fig. 3E4). These behav-

iors would in many evaluations with a short test (e.g.

evolutionary algorithms) already be considered solu-

tions, but it shows that even slight weaknesses due

to an unfortunate sequence of target light sources can

lead to a destruction of such almost stable networks

in the long run. As in E3, temporary solutions are

found quite fast (Fig. 4B-E4), but are destroyed later,

so that most of the time is spent trying new network

conﬁgurations (Fig. 4D-E4).

The pendulum behavior again is an example of a

simpler single-goal task. The number of successful

runs is, with almost 50%, quite high and the networks

are also found fast within the ﬁrst 2 hours (of a total

of 4 hours). Due to the characteristics of the exper-

iment, there are almost no temporary solutions: if a

solution is found, then this solution tends to be sta-

ble in the long run, because there are no disturbances

in the simple pendulum motion (compare Fig. 4A-E5,

4B-E5, and 4C-E5).

An interesting observation can be made concern-

ing the network complexity. It was expected, that the

performance of the experiments primarily depends on

the size of the neural substrate, because with an in-

creasing search space the probability of ﬁnding a sta-

ble solution should drop down signiﬁcantly. However,

at least for the network sizes used in these experi-

ments, there is only a small inﬂuence of the network

substrate on the performance (Fig. 3). Only in E2 the

largest network showed a signiﬁcant drop in the num-

ber of solutions compared to the other substrates in

the same experiment. And in E5 it seems that the

layered network has an advantage over the fully re-

current neural networks. This may indicate, that – as

long as the topology can vary within the substrate –

there are similar or equivalent network conﬁgurations

contained in all substrates and that with an increas-

ing number of synapses, the fraction between feasible

and improper network conﬁgurations may remain in

the same order of magnitude. In forthcoming experi-

ments, larger networks have to be tested to ﬁnd the ac-

tual limiting size for this simple class of robot exper-

iments. In these experiments, anyway, the impact of

the chosen experiment complexity has a much higher

impact on the performance than the chosen network

substrate, so the major effort in designing such ex-

periments should probably be focused on deﬁning a

well suited experiment, not on choosing a particularly

suited network substrate.

To examine the learning process in more detail,

ﬁgure 5 shows the weight changes and the related

neuromodulator concentrations for one of the learn-

ing runs in experiment E2. As expected, the weight

changes in learning phases are random and undi-

rected. However, from time to time, the system sta-

bilizes in a network conﬁguration, because no neuro-

modulator is produced as a response to the (partially)

working behavior. It can also be seen in the lower

part of ﬁgure 5 that even during these stable states,

the stimulation of the NMCs is not just zero, but that

their stimulation level remains active, though not high

enough to enter their production mode. So, slight vi-

olations of the behavior restrictions still take place,

but these violations are not strong enough to be in-

terpreted as a failing behavior. But if the stimulation

level exceeds the limit to production mode, then of-

ten one of the ﬁrst random changes destabilizes the

system so much, that other neuromodulators are trig-

gered as side-effect. This leads to a strong relearn-

ing, usually destroying the previous temporary solu-

tion, until the modulation stops when a new poten-

tially working conﬁguration has been found.

EvaluatingNeuromodulator-ControlledStochasticPlasticityforLearningRecurrentNeuralControlNetworks

495

5 CONCLUSIONS

We demonstrated with ﬁve typical experiments from

the ﬁeld of robot learning and early evolutionary

robotics, that a simple random search on a given net-

work topology is sufﬁcient to ﬁnd many suitable so-

lutions, as long as the network changes are started

and stopped by a reasonable feedback signal. In our

case, this feedback is realized with neuromodulators

that are triggered as a reaction to the sensed behav-

ior. Because of this, and the simplicity of the im-

plementation, the learning should also work directly

on physical robots without external supervision. The

benchmarks show that the feasibility of the method

strongly depends on the experiment complexity, not

so much on the chosen network substrate. Also, tem-

porary solutions appear and get relearned when the

behavior proves ineffective in some situations. These

aspects – already available in such a simple approach

– are highly desired in the ﬁeld of robot learning to

allow adaptive, self-contained robots with life-long

learning capabilities. The method, however, is not

meant to be used as a competitive learning paradigm

for real robots. Instead, one intention of the bench-

mark is to provide a minimal testbed to evaluate new

learning paradigms for recurrent neural networks in

the sensori-motor loop. These paradigms should be

better in some aspects compared to such a simple ran-

dom search to justify their usually much higher com-

plexity. For this, the benchmarks are also publicly

available at the supplementary page.

Supplementary Material can be found at:

nerd.x-bot.org/neuromodulator-benchmarks

ACKNOWLEDGEMENTS

This work was partially funded by DFG-grant PA

480/7-1. We thank Josef Behr and Florian Ziegler for

testing and reﬁning the simulation model and for their

contributions to the NERD toolkit.

REFERENCES

Ashby, W. R. (1960). Design for a brain: The origin of

adaptive behavior (2nd edition). Chapman and Hall,

London UK.

Buckley, C. L. (2008). A systemic analysis of the ideas im-

manent in neuromodulation. PhD thesis, University of

Southampton.

Doya, K. (2002). Metalearning and neuromodulation. Neu-

ral Networks, 15(4-6):495–506.

urr, P., Mattiussi, C., Soltoggio, A., and Floreano, D.

(2008). Evolvability of neuromodulated learning for

robots. In Proc. of the 2008 ECSIS Symposium on

Learning and Adaptive Behavior in Robotic Systems,

pages 41–46.

Fellous, J. and Linster, C. (1998). Computational models

of neuromodulation. Neural Computation, 10(4):771–

805.

Floreano, D. and Urzelai, J. (2001). Neural morphogene-

sis, synaptic plasticity, and evolution. Theory in Bio-

sciences, 120(3):225–240.

Hoinville, T. and H

enaff, P. (2004). Comparative study of

two homeostatic mechanisms in evolved neural con-

trollers for legged locomotion. In Proc. of IEEE/RSJ

International Conference on Intelligent Robots and

Systems, IROS 2004, volume 3, pages 2624–2629.

Husbands, P. (1998). Evolving robot behaviours with

diffusing gas networks. In Proc. of Evolutionary

Robotics, EvoRob’98, volume 1468 of LNCS, pages

71–86. Springer.

Moioli, R., Vargas, P., and Husbands, P. (2009). A multiple

hormone approach to the homeostatic control of con-

ﬂicting behaviours in an autonomous mobile robot. In

Proc. of IEEE Congress on Evolutionary Computa-

tion, CEC’09, pages 47–54.

O’Keefe, J. and Dostrovsky, J. (1971). The hippocampus as

a spatial map: Preliminary evidence from unit activity

in the freely-moving rat. Brain Research, 34(1):171–

175.

Pitonakova, L. (2012). Ultrastable neuroendocrine robot

controller. Adaptive Behavior, 21(1):47–63.

Rempis, C. W., Thomas, V., Bachmann, F., and Pasemann,

F. (2010). NERD - Neurodynamics and Evolutionary

Robotics Development Kit. In SIMPAR 2010, volume

6472 of LNAI, pages 121–132. Springer.

Rempis, C. W., Toutounji, H., and Pasemann, F. (2013).

Controlling the learning of behaviors in the sensori-

motor loop with neuromodulators in self-monitoring

neural networks. In Workshop on Autonomous Learn-

ing at the IEEE International Conference on Robotics

and Automation, ICRA 2013.

Soltoggio, A. and Stanley, K. (2012). From modulated

hebbian plasticity to simple behavior learning through

noise and weight saturation. Neural Networks, 34:28–

41.

Timmis, J., Neal, M., and Thorniley, J. (2009). An adap-

tive neuro-endocrine system for robotic systems. In

Proc. of the IEEE Workshop on Robotic Intelligence

in Informationally Structured Space, RIISS’09, pages

129–136.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

496