
The Problem of Organizing and Partitioning Large Data Sets in
Learning Algorithms for SOM-RBF Mixed Structures
Application to the Approximation of Environmental Variables
José A. Torres, Sergio Martínez, Francisco J. Martínez and Mercedes Peralta
Dep. de Informática, University of Almería, 04120 Almería, Spain
Keywords: Neural Networds, Large Training Sets, SOM-RBF Mixed Model, Ensemble of Neural Networks,
Environmental Applications.
Abstract: The paper presents a technique to partition and sort data in a large training set for building models of envi-
ronmental function approximation using RBFs networks. This process allows us to make very accurate ap-
proximations of the functions in a time fraction related to the RBF networks classic training proccess. Fur-
thermore, this technique avoids problems of buffer overflow in the training algorithm execution. The results
obtained proved similar accuracy to those obtained with a classical model in a time substantially less, open-
ing, on the other hand, the way to the parallelization process using GPUs technology.
1 INTRODUCTION
The concept of subdividing a complex problem into
simpler ones whose solutions are the basis for con-
structing an overall solution is a much-studied field
in computing. The concept of modular networks was
first formalized by (Jacobs, 1991) as neuronal archi-
tecture in which different processing modules, with
different inputs can be distinguished, which use
different mechanisms than the final output, which, in
turn is a function of the outputs of the various mod-
ules. The concept of modularity is inherent to the
nervous system of living beings, where specialized
neuronal structures make interconnections in order
to realize superior capabilities (de Felipe, 1997). If
we restrict ourselves to the field of connectionist
computing, many authors have applied calculus
models based on the composition of neuronal classi-
fiers as a means of problem-solving. Thus, in a study
by (Arriaza et al., 2003), a system for classification
and detection of clouds in satellite images was de-
veloped in which the classification is processed by
means of a cascade of interconnected networks.
Perhaps, the most accepted model in this context
would be the utilization of specialized classifiers in
one domain of the problem, whose outputs are stud-
ied and treated by a subsequent function that deliv-
ers the final output.
These structures, known as Neural Network En-
sembles have been described in the literature as a
finite set of neural networks trained to perform a
common task, together with a process that combines
their outputs to obtain a general solution. This tech-
nique, combined with various techniques for recom-
bining outputs, generates systems with a greater
capacity for generalization than the simple neural
network models (Rao, 2005).
Radial basis function (RBF) networks are very
useful for solving problems where knowledge is
scarce, fitting non-adjustable functions using statis-
tical procedures and, in some cases, of conflicting
knowledge. RBFs were introduced in the literature
by (Broomhead, 1988) but it was (Poggio, 1990)
who later offered the technique that allows a RBF
the possibility of generalizing the solution of a prob-
lem.
2 RADIAL BASIS FUNCTION
NETWORKS
RBF networks make approximations of functions
that are scarcely known, that cannot be fitted using
statistical procedures and, in some cases, are contra-
dictory. RBFs were first described by (Broomhead,
1988), whilst (Poggio, 1990) offered the technique
by which an RBF could be applied to provide a
generalized solution to a problem. A RBF is a net-
497
Torres J., Martinez S., Martinez F. and Peralta M..
The Problem of Organizing and Partitioning Large Data Sets in Learning Algorithms for SOM-RBF Mixed Structures - Application to the Approximation
of Environmental Variables.
DOI: 10.5220/0004554604970501
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 497-501
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

work consisting of two levels: one level is construct-
ed from a set of kernel functions, called the radial
base functions, while the second, called the integra-
tion layer integrates the output of these functions in
a linear fashion.
RBFs networks have certain functional features
that make them attractive for solving problems, such
as:
• Pattern recognition
• Generalization of future events based on past
actions
• Non-linear regressions.
2.1 Training of a RBF Net
The scientific literature shows a number of RBF
networks training techniques.
We consider, however, these techniques are di-
vided into two blocks:
• Algorithms for exact alignment of the training
set. In this case the number of kernel functions
of the network is equal to the cardinal of the
training set.
• No exact training algorithms. In these algo-
rithms, the number of kernel functions is below
the cardinal of the training set.
For the present case, the process of training a
network using RBFs accurate approximation of all
the elements of the training set is the following:
In a set of m elements that belongs to a training
set E
mxn
= {e
1
, e
2
, …, e
m
} (with n characteristics per
sample), and where W = {w
1
,w
2
, … ,w
m
} are the
weights of the neurons that comprise the network,
the expression on which training of the RBF is based
is:
∑
∙
‖
‖
(1)
where φi the radial base function (Gaussian).
If we express this as a matrix we have (Haykin,
1994):
⋯
⋮⋱⋮
⋯
⋮
⋮
(2)
Thus, to obtain the unknown
(which is what the
training stage consists of), the expression would be:
⋮
⋯
⋮⋱⋮
⋯
⋮
(3)
2.2 Layout, Typeface, Font Sizes
and Numbering
The time required for the training process means that
it is very costly to train a RBF. If we analyse the
final expression of the training process, we observe
that to train a RBF we have two large operations
(Brassard, 1995):
• Finding the inverse of a m × m matrix: order of
complexity O(n3)
• Multiplying the two matrices: order of
complexity O(n3)
Although the order of complexity is polynomial
in some applications where the data set is very large,
the general algorithm is inapplicable, because there
are problems of buffer overflow and excessive CPU
time.
The use of non exact algorithms to solve the
problem at the expense of CPU time increase and /
or decrease the precision of approximation.
3 MIXED OPERATING MODEL
(SOM-RBF)
The proposed operational model, once trained,
makes use, on one hand, of a SOM reference vectors
to determine the "position" within the approximate
curve of the input vector, and furthermore, a set
RBFs networks formed, trained, each in the context
of the curve to approximate.
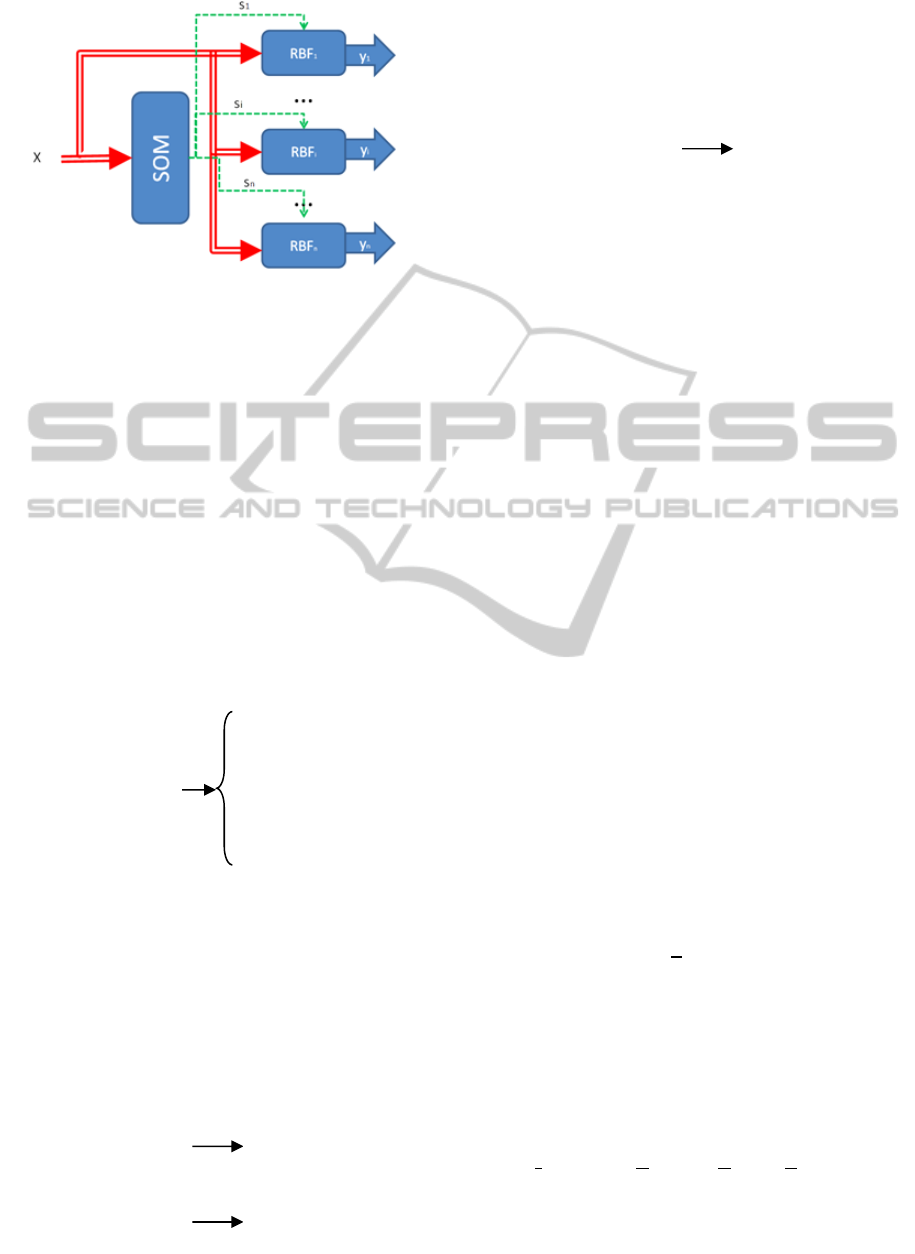
The proposed architecture is defined by a pair
{RBFi}, {Ci}, where {RBFi} is a set of RBFs
applied, one by one, to a subset of the input space,
and {Ci} are the reference vectors of a Self Organ-
izing Map (SOM). The vectors Ci act as activators
of the RBFs that have to be used for a given input.
Schematically, the model has the structure given in
Figure 1.
X is an input vector belonging to the input space,
SOM is a Self Organizing Map that generates an
output Si for a given input, and which operates as an
activation signal for the RBF, which is responsible
for generating the output. As the scheme shows, the
input X is also applied to each of the RBFs in this
structure, since it is they that really generate the
output.
3.1 Training the RBF-SOM Mixed
Operating Model
The new algorithm proposed in this paper consists of
dividing the training set into N subgroups and, in
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
498
,
⋯
,
⋮⋱⋮
∗∗,
⋯
∗∗,
z centroids
Figure 1: Structure of the RBF-SOM mixed Operating
Model. The signal s
i
enables or disables for each input
vector, a unique network of RBFs.
this way, creating N RBFs that approximate the
curve of the problem. To illustrate the process, we
start with a real situation: the process of approxima-
tion of an environmental variable, of which there are
16,000 samples obtained with 20 variables that de-
fine them.
Nevertheless, this division of elements from the
training set must be ordered rather than randomized.
The ordering process uses the SOMs described in
(Kohonen, 1990) as tools for separating and ordering
the training vectors.
Algebraically, the ordering process is as follows:
1. Make a preliminary random partition of the
training set into N groups:
(4a)
The reason for this (using a first partition at
random and not based on any statistical proce-
dure) is due to our efforts to reduce the compu-
tational requirements.
2. Training a SOM for each of the training sub-
sets. (In our case, we used a hexagonal topolo-
gy of p rows and k columns)
3. From step 2, we are interested in the p
∗
k cen-
troids of each of the SOMs.
(4b)
After this step, we will have N
∗
p
∗
k cen-
troids: C = {c1, c2, . . , cN
∗
p
∗
k}
4. Apply a new SOM to the set of centroids C, in
order to generate z new centroids:
(4c)
5. Use the z centroids to divide the elements of
the training set into z training subsets.
a. Measure the Euclidean distance of the train-
ing element to each centroid.
b. Calculate which is the minimum distance.
c. Assign the training element to the closest
training subset (as measured to its reference
centroid).
6. Train the z RBFs using the exact algorithm
procedure.
In this way, the product of the training is not a single
trained RBF, but z RBFs.
Faced with this change, when we undertake the
classification, we have to:
1. Check which RBF it is most suitable to use for
classification (using the Euclidean distances to
the centroids mentioned).
2. Classify using the RBF obtained.
3.2 Theoretical Study of the
Improvement
The improvement arises mainly from the fact that
the most costly operations of training the RBF,
namely the inverse of the matrix and the multiplica-
tion of the matrices together, do not have to be exe-
cuted so many times, since we are working with z
RBFs and not just a single RBF.
In this way, we can express the order of com-
plexity of both algorithms, after the proposed im-
provement, as:
∙
,
(5)
where z is the number of centroids and n the
number of elements in the matrices that must be
operated on.
Simply put, it can be demonstrated that a cubic
algorithm takes substantially less time to solve after
the improved method is applied. Let us see the theo-
retical demonstration.
↔
↔
↔1
↔
1(6)
Then, since z ≥ 1, we have z
2
≥ 1, and, therefore,
we conclude that the efficiency of the algorithm of
,
⋯
,
⋮⋱⋮
,
⋯
,
,
⋯
,
⋮⋱⋮
,
⋯
,
⋮
,
⋯
,
⋮⋱⋮
,
⋯
,
,
⋯
,
⋮⋱⋮
,
⋯
,
⋮
,
⋯
,
⋮⋱⋮
,
⋯
,
p*k centroids
p*k centroids p*k centroids p*k centroids
TheProblemofOrganizingandPartitioningLargeDataSetsinLearningAlgorithmsforSOM-RBFMixedStructures-
ApplicationtotheApproximationofEnvironmentalVariables
499

order ∙
is greater than that of an algorithm of
order n
3
.
This variation significantly delay the process of
polynomial growth, reducing the cost of memory
and CPU time.
4 CASE STUDY. MODELING
ECOLOGICAL VARIABLES
USING REMOTE SENSING
DATA
Within the framework of a study of environmental
variables, the objective of the present study has been
to substitute a RBF network used as an approxima-
tion function for the ecological variables, by a RBF
structure that approximates these variables with
comparable precision, but with shorter training
times.
The study of ecological variables is a fundamen-
tal component of the environmental sciences, for
environmental impact analysis and for determining
ecological partitions in a geographical area. This
work is essentially carried out by means of costly
field surveys, which require heavy investment and
slow down the rate at which results can be obtained.
The use of satellite information to obtain the same
data comprises an effective tool that is quick and of
modest cost.
Nevertheless, there is a need to understand the
relationship between the satellite information and
the ecological variables. Studies undertaken until
now have determined the relationship between in-
formation collected by LANDSAT sensors using
RBFs, and have identified the geographical zones
that share the same values of the ecological varia-
bles. There are a good number of studies which
correlate LANDSAT information with vegetation
data; however, the correlation of this information
with ecological variables is more complex (Cruz et
al., 2010).
Two restrictions were imposed on the new meth-
od of approximation: It should yield a precision
similar to that obtained using a single RBF and
There should be an exact fit for all cases in the input
set.
One of the operative characteristics of these prob-
lems is that training sets are very large (order of tens
of thousands of vectors). In this case, training sets
containing 22000 vectors were used, each with 20
elements, obtained from LANDSAT information,
with 16000 used for training of the RBFs and 6000
for calibrating the results.
We experimented using the 25 test sets corre-
sponding to the 25 different ecological variables (out
of a total of 45 that were used in the environmental
study (Cruz et al., 2010)).
Applying the algorithm our experiment took the
following values:
1. The random partition contained 100 groups.
a) To each group, we applied the SOM, with the
following features: Topology: hexagonal,
Number of rows: 32, Number of columns: 1.
2. We obtained 32 centroids for each of the 100
SOM, yielding a total of 3, 200 centroids.
a) In the fourth step, we applied the SOM to the
3200 earlier centroids, with the following fea-
tures: Topology: hexagonal, Number of rows:
5, Number of columns: 5.
3. In this way, we obtained 25 centroids and,
therefore, 25 RBFs.
When we analize the results of the
experiment, we
can see that, while the average time of execution of
the classic training of an RBF is approximately 1
hour 30 minutes for each training, the proposed new
method gives better results, Table 1 show the result
of these experiments.
Of course, we checked that the improvement in
the training phase did not cause a deterioration of the
goodness of fit in the subsequent classification
Table 1: Results of experiments using as application field, the approximation of environmental variables 25 and the training
process described above.
Training file training1.csv training2.csv training3.csv training4.csv training5.csv
Training time 48 seconds 44 seconds 45 seconds 45 seconds 47 seconds
Training file training6.csv training7.csv training8.csv training9.csv training10.csv
Training time 43 seconds 45 seconds 45 seconds 47 seconds 46 seconds
Training file training11.csv training12.csv training13.csv training14.csv training15.csv
Training time 44 seconds 42 seconds 45 seconds 45 seconds 46 seconds
Training file training16.csv training17.csv training18.csv training19.csv training20.csv
Training time 42 seconds 45 seconds 44 seconds 44 seconds 45 seconds
Training file training21.csv training22.csv training23.csv training24.csv training25.csv
Training time 47 seconds 46 seconds 44 seconds 47 seconds 46 seconds
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
500

process, by measuring the classification error against
several calibration files (one for each training set). In
this way, we measured the percentage accuracy, by
comparing the output value against a threshold error
of either ±0.01 and ±0.001.
In both cases, the accuracy was similar to results
obtained using a single RBF.
Therefore, since the percentage effectiveness us-
ing the actual algorithm is basically the same, we
have demonstrated the efficiency of the proposed
method on reducing training time (Sedgewick,
2002).
Time efficiency = New process time/
Usual process time · 100 (7)
The results give a mean efficiency of
0.836182336%; in other words the execution time,
on average, is reduced by 99.1638177%, and thus
we can conclude that the proposed technique is quite
acceptable.
ACKNWOLEDGEMENTS
This study was financed from Project TIN2010-
15588 of the Spanish Ministry for Science and Inno-
vation.
This work has been financed from Project of ex-
cellence financed by Junta de Andalucía with refer-
ence P10-TIC-6114 JUNTA ANDALUCIA.
REFERENCES
Jacobs, R. J.; “A competitive modular connectionist archi-
tecture,” Advances in Neural Information Processing
Systems, vol. 3, pp. 767–773, 1991.
de Felipe, J.; “Microcircuits in the brain,” in Proceeding of
the IWANN’97, pp. 1–14. 1997,
Arriaza, José A. Torres, Francisco Guindos Rojas, Mer-
cedes Peralta Lopez, Manuel Cantón “An automatic
cloud-masking system using backpro neural nets for
avhrr scenes,” IEEE Transactions on Geoscience and
Remote Sensing, vol. 41, no 4, pp. 826-831, 2003.
Rao, K. V. G.; “Soft computing-neural networks ensem-
bles,” Journal of Theoretical and Applied Information
Technology,pp. 45–50, 2005.
Broomhead, D. L.; “Multivariable functional interpolation
and adaptive networks,” Complex Systems, vol. 2, pp.
321–355, 1988.
Poggio, T.; “Networks for approximation and learning,”
IEEE, vol. 78, pp. 1481–1497, 1990.
Haykin, S.; “Neural networks, a comprehensive founda-
tions,” IEEE press, 1994.
Brassard, P.; Fundamentals of algoritmics. Prentice Hall,
1995.
Aho, A. V., J. E. Hopcroft, J. D. Ullman, Estructuras de
datos en Java. Addison-Wesley, 2000/2004.
Kohonen, T.; Self-Organizing Maps. Springer, 1990.
Sedgewick, R.; Algorithms. Addison-Wesley, 2002.
Cruz, M., M. Espínola, R. Ayala, M. Peralta, José
A.Torres, “How Can Neural Networks Speed Up Eco-
logical Regionalization Friendly?. ICCN 2010. Inter-
national Conference on Neural Computation. Part of
2th. International Joint Conference on Computational
Intelligence. INSTICC. 2010.
TheProblemofOrganizingandPartitioningLargeDataSetsinLearningAlgorithmsforSOM-RBFMixedStructures-
ApplicationtotheApproximationofEnvironmentalVariables
501
