
Analysis of Co-evolutionary Approach for Robotic Gait Generation
Jan
ˇ
Cern
´
y and Ji
ˇ
r
´
ı Kubal
´
ık
Department of Cybernetics, Faculty of Electrical Engineering,
Czech Technical University, Technick
´
a 2, 166 27 Prague 6, Czech Republic
Keywords:
Evolutionary Algorithms, Genetic Programming, Legged Robots, Robotic Gait, Co-evolution, Motion
Patterns, Evolutionary Robotics.
Abstract:
Recently, a new co-evolutionary approach for generating motion patterns for multi-legged robots which ex-
hibit symmetry and module repetition was proposed. The algorithm consists of two evolutionary algorithms
working in co-evolution. The first one, a genetic programming module, evolves a motion of a single leg. The
second one, a genetic algorithm module, seeks for the optimal deployment of the single-leg motion pattern
to all legs of the robot. Thus, the whole task is decomposed into two subtasks that are to be solved simulta-
neously. First proof-of-concept experiments proved such a decomposition helps to produce better solutions
than a simple GP-based approach that tries to evolve individual motion patterns for all legs of the robot. This
paper further analyzes the co-evolutionary algorithm focusing on two things – the way it handles the problem
decomposition and the type of functions it uses to control joints of the robot. The experiments carried out in
this work indicate that both design choices positively contribute to its performance.
1 INTRODUCTION
Walking robots have advantage over wheeled ones
when navigating complex and uneven environments.
However, to fully use abilities of a particular legged
robot it is necessary to optimize its gait specifically
for its mechanical structure, dimensions and parame-
ters.
This is a highly challenging task seeking for a co-
ordinated control of many joints, given multiple (of-
ten contradictory) optimization objectives such as the
maximal or some specific speed of locomotion, low-
energy operational mode, stability of the robot, etc.
The solution sought must also comply with multi-
ple constraints. Typically, the state transitions have
to be continuous in order to attain smooth gait pat-
terns. Other constraints can be determined by limited
resources and mechanical parameters that determine
inherent capability limits of the robot (Gong et al.,
2010). Moreover, the optimization objectives as well
as the constraints are non-linear, in general.
Obviously, manual generation of gaits is very dif-
ficult, if feasible at all, due to the aspects mentioned
above. Utilization of standard numerical optimization
methods is limited since the objective functions are
not defined analytically (each candidate gait is eval-
uated by a real experiment or through a simulation),
hence no information about continuity or differentia-
bility of the objective function is available. Single-
state heuristic methods that work in point-to-point
manner are ineffective as well since they are very
prone to get stuck in some sub-optimal solution when
searching huge space with many local optima.
On the contrary, evolutionary algorithms (EAs)
are population-based search and optimization tech-
niques that have been used for solving hard opti-
mization problems of the black-box type. Unlike the
single-state heuristics, the search direction is adjusted
using the information accumulated over all candidate
solutions of the population in each generation step of
the EA run. Thus, the EAs are more resistant to get-
ting trapped in a local optimum. They are also resis-
tant to noise in the evaluation function, which is very
important for this particular optimization domain.
There have been many studies devoted to the evo-
lutionary design of systems for automated gait gener-
ation and gait optimization of biped, quadruped, and
hexapod robots (Gong et al., 2010). Several types
of gait representation has been used by evolutionary-
based gait generators. Genetic Programming and
Grammatical Evolution evolve directly the functions
defining the joint angle trajectories (Seo and Hyun,
2008). One example of this approach is in the work
of Ivan Tanev who used it to create controllers for ar-
tificial snakes (Tanev and Shimohara, 2008).
37
ˇ
Cerný J. and Kubalík J..
Analysis of Co-evolutionary Approach for Robotic Gait Generation.
DOI: 10.5220/0004554900370046
In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 37-46
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Another approach to this problem is evolution
of Central Pattern Generators (CPG) (Crespi and
Ijspeert, 2008). Those are type of neural network with
the ability to generate rhythmic patterns. CPGs are
nature inspired mechanisms used to generate rhyth-
mic signals useful for periodical motions. This con-
cept comes from neurology. Small clusters of neu-
rons were isolated from brains of many different an-
imals which were able to generate rhythmic signals
hours after any sensory input. Simple CPG can be
sine wave generator or multiple sine wave generators
with different frequency amplitude and phase, more
complex ones are usually constructed from artificial
neural network. CPGs in robotics are used the same
way as in living organism for periodical motions like
walking or swimming.
In (Parker, 2001) Parker used the idea of two stage
evolution. He used an evolution algorithm to evolve
the motion of single limb of hexapod robot and then
combined those moves into gait in another stage of
evolution. This approach simplifies the task by evolv-
ing part of the problem in advance, but it also has
some limitations. Because the movement of entire
robot cannot be observed during the first stage of the
evolution it is not part of fitness function. The motion
pattern which has a good fitness when used for a sim-
plified problem of the first stage might behave poorly
when used for final robot.
Neuroevolutionary approach to generate con-
trollers for entire robot has been described in (Yosin-
ski, 2011). Yosinski et al. used HyperNEAT gen-
erative encoding to evolve controller for a physical
quadruped robot. The gaits produced by HyperNEAT
performed significantly better than locally optimized
parameterized motion models. This has been at-
tributed to an ability of HyperNEAT to discover a va-
riety of gait regularities. However, the gaits evolved
by HyperNEAT directly on a physical robot were not
impressive. Evolution on real hardware proved to be
impractical. Since the robot would constantly over-
heat or break, number of evaluations in evolution has
to be greatly reduced and this led to inferior results.
Thus, further improvement of the gaits was achieved
only after it has been moved to the simulated environ-
ment (Lee et al., 2013).
In (Cerny, 2012; Cerny, 2013) a new co-
evolutionary approach for automatic generation of
robotic gait was presented. The method was designed
for modular robotic creatures that are composed of a
number of simple cubic-shaped robotic blocks
1
. The
robotic blocks are endowed with a movable arm and
1
Multi-legged robots that exhibit features of symme-
try and module repetition were considered (particularly a
quadruped robot).
several slots that they use to connect to each other (re-
alizing joint-like connections) to form complex struc-
tures. Joint angles are controlled by functions of a
single input, time, that return desired joint positions
at discrete time steps. Thus, the generation of the gait
consists in finding a set of functions (a single func-
tion for each joint) that make the whole robotic crea-
ture to move in a desired way. The gaits were gen-
erated through a simultaneous evolution of (1) opti-
mal single-leg motion and (2) its coordinated deploy-
ment to all legs of the robot. The results presented in
(Cerny, 2013) show that such a decomposition of the
whole problem can lead to better motion patterns than
simple GP approach that evolves individual control
function to all legs. However, there are still a number
of open issues that has to be investigated in order to
conclude about the relevance of the co-evolutionary
approach.
The primary goal of this work is to investigate
the impact of key features of the co-evolutionary ap-
proach on its performance. Particularly, we focus on
the following two design choices:
• Co-evolution vs. Single-population Evolution.
The robotic gait is sought through the co-
evolution of the single-leg motion pattern and the
coordination strategy. Another way to approach
the gait generation problem using decomposition
is to evolve a single population of individuals,
where each one encodes both the single-leg mo-
tion and the coordination strategy. Thus, the ques-
tion is whether the co-evolution of the two aspects
of the complete robotic gait is better than single
evolution of composite individuals.
• Complexity of the Control Functions. The single-
leg motion patterns are represented as arbitrary
functions that are sought by the GP. Another way
to realize the motion patterns is to some periodic
function, such as the sine wave, to control mod-
ules of the robot and then to tune just the pa-
rameters of the sine waves (amplitude, phase, fre-
quency) of each module. Thus, the question is
whether the more general functions evolved by
GP are advantageous and can allow for generating
better motion patterns than the sine wave ones.
Series of experiments were carried out in or-
der to compare a performance of the baseline co-
evolutionary GP approach with its variants that differ
in the above mentioned aspects.
This paper is structured as follows. In section 2,
characteristics of robots simulated in the simulation
platform Sim are described. Section 3 describes
the co-evolutionary approach for automatic robot gait
generation. Section 4 describes algorithms used to
empirically validate the design of the co-evolutionary
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
38

Figure 1: A single robotic block used as a building block of
robotic creatures.
algorithm. Section 5 describes the experimental sce-
nario and presents the achieved results. Final section
concludes the paper and lists further extensions of the
presented approach.
2 SIMULATION PLATFORM AND
EXPERIMENTAL ROBOT
In this work, we use just a simulation platform Sim
(Vonasek and Fiser, 2012), not the real physical
robots. However, the simulation platform, which is
based ODE physics simulator, provides very realistic
and accurate experimental environment.
In Sim, robots composed of a number of simple
cubic-shaped robotic blocks, see Fig. 1, can be inves-
tigated. Each block consists of the main body and one
movable arm. This arm has its axle in the center of the
body and can be moved between −
π
2
and
π
2
. While the
main body of the block has wheels which can be used
to move it on the flat ground, those are not used as
a means of motion. Instead, the blocks are endowed
with slots (three of them on the main body and one is
on the movable arm) that enable them to connect to
each other and form more complex robots capable of
walking motion.
By connecting a slot on the movable arm of one
block to the slot on the main body of another block
a joint-like functionality is realized. Motors moving
with arms are controlled by input signals which ex-
press a desired angle of the arm. This means that the
motor tries to move the arm to the desired angle, how-
ever it may fail to reach exactly the desired position
due to the physical constraints.
Figure 2: Tested configuration of the complete robot in
starting position (i.e. lying on the floor) and a higher-level
abstraction of the same robot in standing position.
In this work we focus on multi-legged robots that
exhibit features of symmetry and module repetition.
Particularly, a quadruped robot was investigated, see
Fig. 2. This structure of the robot was fixed for all
experiments as the search for ideal morphology is not
part of this work. This robot is assembled from 17
blocks, five of these blocks form a torso of the robot
and remaining twelve blocks are used for four iden-
tical legs. Note that the movable arms do not realize
spherical joints, they can move only in one plane, ei-
ther the vertical or the horizontal one. Thus the con-
nection types chosen for individual joints of the robot
determine the character of gait the robot can perform.
The robot used in our experiments is designed to walk
sideways just as crabs do.
3 CO-EVOLUTIONARY
APPROACH TO MOTION
PATTERN GENERATION
In this work we assume multi-legged robots that ex-
hibit symmetry and module repetition properties and
propose a gait generation algorithm that makes use of
these properties to decompose the whole task in or-
der to efficiently evolve gaits of such complex robots.
There are two modules, genetic programming mod-
ule (GP-module) and genetic algorithm module (GA-
module), involved in the algorithm, each devoted to
evolution of a specific trait of the resulting gait:
• The GP-module is responsible for evolution of a
single-leg motion pattern, i.e. evolution of func-
tions controlling movement of individual joints of
a single leg and their coordination. A standard
tree-based GP is used to realize this module.
• The GA-module is responsible for evolution of a
coordination strategy that optimally deploys the
single-leg motion pattern, evolved by the GP-
module, to all legs of the robot. This module is
realized by genetic algorithm as the coordination
strategy is represented by a linear vector of con-
trol parameters that are to be tuned.
The two modules co-evolve simultaneously in a
sense that the single-leg motion patterns are coupled
with coordination strategies for the purpose of assess-
ing their quality. So, when evaluating one particular
individual of GP-module some individual of the GA-
module has to be assigned in order to make a com-
plete gait, and vice versa. The motivation for this co-
evolutionary approach is to let the system seek for a
good single-leg motion pattern that could be re-used,
with certain adjustment for left/right and fore/hind
leg, multiple times for all legs of the complete robot.
AnalysisofCo-evolutionaryApproachforRoboticGaitGeneration
39

Clearly, this approach could be used only if all legs
of the robot have the same structure and the motion
patterns they perform are expected to be similar
2
.
3.1 Genetic Programming Module
3.1.1 Representation
Given that each leg is composed of k connected
blocks, where each of the k joints is controlled by
its own function, the single-leg motion pattern is then
represented by k trees which use the following sets of
terminals and non-terminals:
• non-terminals: +, -, unary -, sin, cos, *, /, max,
min
• terminals: input variable time t, π, real-valued
constants r = h−1,1i
3.1.2 Genetic Operators
Standard GP subtree-swapping crossover operator
was implemented. On the other hand, no mutation
operator was used. To select individuals for reproduc-
tion, the tournament selection method was chosen.
To reduce the bloat and increase the computational
efficiency of the algorithm, a bloat control method
called Proportional Tournament (Panait and Luke,
2004) was used. In this method, a proportion of tour-
naments, given by parameter R, are based on parsi-
mony and the remaining tournaments, 1−R, are based
on fitness. This means that either well-fit or small tree
wins the tournament.
3.1.3 Evolution Model and Initialization
This algorithm uses generational evolution model.
The first generation is initialized by ramped-half-and-
half method with the maximal depth limit of 5.
3.2 Genetic Algorithm Module
3.2.1 Representation
This module evolves coordination strategies that de-
termine the way a particular single-leg motion pattern
is deployed to all legs of the robot. The coordination
strategy is given by the following parameters defined
for each leg:
2
Note, the joints connecting the blocks of the robot’s
torso are fixed, they are not included into the evolved gait
control strategy.
• Direction, d, specifies whether the single-leg mo-
tion will be applied in the direct or its reverse
mode. If the reverse mode is chosen for a partic-
ular leg then the input time parameter passed into
its joints functions is negated so that the leg per-
forms a motion which is a ”mirrored” version of
the original single-leg motion. This is important
for the crab like motion as it allows legs on one
side of the robot to pull and legs one the other side
to push. The direction parameter is represented by
a single bit for each leg.
• Phase, ϕ, specifies phase shift in legs movement.
This makes it possible to have different legs in dif-
ferent phases of the gait at the same time. This pa-
rameter is represented by a real number from in-
terval h0.0,1.0i, where the interval covers all pos-
sible shifts within one period of the corresponding
single-leg motion.
The final structure of the chromosome represent-
ing a coordination strategy for n legs is as follows
[d
1
...d
n
| ϕ
1
...ϕ
n
] (1)
where the direction bits are grouped in the head
part and the phase real numbers in the tail part of the
chromosome.
3.2.2 Genetic Operators
The representation described above requires a
crossover operator that operates differently for the
two parts of the chromosome. Standard one-point
crossover is used for the binary string of direction
bits. For the real-valued tail part of the chromosome,
a variant of the Blend crossover was implemented.
Given two parents p1 and p2, the offspring phase
value at position i, o
ϕi
, is taken at random (with uni-
form distribution) from the following set of possible
choices
o
ϕi
∈ {p1
ϕi
, p2
ϕi
,(p1
ϕi
+ p2
ϕi
)/2,
min(p1
ϕi
, p2
ϕi
) − 0.5 ∗ range,
max(p1
ϕi
, p2
ϕi
) + 0.5 ∗ range}
(2)
where range = abs(p1
ϕi
− p2
ϕi
). Every newly
generated value o
ϕi
is further adjusted to fall into the
interval of admissible values h0.0, 1.0i.
For the binary direction parameters, simple bit-flip
mutation operator was used. When a phase parameter
is selected for mutation, it is replaced by a new value
randomly generated from h0.0,1.0i. Tournament se-
lection is used to select parents for crossover and mu-
tation.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
40

3.2.3 Evolution Model and Initialization
This algorithm uses a steady-state evolution model
where the newly generated individual replaces the
worst individual in the population. The first gener-
ation is initialized randomly.
3.3 Co-evolution of GP-module and
GA-module
As mentioned at the beginning of this section, the
co-evolution of GP-module and GA-module is based
on pairwise relationships between individuals from
these two populations. These relationships are nec-
essary for assessing the quality of the individuals so
that when evaluating an individual from GP-module
its counterpart from GA-module is used to make up
the whole gait strategy, and vice versa. Below, the
fitness function used to assess evolved gait strategies
and the scheme used for maintaining the pairwise re-
lationships are described.
3.3.1 Fitness Function
The same minimization fitness function is used to as-
sess individuals from GP-module and GA-module. It
takes into account two aspects of the evaluated gait -
(i) a distance covered by the robot in desired direction
and (ii) a body posture of the robot during its move-
ment.
The covered distance term is measured as the dis-
tance of the central block of the robot’s torso from
desired destination point. The body posture term is
defined as a penalty punishing robots that show ten-
dency to drag its body on the ground. This is realized
so that a minimum height of the central block of the
robot is specified and then certain value is added to
the final penalty for each step of the whole simula-
tion of the robot’s movement
3
the robot made in lower
posture. Note, the penalty is in fact very high, hence
strongly encouraging evolution of walking gaits in-
stead of crawling ones.
3.3.2 Pairing off Individuals of GP-module and
GA-module
At the beginning of the run, individuals of the GP-
module are randomly paired off with individuals of
the GA-module so that each GP-module individual
has exactly one counterpart in GA-module. On the
3
The simulations are carried out in discrete steps, with
frequency 125 steps per second.
other hand, the GA-module individual can have arbi-
trary number of links (0 to many) to individuals in
GP-module.
Then, the co-evolution proceeds by phases, alter-
ing M generations of GP-module and N generations
of GA-module in each phase. When the GP-module
generates a new population, each newly generated in-
dividual inherits the relationship with the GA-module
individual from one of its parents. This way it is en-
sured that every individual in GP-module has always
assigned its counterpart in the GA-module for evalua-
tion purposes.
When GA-module evolves its population, each
newly generated individual is evaluated with several
candidates from GP-module and the best value is set
as its fitness. Moreover, it may happen that some of its
individuals has lost its counterpart in the GP-module
(because they were replaced by new individuals in
some of the previous generations of GP-module). In
this case, the fitness of such unpaired GA-module in-
dividual is penalized. This way individuals with no
link to GP-module can still compete between each
other but will always lose against those that are linked
to someone in GP-module. Also, whenever an indi-
vidual from GA-module is deleted it is important to
find a new GA-module individual for all GP-module
individuals which were connected to it.
4 COMPARED ALGORITHMS
In this section algorithms for automatic robot gait
generation, used for comparisons with the original
co-evolutionary approach (Cerny, 2013), will be de-
scribed. The algorithms vary in the way they han-
dle the problem decomposition and the type of func-
tions they use to control joints between modules of
the robot.
4.1 GP-based Algorithms
These are the variants of the original approach that all
evolve general functions using the GP. The original
co-evolutionary algorithm will be denoted as GP
co-
evolution.
4.1.1 GP with composite Individuals
This algorithm, denoted as GP composite, handles
the problem decomposition via composite individu-
als, where each individual encodes both
• the trees representing functions for controlling
joints of a single leg and
AnalysisofCo-evolutionaryApproachforRoboticGaitGeneration
41

• the set of synchronization parameters for coordi-
nated deployment of the single-motion to all legs
of the robot, as defined in Section 3.2.1.
Note, in the GP co-evolution approach, each
newly generated set of synchronization parameters is
tried with several single-leg motion patterns being as-
sessed and linked with the best performing one in the
end. In GP composite variant, the newly created set
of synchronization parameters is always linked with
the single-leg pattern inherited from its parents irre-
spectively of whether such a linkage performs well or
not.
4.1.2 GP without Decomposition
This algorithm, denoted as GP, does not make use of
the problem decomposition at all. It evolves functions
to all of the joints of the robot in a single population.
In particular, the GP evolves individuals, each repre-
senting twelve functions (4 legs times 3 joints).
4.2 Sine Wave based Algorithms
Approaches in this group do not use general func-
tions for controlling the joints of the robot. Instead, a
sine wave functions are used for controlling the joints’
movements. These algorithms thus evolve just a set
of parameters determining particular sine wave func-
tions. There are four parameters that determine the
sine wave – amplitude, center amplitude, frequency
and phase.
4.2.1 Sine Waves with Co-evolution
This algorithm, denoted as Sine co-evolution, is in
principle very much like the GP co-evolution – it co-
evolves two populations. The first population evolves
individuals that encode 12 sine wave parameters for a
single leg (3 joints times 4 parameters). These are rep-
resented as a vector of 12 real values. Standard Simu-
lated Binary Crossover (Deb and Agrawal, 1995) and
Gaussian mutation operators designed for the real rep-
resentation were used for generating new individuals.
The second population evolves the synchroniza-
tion strategies like in the GA-module described in Sec-
tion 3.2. The only difference is that here only the
phase parameters, ϕ, are considered because the di-
rection does not make sense for the sine function.
4.2.2 Sine waves with Composite Individuals
This algorithm, denoted as Sine composite, is an ana-
logue of the GP composite algorithm. It evolves a
population of composite individuals composed of the
12 sine wave parameters for a single leg motion plus
the phase synchronization parameters.
4.2.3 Sine Waves without Decomposition
This algorithm, denoted as Sine, does not make use of
the problem decomposition. It evolves a population
of individuals, each encoding parameters sine waves
controlling all joints of the robot. Thus, each individ-
ual is represented as a vector of 48 real-valued param-
eters (12 joints times 4 parameters).
5 EXPERIMENTAL EVALUATION
Series of experiments were carried out in order to
analyze impact of the two design choices of the co-
evolutionary approach, namely the way the algorithm
handles the problem decomposition and the utiliza-
tion of general functions for controlling joints of the
robot. In this work we consider just simulations of the
robot and its gaits that are carried out using a simula-
tion platform Sim, based on ODE physics simulator
4
,
which has been developed within the SYMBRION
and REPLICATOR
5
projects (Kernbach et al., 2008),
focused on an application of evolutionary and swarm
techniques in robotics.
5.1 Experimental Scenario
To evaluate performance of implemented methods a
simple experiment was set up. Gaits for the robot de-
scribed in Section 2 were evolved in an arena where
the environment was just a flat surface without any
obstacles. When simulating the robot with a candi-
date gait, the robot was always placed in the center
of the simulation arena in laying position. First, the
robot was given a fixed amount of simulation steps to
start moving, hopefully to stand up, and then it was let
to walk as far as possible for specified amount of time
(10 seconds in this case). Finally, the distance of its
final position from the specified target point was mea-
sured. In this work, the target point is located straight
to the north at [0, 40].
5.2 Experimental Set-up
Control parameters of the co-evolutionary algorithms
were set as follows:
• GP-module:
– population size 500
4
www.ode.org
5
http://www.symbrion.eu/tiki-index.php
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
42

Figure 3: Movement of a robotic creature.
– generations 200
– tournament size 7
• GA-module:
– population size 50
– tournament size 3
• synchronization: start-up phase of 20 generations
of the GP-module and then repeatedly carrying
out 2 generations of GP-module followed by 30
newly generated individuals in the GA-module;
Control parameters for the non-co-evolutionary
algorithms were set as follows:
• population size 600
Table 1: Mean and best results of all tested algorithms.
Algorithm Mean (StDev) Best
GP co-evolution 35.98 (1.58) 33.08
GP composite 39.83 (1.71) 35.91
GP 38.67 (1.78) 35.16
Sine co-evolution 39.13 (1.28) 35.54
Sine composite 39.26 (1.03) 37.78
Sine 39.14 (1.61) 34.07
• generations 250
• tournament size
This configuration ensures that the simple GP al-
gorithms should compute at least as many fitness eval-
uations (i.e. simulations) as the co-evolutionary ones.
5.3 Results
All motions generated by all algorithms managed to
at least put the robot into standing position, but not all
of them were able to walk or move significantly far
from the starting position in the desired direction.
The overall best and the mean best results calcu-
lated from ten independent runs for all algorithms are
in Table 1. Note, the less the better since the val-
ues represent distances of the robot’s final position
from the desired target point. The GP co-evolution
algorithm achieved the mean best distance 35.98 and
the overall best distance of 33.08. These results are
the best out of the group of the compared algorithms.
The Mann-Whitney rank sum test gives significant ev-
idence (p < 0.05, two-tailed) for the observed dif-
ferences between GP co-evolution and all other al-
gorithms. The typical pattern evolved by the GP co-
evolution can be seen in Figure 3.
AnalysisofCo-evolutionaryApproachforRoboticGaitGeneration
43
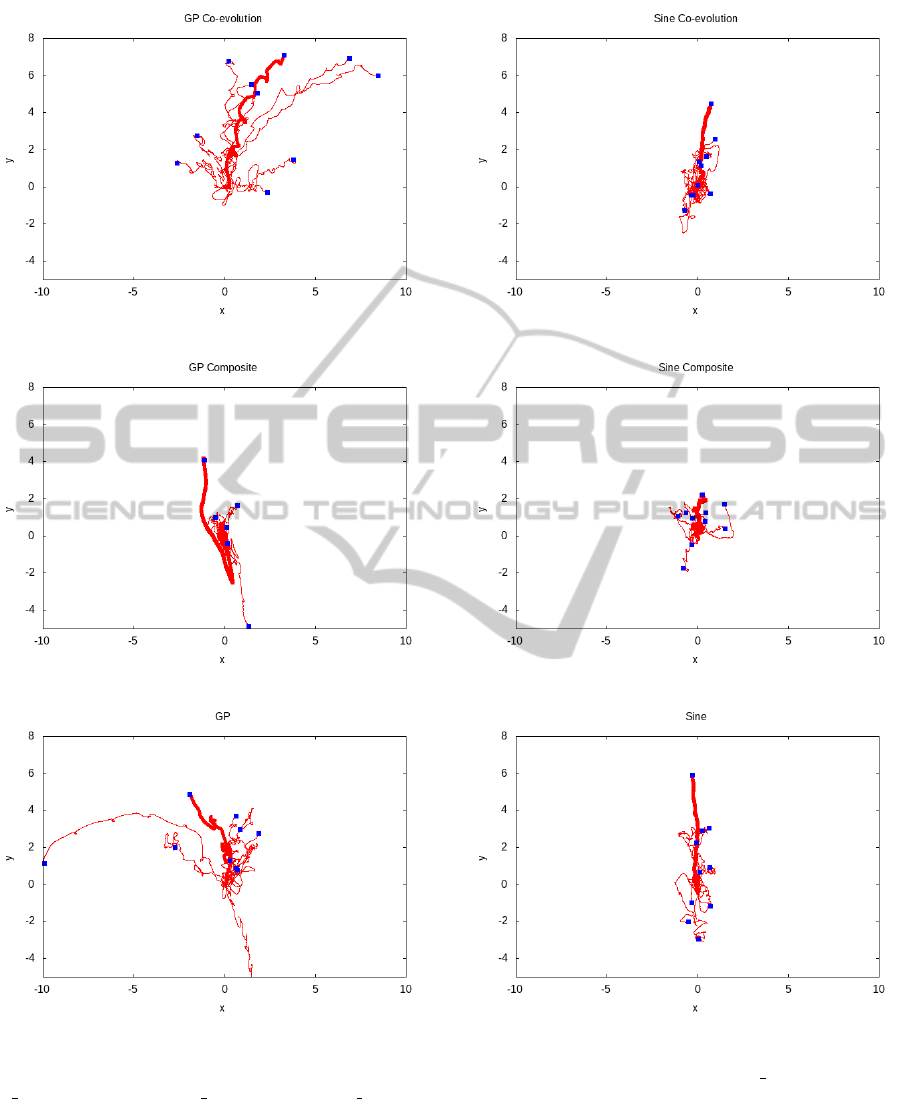
a) d)
b) e)
c) f)
Figure 4: Trajectories of robots with control functions evolved by the compared algorithms - a) GP co-evolution, b)
GP composite, c) GP, d) Sine co-evolution, e) Sine composite and f) Sine.
There are several important observations based on
the achieved results
• Tuning parameters of sine waves is less effective
than the evolution of general functions by means
of the GP. This indicates that sine waves might not
be sufficient for efficient generation of appropri-
ate motion patterns which can be more easily pro-
duced with general functions. For example, sine
wave is not able to produce intervals with constant
value, that can be interpreted as ”do not change
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
44

the joint angle” control action.
• The problem decomposition is important and pro-
duces better results than approaches not utilizing
the decomposition. This is rather expected con-
clusion since the decomposition reduces the size
of the search space.
• The decomposition realized via co-evolution is
better than evolution of a single population of
composite individuals. A possible explanation of
this observation can be that it is harder to find an
optimal composite individual than to find the so-
lution in parts. In case of the evolution of the
composite individuals each individual has fixed
pair of the single-leg motion pattern and the syn-
chronization scenario. So if one part of the indi-
vidual is not good the fitness of the whole indi-
vidual is very likely bad as well irrespectively of
the quality of the other part. On the contrary, in
the co-evolutionary algorithm each individual of
one population is evaluated based on a number of
trials when coupled with individuals of the other
population. This way the possibility of accidental
suppressing of good individuals is reduced.
Evolved paths are shown in Figure 4. All dia-
grams show 10 trajectories tracked by the robot driven
by the evolved control strategies for 10 seconds. It can
be observed several times that the best rewarded mo-
tion pattern lead the robot in the opposite direction to
the desired one, i.e. to the south. This happens due to
the fitness function definition, which strongly forces
the robot to walk with elevated body and not to crawl
on the ground (note that all crawling movements are
rewarded less than any movement with the elevated
body). It is evident, that in these cases the algorithms
only managed to evolve ”well-rewarded” walking gait
that made the robot walk backwards.
6 CONCLUSIONS
In this paper we analyze the recently proposed co-
evolutionary GP-based approach for automatic gen-
eration of robotic gaits. The approach is based on the
decomposition of the whole problem so that it simul-
taneously evolves single-leg motion and synchroniza-
tion scheme that determines coordinated deployment
of the single-leg motion to all legs of the robot.
We focus on two key components of the co-
evolutionary algorithm – the way it handles the prob-
lem decomposition and the type of functions it uses to
control joints of the robot.
The experiments carried out in this work indicate
that both the co-evolution of two separate populations
and the evolution of general function controlling the
joints positively contribute to the overall algorithm
performance.
There are a number of possible further extensions
of the co-evolutionary approach. One of them is evo-
lution of multiple motion primitives like left and right
turn and forward and backward walking. For exam-
ple, it is assumed that when given an efficient forward
walking gait the co-evolutionary approach should be
able to change the direction of walking just by evolv-
ing new leg-synchronizing strategy in GA-module for
the fixed single-leg motion patterns. Those walk-
ing primitives can be further used to navigate a robot
along some desired path. Another area of interest is
evolution of gaits for more challenging environments
such as sloped surfaces or walking up and down stairs.
Since the most time- and resource-consuming compu-
tations are related to the simulations it might be useful
to design the evaluation procedure in a staged manner
so that the candidate gait first undergoes simple and
short simulations and only if it passes them it pro-
ceeds to the main simulation that returns the objective
value.
ACKNOWLEDGEMENTS
This work has been supported by the research pro-
gram No. MSM 6840770038 ”Decision Making and
Control for Manufacturing III” of the CTU in Prague
and by the Grant Agency of the CTU in Prague, grant
No. SGS12/145/OHK3/2T/13.
REFERENCES
Cerny, J. (2012). Evolutionary design of robot motion pat-
terns.
Cerny, J. and Kubalik, J. (2013). Co-evolutionary Approach
to Design of Robotic Gait. In Proceedings of 16th Eu-
ropean Conference on the Applications of Evolution-
ary Computation – EvoApplications 2013. LNCS, vol.
7835, Springer, pages 550–559.
Crespi, A. and Ijspeert, A. (2008). Online optimization
of swimming and crawling in an amphibious snake
robot. IEEE Transactions on Robotics, vol. 24, no.
1, pp. 75–87.
Deb, K. and Agrawal, R. B. (1995). Simulated binary
crossover for continuous search space. Complex sys-
tems, vol. 9, pp. 115–148.
Gong, D., Yan, J., and Zuo, G. (2010). A review of gait
optimization based on evolutionary computation. Ap-
plied Computational Intelligence and Soft Computing,
2010.
Kernbach, S., Meister, E., Schlachter, F., Jebens, K., Szy-
manski, M., Liedke, J., Laneri, D., Winkler, L.,
AnalysisofCo-evolutionaryApproachforRoboticGaitGeneration
45

Schmickl, T., Thenius, R., et al. (2008). Symbiotic
robot organisms: Replicator and symbrion projects.
In Proceedings of the 8th Workshop on Performance
Metrics for Intelligent Systems. ACM, pages 62–69.
Lee, S., Yosinski, J., Glette, K., Lipson, H., & Clune, J.
(2013). Evolving Gaits for Physical Robots with the
HyperNEAT Generative Encoding: The Benefits of
Simulation. In Proceedings of 16th European Confer-
ence on the Applications of Evolutionary Computation
– EvoApplications 2013. LNCS, vol. 7835, Springer,
pp. 540–549.
Panait, L. and Luke, S. (2004). Alternative bloat control
methods. In Proceedings of the Genetic and Evo-
lutionary Computation Conference – GECCO 2004.
LNCS, vol. 3102, Springer, pages 630–641.
Parker, G. (2001). ”The incremental evolution of gaits
for hexapod robots.” In Proceedings of the Genetic
and Evolutionary Computation Conference (GECCO
2001) (pp. 1114-1121).
Seo, K. and Hyun, S. (2008). Genetic programming based
automatic gait generation for quadruped robots. In
Proceedings of the 10th Genetic and Evolutionary
Computation Conference – GECCO 2008. New York,
NY, USA, ACM, pages 293–294.
Tanev, I. and Shimohara, K. (2008). Co-evolution of active
sensing and locomotion gaits of simulated snake-like
robot. In Proceedings of the Genetic and Evolutionary
Computation Conference – GECCO 2008. New York,
NY, USA, ACM, pages 257–264.
Vonasek, V. and Fiser, D. (2012). Sim: a general purpose
3d robotic simulator.
Yosinski, J., Clune, J., Hidalgo, D., Nguyen, S., Zagal, J.,
Lipson, H. (2011) Evolving robot gaits in hardware:
the HyperNEAT generative encoding vs. parameter
optimization. In Proceedings of the 20th European
Conference on Artificial Life, pp. 11–18
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
46
