The L-Co-R Co-evolutionary Algorithm

A Comparative Analysis in Medium-term Time-series Forecasting Problems

E. Parras-Gutierrez

, V. M. Rivas

and J. J. Merelo

Department of Computer Sciences, University of Jaen, Campus Las Lagunillas s/n, 23071, Jaen, Spain

Department of Computers, Architecture and Technology, University of Granada,

C/ Periodista Daniel Saucedo s/n, 18071, Granada, Spain

Keywords:

Time Series Forecasting, Co-evolutionary Algorithms, Neural Networks, Signiﬁcant Lags.

Abstract:

This paper presents an experimental study in which the effectiveness of the L-Co-R method is tested. L-

Co-R is a co-evolutionary algorithm to time series forecasting that evolves, on one hand, RBFNs building

an appropriate architecture of net, and on the other hand, sets of time lags that represents the time series in

order to perform the forecasting using, at the same time, its own forecasted values. This coevolutive approach

makes possible to divide the main problem into two subproblems where every individual of one population

cooperates with the individuals of the other. The goal of this work is to analyze the results obtained by L-Co-R

comparing with other methods from the time series forecasting ﬁeld. For that, 20 time series and 5 different

methods found in the literature have been selected, and 3 distinct quality measures have been used to show the

results. Finally, a statistical study conﬁrms the good results of L-Co-R in most cases.

1 INTRODUCTION

Formally deﬁned, a time series is a set of observed

values from a variable along time in regular periods

(for instance, every day, every month or every year)

(Pe

na, 2005). Accordingly, the work of forecasting in

a time series can be deﬁned as the task of predicting

successive values of the variable in time spaced based

on past and present observations.

For many decades, different approaches have been

used for to modelling and forecasting time series.

These techniques can be classiﬁed into three different

areas: descriptive traditional technologies, linear and

nonlinear modern models, and soft computing tech-

niques. From all developed method, ARIMA, pro-

posed by Box and Jenkins (Box and Jenkins, 1976), is

possibly the most widely known and used. Neverthe-

less, it yields simplistic linear models, being unable

to ﬁnd subtle patterns in the time series data.

New methods based on artiﬁcial neural networks,

such as the one used in this paper, on the other hand,

can generate more complex models that are able to

grasp those subtle variations.

The L-Co-R method (Parras-Gutierrez et al.,

2012), developed inside the ﬁeld of ANNs, makes

jointly use of Radial Basis Function Networks

(RBFNs) and EAs to automatically forecast any given

time series. Moreover, L-Co-R designs adequate neu-

ral networks and selects the time lags that will be

used in the prediction, in a coevolutive (Castillo et al.,

2003) approach that allows to separate the main prob-

lem in two dependent subproblems. The algorithm

evolves two subpopulations based on a cooperative

scheme in which every individual of a subpopulation

collaborates with individuals from the other subpopu-

lation in order to obtain good solutions.

While previously work (Parras-Gutierrez et al.,

2012) was focused on 1-step ahead prediction, the

main goal of this one is to analyze the effectiveness

of the L-Co-R method in the medium-term horizon,

using the own previously predicted values to perform

next predictions. For this reason, L-Co-R has been

tested over 20 databases, taken from real world, or

used in well-known research publications and time

series competition. As section 4 shows, the method

has been compared against 5 time series forecasting

methods.

The rest of the paper is organized as follows: sec-

tion 2 introduces some preliminary topics related to

this research; section 3 describes the method L-Co-R;

section 4 presents the experimentation and the statis-

tical study carried out, while section 5 presents some

conclusions of the work.

144

Parras-Gutierrez E., M. Rivas V. and Merelo J..

The L-Co-R Co-evolutionary Algorithm - A Comparative Analysis in Medium-term Time-series Forecasting Problems.

DOI: 10.5220/0004555101440151

In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 144-151

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 PRELIMINARIES

Approaches proposed in time series forecasting can

be mainly grouped as linear and nonlinear models.

Methods like exponential smoothing methods (Win-

ters, 1960), simple exponential smoothing, Holt’s lin-

ear methods, some variations of the Holt-Winter’s

methods, State space models (Snyder, 1985), and

ARIMA models (Box and Jenkins, 1976), have stand

out from linear methods, used chieﬂy for modelling

time series. Nonlinear models arose because linear

models were insufﬁcient in many real applications;

between nonlinear methods it can be found regime-

switching models, which comprise the wide variety

of existing threshold autoregressive models (Tong,

1978). Nevertheless, soft computing approaches were

developed in order to save disadvantages of nonlinear

models like the lack of robustness in complex model

and the difﬁculty to use (Clements et al., 2004).

ANNs have also been successfully applied (Jain

and Kumar, 2007) and recognized as an important tool

for time-series forecasting. Within ANNs, the utiliza-

tion of RBFs as activation functions were considered

by works as (Broomhead and Lowe, 1988) and (Rivas

et al., 2004), while Harpham and Dawson (Harpham

and Dawson, 2006) or Du (Du and Zhang, 2008) fo-

cused on RBFNs for time series forecasting.

On the other hand, an issue that must be taken

into account when working with time series is the cor-

rect choice of the time lags for representing the series.

Takens’ theorem (Takens, 1980) establishes that if d,

a d-dimensional space where d is the minimum di-

mension capable of representing such a relationship,

is sufﬁciently large is possible to build a state space

using the correct time lags and if this space is cor-

rectly rebuilt also guarantees that the dynamics of this

space is topologically identical to the dynamics of the

real systems state space.

Many methods are based in Takens’ theorem (like

(Lukoseviciute and Ragulskis, 2010)) but, in gen-

eral, the approaches found in the literature consider

the lags selection as a pre or post-processing or as

a part of the learning process (Ara

ujo, 2010),(Maus

and Sprott, 2011). In the L-Co-R method the selec-

tion of the time lags is jointly faced along with the

design process, thus it employs co-evolution to simul-

taneously solve these problems.

Cooperative co-evolution (Potter and De Jong,

1994) has also been used in order to train ANNs

to design neural network ensembles (Garc

ıa-Pedrajas

et al., 2005) and RBFNs (Li et al., 2008). But in addi-

tion, cooperative co-evolution is utilized in time series

forecasting in works as the one by Xin (Ma and Wu,

2010).

3 DESCRIPTION OF THE

METHOD

This section describes L-Co-R (Parras-Gutierrez

et al., 2012), a co-evolutionary algorithm developed

to minimize the error obtained for automatically time

series forecasting. The algorithm works building at

the same time RBFNs and sets of lags that will be

used to predict future values. For this task, L-Co-R

is able to simultaneously evolve two populations of

different individual species, in which any member of

each population can cooperate with individuals from

the other one in order to generate good solutions, that

is, each individual represents itself a possible solution

to the subproblem. Therefore, the algorithm is com-

posed of the following two populations:

• Population of RBFNs: it consists of a set of

RBFNs which evolves to design a suitable ar-

chitecture of the network. This population em-

ploys real codiﬁcation so every individual repre-

sent a set of neurons (RBFs) that composes the

net. Each neuron of the net is deﬁned by a center

(a vector with the same dimension as the inputs)

and a radius. The exact dimension of the input

space is given by an individual of the population

of lags (the one chosen to evaluate the net). Dur-

ing the evolutionary process neurons can grow or

decrease since the number of neurons is variable,

and centers and radius can also be modiﬁed by

means of muatation.

• Population of lags: it is composed of sets of lags

evolves to forecast future values of the time series.

The population uses a binary codiﬁcation scheme

thus each gene indicates if that speciﬁc lag in the

time series will be utilized in the forecasting pro-

cess. The length of the chromosome is set at the

beginning corresponding with the speciﬁc param-

eter, so that it cannot vary its size during the exe-

cution of the algorithm.

As the fundamental objective, L-Co-R forecasts

any time series for any horizon and builds appropriate

RBFNs designed with suitable sets of lags, reducing

any hand made preprocessing step. Figure 1 describes

the general scheme of the algorithm L-Co-R.

L-Co-R performs a process to automatically re-

move the trend of the times series to work with, if

necessary. This procedure is divided into two main

phases: preprocessing, which takes places at the be-

ginning of the algorithm, and post-processing, at the

end of co-evolutionary process. Basically, the algo-

rithm checks if the time series includes trend and, in

afﬁrmative case, the trend is removed.

TheL-Co-RCo-evolutionaryAlgorithm-AComparativeAnalysisinMedium-termTime-seriesForecastingProblems

145

Trend preprocessing

t = 0;

initialize P lags(t);

initialize P RBFNs(t);

evaluate individuals in P lags(t);

evaluate individuals in P RBFNs(t);

while termination condition not satisﬁed do

begin

t = t+1;

/* Evolve population of lags */

for i=0 to max gen lags do

begin

set threshold;

select P lags’(t) from P lags(t);

apply genetic operators in P lags’(t);

/* Evaluate P lags’(t) */

choose collaborators from P RBFNs(t);

evaluate individuals in P lags’(t);

replace individuals P lags(t) with P lags’(t);

if threshold < 0

begin

diverge P lags(t);

end

/* Evolve population of RBFNs */

for i=0 to max gen RBFNs do

begin

select P RBFNs’(t) from P RBFNs(t);

apply genetic operators in P RBFNs’(t);

/* Evaluate P RBFNs’(t) */

choose collaborators from P lags(t);

evaluate individuals in P RBFNs’(t);

replace individuals with P RBFNs’(t);

end

train models and select the best one

forecast test values with the ﬁnal model

Trend postprocessing

Figure 1: General scheme of method L-Co-R.

The performance of L-Co-R starts with the cre-

ation of the two initial populations, randomly gener-

ated for the ﬁrst generation; then, each individual of

the populations is evaluated. The L-Co-R algorithm

uses a sequential scheme in which only one popu-

lation is active, so the two population take turns in

evolving. Firstly, the evolutionary process of the pop-

ulation of lags occurs: the individuals which will be-

long to the subpopulation are selected; following the

CHC scheme (Eshelman, 1991), genetic operators are

applied; the collaborator for every individual is cho-

sen from the population of RBFNs; and the individu-

als are evaluated again and assigned the result as ﬁt-

ness. After that, the best individuals from the sub-

population will replace the worst individuals of the

population. During the evolution, the population of

lags checks that al least one gene of the chromosome

must be set to one because necessarily the net needs

one input to obtained the forecasted value.

In the second place, the population of RBFNs

starts the evolutionary process. For the ﬁrst gener-

ation, every net in the population has a number of

neurons randomly chosen which may not exceed a

maximum number previously ﬁxed. As in population

of lags, the individuals for the subpopulation are se-

lected, the genetic operators are applied, every indi-

vidual chooses the collaborator from the population

of lags, and then, the individuals are evaluated and

the result is assigned as ﬁtness. Fitness function is

deﬁned by the inverse of the root mean squared error

At the end of the co-evolutionary process, two mod-

els formed by a set of lags (from the ﬁrst population)

and a neural network (from the second population) are

obtained. On the one hand, a model is composed of

the best set of lags and its best collaborator, and on

the other hand, the other model is composed of the

best net found and its best collaborator. Then, the two

models are trained again and the ﬁnal model chosen is

the one that obtains the best ﬁtness. This ﬁnal model

obtains the future values of the time series used for

the prediction, and then, forecasted data will be used

to ﬁnd next values.

The collaboration scheme used in L-Co-R is the

best collaboration scheme (Potter and De Jong, 1994).

Thus, every individual in any population chooses the

best collaborator from the other population. Only at

the beginning of the co-evolutionary process, the col-

laborator is selected randomly because the population

has not been evaluated yet.

The method has a set of speciﬁc operators spe-

cially developed to work with individuals from every

population. The operators used by L-Co-R are the fol-

lowings:

• Population of RBFNs: tournament selection, x ﬁx

crossover, four operators to mutate randomly cho-

sen (C random, R random, Adder, and Deleter)

and replacement of the worst individuals by the

best ones of the subpopulation.

• Population of lags: elitist selection, HUX

crossover operator, replacement of the worst in-

dividuals, and diverge (the population is restarted

when it is blocked).

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

146

4 EXPERIMENTATION AND

STATISTICAL STUDY

The main goal of the experiments is to study the be-

havior of the algorithm L-Co-R comparing with other

5 methods found in the literature and for 3 different

quality measures.

4.1 Experimental Methodology

As in (Parras-Gutierrez et al., 2012), the experimen-

tation has been carried out using 20 data bases, most

of then taken from the INE

. The data represent ob-

servations from different activities and have differ-

ent nature, size, and characteristics. The data bases

have been labeled as: Airline, WmFrancfort, Wm-

London, WmMadrid, WmMilan, WmNewYork, Wm-

Tokyo, Deceases, SpaMovSpec, Exchange, Gasoline,

MortCanc, MortMade, Books, FreeHouPrize, Prison-

ers, TurIn, TurOut, TUrban, and HouseFin. The num-

ber of samples in every database is between 43 (for

MortCanc) and 618 (for Gasoline, a database used in

the NN3 competition).

To compare the effectiveness of L-Co-R, 5 ad-

ditional methods have been used, all of them found

within the ﬁeld of time series forecasting: Exponen-

tial smoothing method (ETS), Croston, Theta, Ran-

dom Walk (RW), and ARIMA (Hyndman and Khan-

dakar, 2008).

In order to test and compare the generalization ca-

pabilities of every method, databases have been split

into training and test sets. Training sets have been

given the ﬁrst 75% of the data, while test sets are com-

posed by the remaining 25% samples.

An open question when dealing with time series is

the measure to be used in order to calculate the accu-

racy of the obtained predictions. Mean Absolute Per-

centage Error (MAPE) (Bowerman et al., 2004) was

intensively used until many other measures as Geo-

metric Mean Relative Absolute Error, Median Rel-

ative Absolute Error, Symmetric Median and Me-

dian Absolute Percentage Error (MdAPE), or Sym-

metric Mean Absolute Percentage Error were pro-

posed (Makridakis and Hibon, 2000). However, a

disadvantage was found in these measures, they were

not generally applicable and can be inﬁnite, unde-

ﬁned or can produce misleading results, as Hyndman

and Koehler explained in their work (Hyndman and

Koehler, 2006). Thus, they proposed Mean Absolute

Scaled Error (MASE) that is less sensitive to outliers,

less variable on small samples, and more easily inter-

preted.

National Statistics Institute (http://www.ine.es/)

In this work, the measures used are MAPE (i.e.,

mean(| p

|)), MASE (deﬁned as mean(| q

|)), and

MdAPE (as median(| p

|) ), taking into account that

is the observation at time t = 1, ...,n; F

is the fore-

cast of Y

; e

is the forecast error (i.e. e

= Y

− F

);

= 100e

is the percentage error, and q

is deter-

mined as:

n − 1

∑

i=2

| Y

−Y

i−1

Due to its stochastic nature, the results yielded by

L-Co-R have been calculated as the average errors

over 30 executions with every time series. For each

execution, the following parameters are used in the

L-Co-R algorithm: lags population size=50, lags pop-

ulation generations=5, lags chromosome size=10%,

RBFNs population size=50, RBFNs population gen-

erations=10, validation rate=0.25, maximum num-

ber of neurons of ﬁrst generation=0.05, tournament

size=3, replacement rate=0.5, crossover rate=0.8, mu-

tation rate=0.2, and total number of generations=20.

Tables 1, 2, and 3 show the results of the L-Co-

R and the utilized methods to compare (ETS, Cros-

ton, Theta, RW, and ARIMA), for measures MAPE,

MASE, and MdAPE, respectively (best results are

emphasized with the character *). As mentioned be-

fore, every result indicated in the tables represent the

average of 30 executions for each time series. With

respect to MAPE, the L-Co-R algorithm obtains the

best results in 15 of 20 time series used, as can be

seen in table 1. Regarding MASE, L-Co-R stands out

yielding the best results for 5 time series; ETS, Cros-

ton and Theta for 3 time series; RW only for 2; and

ARIMA for 4 time series; as can be observed in ta-

ble 2. Concerning MdAPE, L-Co-R acquires better

results than the other methods in 12 of 20 time series,

as table 3 shows. Thus, the L-Co-R algorithm is able

to achieve a more accurate forecast in the most time

series for any of the quality measures considered.

4.2 Analysis of the Results

To analyze in more detail the results and check

whether the observed differences are signiﬁcant, two

main steps are performed: ﬁrstly, identifying whether

exist differences in general between the methods used

in the comparison; and secondly, determining if the

best method is signiﬁcant better than the rest of the

methods. To do this, ﬁrst of all it has to be decided if

is possible to use parametric o non-parametric statisti-

cal techniques. An adequate use of parametric statis-

tical techniques reaching three necessary conditions:

independency, normality and homoscedasticity (She-

skin, 2004).

TheL-Co-RCo-evolutionaryAlgorithm-AComparativeAnalysisinMedium-termTime-seriesForecastingProblems

147

Table 1: Results of the methods L-Co-R, ETS, Croston, Theta, RW, and ARIMA, with respect to MAPE. Best result per

database is marked with character *.

Time series L-Co-R ETS Croston Theta RW ARIMA

Airline 30.380 * 274.770 72.606 141.452 137.986 53.636

WmFrancfort 16.423 17.393 40.544 22.745 25.169 12.136 *

WmLondon 2.860 * 5.383 27.682 10.136 13.397 5.212

WmMadrid 20.101 27.035 44.285 25.505 27.034 12.930 *

WmMilan 30.529 * 34.858 49.750 34.078 34.823 34.823

WmNewYork 8.259 7.182 * 30.297 14.669 18.073 7.536

WmTokyo 4.764 * 12.807 20.556 10.575 12.591 12.591

Deceases 5.981 * 8.002 7.472 7.264 8.040 8.040

SpaMovSpec 53.788 * 217.978 78.648 70.500 78.935 88.197

Exchange 43.044 46.025 31.121 * 39.138 33.631 45.254

Gasoline 1.654 * 7.986 9.587 6.701 7.974 9.359

MortCanc 1.137 * 12.979 32.489 5.889 6.256 5.440

MortMade 3.931 * 13.526 46.362 40.272 12.800 31.000

Books 13.787 * 23.588 23.122 22.360 22.640 23.476

FreeHouPrize 3.424 * 8.540 29.271 5.215 9.220 10.227

Prisoners 8.392 3.103 * 14.220 6.888 9.474 3.150

TurIn 1.357 * 7.074 11.234 7.084 7.110 6.377

TurOut 8.133 * 13.261 12.159 15.238 13.226 9.634

TUrban 2.734 * 11.957 9.067 8.949 10.116 9.291

HouseFin 16.452 * 22.296 21.548 19.947 22.887 19.555

Table 2: Results of the methods L-Co-R, ETS, Croston, Theta, RW, and ARIMA, with respect to MASE. Best result per

database is marked with character *.

TS L-Co-R ETS Croston Theta RW ARIMA

Airline 1.913 12.707 2.738 5.853 5.664 1.441 *

WmFrancfort 3.578 * 3.608 7.984 4.673 5.159 7.988

WmLondon 1.648 1.603 * 8.410 3.099 4.119 3.484

WmMadrid 4.442 * 5.686 9.126 5.362 5.685 8.625

WmMilan 5.967 * 6.684 9.263 6.534 6.678 19.327

WmNewYork 2.667 1.837 * 7.982 3.942 4.879 6.228

WmTokyo 2.791 2.443 3.935 2.129 2.402 1.628 *

Deceases 1.059 1.059 0.952 * 0.955 1.064 1.144

SpaMovSpec 1.027 2.027 1.009 * 1.023 1.010 1.933

Exchange 41.181 44.039 30.448 * 37.807 32.825 70.734

Gasoline 1.198 * 1.543 1.864 1.274 1.541 1.698

MortCanc 0.646 1.618 4.098 0.725 0.796 0.277 *

MortMade 1.314 1.303 * 4.500 3.869 1.315 1.712

Books 0.762 0.965 0.936 0.894 0.759 * 1.147

FreeHouPrize 3.339 * 5.642 19.468 3.487 6.183 6.805

Prisoners 14.482 5.485 23.979 11.934 16.305 4.031 *

TurIn 1.903 1.902 3.151 1.824 * 1.916 1.950

TurOut 2.005 2.000 2.088 2.239 1.996 * 2.241

TUrban 0.886 0.978 0.772 0.744 * 0.887 0.897

HouseFin 1.319 1.283 1.234 1.095 * 1.322 1.502

Owing to the former conditions are not fulﬁlled,

the Friedman and Iman-Davenport non-parametric

tests have been used. Tables 4 and 5 shows the results

for MAPE, MASE and MdAPE, for these tests. From

left to right, tables show the Friedman and Iman-

Davenport values (χ

and F

, respectively), the cor-

responding critical values for each distribution by us-

ing a level of signiﬁcance α = 0.05, and the p-value

obtained for the measures utilized.

As can be observed, the critical values of Fried-

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

148

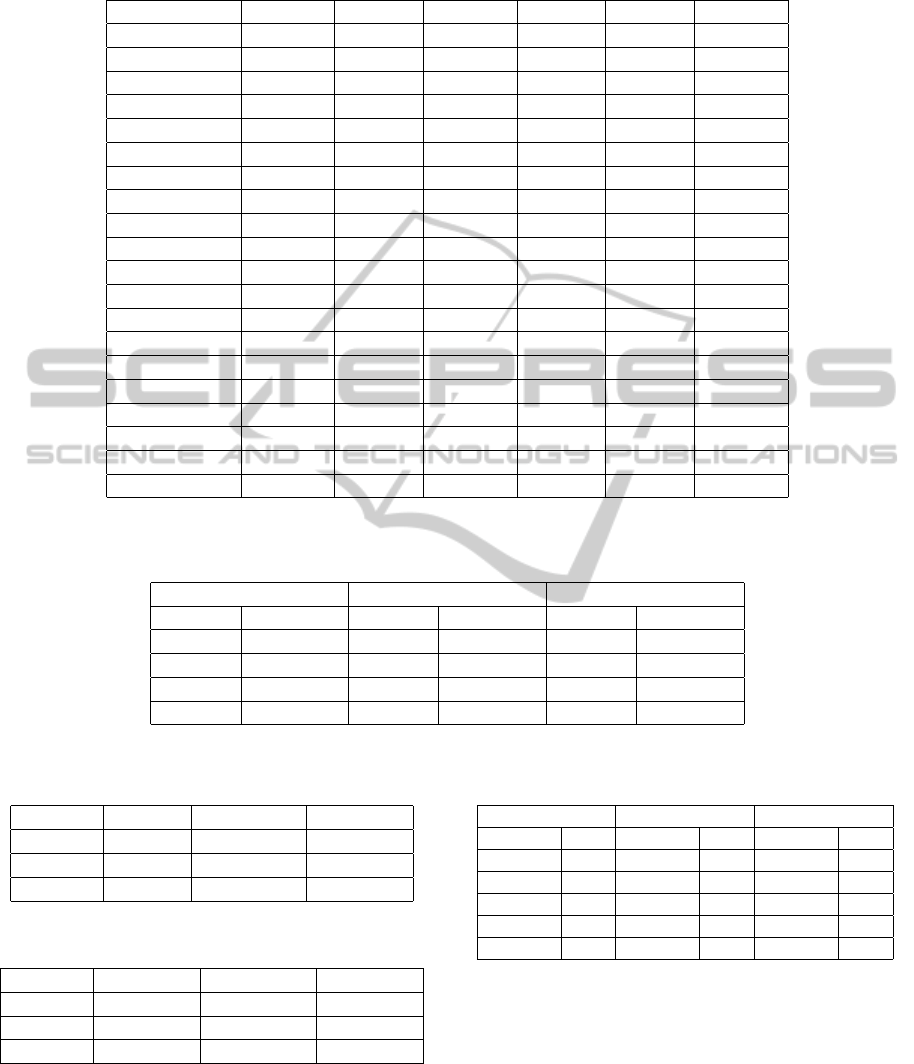
Table 3: Results of the methods L-Co-R, ETS, Croston, Theta, RW, and ARIMA, with respect to MdAPE. Best result per

database is marked with character *.

Time series L-Co-R ETS Croston Theta RW ARIMA

Airline 15.057 * 233.934 54.657 119.754 118.090 15.212

WmFrancfort 14.610 14.603 39.259 19.960 22.750 11.026 *

WmLondon 3.498 * 5.430 30.550 10.474 15.722 5.099

WmMadrid 22.718 28.116 45.817 26.787 28.116 11.446 *

WmMilan 30.476 * 34.685 50.040 33.872 34.643 34.643

WmNewYork 9.114 4.598 * 35.253 16.505 23.137 5.712

WmTokyo 5.517 * 9.864 18.782 9.075 9.556 9.556

Deceases 4.267 * 5.464 6.121 4.440 5.458 5.458

SpaMovSpec 17.669 * 107.283 51.653 53.104 51.568 54.033

Exchange 44.368 46.597 34.121 * 38.832 36.521 45.961

Gasoline 1.792 * 7.587 9.045 6.429 7.563 8.923

MortCanc 11.25 9.694 30.568 4.047 * 5.339 5.116

MortMade 3.459 * 12.111 45.704 41.989 15.629 28.374

Books 4.868 * 18.111 17.230 16.566 11.567 18.093

FreeHouPrize 1.803 * 5.222 29.683 5.201 9.748 6.572

Prisoners 6.766 1.512 * 12.651 5.287 7.817 1.621

TurIn 2.945 * 6.627 11.696 4.779 6.669 4.605

TurOut 5.289 * 11.331 11.518 10.873 11.392 7.689

TUrban 5.290 8.262 6.822 4.922 * 8.900 6.374

HouseFin 18.286 22.623 21.279 18.845 23.684 17.297 *

Table 7: Adjusted p values of Holm’s procedure between the control algorithm (L-Co-R) and the other methods for MAPE,

MASE, and MdAPE. Values lower than alpha = 0.05 indicate signiﬁcant differences between L-Co-R and the corresponding

algorithm.

MAPE MASE MdAPE

Croston 2.433E-08 ARIMA 1.138E-03 Croston 2.432E-08

ETS 3.346E-06 Croston 1.528E-03 ETS 1.692E-04

RW 9.120E-06 ETS 1.083E-01 RW 2.002E-04

ARIMA 4.636E-03 RW 1.179E-01 Theta 6.298E-02

Theta 5.287E-03 Theta 7.673E-01 ARIMA 6.920E-02

Table 4: Results of the Friedman, showing signﬁcant differ-

ences as p −values < 0.05.

Measure F. Value Value in χ

p value

MAPE 39.364 5 2.101E-10

MASE 18.893 5 2.012E-03

MdAPE 38.350 5 3.209E-07

Table 5: Results of the Iman-Davenport test, showing sign-

ﬁcant differences as p − values < 0.05.

Measure I-D. Value Value in F

p value

MAPE 12.283 5 and 95 3.416E-09

MASE 4.426 5 and 95 1.146E-03

MdAPE 11.819 5 and 95 6.717E-09

man and Iman-Davenport are smaller than the statis-

tic, it means that there are signiﬁcant differences

among the methods in all cases. In addition, Fried-

man provides a ranking of the algorithms, so that the

method with a lowest result is taken as the control al-

Table 6: Friedman’s test ranking. Control algorithms are

located in ﬁrst row.

MAPE MASE MdAPE

L-Co-R 1.50 L-Co-R 2.53 L-Co-R 1.85

Theta 3.15 Theta 2.70 ARIMA 2.93

ARIMA 3.18 RW 3.45 Theta 2.95

RW 4.13 ETS 3.48 RW 4.05

ETS 4.25 Croston 4.40 ETS 4.08

Croston 4.80 ARIMA 4.45 Croston 5.15

gorithm. For this reason, and according to table 6, the

L-Co-R algorithm results to be the control algorithm

for the three quality measures.

In order to check if the control algorithm has sta-

tistical differences regarding the other methods used,

the Holm procedure (Holm, 1979) is used. Table 7

presents the results of the Holm’s procedure since

shows the adjusted p values from each comparison

between the algorithm control and the rest of the

TheL-Co-RCo-evolutionaryAlgorithm-AComparativeAnalysisinMedium-termTime-seriesForecastingProblems

149

methods for MAPE, MASE, and MdAPE, consider-

ing a level of signiﬁcance of al pha = 0.05.

As can be seen in table 7, there are signiﬁcant

differences among L-Co-R and all the rest methods

for MAPE. With respect to MASE, there exist signif-

icant differences between the L-Co-R algorithm and

ARIMA and Croston, although it is not appropriate to

assure that with methods ETS, RW, and Theta. Re-

garding MdAPE, L-Co-R has signiﬁcant differences

with methods Croston, ETS, and RW.

In conclusion, it is possible to conﬁrm that the L-

Co-R method is able to achieve a better forecast in

majority of cases comparing with the other 5 meth-

ods utilized and concerning to 3 different quality mea-

sures.

5 CONCLUSIONS

In this contribution, the behavior of the L-Co-R

method, a recent algorithm developed for minimizing

the error when predicting future values of any time

series given, for automatic time series forecasting is

studied.

The algorithm has been tested with 20 different

time series and contrasted with a set of 5 representa-

tive methods. In addition, 3 distinct quality measures

have been used to check the results. L-Co-R obtains

the best results in the majority of the cases tested for

every measure considered.

A statistic study has been done in order to conﬁrm

the results achieved. With respect to MAPE, L-Co-

R is signiﬁcantly better than the rest of the method;

regarding MASE, it has signiﬁcant differences with

ARIMA and Croston; and with respect to MdAPE, it

obtains signiﬁcantly better results than Croston, ETS

and RW.

Thus, it can be concluded that the L-Co-R algo-

rithm yields better results in most time series used

than the other methods utilized.

ACKNOWLEDGEMENTS

This work has been supported by the regional projects

TIC-3928 and -TIC-03903 (Feder Funds), the Span-

ish projects TIN 2012-33856 (Feder Founds), and

TIN 2011-28627-C04-02 (Feder Funds). The authors

would also like to thank the FEDER of European

Union for ﬁnancial support via project ”Sistema de

Informaci

on y Predicci

on de bajo coste y aut

onomo

para conocer el Estado de las Carreteras en tiempo

real mediante dispositivos distribuidos” (SIPEsCa) of

the ”Programa Operativo FEDER de Andaluc

ıa 2007-

2013”. We also thank all Agency of Public Works of

Andalusia Regional Government staff and researchers

for their dedication and professionalism.

REFERENCES

Ara

ujo, R. (2010). A quantum-inspired evolutionary hybrid

intelligent apporach fo stock market prediction. Inter-

national Jorunal of Intelligent Computing and Cyber-

netics, 3(10):24–54.

Bowerman, B., O’Connell, R., and Koehler, A. (2004).

Forecasting: methods and applications. Thomson

Brooks/Cole: Belmont, CA.

Box, G. and Jenkins, G. (1976). Time series analysis: fore-

casting and control. San Francisco: Holden Day.

Broomhead, D. and Lowe, D. (1988). Multivariable func-

tional interpolation and adaptive networks. Complex

Systems, 2:321–355.

Castillo, P., Arenas, M., Merelo, J., and Romero, G. (2003).

Cooperative co-evolution of multilayer perceptrons.

In Mira, J. and

Alvarez, J. R., editors, Computational

Methods in Neural Modeling, volume 2686 of Lecture

Notes in Computer Science, pages 358–365. Springer

Berlin Heidelberg.

Clements, M., Franses, P., and Swanson, N. (2004). Fore-

casting economic and ﬁnancial time-series with non-

linear models. International Journal of Forecasting,

20(2):169–183.

Du, H. and Zhang, N. (2008). Time series prediction us-

ing evolving radial basis function networks with new

encoding scheme. Neurocomputing, 71(7-9):1388–

1400.

Eshelman, L. (1991). The chc adptive search algorithm:

How to have safe search when engaging in nontra-

ditional genetic recombination. In Proceedings of

1st Workshop on Foundations of Genetic Algorithms,

pages 265–283.

Garc

ıa-Pedrajas, N., Hervas-Mart

ınez, C., and Ortiz-Boyer,

D. (2005). Cooperative coevolution of artiﬁcial

neural network ensembles for pattern classiﬁcation.

IEEE Transactions on Evolutionary Computation,

9(3):271–302.

Harpham, C. and Dawson, C. (2006). The effect of different

basis functions on a radial basis function network for

time series prediction: A comparative study. Neuro-

computing, 69(16-18):2161–2170.

Holm, S. (1979). A simple sequentially rejective multi-

ple test procedure. Scandinavian Journal of Statistics,

6(2):65–70.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

150

Hyndman, R. and Koehler, A. (2006). Another look at mea-

sures of forecast accuracy. International Journal of

Forecasting, 22(4):679–688.

Hyndman, R. J. and Khandakar, Y. (2008). Automatic time

series forecasting: The forecast package for r. Journal

of Statistical Software, 27(3):1–22.

Jain, A. and Kumar, A. (2007). Hybrid neural network mod-

els for hydrologic time series forecasting. Applied Soft

Computing, 7(2):585–592.

Li, M., Tian, J., and Chen, F. (2008). Improving multiclass

pattern recognition with a co-evolutionary rbfnn. Pat-

tern Recognition Letters, 29(4):392–406.

Lukoseviciute, K. and Ragulskis, M. (2010). Evolution-

ary algorithms for the selection of time lags for time

series forecasting by fuzzy inference systems. Neuro-

computing, 73(10-12):2077–2088.

Ma, X. and Wu, H. (2010). Power system short-term load

forecasting based on cooperative co-evolutionary im-

mune network model. In Proceedings of 2nd Interna-

tional Conference on Education Technology and Com-

puter, pages 582–585.

Makridakis, S. and Hibon, M. (2000). The m3-competition:

results, conclusions and implications. International

Journal of Forecasting, 16(4):451–476.

Maus, A. and Sprott, J. C. (2011). Neural network method

for determining embedding dimension of a time se-

ries. Communications in Nonlinear Science and Nu-

merical Simulation, 16(8):3294–3302.

Parras-Gutierrez, E., Garcia-Arenas, M., Rivas, V., and del

Jesus, M. (2012). Coevolution of lags and rbfns for

time series forecasting: L-co-r algorithm. Soft Com-

puting, 16(6):919–942.

na, D. (2005). An

alisis de Series Temporales. Alianza

Editorial.

Potter, M. and De Jong, K. (1994). A cooperative co-

evolutionary approach to function optimization. In

Proceedings of Parallel Problem Solving from Nature,

volume 866 of Lecture Notes in Computer Science,

pages 249–257. Springer Berlin/Heidelberg.

Rivas, V., Merelo, J., Castillo, P., Arenas, M., and Castel-

lano, J. (2004). Evolving rbf neural networks for time-

series forecasting with evrbf. Information Sciences,

165(3-4):207 – 220.

Sheskin, D. (2004). Handbook of parametric and nonpara-

metric statistical procedures. Chapman & Hall/CRC.

Snyder, R. (1985). Recursive estimation of dynamic linear

models. Journal of the Royal Statistical Society. Series

B (Methodological), 47(2):272–276.

Takens, F. (1980). Dynamical Systems and Turbulence, Lec-

ture Notes In Mathematics, volume 898, chapter De-

tecting strange attractor in turbulence, pages 366–381.

Springer, New York, NY.

Tong, H. (1978). On a threshold model. Pattern recognition

and signal processing, NATO ASI Series E: Applied

Sc., 29:575–586.

Winters, P. (1960). Forecasting sales by exponentially

weighted moving averages. Management Science,

6(3):324–342.

TheL-Co-RCo-evolutionaryAlgorithm-AComparativeAnalysisinMedium-termTime-seriesForecastingProblems

151