
Dynamically Reconfigurable Online Self-organising Fuzzy Neural
Network with Variable Number of Inputs for Smart Home
Application
Anjan Kumar Ray, Gang Leng, T. M. McGinnity, Sonya Coleman and Liam Maguire
Intelligent Systems Research Centre, University of Ulster, Magee Campus, Londonderry, BT48 7JL, U.K.
Keywords: Self-organising System, Fuzzy Logic, Neural Network, Cognitive Reasoning.
Abstract: A self-organising fuzzy-neural network (SOFNN) adapts its structure based on variations of the input data.
Conventionally in such self-organising networks, the number of inputs providing the data is fixed. In this
paper, we consider the situation where the number of inputs to a network changes dynamically during its
online operation. We extend our existing work on a SOFNN such that the SOFNN can self-organise its
structure based not only on its input data, but also according to the changes in the number of its inputs. We
apply the approach to a smart home application, where there are certain situations when some of the existing
events may be removed or new events emerge, and illustrate that our approach enhances cognitive reasoning
in a dynamic smart home environment. In this case, the network identifies the removed and/or added events
from the received information over time, and reconfigures its structure dynamically. We present results for
different combinations of training and testing phases of the dynamic reconfigurable SOFNN using a set of
realistic synthesized data. The results show the potential of the proposed method.
1 INTRODUCTION
Activity recognition within a smart home
environment is a challenging research problem.
Researchers are exploring different solutions for
low-level data collection, information processing
and high-level service delivery. The main objectives
of presenting intelligence into a smart home
environment are to identify the importance of events
and automatically activate suitable responses
(Bregman, 2010). Another important aspect of
situation awareness within a smart home is to detect
anomalous events. Jakkula and Cook (2011) used
One Class Support Vector Machines (OCSVM)
techniques to address this issue. Gaddam,
Mukhopadhyay, and Gupta (2011) presented a home
monitoring system based on a cognitive sensor
network for elderly-care applications. Processing of
the sensory information is essential to recognise the
context of the ecology. Wang, Chuang, Lai, and
Wang (2005) proposed CASSHA (Context-Aware
System for Smart Home Applications) for
processing, representation, and coordination of smart
home applications. Youngblood, Cook and Holder
(2005) proposed a home automation model to
understand the needs of inhabitants within the
MavHome project. Lin and Fu (2007) used Bayesian
Networks (BNs) to learn multiple users’ preferences;
these represent relationships among users and
related sensor observations. Zheng, Wang, and
Black (2008) developed a self-adaptive neural
network based on Growing Self-Organizing Maps
(GSOM) to analyse human actions within a smart
home environment. Chen et al. (2009) proposed a
hybrid system, which explored the relationship
between an activity model and a preference model to
provide appropriate services. Roy et al. (2010)
discussed an initial framework of activity
recognition based on possibility theory and
description logic (DL). Mastrogiovanni, Sgorbissa,
and Zaccaria (2010) integrated ontology and logic
based approaches for context representation and
recognition to map numerical data to symbolic
representations. Chen and Nugent (2010) discussed
the concept of semantically enhanced situation
awareness for activity of daily living (ADL)
assistance. This work was extended in Chen,
Nugent, and Wang (2012) with an ontology-based
knowledge-driven approach for activity recognition.
Son, Park, Moon, and Lee (2011) reported a
507
Kumar Ray A., Leng G., M. Mcginnity T., Coleman S. and Maguire L..
Dynamically Reconfigurable Online Self-organising Fuzzy Neural Network with Variable Number of Inputs for Smart Home Application.
DOI: 10.5220/0004555405070514
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 507-514
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

resource-aware smart home management system.
Alam, Reaz, and Ali (2012) proposed an algorithm,
called sequence prediction via enhanced episode
discovery (SPEED), to predict user activity in smart
homes. Zhang, McClean, and Scotney (2012)
proposed a learning algorithm to understand multi-
inhabitant activity profiles from a limited number of
data from unreliable low-level sensors. Ray, et al.
(2012) described a cognitive reasoning model based
on a SOFNN that analyses events of a smart home
ecology and reasons across those events to
determine situational awareness. The SOFNN is
suitable for dynamic model compactness as it
identifies its structure and parameters of fuzzy
neural networks from the available data. This makes
the approach suitable for a dynamic smart home
environment. The above mentioned approaches have
a common deficiency in that the processes are built
on a fixed number of contexts. However in a smart
home application, situations change over time as
new sensors and/or actuators are introduced or
behaviours of users change. In this work, we address
this problem. We first develop a dynamic online
SOFNN which reorganises its structure based on a
variable number of inputs which changes
dynamically over time. Then we demonstrate the use
of this proposed method for cognitive reasoning for
a smart home environment.
The remainder of the paper is organised as
follows: section 2 describes the design and
implementation issues of the dynamic SOFNN,
which self-organises its structure depending on the
number of inputs and their values. A brief overview
is presented for neuron addition and pruning
strategies. Section 3 presents the results of the
proposed work. A set of anticipated events and
reasoning outputs are chosen to validate the
proposed idea. The results on structural growth of
the SOFNN and the cognitive reasoning capabilities
under synthesized scenarios with different training
and testing situations are presented. In section 4, we
present the overall conclusions of this work.
2 DYNAMIC ONLINE SOFNN
The SOFNN has a five layer structure as shown in
Figure 1. The current structure, as reported in our
previous work (Ray, 2012) has a fixed number of
inputs. Consider that for the t-th observation (X
t
, d
t
),
we define X
t
=[x
1t
x
2t
…. x
rt
] as the input vector, r as
the number of inputs, d
t
as the desired output
(target), y
t
as the output of the current network, then
the output in layer 5 is obtained as (Ray et al., 2012)
Figure 1: The structure of the SOFNN.
u
k
r
i
ik
iki
u
j
r
i
ij
iji
j
cx
cx
w
Xy
11
2
2
11
2
2
2
2
)(
exp
2
)(
exp
)(
(1)
where u is the number of neurons; c
ij
and
ij
are the
centre and width of the i-th membership function
(MF) in the j-th neuron; w
2j
is the weighted bias (B)
which is defined for the TS model (Takagi and
Sugeno, 1985) as
ujxaxaaw
rjrjjj
,,2,1;
1102
(2)
During the training process, the first ellipsoidal basis
function (EBF) neuron is created based on the first
input vector. The number of membership functions
in each EBF neuron is the same as the number of
inputs. Further details on the sliding window based
training process are available in (Leng et al., 2005)
and (Ray et al., 2012). Figure 2 shows the procedure
for adding new EBF neurons to the existing structure
(Ray et al., 2012) where threshold for output of
neuron is set at 0.1354 (equivalent to 2 standard
deviations from mean). During training, there are
some neurons which have insignificant contributions
for the desired output. These neurons are deleted
from the network for model compactness. The
procedure for pruning insignificant neurons is shown
in Figure 3 (Ray et al., 2012).
There are some applications e.g. smart homes
where the number of inputs is not fixed. As new
sensors and actuators are added to the system, the
number of inputs will change dynamically.
Moreover, there exists the possibility that some of
the inputs may not be available due to
sensor/actuator failures. One option would be to
consider those inputs as having ‘0’ values. But, a ‘0’
value may have significance in certain cases (e.g.
on/off sensor status). Moreover, if we consider
unavailable inputs within the network, then certain
contributions are reflected within the EBF and
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
508

normalised layers. So, a dynamic change of the
number of inputs to the network poses a significant
design constraint but one which needs to be
accommodated in real life.
Figure 2: The process of adding a new EBF neuron.
Figure 3: The process of pruning neurons.
To address this issue, we propose a dynamic
SOFNN structure, which can handle a variable
number of inputs. We aim to provide a facility to
accommodate dynamical changes in the network
structure, where the number of inputs to the network
changes over time.
2.1 Layer 1: Input Layer
We define X
e
as the set of pre-existing inputs to the
network, X
r
as the set of existing inputs that are
removed from the network at time t, X
a
as the set of
new inputs that are added to the network at time t, X
n
as the new set of inputs in the input layer, and X
c
as
the common inputs in X
e
and X
n
. So, we can present
the above understanding as follows:
)(],,,2,1[:),(
],,2,1[:),(
eoer
eroroororor
eepepe
<r, r X X
X,xidroxidX
rpxidX
aren
nec
cckckc
ninin
ealalaalala
XXXX
XXX
rkxidX
mixidX
Xxid,rl)xidX
)\(
],,2,1[:),(
],,2,1[:),(
),(],,2,1[:,(
(3)
where r
e
is the number of existing inputs, r
o
is the
number of removed inputs from the existing inputs,
r
a
is the number of newly added inputs, r
c
is the
number of common inputs, id refers to the input id,
and m=r
e
-r
o
+r
a
. The network receives the set of
inputs X
n
at each sample where an input refers to
corresponding id and its value. The rules to obtain
X
a
, X
r
, r
a
, r
o
are as follows:
1. Check X
e
and X
n
for common inputs X
c
and r
c
a. Find I
xe
(k), k=[1 2 … r
c
] i.e.
index of common inputs in X
e
b. Find I
xn
(k), k=[1 2 … r
c
] i.e.
index of common inputs in X
n
2. Check for inputs that are present in
X
e
but excluded in X
n
a. Get X
r
and r
o
b. Find I
xr
(o), o=[1 2 … r
o
] i.e.
index of removed inputs in X
e
3. Check for inputs that are present in
X
n
but not available in X
e
a. Get X
a
and r
a
b. Find I
xa
(l), l=[1 2 … r
a
] i.e.
index of added inputs in X
n
Depending on the values of r
o
and r
a
, the
membership functions (MFs), bias and weighting
matrix will change accordingly.
2.2 Layer 2: EBF Layer
The addition and/or removal of inputs requires
modification of the number of the MFs associated
with each neuron, and their relative organisation
within it. Let’s consider, C
eje
,
eje
to be the sets of
centres and widths of MFs of the je-th EBF neuron
in the existing structure respectively and C
nj
,
jn
to
be the sets of centres and widths of MFs of the j-th
EBF neuron in the new structure where je = 1, 2 …
u
e
, j = 1 2 … u
n
; u
e
and u
n
represent the number of
EBF neurons in the existing and new structures and
u
n
=u
e.
. Hence we obtain:
DynamicallyReconfigurableOnlineSelf-organisingFuzzyNeuralNetworkwithVariableNumberofInputsforSmart
HomeApplication
509
]},,2,1[],,,2,1[:{
]},,2,1[],,,2,1[:{
]},,2,1[],,,2,1[:{
]},,2,1[],,,2,1[:{
nnijnj
nnijnj
eeepjeeje
eeepjeeje
u jmi
u jmicC
u jerp
u jerpcC
(4)
As the number of inputs changes in the layer 1, so in
general,
0},,min{,,2,1 > r m}r q
cc
oe
nqjeqje
nqjeqje
(5)
The update rule for centres and widths of the MFs
are as follows:
1. If m=r
e
and r
c
=r
e
then no change in
input structure and
c
nij
=c
eij
nij
=
eij
i=[1 2 … m]; j=[1 2 … u
n
]
2. Othewise, follow steps 3 to 5
3. Get I
xe
and I
xn
of common inputs in
X
e
and X
n
from layer 1
4. Update MFs of each EBF neurons as
follows:
a = I
xn
(k)
b = I
xe
(k)
c
naj
= c
ebj
naj
=
ebj
k=[1 2 … r
c
], j=[1 2 … u
n
]
5. If r
a
>0 then add new r
a
number of
MFs to each existing EBF neuron and
update as follows:
c = I
xa
(l)
c
ncj
= x
nc
ncj
= chosen predefined value
l= [1 2 … r
a
], j= [1 2 … u
n
]
So the new i-th membership function in the j-th
neuron is
n
nij
nijni
nij
ujmi
cx
,,2,1;,,2,1;
2
exp
2
2
(6)
Accommodating the changes in the previous layer,
the output of each EBF neuron in layer 2 is given by
m
i
nnijnj
uj
1
,,2,1;
(7)
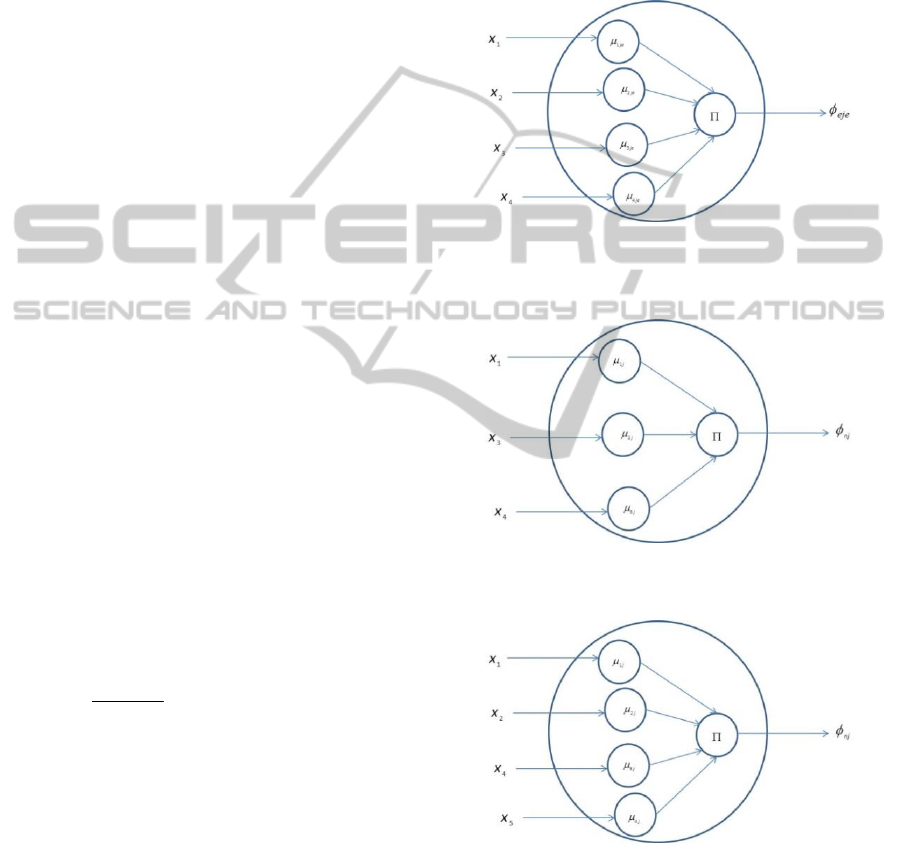
Any change in input number will change the internal
structure of the EBF neurons. Let the current
structure of the je-th EBF neuron be given as in
Figure 4. It shows four MFs corresponding to four
inputs. If input x
2
is removed from the network then
the structure of the EBF neuron will change. Figure
5 depicts that the neuron has three MFs and MFs
two and three are related to inputs x
3
and x
4
. When
r
o
=r
a
, the total number of inputs to the network does
not change. But the internal structure of the neuron
changes and represents a new EBF neuron. Figure 6
depicts that input x
3
is removed and input x
5
is
added. Although the neuron has four MFs, they are
different as compared to the MFs in Figure 4 Here
the new MFs three and four correspond to the inputs
x
4
and x
5
respectively.
Figure 4: Structure of an existing EBF neuron with four
inputs and four membership functions corresponding to
each input.
Figure 5: Modified MFs as per change in the number of
inputs (input number two is removed).
Figure 6: Modified MFs as per change in the number of
inputs (input three is removed and input 5 is added).
2.3 Layer 3: Normalised Layer
The number of neurons in this layer is the same as
layer 2. The new output of the j-th neuron in this
layer will reflect the changes in inputs to the
network and is given by
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
510

n
n
u
n
k
n
k
nj
nj
uj ,,2,1;
1
(8)
2.4 Layer 4: Weighted Layer
The output of this layer depends on the outputs of
layer 3 and the weighted bias. Let, the existing bias
vector and parameter vector be given respectively by
B
e
= [1 x
e1
x
e2
… x
ere
]
T
A
e
j
e
= [a
e
j
e0
a
e
j
e1
a
e
j
e2
… a
e
j
ere
]; je = 1 2 … u
e
(9)
So, the existing weighted bias is
w
eje
= A
eje
B
e
= a
eje0
+ a
eje1
x
e1
+ a
eje2
x
e2
+ … + a
ejere
x
ere
(10)
As the inputs change in number as well as positions
within the input set, the bias and parameter vectors
are also changed. Let, the new bias and parameter
vectors be given by
B
n
= [1
x
n1
x
n2
… x
nm
]
T
A
n
j
= [a
n
j
0
a
n
j
1
a
n
j
2
… a
n
j
m
]; j=1 2 … u
n
(11)
The update for B
n
is straightforward according to the
received inputs. The update rule for A
nj
is as follows:
1. If m=r
e
and r
c
=r
e
then
A
nj
=A
ej
,
j=[1 2 … u
n
]
2. Othewise, follow steps 3 to 5
3. Get I
xe
and I
xn
of common inputs in
X
e
and X
n
from layer 1
4. Update A
nj
as follows:
g = I
xn
(k)+1
h = I
xe
(k)+1
a
nj0
= a
ej0
a
njg
= a
ejh
k=[1 2 … r
c
], j=[1 2 … u
n
]
5. If r
a
>0 then add new r
a
number of
elements in A
nj
as follows:
c = I
xa
(l)+1
a
njc
= 0
l= [1 2 … r
a
], j= [1 2 … u
n
]
The above steps are referred to as the initialisation of
new parameters. The weighted bias of the new
structure is given by
nmnjmnnjnjnnjnj
xaxaaBAw
110
(12)
The output of each neuron in this layer is given by
njnjnj
wf
(13)
2.5 Layer 5: Output Layer
The output of this layer is a summation of the
overall outputs from layer 4 and is given by
n
u
j
njn
fXy
1
)(
(14)
This will restructure the existing network to adapt to
the changes in the number of inputs. This will
produce an initial network structure which can
accommodate a dynamic change in inputs.
3 RESULTS
To validate our proposed system, we consider a
smart home situation with different sensors and
actuators. Different events that are obtained from
sensory data within the environment reflect the
activities of a user. The developed SOFNN is used
to extract high level understanding from these events
related to the user activities. We consider a set of 19
initial event inputs and 10 reasoning outputs for this
situation. The chosen inputs and reasoning outputs
are shown in Table 1 and Table 2 respectively.
Values of inputs and outputs represent confidence
levels between 0 and 1. We synthesize 4500 data
samples. The dataset ensures a richness of variability
with sufficient complexity to exercise the reasoning
capabilities of the system. First, we consider training
results for 3 different cases with sliding window of
300 data samples. In the first case the network is
trained with 19 inputs. Then we consider the
network with deletion of an input event (from 19 to
18 inputs) after 900 samples (the visitor detection
event is removed). In case 3, the number of inputs
changes from 19 to 20 after 900 samples. The
objective is to observe the online adaptation as a
result of the change in the number of inputs. Figure
7 shows the neuronal structure for the 3 cases when
the network reasons across the ‘user relaxing’
situation. It is observed that the network produces
different structures according to addition and
pruning of neurons. The overall neuronal structures
of the network for these cases are shown in Figure 8
and Table 3. The network has 17, 22, and 23 neurons
for these cases respectively. From these results, it is
clear that the proposed network is capable of
handling changes in its input numbers. Table 4
shows the root mean square errors (RMSE) during
training to obtain the expected reasoning outputs.
Next, we consider different testing situations
using a trained network with 4500 data samples for
19 inputs. We show testing results with 300 data
samples (4201 to 4500) for 3 cases. In case 1, we
consider 19 inputs. In case 2, we consider 18 inputs
where input id 12 (TV usage) is dropped. In case 3,
we consider deletion of input id 4 ( Visitor
DynamicallyReconfigurableOnlineSelf-organisingFuzzyNeuralNetworkwithVariableNumberofInputsforSmart
HomeApplication
511

Figure 7: Change of the number of EBF neurons for the
‘user relaxing’ situation for different training cases: (a)
network with 19 inputs; (b) network with deletion of an
input (from 19 to 18 inputs) after 900 samples; (c) network
with addition of an input (from 19 to 20 inputs) after 900
samples.
Table 1: The event inputs for the smart home application.
Synthesized input ids Events
1 User in room 1
2 User in room 2
3 User in room 3
4 Visitor detection
5 Phone event
6 Doorbell event
7 Dripping event
8 Music event
9 Fire alarm
10 Microwave usage
11 Dishwasher usage
12 TV usage
13 Cleaning operation
14 Cooking
15 Use of oven
16 Smoke detection
17 Room temperature
18 Burglary alarm
19 Front door usage
Table 2: The target outputs for SOFNN reasoning.
Output ids Reasoning outputs
1 User exercise
2 User relaxing
3 User in kitchen
4 Bring phone
5 Open door
6 Cooking activity
7 Fire alert situation
8 Burglary alert situation
9 Dripping alert situation
10 Cleaning situation
Figure 8: Change of the number of EBF neurons for the
overall network for different training cases: (a) network
with 19 inputs; (b) network with deletion of an input event
(from 19 to 18 inputs) after 900 samples; (c) network with
addition of an input event (from 19 to 20 inputs) after 900
samples.
Table 3: Total number of EBF neurons for the reasoning
outputs in different training cases.
Reasoning outputs Case 1 Case 2 Case 3
User Exercise 1 1 1
User Relaxing 4 6 6
User in Kitchen 1 1 1
Bring Phone 1 1 1
Open Door 1 2 1
Cooking Activity 2 2 2
Fire Alert Situation 2 2 2
Burglary Alert
Situation
1 2 2
Dripping Alert
Situation
1 1 2
Cleaning Situation 3 4 5
Total Neurons 17 22 23
Detection). Figure 9 and Figure 10 show the
reasoning outputs from the network when there are
19 inputs (case 1) and 18 inputs (case 2). It is
observed in Figure 9 that the confidence level of
“user relaxing” is reduced when the TV usage event
is removed. The network identifies all other
reasoning outputs as expected. Figure 11 and Figure
12 show the reasoning outputs from the network
when there are 19 inputs (case 1) and 18 inputs (case
3). It is observed in Figure 12 that the confidence
level of the “open door” situation is reduced as the
“visitor detection” event is dropped from the input
set. The network identifies all other reasoning
outputs as expected. The RMSEs for these testing
cases are shown in Table 5. It is observed that the
RMSEs for the “user relaxing” in case 2 and “open
door situation” in case 3 have higher values.
500 1000 1500 2000 2500 3000 3500 4000 4500
0
5
10
User relaxing
(a)
500 1000 1500 2000 2500 3000 3500 4000 4500
0
5
10
(b)
Total number of EBF neurons
500 1000 1500 2000 2500 3000 3500 4000 4500
0
5
10
(c)
Number of samples
500 1000 1500 2000 2500 3000 3500 4000 4500
10
20
30
Self-organisation of the network
(a)
500 1000 1500 2000 2500 3000 3500 4000 4500
10
20
30
(b)
Total number of EBF neurons
500 1000 1500 2000 2500 3000 3500 4000 4500
10
20
30
(c)
Number of samples
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
512

Table 4: RMSE of different training cases.
Reasoning outputs Case 1 Case 2 Case 3
User Exercise
0.0828 0.0810 0.0817
User Relaxing
0.0482 0.0421 0.0423
User in Kitchen
0.0658 0.0649 0.0650
Bring Phone
0.0667 0.0661 0.0656
Open Door
0.0531 0.0668 0.0521
Cooking Activity
0.0621 0.0611 0.0579
Fire Alert Situation
0.0319 0.0292 0.0311
Burglary Alert
Situation
0.0812 0.0693 0.0698
Dripping Alert
Situation
0.0842 0.0832 0.0799
Cleaning Situation
0.0454 0.0590 0.0547
Figure 9: Set 1 of reasoning outputs during testing with 19
inputs and 18 inputs (TV event removed).
Figure 10: Set 2 of reasoning outputs during testing with
19 inputs and 18 inputs (TV event removed).
Figure 11: Set 1 of reasoning outputs during testing with
19 inputs and 18 inputs (Visitor detection event removed).
Figure 12: Set 2 of reasoning outputs during testing with
19 inputs and 18 inputs (Visitor detection event removed).
Table 5: RMSEs of different testing cases.
Reasoning outputs Case 1 Case 2 Case 3
User Exercise 0.0681 0.0697 0.0716
User Relaxing 0.0527 0.2260 0.0513
User in Kitchen 0.0671 0.0730 0.0671
Bring Phone 0.0662 0.0666 0.0699
Open Door 0.0529 0.0556 0.2062
Cooking Activity 0.0671 0.0733 0.0674
Fire Alert Situation 0.0345 0.0515 0.0372
Burglary Alert
Situation
0.0613 0.0652 0.0619
Dripping Alert
Situation
0.0844 0.0846 0.0835
Cleaning Situation 0.0283 0.0396 0.0282
4 CONCLUSIONS
This paper presents a dynamically reconfigurable
online SOFNN for application in a robot ecology
environment. In this work we address the situation
DynamicallyReconfigurableOnlineSelf-organisingFuzzyNeuralNetworkwithVariableNumberofInputsforSmart
HomeApplication
513

when the number of inputs varies over time. We
then implemented and utilized this network to
extract knowledge from realistic events occurring
within a smart home environment. A set of realistic
synthesized training and testing data have been
employed to observe different scenarios. We show
the structural modifications of the network when the
number of inputs changes for the network during the
training phase. We also show the impact of
removing event inputs from the network during
different testing phases. The results show that the
network has the ability to adapt to the dynamics of
the environment and show its cognitive capability.
ACKNOWLEDGEMENTS
This work is partially supported by the EU FP7
RUBICON project (contract no. 269914) –
www.fp7rubicon.eu.
REFERENCES
Alam, M. S., Reaz, M. B. I., and Ali, M. A. M., 2012.
SPEED: An inhabitant activity prediction algorithm
for smart homes. IEEE Transactions on Systems, Man,
and Cybernetics—Part A: Systems and Humans,
42(4), 985-990.
Bregman, D., 2010. Smart home intelligence - the ehome
that learns. International journal of smart home, 4(4).
Chen, L., and Nugent, C. D., 2010. Situation aware
cognitive assistance in smart homes. Journal of
Mobile Multimedia, 6(3), 263-280.
Chen, L., Nugent, C. D., and Wang, H., 2012. A
knowledge-driven approach to activity recognition in
smart homes. IEEE Transactions on Knowledge and
Data Engineering, 24(6), 961-974.
Chen, Y. H., Lu, C. H., Hsu, K. C., Fu, L. C., Yeh, Y. J.,
and Kuo, L. C., 2009. Preference model assisted
activity recognition learning in a smart home
environment. IEEE/RSJ International Conference on
Intelligent Robots and Systems, 4657 - 4662.
Gaddam, A., Mukhopadhyay, S. C., and Gupta, G. S.,
2011. Elder care based on cognitive sensor network.
IEEE Sensors Journal, 11(3).
Jakkula, V., and Cook, D. J., 2011. Detecting anomalous
sensor events in smart home data for enhancing the
living experience. AAAI Workshop, 33-37.
Leng, G., McGinnity, T. M., and Prasad, G., 2005. An
approach for on-line extraction of fuzzy rules using a
self-organising fuzzy neural network. Fuzzy Sets and
Systems, 150(2), 211-243.
Lin, Z. H., and Fu, L. C., 2007. Multi-user preference
model and service provision in a smart home
environment. IEEE International Conference on
Automation Science and Engineering, 759 – 764.
Mastrogiovanni, F., Sgorbissa, A., and Zaccaria, R., 2010.
A cognitive model for recognizing human behaviours
in smart homes. Ann. Telecommunication, 65, 523–
538.
Ray, A. K., Leng, G., McGinnity, T. M., Coleman, S. A.,
and Maguire, L. P., 2012. Development of cognitive
capabilities for smart home using a self-organizing
fuzzy neural network. 10th IFAC Symposium on Robot
Control, Dubrovnik, Croatia, 447-454.
Roy, P. C., Giroux, S., Bouchard, B., and Bouzouane, A.,
Phua, C., Tolstikov, A., and Biswas, J., 2010.
Possibilistic behavior recognition in smart homes for
cognitive assistance, AAAI Workshop, 53-60.
RUBICON project., 2011. EU FP7 project. FP7 challenge
2, cognitive systems and robotics. Available:
http://www.fp7rubicon.eu.
Son, J. Y., Park, J. H., Moon, K. D., and Lee, Y. H., 2011.
Resource-aware smart home management system by
constructing resource relation graph. IEEE
Transactions on Consumer Electronics, 57(3).
Takagi, T., and Sugeno, M., 1985. Fuzzy identification of
systems and its applications to modeling and control.
IEEE Transactions on Systems, Man, and Cybernetics,
15(1), 116-132.
Wang, W. Y., Chuang, C. C., Lai, Y. S., and Wang, Y. H.,
2005. A context-aware system for smart home
applications. EUC Workshops, LNCS 3823, 298-305.
Youngblood, G. M., Cook, D. J., and Holder, L. B., 2005.
Managing adaptive versatile environments. Pervasive
and Mobile Computing, 1(4), 373-403.
Zhang, S., McClean, S. I., and Scotney, B. W., 2012.
Probabilistic learning from incomplete data for
recognition of activities of daily living in smart homes.
IEEE Transactions on Information Technology in
Biomedicine, 16(3), 454-462.
Zheng, H., Wang, H., and Black, N., 2008. Human
activity detection in smart home environment with self-
adaptive neural networks. IEEE ICNSC, 1505–1510.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
514
