
Neural Networks Ensemble for Quality Monitoring
P. Thomas, M. Noyel, M. C. Suhner, P. Charpentier and A. Thomas
Centre de Recherche en Automatique de Nancy (CRAN-UMR 7039), Lorraine-Université,
CNRS Faculté des Sciences et Techniques, BP 70239, 54506 Vandoeuvre lès Nancy Cedex, France
Keywords: Neural Network, Product Quality, Neural Network Ensemble, Multivariate Quality Control, Classification,
Classifiers Ensemble.
Abstract: Product quality level is a key concept for companies' competitiveness. Different tools may be used to
improve quality such as the seven basic quality tools or experimental design. In addition, the need of
traceability leads companies to collect and store production data. Our paper aims to show that we can ensure
the required quality thanks to an "on line quality approach" based on exploitation of collected data by using
neural networks tools. A neural networks ensemble is proposed to classify quality results which can be used
in order to prevent defects occurrence. This approach is illustrated on an industrial lacquering process.
Results of the neural networks ensemble are compared with the ones obtained with the best neural network
classifier.
1 INTRODUCTION
One of the main goals in the mass customization
context is the product quality control. Statistical
process control is one of the most effective tools of
Total Quality Management (TQM). The American
Production and Inventory Control Society (APICS)
defines Total Quality Management as "A
management approach to long-term success through
customer satisfaction. TQM is based on the
participation of all members of an organization in
improving processes, goods, services, and the
culture in which they work". This definition is very
related to the definition of Just in Time (JiT) because
APICS presents JiT as “A philosophy of
manufacturing based on planned elimination of all
wastes and on continuous improvement of
productivity. One of the main elements of JiT is to
improve quality to zero defects. In the broad sense, it
applies to all forms of manufacturing”. JiT and TQM
are two major concepts related to Lean
manufacturing –LM- (Vollmann et al., 1984).
Different tools may be used to improve quality such
as the seven basic quality tools (Ishikawa chart,
check sheet, control charts, histogram, Pareto chart,
scatter diagram, stratification), or experimental
designs. These tools, along with the Taguchi
Method, are well known in the industry. Initially,
quality products was controlled a posteriori and this
a posteriori control led to reject or to downgrade a
large part of the production. Taguchi is the first to
propose to control quality before the product
origination with the set-up parameters control. this
approach based on the experimental design present
the drawback to be off-line.
In addition, the seek of traceability imposes to
companies to collect and store production data. We
propose to exploit these data in order to perform on-
line quality monitoring. The proposed approach
relies to the same philosophy as Taguchi approach.
The main goal is to set-up production parameters in
order to prevent defects occurence. This set-up is
performed on-line by taking into account the
variation in the operating range.
The first step is to extrack from data, knowledge
on the defects production. One important step of the
knowledge discovery in data processus is the
datamining step which may be performed by using
neural networks. Other tools may be used to perform
this step as fuzzy logic when expert knowledge is
available or naïve Bayes or decision tree where only
discret data are used. Neural network performs a
local search of optimum. This fact implies that the
neural network design needs to perform many
learning with different initial weights sets in order to
avoid local minimum trapping problem. These
different learning produces different classifiers more
or less performant. The simplest strategy could be to
515
Thomas P., Noyel M., Suhner M., Charpentier P. and Thomas A..
Neural Networks Ensemble for Quality Monitoring.
DOI: 10.5220/0004556505150522
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 515-522
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

select the single, best performing classifier. Another
approach consists to use an ensemble of these
classifiers (Hansen and Salomon, 1990). This
approach based on the Condorcet's jury theorem
allows to improve the results. The second step is to
performed an on-line optimal production parameter
set-up based on the classifier ensemble results and
which may vary in function of the operating range.
The main goal of this paper is to evaluate the use
of a neural network ensemble classifier for quality
monitoring process comparing with a single neural
classifier. The design of a Taguchi experiments by
using these classifiers is also investigated in order to
find optimal tuning of controllable parameters for
considered operating point.
First, we will recall succinctly the knowledge
discovery in data process. In a second step, the
neural network structure, its learning and pruning
procedure are recalled before to present neural
network ensemble. After, the industrial application
case and the results obtained are presented before to
conclude.
2 KNOWLEDGE DISCOVERY
IN DATA FOR QUALITY
To control quality, we must understand it. So we
need to know precisely factors affecting quality.
These factors can be classified according to 6M
(Ishikawa, 1986) of the Ishikawa chart (Machine
(technology), Method (process), Material, Man
Power, Measurement (inspection), Milieu
(environment). When considering their
controllability, only 4 of the 6M must be considered:
Environmental Factors (Environment-Milieu) such
as temperature or humidity. These factors are
generally low- or non-controllable.
Technical Factors (Machine and Method) resulting
primarily from the machine state during
operations. They are controllable factors.
Human Factors (Man Power) in manual
operations. They are difficult to take into account
because they sometimes vary consequently
between operators. So far, the attempts to control
human factors (establishing standards, poka yoke)
have limitations and constraints.
Knowledge on the controllability of factors is
needed in order to determine if a factor may be
tuned or considered as constraint or even as noise.
When the influential factors are correctly analyzed,
we can focus on the challenge for quality control.
The "zero defect" can be obtained in two ways:
By optimizing the initial settings of various
factors.
By drifts monitoring and prevention.
This paper focuses on the first way. Historically,
there are two approaches to manage quality. The
first one, and also the easiest, is to use the seven
basic quality tools (Ishikawa chart, check sheet,
control charts, histogram, Pareto chart, scatter
diagram, stratification). In this approach, the
finished parts are a posteriori controlled and
improvement propositions are performed by using
expert knowledge. In a second approach, the main
goal is to control the process and no longer the
finished parts in order to tune the technical factors
off-line by using experimental design methods.
In our approach, the production data collected
are used in order to determine the conditions of
defects apparition. To do that, a Knowledge
Discovery in Data (KDD) process may be
performed. KDD process is performed in different
steps (Patel and Panchal, 2012). We assign a letter to
each step in order to refer more easily to them later.
Selection: obtain data from various sources (a),
Preprocessing: cleanse data (b),
Transformation; convert to common format,
transform to new format (c),
Data mining: obtain desired results (d),
Interpretation/Evaluation/Presentation: present
results to user in meaningful manner (e).
The two main steps are selection (a) and data
mining (d). Data mining which is the core part of
KDD is the process of analysing data and summarize
it into useful information. Different approaches can
be used to perform it such as artificial intelligence,
machine learning, statistics and database systems.
Data mining may perform different tasks:
Classification: maps data into predefined group or
classes,
Regression: maps data from an input space to an
output space,
Clustering: groups similar data together into
clusters,
Summarization: maps data into subsets with
associated simple descriptions,
Link Analysis: uncovers relationships among data.
In a quality monitoring problem, the data mining
must perform a classification of data into 2 classes:
defect occurrence and no defect occurrence.
2.1 Selection (a), Preprocessing (b)
and Transformation (c) of Data
An important task in KDD process is the data
collection (a). It is possible to collect the values of
the different factors that influence quality in the
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
516

same way. The availability of data is a crucial point
for the quality analysis. Ideally, the collect of data
must be automated. In the case of manual data
collection we need to increase operator awareness of
the importance of this task. Manual data collection is
often seen as a waste of time because the operator
must stop his work to write information not used
directly in production. If this task is not correctly
performed, the whole database becomes unworkable.
However, manual data collection is often inevitable,
because quality checking is often manually
performed. It is necessary to consolidate the two
types of data (production information and quality
factor values). The data must be preprocessed (b) in
order, for example, to synchronize the different
database, delete evident outliers, and digitize
qualitative data as color (c)...
2.2 Datamining (d)
The volume of data to be analyzed is often weighty
(Agard and Kusiak 2005). Companies collect and
store data for traceability reasons but they rarely use
their well of information and only as indicators for
real-time management methods (Kusiak, 2001). Data
mining is the part of Knowledge Discovery in Data
which consists in analyzing data in order to
summarize it into useful information. In our case,
data mining should perform a classification of data
into two classes: defect occurrence and no defect
occurrence. To do that, different tools may be used
such as Naïve Bayes, Decision tree, Support Vector
Machine (SVM), neural networks (NN)... Decision
tree is faster to classify data but does not work well
with noisy data (Patel and Panchal, 2012). So in the
case of industrial data, the use of this approach is not
pertinent. Naïve Bayes is dedicated to the treatment
of discrete data and the use of continuous ones needs
to perform a discretization of these data. Support
Vector Machine and Neural network both use very
close concepts which lead to very close results.
Sometimes, SVM gives better results (Meyer et al.,
2003), sometimes it is NN (Paliwal and Kumar,
2009; Hajek and Olej, 2010). This work focuses on
neural network tools which are presented in the next
section.
3 NEURAL NETWORK TOOLS
3.1 Multilayers Perceptron
We propose the use of neural networks (NN) to
model systems in order to classify quality products.
The final goal is to determine the best on-line
settings for each factor. The advantages of this
approach are:
Exploitation of real data without carrying out
dedicated experiments as in experiments plan by
using database collected during the production.
Simple implementation of the approach because
the neural model design is partially automated.
On-line tuning of the quality monitoring process
by using actual production data in order to
improve and adapt the process to change.
In our approach, the neural model is performed
by using production data representatives of all the
conditions encountered in the past and so, it can
adapt itself to these changeable conditions. This
model is able to provide lower and upper limits for
each controllable factor settings based on all non-
controllable factors.
The multilayer perception (MLP) seems to be the
neural network best suited to our case. Works of
Cybenko (1989) and Funahashi (1989) have proved
that a MLP with only one hidden layer using a
sigmoïdal activation function and an output layer
can approximate all non-linear functions with the
wanted accuracy. Its structure is given by:
01
2101
21
11
..
n
n
iihhi
ih
zg wg wx b b
(1)
where
0
h
x
are the n
0
inputs of the neural network,
1
ih
w are the weights connecting the input layer to the
hidden layer,
1
i
b are the biases of the hidden
neurons,
g
1
(.) is the activation function of the hidden
neurons (here, the hyperbolic tangent),
2
i
w are the
weights connecting the hidden neurons to the output
one,
b is the bias of the output neuron g
2
(.) is the
activation function of the output neuron and
z is the
network output. Because of the problem is to obtain
a classification of product into two classes: defect
occurrence and no defect occurrence,
g
2
(.) being
chosen sigmoïdal.
3.2 Initialisation, Learning
and Pruning
Three steps must be performed in order to design the
neural model.
3.2.1 Initialisation
The first one is the determination of the initial set of
weights and biases. This step is important because
learning algorithm performs a local search of
NeuralNetworksEnsembleforQualityMonitoring
517

minimum. So, in order to avoid local minimum
trapping, different initial sets must be constructed
which allow beginning learning in different zones of
the criteria domain. Different initialisation
algorithms have been proposed in the literature
(Thomas and Bloch, 1997). The initialisation
algorithm used is the one proposed by Nguyen and
Widrow (1990) which allows associating a random
initialization of weights and biases to an optimal
placement in input and output spaces. This step
allows improving the diversity of the neural
classifiers which is an important notion for neural
network ensemble.
3.2.2 Learning
The second step is performed by the learning
algorithm which must fit the network output with the
data. In industrial application data are noisy and
corrupted with many outliers. In order to limit the
impact of outliers on the results, a robust Levenberg-
Marquardt algorithm is used (Thomas et al., 1999).
Levenberg–Marquard algorithm allows associating
the speed of the Hessian methods to the stability of
the gradient methods. This is performed by adding a
parameter multiplied by the identity matrix in order
to permit the inversion of the Hessian matrix even if
it is singular. The tuning of this parameter during the
learning allows the Levenberg–Marquard algorithm
to work as a gradient descent algorithm when this
parameter is large and as a Gauss–Newton algorithm
when this parameter is small. The use of a robust
criterion allows avoiding the influence of outliers
and, has a regularization effect in order to prevent
overfitting.
3.2.3 Pruning
An important issue in neural network design is the
determination of its structure. To determine it, two
approaches can be used. The first is constructive,
where the hidden neurons are added one after
another (Ma and Khorasani, 2004). The second
approach exploits a structure with too many hidden
neurons, and then prunes the least significant ones
(Setiono and Leow, 2000; Engelbrecht, 2001). We
focus on pruning approach that allows the selection
simultaneously of the input neurons and the number
of hidden neurons. The pruning phase is performed
in two steps. First, the Engelbrecht algorithm is used
which allows to quickly simplifying the structure
and second the Setiono and Leow algorithm is used
which is slower but also more efficient (Thomas and
Thomas, 2008). This step is also very important for
neural networks ensemble because it allows
improving performances of each classifier, and the
diversity of different classifiers by differentiating
there structures (pruning of inputs, hidden neurons
or weights are different for the different networks).
3.3 Neural Networks Ensemble
Neural networks ensemble is an interesting approach
to improve quality of classifier. Typically, an
ensemble classifier can be built at four different
levels (Kuncheva, 2004): Data level (Breiman,
1996), feature level (Ho, 1998), classifier level and
combination level (Kuncheva, 2002). We focus here
on classifier and combination level. The principle of
neural network ensemble is presented figure 1.
Design of ensemble neural networks consists of two
main steps: the generation of multiples classifiers
and their fusion (Dai, 2013). This leads to two
problems: how many classifiers are needed and how
to perform their fusion.
Figure 1: A neural network ensemble.
The classifier selection is a problem addressed by
many authors (Ruta and Gabris, 2005; Hernandez-
Lobato et al., 2013; Dai, 2013). Two approaches
may be used to perform it (Ruta and Gabrys, 2005):
Static classifiers selection. The optimal selection
solution found for the validation set is fixed and
used for the classification of unseen patterns.
Dynamic classifiers selection. The selection is
done on-line, during classification, based on
training performances and also various parameters
of the actual unlabelled pattern to classify.
In order to preserve speed of classification, we
use here a static classifiers selection. Different
selection criterions have been proposed. Individual
best performance is an universal indicator for
selection of the individual best classifiers, which is
the simplest and is reliable and robust is generally
preferred in industrial applications (Ruta and Gabrys
2005). This indicator calls minimum individual error
Network 1 Network 2 Network N
…
Combining
outputs
Input
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
518

(MIE) represents the minimum error rate of the
individual classifier and promotes individual best
classifiers selection strategy:
1
1
min ( )
n
j
j
i
M
IE e i
n
(2)
where e
j
(i) represents the error classification of
classifier j on data i.
We use this criterion to select 100 classifiers in
order to benefit of a large classifiers set and to
obtain directly a percentage of vote representative to
the confidence of classification. Ensemble pruning
algorithm may also be used in order to optimize the
size of the classifiers ensemble (Tsoumakas et al.,
2009; Guo and Boukir, 2013).
The fusion of classifiers is generally performed
by majority vote. Kuncheva et al. (2003) have
proposed to implement limits on the majority vote
accuracy in classifier fusion. They studied the
problem of lack of independence in the classifiers
which may limit the interest of classifiers ensemble.
We implement majority vote which presents the
advantage that it could be also used as a confidence
interval on the classification results. This approach
is applied on an industrial quality control.
4 INDUSTRIAL APPLICATION
4.1 Presentation of the Process
The considered company produces high quality
lacquered panels made in MDF (Medium Density
Fiberboard) for kitchens, bathrooms, offices, stands,
shops, hotel furniture. Its main process is a robotic
lacquering workstation. Even if this workstation is
free of human factors, the production quality is
unpredictable (we cannot know if there is a risk that
products will have defects) and fluctuates (the
percentage of defects may be of 45% one day and
down to 10% the next day without changing the
settings). After a brainstorming about the factors
influencing the quality level, we were able to
classify them in three categories specified in
paragraph 2. We could imagine the potential drifts
and associate a type of defect. This preliminary work
results of expert knowledge. Only after the complete
study can we know accurately which factors affect
which defects. Thanks to a production and quality
management system, data corresponding to the
factors studied since february 2012 to september
2012 have been collected. Upstream of the robotic
lacquering workstation, experts decided to collect
factors such as load factor, number of passes, time
per table (lacquering batches), liter per table, basis
weight, number of layers, number of products and
drying time. We could add to these technical factors
environmental ones such as temperature,
atmospheric pressure and humidity. According to the
experimental design approach, we can classify these
variables into two types of factors: internal ones
(load factor, number of passes, time per table, liter
per table, basis weight, number of layers, number of
products and drying time) and external ones
(temperature, humidity, pressure). Two factors
(passes number and number of layers) are discrete
ones that can each take three states and that are
binarized (Thomas and Thomas 2009).
We have 15 inputs to apply to the neural network
which 6 are binary ones. Downstream of the
machine, we were able to detect up to 30 different
types of defects. The first works with the neural
network prediction concerning a type of defects:
"Stains on back." We have a total of 2270 data we
will split into 2 data sets for identification (1202
data) and validation (1068 data). First, learning is
achieved by exploiting 25 neurons in the hidden
layer. Pruning phase can then eliminate spurious
inputs and hidden neurons. This is done 150 times
with different initial weights sets to avoid problem
of trapping in local optimum. The 100 better
classifiers are used in the neural networks ensemble
and the performances of the neural networks
ensemble are compared with the best neural
classifier. The different initialisation sets and the
pruning phase allows to assure diversity into the
classifers set.
During the validation phase, we therefore
compare the results of the best neural classifier with
the real defects detection. For the defect "Stains on
back", we know that it occurs 127 times on the 1068
data validation set. The best neural classifier can
detect 112 defects which lead to a non-detection rate
of 11.8%. The proportion of false positive is 19.2%,
which may be partly explained by the fact that some
defects haven’t been identified out of the machine.
The quality control is performed manually. This fact
induces that some defects are not notice.
The using of neural networks ensemble on the
same validation data set gives a non-detection rate of
10.2%. The proportion of false positive is 16.4%.
These results show an improvement of 14% of the
non-detection rate and 15% on the false alarme rate.
The same work performed on a second defect (grain
on face, 477 defects on the 1068 data validation set)
allows to reduce the non detection rate from 42% to
NeuralNetworksEnsembleforQualityMonitoring
519

32% (24% of improvement) and a false alarme rate
from 21% to 16% (24% of improvement).
Another advantage of the neural networks
ensemble is that the result of the vote may be use as
a confidence interval on the classification result. As
example, for a data, a vote with 40% of defect and
60% on non defect may induces to suspect the
occurence of defect even if the classification result
leads to a non defect classification.
It is obvious that these defects are largely
explained by the archived operating conditions and
it’s possible to use neural networks ensemble
upstream of the workstation to prevent the risk of
defects. However, there are defects which cannot be
predicted with the neural networks ensemble in the
conditions described above. This is for example the
case for “knock” where you get 73% non-detection
for 11% false positives. The non predictable defects
depend certainly on other factors that we need to
determine and collect if we want to predict them. In
total, on the 30 identified defects, 7 can be partially
explained using the variables collected. For the
predictable defects, there are 2 possible approaches:
Warning. By analyzing the inputs through the
neural networks ensemble, it becomes possible to
predict defects occurrence and report it when
conditions are met to create risk.
Limitation. By using neural networks ensemble to
limit the input factors by upper and lower limits
and prohibit the production lot when one of the
inputs is outside these limits. If it’s a controllable
factor, operators can modify it to allow production.
Otherwise, the production lot will be rejected. It
must be scheduled later when conditions become
acceptable. To do that, factors must be classified
into controllable ones (load factor, basis weight,
drying time, liters per table), non-controllable ones
(temperature, humidity, pressure) and protocols
(number of passes, time per table, number of
layers, and number of products). The neural
networks ensemble is then used instead of the real
system to perform experiments that achieve an
entire plan without increasing the cost. The results,
however, still to be validated on the real system.
Figure 2 and 3 present the results of an entire
Taguchi plan in which 10 levels were chosen for the
3 controllable factors. In this example, for protocol
factors, we set the number of passes and layer to 1;
the time per table, and the liter of lack to their
average values; and the number of products to its
median value. We also fixed non-controllable factors
values to their average values. The effect of each
factor x
i
to a level A
i
is given classically by the mean
of all the results (defect occurence) obtained when
x
i
= A
i
minus the mean of the results obtained with
all the experiences. When an effect is positive, this
implies that the considered level increase the
occurence of defects, when it is negative, the
considered level reduce the occurence of defects.
The interractions between factor may be investigated
in the same way.
Figure 2 presents the results obtained with the
best neural classifier. It shows that the load factor
has a relatively small impact on the defects
occurrence. However, the increase in weight has a
significant effect. High basis weights tend to create
more defects. Drying time has also an impact
because too short drying time greatly increases the
occurrence of defects.
Figure 3 presents the same work performed by
using neural networks ensemble. Due to the
diversity of the different classifiers, the impact of
each effect are presented in the forme of an
enveloppe including the effects for all the classifiers.
We can see that the information given by the neural
networks ensemble is more complete than the one
given by the best neural classifier. If, for the load
effect, the neural networks ensemble confirms that it
has a very small impact on the defects occurence, for
the basis weight effect and dry effect, it shows that
small and large values may lead to defects
occurence.
This information can not be obtained by using
uniquely the best neural classifier. These results are
useful to tune the process parameter to their best
values under the constraint of uncontrollable factors
as meteorological ones.
As example, with the operating range considered
here, the set-up of the basis weight may be tuned
between 90 and 190 when the tuning of dry time
may be tuned between 400 and 1100 in order to limit
the risk of defects occurence.In order to obtain the
same results by using an experiments plan, we need
to use 5 modalities for drying time and basis weight
and 2 for the load factor that lead to many
experiments even using Taguchi plan. These
preliminary results need to be confirmed by taking
into account the variation of non-controllable factors
(temperature, pressure and humidity) and validating
the results on the real system.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
520
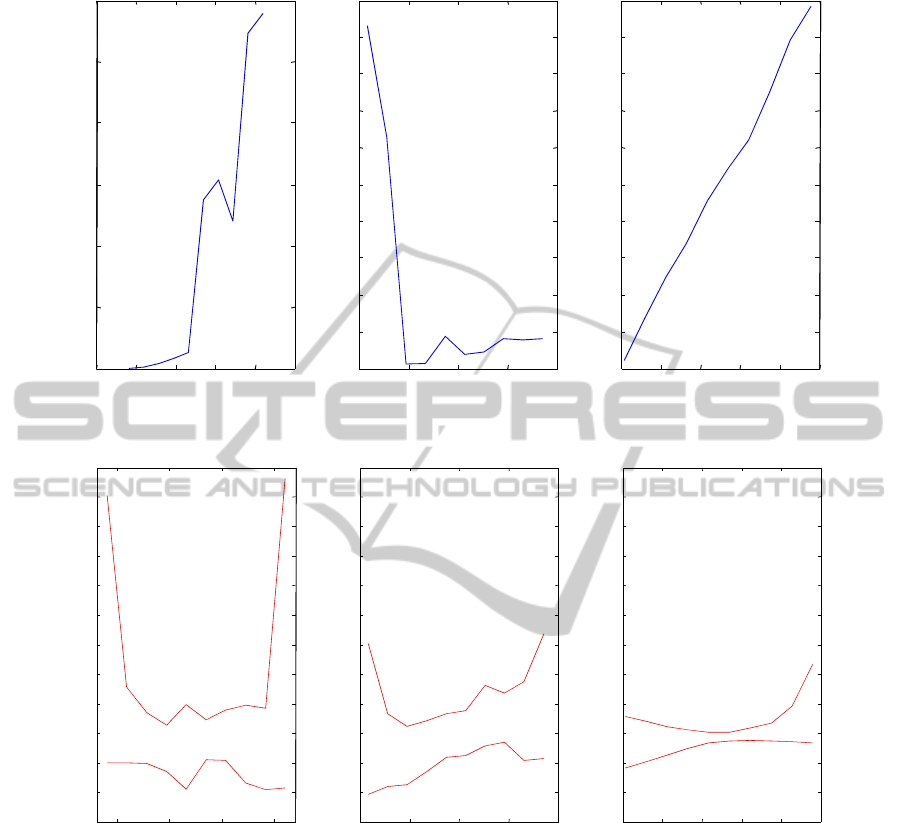
Figure 2: Experiment plan results by using best NN classifier.
Figure 3: Experiment plan results by using neural networks ensemble.
5 CONCLUSIONS
This paper presents neural networks ensemble for
quality monitoring comparing to single neural
classifier. The approach is applied and tested on an
industrial application. The results show that a neural
networks ensemble allows improving greatly the
classification performance. We show that neural
networks ensemble, as single classifier, allows
performing Taguchi experiments in order to find the
best tuning of parameters in order to avoid defects
occurrence. Due to diversity of classifier, the results
of Taguchi experiments obtained by using neural
networks ensemble are more complete and useful.
Two ways of improvement must be performed in
the future works. The first one is to use pruning
ensemble algorithm in order to optimize the size of
the ensemble in function of the results. The second
one is to improve the diversity of classifiers by using
other classifiers tools as support vector machines,
fuzzy logic or genetic algorithms.
REFERENCES
Agard, B., Kusiak, A., 2005. Exploration des bases de
0 50 100 150 200 250
-0.02
-0.01
0
0.01
0.02
0.03
0.04
Levels for basis weight factor
0 500 1000 1500 2000
-0.02
-0.01
0
0.01
0.02
0.03
0.04
0.05
0.06
0.08
Level s for dry time factor
0 1 2 3 4 5
-5
-4
-3
-2
-1
0
1
2
3
5
x 10
-3
Levels for load factor
effect
on defects
occurrence
effect
on defects
occurrence
effect
on defects
occurrence
50 100 150 200
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Levels for basis weight factor
0 500 1000 1500 2000
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Levels for dry time factor
0 1 2 3 4 5
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Levels for load factor
Effect on
defect
occurrence
Effect on
defect
occurrence
Effect on
defect
occurrence
NeuralNetworksEnsembleforQualityMonitoring
521

données industrielles à l’aide du datamining –
Perspectives. 9
ème
colloque national AIP PRIMECA.
Breiman, L., 1996. Bagging predictors. Machine Learning,
24, 2, 123-140.
Cybenko, G., 1989. Approximation by superposition of a
sigmoïdal function. Math. Control Systems Signals, 2,
4, 303-314.
Dai, Q., 2013. A competitive ensemble pruning approach
based on cross-validation technique. Knowledge-
Based Systems. 37, 394-414.
Engelbrecht, A. P., 2001. A new pruning heurisitc based
on variance analysis of sensitivity information. IEEE
trasanctions on Neural Networks, 1386-1399.
Funahashi, K., 1989. On the approximate realisation of
continuous mapping by neural networks. Neural
Networks, 2, 183-192.
Guo, L., Boukir, S., 2013. Margin-based ordered
aggregation for ensemble pruning. Pattern
Recognition Letters, 34, 603-609.
Hajek, P., Olej, V., 2010. Municipal revenue prediction by
ensembles of neural networks and support vector
machines. WSEAS Transactions on Computers, 9,
1255-1264.
Hansen, L. K., Salomon, P., 1990. Neural network
ensembles. IEEE Transactions on Pattern Analysis
and Machine Intelligence. 12, 10, 993-1001.
Hernandez-Lobato, D., Martinez-Munoz, G., Suarez, A.,
2013. How large should ensembles of classifiers be?
Pattern Recognition. 46, 1323-1336.
Ho, T., 1998. The random subspace method for
constructing decision forests. IEEE Transactions on
Pattern Analysis and Machine Intelligence. 20, 8, 832-
844.
Ishikawa, K., 1986. Guide to quality control. Asian
Productivity Organization.
Kuncheva, L. I., 2002. Switching between selection and
fusion in combining classifiers: An experiment. IEEE
Transactions on Systems, Man and Cybernetics, part
B: Cybernetics. 32, 2, 146-156.
Kuncheva, L. I., 2004. Combining pattern classifiers:
Methods and algorithms. Wiley-Intersciences.
Kuncheva, L. I., Whitaker, C. J., Shipp, C. A., 2003.
Limits on the majority vote accuracy in classifier
fusion. Pattern Analysis and Applications. 6, 22-31.
Kusiak, A., 2001. Rough set theory: a data mining tool for
semiconductor manufacturing. Electronics Packaging
Manufacturing, IEEE Transactions on, 24, 44-50.
Ma, L., Khorasani, K., 2004. New training strategies for
constructive neural networks with application to
regression problems. Neural Network, 589-609.
Meyer, D., Leisch, F., Hornik, K., 2003. The support
vector machine under test. Neurocomputing, 55, 169-
186.
Nguyen, D., Widrow, B., 1990. Improving the learning
speed of 2-layer neural networks by choosing initial
values of the adaptative weights. Proc. of the Int. Joint
Conference on Neural Networks IJCNN'90, 3, 21-26.
Paliwal, M., Kumar, U. A., 2009. Neural networks and
statistical techniques: A review of applications. Expert
Systems with Applications, 36, 2-17.
Patel, M. C., Panchal, M., 2012. A review on ensemble of
diverse artificial neural networks. Int. J. of Advanced
Research in Computer Engineering and Technology,
1, 10, 63-70.
Ruta, D., Gabrys, B., 2005. Classifier selection for
majority voting. Information Fusion. 6, 63-81.
Setiono, R., Leow, W.K., 2000. Pruned neural networks
for regression. 6th Pacific RIM Int. Conf. on Artificial
Intelligence PRICAI’00, Melbourne, Australia, 500-
509.
Thomas, P., Bloch, G., 1997. Initialization of one hidden
layer feedforward neural networks for non-linear
system identification. 15
th
IMACS World Congress on
Scientific Computation, Modelling and Applied
Mathematics WC'97, 4, 295-300.
Thomas, P., Bloch, G., Sirou, F., Eustache, V., 1999.
Neural modeling of an induction furnace using robust
learning criteria. J. of Integrated Computer Aided
Engineering, 6, 1, 5-23.
Thomas, P., Thomas, A., 2008. Elagage d'un perceptron
multicouches : utilisation de l'analyse de la variance de
la sensibilité des paramètres. 5
ème
Conférence
Internationale Francophone d'Automatique CIFA'08.
Bucarest, Roumanie.
Thomas, P., Thomas, A., 2009. How deals with discrete
data for the reduction of simulation models using
neural network. 13
th
IFAC Symp. On Information
Control Problems in Manufacturing INCOM’09,
Moscow, Russia, june3-5, 1177-1182.
Tsoumakas, G., Patalas, I., Vlahavas, I., 2009. An
ensemble pruning primer. in Applications of
supervised and unsupervised ensemble methods O.
Okun, G. Valentini Ed. Studies in Computational
Intelligence, Springer.
Vollmann, T. E., Berry, W.L. and Whybark, C. D., 1984.
Manufacturing Planning and Control Systems, Dow
Jones-Irwin.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
522
