
Module Isolation for Efficient Model Checking and its Application
to FMEA in Model-driven Engineering
Vladimir Estivill-Castro and Ren
´
e Hexel
School of Information and Communication Technology, Griffith University, Nathan, QLD, Australia
Keywords:
Model-driven Engineering, Formal Methods, Software Modelling, Failure Mode Effects Analysis.
Abstract:
Model-driven development results in directly runnable implementations, and therefore it is of utmost impor-
tance to formally verify and validate such models. However, model-checking usually faces the challenge of
concurrent modules generating a state space equal to the Cartesian product of the state spaces of all mod-
ules. This is even more dramatic as recent trends in model-driven-engineering aim at not only modelling the
software in question, but other components of the system as well, in order to perform Failure Mode Effects
Analysis (FMEA). These additional components further enlarge the collective state space. We provide an algo-
rithm that identifies the sections of the system that are independent, enabling verification of separate sections
of the system. As a consequence, formal verification of the system as well as the corresponding FMEA can be
performed much more efficiently.
1 INTRODUCTION
Model-driven engineering is proving to be a widely
successful approach to developing software. Tools
and techniques are resulting in faster and simpler (eas-
ier to maintain) products and applications than tra-
ditional language parser/compiler or interpreter ap-
proaches. Model-driven engineering ensures trace-
ability, validation against requirements, and plat-
form independence (Schmidt, 2006). Finite state
machines in particular are ubiquitous, for instance
those of executable UML (Mellor and Balcer, 2002),
MathWorks
R
, StateFlow or StateWorks (Wagner
et al., 2006). There are now several commercial tools
and standards to represent and compose behaviours
for software that will execute in embedded sys-
tems. Among others, these include SysML (Frieden-
thal et al., 2009) and MathWorks
R
StateFlow with
Symlink. Penetration of these technologies includes
large industrial sectors such as the automotive indus-
try (SLSF, 2009; GMG, 2009)
The safety of such systems is critically linked to
the verification of the models as models are directly
implemented. However, model-checking of concur-
rent finite state machines (FSMs) (or analogous mod-
elling approaches, such as decision trees and Require-
ment Refinement Modeling Diagrams (RRMDs) (Sat-
pathy et al., 2013)) face the challenge that the num-
ber of possible state combinations of the system is the
Cartesian product of the possible states of the compo-
nents. This can significantly hamper the use of for-
mal methods and model-checking to verify models.
Moreover, showing that a model is correct is just the
first step. Systems are also examined using fault in-
jection and extensive Failure Mode Effects Analyses
(FMEAs). These FMEAs provide confidence that the
software robustly handles failures of subsystems and
other components. But, the automation of such an
analysis starts by complementing the software models
with models representing the hardware (i.e., sensors,
actuators, and effectors). Thus, FSMs are used to rep-
resent the possible states of buttons, levers, or even
operators. The entire system (software plus modelled
external components) is then submitted to exhaustive
exploration. Fault injection is then used on each mod-
elled component to generate FMEA tables that con-
tain information about violations of requirements or
safety properties (Grunske et al., 2011; Estivill-Castro
et al., 2012b). This is achieved by simulation or
through formal model-checking. However, these ex-
tra FSMs required to model the additional hardware
components, contribute multiplicatively to the overall
size of the system state space; this further explosion of
the state space makes it prohibitively costly (or even
impossible) to use standard model-checking tools.
We show that the process described above can be
significantly improved by systematically identifying
independent components or groups of components
218
Estivill-Castro V. and Hexel R..
Module Isolation for Efficient Model Checking and its Application to FMEA in Model-driven Engineering.
DOI: 10.5220/0004557502180225
In Proceedings of the 8th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2013), pages 218-225
ISBN: 978-989-8565-62-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
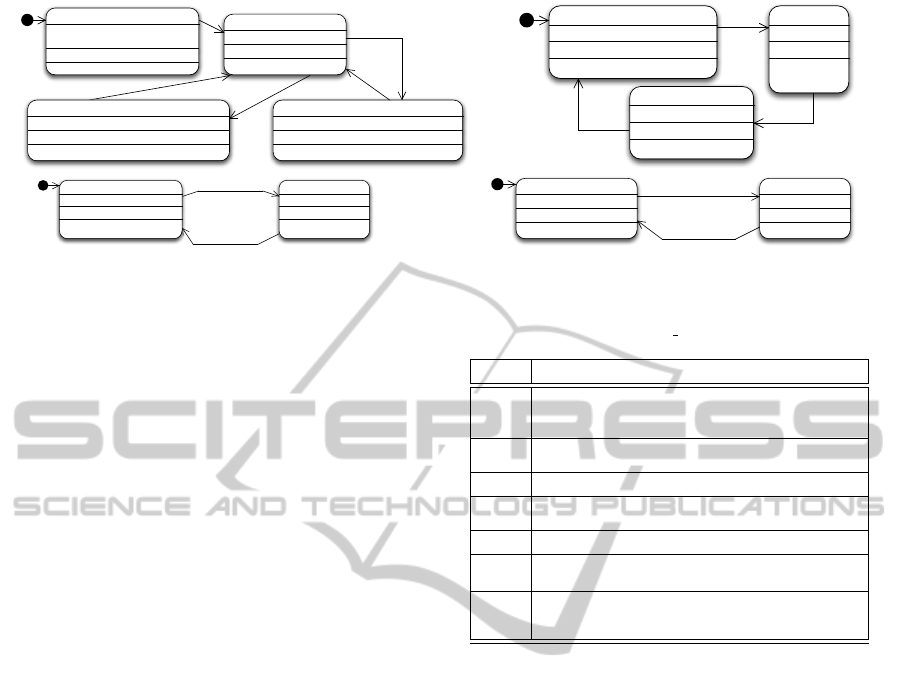
a)
INIT
OnEntry
{int currentTime; currentTime=0;}
OnExit {}
{}
CHECK
OnEntry {}
OnExit {}
{timeLeft=0<currentTime;}
1
1
DECREMENT_1_MINUTE
OnEntry {currentTime=currentTime-1;}
OnExit {}
{}
buttonPushed && !doorOpen
ADD_1_MINUTE
OnEntry {currentTime=1+currentTime;}
OnExit {timeLeft=1;}
{}
!buttonPushed
!doorOpen && timeLeft && timeout(60000000)
b)
OFF
OnEntry {int sound; sound=0;}
OnExit {}
{}
ARMED
OnEntry {}
OnExit {}
{}
timeLeft
timeout(2000000)
RINGING
OnExit {}
OnEntry {sound=1;}
{}
!timeLeft
c)
NOT_COOKING
OnEntry {int motor; motor=0;}
OnExit {}
{}
COOKING
OnEntry {motor=1;}
OnExit {}
{}
!doorOpen && timeleft
doorOpen || ! timeLeft
d)
DARK
OnEntry {int light; light=0;}
OnExit {}
{}
ILLUMINATED
OnEntry {light=1;}
OnExit {}
{}
doorOpen || timeLeft
!doorOpen && ! timeLeft
Figure 1: Complete model of one-minute microwave. a) A 4-state FSM for the timer. b) A 3-state machine for controlling
the bell. c) A 2-state machine for controlling the cooking engine. d) A 2-state machine for the light.
that we can demonstrate can be verified separately.
Thus, without loss of generality, model-checking of
the system can be partitioned. Similarly, the same
model-checking process that performs FMEA can
also be completed on the independent partitions while
still being able to provide the complete FMEA table
for the system. That is, our approach enables com-
plete validation of models as well as comprehensive
failure analysis in scenarios that would otherwise be
too complex or costly to formally verify.
There is a further aspect where our approach of-
fers a significant improvement on previous work.
Estivill-Castro, Hexel and Rosenblueth (Estivill-
Castro et al., 2012c) reduced the challenge of model-
checking concurrent executable models by prescrib-
ing a deterministic sequential schedule on a single
CPU. That approach reduced all possible permuta-
tions of states of computation to only those that
where derived from the schedule. Similarly, the
RRMDs (Satpathy et al., 2013) approach removes all
parallelism, and converts the program into a totally
deterministic behavior. Deterministic scheduling fa-
cilitates model-checking but prevents truly parallel
execution of the system. If such software is to ex-
ecute on hardware that supports more than one CPU
(or a multi-core CPU, which is becoming increasingly
common now, even on mobile or embedded systems),
then such a sequential approach is not able to not take
advantage of the true parallelism available on these
systems. With our approach here, we can identify
groups of modules that can be scheduled in parallel
and still have completely verified models under con-
sequential parallel schedules.
We will use two case studies to support the ar-
gument. Both examples are a widely used exam-
ple in the literature of model-checking, model-driven
development and safety: the one-minute microwave
and the mine pump. The one-minute microwave has
analogies for safety with well-publicised cases such
as the failure of the Therac-25 X-Ray machine.
Table 1: Microwave Oven requirements.
Req. Description
R 1
There is a single control button available for the use of the oven.
If the oven is closed and you push the button, the oven will start
cooking (that is, energise the power-tube) for one minute.
R 2
If the button is pushed while the oven is cooking, it will cause the
oven to cook for an extra minute.
R 3
Pushing the button when the door is open has no effect.
R 4
Whenever the oven is cooking or the door is open, the light in the
oven will be on.
R 5
Opening the door stops the cooking.
R 6
Closing the door turns off the light. This is the normal idle state,
prior to cooking when the user has placed food in the oven.
R 7
If the oven times out, the light and the power-tube are turned off
and then a beeper emits a warning beep to indicate that the cooking
has finished.
2 TACKLING COMPLEXITY
The one minute microwave is a good case study for
modelling requirements. Scholars discussing this ex-
ample typically present a series of requirements in
natural language like those in Table 1. Techniques
such as behavior-trees, Petri Nets, plain finite-state
machines (Wagner et al., 2006) and logic-labeled fi-
nite state machines (Estivill-Castro et al., 2012b) have
been used to model this case study.
Fig. 1 shows the model that uses logic-labeled
finite state machines (Estivill-Castro et al., 2012b)
for the microwave controller (Estivill-Castro et al.,
2012a). It consists of four finite state machines that
are executed in a round robin fashion. Through such
sequential execution, all possible state combinations
that can occur in the system can be derived (Estivill-
Castro et al., 2012c).
The sequential program corresponds to a
Kripke structure by standard transformation tech-
niques (Clarke et al., 2001, Chap. 2), and thus,
standard model-checking tools such as NuSMV can
be applied to establish that this software controller
fulfils safety properties. For the microwave, safety
ModuleIsolationforEfficientModelCheckinganditsApplicationtoFMEAinModel-drivenEngineering
219

SPEC
AG( (E$$doorOpen=1 & M0$$motor=1) -> AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
(E$$doorOpen=1 -> M0$$motor=0) | AX(
M0$$motor=0)))))))))
SPEC
! E [ ! (E$$doorOpen=0) U (M0$$motor=1 & ! ( pc = M0S2R0M1S1R0 ))]
SPEC
AG( (timeLeft=0 & M0$$motor=1) -> AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
(timeLeft=0 -> M0$$motor=0) | AX(
M0$$motor=0
))))))))))
Figure 2: NuSMV coding of the property that the cooking
must stop if the door is held open.
properties include the following
Property-1 “Necessarily, the oven stops (after several
steps, i.e. a small, finite number of transitions in
the Kripke structure) after the door opens.”
Property-2 “It is necessary to pass through a state
in which the door is closed to reach a state in
which the motor is working and the machine has
started.”
Property-3 “Necessarily, the oven stops (after several
steps, i.e. again, a small, finite number of transi-
tions in the Kripke structure) after the timer has
expired.”
Property-4 “Cooking may go on for ever (e.g. if the
user repeatedly keeps pressing the add button
while the timer is still running).”
The NuSMV coding using a CTL (Computation-
Tree Logic (Clarke and Emerson, 1981; Huth and
Ryan, 2004)) formula for Property 1, for Property 2,
and Property 3 appears in Fig. 2.
However, the next step is the Failure Mode Ef-
fects Analysis of these properties. For that, two
types of fault injection are used. The first type con-
sist on introducing a fault into one or more of the
components of the software model. That is, we
perturb the components displayed in Fig. 1. The
suggested fault injection consist of the following
operations (Grunske et al., 2011), loosely follow-
ing the well-established original classification (Bon-
davalli and Simoncini, 1990):
1. to remove behaviour from the model (an omission
failure) and test all properties, and
2. to modify (a value failure) behaviour and test all
properties.
We can then build the FMEA table of failures and
their consequences. Removal or modification of be-
haviour are indeed explored in detail. Each transi-
tion (arrow), state, or any value assignments in the
corresponding sections of the states can be modified
or removed. One such modification/removal consists
of a single fault injection from the table (level 1). If
we perform two such operations, we inject a level 2
fault. (Generally, the likelihood of higher level inde-
pendent faults occurring quickly becomes infinitesi-
mally small; consequently fault-tolerant systems aim
at tolerating at least every possible level 1 fault, while
only being able to handle some, clearly defined level 2
faults (Hexel, 2003)). After each fault-injection oper-
ation, we have a (faulty) model for which NuSMV is ex-
ecuted to determine the affected properties. The faults
injected constitute the rows of the FMEA table while
the columns constitute the properties. Note that auto-
matic completion of the table requires the execution
of a model checker. And therefore, there are as many
entries in the FMEA table as properties and possible
modifications/removals to/from the model.
If execution a model checker is already a costly
exercise, completing the FMEA table multiplies this
further by a large factor.
The useful set of modelling tools (such as logic-
labeled finite-state machines or behavior trees), en-
ables extending models to also represent hardware
components. So the second type of fault injection
concerns the simulation of hardware faults through
software (Hexel, 2003)). For example, in the case of
the microwave, we could model the actual bulb that
produces the light. This example is for illustration
only, but the point is that Fig. 1b) is a model, in soft-
ware, of that hardware component. The variable int
light models the belief of the software (along with
the current state identifier) of whether the light has
been asked to be on or off. A separate finite state ma-
chine as per Fig. 3 models the actual light bulb hard-
ware (and any other connections and communications
that turn the light on or off). In this particular illustra-
tion, the modelling of the hardware components of the
system may not seem add much to the original analy-
sis, but in other examples (such as the industrial press
example (Grunske et al., 2011) it is common to model
hardware components that may be faulty in different
ways, or sometimes even possible behaviour by peo-
ple, e.g. mistakes made by a human operator.
These additional components ( beyond the soft-
ware model) enable simulation of the system as a
whole, allowing validation of that system. Naturally,
to actually perform verification and to carry out the
analysis of building an FMEA table, the next step is
to systematically inject faults into the model. For in-
ENASE2013-8thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
220

2 BULB_OFF
OnEntry {int On; On=0;}
OnExit {}
{}
1 BULB_ON
OnEntry {On=1;}
OnExit {}
{}
light
!light
Figure 3: A model of the light bulb hardware component.
stance, the addition of faults into the model for Fig. 3
corresponds to faults of the hardware, e.g. the light
bulb being poorly connected, or busted. These ad-
ditional components enable verification of some very
important initial and shut-down conditions of the sys-
tem. One can observe the behaviour of the software, if
it starts running with error states of other components.
For instance, in the microwave example, it could be
starting with a faulty door sensor always reporting a
doorOpen condition.
The point we want to make here is that these ad-
ditional models that represent the hardware as well
as the software, while very effective for FMEA table
completion, result in a much larger Kripke structure
for the model-checker. Simply put, now we have a
larger set of components that we are formally veri-
fying. More importantly, for each component that is
added, the total number of possible states (of the hard-
ware and software in simulation) gets multiplied by
the number of states of the additional component.
A very important observation is that, typically,
such hardware components only depend on a very
small software module – let’s call it the driver soft-
ware (in the above example, that role is played by the
state machine in Fig. 1b) – and they do not depend
on the many other components or software modules.
Thus, one shall identify independent sub-models, for
the purposes of model checking, whose state-space
would be much smaller. The end result is that the
model-checking that is repeated for every entry of the
FMEA table would be, in fact, much faster, having
an overall dramatic improvement in verification times
and the completion of the FMEA table.
3 INDEPENDENT SUB-MODEL
IDENTIFICATION
We propose a method to identify dependencies be-
tween components. We use the semantics and sequen-
tial scheduling (Estivill-Castro et al., 2012b; Estivill-
Castro et al., 2012a) proposed for logic-based finite-
state machines (FSMs). These FSMs consist of a
set S of states and a transition table T : S × E → S
. There is an initial state s
0
∈ S, and for each state,
the transitions leading out of the state are ordered in
a sequence. Transitions are labeled by an expression
e ∈ E, and these expressions are evaluated in deter-
ministic order (and time) by an expert system (the ex-
amples in the literature use Decisive Plausible Logic
(DPL) (Estivill-Castro et al., 2012b; Estivill-Castro
et al., 2012a), but the expressions can also be Boolean
expressions of an imperative programming language
such as C, C++, or Java (or any decidable logic, that
provides an answer in predictable time). The point is
that execution of an vector of these machines (such as
the ones in Fig. 1 in the previous section) is sequenced
deterministically by a pre-defined schedule. Each ma-
chine in the vector receives a pre-defined number of
ringlets it executes before execution passes to the next
machine in the vector. The execution token passes
back to the first machine after the last machine com-
pletes its allocated ringlets. A ringlet consist of eval-
uating the OnEntry section of the current state (if it
is the first time control arrives to this state from an-
other state in this machine), followed by evaluation of
the expressions in the list of transitions until an ex-
pression evaluates to true. In this case, the OnExit
section is evaluated and the ringlet concludes. If the
list of transitions is exhausted without any expres-
sion becoming true; then the Internal section of the
state completes and the ringlets also conclude. Thus a
ringlet is the complete assessment of the current state.
The shared variables between the different mod-
ules (FSMs) are called external variables and are man-
aged on a repository architecture named the white-
board (Hayes-Roth, 1988). When the execution token
arrives at a machine, it makes a local copy of any ex-
ternal variables it will use in the current state. We re-
fer to this as the READ footprint on the whiteboard.
Before the execution token of an FSMs is handed
back, the machine copies to the whiteboard any ex-
ternal variables it has modified locally. We refer to
this as the WRITE footprint of the state. This ensures
there is never a race condition between the FSMs that
are running concurrently under the predefined sched-
ule (and thus, there is no need for further mechanisms
to protect shared variables or synchronise FSMs).
For a FSM, the union of all the READ footprints
of its states is called the REQUIRES set of the FSM.
Similarly, the union of all the WRITE footprints of
its states is called the PROVIDES set. Note that
it has been shown that the REQUIRES set and the
PROVIDES set of an FSM can be computed from the
static analysis of the FSM description (Estivill-Castro
and Hexel, 2011).
We can compute a dependency (impact) graph be-
tween the FSMs in a vector, given the REQUIRES
set and the PROVIDES set of the FSMs in that vec-
tor. That is, we can find the dependency graph of the
ModuleIsolationforEfficientModelCheckinganditsApplicationtoFMEAinModel-drivenEngineering
221

modules that constitute the software. There, nodes
of the graph are the modules (the FSMs), while there
is a directed edge from FSM M
1
to FSM M
2
if the
REQUIRES set of M
2
has a not empty intersection
with the PROVIDES set of M
1
.
It is clear that in this graph, if we find sev-
eral disjoint, connected components, then these are
completely independent, and any model-checking of
the entire system is equivalent to performing model-
checking of each connected component separately.
Simply put, none of the external variables of the
connected components are shared. That is, there is
no communication whatsoever between FSMs in one
connected component and another. They can actually
be scheduled in parallel and not sequentially, and each
would have no impact on the other. This is an extreme
case that would rarely appear in practice as it indicates
that a system is made of completely independent sys-
tems without communication between them. How-
ever, this is an important precursor to the principle we
shall discuss next, as such partitioning illustrates that
the model-checker no longer has to explore a Kripke
state space consisting of the product of all the state
spaces, but indeed we can get away with exploring
essentially separate spaces, only adding their number
of states (rather than multiplying them).
This directed graph can now be analysed by tra-
ditional digraph algorithms. Consider the following
procedure. Let v
1
be a node with a non-zero in-
degree. We can find an ancestor (as v
1
has an in-
degree larger or equal to 1). If the ancestor has an
in-degree greater than 0, we find an ancestor of the
ancestor. In fact, we conduct a depth-first search con-
sidering the edges in reverse orientation from v
1
. We
call this graph A
v
1
(and although we refer to it as the
ancestors of v
1
, we consider v
1
∈ A
v
1
).
Lemma 3.1. For any vertex u
1
∈ A
v
1
, there is a di-
rected path from u
1
to v
1
in G; and therefore the
WRITE set of u
1
may influence the READ set of v
1
.
Proof. This follows by induction and transitivity on
the length of the path from u
1
to v
1
.
We refer to the construction of A
v
1
for a vertex v
1
as the ancestor exploration step with focus v
1
.
As a consequence of Lemma 3.1 we have the fol-
lowing observation.
Observation 3.2. If there is a directed path from a
node v
1
to a node v
2
, then v
1
and v
2
must be analysed
jointly.
Conversely, if there are two nodes v and u, and
there is no directed path from v to u and there is no
directed path in the other direction either (from u to
v), then then nodes u and v can be analysed separately.
1"
2"
3"
4"
5"
6"
7"
8"
9"
1"
3"
4"
5"
9"
2"
3"
4"
5"
9"
5"
6"
7"
8"
9"
a)" b)"
Figure 4: A dependency graph, and b) its cover into 3 com-
ponents.
Thus, what we are aiming for is a decomposition
of the graph G = (V, E) of dependencies into a cover
ˆ
C = {C
1
, . . . , C
t
} so that
1. every node is included; that is
S
C∈
ˆ
C
C = V,
2. each component C ∈
ˆ
C of this cover has the prop-
erty that if u and v are vertices in C, then there is
a path in C form u to v or a path in C from v to u,
3. each component is ancestor-maximal, that is,
there is no vertex v 6∈ C so that there is a path from
v to some vertex u ∈ C.
Moreover, we aim for a cover with minimum number
of components. For illustration, consider the graph in
Fig. 4a). This graph’s cover is shown by the 3 compo-
nents in Fig. 4b). Note that there is no further ancestor
to any vertex that belongs to a component outside the
component. Also, vertex 1 and vertex 2 are in dif-
ferent components, as in the graph itself, there is no
directed path in either direction.
To compute this cover we recall the classical de-
scription (Aho et al., 1974) of depth-first search (both
for a directed graph and an undirected graph). We
reduce the problem to connected components by ap-
plying depth-first search to the undirected version of
the graph. Thus, in what follows, we assume that the
undirected version of the graph is connected. Then,
we can take any vertex v
1
with a non-zero in-degree
and find its ancestors by using directed depth first
search (but following the directed edges in reverse
direction). Moreover, the depth directed depth first
search produces (Aho et al., 1974, page 188)
tree edges which lead to new vertices during the
search and form the topological-sort tree,
forward edges which go from ancestors to proper de-
scendants but are no tree edges
back edges which go from descendants to ancestors,
cross edges which go between vertices that are nei-
ther ancestors not descendants of one another.
Thus, the depth-first search in reverse direction from
v
1
has leave nodes of the topological-sort tree. Let u
be a leave node. If such a leave u does not have a back
edge, then u is a maximal ancestor. The starting set of
ENASE2013-8thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
222

ancestors consist of u alone. If u has a back edge,
then u is in a cycle and we take all the vertices in all
the cycles involving u as the starting set of ancestors.
The next step consists of performing a directed
depth first search from each vertex in the set of an-
cestors. We obtain the same classification as before
of all the edges of the graph. However, we find com-
ponents every time
1. there is a node v that has two or more children in
the topological-sort tree,
2. there is no back edge from any descendant of v in
the topological-sort to an ancestor of v
3. there is no forward edge from an ancestor of v to
a descendant of v.
When such a node v is found, then we have a candi-
date component that consists of all the ancestors of v
with the child branch B
i
that has no back edges em-
anating and no forward edges arriving. The candi-
date components share v and the ancestor of v. That
is, they are of the form B
i
∪ A
v
and are as many as
child branches B
i
of v that have no back edges and no
forward edges. However, candidate components may
need to be extended to be ancestor closed. This is be-
cause, although we built the starting set of ancestors
from v
1
and because v is a descendant of v
1
, there may
be nodes in B
i
that have other ancestors. But complet-
ing each candidate component B
i
∪A
v
to a component
consist of a depth-first search (with edges considered
in the reverse direction). This may actually result in
fusing some candidate components.
If finding components from the starting set of an-
cestors of v
1
covers the entire graph, then the process
terminates. If not, then the process is repeated with a
new vertex of in-degree larger than zero in the part not
covered playing the role of v
1
in the above algorithm.
Since depth-first search is linear on the number
of edges and the number of vertices of a graph, and
clearly, the process of identifying the decomposition
only processes a vertex at most 3 times, the entire
algorithm finds the decomposition into independent
components for model-checking in linear time.
4 EVALUATION
To demonstrate our point we now review the situa-
tion with the Microwave Oven case study introduced
earlier. We suggest that this case study is particularly
illustrative of the situation where many actuators are
controlled by combinations of a few sensors. This is
perhaps where our approach has the highest impact
in practice. Fig. 5 shows the dependencies of the mi-
crowave modules. Actuators are shown in dark boxes,
Microwave_Engine.Microwave_Bell. Microwave_Light.
Microwave_Timer.
Door.Bu8on.
Light.Engine_Mo9on.Sound_Speaker.
Figure 5: The dependencies of the modules of the
Microwave Oven.
Microwave_+
Bell+
Microwave_+
Timer+
Door+Bu2on+
Sound_Speaker+
Microwave_+
Engine+
Microwave_+
Timer+
Door+Bu2on+
Engine_Mo:on+
Microwave_+
Light+
Microwave_+
Timer+
Door+Bu2on+
Light+
Figure 6: The cover of the dependencies graph (Fig. 5) into
ancestor closed and maximal components.
while sensors appear in clear boxes. Software mod-
ules appear in shaded boxes. These dependencies can
also be found by converting the logic-based FSMs to
decision trees (Billington et al., 2010) and using tools
such as BECCIE (Wen and Dromey, 2004).
Although all modules depend on the two sensors
(the door and the button), there is a clear three-way
split at the software module (the FSM in Fig. 1a) that
acts as the timer. Thus, we can decompose the depen-
dency graph into the modules shown in Fig. 6.
We now compare the resources required to per-
form traditional model checking (involving all the
modules) with our approach here. The results in Ta-
ble 2 show a clear improvement in both time and
space when generating NuSMV data with gufsm com-
pared to the explosion of considering all FSMs in
combination. The Kripke structure for the complete
model of the Microwave Oven is 2 orders of magni-
tude larger! As a result, the CPU time to process is
4 orders of magnitude larger. In this example, it is
Table 2: Comparisons Kripke structure size (NuSMV
file size) and generation time (gufsm CPU time) of the
Microwave Oven case study.
Component CPU Time Space
Combined graph 2,557.32 s 287,877,511 bytes
Bell subgraph 0.27 s 2,817,073 bytes
Engine subgraph 0.22 s 2,457,880 bytes
Light subgraph 0.22 s 2,458,762 bytes
ModuleIsolationforEfficientModelCheckinganditsApplicationtoFMEAinModel-drivenEngineering
223
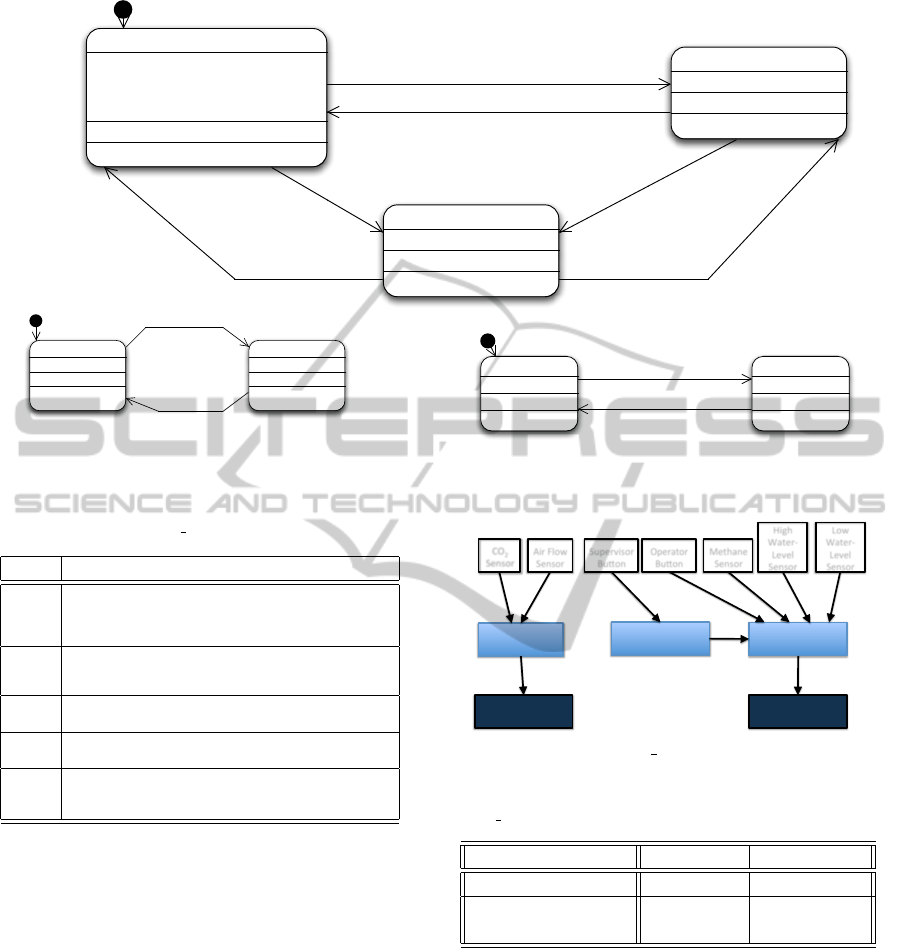
a)
INACTIVE
OnEntry {extern supervisorButtonOn;
extern supervisorButtonOff;
extern supervisorButtonInactive;
indicateOn=0; indicateOff=0; }
OnExit {}
{}
!supervisorButtonOn && !supervisorButtonOff
supervisorButtonOn && !supervisorButtonOff
supervisorButtonOff && !supervisorButtonOn
!supervisorButtonOn && !supervisorButtonOff
supervisorButtonOff && !supervisorButtonOn
supervisorButtonOn && !supervisorButtonOff
INDICATE_ON
OnEntry { indicateOn=1; }
OnExit { indicateOn=0; }
{}
INDICATE_OFF
OnEntry { indicateOff=1; }
OnExit { indicateOff=0; }
{}
b)
(indicateOn ||
(!lowWaterSensorOn && (highWaterSensorOn ||operatorButtonOn)))
&& !indicateOff
&& !methaneSensorHigh
(!indicateOn && ||
(lowWaterSensorOn || (!highWaterSensorOn && !operatorButtonOn))
|| indicateOff
|| methaneSensorHigh
NOT_RUNNING
OnEntry { motor=0;}
OnExit {}
{}
RUNNING
OnEntry {motor=1;}
OnExit {}
{}
c)
!CO2SensorHigh && !airFlowLow
CO2SensorHigh || airFlowLow
RINGING
OnEntry {bell=1;}
OnExit {}
{}
NOT_RINGING
OnEntry {bell=0;}
OnExit {}
{}
Figure 7: Complete model of the mine pump. a) A 3-state FSM for the supervisor. b) A 2-state machine for controlling the
pump. c) A 2-state machine for controlling the alarm.
Table 3: Mine Pump requirements.
Req. Description
R 1
The pump extracts water from a mine shaft. When the water vol-
ume has been reduced below the low-water sensor, the pump is
switched off. When the water raises above the high-water sensor
it shall switch on.
R 2
An human operator can switch the pump on and off provided the
water level is between the high-water sensor and the low-water
sensor.
R 3
Another button accessed by a supervisor can switch the pump on
and off independently of the water level.
R 4
The pump will not turn on if the methane sensor detects a high
reading.
R 5
There are two other sensors, a carbon monoxide sensor and an air-
flow sensor, and if carbon monoxide is high or air-flow is low, and
alarm rings to indicate evacuation of the shaft.
the difference from fractions of a second of CPU time
versus close to hours of CPU time. Note that the 3 in-
dependent subgraphs together do not add to one single
second of CPU time (but achieve the same in terms of
formal verification)!
Another example is the mining pump. This case is
also discussed prominently in the literature (Shrivas-
tava et al., 1993; Sloman and Kramer, 1987; Grunske
et al., 2011; Winter and Yatapanage, 2011). It is
also linked to the literature of software controlling
safety-critical systems (Kramer et al., 1983). It has
been used to present model-driven engineering, for
performing model checking, for performing failure
modes and effect analysis. The requirements (Burns
and Lister, 1991) are reproduced in Table 3.
Fig. 7 shows the logic-labeled finite-state
machines that constitute the controlling soft-
ware (Estivill-Castro et al., 2012a). The most
!"#$%&'()%*+),-%)./
0.1%2*+),-%)./
3"2#*+),-%)./
!"#$%&'()%/
4"5),/
3"2#*6,7',$/!)",8*!#$19$%/
+:
;
//
!$,()%/
<$-=1,$/
!$,()%/
0'%/>.)?/
!$,()%/
@)?/
A1-$%B
@$&$./
!$,()%/
C'7=/
A1-$%B
@$&$./
!$,()%/
:#$%1-)%/
4"5),/
Figure 8: Mine Pump Dependencies.
Table 4: Resource comparison for Kripke structure of the
Mine Pump case study using gufsm and NuSMVas in Table 2.
Component CPU Time Space
Combined graph 22,356.51 s 2,611,097 Kb
Alarm subgraph 0.003 s 10 Kb
Supervisor subgraph 3.025 s 25,703 Kb
interesting part in this example is that the dependency
graph consists, in fact, of two disjunct, connected
components (Fig. 8). Therefore, when we split
independent subgraphs, we find the two connected
components. The resulting differences in Table 4 are
even more impressive (5 orders of magnitude in size
7 orders of magnitude in time for the alarm).
5 CONCLUSIONS
Formal verification by model checking and the con-
ENASE2013-8thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
224

struction of FMEA tables had been reported to take
CPU times of the order of days or weeks for some
well-discussed case studies (Grunske et al., 2011).
We have shown here that for logic-labeled FSMs we
can efficiently split the corresponding dependency
graph and obtain components of the graph that can
be analysed independently. Such components are
found by simple depth-first search exploration, in lin-
ear time, which is negligible with respect to the time
required to perform the model-checking. With de-
composition, even only identifying two or three such
components results in improvements in performance
of several orders of magnitude for a single model-
checking exercise (as demonstrated in two important
case studies, that have received much attention in the
literature). Consequently, Kripke structures in de-
scription languages of common tools such as NuSMV
can be generated and verified much more efficiently.
REFERENCES
Aho, A., Hopcroft, J., and Ullman, J. (1974). The De-
sign and Analysis of Computer Algorithms. Addison-
Wesley, Reading, MA.
Billington, D., Estivill-Castro, V., Hexel, R., and Rock, R.
(2010). Modelling behaviour requirements for auto-
matic interpretation, simulation and deployment. In
SIMPAR 2nd Int. Conf. on Simulation, Modeling and
Programming for Autonomous Robots, vol. 6472 of
LNCS, pp. 204–216. Springer.
Bondavalli, A. and Simoncini, L. (1990). Failures classifi-
cation with respect to detection. In 2nd. IEEE Work-
shop on Future Trends in Distributed Computing Sys-
tems, pp. 47–53, Cairo, Egypt. 1990.
Burns, A. and Lister, A. (1991). A framework for build-
ing dependable systems. The Computer Journal,
34(2):173–181.
Clarke, E. M. and Emerson, E. A. (1981). Design and syn-
thesis of synchronization skeletons using branching
time temporal logic. In Proc. Workshop on Logics of
Programs, vol. 131 of LNCS, pp. 52–71, IBM Watson
Research Center.
Clarke, E. M., Grumberg, O., and Peled, D. (2001). Model
checking. MIT Press.
Estivill-Castro, V. and Hexel, R. (2011). Module interac-
tions for model-driven engineering of complex behav-
ior of autonomous robots. The Sixth Int. Conf. on Soft-
ware Engineering Advances. ICSEA 2011, pp. 84–91,
Barcelona, Spain. IARIA.
Estivill-Castro, V., Hexel, R., and Rosenblueth, D. A.
(2012a). Efficient model checkign and FMEA analy-
sis with deterministic scheduling of transition-labeled
finite-state machines. 2012 3rd World Congress
on Software Engineering (WCSE 2012), pp. 65–72,
Wuhan, China.
Estivill-Castro, V., Hexel, R., and Rosenblueth, D. A.
(2012b). Efficient modelling of embedded software
systems and their formal verification. The 19th Asia-
Pacific Software Engineering Conf. (APSEC 2012),
pp. 428–433, Hong Kong. IEEE Computer Soc., CPS.
Estivill-Castro, V., Hexel, R., and Rosenblueth, D. A.
(2012c). Failure mode and effects analysis (FMEA)
and model-checking of software for embedded sys-
tems by sequential scheduling of vectors of logic-
labelled finite-state machines. In 7th Int. IET System
Safety Conf., 2012, Edinburgh, UK.
Friedenthal, S., Moore, A., and Steiner, R. (2009). A Practi-
cal Guide to SysML: The systems Modeling Language.
Morgan Kaufmann, San Mateo, CA.
GMG, M. A. (2009). Generic modelling design and style
guidelines. The Motor Industry Software Reliability
Association, Warwickshire, UK.
Grunske, L., Winter, K., Yatapanage, N., Zafar, S., and
Lindsay, P. A. (2011). Experience with fault injec-
tion experiments for FMEA. Software, Practice and
Experience, 41(11):1233–1258.
Hayes-Roth, B. (1988). A blackboard architecture for con-
trol. Distributed Artificial Intelligence, pp. 505–540,
San Francisco, CA. Morgan Kaufmann.
Hexel, R. (2003). FITS – a fault injection architecture for
time-triggered systems. Australian Computer Science
Communications, 25(1):333–338.
Huth, M. and Ryan, M. (2004). Logic in Computer Science.
Cambridge University Press, UK, second edition.
Kramer, J., Magee, J., Sloman, M., and Lister, A. (1983).
Conic: an integrated approach to distributed computer
control systems. Computers and Digital Techniques,
IEE Proceedings E, 130(1):1.
Mellor, S. J. and Balcer, M. (2002). Executable UML: A
foundation for model-driven architecture. Addison-
Wesley, Reading, MA.
Reifer, D. J. (1979). Software failure modes and ef-
fects analysis. Reliability, IEEE Transactions on, R-
28(3):247 –249.
Satpathy, M., Snook, C., Arora, S., Ramesh, S., and Butler,
M. (2013). Systematic development of control designs
via formal refinement. In Int. Conf. on Model-Driven
Engineering and Software Development.
Schmidt, D. (2006). Model-driven engineering. IEEE Com-
puter, 39(2).
Shrivastava, S., V., M. L., and Randell, B. (1993). The du-
ality of fault-tolerant system structures. Software —
Practice and Experience, 23(7):773–798.
Sloman, M. and Kramer, J. (1987). Distributed systems and
computer networks. Prentice-Hall, Hertfordshire, UK.
SLSF, M. A. (2009). Modelling design and style guide-
lines for the application of Simulink and Stateflow.
The Motor Industry Software Reliability Association,
Warwickshire, UK.
Wagner, F., Schmuki, R., Wagner, T., and Wolstenholme,
P. (2006). Modeling Software with Finite State Ma-
chines: A Practical Approach. CRC Press, NY.
Wen, L. and Dromey, R. G. (2004). From requirements
change to design change: A formal path. In 2nd
Int. Conf. on Software Engineering and Formal Meth-
ods (SEFM 2004), pp. 104–113, Beijing, China. IEEE
Computer Society.
Winter, K. and Yatapanage, N. The mine pump case study.
Technical report, University of Queensland. supple-
ment in www.itee.uq.edu.au/∼docs/FMEA.
ModuleIsolationforEfficientModelCheckinganditsApplicationtoFMEAinModel-drivenEngineering
225
