
Ontologies as Theories
Marco A. Casanova
1
, Angela Pinheiro
2
, Jose Antonio F. Macedo
2
, Eveline Sacramento
1
and Vania M. P. Vidal
2
1
Departamento de Informática, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil
2
Departamento de Computação, Universidade Federal do Ceará, Fortaleza, Brazil
Keywords: Constraint Specification, Ontology Design, Linked Data Publication.
Abstract: This position paper argues that certain familiar ontology design problems are profitably addressed by
treating ontologies as theories and by defining a set of operations that create new ontologies, including their
constraints, out of other ontologies. The paper first illustrates how to use the operations in the context of
ontology reuse. It goes further and shows how to take advantage of the operations to compare different
ontologies, or different versions of an ontology, and to design mediated schemas in a bottom up fashion.
The discussion in this position paper is backed up by a tool that implements the operations and that offers
other facilities to manipulate ontologies.
1 INTRODUCTION
In this position paper we argue that certain familiar
ontology design problems are profitably addressed
by treating ontologies as theories and by defining a
set of operations on ontologies.
In more detail, we define an ontology as a pair
O=(V,
) such that V is a vocabulary and
is a set of
constraints in V. The theory of
is the set of all
constraints that are logical consequences of
. We
emphasize that the constraints in
capture the
semantics of the terms in V and must, therefore, be
brought to the foreground. The theory of
identifies
the constraints that are implicitly defined, but which
must be considered when using the ontology.
The operations we propose create new
ontologies, including their constraints, out of other
ontologies. Such operations extend the idea of
namespaces to take into account constraints and help
address familiar ontology design problems, which
we now outline to further motivate the discussion.
Consider first the problem of designing an
ontology to publish data on the Web. If the designer
follows the Linked Data principles (Bernes-Lee,
2006); (Bizer et al., 2007), he must select known
ontologies, as much as possible, to organize the data
so that applications “can dereference the URIs that
identify vocabulary terms in order to find their
definition”. We argue that the designer should go
further and analyze the constraints of the ontologies
from which he is drawing the terms to construct his
vocabulary. Furthermore, he should publish the data
so that the original semantics of the terms is
preserved. To facilitate ontology design from this
perspective, we introduce three operations on
ontologies, called projection, union and deprecation.
Consider now the problem of comparing the
expressive power of two ontologies, O
1
=(V
1
,
1
) and
O
2
=(V
2
,
2
). If the designer wants to know what they
have in common, he should create a mapping
between their vocabularies and detect which
constraints hold in both ontologies, after the terms
are appropriately mapped. The intersection
operation answers this question. We argued
elsewhere (Casanova et al., 2010) that intersection is
also useful to address the design of mediated
schemas that combine several export schemas in a
way that the data exposed by the mediator is always
consistent.
On the other hand, if the designer wants to know
what holds in O
1
=(V
1
,
1
), but not in O
2
=(V
2
,
2
), he
should again create a mapping between their
vocabularies and detect which constraints hold in the
theory of
1
, but not in the theory of
2
, after the
terms are appropriately mapped. The difference
operation answers this question.
Finally, a variant of ontology comparison is the
problem of analyzing what changed from one
version of an ontology to the other. Difference is
317
A. Casanova M., Pinheiro A., F. Macedo J., Sacramento E. and M. P. Vidal V..
Ontologies as Theories.
DOI: 10.5220/0004562603170322
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 317-322
ISBN: 978-989-8565-60-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

especially useful here.
The presentation of this position paper is
necessarily informal to stress the major point:
familiar ontology design problems can be properly
addressed by treating ontologies as theories and by
defining a set of operations on ontologies. The
machinery to handle constraints developed in
(Casanova et al., 2010; 2011; 2012a; 2012b)
provides the theoretical foundations of the paper.
Previous work by the authors (Casanova et al., 2011)
introduced the notion of open fragment, which is
captured by projection. The design of mediated
schemas was addressed in (Casanova et al., 2010). A
tool that implements the operations and that offers
other facilities to manipulate ontologies (Pinheiro,
2013) covers the practical aspects of the discussion.
The paper is organized as follows. Section 2
reviews background concepts and notation. Section
3 introduces the operations. Sections 4 and 5 discuss
how to use the operations to address ontology design
problems. Section 6 summarizes related work.
Section 7 contains the conclusions.
2 BACKGROUND
The examples in Sections 4 and 5 use the basic
notation of Description Logic (Baader et al., 2003).
Very briefly, a vocabulary V consists of a set of
atomic concepts, a set of atomic roles, and the
bottom concept . A language in V is a set of
strings, using symbols in V, defining the set of
concept descriptions in V and the set of role
descriptions in V.
An inclusion in V is a string of the form u ⊑ v,
where u and v both are concept descriptions in V or
both are role descriptions in V. Table 1 shows the
common types of inclusions used in the examples.
An ontology is a pair O=(V,
) such that V is a
vocabulary and
is a set of inclusions in V, called
the ontology constraints.
The theory of
(or the theory of O), denoted
[
] (or O[
]), is the set of all logical consequences
of
.
We say that two sets of inclusions,
and
, are
equivalent, denoted
, iff their theories are
equal, that is, the set of all logical consequences of
is equal to that of
. Likewise, two ontologies
O
1
=(V
1
,
1
) and O
2
=(V
2
,
2
) are equivalent, also
denoted O
1
O
2
, iff
1
and
2
are equivalent.
3 ONTOLOGY OPERATIONS
This section introduces the ontology operations we
propose. Sections 4 and 5 illustrate their application
to ontology design problems.
Definition 1: Let O
1
=(V
1
,
1
) and O
2
=(V
2
,
2
) be two
ontologies, W be a subset of V
1
, and
be a set of
constraints in V
1
.
(i) The projection of O
1
=(V
1
,
1
) over W, denoted
[W](O
1
), returns the ontology O
P
=(V
P
,
P
),
where V
P
=W and
P
is the set of constraints in
[
1
] that use only classes and properties in W.
(ii) The deprecation of
fromO
1
=(V
1
,
1
),
denoted
[
](O
1
), returns the ontology
O
D
=(V
D
,
D
), where V
D
=V
1
and
D
=
1
.
(iii) The union of O
1
=(V
1
,
1
) and O
2
=(V
2
,
2
),
denoted O
1
O
2
, returns the ontology
O
U
=(V
U
,
U
), where V
U
=V
1
V
2
and
U
=
1
2
.
(iv) The intersection of O
1
=(V
1
,
1
) and O
2
=(V
2
,
2
),
denoted O
1
O
2
, returns the ontology
O
N
=(V
N
,
N
), where V
N
=V
1
V
2
and
N
=
[
1
]
[
2
].
(v) The difference of O
1
=(V
1
,
1
) and O
2
=(V
2
,
2
),
denoted O
1
O
2
, returns the ontology
O
F
=(V
F
,
F
), where V
F
=V
1
and
F
=
[
1
]
[
2
].
Note that deprecation does not reduce to difference
since, in general, we have
[
D
] =
[
1
] ≠
[
1
]
[
]
We also note that the ontology O
R
that results from
an operation is unique, by definition. However, there
might be several ontologies that are equivalent to
O
R
. For example, if O
P
= (V
P
,
P
) is the projection of
O
1
on W, there might be several sets of constraints
that are equivalent to the set of constraints in the
theory of O
1
that use only terms in W. This simple
observation impacts the implementation of the
operations, discussed elsewhere (Pinheiro, 2013).
Finally, we observe that we may generalize
union, intersection and difference by considering a
renaming of one or both vocabularies of the
ontologies involved and appropriately renaming the
terms that occur in the constraints when comparing
the theories. This extension is considered in the first
example presented in Section 5 (Table 2).
4 PROJECTION, DEPRECATION
AND UNION
Projection allows the designer to define a set W
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
318

Table 1: Common inclusion types used in conceptual modeling.
Name Inclusion type Informal semantics
Domain Constraint
( 1 P) ⊑ C
property P has class C as domain, that is,
if (a,b) is a pair in P, then a is an individual in C
Range Constraint
( 1 P¯) ⊑ C
property P has class C as range, that is,
if (a,b) is a pair in P, then b is an individual in C
minCardinality
Constraint
C ⊑ ( k P) or
C ⊑ ( k P¯)
property P or its inverse P¯ maps each individual
in class C to at least k distinct individuals
maxCardinality
Constraint
C ⊑( k+1 P) or
C ⊑ ( k+1 P¯)
property P or its inverse P¯ maps each individual
in class C to at most k distinct individuals
Subset Constraint
C ⊑ D
each individual in C is also in D, that is,
class C denotes a subset of class D
Disjointness
Constraint
C ⊑ D
no individual is in both C and D, that is,
classes C and D are disjoint
Table 2: Partial Intersection of the DBLP and Lattes ontologies.
(a) DBLP (b) Lattes (c) Intersection
1
Article ⊑Publication Article ⊑Document Article ⊑Publication
2
Conference ⊑Event Book ⊑Document
3
ConferencePaper ⊑Article Collection ⊑Document
4
Continent ⊑Place Phdthesis ⊑Document
5
Proceedings ⊑Publication Proceedings ⊑Document Proceedings ⊑Publication
6
Professor ⊑Person Series ⊑Document
7
ConferencePaper ⊑Document ConferencePaper ⊑Publication
containing just a few terms from the vocabulary of
an ontology and retain the semantics of the terms in
W through the constraints, derivable from those of
the ontology, that apply to the terms in W.
Deprecation simply allows the designer to drop
constraints from an ontology. Finally, union allows
the designer to combine two ontologies. These three
operations offer the designer powerful tools to
(partially) reuse vocabularies and to preserve the
semantics of the terms. In the rest of this section, we
further motivate this argument with the help of an
example that uses the Music Ontology (Raimond et
al., 2010).
The Music Ontology (MO) provides concepts
and properties to describe artists, albums, tracks,
performances, arrangements, etc. on the Semantic
Web. It is used by several Linked Data sources,
including MusicBrainz and BBC Music. The Music
Ontology RDF schema uses terms from the Friend
of a Friend (FOAF) (Brickley and Miller, 2010) and
the XML Schema (XSD) vocabularies. We
respectively adopt the prefixes “mo:”, “foaf:” and
“xsd:” to refer to these vocabularies.
Figure 1 shows the class hierarchies of MO
rooted at classes foaf:Agent and foaf:Person. Let us
focus on this fragment of MO.
We first recall that FOAF has a constraint
informally formulated as:
foaf:Person and foaf:Organization are disjoint classes
Let V
1
be the following set of terms from the FOAF
and the XSD vocabularies, and let V
2
contain the rest
of the terms that appear in Figure 1:
V
1
= { foaf:Agent, foaf:Person, foaf:Group,
foaf:Organization, foaf:name, xsd:string }
V
2
= { mo:MusicArtist, mo:CorporateBody,
mo:SoloMusicArtist, mo:MusicGroup,
mo:Label, mo:member_of }
Let O
1
=(V
1
,
1
) be the ontology obtained by the
projection of FOAF over V
1
and defined in such a
way that
1
is the set of constraints over V
1
that are
logical consequences of the constraints of FOAF:
1
= { (1 foaf:name) ⊑ foaf:Person,
(1 foaf:name¯
) ⊑ xsd:string,
foaf:Person ⊑ foaf:Organization,
foaf:Group ⊑ foaf:Agent,
foaf:Organization ⊑ foaf:Agent }
Let O
2
=(V
2
,
2
) be such that
2
contains just the
subset constraints over V
2
shown in Figure 1:
2
= { mo:SoloMusicArtist ⊑mo:MusicArtist,
mo:MusicGroup ⊑mo:MusicArtist,
mo:Label ⊑mo:CorporateBody }
Then, most of Figure 1 is captured by the union of
O
1
and O
2
, defined as the ontology O
3
=(V
3
,
3
),
where V
3
= V
1
V
2
and
3
=
1
2
.
The constraints shown in Figure 1, but not
included in O
3
, are obtained by the union of
OntologiesasTheories
319
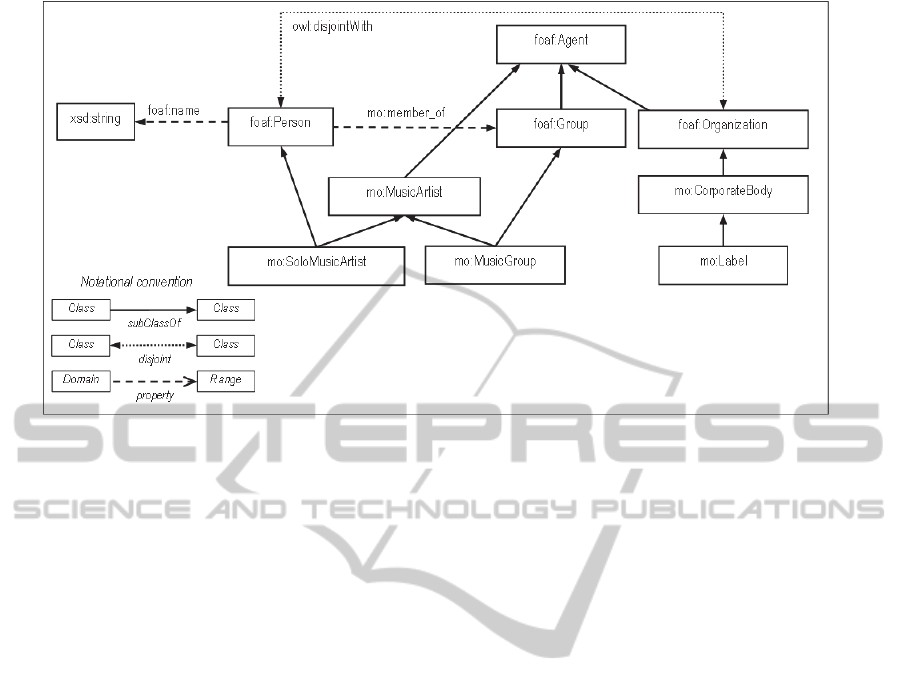
Figure 1: The class hierarchies of MO rooted at classes foaf:Agent and foaf:Person.
O
3
=(V
3
,
3
) with O
4
=(V
3
,
4
) (the ontologies have the
same vocabulary), where
4
= { mo:SoloMusicArtist ⊑foaf:Person,
mo:MusicGroup ⊑foaf:Group,
mo:MusicArtist ⊑foaf:Agent,
mo:CorporateBody ⊑foaf:Organization,
(1 mo:member_of) ⊑foaf:Person,
(1 mo:member_of¯) ⊑foaf:Group }
The union returns the ontology O
5
=(V
5
,
5
), where V
5
= V
3
and
5
=
3
4
. Finally, we construct
O
0
=(V
0
,
0
), the ontology that corresponds to Figure
1 as:
O
0
= (([V
1
](FOAF) O
2
) O
4
)
The reader is invited to reflect upon the definition of
O
0
. We contend that the expression defined using the
operations provides a reasonable explanation of how
O
0
is constructed from FOAF and additional terms
and constraints.
5 INTERSECTION
AND DIFFERENCE
Intersection and difference help the designer
compare the expressive power of two ontologies. If
the designer wants to know what the ontologies have
in common, he should use intersection. On the other
hand, if he is interested in what holds in O
1
=(V
1
,
1
),
but not in O
2
=(V
2
,
2
), he should use difference.
To illustrate the use of intersection, we analyze
two data sources from the scientific research
domain, DBLP and Lattes. DBLP (Digital
Bibliographic and Logic Programming) stores
Computer Science bibliographic references – over
half a million references – and links to researchers’
homepages. Lattes is a database, organized by CNPq
– the Brazilian Research Agency, storing
researchers’ CVs and research group descriptions.
Assume that the Lattes vocabulary suffers a
renaming where Document is mapped to Publication.
To simplify the discussion, Table 2 shows just a
few constraints from each data sources. Column (a)
shows the DBLP constraints, Column (b), the Lattes
constraints, and Column (c) the constraints in the
intersection.
For example, Line 1 of the table indicates that Article
⊑Publication is a constraint in both ontologies, after
Document is renamed to Publication, and hence is in
their intersection. Line 7(b) indicates that
ConferencePaper ⊑ Publication is a constraint of the
Lattes ontology, again after Document is renamed to
Publication; whereas Lines 1(a) and 3(a) implies that
ConferencePaper ⊑ Publication is in the theory of the
DBLP ontology; hence this constraint is in the
intersection of the ontologies, as shown in Line 1(c).
To illustrate the use of difference, consider a
scenario where a domain specialist adopted the
version of the FOAF ontology released on January
1
st
, 2010 (call it FOAF1). However, on August 9
th
,
2010, a new release of the FOAF ontology was
published (call it FOAF2). The specialist then wants
to verify what changed from one version to the
other. He can then compute the difference between
FOAF1 and FOAF2 (and vice-versa).
Given this scenario, Table 3 shows the (partial)
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
320

Table 3: Partial difference between two versions of the FOAF ontology.
(a) FOAF1 (January 1
st
, 2010) (b) FOAF2 (August 9
th
, 2010) (c) Difference
1
Agent ⊑
Document
2
Project ⊑Document Project ⊑
Document Project ⊑
Image
3
Person ⊑
Document
4
Organization ⊑Document Organization ⊑
Document Organization ⊑Image
5
Group ⊑Agent Group ⊑Agent
6
Image ⊑Document
Image ⊑Document
difference between FOAF1 and FOAF2.
Line 2(c) indicates that the constraint
Project ⊑ Image is in the difference between
FOAF1 and FOAF2. Indeed, since
Image ⊑Document is in the theory of FOAF1, we
have that Document ⊑Image is also in the theory
of FOAF1. Hence, since Project ⊑ Document is in
the theory of FOAF1 (in fact, it is a constraint of
FOAF1, according to Line 2(a)), we infer that
Project ⊑ Image is in the theory of FOAF1.
However, this constraint is not in the theory of
FOAF2.
Likewise, Line 4(c) indicates that
Organization ⊑Image is in the theory of FOAF1, but
not in the theory of FOAF2.
Finally, Line 6(a) indicates that FOAF1 has a
constraint, Image ⊑ Document, which is not in the
theory of FOAF2.
6 RELATED WORK
The results reported in the paper cover a topic –
improving Linked Data design by constraint reuse –
that is still neglected in the literature. The question
of Linked Data semantics is not new, though. For
example, recent investigation (Halpin and Haynes,
2010); (Jaffrin et al., 2008); (McCuster and
McGuinness, 2010) in fact questions the correct use
of owl:sameAs to inter-link datasets.
Jain et al., (2010) argues that the Linked Open
Data (LoD) Cloud, in its current form, is only of
limited value for furthering the Semantic Web
vision. They discuss that the Linked Open Data
Cloud can be transformed from “merely more data”
to “semantically linked data” by overcoming
problems such as lack of conceptual descriptions for
the datasets, schema heterogeneity and absence of
schema level links. Along this line, we advocated
that the design of Linked Data sources must include
constraints derived from those of the underlying
ontologies.
We note that the problem we cover in this paper
cannot be reduced to a question of ontology
alignment in the context of Linked Data, addressed
for example in (Prateek et al., 2010); (Wang et al.,
2011). Indeed, we stress that the problem we focus
on refers to bootstrapping a new ontology (including
its constraints) through the implementation of
ontology algebra operations (projection, deprecation,
union, intersection and difference) over one or more
existing ontologies.
Some tools, such as Prompt (Noy and Musen,
2000) and ODEMerge (Ramos, 2001), allow the user
to combine two or more ontologies in a
semiautomatic or in an automatic way. Other tools,
such as PromptDiff (Noy et al., 2004) and OntoDiff
(Tury and Bieliková, 2006), deal with ontology
change detection. However, these tools cannot
capture changes in the semantics of the terms, as the
OntologyManagement tool described in (Pinheiro,
2013), which is based on the operations described in
this paper. Furthermore, the OntologyManagement
tool offers to the user a complete environment to
design and maintain ontologies, which allows
applying a series of operations over one or more
ontologies and enabling reuse, versioning, evolution
and integration of ontologies. Volz et al., (2003)
proposes a tool that implements the projection
operation by the creation of a database view
resulting from query execution. However, this tool
does not allow the generation of semantic
information captured by the constraints that apply to
the vocabulary terms.
Finally, previous work by the authors (Casanova
et al., 2011) introduced the notion of open fragment,
captured by the projection operation, and (Casanova
et al., 2012b) covered some of the operations
discussed in this paper.
7 CONCLUSIONS
In this position paper we argued that certain familiar
ontology design problems could be profitably
addressed by treating ontologies as theories and by
defining a set of operations on ontologies. Such
operations extend the idea of namespaces to take
into account constraints.
A tool that implements the operations and that
OntologiesasTheories
321

offers other facilities to manipulate ontologies is
operational (Pinheiro, 2013). This tool and was used
to test the ideas and to generate the examples partly
described in Sections 4 and 5.
As for future work, we intend to integrate the
ontology management tool with the Protégé
ontology editor. The goal of this integration is to
take advantage of all functionalities already
available in Protégé, such as ontology modeling and
visualization, inference and reasoning tasks.
ACKNOWLEDGEMENTS
This work was partly supported by CNPq, grants
301497/2006-0, 483552/2009-7, 308247/2009-4,
475717/2011-2, by FAPERJ under grant E-
26/103.070/2011, by CAPES under grant NF
21/2009, and by FUNCAP under grant GPF
2151/22.
REFERENCES
Artale, A., Calvanese, D., Kontchakov, R.,
Zakharyaschev, M., 2009. The DL-Lite family and
relations. J. of Artificial Intelligence Research 36(1),
1–69.
Baader, F., Nutt, W. 2003. Basic Description Logics. In:
F. Baader, D. Calvanese, D.L. McGuiness, D. Nardi,
P. F. Patel-Schneider (eds), The Description Logic
Handbook: Theory, Implementation and Applications,
Cambridge U. Press, Cambridge, UK, 43–95.
Berners-Lee, T., 2006. Linked Data - Design Issues. W3C.
Bizer, C., Cyganiak, R., Heath, T., 2007. How to publish
Linked Data on the Web. http://www4.wiwiss.fu-
berlin.de/bizer/pub/LinkedDataTutorial/
Brickley, D., Miller, L., 2010. FOAF Vocabulary
Specification 0.98. Namespace Document 9. Marco
Polo Edition.
Casanova, M. A., Lauschner, T., Leme, L. A. P. P.,
Breitman, K. K., Furtado, A. L., Vidal, V. M. P., 2010.
Revising the Constraints of Lightweight Mediated
Schemas. Data & Knowledge Engineering 69(12),
1274–1301.
Casanova, M. A., Breitman, K. K., Furtado, A. L., Vidal,
V. M. P., Macêdo, J. A. F., 2011. The Role of
Constraints in Linked Data. Proceedings of the
Confederated International Conferences: CoopIS,
DOA-SVI, and ODBASE 2011, Part II. Lecture Notes
in Computer Science v.7045. Springer, 781–799.
Casanova, M. A., Breitman, K. K., Furtado, A. L., Vidal,
V. M. P., Macêdo, J. A. F., 2012a. An Efficient Proof
Procedure for a Family of Lightweight Database
Schemas. In: Michael G. Hinchey (ed.), Conquering
Complexity, Springer, 431–461.
Casanova, M. A., Macêdo, J. A. F., Sacramento, E.,
Pinheiro, A. M. A., Vidal, V. M. P., Breitman, K. K.,
Furtado, A. L., 2012b. Operations over Lightweight
Ontologies. Proc. 11th International Conference on
Ontologies, DataBases, and Applications of Semantics
- ODBASE 2012 (Sept. 11-12, 2012), Rome. LNCS
7566, 646–663.
Halpin, H., Hayes, P. J., 2010.When owl:sameAs isn’t the
same: An analysis of identity links on the semantic
web. In Proc. Int’l. Workshop on Linked Data on the
Web.
Jaffri, A., Glaser, H., Millard, I., 2008. URI
disambiguation in the context of linked data. In Proc.
1st Int’l. Workshop on Linked Data on the Web.
Jain, P., Hitzler, P., Yeh, P. Z., Verma, K., Sheth, A. P.,
2010. Linked Data is Merely More Data. In: Proc.
AAAI Spring Symp. ‘Linked Data Meets Artificial
Intelligence’, 82–86.
McCusker, J., McGuinness, D.L., 2010. owl:sameAs
considered harmful to provenance. In Proc. ISCB
Conference on Semantics in Healthcare and Life
Sciences.
Noy N. F., Kunnatur, S., Klein, M. and Musen, M. A.,
2004. Tracking changes during ontology evolution. In
Sheila A. Mcilraith, Dimitris Plexousakis and Frank
van Harmelen. In: Proc. 3rd International Semantic
Web Conference, 259–273, Hiroshima, Japan.
Pinheiro, A. M. A., 2013. “OntologyManagement Tool –
Uma Ferramenta para Gerenciamento de Ontologias
como Teorias Lógicas”. M.Sc. Dissertation, Dept.
Computing, UFC.
Prateek, J., Hitzler, P., Sheth, A. P., Verma, K., Yeh, P. Z.,
2010. Ontology alignment for linked open data. In:
Proc. 9th Int’l. Semantic Web Conf. Springer-Verlag,
402–417.
Raimond, Y., Giasson, F., 2010. Music Ontology
Specification. Specification Document.
Ramos, J. A. Mezcla automática de ontologías y catálogos
electrónicos, 2001, Final YearProject. Facultad de
Informática de la Universidad Politécnica de Madrid.
Spain.
Tury, M. and Bieliková, M., 2006. An Approach to
Detection Ontology Changes. In: Proc. 6th
Internacional Conference on Web Engineering, 14,
New York, NY, USA. ACM Press.
Volz, R., Oberle, D. and Studer, R., 2003. Implementing
Views for Light-Weight Web Ontologies. In: Proc. of
Int’l Database Engineering and Application
Symposium - IDEAS, 160–169, Hong Kong, China.
IEEE Computer Society.
Wang, Z., Zhang, X., Hou, L., Li, J. 2011. RiMOM2: A
Flexible Ontology Matching Framework. In: Proc.
ACM WebSci'11, Koblenz, Germany, 1–2.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
322
