A New Simple Method for Kinematic Detection of Gait Events

Xiaolei Lv

1,2

, Yi Wei

and Shihong Xia

The Beijing Key Laboratory of Mobile Computing and Pervasive Device,

Institute of Computing Technology, Chinese Academy of Sciences, Beijing, China

University of Chinese Academy of Sciences, Beijing, China

Keywords:

Gait Event, Heel Strike, Toe Off, Gait Cycle, Kinematic Detection.

Abstract:

The detection of gait events in locomotion, such as toe-off and heel-strike, provides a basic criterion for the

division of a step cycle. This paper presents a new simple method for kinematic detection of gait events using

kinematic data captured from only one marker attached to heel. We analyze the geometric distribution of

the markers spatial positions over a small window of frames, and ﬁnd there are new characteristics on the

curve. These characteristics are used to detect the gait events for normal gaits. True errors (mean ± standard

deviation) in the experiments on normal gaits are 8 ± 8 ms for heel-strike and 12 ± 20 ms for toe-off, where

above 91% of subjects’ heel strike events can be determined, with at most one frame (8.3 ms) error away from

the ground reaction force (GRF) results.

1 INTRODUCTION

The detection of heel-strike (HS) and toe-off (TO)

plays a very important role in walking gait analysis,

which determines the stance and swing phase and al-

lows normalization of gait kinematics. The gold stan-

dard method of deﬁning gait events is dependent on

the force plate. It would be necessary for a labora-

tory to be equipped with at least two force platforms

to determine the temporal components of a complete

strike. Unfortunately, the number of available force

plates limits the number of consecutive gait cycles

that can be analyzed (Hreljac and Marshall, 2000).

As a result, researchers have discussed and presented

many methods to detect gait events using other equip-

ments, such as pressure-sensitive switches (Aber-

nethy et al., 1995), photocell contact mat (Viitasalo

et al., 1997), accelerometer (Mayagoitia et al., 2002),

optical motion capture system (O’Connor et al., 2007;

Desailly et al., 2009; Zeni Jr et al., 2008; Kiss, 2010).

The idea of methods using the optical motion cap-

ture device is to extract the characteristics of trajec-

tories of markers attached to the speciﬁed location

on the body and then infer the gait events by these

characteristics. In the early research (Mickelborough

et al., 2000) on kinematic detection of gait events, the

events of the heel-strike and toe-off were inferred by

naked eyes, where one made a subjective decision by

observing the plots of marker’s trajectory and veloc-

ity. It is difﬁcult to implement this method (O’Connor

et al., 2007), because of the inherent inaccuracy of

the visual inspection. Automatic algorithms were

proposed (Ghoussayni et al., 2004; Kar

cnik, 2003),

where thresholds on the height and velocity of mark-

ers are needed. Hreljac and Marshall (2000) proposed

a Hreljac-Marshall algorithm (HMA) method for de-

tecting gait events based on the displacement, accel-

eration and jerk of heel and toe markers. O’Connor et

al. (2007) introduced a foot velocity algorithm (FVA)

which relies on the identiﬁcation of local maximum

and minimum of the vertical velocity signal from the

midpoint of the heel and toe marker locations. Be-

cause the optimal ﬁltering of each marker is used as

an initial step in the HMA and FVA methods, results

could be sensitive to the choice of cutoff frequency

(Tirosh and Sparrow, 2003). By observing the char-

acteristics of the gait events, Zeni Jr et al. (2008) used

the distance between the projection of the sacrum’s

marker on the ground and the heel’s or toe’s marker

to detect the gait events.

It can be seen that the advances of recent research

using optical motion capture device are moving to-

ward a more and more simple, robust and automatic

direction. For example, some simple kinematic char-

acteristics of locomotion are deﬁned as the distance

between the projection of root’s marker on the ground

and the heel’s or toe’s marker (Zeni Jr et al., 2008), or

as local maximum and minimum in the vertical ve-

Lv X., Wei Y. and Xia S..

A New Simple Method for Kinematic Detection of Gait Events.

DOI: 10.5220/0004563600250029

In Proceedings of the International Congress on Sports Science Research and Technology Support (icSPORTS-2013), pages 25-29

ISBN: 978-989-8565-79-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: DPN as a function of frame number throughout a gait cycle with the gait events of toe-off and heel-strike indicated.

locity signal from the midpoint of the heel and toe

marker locations (Desailly et al., 2009). Many efforts

and achievements have been done, however, some re-

search issues are not known yet. For example, could

the number of markers used in gait event detection be

reduced or not? Is there any new marker placement

can be used to discover new gait patterns?

Different from previous work, we investigate how

to deﬁne kinematic characteristics and explore gait’s

characteristics of locomotion using only one marker

attached to heel. The key idea of our method is based

on the fact that the velocity of the swing leg is greater

than that of the supporting leg during locomotion. We

consider the geometric distribution of the marker’s

spatial positions over a small window of frames, and

introduce a metric called dispersion (DPN) for dis-

tinguishing whether the spatial data are dense or not.

Experiments demonstrate the curve of DPN encodes

the gait’s characteristics.

2 METHOD

In this section, DPN is used to describe the move-

ment range of the marker on the heel in some consecu-

tive frames. The computation of DPN is illustrated as

follows. This method analyzes the DPN and detects

the gait events by some characteristics of the curve of

DPN.

(1) For any i −th frame, 2k+ 1 frames (i− k ≤ t ≤

i +k) are taken into consideration. The geometry cen-

ter (x, y, z) of 2k + 1 consecutive markers’ positions

are computed by

x =

t=i+k

∑

t=i−k

2k + 1

y =

t=i+k

∑

t=i−k

2k + 1

z =

t=i+k

∑

t=i−k

2k + 1

(1)

(2) The distances between the 2k + 1 markers’ po-

sitions to the position of the geometry center are com-

puted.

− x)

+ (y

− y)

+ (z

− z)

(i−k ≤ t ≤ i+k) (2)

(3) The average distance of d

(i − k ≤ t ≤ i + k) is

computed:

t=i+k

∑

t=i−k

2k + 1

(3)

(4) The dispersion of the markers is deﬁned as fol-

lows:

DPN = d

(4)

When plotting the curve of DPN, a very clear char-

acteristic can be observed (see Figure 1). The point of

the speciﬁed local maximum is the moment of the toe-

off. The point of the speciﬁed local minimum is the

moment of the heel-strike.

In our experiments, kinematic data of the marker

attached to heel and analog data which are output of

the dual integrated force plates (Kistler 9286BA) are

collected synchronously at 120 Hz using a 12-camera

Vicon workstation. The analog data are ﬁltered with a

cutoff frequency of 20 Hz. Heel strike is determined

when the vertical GRF is greater than 20 N for a width

of at least 40 frames (Zeni Jr et al., 2008). Similarly,

icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport

toe-off is determined when the vertical GRF is less

than 20 N for a width of 40 frames. Only one marker

is attached to each heel (see Figure 2).

Normal subjects’ kinematic data with analog data

(#subjects=7, 6 males, 1 female, age 22-26 years,

mean ± standard deviation 23.3 ± 1.3 years, 64

groups of data, 64 cycles) are captured. All sub-

jects have been given a copy of the informed consent.

Walking speed was neither monitored nor controlled.

Figure 2: Marker placement.

3 RESULTS

True errors in the experiments (mean ± standard de-

viation) are 8 ± 8 ms for heel-strike and 12 ± 20 ms

for toe-off. Above 91% of the normal subjects’ heel

strike events can be determined, with at most one

frame (8.3 ms) error away from the ground reaction

force (GRF) results. The Figure 3 and Table 1 show

the detailed results. LHS refers as left heel strike.

LTO refers as left toe off. RHS refers as right heel

strike. RTO refers as right toe off.

Table 1: Percentages of computationally determined events

offset by the frame error of the normal subjects.

Absolute

Error(frame)

0 1 2 ≥ 3

LHS 44.90 55.10 0 0

LTO 71.43 20.40 8.17 0

RHS 34.28 57.14 8.58 0

RTO 57.14 32.65 8.16 2.05

In our experiments, the variable k can be manu-

ally changed. As k increases, the curve of DPN be-

comes more and more smooth. Experiments show

that a good result can be achieved when the k is set

to 3 (see Figure 4).

The advantages of the method could be summa-

rized as follows. Firstly, only one marker attached

to heel is used in gait event detection. It would be

helpful to set up a gait laboratory using optical mo-

tion capture system. Secondly, new gait’s character-

istics are explored and used for gait event detection.

The accuracy of the detection of heel-strike is very

high. Above 91% of the normal subjects heel strike

events can be determined, with at most one frame

(8.3 ms) error away from the ground reaction force

(GRF) results. Thirdly, this method is easy to be im-

plemented for automatic event detection without the

use of thresholds and optimal ﬁltering of kinematic

data.

There are still some limitations in the proposed

method. The result of the gait events’ detection of

the toe off is not satisfying. Feet’s gestures are not the

same for different subjects when the gait event of the

toe off happens. There are many ways to measure the

geometric distribution of marker’s spatial positions.

There may be a better measurement to achieve better

results. The event detection of pathological gaits is

still an open problem. In future, we will do further

research on this issue especially for the pathological

gaits.

4 CONCLUSIONS

In conclusion, the method proposed in this paper is

simple and robust, which is accurate in the detection

of heel strike. It validates that we can detect the gait

events accurately with only one marker. The future

work is to ﬁnd a robust algorithm for the event detec-

tion of pathological gaits.

ACKNOWLEDGEMENTS

This paper was supported in part by the National Nat-

ural Science Foundation of China, No. 61173055.

REFERENCES

Abernethy, B., Burgess-Limerick, R., Engstrom, C., Hanna,

A., and Neal, R. J. (1995). Temporal coordination of

human gait. Advances in Psychology, 111:171–196.

Desailly, E., Daniel, Y., Sardain, P., and Lacouture, P.

(2009). Foot contact event detection using kinematic

data in cerebral palsy children and normal adults gait.

Gait and Posture, 29(1):76.

Ghoussayni, S., Stevens, C., Durham, S., and Ewins, D.

(2004). Assessment and validation of a simple au-

tomated method for the detection of gait events and

intervals. Gait and Posture, 20(3):266–272.

Hreljac, A. and Marshall, R. N. (2000). Algorithms to deter-

mine event timing during normal walking using kine-

matic data. Journal of Biomechanics, 33(6):783–786.

ANewSimpleMethodforKinematicDetectionofGaitEvents

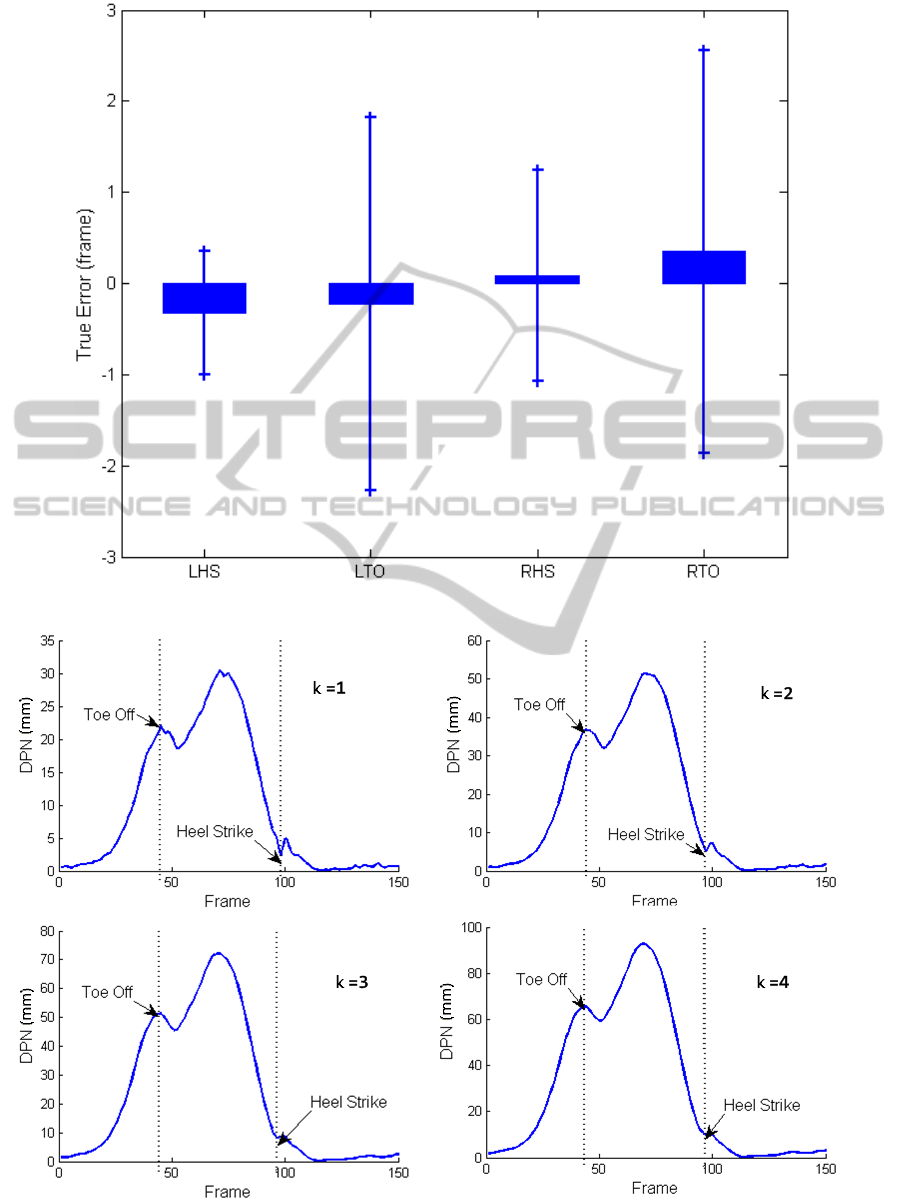
Figure 3: Candlestick chart with means and standard deviation of the true errors of normal gaits.

Figure 4: Curves of the DPN as the k varies. As k increases, the curve of DPN becomes more and more smooth.

icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport

Kar

cnik, T. (2003). Using motion analysis data for foot-

ﬂoor contact detection. Medical and Biological Engi-

neering and Computing, 41(5):509–512.

Kiss, R. M. (2010). Comparison between kinematic and

ground reaction force techniques for determining gait

events during treadmill walking at different walking

speeds. Medical Engineering and Physics, 32(6):662–

667.

Mayagoitia, R. E., Nene, A. V., and Veltink, P. H. (2002).

Accelerometer and rate gyroscope measurement of

kinematics: an inexpensive alternative to optical mo-

tion analysis systems. Journal of Biomechanics,

35(4):537–542.

Mickelborough, J., Van Der Linden, M., Richards, J., and

Ennos, A. (2000). Validity and reliability of a kine-

matic protocol for determining foot contact events.

Gait and Posture, 11(1):32–37.

O’Connor, C. M., Thorpe, S. K., OMalley, M. J., and

Vaughan, C. L. (2007). Automatic detection of

gait events using kinematic data. Gait and Posture,

25(3):469–474.

Tirosh, O. and Sparrow, W. (2003). Identifying heel contact

and toe-off using forceplate thresholds with a range

of digital-ﬁlter cutoff frequencies. Journal of Applied

Biomechanics, 19(2):178–184.

Viitasalo, J., Luhtanen, P., Mononen, H., Norvapalo, K.,

Paavolainen, L., and Salonen, M. (1997). Photocell

contact mat: a new instrument to measure contact and

ﬂight times in running. Journal of Applied Biome-

chanics, 13:254–266.

Zeni Jr, J., Richards, J., and Higginson, J. (2008). Two sim-

ple methods for determining gait events during tread-

mill and overground walking using kinematic data.

Gait and Posture, 27(4):710–714.

ANewSimpleMethodforKinematicDetectionofGaitEvents