Slope based Grid Creation using Interpolation of LIDAR Data Sets

Jan Hovad, Jitka Komarkova and Pavel Sedlak

Faculty of Economics and Administration, University of Pardubice, Studentska 84, 532 10 Pardubice, Czech Republic

Keywords: DTM, LIDAR, Interpolation, Grid, Surface.

Abstract: This article proposes a new approach of DTM creation from irregular LIDAR data scan. It shows the new

way how to utilize GIS results in the 3D modelling branch. LIDAR has a form of digital model of relief

which does not include artificial objects on the surface. DEM is created on the basis of individual points and

their elevation values and is further used for segmentation and classification of the terrain. Key attribute for

this operation is computation of the slope in the area of interest. Resulting classes are used as vector

outlines. These outlines are intended to divide the point cloud into groups. Each of them has specific

requirements for resolution. Flat areas can be modelled with less detail whilst hilly regions with sharp

elevation changes require higher resolution. LIDAR input is processed by chosen interpolation method, in

this case IDW and Renka-Cline algorithm. Irregular structure of the point cloud is converted into regular

grid of points. This process is semi-automatic. It is implemented in C++ library in the application Origin.

Output is automatically saved in predefined variable resolution (set of grids) and prepared to be processed in

3D.

1 INTRODUCTION

Light detection and ranging (LIDAR) is technology

that provides information about elevation of scanned

objects and their position. This technology is utilized

in this article. Goal of this study is based on the

previous research of authors. In this case, authors

were looking for a method that could eliminate the

disadvantages of triangulated irregular networks

(TINs) and that lowers the hardware requirements as

much as possible (Axelsson, 2000).

Current applied utilization of LIDAR is very rich

and intersects a wide range of scientific disciplines.

Most frequent example is creation of Digital Terrain

Model (DTM). Practical example of the DTM

creation can be found in research from Mandlburger

et al. (2009) who studied hybrid terrain models in

the river flow modelling. Next one is the Digital

Elevation Model (DEM). It is frequently used to

compute elevation based analyses. The Digital

Height Canopy Model (DHCM) is used for

reconstruction of forests and vegetation. This

research was done by Klimanek (2006) who used

LIDAR technology in the forestry.

Reconstructed model of terrain relief can be

enriched by buildings in the form of the Digital

Building Model (DBM) and can be used for example

for antennae signal prediction or navigation (Li et al.

(2007). All of these parts can be merged together to

form one complex model. Prerequisite for this

operation is data processing described in this text.

2 IDENTIFIED ISSUES

AND GOALS IN GRID

CREATION

The main goal of this paper is to create slope based

set of quadrilateral grids. This grid set can be made

by chosen interpolation method which can compute

unknown value at a specific grid from the known,

measured values. It is usually represented with

certain error. Interpolated outputs can be stored as a

set of LIDAR XYZ files. These files can be further

processed by 3D applications in parametrical and

procedural way to form almost photo-realistic

visualisation with maintaining the presence of GIS

analyses.

Partial steps can be summarized as follows: (1)

Batch operations are handled by basic scripting and

programming (C++) (2) Resulting grids have a form

of quadrilaterals and they are saved as XYZ files in

the form that will be handled by any 3D scripting

227

Hovad J., Komarkova J. and Sedlak P..

Slope based Grid Creation using Interpolation of LIDAR Data Sets.

DOI: 10.5220/0004574402270232

In Proceedings of the 8th International Joint Conference on Software Technologies (ICSOFT-EA-2013), pages 227-232

ISBN: 978-989-8565-68-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

language in next research. (3)This processed grid

can be used further for visualization, simulation or it

can be utilized in any other scientific field, previous

steps are prerequisites for this operation (4)

Demonstration in the large area in the form of terrain

model by use of constant grid.

2.1 Inputs and Outputs of Individual

Operations

Outline of all key operations to reach set goals can

be expressed by a simplified scheme of inputs and

outputs (Figure 1). This expression represents the

chained pipeline. The first input (LIDAR irregular

data set) is processed through the entire process

while partial output files are generated and re-used

in the next steps.

Figure 1: Processing scheme.

2.2 Used Data and Software

This chapter describes the used data and software

that was needed to finish set goals. Authors had

mainly one available input to finish them. LIDAR

scan for area size 10×20 km. Source of data is from

the Military Office for Geography and

Hydrometeorology of Army of the Czech Republic.

Data set is scanned by aircraft Turbolet L-410 FG.

Scanning parameters are set to, fly height = 1200 m,

plane speed = 250 km/h, beam frequency = 80-120

kHz, scan angle = 60°, scan direction = East-West,

width and length of scanned stripe = 0,8 - 25/60 km

and sides are overlapped by 50 %. Outputs resulted

in two types of LIDAR models. First, the Digital

Surface Model 1st generation (DSM 1G) which

included all objects on the surface (terrain +

vegetation, buildings,…). Second, the Digital Model

of Relief 5

generation (DMR 5G). For this purpose

is the DMR sufficient because authors solved only

problems directly connected with terrain (Belka,

2012).

Scanned data are stored as XYZ text files. Each

scanned point is represented by separate line with

information about X/Y coordinate (WGS 1984) and

Z elevation attribute (meters above sea level). Area

is scanned and saved separately into 50 files that

formed a rectangular matrix. These individual files

are merged together and formed 800 MB big file that

consisted 21 000 000 records (points). XYZ object

representation is plain and can be demonstrated by

basic object primitives (Figure 2).

Figure 2: XYZ file object representation.

This simplicity is from other side compensated by

hardware requirements. Authors used two computers

to perform individual operations. AMD Opteron and

Intel i7 2600K CPU, with minimum of 16 GB

memory, fast SATA III SSD (500 MB/s) and

GeForce 460 GTX. The most important is high

amount of memory to work with a large number of

points. This fact is reflected in the used software that

is mainly used as 64 bit versions to fully utilize

RAM capacity. The first one is ArcGIS 10 from

ESRI - this application fully sufficed in all

interpolation tasks based on local IDW algorithm

and also prepared the LIDAR data set. Batch tasks in

ArcGIS are made with the help of scripting language

Python. The second suitable application is

OriginLab. This application supports scripting,

utilizes national algorithm library (NAG) and

connects all the features within C++.

3 SIMPLIFYING LIDAR DATA

SET BY INTERPOLATION

This chapter characterizes the basic principle of

interpolation in case of simplifying irregular LIDAR

scan to regular grid structure.

3.1 LIDAR Interpolation

Interpolation is the estimation of attribute (in this

case elevation-Z) at unmeasured-unknown points

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

228

from measured points (known points). Weather

forecast is a typical example of interpolation used in

real life. Temperatures are measured at

meteorological stations (known values) and

interpolated throughout the whole area of interest.

Points outside of it can be extrapolated. DEM is

often created from contour lines. To create

continuous raster surface, attributes (Z) from the

contour polyline must be interpolated into the

required grid with predefined unit resolution.

This is called the 2D interpolation because the

values are interpolated on the surface that is defined

by X and Y coordinates. It must be taken on mind

that even contour lines are frequently already based

on interpolation. In addition to these core

applications there are other input data types that can

be chosen for interpolation (points, lines, areas).

Interpolation process can be divided in two main

groups. Global interpolation considers all known

points and computes the unknown values at

specified location. Local interpolation method

usually sets the distance radius (variable or fixed)

around the known point and searches within it

throughout the limited number of neighbourhood

points for the computed value at specified position.

The difference between them is the sensitivity to an

outlier values.

This problem points to the fact that global

method creates smooth surfaces and local method

less smooth surfaces. Local method is not so

sensitive to outliers but creates spikes. This issue

must be considered before using available LIDAR

data set which can be noisy and uncorrected from

outlier values that were reflected from the unwanted

objects (Figure 3).

Figure 3: Global and Local interpolation methods.

Global interpolation can be represented by a surface

which is calculated with a polynom of specified

polynomial grade. For example linear (first grade),

quadratic (second grade), cubic (third). Higher grade

of polynom causes better curve/plane fitting through

the points. But from another aspect it cases so called

“Runges phenomenon” which computes wrong

estimations of attributes for unknown points (peaks).

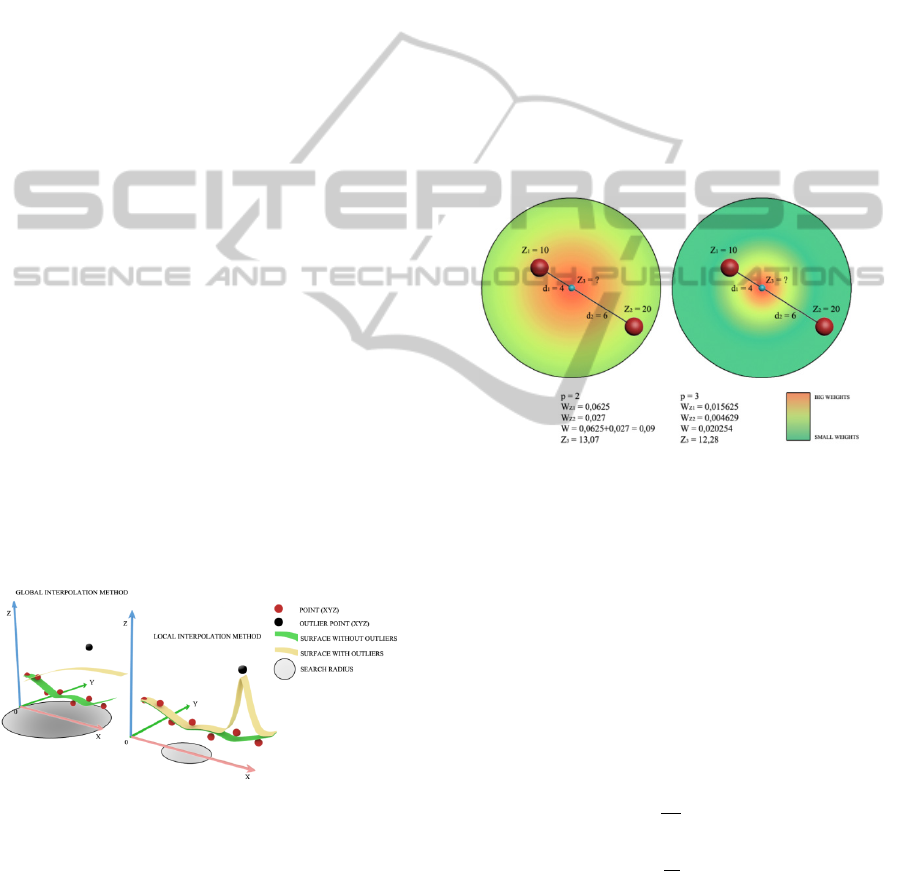
The most used local interpolator which is used

also in this text is Inverse Distance Weighted

Average (IDW). This method is based on the

weighting the known attributes by an inverse power

of distance between known and unknown point. The

closer the unknown point is to a known point, the

stronger the influence of the distance.

User can specify parameters which affect the

output. p = exponent, 0 = no matter where the

unknown point is, 1 = direct correlation with the

distance, 2 = inverse power correlation with

distance, 3 and more = higher influence of

neighbourhood known points on the unknown points

computation. Radius and number of known points

used for computation - spatially affects the output.

All these parameters must be carefully checked

based on distribution of known data points (Figure

4) (Longley et al., 2011).

Figure 4: IDW power influence.

3.2 Batch Implementation

This text uses local interpolation of IDW and global

version of Renka-Cline interpolation (Renka and

Cline, 1984). IDW is computed in ArcGIS 10. Raw

LIDAR data are loaded as 3D features. XY

coordinates are additionally attached and the whole

irregular structure is batch processed by a Python

script. Script saves all interpolated grid outputs into

specified folder. Each output is saved in different

resolution defined by a target size of required

polygon.















(1)















(2)

Where, i = item in the array of resolutions, C

number of columns (X axis), R

= number of rows

(Y axis), W = width of the area of interest, H =

height of the area of interest, P

= target size of the

polygon.

SlopebasedGridCreationusingInterpolationofLIDARDataSets

229

The whole area of interest has a size of 10×20

km. Target size of polygons is set to array of {5 10

20 40 60 100} meters. Computation resulted in two

input arrays, COLS {100,167,251,502,1005,2010},

ROWS {199,332,498,997,1995,3990}. Besides

Python script in ArcGIS, authors use application

OriginLab which combines scripting and

programming steps to fully customize the

computational process.

OriginLab uses C++ compiler and a NAG library

(Numerical Algorithm Group) which contains

approx. 1600 mathematical and statistical

algorithms. Following C++ code shows the batch

solution of performing Renka-Cline within an

application OriginLab. Source code shows only

basic procedure and script text output due to the

limits of article size. User specifies the input file

with LIDAR scan. In this case it is 800 MB big XYZ

data set. Active layer is loaded into XYZFile object.

XFBase class provides an access to scripting

functions, in this study xyz_renka from NAG

library. After that, data are iteratively processed and

saved separately. Timer shows the length of the

computational process and saving operations. Saving

a large xyz file can take a significant amount of

time. In case of grid resolution = 2010×3990 (8

million of points) over 2 minutes and iteration

generated 300 MB big grid file. Files are stored in

created directory.

void renka()

{

Alg = "RENKA-CLIME";

open_file();

Worksheet XYZFile =

Project.ActiveLayer();

for (int i=0;i<max;i++)

{

timerStart = GetTickCount();

int_to_fixed_str(gridValuesX[i],3,bufX)

int_to_fixed_str(gridValuesY[i],3,bufY)

outRes = bufX +" "+ bufY;

XFBase xf("xyz_renka_nag");

data.Add(XYZFile, 0, "X");

data.Add(XYZFile, 1, "Y");

data.Add(XYZFile, 2, "Z");

xf.SetArg("iz",data);

xf.SetArg("rows",gridValuesX[i]);

xf.SetArg("cols",gridValuesY[i]);

xf.Evaluate();

timerEnd = GetTickCount();

line;

printf("Algorithm: Renka-Clime\n");

printf("Resolution:%d",gridValuesX[i],"

× ",gridValuesY[i]);

printf("\nValues:%d\n",gridValuesX[i]*g

ridValuesY[i]);

printf("Pure computation completed

in:%d ms\n",timerEnd-timerStart);

convertMatrix();

Export_ASCII();

timerEndSave = GetTickCount();

printf("Saving the output file took :

%d ms\n",timerEndSave-timerEnd);

printf("Total time: %d

ms\n",timerEndSave-timerStart);

line;

}

printf("\n");

}

***************************

Algorithm: Renka-Clime

Resolution: 2010

Values: 8019900

Pure computation completed in : 11544

Saving the output file took : 3370 ms

Total time: 14914 ms

***************************

Following figure shows the data output of

interpolation process. Set of grids are characterized

by an ascending resolution (Figure 5).

Figure 5: Data output of interpolation process.

The same situation applies to IDW grid set which is

created in ArcGIS. Grid can be stored either as a

point feature or a raster image. Figure 6 shows three

of six created grids in both forms, as raster and point

features. The big sized image on the left is the whole

area of interest. Black square outline magnifies the

area to show the finest details in the grid resolution.

Figure 6: Interpolated grids as raster and point features.

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

230

4 GRID SEGMENTATION USING

DEM SLOPE ANALYSIS

This part is focused on the creation of clip polygons

in ArcGIS. These polygons will be used to clip the

computed set of XYZ grids which resulted from the

interpolation process. In this example authors used

three types of grids. Grid 1 has cell size of 5 meters,

suitable for hilly regions with sudden elevation

changes. Then Grid 2 has the cell size of 20 meters,

for highlands. The Grid 3 has the cell size of 60

meters, for flat lands. Reason for excluding other

grids is based in grid comparison. This comparison

is made by computing grid volumes and split sample

validation. Detailed results of these tests go beyond

of the subject of this article. They will be explained

further in next research. This fragmentation provides

the ability to process large territory. It would not be

possible with constant grid of 5×5 meters because of

hardware requirements.

The main steps can be summarized as following.

Irregular LIDAR data set is converted to raster form

(DEM). This conversion is targeted to adequate cell

size and based on chosen method (e. g. most

frequent, mean,). Precision in the preservation of

real-measured values decreases but it is sufficient for

finding the outlines for all grids. In the next step the

slope analysis is performed. Quality of analysis is

based on the DEM cell size. Slope tool calculates the

maximum rate of change between each cell in the

raster and its eight neighbours.

These steps are shown magnified to recognize

cell size, on the Figure 7.

Figure 7: Slope analysis based on DEM.

To simplify the situation, ranges are aggregated into

3 groups (the same number of used grids). Flat,

semi-steep and steep regions (Table ).

Table 1: Aggregated ranges.

Slope class Gradient [%]

Flat region 0-20

Semi-steep region 21-35

Steep region >36

Decimal values of the raster are converted to

integers. This operation is prerequisite for raster to

polygon conversion. This conversion is made in high

precision to match individual outlines without blank

spaces. The process can be adjusted according to the

terrain type. Mainly by slope requirements, norms or

by DEM cell sizes (Figure 8).

Figure 8: Polygons used to clip interpolated grids.

Minor buffer can be also applied to each polygon

class to extend the boundary. This boundary will

provide an easier intersection of reconstructed

surfaces.

The final step in data preparation is to clip each

selected grid with associated polygon - 5×5 m grid

with orange coloured polygon, 20×20 m grid with

green polygon and 60×60 m with black polygon.

Some overlaps are apparent along the outlines of

each class. These overlaps will work like

intersection areas in the future research which will

utilize these data files for 3D scripting (Figure 9).

Figure 9: Assigned grids based on the slope analysis.

5 DISCUSSION

AND CONCLUSIONS

This section summarizes the results and outlines

possible ways forward in the future research.

5.1 Discussion

Authors performed a hybrid method of DTM

creation. This method is based on the classification

and segmentation of interpolated grids by chosen

method (IDW and Renka-Cline). This method

should lower hardware requirements by lowering the

resolution in certain areas and increasing the

resolution in high slope locations. Adaptive slope

adjustment of the interpolated grid resolution in

certain topographic locations can increase

reconstructed DTM dimensions significantly. This

SlopebasedGridCreationusingInterpolationofLIDARDataSets

231

study is based on the previous research where

authors explained parametric and procedural

visualisation which is built on the single grid with

constant resolution. Output from the previous

research with constant grid can be demonstrated by

following figure and will be very similar even in this

study but in much larger area (Figure 10).

Figure 10: Constant grid used in 3D visualisation in

previous research (Processed in 3D Studio Max).

The future work will be directed to area of 3D

scripting (Maxscript). Set of XYZ files - interpolated

grids will be processed in 3D environment (3D

Studio Max). Each of chosen grids will form

quadrilateral polygonal surface. By help of

parametric, procedural and set operations, the DTM

will be fitted by a set of models to form digitized

photo realistic 3D polygonal version of terrain

model. Real-world attributes (height, density,

coordinates and sizes) will be maintained along with

possibility to combine all features with analyses.

5.2 Conclusions

The main goal and partial steps are completed

successfully. Solution of these steps, however,

resulted in other issues which will be further

explained in following research. These issues are

mentioned in the discussion. Results can be used for

example for simplifying computational tasks related

to LIDAR car control by means of substitution of

point cloud by DTM which provides faster results.

ACKNOWLEDGEMENTS

This work was supported by the project No.

CZ.1.07/2.2.00/28.032 Innovation and support of

doctoral study program (INDOP), financed from EU

and Czech Republic funds.

REFERENCES

Axelsson, P., 2000. DEM generation from laser scanner

data using adaptive TIN models, International Archive

of Photogrammetry and Remote Sensing, 33 (B4),

110-117.

Belka, L., 2012. Airborne laser scanning and production of

the new elevation model in the Czech Republic,

Vojenský geografický obzor, 55 (1), 19-25.

Klimanek, M., 2006. Optimization of digital terrain model

for its application in forestry, Journal of Forest

Science, 52 (5), 233-241.

Li, J., Taylor, G., Kidner, D. and Ware, M., 2008.

Prediction and visualization of GPS multipath signals

in urban areas using LIDAR Digital Surface Models

and building footprints, International Journal of

Geographical Information Science, 22 (11-12), 1197-

1218.

Longley, P., A. et al., 2011. Geographic Information

Systems and Science, 3,539

Mandlburger, G., Hauer, C., Hofle, B., Habersack, H. and

Pfeifer, N., 2009. Optimization of LIDAR derived

terrain models for river flow modeling, Hydrology and

Earth System Sciences, 1453-1466.

Renka, R. J. and Cline, A. K., 1984. A triangle-based C

Interpolation Method. Journal of Mathematics, 14,

223-237.

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

232