
A PSO/Snake Hybrid Algorithm for Determining Differential
Rotation of Coronal Bright Points
E. Shahamatnia, I. Dorotovic, R. A. Ribeiro and J. M. Fonseca
UNINOVA, Campus da FCT/UNL, 2829-516 Caparica, Portugal
Keywords: Particle Swarm Optimization, Snake Model, Hybrid Algorithm, Image Processing, Tracking, Solar Images.
Abstract: Particle swarm optimization (PSO) algorithm is a successful general problem solver, thanks to its
computationally inexpensive mechanisms. On the other hand, snake model is a specialized image processing
algorithm widely used in applications such as boundary delineation, image segmentation, and object
tracking. In this paper we discuss the suitability of a hybrid PSO/Snake algorithm for determining the
differential rotation of the Sun’s coronal bright points. In the Snake/PSO hybrid algorithm each particle in
the population represents only a portion of the solution and the whole population altogether will converge to
the final complete solution. In this model a one-to-one relation between Snake model snaxels and PSO
particles have been created and PSO’s evolution equations have been modified with snake model concepts.
This hybrid model is tested for tracking the coronal bright points (CBPs) along time, on a set of full-disc
solar images obtained with the Atmospheric Imaging Assembly (AIA) instrument, onboard the Solar
Dynamics Observatory (SDO) satellite. The algorithm results are then used for determining the differential
rotation of CBPs. These final results are compared with those already reported in the literature, to assess the
versatility of the PSO/Snake hybrid approach.
1 INTRODUCTION
Particle swarm optimization (PSO), first introduced
by (Kennedy and Eberhart, 1995), has become very
popular as a general search strategy. It is
computationally inexpensive to implement and yet it
demonstrates a fast and reasonable performance. It is
a stochastic algorithm based on the analogy of
collective behavior of birds´ swarms. PSO consists
of a population of particles, each similar to a bird
searching for the best place to find food. Each
particle in PSO is a candidate solution. In PSO,
particles are governed under their cognitive and
social behaviors. These mechanisms make it
possible for particles to communicate and diffuse
their experience of explored space, and finally
converge towards the optimum of search space,
which is the solution to the formulated problem.
Image segmentation is one of the frequently
addressed issues in digital image processing.
Deformable contour was first used for object
boundary delineation in the late 80s and its
variations have been popular approaches ever since.
Kass et al (1988) introduced a new kind of
deformable contour called active contour model
(ACM), which deforms contours to lock onto
features of interest within an image. Active contour
model is also known as snake model, since the
evolution of contour resembles snakes crawling.
Snakes are widely used as an interesting approach in
many applications, including image segmentation,
stereo matching and object tracking (Ballerini and
Bocchi 2003; Tsechpenakis et al., 2004; Kass et al.,
1988).
Snake model is an energy minimization
algorithm induced not only by low level image
features such as image gradient or image intensity,
but also with higher level information such as object
shape, continuity of the contour and user interaction.
Given an approximation of the object boundary, the
snake model will be able to find the precise
boundary of that object (Ballerini 1999; Ballerini
and Bocchi, 2003). Snake model is in essence an
optimization algorithm. Original snake model
achieves this minimization by iteratively solving a
pair of Euler equations on the discrete grid.
Traditional active contour algorithms suffer from
some limitations. One main drawback is the
sensitivity of the initial contour; it must be within
the vicinity of object boundary. An improper
56
Shahamatnia E., Dorotovic I., A. Ribeiro R. and M. Fonseca J..
A PSO/Snake Hybrid Algorithm for Determining Differential Rotation of Coronal Bright Points.
DOI: 10.5220/0004576100560063
In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 56-63
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

initialization may lead the algorithm to fail. A
solution to this problem is to expand the search
domain or increase the capture range of image force
to guide the contour evolution (Leroy et al., 1996;
Park et al., 2001; Cohen and Cohen, 1993). Another
limitation is that it can hardly converge on concave
object boundaries (Bresson et al., 2007; Davatzikos
and Prince, 1994). There are a number of other
problems associated with classical active contours
such as sensitivity to noise, convergence to local
minima, parameter selection and instability (Amini
et al., 1988; Bresson et al., 2007; Mun et al., 2004) .
Several works addressed these problems but very
few have produced satisfactory results. They either
cannot address all the problems or if they can, they
usually raise new drawbacks and impose further
complexity and computational cost to the model.
One successful approach is to minimize the snake
energy by alternate strategies such as dynamic
programming (Amini et al., 1988), greedy
algorithms (Lam and Yan, 1994), genetic algorithms
(Ballerini, 1999; Ballerini and Bocchi 2003; Mun et
al., 2004) and swarm based optimization algorithms
(Zeng and Zhou 2008; Nebti 2009; Tseng et al.,
2009; Li et al., 2009; Shahamatnia and Ebadzadeh,
2011; Asl, 2006).
PSO can be applied to drive control points on the
snake, but particles must be prevented from
convergence to the global best position experienced
by the swarm. In the literature this is done by
restraining the particle search space. (Tseng et al.,
2009; Li et al. 2009) use multi-population PSO in
which each control point is confined to a sub-swarm
spatially distinct from other sub-swarms. In
(Ballerini, 1999; Nebti, 2009), polar coordinate
system is used to restrict the search space of each
contour control point. In (Zeng and Zhou, 2008) an
iterative method has been used to rank the best
position set of particles at each epoch and according
to some equations prevent particles from
intersecting.
Most of the aforementioned methods act only as
a general problem solver and take the approach of
formulating the snake model calculations as a
minimization problem and then just solving this
optimization problem. In this paper, we take the
hybrid PSO/Snake approach introduced in
(Shahamatnia and Ebadzadeh, 2011) and show its
versatility by further extending it to solve a real
world problem from astrophysics domain. The
method presented here customizes PSO algorithm to
overcome snake model drawbacks including snake
initialization, concave boundaries, sensitivity to
noise and local minima. Yet, the simple structure of
PSO is preserved yielding to an algorithm with low
order of complexity and hence good processing
time. These factors are of utmost importance for
precisely calculating the differential rotation of solar
features.
Specifying the exact nature of the differential
rotation of both the solar surface and the solar
interior is a very important issue of solar physics.
The solar surface rotates differentially. However, the
differential rotation (DR) mechanism, most likely
caused by interactions between convection and
overall rotation, is not exactly known. DR plays an
important role in generating solar activity (SA) –
every manifestation of SA is related to changes in
the local magnetic field and local changes of the
differential rotation. Rotational irregularities may
also serve as indicators of hypothetical processes,
going on beneath the solar surface. One example
could be the location of a layer where rotational
speed changes abruptly (the so-called jet stream).
Sometimes it is called a layer of torsional oscillation
(Ulrich and Boyden, 2005). The location of this
layer (its heliographic latitude) is likely related with
a phase of the solar activity cycle, therefore it would
be rather useful to have a tool for regular
determination of its location. During a series of
consecutive days or within an interval of a few days,
we plan also to trace a location of a jet stream in
images obtained by the Atmospheric Imaging
Assembly (AIA) instrument on board the space
Solar Dynamics Observatory (SDO).
Coronal bright points (CBPs) or bright points,
are small and bright structures observed in the
extreme ultraviolet (EUV) and the X-ray part of the
solar spectrum (Brajsa et al., 2001). They are known
to have a mean lifetime of about 8 hours, a typical
maximum area of 2×10
8
Km
2
, but still they look like
a tiny shape on the solar images. Figure 1 illustrates
several CBPs. Bright points are associated with
bipolar magnetic features and a large quantity of
them (several thousands) emerge over the surface of
the Sun per day and thereby in total they bring up
huge magnetic fluxes. Precisely tracking the coronal
bright points over extended periods of time will help
solar physicists and space weather scientists to better
understand this important solar feature. Such
automatic tools will allow solar researchers to
precisely process large amount of solar data and
hence improve solar models. The aim of this paper is
to present the result of applying a hybrid PSO/Snake
algorithm for tracking coronal bright points. The
result of tracking is then used for calculating the
differential rotation of coronal bright points. Further,
the result of PSO/Snake hybrid algorithm is cross
APSO/SnakeHybridAlgorithmforDeterminingDifferentialRotationofCoronalBrightPoints
57
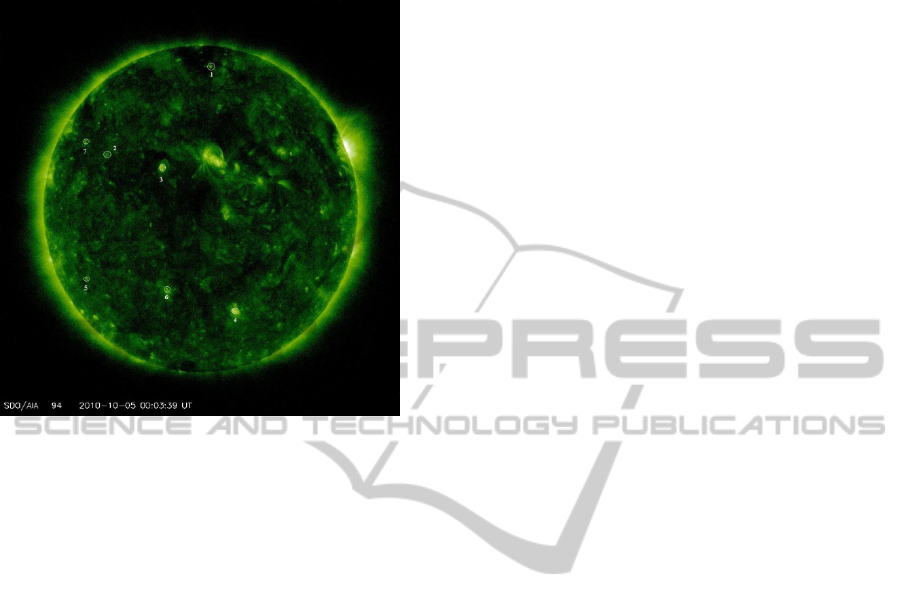
referenced with a state of the art study which entails
manual procedure done by an expert (Lorenc et al.,
2012).
Figure 1: A sample solar image with several CBPs
marked. (Image courtesy of NASAS/DO).
The rest of this paper is organized as follows: Snake
model, PSO, and PSO/Snake algorithms are
reviewed in section 2. Section 3 provides the
experimental results and discussions. Finally,
conclusions are provided in section 4.
2 PSO/SNAKE HYBRID
ALGORITHM
The hybrid algorithm is a merge of the snake model
and PSO. It integrates the active contour evolving
paradigms with PSO dynamics. Snake model also
known as Active Contour Model, is an energy
minimization algorithm which takes into account
both low level image features such as image gradient
or image intensity and higher level information such
as object shape, continuity of the contour and user
interaction (Kass et al., 1988). After that
whereabouts of the Region Of Interest (ROI) is
approximated, the snake model will be able to find
the precise boundary of that object. Due to their
flexibility snakes are widely used in several
applications such as image segmentation, shape
modeling, stereo matching and object tracking (Niu,
2006; Ballerini and Bocchi, 2003; Wildenauer et al.,
2006; Karlsson et al., 2003).
In our model, contour or snake has an energy
associated with it, which correlates with the location
of the snake in the image and its geometrical
characteristics. The idea is to minimize the integral
measure which represents the total snake energy, by
evolving the snake over time. Original snake model
achieves this minimization by iteratively solving a
pair of Euler equations on the discrete grid, resulting
in a computationally expensive algorithm (Karlsson
et al., 2003). Two main approaches for snake
presentation are Geometric and Parametric
representations. Geometric models use an implicit
presentation based on the curve evolution theory and
are usually implemented with level-set techniques.
Effectively handling multiple objects and topology
alteration is the advantage of this approach, with the
cost of being computationally more complex. On the
other hand, the parametric approach is
computationally efficient and easy to interact with
users (Horng et al., 2010). In the parametric
implementations, snake is defined as curve p(s) =
(x(s),y(s)), having arc length s. As it is shown in
equation (1), a number of discrete points called
control points or snaxels characterize the snake
(Kass et al., 1988). PSO/Snake hybrid uses this
presentation since it well matches the snaxels and
particles. The parametric implementation is as
follows:
,
,
,
,
, ∈
0,1
(1)
where t is the time step. Total snake energy is the
sum of its internal (spatial) and external
(geometrical) integrals as shown in equation (2). In
the PSO/Snake hybrid algorithm, the objective
function calculates the total snake energy. Since in
this implementation the whole population altogether
represents one candidate solution to the problem, the
objective is to find the contour with the least total
snake energy. The lesser the total snake energy, the
better it matches the ROI or moves towards it.
1
0
1
0
(2)
The snake model is considered to be a controlled
continuity spline under the influence of internal and
external forces, which induce the snake energy.
Internal energy consists of two terms which are first
and second derivatives of the snake with respect to s.
First term coerces the spline to act like a membrane
and the second term makes the snake act like a thin
plate (Kass et al., 1988). The external energy
determines the snake relationship to the image. It is
formulated in a way that its local minima
corresponds the image features of interest. Various
external energies can be employed such as image
intensity, image gradient, object size or shape. One
common definition used for gray-level images is the
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
58

gradient of Gaussian.
The leading part of PSO/Snake hybrid algorithm,
is its PSO component. PSO is a population based
evolutionary optimization algorithm. The population
in the PSO is called swarm and consists of a number
of particles; each potentially can be a solution to the
optimization problem. Each particle has a position
and a speed which are initialized with random
values. Over a set of iterations, each particle’s
position on the search space is updated by revising
its velocity according to its best experience and also
its neighbors’ experiences. Particle position and its
corresponding fitness value are stored as personal
best experience and form the cognitive aspect of
particle evolution. Other aspect of the particle
position update is called the social behavior and
shows particles influence from its neighbors. The
neighborhood can be defined with various
topologies such as ring, star, Von Neumann and
random. If the particle neighborhood is restricted to
a subset of swarm it is called local best (lbest) PSO,
while if the neighborhood equals whole swarm it is
called global best (gbest) PSO. PSO/Snake hybrid
used lbest with ring structure and radius of 3. The
following equations show the dynamics of the
canonical PSO algorithm for updating particle
velocity and position:
1
1
1
(4)
Where x
i
(t) and v
i
(t) are position and velocity of i-th
particle at time t, y
i
(t) and ŷ
i
(t) denote the best
positions discovered by the i-th particle and its
neighborhood up to the time t, i.e. pbest and lbest
respectively.
(t) is the inertia weight which
controls the impact of the previous velocity and
prevents radical changes. Usually inertia weight is
decreased dynamically during the run time to
balance between exploration in the early iterations
and exploitation in the later iterations. Coefficients
r1 and r2 are random numbers. Weights of cognitive
and social aspects of the algorithm are represented
by acceleration factors c1 and c2 respectively. As it
is shown in (Van den Bergh, 2002) regulated values
for inertia and acceleration weights can be used to
achieve guaranteed convergence.
The PSO/Snake hybrid algorithm integrates the
snake model mechanisms with PSO dynamics.
While most of swarm intelligence approaches in
the literature used in conjunction with snake model
try to optimize the snake model equations,
PSO/Snake hybrid does not employ PSO algorithm
only as a general problem solver to optimize snake
energy minimization, but it also customizes the
standard PSO to better solve this specific type of
image processing problems. Early experiments on
medical image segmentation (Shahamatnia &
Ebadzadeh 2011) and sunspot tracking (Shahamatnia
et al. 2012) reported promising results. The hybrid
model helps to overcome the major drawbacks of
traditional snakes; initialization and poor
convergence to the boundary concavities, while
benefitting from PSO robustness and simplicity. In
the Hybrid PSO/Snake model we use a population of
particles where each particle is a snaxel of the
contour. All particles together form the contour and
hence the population is the final solution. As the
algorithm runs, each particle updates its position and
its velocity according to its personal best experience,
local best experience, and also according to the
internal force of the snake and external force of the
image. This gives the PSO/Snake dynamics a wider
range of informative guides to update the particle
position so that it converges to the ROI.
PSO/Snake hybrid explores the search space
according to PSO trajectory disciplines. This
eliminates the need to have a separate searching
window around each particle as many swarm based
snake optimization algorithms do (Nebti 2009;
Horng et al. 2010; Tseng et al. 2009) . These
methods consider a searching window around each
particle and evaluate every position inside that
window to determine the snaxels’ next position.
Since this local search is performed for each particle
per iteration, it is a computationally expensive
operation that is avoided in the PSO/hybrid model.
The velocity update equation in PSO/Snake is as
follows:
1
̅
.
(5)
where pbest
i
(t) and lbest
i
(t) are personal best
velocity and local best velocity terms respectively.
x
̄
(t) is the average of positions at time step t,
approximating center of mass of particles. This term
pushes the snake to contract or expand with respect
to the sign of its weighting factor, r
3
. This term
speeds up the algorithm and is particularly useful
when the snake is stagnated and there is no other
compelling force. If the snake is initialized far from
the ROI, this term allows the snake to either expand
or shrink towards the ROI and hence it increases the
APSO/SnakeHybridAlgorithmforDeterminingDifferentialRotationofCoronalBrightPoints
59
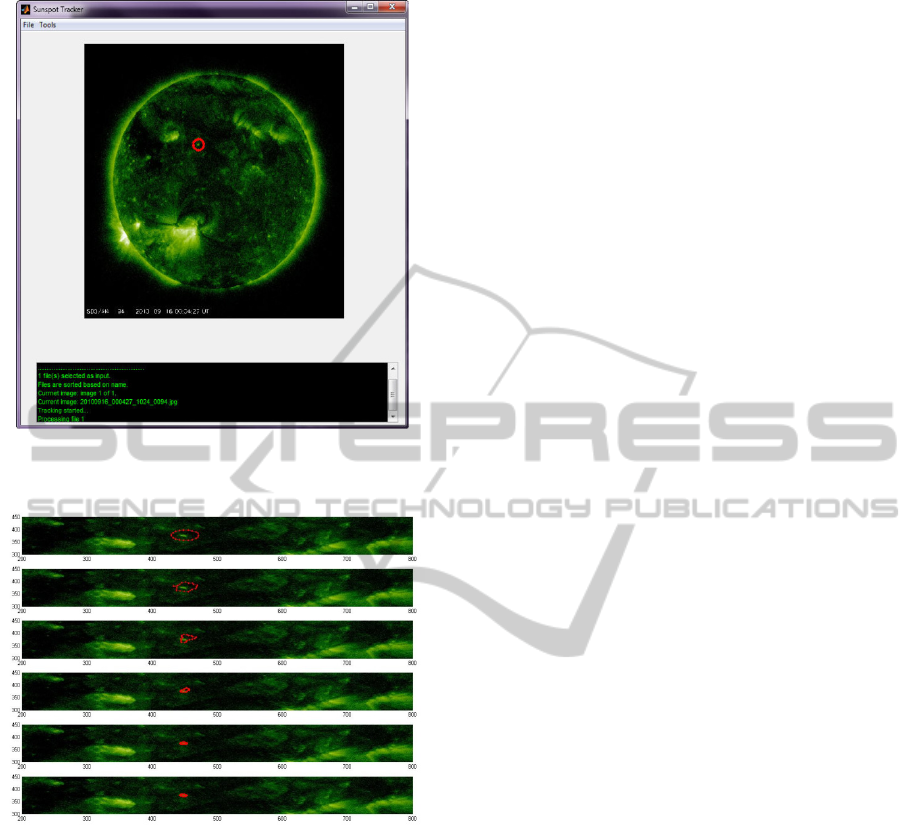
Figure 2: Red circle denotes the initial snake around a
CBP on the first image (16 June 2010).
Figure 3: Detection and tracking process of the selected
CBP (16 June 2010). In this figure the evolution of the
snake to detect CBP boundaries can be seen.
convergence rate and speed. f.Image
i
is the
normalized image force corresponding to external
energy from snake model principles. For particle i,
f.Image
i
gives the image force at the position
specified by that particle. Image force can be any
arbitrary function depending on the application, but
generally external energies such as image gradient
and gradient of Gaussian functional are enough for
satisfactory performance. It must also be noted that
image force does not vary by time and it is
calculated only once for an image pixel. c
4
is the
weighting factor to control the effect of image force.
Inertia weight,
, is taken to be a relatively small
constant and r
1
, r
2
and
r
3
denote random numbers.
Coefficients c
1
, c
2
, c
3
and c
4
are determined
dynamically in a way that if there is a higher image
force c
4
always gets a higher value. It ensures that if
a snaxel is next to the object boundary, it will latch
to the object of interest. The whole process can be
summarized as:
Step 1. Initialization. A pre-processing of images
is done if required, i.e. normalizing the size of
images, correcting the orientation and contrast of
images, etc.
Step 2. Initial Contour. The ROI is chosen by the
operator. This is the initial snake. For most cases a
rough estimation of the initial contour is enough.
This step is done only once when the coronal bright
point appears.
Step 3. Internal parameters set-up. The weight
parameters for the PSO/Snake hybrid algorithm are
initialized in this step.
Step 4. Snake force calculation. The external
force (image force) is calculated, once for every
image.
Step 5. Calculation of social and cognitive parts.
In this step we update the pbest value (the best
velocity the snaxel ever experienced) and the lbest
value as average of velocities of neighboring
particles.
Step 6. Moving snaxels. For each snaxel its
velocity is evaluated and then each snaxel velocity
and position are updated.
Step 7. Snake detection. This step checks the
convergence of snake contour to the coronal bright
point outline, i.e. choosing the snake with the lowest
total energy calculated. If the results are not
satisfactory, algorithm goes back to step 5. The
outcome of this step is the CBP contour for an image
frame.
Step 8. Tracking CBPs. This step tracks the same
CBP in the next image by feeding the subsequent
image frame to the system as input. The algorithm
loops back to step 4, and passes the specifications of
the detected SBP.
Step 9. Stopping tracking. Tracking a CBP stops
when it reaches the solar limb and disappears into
the other side of the Sun, or when the CBP shrinks
to a size smaller than a predefined threshold,
according to the size and resolution of image.
3 RESULTS AND DISCUSSIONS
Our benchmark data are corona images at 9.4 nm.
This line is emitted by the FeXVIII ion. We have
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
60

used selected JPEG images taken between 14
September 2010 and 20 October 2010 downloaded
from a freely accessible database at internet site
http://sdo.gsfc.nasa.gov/ data/aiahmi/ browse.php.
256 gray levels per pixel and image force is
calculated by a gradient of Gaussian functional with
=3. Images are resized to 512x512 resolutions. In
Figure 4: Initial snake on first image (top panel, 16 June
2010) and tracking process of the selected CBP during
time (middle and bottom panels). The cyan contour is the
boundary of tracked CBP, red square is the experts manual
CBP positioning result and the yellow circle is the
PSO/Snake hybrid algorithms automated tracking result
for CBP’s center of mass.
this automated process, the CBP to be tracked is
chosen by an operator. For test purposes we’ve
chosen the same CBPs for which we have the
benchmark data available from the expert’s manual
CBP positioning. It should be noted that in the
automated process, after that each CBP is chosen
(only once), the tracking process is automatic during
life span of that CBP. Figure 2 shows a screen shot
PSO/Snake hybrid algorithm tracking tool for a test
image. The red circle is the initial snake around a
CBP chosen by an operator. Figure 3 shows how the
initial snake is evolved under PSO/Snake algorithm
and the CBP boundary is detected. After CBP is
detected, its characteristics including the
heliographic coordinates of its center of mass are
calculated and are stored. Then the next frame in the
sequence is fed into the system. Detected CBP
contour from previous frame is used as a baseline to
automatically track the CBP in the new frame.
Figure 4 shows a closer look on a tracked CBP. The
results show that due to the dynamic nature of
PSO/Snake hybrid algorithm, detected contours are
flexible and can conform to the changes in shape and
size of the deformable objects like CBPs.
Altogether we have observed motion of 69 more-
or-less point-like structures in 674 images (4998
measurements). In manual procedure (Lorenc et al.
2012), the CBP structures were observed directly on
a PC monitor in an interactive session. Figure 5
shows latitudinal dependence of sidereal angular
speed of coronal rotation obtained in this study in
comparison with other authors. Further details can
Figure 5: Derived values of the rotational speed with error
bars showing the 95% confidence level intervals for
individual point-like structures. The dotted curve shows
the fit to the mean (b) values as a function of latitude b.
Over-plotted are the results of Howard and Harvey
(1970), in solid line and Hara (2009) and Brajsa et al.
(2004) both in the dashed-dotted curve because they are
almost identical.
be found in (Lorenc et al., 2012). In that paper, an
expert operator manually determines the 4998 CBPs
positions. Then, we run our PSO/Snake hybrid
algorithm on the images. Input images are converted
to grayscale color map with
APSO/SnakeHybridAlgorithmforDeterminingDifferentialRotationofCoronalBrightPoints
61

To compare the precision of the algorithm, we
used several parameters that were reported in
(Lorenc et al., 2012). In that paper, after an expert
manually determined positions of CBPs on the solar
images, the following measurements were calculated
(reported in Table 1 of the referenced paper):
angular rotation velocity denoted by , and
measurement error at 95% confidence level denoted
by Δ. Tables 1 and 2 show the result obtained with
manual CBP tracking and result obtained by
PSO/Snake hybrid algorithm for some structures. In
these tables, the structure is the identifier of CBP, b
is the heliographic latitude of CBP.
E
is the orbital
angular rotation velocity of the Earth which can be
looked up from solar almanacs. Figure 6 illustrates
the difference between our calculated values and the
benchmark values for all 69 CBPs.
Table 2 and Figure 6 show that the obtained
results are very close to the result of manual CBP
tracking. Computed angular rotation velocity is
Table 1: Results reported in (Lorenc et al., 2012).
Structure n B
xy0510.01
86 66.7 10.295 ±0.327 0.986
xy0510.03
86 20.5 14.586 ±0.099 0.986
xy0510.04
86
-
33.8
13.648
±0.209 0.986
xy0510.07 86 27.8 14.478 ±0.116 0.986
Table 2: Results obtained by PSO/Snake hybrid algorithm.
Structure n b
xy0510.01
8
6
67.103 11.213 ±0.642 0.985
xy0510.03
8
6
21.057 14.387 ±0.303 0.9
xy0510.04
8
6
-32.27 13.803
±0.342 0.985
xy0510.07
8
6
28.170 15.112 ±0.439 0.985
Figure 6: Deviation of PSO/Snake hybrid result from
benchmark data. The differences in b, ,Δ, and
E
are
presented with blue, cyan, red and green lines.
within ±0.2 of the benchmark data most of the time.
However, it should be noted that part of this
deviation is due to code implementation differences,
which, in precise calculations, impose a minute
variation. It is also worth mentioning, that in several
cases, results displayed bigger differences, and by
further investigation by a solar physicist expert (co-
author), we found out that PSO/Snake hybrid
algorithm behaves consistently and the user-error is
the main cause.
4 CONCLUSIONS
In this paper the PSO/Snake hybrid algorithm has
been used to solve a real solar physic/space weather
problem. By tracking CBPs over time, the angular
rotational velocity in the Sun can be automatically
calculated.
Based on the results analysis and comparison
with a manual method the obtained values of
rotational speed are reliable. We also observed that
the manual method is laborious and with a large
number of images becomes unworkable for practical
reasons. Therefore, we developed an automatic
image-processing tool (with a hybrid Snake/PSO
algorithm) capable of providing the same precision.
Here we discussed the suitability of using a
computer aided tool for tracking coronal bright
points, which includes a combined optimization
process, based on a Snake model and the PSO
evolutionary algorithm.
The combination of PSO dynamics with snake
model kinematics makes it possible to successfully
overcome active contour difficulties, while
preserving the simplicity of PSO. By adding two
new terms to the PSO velocity update equations,
PSO/Snake model still can evolve even if some of
the components are missing or misleading. The
PSO/Snake model can be used for different
applications in image processing for object
detection, image segmentation or tracking. It is
especially suitable for object tracking, since the
particle/snaxels have embedded velocity
information, which adapts itself to the movement of
the object in the images.
ACKNOWLEDGEMENTS
We would like to thank the SDO (NASA) and AIA
science team for the provided observational material.
This work was partially supported by grant
SFRH/BPD/44018/2008 (I.D.) and SFRH/BD/
62249/2009 (E.S.) from Fundação para a Ciência e
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
62

Tecnologia, MCTES, Lisbon, Portugal.
REFERENCES
Amini, A. A., Tehrani, S. & Weymouth, T.E., 1988. Using
dynamic programming for minimizing the energy of
active contours in the presence of hard constraints. In
Computer Vision., Second International Conference
on. pp. 95–99.
Asl, M. A., 2006. Active Contour Optimization Using
Particle Swarm Optimizer. , pp.522–523.
Ballerini, L., 1999. Genetic snakes for medical images
segmentation. In Evolutionary Image Analysis, Signal
Processing and Telecommunications. Springer, pp.
59–73.
Ballerini, L. & Bocchi, L., 2003. Multiple genetic snakes
for bone segmentation. In Applications of
Evolutionary Computing. Springer, pp. 346–356.
Van den Bergh, F., 2002. An analysis of particle swarm
optimizers. University of Pretoria, South Africa,.
Brajsa, R. et al., 2001. Solar differential rotation
determined by tracing coronal bright points in SOHO-
EIT images I . Interactive and automatic methods of
data reduction. Astronomy and astrophysics, 374,
pp.309–315.
Bresson, X. et al., 2007. Fast global minimization of the
active contour/snake model. Journal of Mathematical
Imaging and vision, 28(2), pp.151–167.
Cohen, L. D. & Cohen, I., 1993. Finite-element methods
for active contour models and balloons for 2-D and 3-
D images. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 15(11), pp.1131–1147.
Davatzikos, C. & Prince, J. L., 1994. Convexity analysis
of active contour models. In Proc. Conf. on Info. Sci.
and Sys. pp. 581–587.
Horng, M.-H., Liou, R.-J. & Wu, J., 2010. Parametric
active contour model by using the honey bee mating
optimization. Expert Systems with Applications,
37(10), pp.7015–7025.
Karlsson, A., Stråhlén, K. & Heyden, A., 2003. A fast
snake segmentation method applied to
histopathological sections. In Energy Minimization
Methods in Computer Vision and Pattern Recognition.
pp. 261–274.
Kass, M., Witkin, A. & Terzopoulos, D., 1988. Snakes:
Active contour models. International journal of
computer vision, 1(4), pp.321–331.
Kennedy, J. & Eberhart, R., 1995. Particle swarm
optimization. In Neural Networks, 1995. Proceedings.,
IEEE International Conference on. pp. 1942–1948.
Lam, K.-M. & Yan, H., 1994. Fast greedy algorithm for
active contours. Electronics Letters, 30(1), pp.21–23.
Leroy, B., Herlin, I. L. & Cohen, L. D., 1996. Multi-
resolution algorithms for active contour models. In
ICAOS’96. Springer, pp. 58–65.
Li, R. et al., 2009. A Novel Multi-Swarm Particle Swarm
Optimization algorithm Applied in Active Contour
Model. , (1).
Lorenc, M., Rybanský, M. & Dorotovič, I., 2012. On
Rotation of the Solar Corona. Solar Physics. Available
at: http://www.springerlink.com/index/10.1007/
s11207-012-0105-7 (Accessed September 11, 2012).
Mun, K.-J. et al., 2004. Active contour model based object
contour detection using genetic algorithm with wavelet
based image preprocessing. International Journal of
Control Automation and Systens, 2, pp.100–106.
Nebti, S., 2009. Predator prey optimization for snake-
based contour detection.
Niu, X., 2006. A Geometric Active Contour Model for
Highway Extraction.
Park, H., Schoepflin, T. & Kim, Y., 2001. Active contour
model with gradient directional information:
directional snake. Circuits and Systems for Video
Technology, IEEE Transactions on, 11(2), pp.252–
256.
Shahamatnia, E. et al., 2012. Towards an automatic
sunspot tracking : Swarm intelligence and snake model
hybrid. Acta Futura, 5, pp.153–161.
Shahamatnia, E. & Ebadzadeh, M.M., 2011. Application
of particle swarm optimization and snake model
hybrid on medical imaging. In 2011 IEEE Third
International Workshop On Computational
Intelligence In Medical Imaging. Paris, France: IEEE,
pp. 1–8.
Tsechpenakis, G. et al., 2004. A snake model for object
tracking in natural sequences. , 19, pp.219–238.
Tseng, C., Hsieh, J. & Jeng, J., 2009. Expert Systems with
Applications Active contour model via multi-
population particle swarm optimization. Expert
Systems With Applications, 36(3), pp.5348–5352.
Available at: http://dx.doi.org/10.1016/j.eswa.
2008.06.114.
Ulrich, R. K. & Boyden, J. E., 2005. The solar surface
toroidal magnetic field. The Astrophysical Journal
Letters, 620(2), p.L123.
Wildenauer, H. et al., 2006. Motion detection using an
improved colour model. In Advances in visual
computing. Springer, pp. 607–616.
Zeng, D. & Zhou, Z., 2008. Invariant Topology Snakes
Driven by Particle Swarm Optimizer. In 2008 3rd
International Conference on Innovative Computing
Information and Control. IEEE, pp. 38–38.
APSO/SnakeHybridAlgorithmforDeterminingDifferentialRotationofCoronalBrightPoints
63
