Application of Mathematical Modelling

for Simulation of Galvanic Corrosion

Vít Jeníček, Martina Pazderová and Linda Diblíková

Aerospace Research and Test Establishment – Testing Laboratories, Beranových 130, Prague, Czech Republic

Keywords: Mathematical Modelling, Galvanic Corrosion, Thin Electrolyte Layer, Polarization.

Abstract: This paper deals with an application of mathematical modelling for simulation of galvanic corrosion. A

programme for simulation of galvanic corrosion in a thin film electrolyte layer is presented. The programme

comprises some mathematical simplifications bringing significant reduction of computational demands and

on the other hand a need of specific form of input data. Necessary background for galvanic corrosion is

mentioned and the simplifications are described as well as the form of input data. An example of measured

input data and their application is shown. Discussion of used assumptions, input data availability and

measuring possibilities of the input data is included.

1 INTRODUCTION

Corrosion is significant problem affecting all

engineering materials and causing technical

problems, safety risks and economical losses.

Prevention or reparations are two different

approaches to restriction of corrosion impacts.

Mathematical modelling is an approach to corrosion

prevention, which enables control of an engineering

structure with regard to corrosion resistivity already

during designing process.

Mathematical model is based on physical

description of solved situation and simulation of

processes taking place in the system needs

appropriate input data. Purpose of this paper is to

define input data for simulation of galvanic

corrosion and conditions under which they are to be

measured. Applicability and limitations due to

employed physical model are shown for presented

corrosion simulation software.

2 GALVANIC CORROSION

Galvanic corrosion is one form of corrosion

occuring when two dissimilar metals are connected

in a presence of an electrolyte. Each metal immersed

into an electrolyte has unique potential called

corrosion potential E

corr

. If two metals are

connected, the potential difference becomes a

driving force for a current flowing between the

metals. The electrical circuit closes through the

electrolyte. The flowing current called corrosion

current I

corr

(or corrosion current density j

corr

converted per unit area) causes dissolution of less

noble metal (metal with lower E

corr

). This metal

becomes an anode of an electrochemical corrosion

cell. The metal with higher E

corr

becomes an

cathode. On the cathode, depolarization processes

proceeds which do not cause the dissolution of the

metal. Current flowing between the metal and the

ellectrolyte changes the potential of the metal. The

relation between the current density and the potential

change is represented by polarization curve.

To predict an impact of galvanic corrosion is

difficult because it depends not only on the material

properties but also on the geometry of the

connection and fast, localized degradation can occur.

If more than two materials are connected, the

situation becobes very complex.

3 SIMULATION SOFTWARE

Software BEASY Corrosion Manager (CM BEASY

Ltd., UK) was used for the simulation. The

programme enables to model galvanic corrosion

under thin layer of electrolyte. In this context it

means, that the thickness of the layer covering

modelled structure is much smaller than the

characteristic dimension of solved structure. For

example atmospheric corrosion can be described as

461

Jení

cek V., Pazderová M. and Diblíková L..

Application of Mathematical Modelling for Simulation of Galvanic Corrosion.

DOI: 10.5220/0004588504610466

In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),

pages 461-466

ISBN: 978-989-8565-69-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

corrosion in a thin layer of adsorbed moisture or thin

layer of electrolyte corresponds with rainfalls

covering upper parts of an aircraft fuselage.

Under assumption of thin layer of electrolyte,

following steps can be done (Palani 2011) to model

galvanic corrosion.

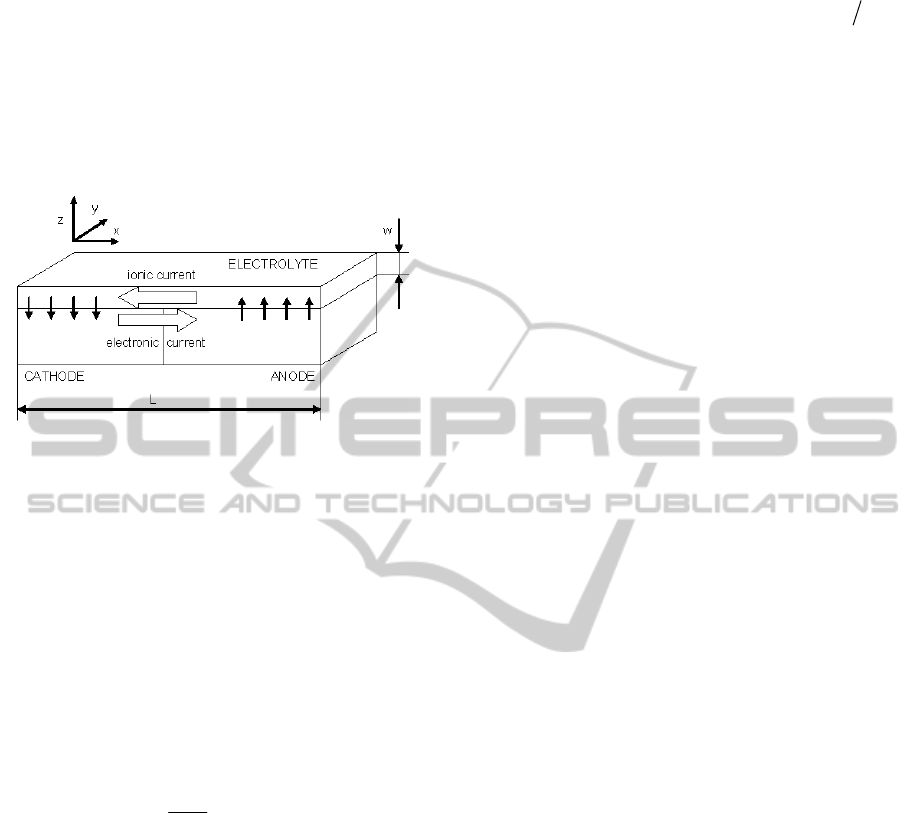
The schematic depiction of galvanic corrosion

under the thin film is in Figure 1.

Figure 1: Schematic depiction of galvanic corrosion under

a thin film of electrolyte, w«L.

Equation to be solved is the charge conservation

equation in the electrolyte under steady state (1):

0j



(1)

where



xVj







is the current density, σ

is the electrolyte conductivity and V

(x) is the

electric potential in the electrolyte at point

Rx  .

The integration domain of the equation (1) is the

volume of the electrolyte.

The boundary conditions for the surface of the

anode and of the cathode are given by equation (2):













(2)

where j

is the current density flowing through

the surface in normal direction and ΔV is the

polarization potential across the metal/electrolyte

interface. Polarization potential is given by

VVV  where V

is the potential of the

metal. This boundary condition is described by the

corresponding polarization curve for the metal of the

anode and of the cathode respectively. These

polarization curves must be contained in input data

for the simulation.

The boundary conditions for insulating surfaces

are j

=0.

In general, it is necessary to solve this problem in

3D. But if the thickness of the electrolyte w is much

smaller than a characteristic dimension of the

problem (see Figure 1), the electrical potential V

can be considered as constant in z direction. This

behaviour allows excluding the





component from the mathematical formulation of

the problem by direct integration of it along the

thickness w and the equation (1) changes into

equation (3):





VfVw

eDD













(3)

where w is the thickness of the electrolyte and



represents two dimensional grad operator

acting on x and y coordinates. The effect of the

charge exchange between the anode and the

electrolyte or the cathode and the electrolyte is

presented as source term and not as a boundary

condition. The dimensionality of the problem is

lowered from three to two.

Even very complex shapes with thin film of

electrolyte can be solved as 2D problem although

this “flat surface” can be twisted in fact. Lowering

of the dimensionality brings furthermore substantial

decrease of the computational demands.

4 INPUTS

Input data for the mathematical modelling are the

geometry of solved structure, the polarization curves

of each included material, conductivity of present

electrolyte and the thickness of the electrolyte layer.

4.1 Geometry

Geometry of solved structure is the basis of

mathematical model. Modelling software BEASY

CM uses universal preprocessor GiD (CIMNE,

Spain), which enables to create a new geometry or to

import an existing geometry in format IGES, DXF,

Parasolid, ACIS, VDA, Rhino, or Shapefile. Because

the corrosion is a matter of a surface of material,

geometry prepared for the simulation of corrosion has

to be composed only of surfaces. For the calculations

the surface is divided into elements by a discretization

mesh. Because the galvanic corrosion takes place in

vicinity of different materials interface, the mesh has

to be thicken in this areas.

4.2 Polarization Curves Measurement

The key input data for the simulation are the

polarization curves. They should be measured under

circumstances similar to those causing galvanic

corrosion. It requests measuring in thin layers of

electrolyte. Thin layer of electrolyte in this context

means layer thinner than 100 μm. Such thin layers

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

462

results in different polarization processes and

different shape of measured polarization curve in

comparison with a bulk electrolyte (Xiao 2012).

Common term in literature is thin electrolyte layer

(TEL).

Polarization curves used for modelling of a

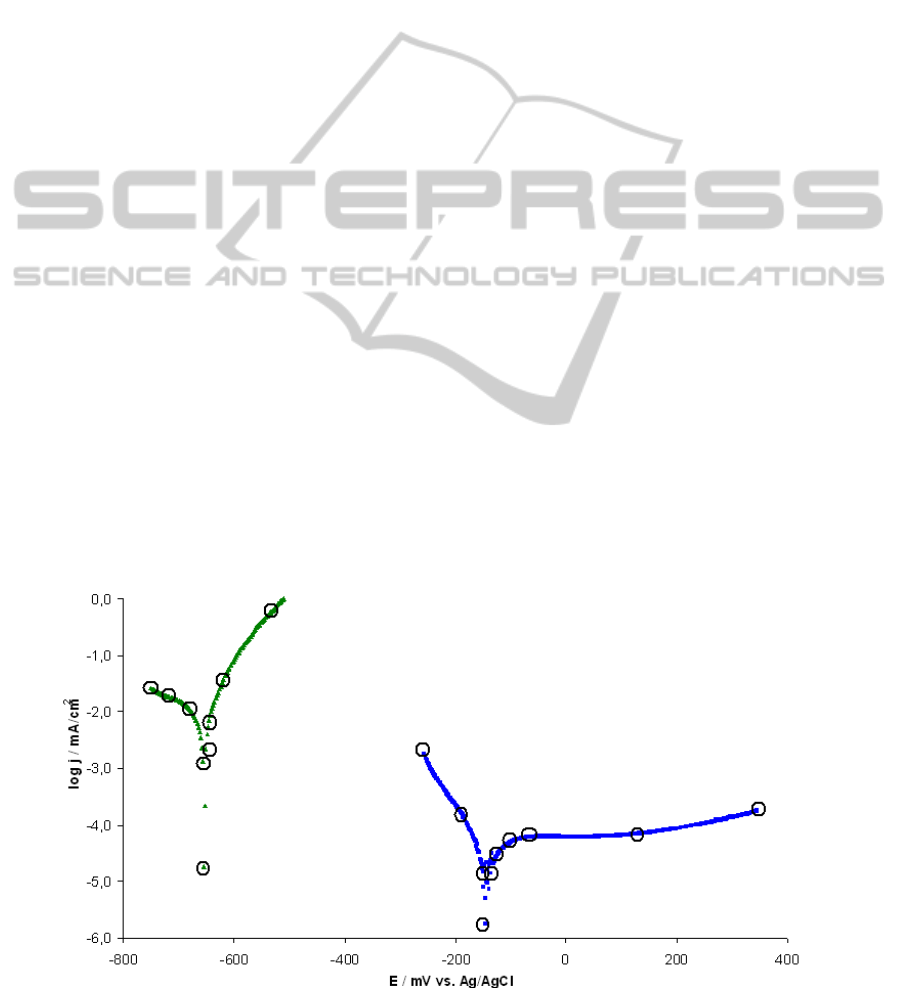
structure presented in this paper as an example are

shown in Figure 2. Measured polarization curves are

modified for the use in the programme. A few

discrete points interconnected by lines represent

them in the programme. The points for this

linearization are shown in Figure 2 too.

Factors influencing the shape of measured

polarization curves are the thickness of the layer,

chemical composition of the electrolyte and the

temperature. Software BEASY CM does not solve

processes on the metal/electrolyte interface.

Influence of all mechanisms (thermodynamics and

kinetics of electrochemical reactions) influencing the

resulting shape of the polarization curve has to be

included in the measured curves. In dependence on

different corrosive conditions to be modelled, there

must be accessible a broad database of polarization

curves, covering all corrosive conditions for all

materials.

4.3 Influence of Coatings

A material with a coating can be modelled as a

surface characterized by a new polarization curve.

Another approach is included, to use a polarization

curve of the plain material and the influence of the

coating model by two variables – breakdown factor

and ohmic resistance. This possibility is appropriate

especially for paints.

Breakdown factor indicates the ratio of area

without coating to the total area of a surface. This

definition enables to model damaged coatings.

Default value is set to 1, describing surface with no

coating. Ohmic resistance characterizes the electrical

properties of the coating. Default value is set to 0,

describing surface with no coating as well.

For coatings capable of electrochemical

reactions, typically galvanic coatings, there is a need

to measure a new polarization curve of the material

with the coating.

4.4 Thickness and Conductivity of TEL

Be the layer of electrolyte thicker than 100 μm or

thinner, the thickness of the layer is a part of input

data together with electrical conductivity of the

electrolyte. For a simulation of atmospheric

corrosion very thin adsorbed layers are used with a

thickness in the range 10-100 µm (Yadav 2007). If

water flowing down or stagnant appears, thicker

layers are modelled. The thickness must be

measured, calculated (Palani 2011) or estimated.

Measured thicknesses for typical situations can be

used repeatedly.

Conductivity of the electrolyte depends on the

composition. Aqueous solutions are most common

although an influence of any type of liquid can be

investigated by presented software on principle.

Conductivity of aqueous solution depends on an

amount of dissolved chemicals (salts, gases etc.).

Composition and conductivity of the electrolyte for

typical situations should be analyzed and

consequently it can be estimated on the basis of

similarity.

Figure 2: Measured polarization curves in thin layer of water: mild steel – green, stainless steel – blue.

ApplicationofMathematicalModellingforSimulationofGalvanicCorrosion

463

5 OUTPUTS

Results of the calculation are potential and current

density distribution over the whole surface of solved

structure. Calculated value of current density

represents the normal component of total current.

This is the current flowing between the metal and

the electrolyte, which is the corrosion current. For a

visualization of the results postprocessor GiD is used

again.

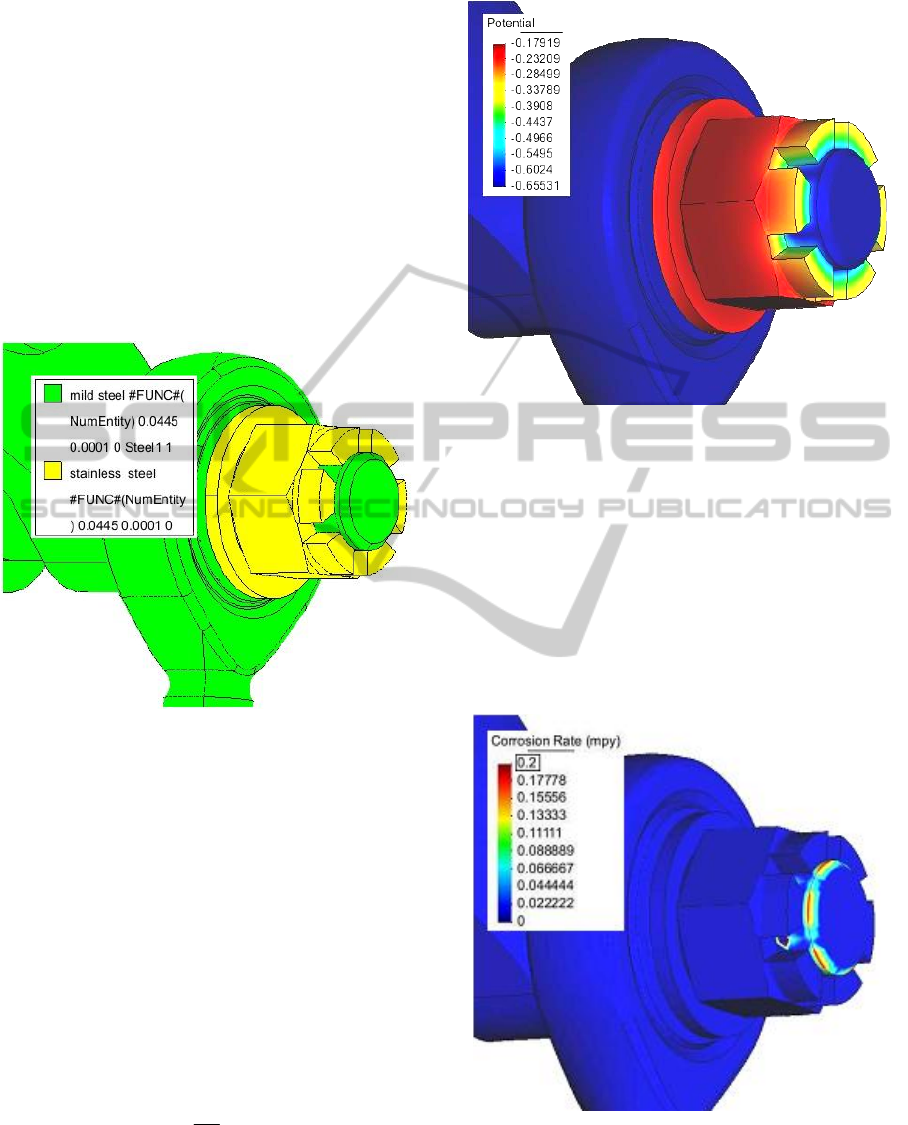
Small construction detail was solved to illustrate

the simulation outputs. It is a connection between a

hydraulic cylinder and a landing gear of an aircraft.

Modelled material composition is shown in Figure 3.

Figure 3: Modelled construction detail and the material

composition.

Modelled distribution of potential in the TEL is

shown in Figure 4. Solved structure includes two

different materials – stainless steel nut and washer

and other parts from mild steel. The stainless steel

has higher E

corr

(is electrochemically more noble)

and the potential of TEL above the nut corresponds

to it. Towards the material interface the potential

lowers and above the mild steel parts far from the

material interface, the potential of TEL is the lowest.

As en improvement, visualization of corrosion

rate was added into the programme. Corrosion rate

CR [mpy] (mils per year) is coupled with calculated

current density by equation 4.

KCR





(4)

where K

=327.2 [mm.kg/(A.m.year)] is a

constant including Faraday’s constant and the unit

conversion factor, ρ is the metal density and EW is

equivalent weight, characteristic for each material.

Figure 4: Modelled distribution of potential. Mild steel

parts and stainless steel nut in thin layer of water (100

μm).

Modelled distribution of corrosion rate is shown

in Figure 5. The figure clearly shows that the

electrochemically less noble mild steel corrodes in

the vicinity of the material interface. Distribution of

the corrosion rate is not uniform. The highest

corrosion rate is near the edges of the stainless steel

nut. Material interface between the washer and the

loop of the hydraulic cylinder is not visible in the

figures.

Figure 5: Modelled distribution of CR. Mild steel parts and

stainless steel nut in thin layer of water (100 μm).

Another quantity characterising the intensity of a

corrosion attack is mass loss rate MLR [g/(day.m

)]

satisfying equation 5.

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

464

EWjKMLR



(5)

where K

=0.8953 [g/(A.day)] is a constant including

Faraday’s constant and the unit conversion factor.

6 DISCUSSION

6.1 Assumptions Discussion

The main assumption used in BEASY CM is the

assumption of the thin layer of electrolyte. This

assumption enables to treat the volume of the

electrolyte as a layer characterized only by the value

of its sheet resistance. Currents flowing through the

layer in the longitudinal direction cause the

continuous distribution of the potential. Mutual

interaction between the electrolyte and the material

of investigated structure is controlled by the

polarization behaviour of the material and is

presented in the electrolyte as a source of current

(positive or negative). This current flows in normal

direction to the surface, represents the corrosion

current and is controlled by the local electrolyte

potential and corresponding polarization curve.

Flow of the current in the volume of the

electrolyte is not solved. This assumption brings

mentioned lowering of computational demand, but

has to be taken into account, when a real situation is

studied. Qualified decision has to be made, if it is

possible to model the situation by BEASY CM or

not. Critical in this case are fine details with

different materials covered by relatively thick layer

of electrolyte. This situation is not common in a case

of atmospheric corrosion, because the thickness of

adsorbed moisture is about 10 – 100 μm. Caution is

needed, when a corrosion in thicker layers is

modeled, for example the layer of stagnant water

covering a part of a car chassis.

Polarization curves are used directly during the

calculation as a binding condition between the

potential of the electrolyte and the flowing corrosion

current. BEASY CM does not solve the mechanisms

of polarization. Therefore, the polarization curves

have to be measured under conditions as close as

possible to those prevailing during the exposition to

the corrosive environment. Factors influencing the

resulting shape of polarization curve are

temperature, composition of the electrolyte,

composition of surrounding atmosphere and the

thickness of the electrolyte layer. For the simulation

of galvanic corrosion by BEASY CM it is necessary

to have a database of polarization curves for all

included materials covering broad spectrum of

measuring conditions or to have a possibility to

arbitrarily measure the curves of included materials

for every specific situation which is to be simulated.

6.2 Input Data Discussion

Because there is no comprehensive database of

polarization data for materials in TEL in the

literature, the measuring of polarization curves is an

essential part of using BEASY CM. Because of large

serial resistance of the TEL, the measuring in the

thin layer requires special techniques. Contactless

measurement (Stratmann, 1990) or a special type of

corrosion cell (Liu, 2010) are most frequently

mentioned in the literature. There is a possibility to

measure polarization curves in TEL in Testing

Laboratories of Aerospace Research and Test

Establishment. The technique is under permanent

development and the minimum achievable thickness

is decreasing.

As mentioned above, the layer of the electrolyte

is characterized with its sheet resistance. This value

is given by a conductivity of the electrolyte and the

thickness of the layer. Factors influencing the

conductivity of an electrolyte are temperature and

the composition of the electrolyte.

The main issue during solving a real situation by

BEASY CM is to determine the thickness of the

electrolyte layer, the composition of the electrolyte

and consequently its conductivity and the

appropriate polarization curve.

7 CONCLUSIONS

Philosophy of a programme BEASY CM for

mathematical modelling of galvanic corrosion was

introduced. As a special tool for modelling of

galvanic corrosion in TEL, the programme uses

mathematical simplifications resulting from physical

description of the situation. The programme solves

the galvanic corrosion as a 2D problem. This

simplification must be considered as a limiting

factor, when decision should be made, if the

software can be used for modelling of particular

situation or not.

On the other hand the programme need special,

precisely measured input data. This data are

polarization curves measured in TEL and the

measuring conditions should cover a broad spectrum

of corrosive environments. The other disputable

variables are the thickness of TEL and the electrical

conductivity of the electrolyte. It is advisable to have

a database of the thicknesses and electrolyte

ApplicationofMathematicalModellingforSimulationofGalvanicCorrosion

465

conductivities for typical corrosive environments.

REFERENCES

Liu, W., Cao, F., Chen, A., Chang, L., Zhang, J. and Cao,

C., 2010. Corrosion behaviour of AM60 magnesium

alloys containing Ce or La under thin electrolyte

layers. Part 1: Microstructural characterization and

electrochemical behaviour. Corrosion Science,

February 2010, Vol.52, No.2, pp 627-638

Palani, S., Hack, T., Perrata, A., Adey, R., Baynham, J.

and Lohner, H., 2011. Modeling approach for galvanic

corrosion protection of multimaterial aircraft

structures. BEASY Software and Services.

http://www.beasy.com/news/pdfs/Aircraft_Structure_

Corrosion_DOD_2011.pdf (accessed May 17, 2013)

Stratmann, M. and Streckel, H., 1990. On the atmospheric

corrosion of metals which are covered with thin

electrolyte layers I-III. Corrosion Science, June/July

1990, Vol.30, No.6/7, pp 681-734

Xiao, K., Dong, C. F., Luo, H., Liu, Q., and Li, X. G.,

2012. Investigation on the Electrochemical Behaviour

of Copper Under HSO

-containing Thin Electrolyte

Layers. International Journal of Electrochemical

Science, August 2012, Vol.7, No.8, pp 7503-7515

Yadav, A. P., Katayama, H., Noda, K., Masuda, H.,

Nishikata, A. and Tsuru, T., 2007. Effect of Al on the

galvanic ability of Zn-Al coating under thin layer of

electrolyte. Electrochimica Acta, February 2007,

Vol.52, No.7, pp 2411-2422

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

466