R-Pref: Rapid Prototyping of Database Preference Queries in R

Patrick Roocks and Werner Kießling

Institute of Computer Science, Augsburg University, D-86159 Augsburg, Germany

Keywords:

R, Preferences, Preference SQL, Text Mining.

Abstract:

Preferences are a well-established framework for database queries with soft constraints. Such queries select

the best objects from large data sets according to a strict partial order induced by intuitive and semantically rich

preference constructors. Together with functionality like grouping and aggregation, adapted from well-known

database mechanisms, a very ﬂexible preference framework has emerged in the last decade. In this paper

we present R-Pref, an implementation of the preference framework in the statistical computing language R.

R-Pref comprises less than 1000 lines of code and adheres to the formal foundations of preferences. It allows

rapid prototyping of new preferences and related concepts. Exemplarily we present a use case in which a

simple text mining example based on pattern matching is enriched by preferences. We argue that R-Pref paves

the way for rapidly exploring new ﬁelds of application for preferences. Especially new semantic constructs

for preference related operations together with equivalences of preference terms, being highly important for

optimization, can be quickly evaluated.

1 INTRODUCTION

Preference queries (Kießling, 2002; Chomicki, 2003)

are an established concept in the database community

and have been intensively studied in the last decade.

Preference are an effective method to reduce very

large datasets to a small set of highly interesting re-

sults and to overcome the empty result set and ﬂood-

ing effect. In general, a preference query selects those

objects from the database that are not dominated by

any other object. Therefore, preferences have shifted

retrieval models from exact matching of attribute val-

ues to the notion of best matching database objects.

Preferences are strict partial orders and a set of

intuitive preference constructors allows for the for-

mulation of preference terms. According to (Ste-

fanidis et al., 2011) Preference SQL (Kießling et al.,

2011) is currently the only comprehensive approach

which implements a general preference query model

for databases.

In this paper we present R-Pref (sources and doc-

umentation at (Roocks, 2013)), an interpreter for pref-

erences which is implemented in the statistical com-

puting language R (R Core Team, 2012). We use

newest language concepts like reference classes al-

lowing for OOP style programming in R. The pref-

erence constructors are implemented sticking closely

to their formal deﬁnition.

In R-Pref, new preference constructors can be

very easily implemented and debugged. Because of

this we call R-Pref a rapid prototyping environment

for database preferences and related concepts.

A traditional example for a preference query is to

ﬁnd optimal products according to a consumer pref-

erence. Assume we are looking for cheap hotels close

to the beach. A query searching for “minimal price

and minimal distance to the beach” returns only those

hotels which are not dominated in both criteria by any

other hotel.

To show that R-Pref allows us to explore quite dif-

ferent application ﬁelds, we present a use case where

preferences serve as a preﬁlter for a text mining appli-

cation. We think that the data mining process could

beneﬁt from the introduction of intuitive semantics

by means of preference terms, in addition to estab-

lished data mining techniques. As preferences are not

in the traditional scope of application for such tasks,

we show the ﬂexibility and expandability of our pref-

erence framework and its R implementation.

In our use case we will focus on text mining in

a dataset of e-mails which are an example for semi-

structured data. The mail content is unstructured, but

there is a structured mail header containing sender, re-

ceiver, date and subject. Our idea is to use preferences

primarily on the header columns to select the relevant

mails. Afterwards, we apply simple pattern matching

methods to extract the relevant information from the

content. Of course, it would be also imaginable to

104

Roocks P. and Kießling W..

R-Pref: Rapid Prototyping of Database Preference Queries in R.

DOI: 10.5220/0004590301040111

In Proceedings of the 2nd International Conference on Data Technologies and Applications (DATA-2013), pages 104-111

ISBN: 978-989-8565-67-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

combine more sophisticated data mining techniques

with preferences which is subject to future research.

We presume that the use of preferences as a pre-

ﬁlter leads to improved results as well as to a reduced

parsing expense. We illustrate the principal use of

preferences for searching in a mail dataset in the fol-

lowing example:

Example 1. Consider a dataset of university internal

e-mails from which we want to extract the topics a

scientist is working on by searching his e-mails. As-

sume that the scientist Dr. Leonard Hofstadter usually

sends a monthly report to his boss (Dr. Eric Gable-

hauser).

Therefore we primarily look out for all mails from

Leonard and to Gablehauser. Less important to this,

we pick out those which are entitled with “Monthly

Report”, as this is the usual subject for these reports.

To formulate this query, assume that the mail

dataset of the university is stored in the table mails

and has the columns subject, date, from, to, content.

Consider the following Preference SQL (Kießling

et al., 2011) query:

SELECT m , conten t FROM ma ils PREFERRING

( ` from ` IN ' h o f s t adter @ c a l t e c h . edu'

AND ` to ` IN ' g a b l e h a u ser@c a l t e c h . ed u' )

PRIOR TO

su b j ec t IN (' Mon t hly Re p ort ' )

GROUPING

ex t r ac t ( m on t h f rom dat e ) AS m

By using AND we state that the preferences on the

columns from and to are equally important. Less im-

portant to this prefer mails with a predeﬁned subject.

This wish is stated as the left hand side of PRIOR TO.

Using the GROUPING construct we execute this query

group-wise for every month. Thereby the aliasing

with AS in the grouping-part is a language feature of

Preference SQL (in contrast to standard SQL where

this would be done in the projection).

The query retrieves the following results: For ev-

ery month in which a mail with exactly these at-

tributes exist, only this mail is returned (exact match).

Assume that in one month Leonard sent nothing to

Gablehauser, but he sent his Report to Sheldon (an-

other scientist), and Sheldon sent it to Gablehauser,

both mails entitled with “Monthly Report”. Accord-

ing to the given preference these two mails are re-

turned as best matches. Even if such mails do not

exist, we retrieve all mails which are from Leonard

or to Gablehauser, as the preference on sender/re-

ceiver is stated as a Pareto-Preference (Mails fulﬁlling

one Pareto-condition dominate those fulﬁlling non of

these conditions). This result might give us ﬁnally

some helpful information what they are doing in this

month. In Figure 1 on page 5 this preference order

will be visualized.

The remainder of the paper is structured as fol-

lows: In section 2 we consider the related work re-

garding preferences as well as related R packages.

In section 3 we introduce the speciﬁcation of prefer-

ences tightly together with the implementation of R-

Pref and present some examples. In section 4 we pro-

vide a use case based on information extraction from

mails concerning the organization of a scientiﬁc sym-

posium. In the ﬁnal section we provide a summary

and outlook.

2 RELATED WORK

The theoretical foundation of preference queries is

the preference algebra which was introduced in

(Kießling, 2002). In R-Pref, query statements are de-

noted in a very similar fashion like terms in the pref-

erence algebra. In (Stefanidis et al., 2011) a compre-

hensive survey of representation, composition and ap-

plication of preferences is given.

The R package sqldf (Grothendieck, 2012) allows

a manipulation of dataframes with SQL statements.

Similarly to our approach established database tech-

niques are made available to the R community. Un-

like to our approach, we do not parse SQL statements

but assume that the “queries” are given as nested calls

of functions.

R-Pref makes use of the igraph-package (Csardi

and Nepusz, 2006) to visualize preference orders as

trees. In this package sophisticated algorithms for a

neat drawing of the graphs turned out to be useful for

the visualization of Better-Than-Graphs.

Additionally we use the RJDBC-package (Ur-

banek, 2012) which allows us to evaluate preference

queries in R-Pref directly on any database system sup-

porting JDBC. Due to the package RServe (Urbanek,

2013) R and therewith also R-Pref can be used by any

Java application.

Established text mining methods (cf. (Zhang

et al., 2011)) predominantly make use of statistical

scoring functions like TF-IDF or LSI. In contrast to

this we suggest to think about a non-numerical and

more semantical approach for selecting relevant doc-

uments. Note that we merely consider the text mining

approach as an idea how to combine semantics and

data mining. We do not strive to compete with es-

tablished data mining technologies solely with pref-

erences.

With the package tm (Feinerer et al., 2008) there is

a variety of text mining functions available within R.

R-Pref:RapidPrototypingofDatabasePreferenceQueriesinR

105

3 PREFERENCES AND THEIR

IMPLEMENTATION IN R

In this section we present the theoretical founda-

tions of preferences according to (Kießling, 2002;

Kießling, 2005) tightly together with their implemen-

tation R-Pref. Due to space restrictions we refer to the

documentation and fully available source code on the

web for further details about R-Pref (Roocks, 2013).

The following code samples are restricted to the es-

sential parts while some technical details are omitted.

The code examples show that the R implementation is

very near to the speciﬁcation.

Deﬁnition 1 (Preference). A preference P = (A, <

where A is a set of attributes, is a strict partial order on

the domain of A. Thus <

is irreﬂexive and transitive.

Thereby x <

y is interpreted as “I like y more than x”.

In R-Pref a preference is an object of the reference

class preference having (amongst others) the ﬁelds

col (a character-vector representing A) and a compare

function cmp (representing <

The result of a preference is computed by the pref-

erence selection, also called winnow by (Chomicki,

2003).

Deﬁnition 2 (Preference Selection). The BMO-set of

a preference P = (A, <

) on an input database rela-

tion R contains all tuples that are not dominated w.r.t.

the preference. It is computed by the preference se-

lection operator σ and ﬁnds all best matching tuples t

for P, where t.A is the projection to the attribute set A.

σ[P](R) := {t ∈ R | @t

∈ R : t.A <

.A}

In the following the projection will be mostly

omitted, i.e., we write just t <

for t.A <

.A.

In R-Pref this is performed by the sigma function.

For a preference pref and a dataset tbl the R code

implementing the BMO-set deﬁnition is essentially:

for( i in 1:nrow( t bl ) )

ind [ i ] = !any( p re f$cmp ( tbl , tbl [ i ,]))

res = tbl [ ind ,]

Therein !any corresponds to @ and the call of cmp

represents <

. Of course, this is not an efﬁcient al-

gorithm but shows that the implementation is a close

representation of its formal foundations.

3.1 Base Preference Constructors

To specify a preference, a variety of intuitive base

preference constructors together with some complex

preference constructors has been deﬁned. Subse-

quently, we present some selected preference con-

structors. More preference constructors as well as

their formal deﬁnition can be found in (Kießling,

2002; Kießling, 2005; Kießling et al., 2011).

Deﬁnition 3 (SCORE

Preference). Assume a scoring

function f : dom(A) → R

, and some d ∈ R

. Then P

is called a SCORE

preference, iff for x,y ∈ dom(A):

x <

y ⇐⇒ f

(x) > f

(y)

where f

: dom(A) → R

is deﬁned as:

(v) :=

(

f (v) if d = 0

f (v)

if d > 0

In R-Pref this is realized with the score(column,

scr_fnc, dval) function in a few code lines.

An important sub-constructor of SCORE

is the

BETWEEN

(A, [low, up]) preference expressing the

wish for a value between a lower and an upper bound.

Its scoring function equals

f (v) = max{low − v, 0, v − up}

In R-Pref the implementation is essentially:

between = function( co lumn , low , up , . .. )

score( colu mn , function( va ls )

pmax( low - vals , 0, vals - up ) , .. .)

Thereby “...” bypasses additional arguments like

the d-parameter to score. The R funtion pmax

is the parallel maximum, which returns a vector

of logicals, if val is a vector. Sub-constructors of

BETWEEN are, e.g., the AROUND

(A, z)-preference

and the HIGHEST

(A)-preference. We just consider

their implementation as this is very close to the deﬁ-

nition:

around = function( c ol um n , cen te r , .. .)

between( column , c en te r , cen te r , .. .)

highest = function( co lumn , ... )

around( co lu mn , s u pre m a [[ co lum n ]] , ...)

Thereby suprema is a variable containing the max-

imal values of the given dataset for every numerical

column, determined initially in sigma. Next to the

numerical preferences there are also preferences on

categorical domains, e.g., the LAYERED-preference.

Deﬁnition 4 (LAYERED

Preference). Let L =

, ..., L

) be an ordered list of m sets forming a par-

tition of dom(A) for an attribute A. The preference P

is a LAYERED

(A, (L

, ..., L

)) preference if its scor-

ing function equals

f (v) = i − 1 ⇐⇒ x ∈ L

For convenience, one of the L

may be named

“OTHERS”, representing the set dom(A)\

j6=i

The essential part in the implementation of the

score-function for LAYERED is:

res = rep( Inf , length( val s ))

for( i in 1:length( lay e rs ))

res [ val s %in% l aye rs [[ i ] ]] = i -1

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

106

An important sub-constructor of LAYERED is the

POS(A, POS-set)-preference which is simply imple-

mented by:

pos = function( column , po sse t )

layered( column , list( po ss et , O THE R S ))

This assigns to all values contained in posset the

score 0 and to all other values the score 1.

Quite similar to this, we implemented a

POS MATCHES(A, reg) preference analogous to

the POS-preference, searching for a regular expres-

sion reg that is contained in the domain values of

column A. Thereby we use the built-in R function

regexec to process the regular expression search.

3.2 Complex Preference Constructors

In order to combine several preferences into more

complex preferences, their relative importance has to

be determined. Intuitively, people speak of “this pref-

erence is more important to me than that one” or

“these preferences are all equally important to me”.

Equal importance is modeled by the so-called Pareto

preference while the Prioritization states that one

preference is more important than another preference.

To realize these complex preferences we need a

notion of equality w.r.t. a preference. Therefore the

SV-semantics for preferences (Kießling, 2005) have

been introduced. As we will only cope with sub-

constructors of score preferences in this paper, we

need an equivalence relation w.r.t. a preference P with

scoring function f . We state

∼

y ⇔ f (x) = f (y)

which is also called regular SV-semantics.

Deﬁnition 5. For the Pareto preference P

⊗ P

and the Prioritization preference P

& P

, where

= (A

, <

), we deﬁne for all tuples x = (x

, x

y = (y

, y

) ∈ dom(A

) × dom(A

, x

) <

⊗P

, y

) ⇐⇒

∧ (x

∨ x

∼

)) ∨

∧ (x

∨ x

∼

))

, x

) <

, y

) ⇐⇒

∨ (x

∼

∧ x

)

For the equivalence relation we state for ? ∈ {&, ⊗}:

, x

) <

? P

, y

) ⇐⇒ x

∼

∧ x

∼

In the R implementation preferences are reference

classes and therefore we can overload their operators.

We deﬁned '

.preference' for the pareto composi-

tion and '&.preference' for the prioritization. We

also overloaded the logical operators & and | for func-

tions allowing for a very compact representation of

the prioritization:

"&. p ref e r e nce " = function(p1 , p2 )

preference( c ol = union( p1$col , p2$col ) ,

cmp = p1$cmp | p1$sv & p2$cmp ,

sv = p1$sv & p2$sv )

This code directly corresponds to Deﬁnition 5.

Example 2. We show the R-Pref formulation for the

complex preference used in Example 1:

p =(pos(' fr om' , ' h o fstad t e r @ c a l tech . e du ' )

pos(' to' , ' gabl e h a u s e r @ calte c h . edu' ))

& pos(' su b jec t ' , ' M o n th l y

Re p ort ' )

Note that the R object p is again a reference class of

the type “preference”.

3.3 Grouped Preferences

A preference P = (A, <

) can also be evaluated in

grouped mode. For a set of attributes G and a function

g with domain dom(G) we deﬁne

σ[P grouping g(G)](R) :=

{t ∈ R | ¬∃t

∈ R : t <

∧ g(t.G) = g(t

.G)}

This means the BMO-set is calculated for each value

of g(dom(G)) separately and then the results are

merged. The function g may be the identity but can be

for example the extract(datepart from date) function

if dom(G) is a Time&Date domain.

In R-Pref there is a grouping(tbl, grp, pref,

...) function realizing this functionality. Its essen-

tial code is, where tbl is the dataset, grp is g(G) and

pref is the preference:

do.call( " rbi nd " , lapply(split( tbl , grp ) ,

function(x) sigma(x , pref )))

In the actual implementation there is some technical

overhead (ca. 70 code lines) for preparing the data

structures; but the essential functionality is realized

with this smart composition of built-in R functions.

Example 3. Now we have everything together to en-

code the grouped preference selection from Exam-

ple 1, where p is deﬁned in Example 2:

res = grouping( m ails ,

list(m = extract(' mo nth ' , da te )) , p)

Note that it is sufﬁcient to write “date” in the

grp-attribute (and not e.g., mails$date) because the

grouping function evaluates this attribute in the

scope induced by tbl via the built-in R functions

substitute and eval. Similar techniques are used

like in the R built-in function subset.

The ﬁnal step is the projection to month and con-

tent. In R-Pref the function project(tbl, lst) real-

izes a projection on tbl where lst is a list of expres-

sions to be projected wherein the grouping attribute m

can also be referenced.

R-Pref:RapidPrototypingofDatabasePreferenceQueriesinR

107

Example 4. To get the same columns as in the Pref-

erence SQL query from Example 1 we ﬁnally apply

the projection to the result res from Example 3:

project( res , list(m , con t ent ))

Note that these nested calls of project,

grouping, etc. are quite near to preference relation

algebra as deﬁned in (Kießling, 2002). To deﬁne the

preference p we formally write:

p = (POS(from, ’hof...’) ⊗POS(to, ’gab...’))

& POS(subject, ’Monthly Report’)

Finally the grouped preference selection together with

the projection is performed by:

content, extract(’month’, date)

(

σ[p grouping extract(’month’, date)](mails) )

Despite of a different notation of the function argu-

ments the missing aliasing, this is the same as the R-

Pref commands in Examples 2–4.

Note that according to (Kießling, 2002)

P grouping A for an attribute A can also ex-

pressed as a preference itself. Let P

 P

the logical

and-composition (also intersection preference, in

R-Pref the “|” operator) of P

and P

. Assume that

is the identity on dom(A), then we have

P grouping A = id

 P .

Formally, id

is not a preference but in R-Pref we can

deﬁne an ident(col) function returning a “prefer-

ence” where the cmp ﬁeld represents the identity. For

example, the search for the most recent mail grouped

by mail authors can be performed in R-Pref in the fol-

lowing ways:

grouping( ma ils , list( f ro m ) , highest( dat e ))

sigma( ma ils , ident( fr om ) | highest( d at e ))

Hence also such interesting interplays can be re-

produced in R-Pref.

3.4 Visualization

As R is especially designed for statistical computa-

tions and data visualizations we can use such func-

tionality to analyze characteristics of preferences.

The grouping function offers an additional parame-

ter proj_agg_lst where aggregating projections (sim-

ilar to GROUP BY in SQL) are possible. Due to this

fact it is possible to count the number of best match-

ing mails for every month. Via the R built-in func-

tion hist we get a histogram visualizing the relevant

mails per month. Such methods offer a quick way to

determine the selectivity of preferences on a dataset.

Example 5. Consider the following R code, where p

is from Example 2:

re s2 = grouping( mails ,

list(m = extract(' mo nth ' , da te )) , p ,

pr oj_agg_lst = list( n =length( m )) )

hist( r es 2 [ ,' n' ])

This generates a histogram with an automatically de-

termined bucket size showing how often BMO-sets

with the same cardinality occur.

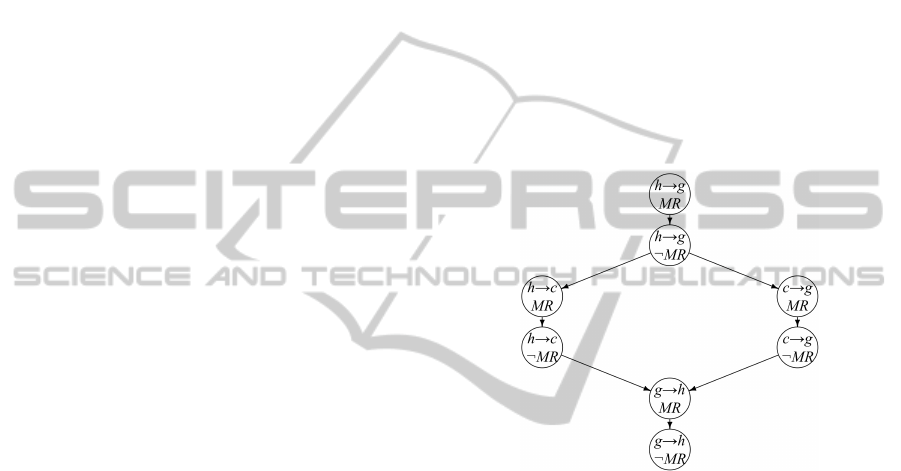
Another interesting visualization of a preference

is its Better-Than-Graph (BTG) which is a Hasse dia-

gram, i.e., the transitive reduction of the preference

order. We use R-Pref do determine the adjacency-

matrix of a given preference and we use the igraph-

package (Csardi and Nepusz, 2006) for R to plot the

graph. In Figure 1 we show an example for a partial

BTG (for some correspondences) based on Example

2 from the introduction, which was created by the vi-

sualization functionality of R-Pref.

Figure 1: BTG for preference p.

In the above ﬁgure h→g stands for mails from Hof-

stadter to Gablehauser, etc. (¬) MR indicates if the

subject of the mail equals “Monthly Report” (or not).

3.5 Other Functions of R-Pref

Up to here we could only sketch a small part of the en-

tire R-Pref functionality; in the actual implementation

(Roocks, 2013) there are more preferences construc-

tors (e.g., EXPLICIT for used-deﬁned orders), more

parameters for the preference selection (e.g., TOP-k

queries) and a plenty of SQL-like projection and ag-

gregation functionality (e.g., complex arithmetic ex-

pressions). Also preferences on spatial domains are

supported. Database joins are also readily available;

the R built-in function merge together with a self-

implemented aliasing mechanism solves this.

Due to the use of the package RJDBC (Urbanek,

2012), R-Pref comes with a direct database connec-

tion. Hence queries can not only processed on csv-

datasets (the “usual” way for importing data in R) but

also directly on any DBMS having a JDBC interface.

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

108

Currently, R-Pref implements the entire current Pref-

erence SQL speciﬁcation, despite of algebraic opti-

mization techniques. They are work under progress as

we will describe further in the outlook in section 5.2.

4 TEXT MINING USE CASE

Assume you organize a symposium and therefore you

get many mails from the participants. Therein they

state their will to attend, or if they are accompanied;

and they announce the titles of their talks. The lat-

ter one is what we are interested in and it is easy to

extract: Mostly the participants will write something

like: “My talk is about: ’...’ ”. Hence we only have

to search for patterns like a colon followed by the title

or for strings in quotation marks.

We took real data from the organization of our in-

ternal chair seminar. Therein 9 of 10 participants used

either a Colon-[Title] or ’[Title]’ schema, hence we

had an easy play with simple pattern matching. But

of course this approach causes many false-positive

matches. In our example we got 9 false-positive

matches (where e.g., people just wrote some words

in quotation marks). It is the task of an appropriate

preference query to ﬁlter out the relevant mails.

As the real dataset contains conﬁdential informa-

tion, we contrived a sample dataset with eight mails

from scientists to the conference organizer. Only four

mails turned out to be relevant, i.e., contain actual

talk titles. The typical problems therein are borrowed

from our real world use case. Because of lack of

space we cannot cite the entire mails here and refer

to (Roocks, 2013) where the dataset (also in a pdf-

version) and the R source ﬁles of this use case are

available.

4.1 Iterative Preference Construction

In the following steps we will iteratively construct ap-

propriate preferences:

Example 6 (First step of use case). Looking at the

matches for talk titles in use case we see – amongst

others – the following results:

wol o wit z | A zero - g r avi t y h uman - wa ste

dis p osa l sy ste m for t he ISS

wol o wit z | Dr . Bern a d e tte R o ste n k o w ski

Obviously the ﬁrst one is his topic while the latter

one is a false positive match. How did this occur?

Looking in the corresponding mail we read:

I fo r got to say I wi ll com e toge t h er w it h :

Dr . Bern a d e tte R oste n k o w ski

In contrast, the mail containing his talk started

with “My topic is: ...”. This leads us to a preference

for mails where “talk” or “topic” occurs in the con-

tent:

p1 = pos_matches(' c ont e nt' , ' ta lk | t op i c' )

But still some mails having ’talk’ or ’topic’ in the

content produce false positive matches.

Example 7 (Second step of use case). We also ﬁnd in

the matches:

co o per | g e nera l l y un d e r sta n d a b l e

co o per | Th e H igg s Bos o n as a bl ack hole

acc e l e r ati n g bac k w ard s th r oug h tim e

Of course the ﬁrst one is not the topic of a talk –

in this mail Sheldon Cooper makes an sarcastic com-

ment on the organizer’s advice that all talks should

be “generally understandable”. Therefore he puts this

phrase in quotation marks. To ﬁlter out false matches

of this kind we stipulate that titles of academic talks

are usually quite long. Because of this we should pre-

fer mails having a string with more than 30 chars in

quotation marks. We put this in a prioritization chain

together with our ﬁrst preference from Example 6.

p2 = p1 &

pos_matches(' c ont e nt' ,' " [ ˆ " ] {30} [ ˆ " ] + " ' )

But what should we do if someone really sends us

two different topics – even if we know he holds only

one talk? Well, it may happen that someone changes

his topic. Consider the following example.

Example 8 (Third step of use case). We also ﬁnd the

following two matches:

hof s t adte r | E x p e rime n t a l ev i den c e s f or

the H ig g s B o so n as a b la c k h ole

hof s t adte r | E x p e rime n t a l ob s e r vat i o n s on

Co o p er s th eor y on Hig gs B o so n s

How could this happen? The latter mail having a later

date starts with the sentence:

Af ter some di s c ussi o n s wit h my co l lea g u e s

I have t o c han ge the tit le of my tal k to :

This means Leonard Hofstadter changes the title

of his talk (because his colleague Sheldon Cooper

does not accept not to be mentioned, as he is the in-

ventor of the theory). How can we catch this? We put

a ﬁnal preference in the prioritization chain: A prefer-

ence taking the newest mail, realized with a HIGHEST

preference on the Date-column:

p3 = p2 & highest(' date ' )

This implies that within all mails being equally

good according to p2, the newest mail is preferred,

which allows the authors to revise their titles.

R-Pref:RapidPrototypingofDatabasePreferenceQueriesinR

109

4.2 Preference Evaluation

So we are nearly done, but we still have not evaluated

the preference. As every sender holds a talk we have

to search for the best matches in every sender-group,

i.e., we have to use a grouped preference where the

from column is the grouping attribute.

Example 9 (Final step of use case). The full prefer-

ence selection for the use case is:

res = grouping( m ails , list( f rom ) , p3 )

But note that preferences are just soft constraints. If a

mail like “I will not attend the symposium” is in the

mails dataset it will also occur in res. This is no prob-

lem for the ﬁnal result as there is no title-pattern in

such a mail. As we aim to ﬁlter out as much as possi-

ble “senseless” information we can enrich the prefer-

ence by a hard selection, requiring that “talk | topic”

has to occur in the content.

subset( res ,matches( co nt en t ,' t alk | top ic' ))

Finally applying the pattern-matching extraction

methods to the remaining four mails of the dataset

gives us exactly four (correct) titles of the talks.

Hence we could construct an optimal preﬁlter for our

sample dataset, just by some base preferences, a prior-

itization chain and ﬁnally the grouping-construct for

preferences.

5 CONCLUSIONS

Having sketched the R-Pref system and the text min-

ing use case we will now sum up the achievements of

R-Pref and conclude with our ideas for future research

in prototyping preferences and related concepts.

5.1 Summary

For the presented use case we implemented new

preferences like POS MATCHES supporting pattern

matching in R. This was quite easy as we could build

on the R functionality for regular expressions and the

R-Pref framework. Together with a user-friendly R-

IDE (we used “RStudio”) R-Pref turns out to be a

comfortable rapid-prototyping environment allowing

to experiment with different preferences and related

approaches. New constructors can be implemented in

a few minutes and in few lines of code. The easily ap-

plicable internal visualization functionality of R (his-

tograms, bar plots, etc.) and external packages like

igraph can be used to visualize the results and charac-

teristics of preferences. Additionally preferences and

statistical approaches can be compared as R is espe-

cially designed for statistic calculations.

Even with R being originally designed for statis-

tical applications, nowadays its application scope is

much more widespread to due a plenty of packages

for e.g., databases or data mining. New developments

like reference classes together with operator overload-

ing offer the possibility for an extremely concise cod-

ing, which we use for the composition of preferences

in an algebraic style. Due to all these considerations,

it was the logical consequence to make our compre-

hensive preference framework available for R.

In analogy to the algebraic optimization rules of

Preference SQL like “Push preference over join” one

can see our text mining use case under the paradigm

“Push preference into code”. Therein “code” rep-

resents the common text mining techniques as e.g.,

clustering, summarizing or ﬁnding associations. For

future research, established concepts for exploring

semi-structured data can be combined with the

approach of preferences.

5.2 Outlook

The development of R-Pref just started in November

2012 and this project is still in the beginning. Al-

though we are supporting a comprehensive preference

framework, there is still a lot of work to do.

In one part of our project we are developing an

R-based automatic correctness test application for

the Preference SQL system (Kießling et al., 2011).

Therein datasets and queries are randomly generated

and executed on both systems, R-Pref and Preference

SQL. Afterwards the results are compared and differ-

ences are returned as potential errors. Of course, such

an approach just offers “probable correctness” but it is

highly improbable that both implementations have ex-

actly the same errors. The speciﬁcation-near coding

style of R-Pref together with a sufﬁcient large search

space (of queries and datasets) gives a strong hint for

correctness in general.

In (Hafenrichter and Kießling, 2005) sophisti-

cated optimization techniques like “Push preference

over join” are introduced. In the context of R these

can be considered as transformations on expressions.

Syntactically, due to expression([query]) R offers

a neat semantic layer to manipulate function calls be-

fore evaluating. Because R-Pref queries are near to

the relational algebraic representation it seams rea-

sonable to study different optimization techniques

based on transformations of R expressions. We are

working on an optimizer in a “formal style” just con-

sisting of a set of algebraic optimization rules and

their preconditions. Therein the optimization rules

should not be subjected to an error-prone application-

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

110

speciﬁc parsing process, but highly beneﬁt from the

general semantic structure of expressions and refer-

ences classes in R.

Regarding the text mining use case, at the cur-

rent stage of development this project cannot com-

pete with established data mining techniques. But we

think that the data mining process will beneﬁt from

the semantical structure of preferences and the best

matches only query model in many aspects. Most data

mining algorithms are based on many weighting fac-

tors, which have little intuitive meaning to the data

analyst. In contrast, preferences terms are quite intu-

itively understandable and therefore we think the ﬁeld

of semantics in query languages is an interesting re-

search ﬁeld for decision support, data mining, etc.;

a ﬁeld where the statistical computing language R is

very popular. A close connection of preferences and

established algorithms in this area might lead to sub-

stantial new results.

In a nutshell, our vision is to use R-Pref as an

experimental incubator for rapidly exploring new re-

search ideas. Ideas found promising will then be

implemented efﬁciently in our main Preference SQL

system.

ACKNOWLEDGEMENTS

This work has been funded by the Bavarian Ministry

of Economic Affairs, Infrastructure, Transport and

Technology, grant no. IUK-1109-0003//IUK398/002.

REFERENCES

Chomicki, J. (2003). Preference Formulas in Relational

Queries. In TODS ’03: ACM Transactions on

Database Systems, volume 28, pages 427–466, New

York, NY, USA. ACM Press.

Csardi, G. and Nepusz, T. (2006). The igraph software

package for complex network research. InterJournal,

Complex Systems:1695.

Feinerer, I., Hornik, K., and Meyer, D. (2008). Text Mining

Infrastructure in R. Journal of Statistical Software,

25(5):1–54.

Grothendieck, G. (2012). sqldf: Perform SQL Selects on R

Data Frames. R package version 0.4-6.4.

Hafenrichter, B. and Kießling, W. (2005). Optimization

of Relational Preference Queries. In Proceedings of

the 16th Australasian database conference - Volume

39, ADC ’05, pages 175–184, Darlinghurst, Australia,

Australia. Australian Computer Society, Inc.

Kießling, W. (2002). Foundations of Preferences in

Database Systems. In VLDB ’02: Proceedings of

the 28th International Conference on Very Large Data

Bases, pages 311–322, Hong Kong, China. VLDB.

Kießling, W. (2005). Preference Queries with SV-

Semantics. In Haritsa, J. R. and Vijayaraman, T. M.,

editors, COMAD ’05: Advances in Data Management

2005, Proceedings of the 11th International Confer-

ence on Management of Data, pages 15–26, Goa, In-

dia. Computer Society of India.

Kießling, W., Endres, M., and Wenzel, F. (2011). The

Preference SQL System - An Overview. Bulletin of

the Technical Commitee on Data Engineering, IEEE

Computer Society, 34(2):11–18.

R Core Team (2012). R: A Language and Environment for

Statistical Computing. R Foundation for Statistical

Computing, Vienna, Austria. ISBN 3-900051-07-0.

Roocks, P. (2013). R-Pref Documentation, Sources and

use case http://ursaminor.informatik.uni-augsburg.de/

trac/wiki/R-Pref.

Stefanidis, K., Koutrika, G., and Pitoura, E. (2011). A Sur-

vey on Representation, Composition and Application

of Preferences in Database Systems. ACM Transac-

tion on Database Systems, 36(4).

Urbanek, S. (2012). RJDBC: Provides access to databases

through the JDBC interface. R package version 0.2-1.

Urbanek, S. (2013). Rserve: Binary R server. R package

version 0.6-8.1.

Zhang, W., Yoshida, T., and Tang, X. (2011). A com-

parative study of TF*IDF, LSI and multi-words for

text classiﬁcation. Expert Systems with Applications,

38(3):2758 – 2765.

R-Pref:RapidPrototypingofDatabasePreferenceQueriesinR

111