
Exploring the Potential of Combining Time of Flight and Thermal
Infrared Cameras for Person Detection
Wim Abbeloos and Toon Goedem´e
EAVISE, Campus De Nayer, ESAT/PSI-VISICS, KU Leuven, Kasteelpark Arenberg 10, Heverlee, Belgium
Keywords:
Time of Flight, Range Image, 2.5D, Thermal Infrared, Thermopile Array, Calibration, Camera, Sensor, Data
Fusion, Measurement Errors, Scattering, Multi-path Interference.
Abstract:
Combining new, low-cost thermal infrared and time-of-flight range sensors provides new opportunities. In
this position paper we explore the possibilities of combining these sensors and using their fused data for
person detection. The proposed calibration approach for this sensor combination differs from the traditional
stereo camera calibration in two fundamental ways. A first distinction is that the spectral sensitivity of the two
sensors differs significantly. In fact, there is no sensitivity range overlap at all. A second distinction is that their
resolution is typically very low, which requires special attention. We assume a situation in which the sensors’
relative position is known, but their orientation is unknown. In addition, some of the typical measurement
errors are discussed, and methods to compensate for them are proposed. We discuss how the fused data could
allow increased accuracy and robustness without the need for complex algorithms requiring large amounts of
computational power and training data.
1 INTRODUCTION
Cameras have been used to record and monitor peo-
ple’s activities in a great variety of situations. They
provide an easy, affordable and intuitive way to ob-
serve our surroundings. The automatic detection of
people has important applications in the areas of ma-
chine safety, human-computer interaction, security,
traffic analysis, driver assistance, health-care, etc.
Detecting people in images, however, turns out
to be a surprisingly difficult task. The major prob-
lem when detecting people is the immense variance
in their appearance. Let’s just consider a few causes:
· Intra-class variety: all people are unique. We
all have different body proportions, wear different
clothes and move in a different way.
· The illumination conditions are often uncon-
trolled. They may be completely unknown, or
vary in time.
· A person’s appearance strongly depends on the
point of view.
· When using a regular camera, dimensional infor-
mation is lost by projection. The size of a person
in the image depends on its distance to the camera.
· Articulateness: the human body is highly flexible.
Especially the limbs can take a large variety of
poses.
· Often a person is only partially visible. For exam-
ple, when entering or leaving the cameras’ field of
view, or when occluded by other objects.
Despite these issues, some very powerful computer
vision algorithms for the detection of people from
normal camera images exist. A lot of progress has
recently been made in the detection of pedestrians
(Doll´ar et al., 2011)(Enzweiler and Gavrila, 2009).
Many of these algorithms use a Histogram of Oriented
Gradients-based detector, combined with a part based
model. While the performance of these algorithms
continues to improve, they require a lot of computa-
tional power and a very large annotated dataset for the
training stage. They also rely on some situation spe-
cific assumptions (e.g. only people with an approxi-
mately vertical pose are detected).
An alternative approach, which avoids many of
these issues, is not to detect people specifically, but to
detect any moving object. Especially in applications
with a static camera, this can be done very easily and
efficiently by applying background subtraction algo-
rithms. Methods such as approximatemedian filtering
(McFarlane and Schofield, 1995) and shadow detec-
tion (Rosin and Ellis, 1995) can be used to increase
464
Abbeloos W. and Goedemé T..
Exploring the Potential of Combining Time of Flight and Thermal Infrared Cameras for Person Detection.
DOI: 10.5220/0004595704640470
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 464-470
ISBN: 978-989-8565-71-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
TOF
x
y
z
IR
z
x
y
R,T
Figure 1: Relative pose of the TOF and IR camera. The
translation (T) is known, but the rotation (R) is unknown
and must be determined during the calibration step.
the robustness to varying light conditions.
This approach has been used as a preprocessing
step for pedestrian detection algorithms in order to
segment the image, reducing the search space and
thus the required processing time (Liang et al., 2012).
We explore a similar approach, but instead of
measuring the amount of reflected light from an ob-
ject, as is observed with a normal camera, we pro-
pose a sensor measuring thermal radiation and range.
Measuring these physical properties directly provides
far more informative data, being the temperature of
an object and its geometrical measures, respectively
(Gandhi and Trivedi, 2007). We anticipate that fused
Time-of-Flight (TOF) range measurements and ther-
mal infrared (IR) data will allow significant improve-
ments in three key areas:
1. Accurate and fast segmentation of moving ob-
jects.
2. Reduced complexity of people detection algo-
rithms.
3. Reduction of the required amount of training data.
The following sections provide more details on these
sensors. A prototype combining a TOF and IR camera
is currently being developed. The relative translation
of these sensors is known sufficiently accurately, but
their relative rotation is not (figure 1). To fuse their
data and obtain a 3D thermogram we propose calibra-
tion routine, described in sections 4 and 5. Prelimi-
nary experiments (section 6) show great potential, but
also reveal some challenges. These are discussed in
the future work, followed by our conclusions.
2 TIME-OF-FLIGHT CAMERA
A Time-of-Flight range camera is equipped with a
near infrared light source (with a wavelength of about
850nm) that is modulated with a frequency of about
21 MHz (figure 2). The reflected light is collected
onto a sensor capable of measuring the signal’s phase
(ϕ), amplitude (a) and offset (b) (figure 3, equations 1-
4). These are not measured directly, but can be deter-
mined using the four intensity measurements (A
1
-A
4
).
Figure 2: Time-of-Flight camera principle.
Figure 3: The reflected signal received by the TOF camera
is sampled four times. This allows to determine the signals
phase shift ϕ.
ϕ = arctan(
A
1
− A
3
A
2
− A
4
) + k · 2π (1)
D =
c
4π · f
mod
· ϕ (2)
with c the speed of light in air and f
mod
the modu-
lation frequency.
a =
p
(A
1
− A
3
)
2
+ (A
2
− A
4
)
2
2
(3)
b =
A
1
+ A
2
+ A
3
+ A
4
4
(4)
From the phase difference between the emitted and
received signal, the total distance the light traveled is
determined. By dividing the total distance by two we
obtain the object-camera distance (D).
x
y
D
d
z
P(0,0,0)
P(X,Y,Z)
p (u,v)
p(0,0)
f
Figure 4: TOF camera pinhole model illustrating the projec-
tion of a point P(X,Y,Z) onto the TOF sensor: p(u,v). The
two highlighted triangles are of similar shape, hence the ra-
tio of any two of their equivalent sides is equal. This means
that the known length d and the measured distance D suffice
to determine the 3D coordinates of any point p(u, v).
ExploringthePotentialofCombiningTimeofFlightandThermalInfraredCamerasforPersonDetection
465

If the TOF camera’s focal length (f) is known
we can calculate the 3D coordinates for every point.
These equations are easily deduced from figure 4.
d =
p
f
2
+ u
2
+ v
2
(5)
X
Y
Z
i
=
D
i
d
u
v
f
(6)
If radial distortion is present, this can be compen-
sated by converting the distorted values (index d) to
the undistorted values (index u).
r
u,i
= r
d,i
+ k
1
r
3
d,i
+ k
2
r
5
d,i
(7)
with
r
d,i
=
q
u
2
i
+ v
2
i
(8)
We change the (u,v) coordinates accordingly:
u
v
u,i
=
r
u,i
r
d,i
u
v
d,i
(9)
3 THERMAL INFRARED
CAMERA
All objects emit a certain amount of black body radi-
ation as a function of their temperature. The higher
an object’s temperature, the more infrared radiation
is emitted. A thermal infrared camera consist of an
array of elements that measure this radiation. They
are typically sensitive in the far infrared range, at
wavelengths of about 5-15µm. Silicon or germanium
lenses must be used, as glass does not transmit these
wavelengths.
Several types of IR sensor exist. In general, a dis-
tinction can be made between cooled and uncooled
infrared detectors. We only consider the uncooled va-
riety as they are cheaper and more compact. In our
experiments we use both the thermopile array and mi-
crobolometer type of detector.
In a thermopile array the heat radiated from an ob-
ject is absorbed by a small membrane. The tempera-
ture difference between the membrane and a thermal
mass causes a difference in electric potential. This
is known as the Seebeck effect. This voltage can be
converted to an absolute temperature measurement.
A microbolometer is a very similar device but in-
stead of relying on the Seebeck effect, it uses the tem-
perature coefficient of resistance.
Both sensors are able to simultaneously measure
a number of absolute temperatures, often visualized
dK&;Ƶ͕ǀ͕Ϳ
;y
dK&
͕z
dK&
͕
dK&
Ϳ
;Ĩ͕Ŭ
ϭ
͕Ŭ
Ϯ
Ϳ
dK&
/Z;ƌ͕ƐͿ
;Z͕dͿ
dK&Ͳ/Z
Ĩ
/Z
ϯƚŚĞƌŵŽŐƌĂŵ
;y
dK&
͕z
dK&
͕
dK&
͕d
/Z
Ϳ
;y
/Z
͕z
/Z
͕
/Z
Ϳ
Figure 5: In the data fusion process the range measurements
are projected onto the IR sensor to obtain a 3D thermogram.
as a false color image. While the microbolometer
technology is more mature, the thermopile array is
cheaper and smaller. Although very limited at the mo-
ment (4x16px), an increase in resolution is expected
which will soon make them an interesting alternative.
4 DATA FUSION
To obtain the 3D thermogram we wish to use to de-
tect people, the TOF and IR data must be fused. A
method to fuse TOF range data with images from a
regular camera is proposed in (Hanning et al., 2011).
Their method relies on the cameras being perfectly
parallel, a condition that is not met by our sensor. The
accuracy of the calibration also relies on the accuracy
of the range measurements, which is typically quite
low.
We propose a new data fusion algorithm en-
abling us to assign a temperature measurement to ev-
ery range measurement. Figure 5 gives a graphical
overview.
If the focal length of the TOF camera is known,
every pixels’ 3D coordinates can be calculated using
their distance measurement (equation 6). To obtain
their 3D position in the IR camera reference frame we
simply apply a translation and rotation to the 3D point
cloud (equation 10). Projecting these points onto the
calibrated IR sensor (equation 11) yields their posi-
tion on the IR sensor from which we can obtain each
3D point’s temperature measurement by bilinear in-
terpolating between its four nearest neighbors (Figure
6, equation 12).
X
Y
Z
IR
=
R | T
X
Y
Z
1
TOF
(10)
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
466

dž
LJ
d;Ϭ͕ϬͿ
d;ϭ͕ϬͿ
d;ϭ͕ϭͿd;Ϭ͕ϭͿ
d;dž͕LJͿ
Figure 6: The point (x,y) is the projection of a point (X,Y,Z)
onto the IR sensor. The four other points represent the cen-
ter of the four nearest pixels. We use bilinear interpolation
to determine the temperature T(x,y).
Z
r
s
1
=
f
IR
0 0
0 f
IR
0
0 0 1
X
Y
Z
IR
(11)
T(x, y) =
1− x x
T(0, 0) T(0, 1)
T(1, 0) T(1, 1)
1− y
y
(12)
Other interpolation methods may be investigated later
on.
5 CALIBRATION
Various methods to calibrate the intrinsic parameters
of both TOF and IR cameras exist. A very popular
method uses a simple planar target with a checker-
board pattern (Zhang, 1999). For regular cameras,
these calibration images also allow to determine their
relative pose. The problem in our case is that the two
sensors do not share a common spectral sensitivity
range and that both measure fundamentally different
object properties.
A first part of the solution is to use the TOF
cameras intensity measurements instead of the phase.
This eliminates the need for a complex three dimen-
sional calibration target and problems with measure-
ment errors in the range data.
The second part of the solution is to use a calibra-
tion target that shows contrast in a very wide spectral
range. In the literature, a number of different solu-
tions have been proposed. In (Yang et al., 2011) small
light bulbs that emit light within the sensitivity range
of the regular camera are used, the heat they gener-
ate can be measured by the IR camera (figure 7a) .
A more traditional ’checkerboard’ calibration target
(figure 7b) is used in (Vidas et al., 2012). By illumi-
nating the pattern with a powerful lamp, the black re-
gions will warm more quickly than the white regions
because of the difference in absorption. However, the
Figure 7: IR camera calibration targets suggested in litera-
ture.
temperature will soon even out and the contrast re-
quired to locate the corner points in the IR image ac-
curately will quickly fade. As a solution, they pro-
pose to use a mask with with regularly spaced holes
(figure 7c). The mask is made of a material with con-
trasting colors to the background. As a background,
either a hotter or colder object is used, providing the
required contrast in the IR image. As both materials
can be thermally insulated (e.g. by air), this approach
doesn’t suffer from the fading as much. The mask
however must be designed very carefully. The inside
edges must be made ’infinitely’ thin so that the ’back
edge’ does not interfere with the measurement when
the mask is viewed at an angle. Also, the mask must
be sufficiently rigid to assure it remains perfectly pla-
nar.
A method to calibrate a structured light and IR
camera system is proposed in (Yang and Chen, 2011).
Their method requires higher resolutions sensors and
a large amount of calibration measurements, as they
estimate a large number of parameters in a single op-
timization procedure.
In a first step the calibration of the intrinsic camera
parameters of the TOF and IR cameras is performed.
This is followed by the calibration of the relative pose
of the two cameras. As mentioned before, the 3D
translation between the two cameras is assumed to be
known. This is a reasonable assumption as we can
measure their position sufficiently accurately on the
printed circuit board they are mounted on. Also, a
small error in the translation parameters will result in
a small error in the pixel mapping.
ExploringthePotentialofCombiningTimeofFlightandThermalInfraredCamerasforPersonDetection
467
The only parameters that remain to be estimated
are the relative orientation of the two cameras. To
do this we measure objects at a known distance (this
avoids relying on the distance measurement precision
of the TOF camera) using the TOF camera. As we al-
ready performed the intrinsic calibration, the object’s
image and its distance allow us to calculate its 3D
position in the world ordinate system. An initial es-
timate of the rotation and the known translation are
used to calculate the points’ position in the IR camera
ordinate system. The projected point will not coincide
perfectly with the actual measurement point in the IR
image. This projection error is minimized in order to
find the optimal rotation matrix R. As the error func-
tion we use the euclidean distance between the virtual,
projected point, and the real measurement.
E
i
= |P
m,i
(u
i
, v
i
, D
i
) − P
p,i
(u
i
, v
i
, D
i
, R)| (13)
R = argmin(
∑
i
E
i
) (14)
To find the object’s position in the TOF and IR im-
ages, we may simply pick the pixel with the highest
intensity, or highest temperature respectively. Due to
the low resolution this would result in a significant er-
ror. In order to achieve sub-pixel precision, we can
fit a function to the local neighborhood of this pixel,
and determine the position corresponding to the max-
imum of this function.
6 PRELIMINARY EXPERIMENTS
The experiments are performed with an IFM O3D201
TOF camera with a resolution of 64x50 pixels and at
a modulation frequency of 21MHz. The thermal cam-
era used is the Flir E40bx microbolometer, which has
a resolution of 160x120 pixels.
In a first experiment the TOF camera was fixed to
the ceiling of a room and recorded a sequence of im-
ages. A set of 1000 consecutive frames without mov-
ing objects was averaged and used as ’background’
(figure 8a). The background was subtracted from the
another frame (figure 8c) in an attempt to segment
moving objects (figure 8e,f).
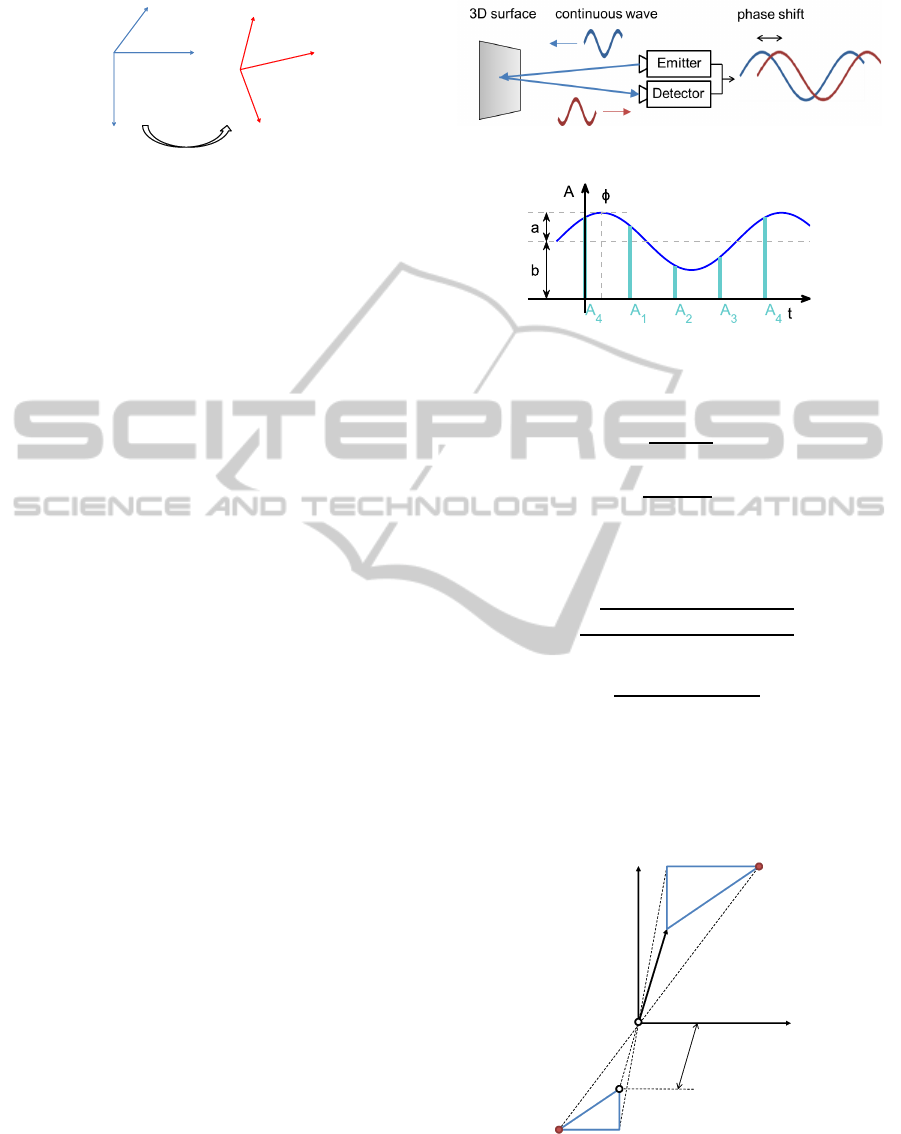
As can be seen in figure 8f, our measurements are
subject to noise. The noise on the phase measurement,
results in a distance error. The standard deviation per
pixel in the 1000 background frames is shown in fig-
ure 9, next to the histogram of the range measurement
of the highlighted pixel. The average error is typi-
cally about one percent, which is acceptable for many
applications. The noise level depends on a variety of
Figure 8: a) Average distance (background). b) Average
intensity. c) Single distance image. d) Single intensity im-
age. e) Background subtracted, absolute difference of a and
c. f) Background subtracted, with rescaled range. The data
contain some outliers due to over or underexposure.
Figure 9: Left: Standard deviation (in meters) of range mea-
surements. Right: Histogram showing the distribution of
the measured distances of the highlighted pixel.
properties such as illumination power, object reflec-
tivity, surface orientation, distance, etc. In general
the error can be modeled (e.g. using gaussian mix-
ture models) quite well. This allows the probability a
pixel belongs to the background or foreground to be
calculated.
However, if we carefully compare the image with
subtracted background (figure 8f) to the standard de-
viations in figure 9, we see that some of the abso-
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
468
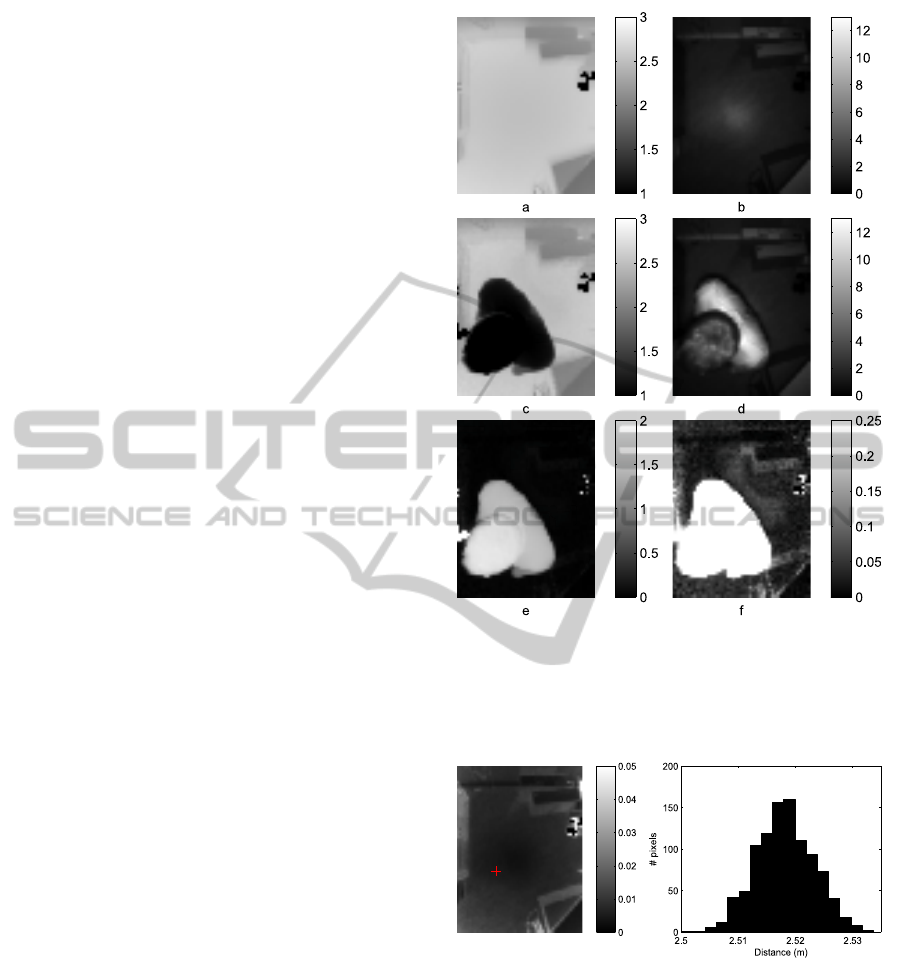
Figure 10: The direct reflection off the wall (blue, solid line)
provides the correct range measurement D. This measure-
ment, however, will be corrupted by other signals (e.g. the
red, dotted line), which will have a larger phase shift as they
have traveled a longer distance. This is known as the multi-
path interference error.
lens sensor
Figure 11: The scattering effect of a ray of light in a TOF
camera. The incoming ray is not completely absorbed by
the pixel but partially scattered. Part of the scattered en-
ergy reflects on the lens surface and back onto the sensor,
disturbing the measurements.
lute differences on the background are substantially
greater than the expected noise. These errors are due
to multi-path interference (figure 10) and scattering
(figure 11).
7 FUTURE WORK
While the current hardware setup has a small field of
view, a prototype with a larger field of view is be-
ing developed. This will allow to monitor a reason-
ably large volume. The calibration routine also al-
lows to fuse data from multiple sensors to extend it
even more.
We intend to integrate the calibration of the intrin-
sic and extrinsic parameters of the combined sensor
into one automatic procedure. To determine the point
spread functions for both the IR and TOF cameras,
a system allowing to systematically repositioning the
calibration target using a robot will be set up. The
generated data will provide a better understanding of
the multi-path interference and scattering errors ob-
served in our experiments. Error compensation meth-
ods such as (Karel et al., 2012) (Mure-Dubois and
H¨ugli, 2007) allow to improve the reliability in seg-
menting moving objects and will increase correspon-
dence accuracy between the IR and range data.
A set of fused range and IR data will be generated
and used to train people detection algorithms. The
three main hypotheses mentioned in the introduction
will be thoroughly tested. Applying 3D tracking al-
gorithms will increase the robustness and enable the
system to cope with occlusion.
8 CONCLUSIONS
A combined sensor for the detection of people us-
ing fused geometric and infrared radiation data was
introduced. We explained the working principles of
both sensors and illustrated and addressed some im-
portant accuracy issues that arose during experiments.
A method to calibrate a system with known relative
position and unknown relative orientation was pro-
posed. Three key areas in people detection that could
benefit greatly from the fused IR and range data were
determined and will be investigated in future work.
ACKNOWLEDGEMENTS
We thank ICRealisations for their input and for pro-
viding a prototype system for experimental work, and
Xenics for providing a thermal infrared camera for
verification purposes.
REFERENCES
Doll´ar, P., Wojek, C., Schiele, B., and Perona, P. (2011).
Pedestrian detection: An evaluation of the state of the
art. PAMI, 99.
Enzweiler, M. and Gavrila, D. M. (2009). Monocular pedes-
trian detection: Survey and experiments. TPAMI,
31(12):2179–2195.
Gandhi, T. and Trivedi, M. (2007). Pedestrian protec-
tion systems: Issues, survey, and challenges. Intel-
ligent Transportation Systems, IEEE Transactions on,
8(3):413–430.
Hanning, T., Lasaruk, A., and Tatschke, T. (2011). Calibra-
tion and low-level data fusion algorithms for a parallel
2d/3d-camera. Information Fusion, 12(1):37 – 47.
Karel, W., Ghuffar, S., and Pfeifer, N. (2012). Modelling
and compensating internal light scattering in time of
flight range cameras. The Photogrammetric Record,
27(138):155–174.
Liang, F., Wang, D., Liu, Y., Jiang, Y., and Tang, S. (2012).
Fast pedestrian detection based on sliding window fil-
tering. In Proc. PCM 2012, pages 811–822, Berlin,
Heidelberg. Springer-Verlag.
McFarlane, N. and Schofield, C. (1995). Segmentation and
tracking of piglets in images. Machine Vision and Ap-
plications, 8(3):187–193.
Mure-Dubois, J. and H¨ugli, H. (2007). Real-time scattering
compensation for time-of-flight camera. Proceedings
ExploringthePotentialofCombiningTimeofFlightandThermalInfraredCamerasforPersonDetection
469

of the ICVS Workshop on Camera Calibration Meth-
ods for Computer Vision Systems.
Rosin, P. and Ellis, T. (1995). Image difference thresh-
old strategies and shadow detection. In Proc. BMVC,
pages 347–356. BMVA Press.
Vidas, S., Lakemond, R., Denman, S., Fookes, C., Sridha-
ran, S., and Wark, T. (2012). A mask-based approach
for the geometric calibration of thermal-infrared cam-
eras. Instrumentation and Measurement, IEEE Trans-
actions on, 61(6):1625–1635.
Yang, R. and Chen, Y. (2011). Design of a 3-d in-
frared imaging system using structured light. Instru-
mentation and Measurement, IEEE Transactions on,
60(2):608–617.
Yang, R., Yang, W., Chen, Y., and Wu, X. (2011). Ge-
ometric calibration of ir camera using trinocular vi-
sion. Lightwave Technology, Journal of, 29(24):3797–
3803.
Zhang, Z. (1999). Flexible camera calibration by viewing
a plane from unknown orientations. In Proc. ICCV,
volume 1, pages 666–673 vol.1.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
470
