Exploratory Modeling of Complex Information Processing Systems

Jochen Kerdels and Gabriele Peters

Chair of Human-Computer Interaction, University of Hagen, Universit¨atsstrasse 1, D-58097 Hagen, Germany

Keywords:

Exploratory Modeling, Modeling of Complex Systems, Emergence, Self Organization.

Abstract:

A widely adopted approach to study and understand complex systems such as ant colonies or economic sys-

tems consists in their modeling and simulation. In contrast to the predominat use of models and simulation

in science as a substitute for the real system in order to predict the system’s beaviour, the methodology of

exploratory modeling uses modeling and simulation as a tool to increase knowledge and understanding of the

systems themselves, for example to better understand the dynamic properties of a system. In this paper we

propose a model which was speciﬁcally devised to support this process of exploratory modeling. The model

deﬁnes four lightweight building blocks such as information processing entities that can be freely combined

to model a particular complex system. Furthermore, the model provides an explicit state representation that

comprises the entire model including an explicit representation of the information that is individually available

to every information processing entity of the model. We illustrate our introduction of the proposed model by

means of short examples of a concrete system for the simulation of motions in a ﬂock of birds.

1 INTRODUCTION

A widely adopted approach to study and understand

complex systems consists in their modeling and sim-

ulation. Typical examples of systems that are being

investigated in that way include ant colonies, eco-

nomic systems, nervous systems or biological evo-

lution (Newman, 2011). Yet, much simpler systems

based on only a small set of ﬁxed rules like board

games or cellular automata are also analyzed in this

context (Evans, 2001; Holland, 1998; Gardner, 1970).

In contrast to the predominat use of models and

simulation as a means to make valid predictions about

the system that is being modeled, the analysis of the

systems themselves typically uses the methodology

of exploratory modeling (Bankes, 1993). Exploratory

modeling is an iterative process which uses modeling

and simulation as a means to test assumptions, to un-

cover unexpected implications of existing knowledge

and to act as a form of intuition pump (Dennett, 1998).

At the center of this approach lies the concept,

that a system is not represented by a single speciﬁc

model but rather by a model space which is con-

strained by what is known aboutthe system and which

is expanded by what is uncertain. This model space

is then explored by conducting series of simulations

with varying model instances drawn from the space

of possible models. These computational experiments

can support the analysis of complex systems in differ-

ent ways. For example:

• Exploration of Parameters The inﬂuence of model

parameters on the dynamic behaviour of a com-

plex system can be estimated by identifying the

parameter ranges that are essential for a stable op-

eration of the system or, conversely, by identify-

ing those parameter ranges under which the sys-

tem breaks down.

• Identiﬁcation of common Patterns. Simulation of

a wide range of complex systems facilitates the

identiﬁcation of common patterns that underlie

phenomena of self-organization and emergence.

These common patterns are the prerequisite for

a more general understanding of the dynamic be-

haviour of complex systems (Holland, 1998).

• Existence Proofs. Modeling of hypothetical, high

level mechanisms or structures that are based on

known basic mechanisms of a system can provide

proof of concept explanations for observed phe-

nomena that are associated with that system.

The methodology of exploratory modeling is not

bound to a speciﬁc form of modeling or simulation.

The types of models used range from simple sets of

mathematical equations (Lempert et al., 1996) to cel-

lular automata (Langton, 1986) or agent-based mod-

514

Kerdels J. and Peters G..

Exploratory Modeling of Complex Information Processing Systems.

DOI: 10.5220/0004598205140521

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 514-521

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

els

(DeAngelis and Mooij, 2005). The choice of a

particular model type is commonly guided by the sim-

ilarity between characteristics of the system and the

model. For example, agent-based models are widely

used in social sciences (Salamon, 2011) and eco-

nomics (Bonabeau, 2002) as the concept of an agent

readily translates into entities of the respective sys-

tems like market participants, employers or friends.

This direct mapping of system entities onto model

entities facilitates an intuitive way of describing a sys-

tem. However, this intuitive approach also empha-

sizes two detrimental tendencies in the resulting mod-

els:

• There is a tendency to focus on modeling the en-

tities of a system rather than a focus on modeling

the interactions occuring in that system.

• There is a tendency to incorporate only a small

number of temporal and spatial scales which

leads to either oversimpliﬁed entities or to entities

which are complex systems by themselves. Some

model types, for example the swarm model (Mi-

nar et al., 1996), mitigate this tendency by allow-

ing nested structures.

Especially in the case of complexsystems that employ

a substantial variety of signaling mechanisms across

several spatial and temporal scales, e.g. neuronal pro-

cesses, these two tendencies can lead to a model that

does not represent the particular system well and thus

impedes the analysis of the system. In the follow-

ing sections we propose a general model for the de-

scription of complex information processing systems

that addresses theses issues by emphasizing the mod-

eling of interactions and employing a description of

the system that is based on the composition of build-

ing blocks which represent functional characteristics

rather than discrete entities.

2 OVERVIEW AND OBJECTIVES

OF OUR APPROACH

In order to support the methodical approach addressed

in the previous section we designed a general model

to describe complex information processing systems.

This approach makes the assumption, that every com-

plex system can be represented by a corresponding

complex information processing system, i.e., that the

complex system can be reduced to a system that only

consists of a set of entities that process and exchange

information. The model we present here was designed

particularly with regard to the following ﬁve objec-

tives:

sometimes also called individual-based models.

1. Generality. It should be possible to model a di-

verse set of complex systems that would other-

wise be modeled by spezialized types of mod-

els like cellular automata, neuronal networks or

agent-based systems. The ability to model a wide

spectrum of different complex systems is a pre-

requisite for the identiﬁcation of common patterns

among those systems.

2. Explicit State Representation. The model of a par-

ticular system should have an explicit representa-

tion of it’s state at any time step resulting in an

explicit representation of the models behaviour as

a sequence of states. Such a representation is par-

ticularly useful for comparing the behaviour of in-

dividual models drawn from the model space of a

complex system.

3. Focus on Interactions. The model should facil-

itate the description of complex interactions oc-

curing in a system including aspects of nontrivial

addressing and temporal as well as spatial propa-

gation of information. Complex interactions are

reckoned as key contributing factor to phenom-

ena of self-organization and emergence (Holland,

1998).

4. Expressiveness. The perceived concepts of a com-

plex system, i.e., its different entities, their possi-

bly dynamic relations, and further characteristics

of interest, should intuitively translate into corre-

sponding elements of the model. The structure of

the resulting models should be highly modular. A

modular structure supports the variation of indi-

vidual model elements and thus facilitates the cre-

ation of a broader model space beyond the mere

variation of numerical parameters.

5. Minimalism. The interference between concepts

and structure inherent to the model itself and those

perceived of the complex system that is mod-

eled should be as minimal as possible, i.e., the

model should mitigate the phenomenon known as

“Maslow’s Hammer” (Maslow and Wirth, 1966).

The subsequent description of the model is structured

as follows: Section 3 introduces the four major build-

ing blocks of the model and describes how theses

building blocks relate to one another and how they can

be combined. Section 4 explains how time is repre-

sented in the model, it deﬁnes what comprises a state

and describes how state transitions are performed. Fi-

nally, section 5 reviews the presented model with re-

spect to the objectives stated above.

To illustrate the description of the proposed model we

will roughly sketch out the modeling of a simple boid

simulation as an example along the way. Boids (bird-

like objects) were introduced by (Reynolds, 1987) as

ExploratoryModelingofComplexInformationProcessingSystems

515

a simple model of ﬂocking behavior. In essence, the

movement behavior of a boid is governed by three

simple rules

1. Separation. Steer to avoid crowding local ﬂock-

mates.

2. Alignment. Steer towards the average heading of

local ﬂockmates.

3. Cohesion. Steer towards the average position of

local ﬂockmates.

In addition to these basic rules the model can be ex-

tended with similar rules to avoid obstacles or to stay

in a certain region. Despite this very simple set of

rules a ﬂock of boids can exhibit a surprising variety

of motion patterns.

3 BUILDING BLOCKS OF OUR

MODEL

The proposed model uses an object-oriented ap-

proach. It’s main idea is to model a complex sys-

tem as a combination of four basic building blocks

(proceties

, messages, address ﬁlters, and procety at-

tributes) which will be described in detail in this sec-

tion. The building blocks can be freely combined to

form descriptive elements that capture speciﬁc char-

acteristics of a complex system that do not necessarily

have to coincide with individual entities of that sys-

tem. In this regardour approach differs from common

modeling approaches like cellular automata or agent-

based models

which typically divide a complex sys-

tem into a set of disjunct, structural entities like cells

or agents and then assess and attribute their particular

functions afterwards. Contrary, in our approach the

functional attributes of a complex system are identi-

ﬁed ﬁrst and then combined in the form of building

blocks into corresponding structural elements of the

model.

The ﬁrst building block of the proposed model are

information processing entities, or proceties in short.

A procety is any element of a complex system that is

able to send and receive information, to create new

proceties and remove existing ones. In case of the

boid simulation, each boid can be interpreted as a pro-

cety: it has to receive information about the positions

and headings of nearby ﬂockmates and it has to send

its own position and heading. Less obvious, possible

See also http://www.red3d.com/cwr/boids/ for a de-

tailed description.

short form of information processing entities.

For an overview of agent-based models see

(Salamon, 2011; Allan, 2010; Railsback et al., 2006).

obstacles in a boid simulation would also be modeled

as proceties that actively send out information about

their presence. As there is no common representa-

tion of an environment in our model, even “passive”

elements have to be modeled explicitly as sources of

information, i.e., proceties, if they are to be perceived

by other entities of the system. At ﬁrst glance this

property of the model may seem to be a serious draw-

back, but contrariwise, this property helps to achieve

the second objective stated in section 2.

The second building block are messages. They en-

capsulate the information that is exchanged between

proceties. The information that is transferred by a

message can be arbitrary. The recipients of a mes-

sage are determined by its address. The address has

the form of a set expression which allows to describe

the recipients of a message on an abstract and concep-

tual level. It is a key component of the model in order

to achieve the third objective stated in section 2.

The set expression used to specify the recipients of

a message is composed of common set operators like

union or intersection, and sets of proceties that are ﬁl-

tered by address ﬁlters – the third building block of

our model. If an address ﬁlter is applied to a set of

proceties the ﬁlter decides for every procety in the set

if the procety should remain in the set or not. The

information on which the address ﬁlter bases its de-

cision is provided by a set of procety attributes that

are exhibited by the individual proceties. Procety at-

tributes are the last building block of the proposed

model. They provide a way to describe attributes that

are shared among a set of proceties. In case of the

boid simulation such a shared attribute could be the

position and the heading of a boid. Based on this in-

formation, a corresponding address ﬁlter could then

select all boids that are within a certain distance of

the boid that originated the message – effectively re-

stricting the ﬂow of information from one boid to its

local neighborhood only. In general, shared attributes

are the basic prerequisite for the deﬁnition of global

relations among proceties. These global relations can

then be represented as address ﬁlters and as such be

used in a set expression to speciﬁy the recipients of a

message.

In addition to this addressing scheme, messages

feature another important property. They can have an

arbitrary long time to live (TTL) once they were sent

by a procety. This property is the basis for a broad

variety of time-dependent interactions between pro-

ceties. As a simple example, the messages sent by

“passive” proceties like the aforementioned obstacles

in the boid simulation can have an unlimited TTL and

thus must be sent only once. More sophisticated uses

are achieved in combination with appropriate, time-

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

516

dependent address ﬁlters. For example, the propaga-

tion of a message over time can be described by an

address ﬁlter that selects different sets of recipients

depending on the age of the message, i.e., depending

on how far the message has “travelled”. In the boid

simulation we could use this to model a message of

type “boid cry” that expands radially over time from

the boid that uttered the cry.

The four building blocks of the proposed model can

be summarized as follows:

1. Proceties are “information processing entities” of

a complex system. As such they process informa-

tion which they send and receive in form of mes-

sages. Furthermore, proceties can create new pro-

ceties and delete existing ones.

2. Messages represent information that is transferred

between proceties. The address of a message has

the form of a set expression which allows to spec-

ify the recipients of a message on a high, con-

ceptual level. Furthermore, messages have a TTL

(time to live). That means, they can exist inde-

pendently of any procety for an arbitrary number

of time steps after they have been sent.

3. Address ﬁlters are used as a mechanism in the

message addressing scheme of the model. They

represent global relations among sets of proceties

that share one or more procety attributes.

4. Procety Attributes represent common attributes

that are shared among a set of proceties. They

can be used by address ﬁlters to determine if the

owner of an attribute should receive a particular

message or not.

As stated at the beginning of this section, the de-

scribed building blocks of our model do not necessar-

ily have an exclusive one-to-one relationship to en-

tities of the complex system that is being modeled.

Instead, an element of a complex system can be rep-

resented by several building blocks at once. For ex-

ample, the procety attribute of a procety could itself

be a procety in its own right that modiﬁes the attribute

values according to the information it receives. A

practical example could be the model of a biological

neuron with its ion channels. In this case, the neuron

as well as the ion channels could be modeled as pro-

ceties, where at the same time the ion channels would

also be procety attributes of the neuron. In such a con-

ﬁguration, the ion channels could independently alter

their behavior in reaction to ion channel speciﬁc sig-

nals, i.e., messages, that are directly processed by the

ion channels themselfes and not by the neuron as a

proxy.

4 TIME, STATES, AND STATE

TRANSITIONS

The proposed model operates on a discrete time scale

with steps t ∈ N. At the beginning of each time step t

the state of the model is given by the current states

of all building blocks in the current model. This state

comprises the states of all proceties, messages, ad-

dress ﬁlters and procety attributes. The transition of

the state at timet to the state at time t + 1 is performed

by the following three substeps:

1. Use the procety scheduler of the model to gener-

ate a processing schedule that governs which pro-

ceties are executed in substep 2.

2. Prompt each procety in the processing schedule

to process the messages in their local message

buffers.

3. Evaluate the addresses of all messages and dis-

tribute the messages according to the resulting

procety sets to the local message buffers of each

procety.

The use of a procety scheduler in the ﬁrst step of

the state transition allows to precisely control, how

the proceties are updated during the state transition.

The default procety scheduler of the model facilitates

the synchronous updating of all proceties, i.e., every

procety is prompted to process its messages in ev-

ery time step. However, there are several models for

complex systems that prefer asynchronous updating,

e.g., many agent based models (Caron-Lormier et al.,

2008). In these cases a custom procety scheduler can

be deﬁned to accurately emulate the updating proce-

dure of the particular model.

The separation of the processing of messages in

step 2 and the delivery of messages in step 3 effec-

tively implements a double buffering scheme. This

means that messages that were sent at time t will be

processed earliest at time t + 1. It also guarantees,

that the order of the proceties inside the processing

schedule has no effect on the behavior of the model.

5 REVIEW OF THE OBJECTIVES

The proposed model was speciﬁcally designed to sup-

port the process of exploratory modeling. In this re-

gard we deﬁned ﬁve objectives to guide the devel-

opment of the model. In this section we review the

model in relation to these objectives.

Generality. There are two main components of the

model that provide the ability to model a wide vari-

ety of different complex system. First, the address-

ing scheme based on procety attributes and address

ExploratoryModelingofComplexInformationProcessingSystems

517

ﬁlters facilitates the description of virtually any kind

of static or dynamic relation between the elements of

a system. Secondly, the state representation of the

model provides an implicit double buffering scheme

which, in combination with a customizable procety

scheduler, allows to implement synchronous as well

as asynchroneous updating during state transitions.

Explicit State Representation. As described in

section 4 the state of a system comprises all build-

ing blocks of the model. In addition, the information

that is individually available to a procety in that time

step is represented by the messages inside the local

message buffer of that procety. This state information

is especially usefull, e.g., to extract a communication

graph for every time step that represents which pro-

ceties exchange information with one another. This

graph representation opens up the possibility to use

common graph measures

to characterize the dynamic

structure of the interactions occuring in the complex

system. As this representation is independent of the

particular system that is being modeled, it facilitates

the comparison of different complex systems and thus

supports the process of exploratory modelling.

Focus on Interactions. As already stated above, the

addressing scheme provides an effective way to de-

scribe a wide variety of interactions between the pro-

ceties. Furthermore, the ability of messages to exists

for arbitrary long periods of time and the possibility to

deﬁne time-dependent address ﬁlters yields a whole

new area of interactions that can be modeled, e.g.,

the spatial propagation of signals. The modulation of

messages was not explicitly addressed. However, as

the building blocks of our model can be freely com-

bined, a message can also be a procety or an address

ﬁlter for instance. The latter, for example, would al-

low for the manipulation of the message content while

it is propagated over time.

Expressiveness. The building blocks of the model

were designed in the spirit of object-orientation to en-

courage the encapsulation of local knowledge. For

example, when proceties interact by exchanging mes-

sages they use a set expression for addressing other

proceties. This set expression contains only address

ﬁlters which typically represent high level concepts

about some relation between the proceties. Thus, a

procety does not need to know much about the other

proceties they are interacting with. The same holds

true for the address ﬁlter itself. The ﬁlter just relies

on the information provided by speciﬁc procety at-

tributes.

An extensive review of graph measures can be found in

(Newman, 2003).

Minimalism. The model uses only four building

blocks which represent functional rather than struc-

tural characteristics of a complex system and which

have a very precise and small “conceptual footprint”.

As the building blocks can be freely combined to form

custom model elements there is no need to “force-

fully” ﬁt a perceived concept of a particular complex

system onto a single, non-custom building block of

the model.

In the context of exploratory modeling the use of

building blocks leads to a highly modular structure

which allows to expand the model space by providing

alternative versions of speciﬁc model elements. For

example, an address ﬁlter that determines the recip-

ients of a message could have a probabilistic coun-

terpart which selects the recipients of a message only

with a certain probability.

6 SIMULATION EXAMPLE

We created a software library using C++ and the

ROOT data analysis framework developed at CERN

(Brun and Rademakers, 1996) to support the imple-

mentation of simulations that use our model. As the

ROOT framework is designed to handle and analyse

large amounts of data, it is well suited for the data

intensive process of exploratory modeling.

As a ﬁrst test case for our model we implemented

a boid simulation as described in section 2. In ad-

dition to the three basic rules of a boid we added a

rule that keeps the boids conﬁned to a local area. The

primary use of this model was to check the implemen-

tation of our library for errors and to gather a ﬁrst set

of simulation data that could be analysed within the

ROOT framework.

To illustrate one application of exploratory mod-

eling, i.e. the exploration of parameters as described

in section 1, we investigated the inﬂuence of the pa-

rameter viewing range of the individual boids on the

observable ﬂocking behaviour. Therefor, we con-

ducted a series of simulations in which we increased

the viewing range stepwise from 5 units to 90 units.

As a measure of “ﬂocking” we used the average num-

ber of clusters that occured within 1000 time steps.

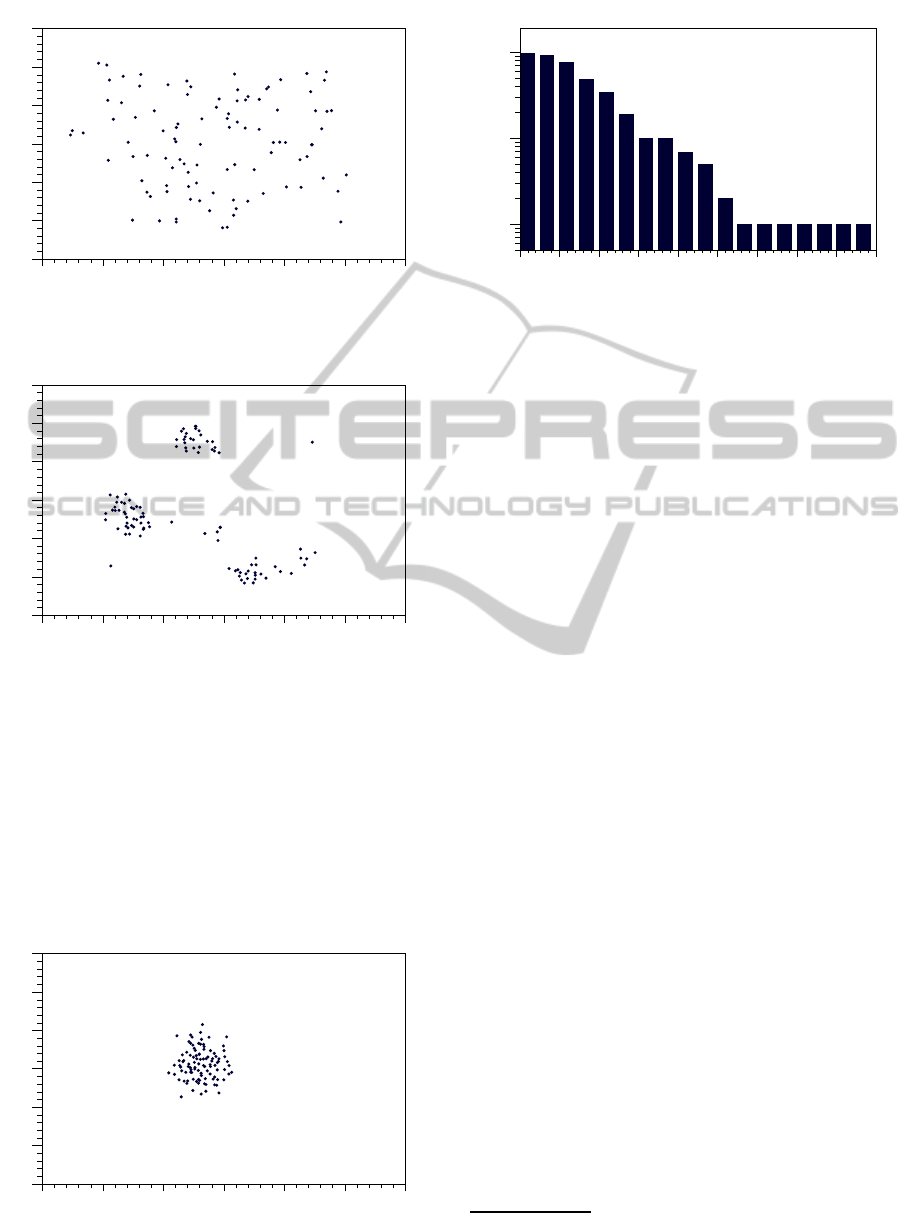
Is the viewing range to short, e.g. only 10 units,

then no observable ﬂocking occurs (s. Figure 1). If

the viewing range is increased to some medium value,

e.g. 35 units, then the emergence of several indepen-

dent ﬂocks can be witnessed (s. Figure 2). However,

if the viewing range is increased further, e.g. to a

value of 80 units, then the dynamic behavior breaks

down and all boids accumulate in a single cluster (s.

Figure 3). Figure 4 summarizes the results of these

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

518

-300 -200 -100 0 100 200 300

-300

-200

-100

100

200

300

boid simulation with a viewing range of 10

Figure 1: A representative distribution of boids with a short

viewing range of 10 units.

-300 -200 -100 0 100 200 300

-300

-200

-100

100

200

300

boid simulation with a viewing range of 35

Figure 2: A representative distribution of boids with a

medium viewing range of 35 units.

experiments. With increasing viewing range the num-

ber of clusters drop rapidly starting with ∼ 100 clus-

ters at a viewing range of 5 units to ∼ 10 clusters at

a viewing range of 35 units. Starting with a viewing

range of 60 units the simulation averages on one sin-

gle cluster, i.e. no ﬂocking occurs anymore.

This simple example illustrates one application of

-300 -200 -100 0 100 200 300

-300

-200

-100

100

200

300

boid simulation with a viewing range of 80

Figure 3: A representative distribution of boids with a long

viewing range of 80 units.

viewing range

5 15 25 35 45 55 65 75 85 95

average number of clusters

Influence of viewing range on the number of clusters

Figure 4: The viewing range of the individual boids inﬂu-

ences the average number of clusters that emerge during a

simulation run.

exploratory modeling to increase the understanding of

the dynamic properties of a given complex system.

It provides a ﬁrst intuition about how the parameter

viewing range inﬂuences the overall dynamic behav-

ior of the system. Yet, a full exploration would en-

compass the exploration of more parameters and their

interrelations. Despite its limitations the given exam-

ple hints at a more general property of emergent phe-

nomena. It appears that emergent phenomena might

require a certain amount of local information, i.e. a

local context of a certain size that is neither too small

nor too big.

Observations such as these, gathered from mod-

eling and simulation of different complex sys-

tems within the same framework, may lead to a

more general understanding of phenomena like self-

organization and emergence.

7 CONCLUSIONS

AND OUTLOOK

In this paper we presented a new model for the de-

scription and simulation of complex information pro-

cessing systems. We designed this model speciﬁcally

to support the exploratory modeling of complex infor-

mation processing systems. The proposed model dif-

fers from common modeling approaches like agent-

based models in a number of ways:

• Model elements are composed out of a set of

four basic building blocks that represent func-

tional rather than structural characteristics of a

particular complexsystem. This contrasts existing

models

where the different model elements such

as cells, agents or messages are used disjunctively.

For example NetLogo (Wilensky, 1999) or repast

(North et al., 2006).

ExploratoryModelingofComplexInformationProcessingSystems

519

• The state of the model – including the information

that is sent at a particular time – has an explicit

representation. This facilitates the creation and

application of measures that describe global, dy-

namic properties of the system enabling the com-

parison of systems that would otherwise be too

different to be compared in a more direct way.

• The model focuses on the interactions between

its information processing entities. The building

blocks of the model are designed such that the

modeling of complex interactions is facilitated.

One aspect of this is the ability of messages to ex-

ist over arbitrary long time intervals which, e.g.,

enables modeling of the spatial propagation of a

message.

In our future work we will use the presented model

to investigate phenomena observed in neuronal infor-

mation processing systems as they are a prime exam-

ple of complex systems. Their operation involves a

substantial variety of mechanisms, e.g., fast signal-

ing through action potentials, complex integration of

signals due to dendrite morphology and electrotonic

properties, change of processing characteristics via

neuromodulators, or the constant adjustment of net-

work topology by means of synaptic plasticity (Koch,

2004; Shepherd and Grillner, 2010). Furthermore,

nervous systems develop by evolutionary processes

over millions of years and are able to “bootstrap”

themselves by a process of self-organized growth

within a timescale of weeks to months (Butler and

Hodos, 2005; Squire et al., 2008).

Among the ﬁrst phenomena that we want to anal-

yse are the mechanisms of self-organization utilized

during nervous system development such as biochem-

ical guidance cues which are used in the context of

neuron migration and axonal path ﬁnding.

We think that modeling and simulation of these

neuronal systems will not only result in a better un-

derstanding of the particular processes themselves but

may provide also insight into more general principles

of self-organization and emergence.

REFERENCES

Allan, R. (2010). Survey of agent based modelling and sim-

ulation tools. Technical report, STFC Daresbury Lab-

oratory, Computational Science and Engineering De-

partment, Daresbury, Warrington WA4 4AD.

Bankes, S. (1993). Exploratory modeling for policy analy-

sis. Operations Research, 41(3):435–449.

Bonabeau, E. (2002). Agent-based modeling: Methods and

techniques for simulating human systems. Proceed-

ings of the National Academy of Sciences of the United

States of America, 99(Suppl 3):7280–7287.

Brun, R. and Rademakers, F. (1996). Root - an object ori-

ented data analysis framework. In AIHENP’96 Work-

shop, Lausane, volume 389, pages 81–86.

Butler, A. and Hodos, W. (2005). Comparative Vertebrate

Neuroanatomy: Evolution and Adaptation. Wiley.

Caron-Lormier, G., Humphry, R., Bohan, D., Hawes, C.,

and Thorbek, P. (2008). Asynchronous and syn-

chronous updating in individual-based models. Eco-

logical Modelling, 212(3-4):522–527.

DeAngelis, D. L. and Mooij, W. M. (2005). Individual-

based modeling of eecological and evolutionary pro-

cesses. Annual Review of Ecology, Evolution, and Sys-

tematics, 36(1):147–168.

Dennett, D. (1998). Brainchildren: Essays on Designing

Minds, 1984-1996. Representation and Mind Series.

Mit Press.

Evans, K. M. (2001). Larger than life: Digital creatures

in a family of two-dimensional cellular automata. In

Cori, R., Mazoyer, J., Morvan, M., and Mosseri, R.,

editors, Discrete Models: Combinatorics, Computa-

tion, and Geometry, DM-CCG 2001, volume AA of

DMTCS Proceedings, pages 177–192. Discrete Math-

ematics and Theoretical Computer Science.

Gardner, M. (1970). Mathematical games: The fantastic

combinations of John Conway’s new solitaire game

‘Life’. j-SCI-AMER, 223(4):120–123.

Holland, J. (1998). Emergence. Oxford University Press,

New York.

Koch, C. (2004). Biophysics of Computation: Information

Processing in Single Neurons. Computational Neuro-

science Series. Oxford University Press, USA.

Langton, C. G. (1986). Studying artiﬁcial life with cel-

lular automata. Physica D: Nonlinear Phenomena,

22(13):120 – 149. Proceedings of the Fifth Annual

International Conference.

Lempert, R. J., Schlesinger, M. E., and Bankes, S. C.

(1996). When we dont know the costs or the bene-

ﬁts: Adaptive strategies for abating climate change.

Change, Climactic Change, 33:235–274.

Maslow, A. and Wirth, A. (1966). The psychology of sci-

ence: a reconnaissance, volume 8 of The John Dewey

Society lectureship series. Harper & Row.

Minar, N., Burkhart, R., Langton, C., and Askenazi, M.

(1996). The swarm simulation system: A toolkit for

building multi-agent simulations. Santa Fe Institute.

Newman, M. (2003). The structure and function of complex

networks. SIAM Review, 45(2):167–256.

Newman, M. E. J. (2011). Resource letter cs-1: Complex

systems. American Journal of Physics, 79:800–810.

North, M., Collier, N., and Vos, J. (2006). Experiences cre-

ating three implementations of the repast agent mod-

eling toolkit. ACM Trans. Model. Comput. Simul.,

16(1):1–25.

Railsback, S., Lytinen, S., and Jackson, S. (2006). Agent-

based simulation platforms: Review and development

recommendations. Simulation, 82(9):609–623.

Reynolds, C. (1987). Flocks, herds and schools: A dis-

tributed behavioral model. In Proceedings of the 14th

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

520

annual conference on Computer graphics and interac-

tive techniques, SIGGRAPH ’87, pages 25–34, New

York, NY, USA. ACM.

Salamon, T. (2011). Design of Agent-Based Models : De-

veloping Computer Simulations for a Better Under-

standing of Social Processes. Academic series. Bruck-

ner Publishing, Repin, Czech Republic.

Shepherd, G. and Grillner, S. (2010). Handbook of Brain

Microcircuits. Oxford University Press, USA.

Squire, L., Bloom, F., Spitzer, N., Squire, L., Berg, D.,

du Lac, S., and Ghosh, A. (2008). Fundamental Neu-

roscience. Fundamental Neuroscience Series. Elsevier

Science.

Wilensky, U. (1999). NetLogo http://ccl.northwestern.edu/

netlogo/. Center for Connected Learning and

Computer-Based Modeling, Northwestern Univer-

sity., Evanston, IL.

ExploratoryModelingofComplexInformationProcessingSystems

521