Efficient Group Signatures with Verifier-local Revocation Employing a
Natural Expiration
Lukas Malina, Jan Hajny and Zdenek Martinasek
Department of Telecommunications, Brno University of Technology, Technicka 12, Brno, Czech Republic
Keywords:
Batch Verification, Cryptography, Efficiency, Group Signatures, Privacy, Pseudonymity, Time-bound Secret
Key.
Abstract:
This paper presents a novel proposal of group signatures with verifier-local revocation employing a natural
expiration to ensure an efficient verification of signatures and a revocation check. Current group signatures
have an expensive verification phase which takes several pairing operations and checks a long-sized revocation
list, especially, if a large number of users are in the group. Generally, the revocation list grows linearly every
time when a new revoked user is added into the list unless group parameters and keys are not reinitialized.
Nevertheless, the reinitialization is not feasible and burdens the communication overhead in many commu-
nication systems. In these schemes, the verification of several signatures with the long-sized revocation list
takes too much time. Our proposed group signature scheme offers the more efficient verification phase which
employs the revocation list that is reduced in time by a natural expiration of group member secret keys. Due
to an optimization in the verification phase, our scheme is more efficient than related solutions.
1 INTRODUCTION
Group signatures can be used in many privacy-
preserving services and authentication schemes. A
user, who is a member of a group, can sign a mes-
sage behalf of the group and send the message anony-
mously to a verifier. Since the first scheme of a group
signature is introduced in (Chaum and Van Heyst,
1991), many of group signature schemes have been
proposed with various attributes and different ways
how to revoke group members. In this paper, we aim
to revocation in group signatures which can be di-
vided into three main mechanisms. The first method
revokes members by the reinitialization of group pub-
lic keyand sending it to all unrevoked members which
must recomputate group member secret keys. This
method burdens communication and adds computa-
tional operations anytime when a member is added
or revoked. The second mechanism is based on
sending the single public broadcast message to all
members without need to recompute secret keys. In
this accumulator-based revocation method, e.g. (Ca-
menisch et al., 2009), users must prove their valid-
ity proofs called witnesses and that are included in a
white-list accumulator (or not present in a black-list
accumulator). Verifiers do not need any revocation
list. Nevertheless, signers have to keep track of the
changes into accumulator and have to be online. The
third option how to check the revoked users is to em-
ploy a list with revoked users (keys, credentials etc.)
maintained by Group Manager (GM). GM sends it to
verifiers who must perform a revocation check. This
method is called Verifier-Local Revocation (VLR).
Since group members have no work with revocation
check, this check must be computed by the verifier,
such as in (Boneh and Shacham, 2004) and (Hajny
and Malina, 2012). VLR solutions provide less inter-
activity so the signer can be off-line and has no ad-
ditional computation in comparing with accumulator-
based solutions. The drawback of VLR solutions is
usually the growth of revocation lists to enormous
sizes in a large group. Our work is aimed to immedi-
ate revocation which is also suitable for off-line sign-
ers in non-large groups. We focus on the verifier-local
revocation approach and propose a group signature
scheme with VLR employing a natural expiration to
reduce the length of revocation list by time. Our pro-
posal focuses on efficiency in the signing phase and
the verification phase including the revocation check.
1.1 Related Work
The verifier-local revocation introduced in (Boneh
and Shacham, 2004) can be an efficient revocation so-
555
Malina L., Hajny J. and Martinasek Z..
Efficient Group Signatures with Verifier-local Revocation Employing a Natural Expiration.
DOI: 10.5220/0004600105550560
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 555-560
ISBN: 978-989-8565-73-0
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

lution for signers. In (Nakanishi and Funabiki, 2007),
the authors extend a group signature scheme (Boneh
and Shacham, 2004) and add Backward Unlinkability
(BU). They employ the revocation tokens of revoked
members for certain time intervals to ensure that for-
mer signatures cannot be linkable if the member is
revoked. Since the proposal (Nakanishi and Funabiki,
2007) is proved in the random oracle model, the work
(Libert and Vergnaud, 2009) presents the VLR group
signature scheme with BU that is proved in the stan-
dard model. Nevertheless, the revocation check also
costs 1 pairing operation per one revocation token as
in (Nakanishi and Funabiki, 2007). To improve com-
putational overhead, one revocation check is reduced
from one pairing to one exponentiation in (Chen and
Li, 2012). In (Bringer and Patey, 2011), the scheme
proposed in (Chen and Li, 2012) is patched to satisfy
backward unlinkability, traceability and exculpability
in the random oracle model. The work (Camenisch
et al., 2010) presents revocation with efficient up-
dates. The validity time of a credentials is encoded
into an attribute. Nevertheless, the solution does not
support an immediate revocation. In time-critic ser-
vices, the solution has to be combined with an accu-
mulator solution. The work (Chu et al., 2012) pro-
poses a pairing-based group signature scheme with
VLR employing time-bound secret keys and without
BU. Each group secret key has an expiration date so
the verifier checks the revocation list that excludes ex-
pired members. Only one exponentiation is needed
to check whether the key is revoked. Nevertheless,
the scheme performs seven pairing operations per one
message in the verification phase.
1.2 Our Contribution
Our scheme provides standard group signature prop-
erties like authenticity, anonymity, data integrity, non-
reputation, correctness and one public key. The
scheme does not need the reinitialization of param-
eters and keys of members when a new user is
added, revoked or epoch is ended. In contrary to
schemes (Nakanishi and Funabiki, 2007), (Libert and
Vergnaud, 2009), (Chen and Li, 2012) and (Bringer
and Patey, 2011) where time intervals are employed,
in our proposal, a Revocation List (RL) is reduced
by the natural expiration of secret keys which is con-
venient for applications where the individual time of
group membership expiration is needed. To our best
knowledge, only the scheme proposed by Chu et al.
2012 (Chu et al., 2012) uses time-bound secret keys
to the natural expiration of these keys. Neverthe-
less, we propose a scheme which is more efficient in
computational overhead than Chu et al. scheme (Chu
et al., 2012) by using a different design and employ-
ing optimization techniques such as the batch verifi-
cation used in (Ferrara et al., 2009) and (Malina et al.,
2013). Our scheme needs only 8 elements per a re-
vocation token in contrary to 14 elements needed in
(Chu et al., 2012). Moreover, to ensure the shorter
revocation tokens, we use time offsets in comparing
with using date formats in (Chu et al., 2012). Accord-
ing to the initial results, see section 4.2, our scheme
has better performance in the verification phase than
the current VLR group signatures.
2 BACKGROUND
In this section, the cryptography background and sys-
tem model are outlined.
2.1 Cryptography Used
Our scheme is based on a group signature scheme
proposed by Boneh and Shacham (the BS04 scheme)
(Boneh and Shacham, 2004) with verifier-local revo-
cation that ensures anonymity, authenticity, message
integrity, non-repudiation, unlinkability and traceabil-
ity. The scheme uses bilinear maps and is based on
the q-SDH problem and Decision Linear problem,
which have been described in (Boneh and Shacham,
2004). We modify this scheme to ensure more effi-
cient verification algorithm by a verifier-local revoca-
tion with time-bound group member secret keys and
batch verification. To make time-bound group se-
cret member keys, we employ the methods called 0-
encoding/1-encoding presented in (Chu et al., 2012).
The 0-encoding and 1-encoding reduce the greater
than predicate to set intersection predicate by convert-
ing a date format in binary string to a value in Z
p
.
2.2 System Model
Our system model consists of three parties:
• Group manager (GM). We assume that GM is a
trusted party. GM initializes all group signature
parameters, one group public key, one group man-
ager secret key and group member secret keys.
GM also manages a revocation list which includes
revoked users.
• Verifier (V). V checks only signed messages by a
group public key and if user is on the revocation
list or not.
• User (U). U, who correctly joins into a group, can
sign any message by his/her group member secret
key and send it to V.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
556

3 PROPOSED SCHEME
In this section, the proposed scheme is outlined. Our
scheme consists of five main phases: setup, join, sign,
verify and open. Our scheme is based on BS group
signature scheme (Boneh and Shacham, 2004) and it
is enhanced on the efficient group signature scheme
with time-bound secret keys with batch verification.
3.1 Setup
In the setup phase, GM sets group signature parame-
ters, group public key and group manager secret key.
Based on the length of the security parameter λ, the
group signature parameters G
1
, G
2
, g
1
, g
2
,ψ, e are es-
tablished since g
1
= ψ(g
2
) if e(ψ(g
2
), g
1
) 6= 1. GM
generates the group manager secret key gmsk = (γ)
where γ
R
← Z
p
. The group public key gpk = (g
1
, g
2
, w)
is published where w = g
γ
2
.
3.2 Join
In the join phase, the i-th user U
i
joins into a group
which is managed by a group manager GM as fol-
lows:
• Based on the variable values such as the length
of revocation list, the reputation of U
i
etc., the
group manager decides about the duration of ex-
piration date τ
i
for the group member secret key
gsk
U
i
. GM encodes the expiration date τ
i
by the 1-
Encoding: {τ
ij
}
j∈[1,l]
←1-Enc(τ
i
) where l is the
length of date format. For ( j = 0; j ≤ l; j + +),
GM computes A
ij
= g
1
τ
ij
x
i
+γ
1
, where x
ij
R
← Z
∗
p
and
τ
ij
x
ij
+ γ 6= 0. GM sends user’s group member
secret key τ
i
, {A
ij
, x
ij
}, the group public key and
public parameters via secured connection to user
(e.g. via TLS). The revocation token τ
i
, {x
ij
} is
saved.
• U
i
encodes the expiration date τ
i
by the 1-
Encoding: {τ
ij
}
j∈[1,l]
←1-Enc(τ
i
) and checks
e(A
ij
, w
τ
ij
g
x
ij
2
) = e(g
1
, g
2
) for each j ∈ {1, 2, ..., l}
if gsk
U
i
is valid.
3.3 Signing
Every user U
i
who wants to send a new message to
a verifier has to sign the message. Every U
i
has a
member secret key gsk
U
i
= τ
i
, {A
ij
, x
ij
} and a group
public key gpk = (g
1
, g
2
, w). U
i
signs a message
M ∈ (0,1)
∗
and outputs the signature of knowledge
σ = (t
cur
, k, T
1
, T
2
, c, s
α
, s
x
, s
δ
, R
2
) as follows:
1. U
i
checks if his/her gsk
U
i
is not expired by t
cur
<
τ
i
, where t
cur
is a current date (e.g. a current
month or a current date in format ’YYMMDD’ as
in (Chu et al., 2012)) or the date of the signature
expiration. If t
cur
≥ τ
i
, the algorithm halts.
2. The dates are converted into intersection check
by the 0/1-Encoding: {τ
ij
}
j∈[1,l]
←1-Enc(τ
i
) and
{t
j
}
j∈[1,l]
←0-Enc(t
cur
) where l is the length of
date format used.
3. The index k ∈ {1, 2, ..., l} is found such that τ
ik
=
t
k
and the pair of A
ik
, x
ik
from gsk
U
i
is selected.
4. U
i
chooses random elements α, r
α
, r
x
, r
δ
∈ Z
∗
p
.
5. U
i
computes the group signature by the following
steps:
Firstly, U
i
sets (
u, v) = H
0
(M, gpk,t
cur
), where H
0
is two-dimensional hash function, mapping 0,1
∗
to G
2
2
. Then, U
i
sets their images in G
1
by (u, v) =
ψ(
u, v) and computes pseudonyms by
T
1
= u
x
ik
, T
2
= A
ik
v
α
, (1)
helper values by
δ = αx
ik
, R
1
= u
r
x
,
R
2
= e(T
2
, g
2
)
−r
x
e(v, g
2
)
r
δ
e(v, w)
r
α
τ
ik
=
e(T
−r
x
2
v
r
δ
, g
2
) e(v, w)
r
α
τ
ik
R
3
= T
r
α
1
u
−r
δ
,
(2)
a challenge value by
c = H(gpk,t
cur
, M, T
1
, T
2
, R
1
, R
2
, R
3
), (3)
and response values by
s
α
= r
α
+ cα,
s
x
= r
x
+ cx
ik
,
s
δ
= r
δ
+ cδ.
(4)
6. U
i
sends the message M with the signature σ =
(t
cur
, k, T
1
, T
2
, c, s
α
, s
x
, s
δ
, R
2
).
3.4 Verification
The verifier (V) verifies messages received from
pseudonymous users. V checks the group signature,
the time validity of signature and if a pseudonymous
user who signed the received message is not in a re-
vocation list RL.
3.4.1 Individual Verification
Individual verification is performed by V as follows:
1. The time validity of signature is checked by t
act
>
t
cur
, if yes then the algorithm halts. To continue
the algorithm, the value t
cur
must be equal or
newer than actual date t
act
measured by verifier.
EfficientGroupSignatureswithVerifier-localRevocationEmployingaNaturalExpiration
557

2. The date t
cur
is converted into the intersection
check by the 0-Encoding: {t
j
}
j∈[1,l]
←0-Enc(t
cur
)
and by k from signature is found t
k
.
3. V restores u, v. . Firstly, V computes (
u, v) =
H
0
(M, gpk,t
cur
), where H
0
is two dimensional
hash function, mapping 0,1
∗
to G
2
2
. Then, V sets
their images in G
1
by (u, v) = ψ(
u, v).
4. V restores
R
1
and R
3
:
R
1
= u
s
x
T
−c
1
, R
3
= u
−s
δ
T
s
α
1
. (5)
5. V computes a new control hash c
′
from the re-
ceived parameters:
c
′
= H(gpk,t
k
, M, T
1
, T
2
, R
1
, R
2
, R
3
).
and checks if c
′
= c. If yes, then V continues with
the verification, otherwise the message is incon-
sistent and is refused.
6. V checks if
R
2
= e(T
2
, g
2
)
−s
x
e(v, w)
(t
k
s
α
)
e(v, g
2
)
(s
δ
)
(e(g
1
, g
2
)e(T
2
, w
t
k
)
−1
)
c
= e(T
−s
x
2
v
s
δ
g
c
1
, g
2
)e(v
s
α
T
−c
2
, w
t
k
)
(6)
7. The signed message is valid if Equations 6 hold.
8. The verification phase continues by a revocation
check in the following subsection.
3.4.2 Revocation Check
The verifier opens the actual revocation list
RL =(τ
i
, {x
ij
}) containing r revoked tokens where
j ∈ [1, l] (l is the length of the date format used) and
i ∈ [1, r] to check if the signed message is received
from a revoked or unrevoked user. The revocation
check is performed as follows:
• For each i-pair of τ
i
, {x
ij
}, V recomputes by the
1-Encoding: {τ
ij
} ←1-Enc(τ
i
) and find index m
(1 ≤ m ≤ l) such that τ
im
= t
k
, selects x
im
from RL
and checks if
T
1
= u
x
im
. (7)
• If Equation 7 holds then user’s signed message
will be discarded because the i-th user with x
im
has been revoked by GM.
If a new user is revoked then GM sends to veri-
fiers the refreshed revocation list. Further, every ver-
ifier discards old records with obsolete pairs τ
i
, {x
ij
}
to reduce the length of RL.
3.4.3 Batch Verification
If V receives more message in one short period
then V verifies the signed messages in one batch.
V uses gpk = (g
1
, g
2
, w) to verify n messages
with σ
z
= (t
zcur
, k
z
, T
z1
, T
z2
, R
z2
, c
z
, s
zα
, s
zx
, s
zδ
) for
z = 1, ..., n, and does:
1. V checks the time validity (of signature) by t
act
>
t
zcur
, if yes then the algorithm aborts. To con-
tinue the algorithm, the value t
zcur
must be equal
or newer than actual date t
act
measured by verifier.
2. The date t
zcur
is converted into intersection check
by the 0/1-Encoding: {t
zj
}
j∈[1,l]
←0-Enc(t
zcur
)
and by k
z
from the signature is found t
zk
.
3. V restores u
z
, v
z
. Firstly, V computes (
u
z
, v
z
) =
H
0
(M
z
, gpk,t
zcur
), where H
0
is two-dimensional
hash function, mapping 0,1
∗
to G
2
2
. Then, V sets
their images in G
1
by (u
z
, v
z
) = ψ(
u
z
, v
z
).
4. V restores
R
z1
and R
z3
:
R
z1
= u
s
zx
z
T
−c
z
z1
,
R
z3
= u
−s
zδ
z
T
s
zα
z1
, (8)
5. V computes a new control hash c
′
z
from the re-
ceived parameters:
c
′
z
= H(M
z
, gpk,t
zcur
, T
z1
, T
z2
,
R
z1
, R
z2
, R
z3
).
and checks if c
′
z
= c
z
. If yes then V continues with
the verification, otherwise the message with the
signature is inconsistent and is refused.
6. V randomly selects θ
1
, θ
2
, ..., θ
n
∈ Z
p
with l
b
bit,
checks the batch if
z=n
∏
z=1
R
θ
z
z2
= e(
z=n
∏
z=1
(T
−s
zx
z2
v
s
zδ
z
g
c
z
1
)
θ
z
, g
2
)
e(
z=n
∏
z=1
(T
c
z
z2
v
−s
jα
z
)
θ
j
,
z=n
∏
z=1
(w
t
zk
))
(9)
7. The batch with signed messages is valid if Equa-
tions 9 hold.
8. V performs the revocation check to ensure that
there are no messages from already revoked users.
We can see from Equations 6 and 9 that the individual
verification costs 2 pairing operations per one mes-
sage but the batch verification costs only 2 pairing op-
erations per n messages. In case the batch verification
is valid, then all messages from the batch continue
are valid. In case the batch verification fails, then the
divide-and-conquer approach is used to identify the
invalid signatures that can be discarded.
3.5 Open
GM stores revocation tokens τ
i
, {x
ij
} of all users. Ev-
ery correctly signed message M with the group signa-
ture σ and group public key can be opened by GM.
User index i which is connected with a user ID stored
in a database can be revealed by the revocation check.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
558

If the revealed user has still the unexpired group mem-
ber secret key then GM puts this user onto the revoca-
tion list and send refreshed RL to verifiers.
4 SCHEME EVALUATION AND
RESULTS
In this section, we evaluate our scheme and com-
pared it with related work. Further, an experimental
implementation and initial results of our scheme are
outlined. Our scheme is based on the BS04 scheme
(Boneh and Shacham, 2004) and inherits all security
assumptions of (Boneh and Shacham, 2004). The se-
curity proof is not included due to the limitation of the
position paper.
4.1 Evaluation and Comparison
We evaluate our solution in the main phases: sign-
ing and verification which includes revocation. Ta-
ble 1 depicts our comparison with related solutions
BS04 (Boneh and Shacham, 2004), CLHZ12 (Chu
et al., 2012), NF07 (Nakanishi and Funabiki, 2007)
and BP11 (Bringer and Patey, 2011). We emphasize
that the verification of n messages also includes the
revocation check of r revoked users. Assuming that
p is a 170-bit prime, the length of elements in G
1
is 171 bits and the length of elements in G
T
is 1020
bits. We use the date format for 255 months (21 years)
formed in an offset since the setup of system. Then,
the date format and index k take only 11 bits (8 bits
for date, 3 bits for index k). Our scheme produces
2059-bit signatures. Comparing with the revocation
token used in CLHZ12 (Chu et al., 2012) which has
14 elements, the revocation token has only 8 elements
in our scheme. In BP11 scheme (Bringer and Patey,
2011), the size of λ is 80 which afflicts the length of
a signature (23301 bits). Due to the batch verification
applied in our scheme, the verification takes only 2
pairings per n messages.
4.2 Experimental Results
To obtain initial results, we have implemented our
proposal as a proof of concept application in JAVA.
The main core of our experimental implementation is
formed by the group signature scheme that uses the
Java Pairing Based Cryptography (jPBC) Library
1
.
The implementation employs the MNT curves type
1
(available on http://gas.dia.unisa.it/projects/jpbc/
index.html)
D with the embedding degree k = 6 and the 171-
bit order of curves. Our implementation is tested
on a machine with Intel(R) Xeon(R) CPU X3440 @
2.53GHz, 4 GB Ram. In our scheme, the signing of
one message takes approx. 120 ms and one verifi-
cation with empty RL takes 132 ms. The revocation
check with one revocation token in the list takes 5.1
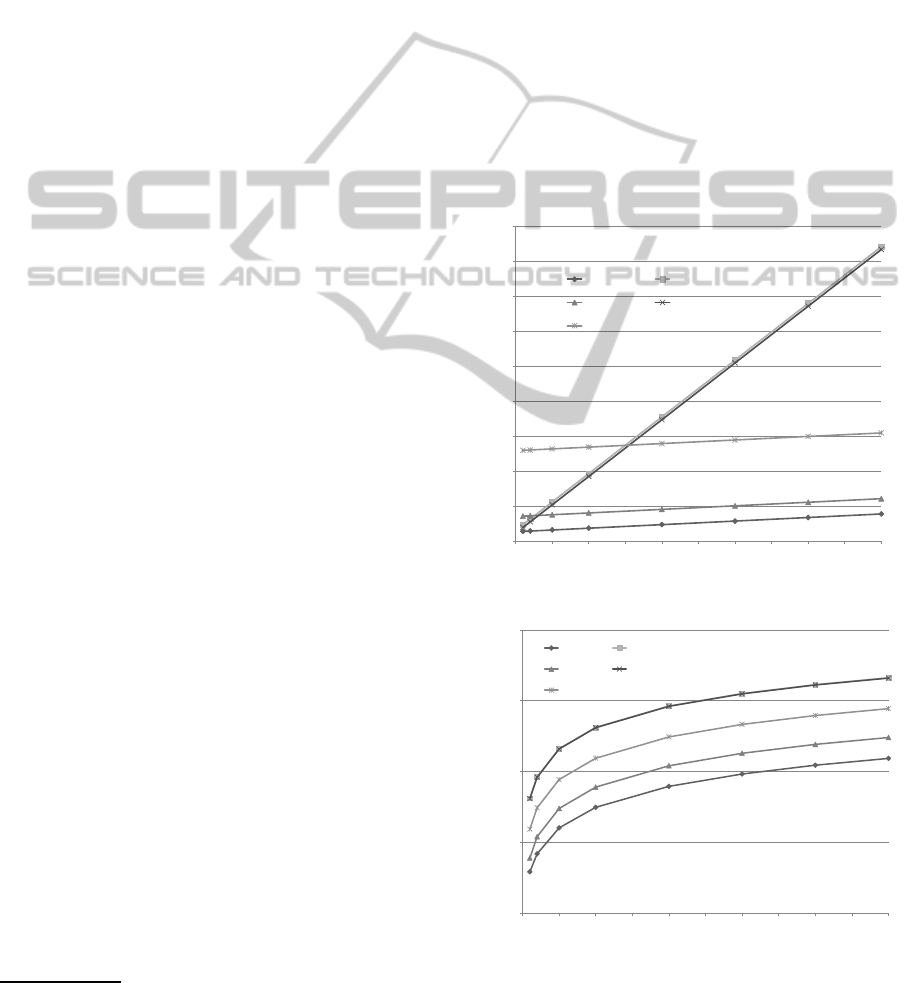
ms. In Figures 1 and 2, the performances of the veri-
fication phase of our scheme and related schemes are
depicted. The Figure 1 shows the performance of ver-
ification of 1 signature with growing the number of
revoked users. The Figure 2 depicts the performance
of verification with the size of RL |RL| = 50 with
growing the number of signatures. Figures 1 and 2
confirms that the verification phase in our scheme is
more efficient than the verification phase in the re-
lated schemes for a variable number of messages and
revoked users. Our scheme is about twice more effi-
cient than the CLHZ12 scheme (Chu et al., 2012).
0
500
1000
1500
2000
2500
3000
3500
4000
4500
0 5 10 15 20 25 30 35 40 45 50
Time [ms]
# Revoked Users
Our Scheme BS04
CLHZ12 NF07
BP11
Figure 1: The performance of verification for 1 signature.
100
1000
10000
100000
1000000
0 5 10 15 20 25 30 35 40 45 50
Time [ms]
# Signatures
Our Scheme BS04
CLHZ12 NF07
BP11
Figure 2: The performance of verification with 50 revoked
users.
EfficientGroupSignatureswithVerifier-localRevocationEmployingaNaturalExpiration
559

Table 1: Performance evaluation of VLR group signature schemes - Signing and verification phases.
GS scheme: Our scheme BS04 (Boneh
and Shacham,
2004)
CLHZ12 (Chu
et al., 2012)
NF07 (Nakan-
ishi and Fun-
abiki, 2007)
BP11 (Bringer
and Patey,
2011)
Batch: yes no no
Length of sig-
nature:
2G
1
, G
T
, 4Z
p
(2059 bits)
2G
1
, 5Z
p
(1192
bits)
4G
1
, 5Z
p
(1549bits)
3G
1
, 6Z
p
(1533
bits)
5G
1
, λ + 6Z
p
(23301 bits)
Verification of n messages with r revoked users in RL:
Pairings 2 3n + 2nr 7n 2n + 2nr 1n
Exponentiation 10n+ 1nr 6n 13n + 1nr 6n 3nλ+1nr+5n
Multiplication 9n+1 6n+1nr 9n 6n+1nr 2nλ+8n
Signing:
Pairings 2 2 5 1 1
Exponentiation 8 8 12 7 16
Multiplication 9 9 10 8 10+λ
5 CONCLUSIONS
We have presented the group signature scheme with
VLR using a natural expiration that can be useful for
many applications where back unlinkability is not de-
manded. Our scheme can be applied in services used
by the middle-sized groups of users who are off-line.
We have employed batch verification to enhance the
performance of our scheme in the verification phase.
Hence, verifiers are able to check more signatures at
once and save their computational overhead. Accord-
ing to our experimental results, our scheme is more
efficient than the related schemes in verification for
the various number of signed messages or revocation
tokens placed in the revocation list. As future work,
we would like to include back unlinkability and inves-
tigate the impact of natural expiration on revocation
check in large groups.
ACKNOWLEDGEMENTS
This work is funded by the Technology Agency
of the Czech Republic projects TA02011260 and
TA03010818; the Ministry of Industry and Trade of
the Czech Republic projects FR-TI4/647 and FR-
TI2/220; and by project SIX CZ.1.05/2.1.00/03.0072.
REFERENCES
Boneh, D. and Shacham, H. (2004). Group signatures with
verifier-local revocation. In Proceedings of the 11th
ACM conference on Computer and communications
security, pages 168–177. ACM.
Bringer, J. and Patey, A. (2011). Backward unlinkability for
a vlr group signature scheme with efficient revocation
check. Technical report, Cryptology ePrint Archive.
Camenisch, J., Kohlweiss, M., and Soriente, C. (2009). An
accumulator based on bilinear maps and efficient re-
vocation for anonymous credentials. In Public Key
Cryptography–PKC 2009, pages 481–500. Springer.
Camenisch, J., Kohlweiss, M., and Soriente, C. (2010).
Solving revocation with efficient update of anony-
mous credentials. In Security and Cryptography for
Networks, pages 454–471. Springer.
Chaum, D. and Van Heyst, E. (1991). Group signatures. In
Advances in CryptologyEUROCRYPT91, pages 257–
265. Springer.
Chen, L. and Li, J. (2012). Vlr group signatures with indis-
putable exculpability and efficient revocation. Inter-
national Journal of Information Privacy, Security and
Integrity, 1(2):129–159.
Chu, C., Liu, J., Huang, X., and Zhou, J. (2012). Verifier-
local revocation group signatures with time-bound
keys.
Ferrara, A. L., Green, M., Hohenberger, S., and Pedersen,
M. Ø. (2009). Practical short signature batch verifi-
cation. In Topics in Cryptology–CT-RSA 2009, pages
309–324. Springer.
Hajny, J. and Malina, L. (2012). Anonymous credentials
with practical revocation. In Satellite Telecommunica-
tions (ESTEL), 2012 IEEE First AESS European Con-
ference on, pages 1–6. IEEE.
Libert, B. and Vergnaud, D. (2009). Group signatures with
verifier-local revocation and backward unlinkability in
the standard model. In Cryptology and Network Secu-
rity, pages 498–517. Springer.
Malina, L., Castell`a-Roca, J., Vives-Guasch, A., and Ha-
jny, J. (2013). Short-term linkable group signatures
with categorized batch verification. In Foundations
and Practice of Security, pages 244–260. Springer.
Nakanishi, T. and Funabiki, N.(2007). A short verifier-local
revocation group signature scheme with backward un-
linkability. IEICE transactions on fundamentals of
electronics, communications and computer sciences,
90(9):1793–1802.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
560