
A Complex Network Approach for Evaluating Query
Similarity Metrics
Rushed Kanawati
LIPN CNRS UMP 7030, University Paris Nord, Villetaneuse, France
Abstract. Query similarity is a core function in many information retrieval appli-
cations. A wide variety of similarity metrics can be defined, varying from simple
term-based similarities to complex document (result) based similarities. However,
no clear evaluation measurement of these different query similarity functions is
yet provided. In this paper we show that effective similarity functions induce
scale-free σ-similarity graphs.
1 Introduction
Web search engines keep track of all received queries in log files. For each query Q
submitted by a user u, we usually find the following information in the log:
1. Q
t
the query processing time.
2. Q
u
the user identifier. This is usually represented by the IP address of user’s ma-
chine.
3. Q
T
is the set of the query terms. In this work we only consider simple queries
composed of a set of words. No boolean operators (i.e. and, or, not) or filtering
operators (i.e. near, language filtering, etc.) are considered.
4. Q
R
is a ranked list of results returned by the search engine in answer to Q.
5. Q
S
⊆ Q
R
is a ranked list of results selected by the user among the list Q
R
. For
each selected document we may save also in the log file the selection time as well
as the visualization time of the document.
Mining query log files has a number of useful applications including: search result
personalization [19], result re-ranking [18], query expansion and reformulation [14],
query recommendation [12] and queries clustering and classification [11]. Defining
an effective query similarity function is a central issue in all above mentioned tasks.
Different similarities have been proposed in the scientific literature [4, 1]. These cover
term-based similarities, result-based similarities, selection-based similarities and graph-
based similarities [1]. In each of the above mentioned types of similarities a wide variety
of concrete similarities can be conceived. The problem we tackle in this work is how
to compare and evaluate different similarity functions in a task-independent way ? Ac-
tually, as far as we are aware, no clear methodology is given in the scientific literature
for evaluating query similarity measures. Some partial work is given in [15, 4]. The
idea we explore in this work is based on defining the concept of σ-similarity induced
Kanawati R..
A Complex Network Approach for Evaluating Query Similarity Metrics.
DOI: 10.5220/0004603200320041
In Proceedings of the 2nd International Workshop on Web Intelligence (WEBI-2013), pages 32-41
ISBN: 978-989-8565-63-1
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

graph. This is simply defined as follows: Let Q be a set queries. Let sim() be a query
similarity function : sim : Q × Q → [0, 1]. Let σ ∈ [0, 1] be a given threshold. The
σ-similarity induced query graph is then defined by: G
(sim,σ)
=< Q, E ⊆ Q × Q >,
where E denotes the set of links in the graph. Two queries Q
i
, Q
j
are linked if their
similarity, as computed by sim(), is greater than σ. The intuition we want to confirm
is that effective similarity functions induce a free-scale similarity graphs [17]. One of
the major characteristics of free-scale graphs is that they exhibit a high clustering coef-
ficient, as compared to random graphs of the same size [16]. The clustering coefficient
defines the probability of having two neighbors of a random selected node linked in
the graph. In social graphs, which are one of the most studied scale-free graphs, this
can be expressed by the high probability of having ” friends of friends being friends
themselves”. This property is not natural in similarity induced graphs since similarity
function in general are not transitive. We claim, that a similarity function inducing a
scale-free graph over the set of queries would be an efficient similarity function. As
a first step towards assessing this claim, we compute different similarities over a real
dataset of query log and we examine if there is any correlation between the scale-free
nature of obtained similarity induced graphs and performances obtained by applying
the correspondent similarity function in the context of a result re-ranking application
[13]. This constitutes no formal proof in any way. However results we obtain allow us
to be more confident in believing this intuition.
Next in section 2, we give a short review of the most used query similarity func-
tions. Our approach for evaluating similarities is then described in detail in section 3.
Experimental results and learned lessons are given and commented in section 4.
2 Query similarity functions
Query similarity functions already proposed in the scientific literature fall into one of
the four following categories:
– Term-based Similarities: The similarity of two queries is measured by the similarity
of used search terms.
– Result-based Similarities: The similarity of two queries is measured by the simi-
larity of document lists returned in answer to these queries. Queries may have no
terms in common but have an important overlap in their result sets.
– Selection-based Similarities: These are basically the same as the result-based func-
tions but applied only to documents selected by users from the whole set of results
returned by the search engine. Next in this paper, this type of similarity function
will not be considered since the target application we use is a result re-ranking ap-
proach in which result selection information is not available at time of similarity
computing (see section 3.3).
– Graph-based Similarity: Different types of relations can be defined between two
queries as described in [1]. These relations can be coded in form of a graph defined
over the query set. Notice that these are different form similarity-induced graphs
which are introduced earlier in this paper. Relational graphs can then be used to
detect similarities among queries in [5, 6].
33

Next, in subsequent sections we give some details about each of the above men-
tioned types of query similarity functions.
2.1 Term-based Metrics
Term-based similarities can further be classified according to the following criteria:
1. Term-order Awareness. One of the simplest way to compute query similarity is
to compute querie’s terms overlap. This is done by applying the classical Jaccard
coefficient as follows:
simJaccard(Q
i
, Q
j
) =
|Q
T
i
∩ Q
T
j
|
|Q
T
i
∪ Q
T
j
|
(1)
This simple metric does not take term order into account. However, in many cases,
term order is significant. For example, the following two queries Q
1
= ” OS X” and
Q
2
=”X OS” have the maximum similarity as computed by simJaccard() metric.
Actually, these queries refer to different computer operating systems: the Mac OS X
operating system and a free flavor of Linux: the X/OS operating system. One direct
way to take term order into account is to treat query terms as strings, then apply a
classical edition similarity [22]. Let C
i
(resp. C
j
) be a the string representing Q
T
i
(resp. Q
T
j
). The edition similarity is given by:
simEdit(Q
i
, Q
j
) = 1 −
editDistance(C
i
, C
j
)
max(len(C
i
), len(C
j
))
(2)
where editDistance is a function computing the minimal cost of transforming
C
i
into C
j
applying atomic edition operations: adding and suppressing characters.
len(c) returns the length of the string c.
2. Terms Pre-processing. Queries terms can be pre-processed before applying sim-
ilarity functions in the same way terms used to indexing full documents are pro-
cessed. Some classical text preprocessing operations are white words cleaning and
terms stemming [3]. However, since query texts are typically very short list of key-
words (in our dataset the average length of query term lists is 2,5), pre-processing
(especially whit words removing) is seldom applied.
3. Term-semantic Awareness. Basic term based similarity metrics treat terms as
atomic entities. However, in different application fields we may benefit from the
availability of a some accepted ontology in order to compute a semantic similarity
between terms [23]. However, in general web searching context, it is hard to select
the right ontology to use for term similarity computing: In which ontology should
we search for jaguar ? Cats, Cars or Operating systems.
2.2 Result-based Metrics
Computing queries similarity by computing the similarity of queries results allow to
handle, in some way, the problem of term ambiguity and the dual problem of using
34

different terms for designating a same concept. Results of a web query are usually a
sequence of U RLs. Different approaches can be applied to compute similarity of two
sequences of URLs
One first, and simple, approach, is to consider U RLs as atomic terms and then
apply the same Jaccard coefficient formula computing URL overlap r of two queries as
follows:
simResultJaccard(Q
i
, Q
j
) =
|Q
R
i
∩ Q
R
j
|
|Q
R
i
∪ Q
R
j
|
(3)
Again, the previous metric does not take into account the sequential order of U RLs
in the results lists. In [4], authors propose a URL-order aware metric based on using
Pearson correlation coefficient. In a formal way, let R = Q
R
i
∩ Q
R
j
be the set r docu-
ments at the intersection of Q
R
i
, Q
R
j
(the result lists of queries Q
i
and Q
j
). Let P os
i,k
be the position of the k
th
document of R in the sequence Q
R
i
. A similarity metric is
then given by:
simResultP earson(Q
i
, Q
j
) = Correlation((P os
i,1
, . . . , P os
i,r
), (P os
j,1
, . . . , P os
j,r
))
(4)
Both previous metrics treat URLs as atomic entities. However, URLs are more rich
components having addresses the can be used to reveal some similarities, as proposed
in [14], and they index generally text documents that can be processed and for which
we can compute some text-based similarity. Thus, more sophisticated result-based sim-
ilarity metrics can be conceived using URL similarity metric. A general formula would
be the following:
simResutlContent(Q
i
, Q
j
) =
P
URL
i
∈Q
R
i
P
URL
j
∈Q
R
j
simURL(U RL
i
, URL
j
)
|Q
R
i
| ∗ |Q
R
j
|
(5)
Where simU RL() is a basic U RL similarity metric. A basic metric from comput-
ing similarities of URL contents is the classical cosin() metric given by:
simURL(U RL
i
, URL
j
) =
P
n
k=1
(w
i
k
∗ w
j
k
)
p
P
n
l=1
(w
i
l
)
2
∗
q
P
n
f=1
(w
j
f
)
2
(6)
Where w
i
k
is the wight of term w
k
in the document indexed by U RL
i
. The term-
vector representation of documents is generated using classical information retrieval
techniques as described in [3].
2.3 Relational Graph-based Metrics
In [1] authors identify different relations that can link queries. These relations are de-
picted on figure 1. The following basic concepts are then defined applied to define
graphs over a set of queries:
35
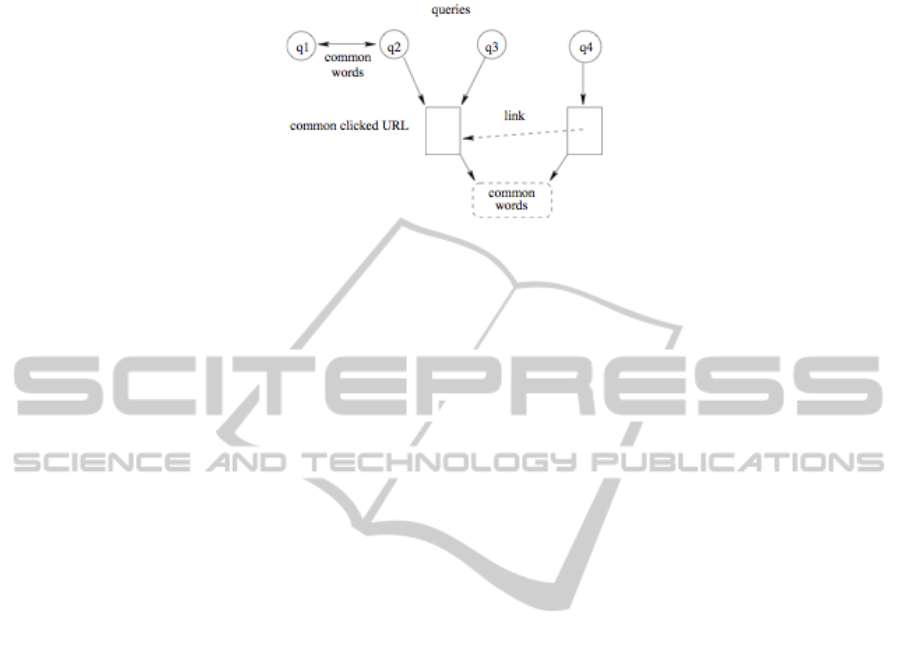
Fig. 1. Different relations among queries (after [1]).
– Query Instance (QI): this is a query terms and a set of selected URL among the list
of results returned by the search engine. Using notations we have introduced in the
introduction this can be define by QI =< Q
T
, p, Q
S
, Q
t
>. Where p is the user
profile if known. p is taken to be Q
u
otherwise.
– Query Session (QS): one or more query instances with the same user profile.
– URL Cover: the set of selected URL : Q
S
.
Based on the above defined concepts, different graphs can be induced:
Word Graph. Vertices are QI (query instances) weighted by the frequency of QI in
the dataset. Two vertices QI
i
, QI
j
are linked if Q
T
i
∩Q
T
j
6= ∅. Notice that this graph
is coding, in some way, the simple term overlap similarity defined in equation (1)
Session Graph. Each vertex is a QI weighted by the number of sessions for whig the
QI belongs. Vertex QI
i
, is linked to QI
j
, by a directed link if both belongs to the
same session and that QI
i
happens before QI
j
.
URL Cover Graph. Again vertices are QIs. Different types of links are defined de-
pending on the selected results overlap: undirected link if both query instances has
the exact selection set, a directed link from QI
i
to QI
i
is Q
S
j
⊂ Q
S
j
, and undi-
rected link if Q
S
i
∩ Q
S
j
6= ∅. Notice that this graph is coding, in some way, the
URL overlap similarity metric defined in equation (3)
URL Link Graph. Vertices are QIs. QI
i
, is linked, by a directed link to QI
j
if there
is at least a hypertext link from selected result in an element in Q
S
i
to an element in
Q
S
j
. Links are weighted by the number of such found hypertext links.
URL Terms Graph. To construct this type of graphs, each selected U RL is first rep-
resented by a vector of terms. Vertices are QIs. Two vertices are linked if there
is l common terms in the intersection of the representations of at least one U RL
of their selected results. Such graph is in straight relation with the content-based
result-based similarity metric defined in equation (5)
The above defined graphs exhibit different characteristics. Authors, mainly evaluate
these in term of sparsity. Word and session graphs are, as expected highly sparse, while
URL term graphs are rather dense ones. Such graphs can then be used to compute a
similarity between queries as proposed in [5], where similarity is computed based on
the flow in such graphs.
This brief summery of main approaches for defining query similarity metrics shows
the wide diversity of approaches the can be used for that purpose.
36

3 Complex Network based Similarity Evaluation Approach
3.1 Informal Description
The approach we propose, for evaluating and comparing different query similarity met-
rics is structured into two main steps:
– Construct the σ-similarity induced graphs. For each graph, we compute the charac-
teristics usually applied to define scale-free graphs (see section 3.2).
– Apply query similarity metric in the context of a web result re-ranking approach
[13]. We search if there is any correlation between the performances obtained from
applying a similarity metric and the characteristics of the similarity graph induced
by the same similarity metric. Evaluating the obtained performances when applying
a given query similarity metric.
The results re-ranking approach is based on mining the log of past processed queries.
For each past query Q
i
we compute a voting function Q
V
i
() that compute a permutation
of Q
R
i
such that Q
S
i
is a prefix of Q
V
i
(Q
R
i
). In other terms, the voting function can
give the ranked result list selected by the user from the list of results returned by the
search engine in answer to Q. Now having a target query Q
T
, the system searches for
past similar queries. Let k be the number of retrieved past similar queries. For each
retrieved similar query we apply the voting function on Q
R
T
. We obtain k potentially
different permutations of Q
R
T
. These different permutations are then merged to obtain
the final re-raking of Q
R
[9]. Hence, the re-ranking framework we propose is structured
in three main hotsopts
1
: 1) The query similarity metric to use, 2) The voting function
to apply and 3) the Permutation merging procedure to apply. Each of these steps can
be implemented by a variety of technical approaches. In the current prototype, we have
implemented four different query similarity metrics summarized in next table.
In the current implementation of the system, we apply a voting function inspired
from the classical voting algorithm [7]. The voting function is implemented as follows:
let Q
R
target
be the set of results returned in answer to target query Q
target
. Let Q
s
be a
past query similar to Q
target
. Let pos(r, Q
R
j
) a function returning the rank of document
r in the list of results Q
R
j
. For each result r ∈ Q
R
target
we compute the following weight
w
r
=
X
rs∈Q
R
s
simURL(rs, r) × pos(rs, Q
R
s
)
Where simU RL(r
i
, r
j
) is a given document similarity metric. Currently this is takes
to be the classical cosine document similarity metric. The result of the voting function
of past query Q
s
is the list Q
R
target
sorted in ascending order with respect to computed
weights w
r
. We apply, the original Borda voting algorithm [7] for merging voting results
obtained from k similar past queries. We propose to evaluate the correctness of the re-
ranking approach by the value of the edit similarity between the rank proposed by the
system and the selection order performed by users (as registered in a log file).
1
In a component framework a hot spot is a place where adaptations can occur.
37

3.2 Scale-free Graphs
Different graphs modeling real complex systems have been showed recently to exhibit
a common set of features that distinguish them from pure random graphs [16]. Let
G =< V, E ⊆ V × V > be a graph. Scale-free graphs have the following main
characteristics:
– Small Diameter. The diameter of a graph is given by highest shortest distance
between any couple of nodes. In scale-free graphs, this distance is very short com-
pared to the number of nodes in the graph. In many real graphs the diameter is
less than 6 stating that we can reach any node from any other nodes by making 6
hops at most. This is the main reason why lot of scale-free graphs are also called
small-world graphs [16].
– Low Density. The density of non-oriented graph G is given by d
G
=
|E|
|V |×(|V |−1)
the number of effective links over the number of possible links. In scale-free graphs
little links do exist, compared to |V | the number of nodes in the graph.
– Power-law Degree Distribution. The number of nodes that have K direct neigh-
bors in the graph is proportional to K
−α
. For many real graphs we have α ∈ [2, 3]
[10].
– Hight Clustering Coefficient. The clustering coefficient is given by
cc(G) =
X
v∈V
2|E ∩ (Γ (v) × Γ (v))|
d(v) × (d(v) − 1)
where Γ (v) denotes the set of neighbors of node v in the graph. d(v) denotes the
degree of node v. This measure estimates the probability that two neighbors of a
randomly selected node are linked directly.
3.3 The CaSE Re-ranking Approach
Roughly speaking, the basic idea underlaying the proposed approach is to associate with
each past query (i.e. source case) Q
i
a voting function Q
V
i
() that compute a permutation
of Q
R
i
such that Q
S
i
is a prefix of Q
V
i
(Q
R
i
). In other terms, the voting function can give
the ranked result list selected by the user from the list of results returned by the search
engine in answer to Q. Now having a target query Q
T
, the system searches for past
similar cases (i.e. queries) using some query similarity measure. Let k be the number
of retrieved past similar queries. For each retrieved similar query we apply the voting
function on Q
R
T
. We obtain k potentially different permutations of Q
R
T
. These different
permutations are then merged to obtain the final re-raking of Q
R
[9]. Hence, the re-
ranking framework we propose is structured in three main hotsopts
2
:
– The query similarity metric to apply for retrieving past similar queries.
– The voting function to apply by each retrieved query in order to re-rank results of
the current query.
– The ranking merging procedure to apply in order to obtain the final rank of results.
38

Table 1. Implemented query similarity metrics. simU RL() is a basic U RL similarity metric.
Similarity metric Formula
Terme overlap (Jaccard) simJaccard(Q
i
, Q
j
) =
|Q
T
i
∩Q
T
j
|
|Q
T
i
∪Q
T
j
|
Query terms Edit Distance simEdit(Q
i
, Q
j
) = 1 −
editDistance(C
i
,C
j
)
max(len(C
i
),len(C
j
))
Result-overlap metric simResultJ accard(Q
i
, Q
j
) =
|Q
R
i
∩Q
R
j
|
|Q
R
i
∪Q
R
j
|
Result-based metric simResutlContent(Q
i
, Q
j
) =
P
URL
i
∈Q
R
i
P
URL
j
∈Q
R
j
simURL(URL
i
,URL
j
)
|Q
R
i
|∗|Q
R
j
|
Each of these steps can be implemented by a variety of technical approaches. In the
current prototype, we have implemented four different query similarity metrics summa-
rized in table 1.
As for the second hotspot, we propose a voting function inspired from the classical
Borda voting algorithm [7]. The voting function is implemented as follows: let Q
R
target
be the set of results returned in answer to target query Q
target
. Let Q
s
be a past query
similar to Q
target
. Let pos(r, Q
R
j
) a function returning the rank of document r in the
list of results Q
R
j
. For each result r ∈ Q
R
target
we compute the following weight
w
r
=
X
rs∈Q
R
s
simURL(rs, r) × pos(rs, Q
R
s
)
Where simU RL(r
i
, r
j
) is a given document similarity metric. Currently this is taken
to be the classical cosine document similarity metric. The result of the voting function
of past query Q
s
is the list Q
R
target
sorted in ascending order with respect to computed
weights w
r
.
Finally, for rank aggregation step, we apply, the original Borda voting algorithm
[7] for merging voting results obtained from k similar past queries. More complex and
effective list rank merging procedures can also be applied [9].
4 Experimentation
Experiments are conducted on a real query log file provided by Microsoft. Data follow
the description of a classical query log file as described in section 1. In this experiment
we use a set of 200000 queries. These contains 80800 distinct query terms and results
are composed of 754000 distinct URLs. We have applied the above described results
re-ranking approach using four different query similarity metrics: J accard
T
, Edit
T
,
Jaccard
R
, and Content
R
. For each metric we vary the similarity threshold σ from 0.6
to 0.9. Characteristics of induced similarity graphs are given in table 2. In this table,
diameter, density and power are those of the biggest connected component.
For all experiments a classical 3-cross validation approach is applied: the query log
is divided into three folds: two are used as a learning set and the third as a validation
set. Each experiment is repeated three times by changing each round the selected learn-
ing/validation folds. Average results of three rounds are given in table1 (last column).
We clearly found that result-based similarities outperforms term-based ones. And
that result-based similarity induced graphs exhibit more scale-free features. Result-
content based similarities give a slightly more enhanced results that results overlap
2
In a component framework a hot spot is a place where adaptations can occur.
39

Table 2. Characteristics of induced similarity graphs with obtained re-ranking correctness.
Similarity Threshold Density Clustering Coeff. Diameter # connected components Power Re-ranking
Jaccard
T
0.6 1.29E-04 0.506 22 16 383 1.581 0.459
0.7 1.93E-04 0.541 1 13 621 1.102 0.501
0.8 2.29E-04 0.561 1 12 259 0.997 0.511
0.9 2.37E-04 0.574 1 11 975 0.992 0.512
Edit
T
0.6 1.43E-04 0.455 25 7 646 2.003 0.406
0.7 1.03E-04 0.459 51 15 286 2.0659 0.430
0.8 1.50E-04 0.530 11 15 652 1.547 0.472
0.9 2.14E-4 0.577 1 12 936 1.259 0.499
Jaccard
R
0.6 3.40E-04 0.784 6 17 250 1.498 0.420
0.7 2.14E-04 0.668 6 15 348 1.95 0.461
0.8 1.65E-04 0.548 5 11 844 2.027 0.514
0.9 1.76E-04 0.399 7 6 646 1.918 0.609
Content
R
0.6 3.23E-03 0.835 5 987 1.28 0.421
0.7 5.29E-03 0.809 3 507 1.287 0.439
0.8 1.15E-02 0.731 2 237 1.032 0.501
0.9 3.15E-02 0.684 2 110 0.849 0.754
similarity. Again results-content graphs is more similar to scale-free graphs (especially
in terms of clustering coefficient which a major metric for characterizing scale-free
graphs [16] ). These results enforce our intuition that effective query similarity metric
induce scale-free similarity graphs.
5 Conclusions
In this work we’ve proposed a new approach for evaluating web search query similar-
ity metrics that can be applied independently of an application type. First experiments,
reported here, show that effective similarity metrics define also a scale-free like graphs.
Obviously, current experimentation does not allow to generalize these findings. More
experimentations are needed in order to take into account other types of similarity met-
rics as well as other types of information retrieval related tasks (other than results re-
ranking). Current extensions of this work include comparing the topological features
of other types of graphs that can be induced by applying a similarity measure on a set
of queries, such as K-nearest neighbors graphs (K-NNG) [8] and relative neighborhood
graphs [20].
References
1. Baeza-Yates, R. (2007). Graphs from search engine queries. SOFSEM 2007: Theory and
Practice of Computer Science, pages 1–8.
2. Baeza-Yates, R. A. (2005). Applications of Web Query Mining. In ECIR, pages 7–22.
3. Baeza-Yates, R. A. and Ribeiro-Neto, B. A. (1999). Modern Information Retrieval. ACM
Press / Addison-Wesley.
4. Balfe, E. and Smyth, B. (2005b). An Analysis of Query Similarity in Collaborative Web
Search. In ECIR, pages 330–344.
5. Boldi, P., Bonchi, F., Castillo, C., Donato, D., Gionis, A., and Vigna, S. (2008). The query-
flow graph: model and applications. In Proceeding of the 17th ACM conference on Infor-
mation and knowledge management, pages 609–618. ACM.
40

6. Boldi, P., Bonchi, F., Castillo, C., Donato, D., and Vigna, S. (2009). Query suggestions using
query-flow graphs. Proceedings of the 2009 workshop on Web Search Click Data - WSCD
’09, pages 56–63.
7. Borda, J. C. (1781). M
´
emoire sur les
´
elections au scrutin. Comptes rendus de l’Acad
´
emie
des sciences, traduit par Alfred de Grazia comme Mathematical Derivation of a election
system , Isis, vol 44, pp 42-51.
8. Dong, W., Charikar, M., and Li, K. (2011). Efficient k-nearest neighbor graph construction
for generic similarity measures. In WWW, pages 577–586.
9. Dwork, C., Kumar, R., Naor, M., and Sivakumar, D. (2001). Rank aggregation methods for
the Web. In WWW, pages 613–622.
10. Guillaume, J.-L. and Latapy, M. (2006). Bipartite graphs as models of complex networks.
371, pages, 2006. Physica A, 37(1):795–813.
11. Hosseini, M. and Abolhassani, H. (2009). Clustering Search Engine Log for Query Recom-
mendation. Advances in Computer Science and Engineering, pages 380–387.
12. Jiang, Q. and Sun, M. (2011). Fast query recommendation by search. In Burgard, W. and
Roth, D., editors, AAAI. AAAI Press.
13. Kanawati, R. (2008). A CBR framework for implementing community-aware web search
engine. In proceedings of second international workshop on adaptive information retrieval
(AIR’08), London, UK.
14. Kanawati, R., Jaczynski, M., Trousse, B., and Anderloi, J.-M. (1999). Applying the broad-
way recommendation computation approach for implementing a query refinement service in
the CBKB meta-search engine. In Trousse, B. and Mille, A., editors, Conf
´
erence franc¸ais
sur le raisonnement
`
a partir de cas (R
`
aPC’99), pages 17–26, Palaiseau, France. AFIA.
15. Kr
¨
omer, P., Sn
´
asel, V., and Platos, J. (2008). Investigating Query Similarity Measures for
Collaborative Web Search. In Sn
´
asel, V., Abraham, A., Saeed, K., and Pokorn
´
y, J., editors,
CISIM, pages 27–32. IEEE Computer Society.
16. Li, L., Alderson, D., Tanaka, R., Doyle, J. C., and Willinger, W. (2005). Towards a theory
of scale-free graphs: Definition, properties, and implications (extended version). CoRR,
abs/cond-mat/0501169.
17. Li, L., Gu, B.-Y., and Chen, L. (2009). The Topological Characteristics and Community
Structure in Consumer-Service Bipartite Graph. In Zhou, J., editor, Complex (1), volume 4
of Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecom-
munications Engineering, pages 640–650. Springer.
18. Rohini, U. and Varma, V. (2007). A Novel Approach for Re-Ranking of Search Results
Using Collaborative Filtering. In ICCTA, pages 491–496. IEEE Computer Society.
19. Tan, B., Shen, X., and Zhai, C. (2006). Mining long-term search history to improve search
accuracy. In Eliassi-Rad, T., Ungar, L. H., Craven, M., and Gunopulos, D., editors, KDD,
pages 718–723. ACM.
20. Toussaint, G. T. (1980). The relative neighbourhood graph of a finite planar set. Pattern
Recognition, 12(4):261–268.
21. Xue, Y., Liu, Y., Zhu, T., Zhang, M., Ma, S., and Ru, L. (2010). Query recommendation
considering search performance of related queries. In Cheng, P.-J., Kan, M.-Y., Lam, W.,
and Nakov, P., editors, AAIRS, volume 6458 of Lecture Notes in Computer Science, pages
410–419. Springer.
22. Zezula, P., Amato, G., Dohnal, V., and Batko, M. (2006). Similarity Search: The metric
Space Approach. Advanced Database Systems. Springer.
23. Zhang, C., Wang, Y.-J., Cui, B., and Cong, G. (2008). Semantic similarity based on compact
concept ontology. In Proceeding of the 17th international conference on World Wide Web -
WWW ’08, page 1125, New York, New York, USA. ACM Press.
41
