
Approaching Encryption through Complex Number Logarithms
George Stergiopoulos, Miltiadis Kandias and Dimitris Gritzalis
Information Security and Critical Infrastructure Protection Research Laboratory, Dept. of Informatics,
Athens University of Economics & Business, 76 Patission Ave., Athens GR-10434, Greece
Keywords: Cryptosystem, Complex Number, Complex Logarithm, Security.
Abstract: In this paper, we approach encryption through the properties of complex logarithm and the complex plane.
We introduce a mathematical concept to be used in cryptography. As an example, we propose a new crypto-
system, by mixing known robust techniques such as chain-block encryption and AES-like structures toget-
her with complex exponentiation to provide robust encryption of plaintext messages. The proposed method
implements encryption by transforming complex numbers into position vectors in a two-dimensional Carte-
sian coordinate system called the complex plane and utilizes the properties of the complex logarithm toget-
her with well-defined techniques from global standards (such as AES), in order to ensure robustness against
cryptanalysis. This is made possible without implementing any computational costly algorithm. This has
two important consequences: First, it may open up viable solutions to known limitations in cryptography
such as relatively complex key schedules (i.e. in Feistel ciphers) and the need for relatively large keys used
in encryption methods (bit-wise). Second, it proposes a new mathematical concept that can be used in future
cryptosystems. An example of this is the preliminary cryptosystem found in this paper. We present its algo-
rithm and show that it can be implemented using fast mechanisms for encryption and decryption.
1 INTRODUCTION
The ever-growing computational capabilities of mo-
dern computers result in an ever-growing need for
complex encryption methods and characteristics,
such as the discovery of ever growing large prime
numbers and complex key schedules to ensure secu-
rity in cryptosystems. In a few years, even AES en-
cryption might not be enough to overcome the com-
putational capabilities of computers-to-come. In this
paper, we propose a new encryption model that can
be used in cryptosystems. We provide an implemen-
tation of a possible encryption method that utilises
the 1-to-many relation found inside the properties of
a complex logarithm.
In Section 2, we present known previous work
on this area. In Section 3, we lay the grounds of our
method by formally presenting the complex loga-
rithm using complex analysis. In Section 4, we de-
monstrate a possible use of the complex logarithm to
encrypt simple plaintext messages and provide an e-
xample algorithm for possible implementation. We
conclude this section by providing some insight on
the robustness of this model using computational
complexity and present all well-defined algorithmic
steps used. Finally, in Section 5 we conclude and
present out plans for future work.
2 RELATED WORK
US Government Federal Information Processing
Standards publicly announced AES (Daemen et al.,
2003) as a standard in encryption, inside “FIPS PUB
197 Advanced Encryption Standard (AES)” in 2001.
No efficient attack can be mounted yet against AES,
though Biryukov, Khovratovich and Nikolić in
(Biryukov et al., 2009) successfully made a related-
key attack on the 192-bit and 256-bit versions of
AES with a complexity of 2
96
for one out of every
2
35
keys which exploits AES's somewhat simple key
schedule. Bogdanov, Khovratovich and Rechberger,
published in 2011 key-recovery attacks on full AES,
based on bicliques (Bogdanov et al., 2011), faster
than brute force by a factor of about four. It requires
2
126.1
operations to recover an AES-128 key. For
AES-192 and AES-256, 2
189.7
and 2
254.4
operations
are needed, respectively.
Blowfish is known to be susceptible to attacks on
reflectively weak keys. Schneier, Blowfish's (Sch-
574
Stergiopoulos G., Kandias M. and Gritzalis D..
Approaching Encryption through Complex Number Logarithms.
DOI: 10.5220/0004604005740579
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 574-579
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

neier, 1994) and Twofish’s (Schneier, 1998) deve-
loper, supposingly said in 2007 "I'm amazed it's still
being used. If people ask, I recommend Twofish in-
stead" (McConnachie, 2007). Twofish is yet unbro-
ken, though computational capability will eventually
catch up since, as claimed in (Shiho, 2000), it will
theoreticaly take roughly 2
51
chosen plain texts to
find a good pair of truncated differentials to break
Twofish.
Technology is bound to catch up to all cryptosy-
stems and surpass their computational limits. For
this reason, any new encryption method should be
welcomed as future input to viable alternatives, es-
pecially suggestions that comply to the “low compu-
tational cost”-“high resilience to cryptanalysis” para-
digm. In this paper, we take the first necessary steps
in trying to provide a new mathematical concept and
suggest a new cryptographic algorithm that may lead
to further solutions and viable cryptosystems.
3 THE LOGARITHM OF A
COMPLEX NUMBER
In complex analysis, a complex logarithm is the
inverse of a complex exponential, similar to natural
logarithm. Ln(x) is the inverse of the real exponen-
tial function e
x
. Thus, a logarithm of z is a complex
number w such that e
w
= z. The basis of our encryp-
tion method relies on the fact that, for one complex
value w, there are infinitely many logarithms, becau-
se we can choose any integer k since the complex
exponential is many-to-one (Zill et al., 2011).
The logarithm of any number, real or complex,
can assume an infinite number of (complex) values,
all with the same modulus, but with different phase
angles.
3.1 Complex Exponentiation
The complex exponential function is not one-to-one,
and all values of e
, z complex are assumed in any
infinite horizontal strip of width 2π in the z-plane
(Zill et al., 2011).
Complex exponentiation is formally defined
ase
cos
t
i∗sint. Thus,
e
∗
e
∗
e
i∗e
This is the formula for the exponential of a general
complex number z = x + i * y expressed in Cartesian
coordinates. In short, this can be rewritten into e
=
w, where z and w are both complex. From here, we
know that z = Log (w), thus, if we let w = a + i * b,
and we solve for x and y in terms of a and b, we get
the equation for the complex logarithm.
a= e
∗
(eq. 1)
b=
e
∗
(eq. 2)
a
2
+ b
2
= e
∗
+ e
∗sin
=
e
∗
=
e
since cos(y)
2
+ sin(y)
2
= 1 for all y. So, using this,
we get:
2x = Loga
b
x =
= Log (
a
b
and
a
b
can be written as |w|, which is the
magnitude of the complex number w.
We then compute y by dividing (eq. 2) by (eq.
1), shown above:
b
a
siny
cosy
tany
yarctan
b
a
If we combine all the above, we get:
x = Log (|w|), y Arg
w
2∗Pi∗k
z x i ∗ y
zLog
|
w
|
i∗
Arg
w
2∗Pi∗k
,
for any integer k. But z = Log(w), so
Log
w
Log
|
w
|
i∗
Arg
w
2∗Pi∗k
, (eq. 3)
for any integer k.
3.2 Inverting the Complex Exponential
Function
For one complex value w, there are infinitely many
logarithms, because we can choose any integer k in
(eq. 3) above. These infinitely many numbers form a
sequence and are all mapped to the same number by
the exponential function. Thus, the complex expo-
nential is many-to-one, a property on which we are
going to base our encryption method.
If w1 and w2 are two solutions, thene
1, in order for w1 and w2 to differ by an integer
multiple of2 ∗ π ∗ i (Figueroa-O’Farrill, 2004).
Any permissible value of w is a called an argument
for z and is denoted by arg(z). We therefore define
ApproachingEncryptionthroughComplexNumberLogarithms
575

logz ln|z| i ∗ arg
z
. To get an actual (sin-
gle-valued) function, we must make particular choi-
ces of arg(z) for each z (Figueroa-O’Farrill, 2004).
Restricting the values of a multiple-valued function
to make it single-valued in some region (in the abo-
ve example in some neighbourhood of z0) is called
choosing a branch of the function (Figueroa-O’
Farrill, 2004).
Let G be an open connected subset of C not
containing the origin. By a branch of arg z in G is
meant a continuous function a in G such that, for
each z in G the value a(z) is a value of arg z. By a
branch of log z in G is meant a continuous function l
in G such that, for each z in G, the value l(z) is a
logarithm of z (Sarason, 2007).
Let a, be a complex number. Then, following
what we have shown in section 2.1, we can show
that, for all z not equal to 0, the a-th power
is
z
e
a∗logz
e
a∗Log|z|i∗a∗argz
Depending on a, there are infinite values forz
for k
= 0, +-1, +-2 etc. Depending on a, we will have
either one, finitely many or infinitely many values of
exponent (i * 2π * a * k). If a is an integer, then the-
re is only one value for
. If a
is rational, then
has a finite number of values but, if a is irrational
then
has infinite number of values. Similarly, if a
is not real, in our case, if it is a complex number,
then a a i ∗ b with b not equal to 0, then
will have an infinite number of values (Figueroa-
O’Farrill, 2004). This is the core of the presented
method.
e
is holomorphic (i.e. is a complex-valued func-
tion that is complex differentiable in every point in
its domain) since it satisfies the Cauchy-Riemann
equations (Sarason, 2007). Thus, log z can have one
or more branches, depending on the open connected
set G used. The use of branches gives a way of deal-
ing with inverses of functions that are not one-to-one
(Sarason, 2007). We consider using a set G with the-
se properties in order to encrypt our messages and
keep the one-to-many property of the complex loga-
rithm.
4 THE COMPLEX LOGARITHM
ENCRYPTION METHOD
Encryption is the standard means of rendering a
communication private (Rivest et al., 1978). The
sender enciphers each message before transmitting it
to the receiver, thus rendering it unreadable (cipher
text) by an eavesdropper.
4.1 Encryption
Here we propose an algorithm implementing the
complex logarithm at its core and give a high-level
description of its steps. It is divided in four basic
steps and, essentially, is a mix of methods, using the
theoretical base of chain-block ciphering (Ehrsam et
al., 1976) and the notion behind the AES encryption
algorithm (Daemen et al., 2003). Nevertheless, with
the necessary mutations, complex exponentials
might be a good alternative to XOR-ing keys in ot-
her algorithms, such as known Feistel ciphers.
Essentially, our proposal replaces the Round Key
step in AES with a new one, in which the encryption
is not performed by using sub-keys derived from the
main key. Instead, a chain encryption is used where
the previous complex number that resulted from
is used as an exponential a in the following
function. This provides an “avalanche effect” since
any erroneous result in solving
in any step of the
way, will propagate the error on all coming complex
functions during the decryption process. This feature
results in increased security against known attacks,
such as the “known-plaintext” attack.
Following, we present a high-level encryption al-
gorithm using our complex logarithm method. For a
better understanding of the Complex Exponential
step of the following algorithm, the reader can sum-
marize the above mathematics in the following equa-
tion, where
(Weisstein, Wolfram
Web Resource)
:
=
∗
Thus, the steps of the algorithm are the following:
1. Complex Randomization: A first complex num-
ber is derived from the binary representation of
the first bit-block of the plaintext together with a
random generator to generate a within the chosen
open, connected group G. The resulting complex
number must conform to set G used. Padding is
used in order to ensure security of the first
encryption (exponentiation) round, as with most
algorithms of the kind (i.e. ElGamal).
2. Initial Round
- Generate random complex number a that
conforms to open group G selected.
- Combine first two parts of plaintext to create
first complex number z1 (each part serves for
real and imaginary part, respectively).
- Compute complex exponential
=C
.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
576
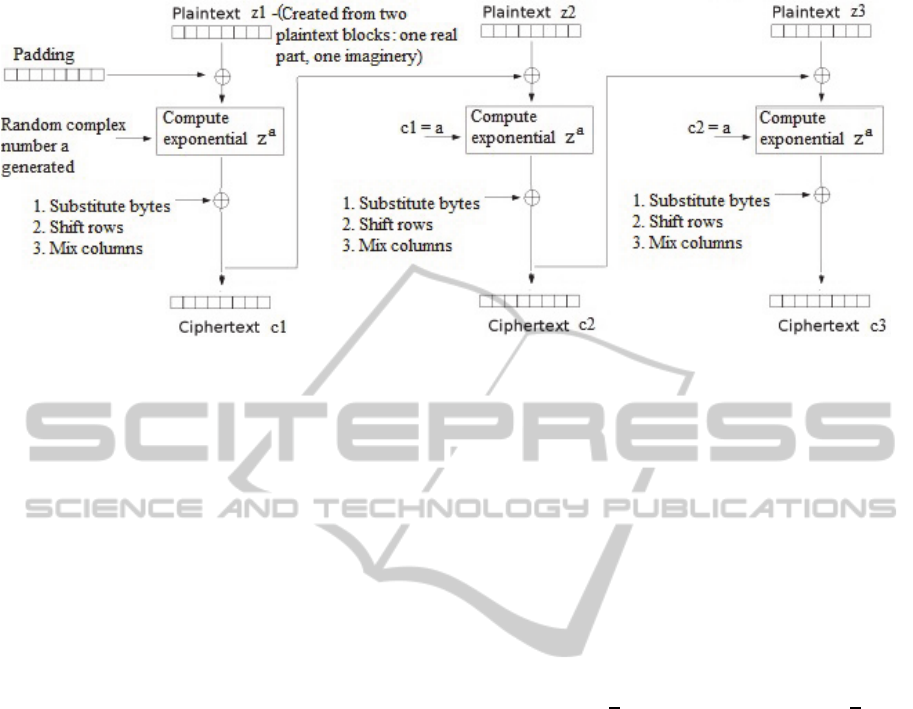
Figure 1: Visual representation of the proposed complex exponential algorithm.
3. Loop for i = 1, 2, ..., k :
- Substitute Bytes: non-linear substitution. Each
byte is replaced on the basis of a lookup table.
- Shift Rows: Transposition step. Each row is
shifted cyclically.
- Mix Columns: Mixing operation which opera-
tes on the columns of the state, combining bytes
in each column.
- Combine first two parts of plaintext to create
first complex number.
-
C
= a.
- Compute complex exponential
= C
.
4. Final Round
- Substitute Bytes
- Shift Rows
- Compute complex exponential
.
Fig. 1 provides a representation of the above algo-
rithm, with a visual analysis of the above mentioned
procedure.
4.2 Decryption
Most cryptosystems implement decryption as the
inverse process used in encrypting a plaintext. Simi-
larly, if someone knows the branch k used in com-
puting the logarithm of a complex exponential, then
he can reverse the entire process by computing each
complex exponential
and using it as input to com-
pute
.
All necessary steps are already formalized since
they follow the same notion as with chain -block
ciphers and the AES encryption/decryption method.
Assuming an appropriate branch cut for the complex
logarithm, logarithms of complex numbers can be
reduced to elementary functions of real numbers
(Sarason, 2007). Keeping that in mind, the decryp-
tion’s computational time is depended on the com-
putation cost of the logarithm. Since complex loga-
rithms can be computed using Taylor series, the
computational cost is within acceptable time bounds.
4.3 Overall Security
We mentioned above in Section 4.2 that logarithms
of complex numbers can be reduced to elementary
functions of real numbers. For example:
Ln
aib
1
2
∗Ln
a
b
i∗arctan
b
a
For a negative real number x<0, if we take into con-
sideration a chosen branch cut, we have
Ln
x
Lnabs
x
i∗Pi
The aforementioned algorithm is used in the imple-
mentation of a cryptosystem using complex expo-
nential. One part of the security of the presented en-
cryption method depends on the properties of the
underlying group G used for
z
as well as any pad-
ding scheme and steps borrowed from well-defined
cryptosystems such as AES. For further information
on how group G affects the complex logarithmic
branches, refer to complex analysis presented in
Section 3.2.
In the following subsections, we shall focus our
attention in analysing the Complex Exponential part
of the method, since this is the base axis of our main
contribution in this article. Padding, Byte substituti-
on etc. are known and well-established techniques in
cryptography (Daemen et al., 2003). In this light, we
will only present them briefly based on knowledge
from (Daemen et al., 2003).
ApproachingEncryptionthroughComplexNumberLogarithms
577

- Substitute bytes: This operation provides the
non-linearity in the cipher.
- Shift rows and Mix columns provide diffusion in
the cipher (i.e. making the relationship between
plaintext and cipher text as complex as possible).
As we have proven earlier in section 3, computing
the logarithm of a complex exponential using two
complex numbers is, under restrictions, a one-to-ma-
ny relation. This applies to plaintext binary represen-
tations and encrypted ones. In the aforementioned
algorithm, chain encryption is used between
and
1
, providing the “avalanche effect” mention-
ed earlier which increases the difficulty in cryptana-
lyzing a text encrypted with the above method.
Our encryption method is probabilistic, meaning
that a single plaintext can be encrypted to many pos-
sible cipher texts, without the consequence of size
expansion between plaintext and cipher text, such as
with the case of ElGamal (ElGamal, 1985). Perfect
secrecy states that a cipher text leaks no information
about the plaintext (to any, even an all-powerful ad-
versary). This is equivalent to stating that the proba-
bility that a given message maps to a given cipher
text is exactly identical for every pair of messages
and cipher texts (for randomly chosen keys) (Raghu-
nathan, 2011). The chain exponential encryption is
depended on a random first complex number. This
choice propagates to all exponential computations
afterwards thus, if the first random complex is diffe-
rent each time, same plain texts encrypt to different
cipher texts with no relation whatsoever.
4.4 Efficiency and Computational
Costs
Knowing that logarithms of complex numbers can
be reduced to elementary functions of real numbers
for a specific branch as we presented earlier, the
computational cost of this complex exponentiation
step is the same as computing an elementary functi-
on of a real logarithm.
Most algorithms compute elementary functions
by composing arithmetic operations. Some known
algorithms use Taylor series applicable to logarithm,
with O ((log n) 2 M (n)) complexity (Chudnovsky et
al., 1988). This shows that encryption and decrypti-
on algorithms for our method can be relatively fast
with no excessive computational cost. On a sample
encryption-decryption test we tested in our labs,
simple transformations of a simple plaintext abide to
the computational costs presented earlier (a simple
plain text sentence was encrypted and decrypted in
less than 0.1 sec (computer time) using open-source,
ready-made complex number calculators).
5 CONCLUSIONS
We proposed a method for implementing a secret-
key cryptosystem using complex logarithms and an
AES-like structure. Its security rests in part on the
difficulty in computing chained functions of comp-
lex logarithms in specific open connected groups
(logarithms computed using the notion of chain-
block encryption for the avalanche effect in the one-
to-many relations between complex logarithms and
their exponentials).
If the security of our method proves to be ade-
quate or our complex logarithm complex proves use-
ful in cryptosystems, it introduces a new concept in
secure communications and also opens up alternati-
ves in creating robust key-schedules or more. In this
case, the method could be utilized for hardening the
protection of critical applications or infrastructures
(Iliadis, 2000, Lekkas, 2006, Marias, 2007).
Future work on the subject with involve real-
world encryptions on relatively big files and tho-
rough testing of the proposed cryptosystem on nu-
merous attacks, involving semantic analysis, known-
plaintext attacks etc. in order to prove its robustness.
On top of that, the average computational complexi-
ty in cryptanalyzing cipher texts must be tested and
proven true, either through reductions in Complexity
Theory using similar, proven algorithms or through
extended testing.
ACKNOWLEDGEMENTS
Authors would like to thank Dr. Nikos Sotiropoulos
for his useful insight in complex analysis and the
complex numbers.
REFERENCES
Biryukov, A., Khovratovich, D., Nikolić, I., 2009. Distin-
guisher and related-key attack on the full AES-256,
Advances in Cryptology, pp. 231-249, Springer.
Bogdanov A., Khovratovich D., Rechberger C., 2011. Bic-
lique Cryptanalysis of the Full AES, Advances in Cry-
ptology, Springer, 2011, p. 344-371.
Chudnovsky, D., Chudnovsky, G. 1988. Approximations
and complex multiplication according to Ramanujan.
Ramanujan revisited, Academic Press.
Daemen, J., Rijmen, V., 2003. AES Proposal: Rijndael,
National Institute of Standards and Technology.
Ehrsam W., Meyer C, Smith J., Tuchman W., 1976. Mes-
sage verification and transmission error detection by
block chaining, US Patent 4074066.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
578

ElGamal, T., 1985. A public key cryptosystem and a signa-
ture scheme based on discrete logarithms, Advances
in Cryptology. Springer Berlin Heidelberg.
Figueroa-O'Farrill J., 2004. Lecture Notes in Mathematical
Techniques III, Edinburgh Mathematical Physics
Group, University of Edinburgh.
Iliadis J., Gritzalis D., Spinellis D., Preneel B., Katsikas
S., 2000. Evaluating certificate status information
mechanisms. Proc. of the 7
th
ACM Computer and
Communications Security Conference, pp. 1-8.
Jorstad D., Smith T., 1997. Cryptographic Algorithm Met-
rics, Institute for Defence Analyses, Science & Tech-
nology Division.
Lekkas D., Gritzalis D, 2006. Long-term verifiability of
healthcare records authenticity. International Journal
of Medical Informatics, 76(5-6), pp. 442-448.
Marias, J., Dritsas, S., Theoharidou, M., Mallios, J. Gritza-
lis, D., 2007. SIP vulnerabilities and antispit mecha-
nisms assessment, Proc. of the 16
th
IEEE International
Conference on Computer Communications and Net-
works, IEEE Press, pp. 597-604.
McConnachie D., 2007. Bruce Almighty: Schneier preac-
hes security to Linux faithful, Computerworld. p.4.
Raghunathan, A., 2011. Proofs in Cryptography, Stanford
University.
Rivest, R. L., Shamir, A., Adleman, L., 1978. A method
for obtaining digital signatures and public-key crypto-
systems. Com. of the ACM, 21(2), 120-126.
Sarason, D., 2007. Complex Function Theory. American
Mathematical Society.
Schneier, B., 1998. Twofish: A 128-bit block cipher, NIST
AES Proposal 15.
Schneier, B.,1994. Description of a new variable-length
key, 64-bit block cipher (Blowfish), Fast Software En-
cryption, pp. 191-204.
Shiho M., Yiqun Lisa Y., 2000. Cryptanalysis of Twofish
(II), NTT Multimedia Communications Laboratories.
Weisstein, Eric W., Complex Exponentiation, MathWorld,
http://mathworld.wolfram.com/ComplexExponentiatio
n.html
Zill, D., Shanahan, P., 2011. A first course in complex a-
nalysis with applications, Jones & Bartlett Learning.
ApproachingEncryptionthroughComplexNumberLogarithms
579
