A Preliminary Application of Generalized Fault Trees to Security

Daniele Codetta-Raiteri

DiSIT, Computer Science Institute, University of Piemonte Orientale, Viale Michel 11, Alessandria, Italy

Keywords:

Attack Trees, Fault Trees, Petri Nets, Dynamic Gates, Repair Box, Parametric Form, Simulation, Reliability,

Security.

Abstract:

Fault trees (FT) are widespread models in the ﬁeld of reliability, but they lack of modelling power. So, in the

literature, several extensions have been proposed and introduced speciﬁc new modelling primitives. Attack

trees (AT) have gained acceptance in the ﬁeld of security. They follow the same notation of standard FT, but

they represent the combinations of actions necessary for the success of an attack to a computing system. In

this paper, we extend the AT formalism by exploiting the new primitives introduced in the FT extensions. This

leads to more accurate models. The approach is applied to a case study: the AT is exploited to represent the

attack mode and compute speciﬁc quantitative measures about the system security.

1 INTRODUCTION

Fault Trees (FT) (Sahner et al., 1996) are a

widespread model in the reliability ﬁeld, and repre-

sent how combinations of component failures (called

basic events) lead to the system failure (top event).

Basic events are Boolean variables whose value turn

from false to true when the component fails. The

intermediate events (subsystem failures) and the top

event are Boolean variables as well, with the same

semantics of basic events, so their value can be deter-

mined by means of Boolean gates (AND, OR, etc.).

From a FT model, we can obtain the minimal cut

sets which are the minimal sets of component fail-

ures (basic events)determining the system failure (top

event). If a probability distribution is associated with

basic events, the FT allows the computation of several

probabilistic measures, such as the system unreliabil-

ity (the probability that the system is failed at a given

time), the probability of minimal cut sets, and impor-

tance (sensitivity) indices. The FT modelling power

is rather limited, mainly because basic events are as-

sumed to be independent. So, in the literature, several

FT extensions have been proposed introducing new

modelling capabilities, as described in Section 2.

Attack trees (AT) (Schneier, 1999) can be consid-

ered the application of FT in the ﬁeld of security. In

other words, an AT follows the same formalism of a

FT, but the goal is representing the combinations of

actions (basic events) by an attacker, in order to suc-

ceed in compromising a system (top event). AT can

be used to both graphically represent the attack mode,

and assess the system security: both the qualitative

analysis (minimal cut sets detection) and the quantita-

tive analysis (computation of probabilistic measures)

can be performed.

AT typically exploit only Boolean gates in order

to express the attack mode. So, AT and FT have the

same modelling power. In this paper, we propose

to include in an AT model all the modelling primi-

tives proposed in the several FT extensions, with the

goal of designing more accurate FT models express-

ing more complex attack modes. In particular, in Sec-

tion 3, we model and evaluate a case study by means

of an AT including Boolean gates, dynamic gates, re-

pair boxes, and the parametric form. The AT model is

evaluated by means of Petri net (Sahner et al., 1996)

generation and simulation, with the goal of computing

quantitative indices concerning the system security.

The use of simulation instead of analysis is justiﬁed

by the presence of repeatable events which lead to an

inﬁnite state space in case of analysis of the model, as

discussed in Section 3.

2 RELATED WORK

An efﬁcient way to perform both the qualitative and

the quantitative analysis (Section 1) of a FT, consists

of the generation and the analysis of the equivalent

Binary Decision Diagram (BDD) (Rauzy, 1993).

One of the ways to improve the reliability of a

609

Codetta-Raiteri D..

A Preliminary Application of Generalized Fault Trees to Security.

DOI: 10.5220/0004612606090614

In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 609-614

ISBN: 978-989-8565-73-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

system, consists of replicating its critical components

or subsystems; in these cases, the construction and

the analysis of the FT may become quite unpracti-

cal because the model will be composed by several

identical (large) sub-trees representing the replicated

parts. Parametric Fault Trees (PFT) (Bobbio et al.,

2003) were proposed with the purpose of providing

the compact modelling of such parts. Using PFT,

identical sub-trees are folded into a single parametric

sub-tree, while the identity of each replica is main-

tained through the possible values of the parameters.

Dynamic Fault Trees (DFT) (Dugan et al., 1992)

introduce dynamic gates representing several kinds of

dependency among events: functional dependencies,

dependencies concerning the order of events, and the

presence of spare components. Due to the dependen-

cies in the model, DFT need the state space solution;

this means generating all the possible system states

and stochastic transitions between states. In other

words, we need to generate and analyze the Continu-

ous Time Markov Chain (CTMC) (Sahner et al., 1996)

equivalent to the DFT.

Repairable Fault Trees (RFT) (Codetta et al.,

2004) introduce a new primitive called Repair Box

representing the presence of a repair process involv-

ing a certain set of components, and activated by the

occurrence of a speciﬁc failure event. This establishes

some dependencies among the failure and the repair

events, so the state space analysis is required, as in

the case of DFT. The state space analysis of a DFT

or RFT can be performed by conversion into a Gen-

eralized Stochastic Petri Net (GSPN) (Sahner et al.,

1996) and by exploiting the available GSPN solution

techniques consisting of the generation and the anal-

ysis of the underlying CTMC. The GSPN model can

undergo simulation as well.

In (Codetta, 2005) the modelling primitives

present in FT, PFT, DFT and RFT formalisms have

been integrated into a single formalism called Gen-

eralized Fault Tree (GFT). So, in a GFT model, we

can exploit in a combined way, the compact mod-

elling of redundancies and symmetries, the dependen-

cies among the events, the repair of components or

subsystems.

There has been a signiﬁcant amount of work on

developing quantitative evaluation tools for computer

security (MATFIA project, 2003; Dacier et al., 1996a;

Dacier et al., 1996b). In particular, the methodol-

ogy of AT has become popular and has been applied

in several contexts, such as SCADA systems (Byres

et al., 2004; Ten et al., 2007). AT can incorporate

defense mechanisms or countermeasures (Roy et al.,

2012). In (Kordy et al., 2011), the point of view of the

attacker as well as the point of view of the defender

can be analysed.

Besides AT, other modelling formalisms have

been applied to security. In (McDermott, 2000) Petri

nets are exploited to represent the attack mode, while

in (Helmer et al., 2007) an AT is converted into Petri

net with the aim of evaluating the model. Stochastic

Activity Networks (SAN) (Sanders and Meyer, 2001)

are a particular form of Petri nets; they have been ap-

plied to security in (Gupta et al., 2003). Bayesian

networks (Langseth and Portinale, 2007) are applied

in (Frigault et al., 2008; Zhang and Song, 2011; Xie

et al., 2010). Other modelling formalisms are priv-

ilege graphs (Dacier and Deswarte, 1994) and AD-

VISE (ADversary VIew security Evaluation) (LeMay

et al., 2011).

3 THE CASE STUDY

The case study consists of the acquisition by a not au-

thorized user (hacker), of the root password of a Unix

server, by means of a privilege escalation attack. We

assume that the Unix server is periodically character-

ized by two vulnerabilities: v1 is the possibility that a

not authorized entity (hacker) logs in the server; v2 is

the possibility to crack the root password.

The privilege escalation attack is performed in this

way: in the time interval between the occurrence of

v1, and the detection and recovery of v1 by the sys-

tem administrator, one or more hackers may try to

IN). After the de-

tection of v1 (event v1REP), the administrator may

discover and remove the not authorized users logged

in (event DISCOVERING). The undiscovered hackers

keep their presence in the system and may discover

the root password in two ways: 1) trying to crack

the root password (event CRACKING) during the oc-

currence of v2; 2) trying to guess the root password

(event GUESSING); this operation does not require

any vulnerability. Also v2 may be detected and recov-

ered by the system administrator (event v2REP). Both

v1 and v2 may occur again after their recovery. The

server becomes compromised if at least one hacker

succeeds in discovering the root password. We as-

sume that users authorized to log in the server are de-

pendable and never try to discover the root password.

We ignore the actions that an intruder may perform in

the system after the discovery of the root password.

All the events described above may occur if al-

lowed by the system state and after an interval of time

which is a random variable ruled by the negative ex-

ponential distribution. In this case study, the values of

the parameter λ have been chosen in an arbitrary way.

Values closer to reality might be obtained by means of

SECRYPT2013-InternationalConferenceonSecurityandCryptography

610

Table 1: The mean times to occurrence and the corresponding rates for each event in the case study.

Event Description Mean time to occurrence 1/λ (h) Occurrence rate λ (h

−1

)

v1 occurrence of v1 24 · 60 0.000694

v2 occurrence of v2 24 · 90 0.000462

v1REP recovery of v1 24 · 10 0.004166

v2REP recovery of v2 24 · 7 0.005952

LOGGING IN attempt to log in 24 · 2 0.020833

CRACKING attempt to crack the root password 24 0.041666

GUESSING attempt to guess the root password 24 · 365 0.000114

DISCOVERING detection and removal of a user logged in 24 0.041666

statistical investigations. Tab. 1 shows the mean time

to occurrence of each event, with the corresponding

parameter λ.

Some events cannot happen before other ones.

For example, the attempt to crack the root password

(eventCRACKING) cannot be performed if the hacker

has not succeeded in logging in and v2 has not oc-

curred. In a similar way, logging in may be attempted

only after the occurrence of v1. These are the tempo-

ral dependencies among the events in this case study

(the symbol ≺ speciﬁes that an event must precede

another one):

v1 ≺ LOGGING

v1 ≺ v1REP

(LOGGING

IN ∧ v2) ≺ CRACKING

LOGGING IN ≺ GUESSING

(LOGGED

IN ∧ v1REP) ≺ DISCOVERING

v2 ≺ v2REP

Some events, once “enabled”, may be repeatable. For

instance, while v1 is occurring, one or more hackers

may log in the server. In a similar way, while v2 is oc-

curring, one ore more hackers may discover the root

password. The occurrence and the recovery of a vul-

nerability are instead alternating events.

3.1 Model Design

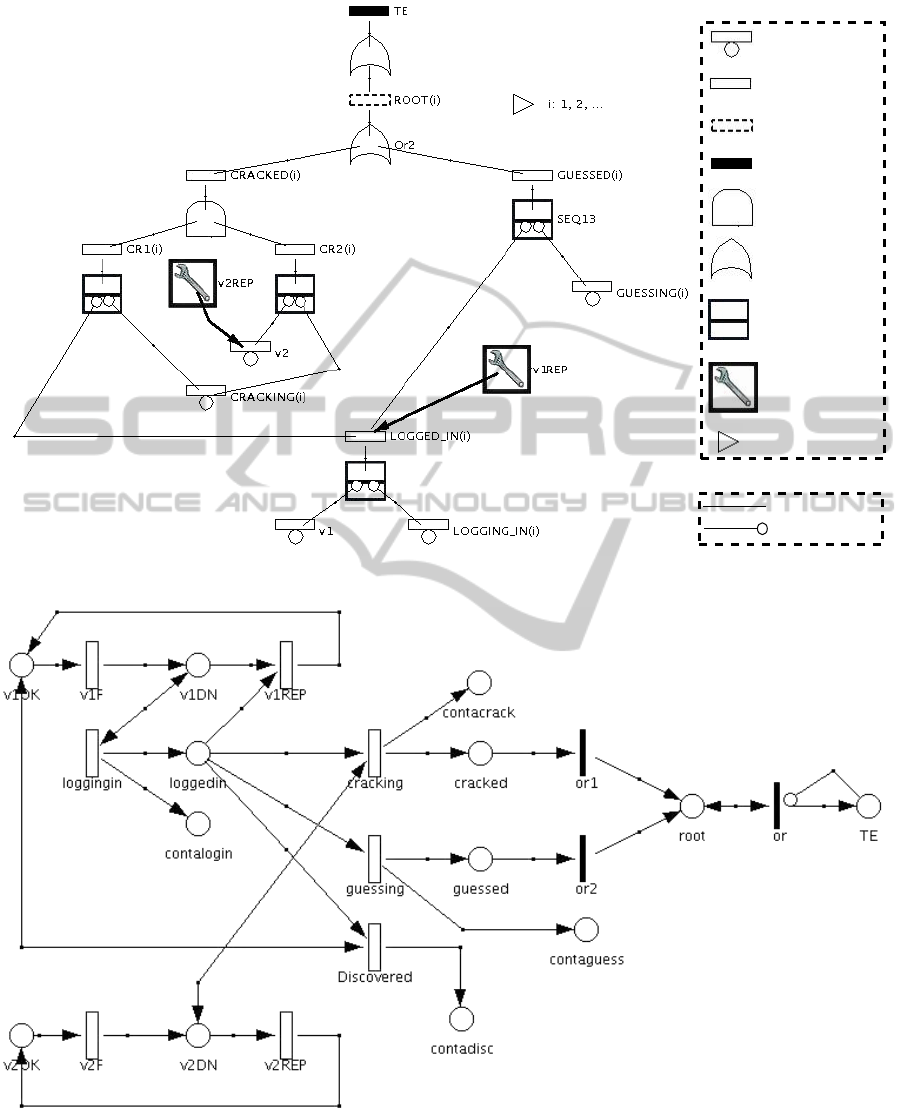
Figure 1 shows the AT representing the case study.

This model uses the modelling primitives collected

in the GFT formalism (Section 2). The top event

(TE), the “root” of the AT, represents the situation

where the server is compromised. This happens if at

least one hacker discovers the root password. There-

fore TE is the output of an OR gate connected to

the event ROOT(i), with i = 1, 2,.. .. ROOT(i) rep-

resents the discovery of the root password by the i-

th hacker introduced inside the system. ROOT(i) is

actually a replicator event. This means that the sub-

tree below ROOT(i) is the compact representation of

several sub-trees with the same structure. The iden-

tity of each sub-tree is maintained by the possible

values of the parameter i which is associated with

the events in the sub-tree, with the exception of v1

and v2 which are instead events shared by all the

replicated sub-trees. So, each sub-tree folded in the

parametric sub-tree, concerns the actions by the i-th

hacker. This notation is called parametric form (Sec-

tion 2). ROOT(i) is the output of another OR gate,

so ROOT(i) happens if the i-th intruder succeeds in

cracking (event CRACKED(i)) or guessing the pass-

word (event GUESSED(i)).

In this model, we use three Sequence Enforcing

(SEQ) gates. SEQ is one of the dynamic gates (Sec-

tion 2) and forces its input events to occur in a speciﬁc

order. The output event of this gate corresponds to

the last input event in the sequence. The basic event

CRACKING(i) (attempt to crack the password by the

i-th hacker) is connected as second input, to two SEQ

gates. Therefore this event may happen only after the

success of the log-in (event LOGGED

IN(i)) and the

vulnerability v2 (basic event v2). In the same way,

the attempt to log in (event LOGGING

IN(i)) may

happen only after the vulnerability v1 (basic event

v1). Also the event GUESSING(i) (attempt to guess

the password by the i-th hacker) is connected to a

SEQ gate: such event may happen only after the event

LOGGED

IN(i).

In the model, two repair boxes (Section 2) are

present. In an AT, the repair box can be used to model

the recovery of a vulnerability. The time to recov-

ery (repair) is a random variable, so a repair box is

ruled by the negative exponential distribution. In Fig-

ure 1, the repair box called v1REP represents the re-

covery of v1 and the detection of the not authorized

users logged in. For this reason, v1REP is connected

to the event LOGGED

IN(i) (success to log in) due

to the sequence of the basic events v1 (vulnerability

v1) and LOGGING

IN(i) (attempt to log in). The re-

pair box v2REP instead, represents only the recovery

of the vulnerability v2, so it is connected to the basic

event v2. The rates of basic events and repair boxes

are the values of λ in Tab. 1.

3.2 Model Evaluation

In this paper, the AT model in Figure 1 is translated

into a Petri Net, and in particular into the GSPN (Sec-

tion 2) in Figure 2. Both models have been edited by

APreliminaryApplicationofGeneralizedFaultTreestoSecurity

611

AND gate

OR gate

sequence enforcing

gate (SEQ)

Repair Box (RB)

Basic Event (BE)

Intermediate Event (IE)

Replicator Event (RE)

Top Event (TE)

parameter

Types of node

Input/Output arc

Order arc

Types of arc

Figure 1: Attack tree model of the case study, using GFT formalism (the labels of the nodes are explained in Tab. 1).

Figure 2: GSPN model of the case study (the details of the model are reported in (Codetta, 2013)).

means of Draw-Net (Codetta et al., 2006).

In FT, basic events are repeatable only in case of

repair. For instance, a component may fail and then,

undergo repair, fail again, and so on. In an AT, a ba-

sic event may be repeatable for an undeﬁned number

of times, even in absence of recovery. For example,

while the system suffers from the vulnerability v1, an

attempt to log in may occur even if another attempt

SECRYPT2013-InternationalConferenceonSecurityandCryptography

612

has already been done. As a consequence, any num-

ber of hackers may log in. The repetitions of basic

events leads the dimensions of the state space to be-

come inﬁnite, so the model cannot undergo analysis.

A remedy to this problem consists of setting a limit to

the number of repetitions of an event. For instance,

we could assume that 10 is the highest number of

hackers logged in. This approach reduces the dimen-

sions of the state space, but they still remain relevant,

and the model may not be realistic. So, the GSPN

obtained from the AT, has been evaluated using sim-

ulation instead of analysis. In this way, we avoid to

impose limits to the number of event repetitions, and

the simulation execution is less expensive than anal-

ysis, in terms of computing complexity. We executed

100000 simulation cycles in order to obtain the results

described below.

Several measures concerning the system security

as a function of the time have been computed by

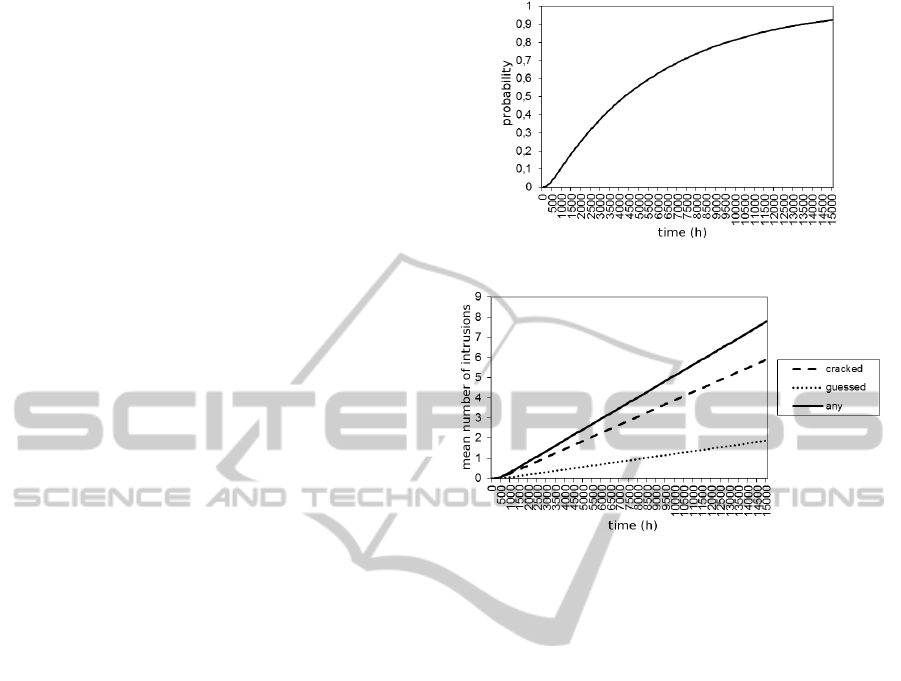
means of GSPN simulation. Figure 3 shows the prob-

ability that the system has been compromised. This

means that at least one intruder has discovered the

root password. Figure 4 shows the mean number of

intruders that have discovered the root password, by

means of password cracking or guessing. Other mea-

sures are computed in (Codetta, 2013) where we de-

scribe the details of the GSPN in Figure 2 and the way

to compute the measures on it.

4 CONCLUSIONS

The aim of this paper is transferring the previous ex-

periences about FT extensions, from reliability to se-

curity. The GFT formalism deﬁned for reliability

evaluation purposes, has been adopted for AT, so that

we can model the attack mode by resorting to a sin-

gle generalized formalism including and integrating

Boolean gates, dynamic gates, the parametric form

and repair boxes. In this way, the modelling power of

AT is improved in a relevant way, so that more accu-

rate models can be designed. The approach has been

applied to a case study characterized by dependencies

among events, recoveries and symmetries. The cur-

rent work is a ﬁrst attempt to use the GFT formalism

for AT, so the case study is rather preliminary; how-

ever, it serves as proof-of-concept to demonstrate the

feasibility of using the GFT formalism, with the con-

sequent improvement of the modelling possibilities.

The approach may be applied to more realistic cases,

for instance by using more accurate probability distri-

bution and rates. Actually the parameters in the case

study have been chosen in an arbitrary way. The AT

of the case study has been evaluated by conversion

Figure 3: Probability that the system is compromised.

Figure 4: The mean number of intruders that have discov-

ered the root password, by means of password cracking,

password guessing, or any of them.

into a Petri net and in particular, a GSPN undergoing

simulation. The goal is to avoid the problem of state

space explosion, due to the repeatable events.

We believe that the formalism needs further im-

provements in order to be suitable for the security

ﬁeld. For example, using GFT formalism, the AT

model takes into account both the attack mode and

the recovery mode. Actually, repair boxes can repre-

sent reactive recovery processes. This means that the

recovery can be performed only as a consequence of a

partial or complete intrusion. The formalism may be

extended by taking into account the preventive recov-

ery as well. In this way, preventive countermeasures

could be included in the AT model. This was already

done in (Roy et al., 2012; Kordy et al., 2011), but

using only Boolean gates. Moreover, we plan to com-

pute indices which are more security-oriented, with

respect to the measures computed in this paper.

Our intention in the future is solving AT mod-

els by means of Dynamic Bayesian Networks

(DBN) (Portinale et al., 2007), already exploited for

FT analysis. The advantage is the possibility of com-

puting predictive, diagnostic, or importance measures

conditioned by observations about the system or com-

ponents state. In the security ﬁeld, observations may

concern the action by intruders, the presence of vul-

nerabilities or countermeasures. Importance mea-

APreliminaryApplicationofGeneralizedFaultTreestoSecurity

613

sures for security, based on conditioned probability,

are deﬁned in (Roy et al., 2012). We plan to use AT

as an high-level model to represent the attack mode

and generate the corresponding DBN.

REFERENCES

Bobbio, A., Franceschinis, G., Gaeta, R., and Portinale,

L. (2003). Parametric fault tree for the dependability

analysis of redundant systems and its high-level Petri

net semantics. IEEE Transactions on Software Engi-

neering, 29(3):270–287.

Byres, J., Franz, M., and Miller, D. (2004). The use of

attack trees in assessing vulnerabilities in SCADA

systems. In International Infrastructure Survivability

Workshop, Lisbon.

Codetta, D. (2005). Extended Fault Trees Analysis sup-

ported by Stochastic Petri Nets. PhD thesis, Dipar-

timento di Informatica, Universit`a di Torino.

Codetta, D. (2013). Generalized fault trees: from reliability

to security. Technical report, DiSIT, Istituto di Infor-

matica, Universit`a del Piemonte Orientale.

Codetta, D., Franceschinis, G., and Gribaudo, M. (2006).

Deﬁning formalisms and models in the Draw-Net

Modelling System. In International Workshop on

Modelling of Objects, Components and Agents, pages

123–144, Turku, Finland.

Codetta, D., Franceschinis, G., Iacono, M., and Vittorini,

V. (2004). Repairable Fault Tree for the automatic

evaluation of repair policies. In International Con-

ference on Dependable Systems and Networks, pages

659–668, Florence, Italy. IEEE.

Dacier, M. and Deswarte, Y. (1994). Privilege graph: an ex-

tension to the typed access matrix model. In Computer

Security, pages 319–334. Springer.

Dacier, M., Deswarte, Y., and Kaˆaniche, M. (1996a). Mod-

els and tools for quantitative assessment of operational

security. Information systems security, pages 177–

186.

Dacier, M., Deswarte, Y., and Kaˆaniche, M. (1996b). Quan-

titative assessment of operational security: Models

and tools. Information Systems Security.

Dugan, J. B., Bavuso, S. J., and Boyd, M. A. (1992). Dy-

namic Fault-Tree Models for Fault-Tolerant Computer

Systems. IEEE Transactions on Reliability, 41:363–

377.

Frigault, M., Wang, L., Singhal, A., and Jajodia, S. (2008).

Measuring network security using dynamic bayesian

network. In Workshop on Quality of protection, pages

23–30. ACM.

Gupta, V., Lam, V., Ramasamy, H. V., Sanders, W. H.,

and Singh, S. (2003). Dependability and performance

evaluation of intrusion-tolerant server architectures.

In Dependable Computing, pages 81–101. Springer.

Helmer, G., Wong, J., Slagell, M., Honavar, V., Miller, L.,

Wang, Y., Wang, X., and Stakhanova, N. (2007). Soft-

ware fault tree and coloured petri net–based speciﬁca-

tion, design and implementation of agent-based intru-

sion detection systems. International Journal of In-

formation and Computer Security, 1(1):109–142.

Kordy, B., Mauw, S., Radomirovi´c, S., and Schweitzer, P.

(2011). Foundations of attack–defense trees. Formal

Aspects of Security and Trust, pages 80–95.

Langseth, H. and Portinale, L. (2007). Bayesian Net-

works in reliability. Reliability Engineering and Sys-

tem Safety, 92:92–108.

LeMay, E., Ford, M. D., Keefe, K., Sanders, W. H., and

Muehrcke, C. (2011). Model-based security metrics

using adversary view security evaluation (advise). In

International Conference on Quantitative Evaluation

of Systems, pages 191–200. IEEE.

MATFIA project (2000-2003). Malicious-and

accidental-fault tolerance for internet applica-

tions. http://research.cs.ncl.ac.uk/cabernet/

www.laas.research.ec.org/maftia/.

McDermott, J. P. (2000). Attack Net Penetration Testing. In

Workshop on New security paradigms.

Portinale, L., Bobbio, A., Codetta-Raiteri, D., and Mon-

tani, S. (2007). Compiling dynamic fault trees into

dynamic Bayesian nets for reliability analysis: The

Radyban tool. CEUR Workshop Proceedings, 268.

Rauzy, A. (1993). New Algorithms for Fault Trees

Analysis. Reliability Engineering & System Safety,

05(59):203–211.

Roy, A., Kim, D. S., and Trivedi, K. S. (2012). Attack coun-

termeasure trees (ACT): towards unifying the con-

structs of attack and defense trees. Security and Com-

munication Networks.

Sahner, R., Trivedi, K., and Puliaﬁto, A. (1996). Perfor-

mance and Reliability Analysis of Computer Systems;

An Example-based Approach Using the SHARPE Soft-

ware Package. Kluwer Academic Publisher.

Sanders, W. and Meyer, J. (2001). Stochastic activity

networks: Formal deﬁnitions and concepts. Lecture

Notes in Computer Science, 2090:315–343.

Schneier, B. (1999). Attack trees. Dr. Dobb Journal of

Software Tools, 24(12):21–29.

Ten, P. C.-W., Liu, C.-C., and Govindarasu, M. (2007).

Vulnerability assessment of cybersecurity for SCADA

systems using attack trees. In Power Engineering So-

ciety General Meeting, pages 1–8.

Xie, P., Li, J. H., Ou, X., Liu, P., and Levy, R. (2010). Us-

ing bayesian networks for cyber security analysis. In

International Conference on Dependable Systems and

Networks, pages 211–220. IEEE.

Zhang, S. and Song, S. (2011). A novel attack graph poste-

rior inference model based on bayesian network. Jour-

nal of Information Security, 2(1):8–27.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

614