
E3SN
Efficient Security Scheme for Sensor Networks
Hassan Noura, Steven Martin and Khaldoun Al Agha
Labaratoire de Recherche en Informatique, Universit´e Paris-Sud CNRS, Paris, France
Keywords:
Secure Wirless Sensor Networks, Data Integrity and Confidentiality.
Abstract:
Sensor networks are widely used in various areas and applications, and the need for effective security systems
is increasingly essential. But most security systems are based on complex algorithms that require a high
complexity and energy consumption, thus have undesirable consequences. To reduce them, a new security
system called E3SN is defined. It is based on an invertible and flexible key dependent matrix to mix the
contents of the packets. Our proposal can achieve simultaneously the information’s confidentiality, packet’s
integrity and source’s authentication, with a minimum of computational complexity, communication overhead
and memory consumption. This matrix is secret and only the transmitter and receiver can produce it in counter
mode. We evaluate our system by comparing E3SN to AES algorithm, considered reliable and robust in
several standards of sensor networks such as ZigBee, WirelessHART and ISA100.11a. The results show that
the proposed technique is much more efficient than AES, with the same quality of cryptography.
1 INTRODUCTION
Recently, the security of Wireless Sensor Networks
(WSN) is becoming principal for researchers and in-
dustry. These kinds of communication are suscepti-
ble to several attacks. The existing attacks can be
divided into two classes: active and passive. The
passive attacks can seriously impair the confidential-
ity of data, while the active attacks can damage their
authentication. Moreover, The nature of passive at-
tacks makes them rather difficult to be detected com-
pared to the active ones. The active attacks may in-
sert, delete or modify packet contents while passive
aim to know them. Encrypting packets among sen-
sor nodes can solve the problems of passive attacks,
but it requires a distributed scheme and a robust key
exchange. The traditional scheme uses symmetric
key cryptography for data encryption, while it pro-
vides efficient memory and computational complexity
compared to Asymmetric Key Cryptography (AKC).
AKC is used for the secret key communication among
sensor nodes. Secured services such as data confi-
dentiality, integrity and source authentication are es-
sential for safe WSN transmission. The confidential-
ity can be achieved using symmetric key cipher like
the Advanced Encryption Standard (AES) (Daemen
et al., 1998). This algorithm is not only known for its
robustness, but also for its complexity and time con-
suming in WSN. In addition, the family of SHA (200,
2002) (e.g. SHA-2, SHA-512) is used to ensure data
integrity while HMAC (Krawczyk et al., 1997) for
source authentication. Moreover, some security pro-
tocols have been presented to provide security so-
lution like IPSec as in (Doraswamy and Harkins,
1999), and others (Perrig et al., 2002), (Karlof et al.,
2004), (Luk et al., 2007), (Rogaway et al., 2001) es-
pecially for WSN.
However, the security of WSN suffers from var-
ious limitations such as higher memory consump-
tion, computation overhead, and power consumption.
Also, it may require a communication overhead. In
general, major techniques of secure WSN have a
trade-off between security and performance. They are
attempting to design a secure Shannon network, but
this causes a decrease in the throughput. The WSN
limitations require cipher scheme with low computa-
tion complexity. This provokes a hard challenge with
the available resource constraints. This paper presents
a new efficient and robust security scheme that attains
low complexity computation. Compared to previous
works, a new technique based on the mixing of sev-
eral packets in a secret dynamic manner is proposed.
Therefore, it can solve the above challenge. The mix-
ing process is realized by using a new method of key
dependent, flexible and invertible matrix. The overall
computation complexity is reduced to one mixing it-
eration in packet level. In addition, a new header is in-
troduced for each packet with 8 bytes length. The ba-
615
Noura H., Martin . and Al Agha K..
E3SN - Efficient Security Scheme for Sensor Networks.
DOI: 10.5220/0004613006150621
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 615-621
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

sic structure of our scheme is a combination between
the HMAC algorithm and the proposed mixing layer.
The aim of this paper is to realize a security pro-
tocol that can ensure a safe transmission with a re-
markable efficiency. The rest of this paper is orga-
nized as follows. Section 2 describes the proposed
secure scheme, and presents a new construction tech-
nique of key dependent, flexible and invertible matrix.
Performance and security of the proposed scheme are
analyzed in section 3. Finally, section 4 presents our
conclusion.
2 THE PROPOSED SECURE
SCHEME
Most security mechanisms that exist today require in-
tensive computation and memory. They apply the se-
curity service on the block level of packets which re-
quires a high computational complexity. This proves
clearly that this method is not efficient especially in
the case of constrained resources as WSN. Our idea is
based on the mixing characteristic of Network Cod-
ing (NC). This section features a new efficient and se-
cure scheme for WSN. Usually, the term efficiency
means having the fastest time while keeping secure
conditions of the WSN. This work can overcome
the above-described disadvantages of previously pre-
sented works and define a new technique to ensure
the security. In fact, the ease of implementation
is attained when operating with constrained devices.
The secure scheme primarily consists of three stages:
source encryption, intermediate forwarding, and des-
tination decryption. The proposed Authentication Ci-
pher Scheme (ACS) and the proposed Authentication-
Decipher Scheme (ADS) is applied at the source and
destination side respectively. No modifications or
supplementary operations are necessary at the inter-
mediate nodes, since our solution is transparent.First,
a general description of the proposed scheme is de-
scribed,then the proposed ACS and ADS are de-
scribed in details.
2.1 The proposed Secure Scheme at
Emitter Side
In practical WSN scenarios, the source may need to
transmit a large volume of data M. In this case, the
source should first divide M into different generations
M
1
,M
2
,....,M
n
. Then divide each generation into dif-
ferent packets M
i
= {m
1
,m
2
,....,m
g
}. We propose
that the authentication and encryption using different
keys to strengthen the level of security. The different
1: procedure KEY UPDATE(MK, adin,i, j,c1,c2)
2: if i ≥ w then
3: c1 ← c1+ 1
4: MK
c1
← SHA
512(MK||c1||adin)
5: else
6: if j ≥ d then
7: V
c
1 ← SHA
256(MK
c1
||adin||c1)
8: c2 ← c2+ 1
9: SK
c1,c2
← SHA
256(V
c1
||adin||c2)
10: end if
11: end if
12: return SK
c1,c2
,c1,c2
13: end procedure
Figure 1: Key update ’s algorithm.
steps of the proposed scheme at the emitter side are
described below in details:
2.1.1 Dynamic Key Generation
This section describes two processes: the first one de-
fines the process of updating the master key and how
produces the section key. Then the process of gen-
erating the dynamic key is presented. This process
is introduced to overcome the problem of fixed key.
The Master Key (MK) should be updated after sev-
eral transmissions to strengthen the level of security.
A new scheme for generating the Section Key (SK)
using the master key (Mk
c1
) is defined. The cycle
length of each master key is w generations. Let Sk
c1,c2
denote the section key used in the c2 interval of Mk
c1
.
The cycle length of each section key is d generations,
which were obtained as described in Figure 1 as a
pseudo code. The variables i and j are integer values
representingthe numberof requests for the master key
and the section key from an instantiation of the sec-
tion key and the master key respectively. Each gener-
ation is encrypted and authenticated using a key pro-
duced different key obtained from the dynamic key
(Kd). The dynamic key is derived from the section
key, Nonce, and the source/ destination nodes (Phys-
ical and/or IP address) as additional information. In
our simulation, the value of the parameters d and w
are set to 2
10
and 2
16
respectively. The elements of
Nonce can be considered as a unique element to guar-
antee that the obtained key is new for each generation.
2.1.2 Construction of the Secret Matrix G
As described above, the process of encryption is im-
plemented using the secret matrix G, which was ob-
tained from the proposed flexible invertible key de-
pendent matrix. This method is divided into two
steps: The first one is the generation of the binary
key-stream that used to construct the sub matrix,
which was used to form the Primary Matrix(PM).
SECRYPT2013-InternationalConferenceonSecurityandCryptography
616

MICKEY 128 is used as a stream cipher. It is de-
fined to be efficient in hardware implementation as in
(Robshaw and Billet, 2008). This matrix has a deter-
minant equal to 1, which means it is invertible (non
singular matrix). Then a shuffle algorithm is applied
to reorder the lines, then the columns of the PM. The
secret matrix G is the result of the shuffling algorithm.
Note. The determinant of the PM of size (h, h) is
equal to 1. Therefore, the determinant of the shuffled
matrix stays equal to 1, this means that the process of
shuffling reserves the invertibility.
KE and KA are calculated by flipping the even and
odd bits of Kd respectively. MICKEY
128 is iterated
with KE as a seed for it iterations to produce the key-
stream S, where it = 2 × m× l. Then S is divided in
two equal parts to form the sub-matrix parameter Mu
and Mv.
This method based on four different invertible ma-
trices as the determinant is ± 1. The proposed tech-
nique is simple, and flexible in an efficient manner
and effortless to implement in hardware. In the fol-
lowing, our method to build dynamic secret matrix is
described.
Note. The determinant of the product of two square
matrices A and B of size (h,h), is equal to the product
of the determinant of two matrices. Thus, if a and b
are respectively, the determinant of the matrix A and
that of the matrix B.Therefore, the determinant of the
matrix, obtained from the multiplication of A× B, is
a× b.
Thus, to ensure a good layer of diffusion among
the packets of a generation, the multiplication of two
different matrices is performed. Which were used the
sub matrices Mu and Mv respectively to form these
matrices. The final form of the secret matrix G de-
pends on the Parity Bit (PB) of the dynamic key:
I f PB = 0,G = M
0
× M
2
, Else G = M
1
× M
3
The four matrices can be used (M
0
,M
1
,M
2
,andM
3
)
to construct the invertible secret matrix G are given as
below:
M
0
=
I
m
Mu
Mv I
l
+ MuMv
, M
1
=
Mu I
m
I
l
+ MuMv Mv
M
2
=
Mv Il +MuMv
I
m
MU
, M
3
=
Il +MuMv Mv
MU I
m
The determinant of the various matrices M
w
,w =
0,1,2, 3 is equal to ±1, then these matrices are invert-
ible. I
m
and I
l
are two identity matrices of size m and l
respectively. M
u
and M
v
are two non-zero matrices of
size m× l and l× m respectively, with m = ⌈h/2⌉ and
l = h − m. The elements of M
u
and M
v
can be freely
chosen from any Galois field such that M
w
is full rank.
In our simulation, the elements of this sub-matrix is
binary {0,1} to avoid the overhead for higher h. M
u
and M
v
are used for the various structures. The use
of different M
u
and M
v
for the various structures in-
crease the key space of secret matrix G but require
double iteration of MICKEY
128. The invertible of
each matrix can be proven as follows.
Having a matrix M constructed from four sub-
matrix (A,B,C, D)
M =
A B
C D
its determinant is given by:
det(M) = det(A) × det(D−CA
−1
B) (1)
For example , if M = M
0
, the determinant of M
0
will
be:
det(M
0
) = det(I
m
) × det(I
l
+ M
v0
M
u0
− M
v0
I
−1
l
M
u0
)
= det(I
m
) × det(I
l
+ M
v0
M
u0
− M
v0
M
u0
)
= det(I
m
) × det(I
l
) = 1
(2)
This means that the necessary condition to possess
an inverse and get the original data at the receivers
is achieved. In Figure 2, an example of the different
steps applied to construct the secret matrix G is shown
for h = 4, PB = 0 and
Mu =
1 0
0 0
, Mv =
0 1
1 1
M
u
or M
v
is formed by the binary key stream with
length h
2
/2. In Figure 3, the primary matrix for
h = 64 is shown. Therefore, the high value of PM
is concentrated in the above right sub-zone. From the
viewpoints of security, it can remain limited to our
proposal. The process of shuffle is applied to dif-
fuse these values in the whole space. The G matrix
is obtained by permuting the rows of PM according to
the permutation vector Ind
L, then the columns is in-
terchanged according to the given permutation vector
Ind
C.
Figure 2: An example of construction secret matrix G for
h = 4.
2.1.3 Encryption of Generation
The buffering model divides the stream of packets
into generations of size g, such the packets of the
E3SN-EfficientSecuritySchemeforSensorNetworks
617
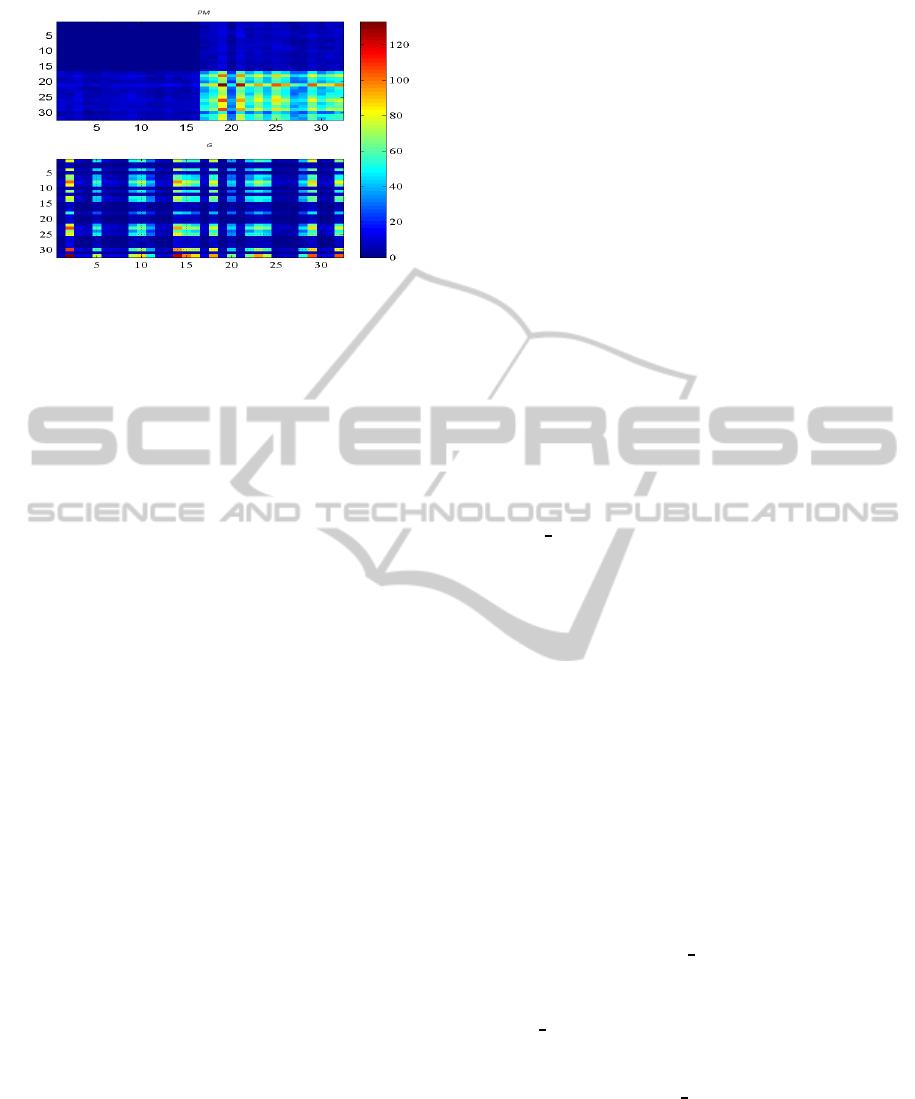
Figure 3: An example of constructed PM and its correspon-
dent G after the process of shuffle for h = 32.
same generation are tagged with a common genera-
tion number NG. When performing encryption on a
series of source packets {m
1
,m
2
,...,m
g
}, a pseudo-
random linear combinations of the source packets are
created and sent instead of the original source packets.
Our scenario of encryption is by performing a mod-
ular multiplication matrix using G to get the cipher
generation X. The process of encryption/decryption
can treat in parallel to reduce the complexity, since
each encrypted packet is independent of others. The
encryption/decryption packets are the result of h ran-
dom linear combination packets in a dynamic man-
ner. The coefficients {c
1
,c
2
,...,c
g
} is described as the
encryption vectors. Each encryption vector is repre-
sented as a sequence of independent random numbers
from a field. The original source packets can be re-
trieved from the encrypted packets when h different
linear independent packets are present at the receiver.
The relationship among encryption packets, encryp-
tion vectors and source packets can be described in
the matrix equation as follows:
X = G × (M)
=
x
1
x
2
.
.
.
x
h
=
G
1,1
G
1,2
···G
1,h
G
2,1
G
2,2
···G
2,h
.
.
.
.
.
.
.
.
.
.
.
.
G
h,1
G
h,2
···G
h,h
·
m
1
m
2
.
.
.
m
h
(3)
Where m
i
is a source packet, c
i, j
is an encryption
coefficient varies between 0 and q − 1 for the line
i and column j and i, j = 1,2,...,h. Moreover, q is
the size of finite field over which WSN is performed.
x
i
is the resulting encryption packets, g is the num-
ber of source packets, h is the number of generating
packets, also known as GS, and h ≥ g to allow re-
ceivers to decrypt when a failure channel decoding
occur. That is, the encrypted packets are combina-
tions of the form c
1
·m
1
+c
2
·m
2
+...+c
h
·m
h
. There-
fore, h = g + ⌈g× pe⌉. While m
i
,i = h − g + 1 is a
null packet (all elements are zero). Another possibil-
ity could be used for the proposed secure scheme is
MDS (Gupta and Ray, 2013). We don’t recommend
it, while it requires a high computational complexity
compared to our proposal.
2.1.4 Authentication of the h Encrypted Packets
The different steps to obtain the MAC value are de-
signed to ensure the effectiveness. The overall cost
for authenticating the stream data is close to that of
hashing these data, especially as data gets large. To
reduce the complexity, the contents of the h encrypted
packets are xored together to form a unique payload
called (temp). HMAC is used with SHA-512 to avoid
hash collision. The input of HMAC is composed of
the vector temp, the extension header NG||GS and the
authentication keyKa. Then, the output of HMAC is
transformedinto matrix with 4 rows and 128 columns.
The 4 rows are xored together to obtain the MAC
value MAC with a size of 128 bits.
2.1.5 Asymmetric Encryption of the MAC value
E
MAC
The MAC is encrypted using the RSA public-key
crypto-system, which was performed with the private
key Kr. Then, it is transmitted to the receiver in an en-
crypted form. The use of private key provides the non
repudiation of the source, which is a principal service.
The algorithm could be more secure, if the (public,
private) keys (Ku, Kr) are renewed after every peri-
odic interval. This interval depends on the area of
application. Two kinds of keys are used for the en-
cryption and the decryption processes.This setting has
additional advantage, since the cryptanalyst requires
applying two different attacks. It is a hard task, while
symmetric and asymmetric cryptosystems have to be
tackled separately (hybrid encryption), which will en-
hance the security level.
2.1.6 Transmission(X,E
MAC)
The transmitted informations to the receiver are the
cipher E
MAC and the encrypted packets X. If the op-
portunity of transmission at an outgoing edge is pos-
sible, the sending node first sends the encrypted gen-
eration, then the cipher E
MAC must be transmitted
for verification of data integrity and source authenti-
cation.The contents of packets are mixed via dynamic
secret matrix G, and the intermediate nodes have no
knowledge about G, it is rather difficult for them to
reconstruct the source packets. In addition, the pro-
posed scheme introduces a small overhead of 8 bytes
per packet (NG||GS||NP).
SECRYPT2013-InternationalConferenceonSecurityandCryptography
618
2.2 The Proposed Secure Scheme at the
Receiver Side
The different steps of the proposed scheme at the re-
ceiver side are described below in details:
2.2.1 Asymmetric Decryption of the MAC Value
At the receiver end, the recipient uses the public emit-
ter RSA key Ku to decrypt E
MAC.
2.2.2 Sort packets Based on NG
The receiver buffering model sorts the packet stream
into generations according to their NG, such that the
packets of the same generation are put in a single
buffer.
2.2.3 Dynamic Key Generation R
Kd
The dynamic keys of authentication (R Ka) and de-
cryption (R Ke)are generated using the same ap-
proach, which was applied at the emitter side.
2.2.4 Verification of Source Authentication
(C MAC,R MAC)
The proposed solution is efficient since it prevents the
attacker from requesting the decrypts of any cipher-
generation unless he verifies correctly using the pro-
posed authentication scheme, which implies that he
already knows the cipher key. Once h different en-
crypted messages are collected from an arbitrary gen-
eration, a new MAC is calculated at the receiver side
called C
MAC using the same approach, which was
applied at the emitter side. If C
MAC is equal to
R MAC, the source is verified. Otherwise, the authen-
tication of the source is not valid.
2.2.5 Decryption of the Encrypted Generation
If the source is verified, then the destination can start
the decryption process. Once h linearly independent
messages are collected, the destination produces the
secret matrix G using its correspondent dynamic key.
The decryption of the encrypted generation X is ob-
tained by using the inverse secret matrix G
−1
as fol-
lows: M = G
−1
× X.
3 PROPERTIES ANALYSIS
To qualify the future usages of our key dependent
invertible matrix, it is important to understand their
characteristics. Two important properties should be
achieved to ensure a high level of security, which are
the random recurrence and the mixing nature. In our
simulation, the proposed security scheme is consid-
ered as a black box and randomly choosing a set of
initial packets with 1500 byte length, which are nor-
mally distributed with a mean equal to 128 and a stan-
dard deviation equal to 16.
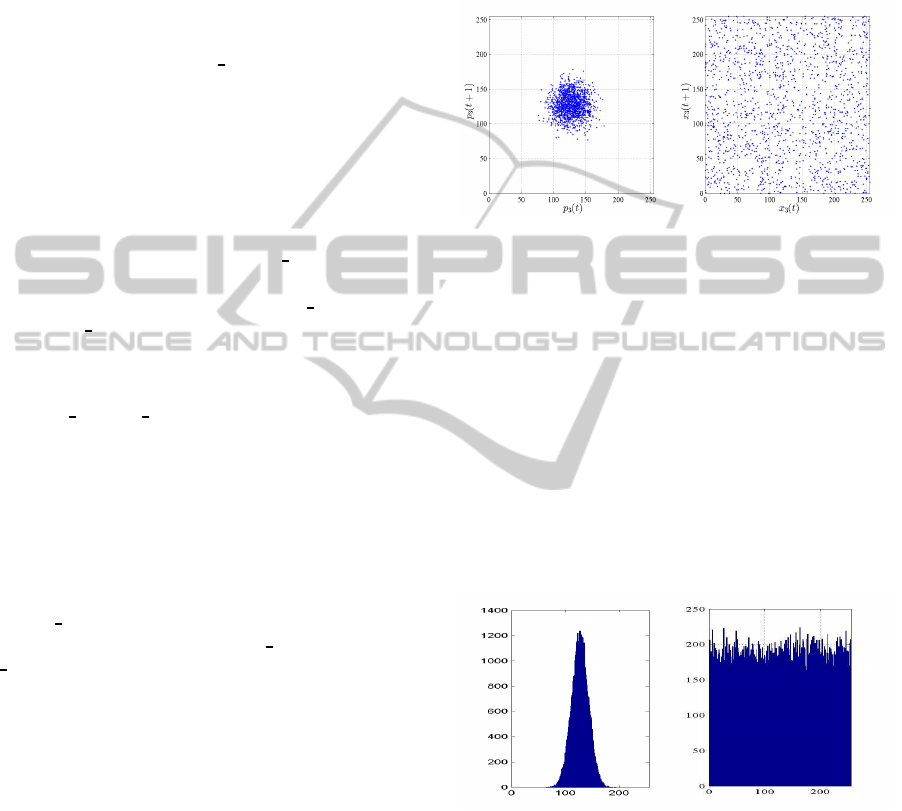
(a) (b)
Figure 4: Recurrence plot of the 1 th original packet (a) and
its correspondent encrypted ones (b).
3.1 Recurrence
The recurrence plot serves to measure the evalua-
tion of randomness and estimates the correlations
among the data of a sequence as in (Rodgers and
Nicewander, 1988). Considering a packet sequence
x
i
= x
i,1
,x
i,2
,...,x
i,m
, a vector with delay t ≥ 1 can
be constructed by: x
i
(t) = x
i
,x
i+t
,x
i,2∗t
,...,x
i,m∗t
. In
Figure 4 a-b, the variation between x
i
(t) and x
i
(t + 1)
from the original and the encrypted packets respec-
tively are shown. It is clearly shown that no clear pat-
tern is obtained after encryption.
(a) (b)
Figure 5: Recurrence plot of the 1 th original packet (a) and
its correspondent encrypted ones (b).
3.2 Correlation Analysis
As a general requirement for all the encryption
schemes, the encrypted data should be greatly dif-
ferent from its original form. The encrypted pack-
ets, should have redundancy and correlation as low
as possible. First, the correlation coefficient between
the original and encrypted packets is measured, then
E3SN-EfficientSecuritySchemeforSensorNetworks
619

Figure 6: The coefficient correlation between the original
and encrypted contents packets for h = 32.
among the different encrypted packets. The correla-
tion coefficient is computed according to the follow-
ing formulas:
ρ
x,y
=
cov(x,y)
p
D(x) × D(y)
(4)
where cov(x,y) = E[{x− E(x)}{y− E(y)}];
E(x) =
1
n
×
n
∑
k=1
x
i
and D(x) =
1
n
×
n
∑
k=1
{x
i
− E[x]}
In Figure 6, the average coefficient correlation be-
tween the original and encrypted packets for 10000
different secret matrix with h = 32 is shown. This re-
sult indicates that no detectable correlation exists be-
tween the original and its corresponding cipher pack-
ets.
3.3 Mixing Nature
The mixing nature serving as a measure of the uni-
formity and it can quantify by a statistical approach.
If the frequency counts of the encrypted generation
are close to a uniform distribution, then it is possi-
ble to categorize that the concerned cipher under test
have a good level of mixing. In Figure 5-a and b,
the distribution of the original generation and its cor-
responding cipher generation respectively is shown.
This result shows clearly that the contents of the en-
crypted packet are spread overall the space and have a
uniform distribution. To validate this uniformity, the
chi-square test (Bates and VA., 1966) is applied and
works as follow:
χ
2
test
=
l
∑
i=1
o
i
− e
i
e
i
(5)
The distribution of the tested histogram is uniform for
h≥12, that means an acceptable mixing and a stronger
mixing property can be obtained when the generation
size is higher.
3.4 Flexibility and Execution Time
Our proposed scheme ensures the flexibility, while
it is able to extend with the increase/decrease of the
number of packets in generation h. Additionally, we
ensure a low computation Complexity and by con-
sequence fast execution time. The operation speed
is significant especially for constrained resources ap-
plication such WSN. The average calculation times
(on 10000 times) to encrypt a generation M against h
in s is presented in Figure 7. These calculations are
given in the following environment software and ma-
terial: Matlab on 2012 and micro-computer Intel Core
2 Duet 2.1 GHZ CPU with 2 GB RAM Intel, under
Windows Live. Clearly, the variation of average time
is linear. The average times necessary against h is es-
timated (approximately) using the linear interpolation
method. It shows that the proposed method is indeed
the fastest and sufficiently fast for WSN applications.
We compare the mean encryption time (in seconds),
versus h, of the proposed cipher with AES.The pro-
posed secure scheme is at least 5× h times faster than
the AES algorithm.
Figure 7: Variations of the average time for encryption gen-
eration versus h.
4 CONCLUSIONS
The WSN security becomes more and more impor-
tant, since WSN are used for many kinds of appli-
cations such as environmental monitoring and mil-
itary applications. The existing schemes use cryp-
tographic algorithms that fail to achieve low execu-
tion time for high security level like AES, which is
considered as robust algorithm but requires a high
complexity and energy consumption. In this paper,
a new security scheme has been described to provide
a safe WSN called E3SN, which requires less com-
plexity and energy consumption. E3SN is based on
a new flexible and invertible key dependent diffusion
layer. It provides at the same time the data confiden-
tiality, integrity and the source authentication. There-
fore, E3SN has been analyzed to quantify its degree of
SECRYPT2013-InternationalConferenceonSecurityandCryptography
620

randomness, uniformity, sensibility of key and cryp-
tographic strengthen (dynamic key in counter mode)
against different attacks (statistical, linear, differen-
tial). In addition, the results in terms of processing
time and complexity indicate a significant reduction
compared to AES CTR, which leads to decrease en-
ergy consumption by consequence. In the future, our
work will be extended to resist against pollution at-
tacks and more WSN security services will be intro-
duced.
REFERENCES
(2002). Secure hash standard. National Institute of Stan-
dards and Technology, Washington. URL: http://
csrc.nist.gov/publications/fips/. Note: Federal Infor-
mation Processing Standard 180-2.
Bates, C. and VA., N. W. L. D. (1966). The Chi-square Test
of Goodness of Fit for a Bivariate Normal Distribu-
tion. Defense Technical Information Center.
Daemen, J., Daemen, J., Daemen, J., Rijmen, V., and Rij-
men, V. (1998). Aes proposal: Rijndael.
Doraswamy, N. and Harkins, D. (1999). IPSec: The New
Security Standard for the Internet, Intranets, and Vir-
tual Private Networks. Prentice Hall PTR, Upper Sad-
dle River, NJ, USA.
Gupta, K. C. and Ray, I. G. (2013). On constructions of mds
matrices from companion matrices for lightweight
cryptography. Cryptology ePrint Archive, Report
2013/056.
Karlof, C., Sastry, N., and Wagner, D. (2004). Tinysec: a
link layer security architecture for wireless sensor net-
works. In Proceedings of the 2nd international confer-
ence on Embedded networked sensor systems, SenSys
’04, pages 162–175, New York, NY, USA. ACM.
Krawczyk, H., Bellare, M., and Canetti, R. (1997). Hmac:
Keyed-hashing for message authentication.
Luk, M., Mezzour, G., Perrig, A., and Gligor, V. (2007).
MiniSec: a secure sensor network communication ar-
chitecture. In IPSN ’07: Proceedings of the 6th inter-
national conference on Information processing in sen-
sor networks, pages 479–488, New York, NY, USA.
ACM Press.
Perrig, A., Szewczyk, R., Tygar, J. D., Wen, V., and Culler,
D. E. (2002). Spins: security protocols for sensor net-
works. Wirel. Netw., 8(5):521–534.
Robshaw, M. J. B. and Billet, O., editors (2008). New
Stream Cipher Designs - The eSTREAM Finalists,
volume 4986 of Lecture Notes in Computer Science.
Springer.
Rodgers, J. L. and Nicewander, A. W. (1988). Thirteen
Ways to Look at the Correlation Coefficient. The
American Statistician, 42(1):59–66.
Rogaway, P., Bellare, M., Black, J., and Krovetz, T. (2001).
Ocb: A block-cipher mode of operation for efficient
authenticated encryption. pages 196–205. ACM Press.
E3SN-EfficientSecuritySchemeforSensorNetworks
621
