A System Dynamics Study of an Emergency Department Impact

on the Management of Hospital’s Surgery Activities

Lucia Cassettari, Roberto Mosca, Andrea Orfeo, Roberto Revetria, Fabio Rolando

DIME Department of Mechanical, Energetic, Management and Transport Engineering, University of Genoa,

Via all’Opera Pia 15, 16145, Genoa, Italy

J. Bradley Morrison

Brandeis International Business School, Waltham (MA), U.S.A.

Keywords: Emergency Department, System Dynamics, Healthcare Management.

Abstract: In Italian hospitals equipped with an Emergency Department (ED), it is possible that patients coming from

such a structure occupy beds that had previously been scheduled for other patients. This happens because of

some law regulations that give these kind of patients preferential access to hospitalization, and it may cause

reduction in, or even stop, scheduled surgery activities. For such a reason operating theaters, surgery teams,

sterilization structure, etc., are often unable to operate in an efficient way. Regarding costs and hospital

management, this issue become considerable, and maybe even more unpleasant for patients on the waiting

list since their scheduled surgery date generally is delayed by a long time. Studying an ED, the authors

decided to build a System Dynamics model to analyze the impact of the admission from ED on other

hospital structures, and thus identify the critical threshold. Some “non trivial” corrective actions have been

evaluated in order to suggest how to address the problem which is currently causing internal conflicts and, if

not managed, is destined to grow over time.

1 INTRODUCTION

The persistence of economic turmoil, which was

originated in the U.S. due to subprime mortgages

and the collapse of Lehman Brothers in 2008, has

forced many sovereign states in Europe to take

drastic policies to limit their debt.

Among all the financial measures adopted by

Italian government, also the Healthcare system, with

a level of annual costs out of control, became the

subject of increasingly frequent budget cuts aiming

to contain the amount of Healthcare spending which

in 2010 reached 9,6% of the Gross Domestic

Product.

As a direct consequence, managers of individual

cost centers (Local Healthcare public utilities - ASL,

hospitals, research laboratories) had to make a

choice between two alternatives: on one side the so-

called "linear cuts" to performances, on the other,

the pursuit and elimination of systemic

inefficiencies, usually quite spread in those systems.

This second way of act is certainly more difficult but

could allow to recoup the amount of money

corresponding to lower state transfers, without

negatively affect the capacity of healthcare

assistance.

Thanks to the experience gained in recent years

by the DIME research group in the healthcare

management field, working jointly with some

hospital managers particularly sensitive to choice

the second route mentioned above, it has been

shown how wide the scope for action for engineers

trained in the management of complex systems

(Cassettari et al., 2011); (Frigato et al., 1999);

(Mosca et al., 2002); (Mosca et al., 2005); (Mosca et

al., 2009); (Mosca et al., 2010); (Revetria et al.,

2011). In fact, with this kind of background culture,

based on the use of ideas and models from the world

of production and services, it is widely possible to

reduce systemic costs through significant

improvements in management efficiency. This paper

arises from a collaboration between DIME research

597

Cassettari L., Mosca R., Orfeo A., Revetria R., Rolando F. and Morrison J..

A System Dynamics Study of an Emergency Department Impact on the Management of Hospital’s Surgery Activities.

DOI: 10.5220/0004617205970604

In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (HA-2013), pages

597-604

ISBN: 978-989-8565-69-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

group and Prof. J. B. Morrison from Boston’s

Brandeis University. It aims to show how, through

the combined use of quantitative analysis and

modeling tools (Briano et al., 2010); (Cassettari et

al., 2010); (Cassettari et al., 2011); (Mosca and

Giribone, 1982); (Mosca et al., 2005); (Mosca et al.,

2010), it is possible both analyze and understand the

reasons that underlie certain inefficiencies, and the

consequences of any corrective actions, before they

are adopted.

The subject of this paper is a classic theme,

namely an analysis of the impact of an Hospital’s

Emergency Department (ED) on the beds

management of the hospital itself. With specific

reference to the examined case, it should be stated

that there are two different kind of access to the

hospital:

 Ordinary admissions: made through booking and

then scheduled in the ordinary surgery activity ;

 Urgent admissions: admissions from the ED,

affected by statistical randomness and with strict

priority on ordinary admissions according to

Regional laws;

This second type of access implies a possible

negative impact on the planning of hospital

departments operating on appointment (ordinary

surgery). In particular, especially in conjunction

with epidemic events, the hospitalization of these

patients in surgical wards reduces availability of

beds to those who are waiting for surgical operation,

reducing, consequently, the activity of whole

divisions. The obvious consequence is the negative

impact on the operators’ utilization indexes and the

reduction in efficiency with the related increase in

costs due to inactivity. In order to better understand

the extent of the problem, it could be highlighted

that the 54% of overall 2011 hospital admissions

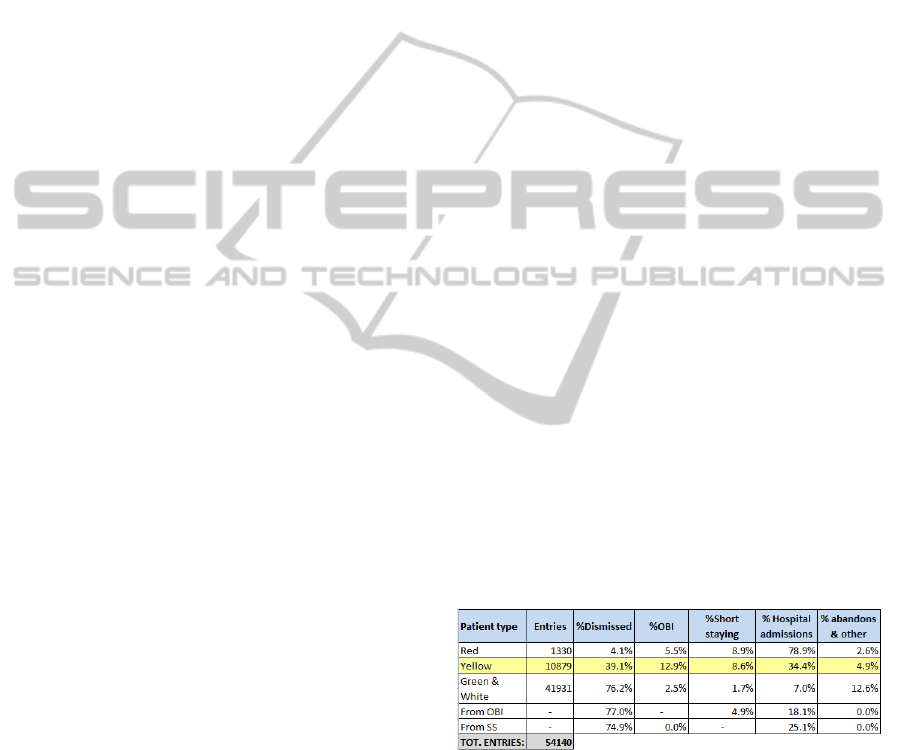
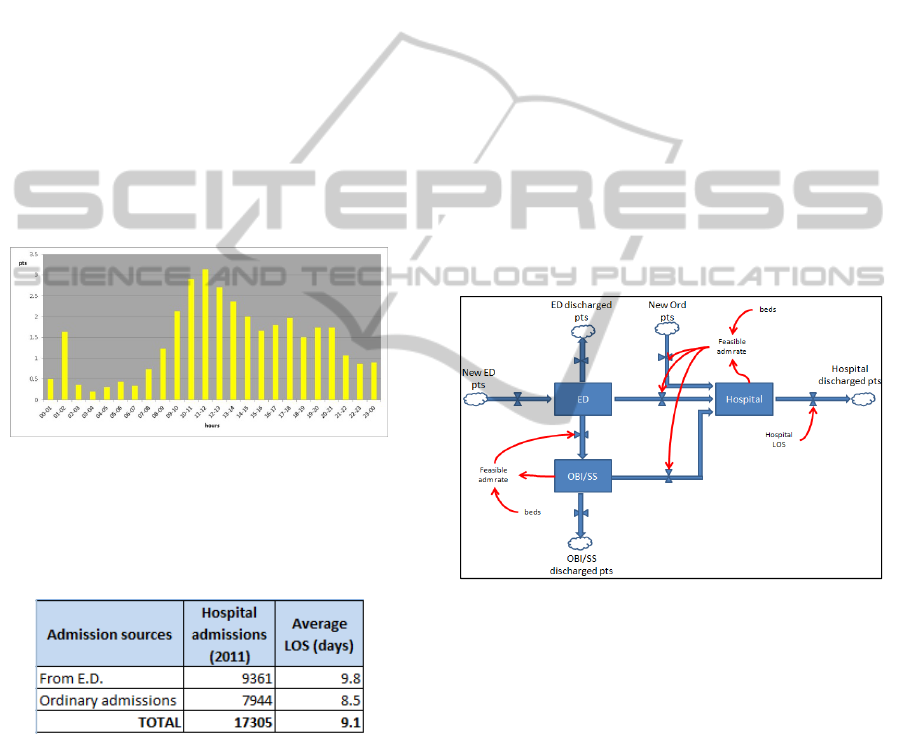
(9361 on 17305) came from ED (Table 2).

It may be interesting to observe how from the

80s up to now the proposed topic has been

considered of primary importance by healthcare

management scholars (especially in North America

and Great Britain) and, consequently, is currently

available an extensive bibliography on such a

subject. For example it may be noted as in the U.S.,

between 1995 and 2005, while the ED visits

increased of 20% (up to 115 million in 2005), the

number of beds dropped by 134.000 units (Nawar et

al., 2007), increasing the ED crowding (Asplin et al.,

2003), and thus forcing many American ED to

operate at peak capacity a day-to-day basis (O’Shea,

2007). In those circumstances it should be

considered that usually the greatest part of hospital

admissions from ED are ascribable to patients with a

yellow code assigned them in the “triage” phase.

The “triage” phase is carried out by specialized

nurses and it consists into the assignment of a color

code to each incoming patient depending on the

seriousness of his conditions:

 Green/white code: non urgent patient, no risks in

worsening his conditions, postponable visit

 Yellow code: medium critical level, possible

evolving risks, possible life danger

 Red code: very critical conditions, danger of life,

extreme priority

(Italian Ministry of Healthcare, government

ordinance, year 1992)

Facing a specific request made by the hospital

management, a System Dynamics (SD) model has

been built in order to evaluate the impact of yellow

codes on the hospital’s beds capacity.

2 DATA COLLECTION PHASE

In a first phase an analysis on data extracted from

the hospital database (related to year 2011) has been

carried out.

ED inflows and outflows, and ordinary

admissions data have been collected and then

examined. This has been done in order to accurately

assess the impact of the sum of these two

contributions (ED + Ordinary admissions) on the

hospital wards.

First step was the evaluation of different “color-

coded” patients incoming to the ED and their

destination after the ED physician visit (Table 1).

Table 1: Emergency Department admissions (2011).

As previously stated in the introduction, each

patient, arriving to the ED, is assigned a color

depending on the seriousness of his condition. After

the triage, the patient should wait in the queue or be

urgently visited (depending on his code). The visit

result could be:

 Discharge

 Admission to the Brief Intensive Observation

(OBI) structure

 Admission to Short Stay (SS) structure

 Admission to ordinary beds (in hospital wards)

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

598

 Abandons and others (i.e. transfer to other

structures)

The OBI is a ward inside the ED where patients

could be monitored up to 24 hours. Patients coming

out from OBI could be discharged, admitted to SS or

admitted to ordinary beds. The SS is an hospital

ward in which patients could be hospitalized in order

to be monitored up to 72 hours. Patients outcoming

from this structure are discharged or admitted to

ordinary beds according to percentages shown in

Table 1.

In the following modeling phase the authors

decided to consider only the yellow-coded patients’

flow because such a category is supposed to be the

one which is most affecting hospital occupancy in

terms of admissions per year.

Arrivals of yellow-coded patients have been

sampled, grouping data by time slot (24 one-hour

slots) in order to take into consideration the real

arrival distribution of ED patients (Fig.1).

Figure 1: Hourly patients arrivals to ED.

Then, average Length Of Stay (LOS) both in the ED

and in OBI/SS structures has been calculated.

Table 2: Hospital admissions (2011).

Table 2 shows the average LOS in hospital wards

calculated through data extracted from the hospital

information system. This quantity will prove to be

crucial as it will be explained later.

As previously mentioned, this data collection

phase was just the necessary prelude to the modeling

phase, phase that will be described in the next

section of this paper. The model was developed both

with a thorough analysis of the real operation of the

Emergency Department, conducted through

observation on site, and as a result of discussions

and interviews with hospital staff.

3 THE SIMULATION MODEL

The authors decided to adopt a continuous modeling

technique, the System Dynamics (SD), in order to

analyze the behavior of the studied system. In

literature some SD studies over emergency

departments can be found: Lattimer et al. (2004)

built a SD model to investigate ways in which

patients flow through EDs and system capacity

could be improved, Morrison and Wears (2011)

evaluated the crowding phenomenon affecting

emergency rooms, Morrison and Rudolph (2011)

studied how the accumulation of small interruptions

on ED’s ongoing activities could lead the dynamics

of such a system into a fragile, crisis-prone one. This

methodology has often been chosen because of its

dynamic complexity, and the delayed feedback loops

imbedded in it, thus it was proved to be particularly

suitable to study the reality under consideration

(Homer and Hirsch 2006).

Fig.2 shows Author’s model in a conceptual

form.

Figure 2: A conceptual scheme of the model.

Patients enter the ED and then, after a visit, could be

sent home, or retained for a certain period in the

hospital structures. In case of hospital admissions,

this flow goes to overlap with the ordinary

admissions flow (patients of pre-scheduled surgical

operations). The admission decision, in both cases,

is a critical point, strictly related to beds availability

and Hospital Length Of Stay as it will be discussed

later.

The simulation model, developed with ISEE’s

iThink 9.1.4, resulted to be a very complex model

because of numerous variables and equations

embedded in it (see Fig.3). Thus some conceptual

schemes, with simplified illustrations, will be

presented in the paper in order to allow the reader to

understand the logical connections between main

stocks.

ASystemDynamicsStudyofanEmergencyDepartmentImpactontheManagementofHospital'sSurgeryActivities

599

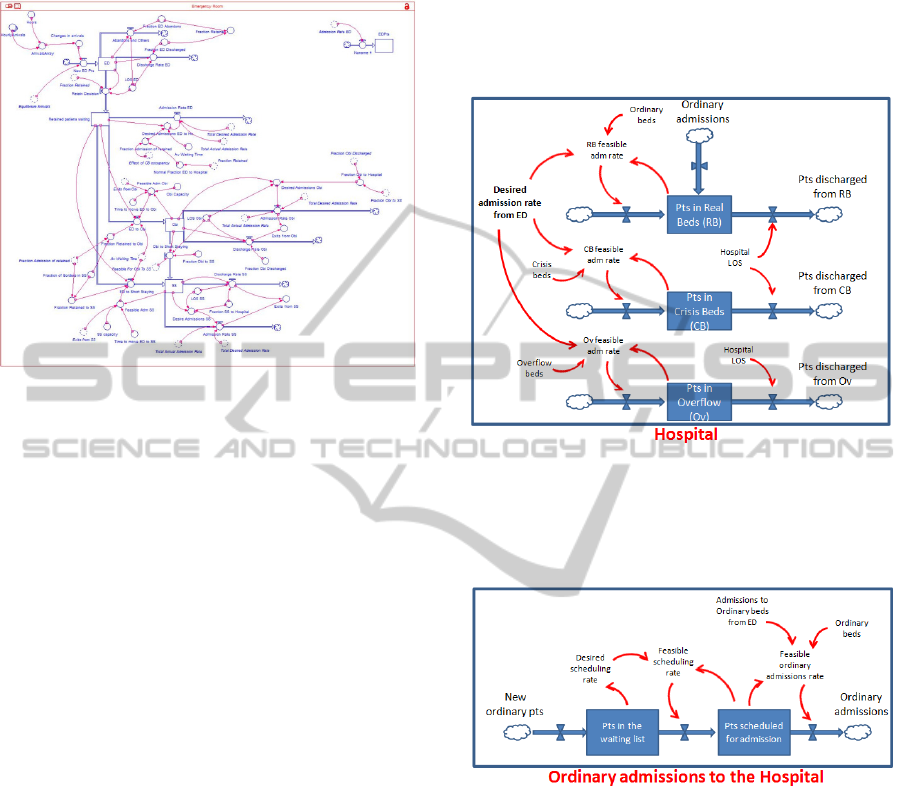
Fig. 3 shows the Emergency Department block.

Patient’s flow enters to the ED block where it stays

Figure 3: SD model – Emergency Department block.

Fig. 3 shows the Emergency Department block.

Patient’s flow enters to the ED block where it stays

for an average time of 3,2 hours (ED LOS,

calculated from hospital database), then a part of it

goes out from the system, and another one is

retained in order to be routed, at a later stage, toward

Hospital, OBI, or SS. Patients are routed to these

different destinations according to Table 1

percentages.

Both OBI and SS structures, and their related

flows, work with the same behavior.

Patients flow addressed to ordinary admissions is

routed to the Pts in Real Beds stock until its capacity

has run out. When there is no more space in real

beds, the flow goes to Pts in Crisis Beds stock and

eventually, when even this stock is full, it goes to the

Pts in overflow stock (Fig.4).

The “Hospital” block (Fig.4), which has a

limited beds capacity, receives patients from both

others model blocks (“ED” and “Ordinary

Admissions”). Patients stay into the Hospital for an

average hospitalization time (Hospital LOS), as

shown in Table 2, and they are then discharged.

Ordinary admissions and discharges usually take

place from 7:00 am to 5:00 pm, while admissions

from ED occur continually during the 24 hours since

they are emergency admissions.

Overall real beds among all Hospital’s wards are

397, plus more 13 “crisis” beds addressed to face

possible emergency situations.

In actual practice, since it is not uncommon for

the capacity to run out, the medical staff is able to

set up a number of additional beds in order to ensure

medical assistance even in the case of capacity limit

reached. In the modeling phase the authors deal with

this practice creating the Pts in Overflow stock

destined to receive patients not able to be

hospitalized neither in Pts in Real Beds nor in Pts in

Crisis Beds.

Figure 4: SD model, Hospital block – a conceptual

scheme.

Third and last block is representing ordinary

admissions dynamics (Fig.5).

Figure 5: SD model, Ordinary admission block - a

conceptual scheme.

New patients requiring surgical intervention are

inserted on a waiting list, and then comparing the

availability of beds with demand from PS, scheduled

to be hospitalized. The model has been built by

implementing a logic of "strict priority" which

focuses on access from ED. This has been made in

order to simulate the real behavior of the Hospital

which must act this way because of regional laws’

requirements.

Model has been validated through the Dynamic

Equilibrium technique (Sterman, 2000) which states

that the model reaches the equilibrium when all

incoming flows equal the total of outcoming flows.

In this specific case the equation is:

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

600

Hospital Exits = New OrdinaryPts + New EDPts

(1)

Once the equilibrium condition has been identified,

the model has been fed with real functioning ED

data in order to evaluate its real behavior. In

particular, yellow-coded patients’ arrival

distribution, daily ordinary admissions (from the

Hospital database), and each structure LOS have

been set.

4 SIMULATION RESULTS

Analyzing the simulations results it can be

immediately put in evidence, as expected, the

importance of the impact of hospitalization time on

the

Hospital’s beds availability.

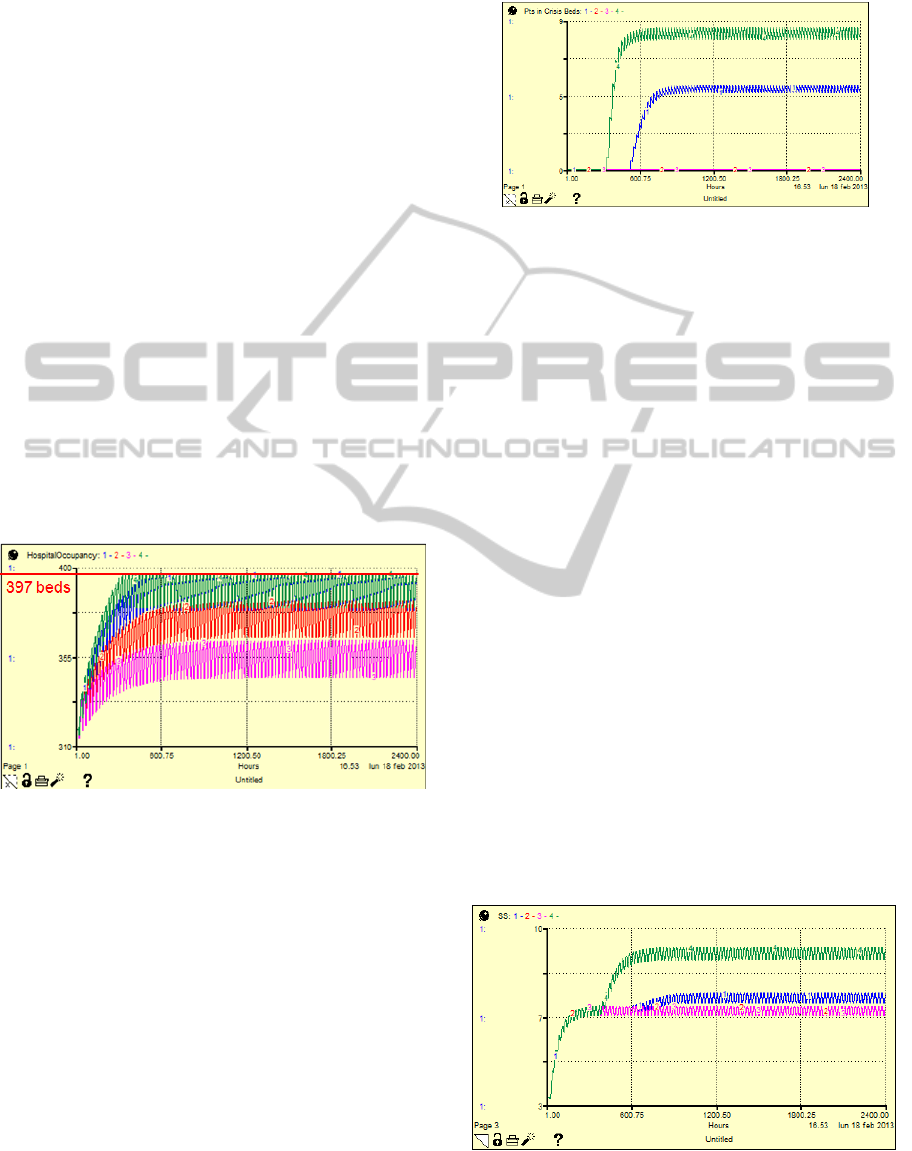
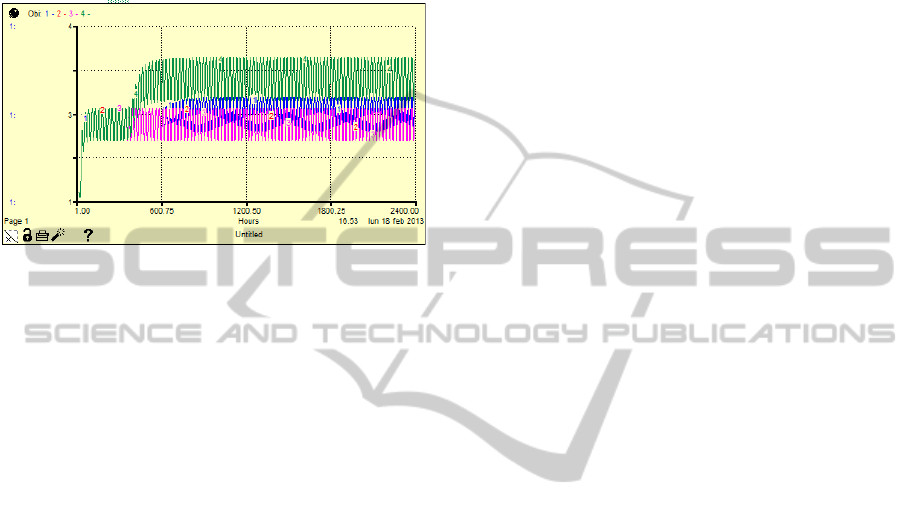
Fig. 6 shows the results of 4 simulation runs,

each one with a different value of AvgLOS.

Different colors have been used to draw each

scenario’s line:

 Green line: LOS = 10 d

 Blue line: LOS = 9.6 d (today)

 Red line: LOS = 9 d

 Purple line: LOS = 8.5 d

Figure 6: Hospital Occupancy during time vs AvgLOS

Oscillations in each individual curves are obviously

due to the daily trend of simulation inputs (ED

admissions and ordinary admissions) and outputs

(discharges). All curves reach the stability condition

after 600 simulated hours (as it can be seen in

Fig.6); this could be considered as the model’s warm

up time, and so results could be reliable only after

this period of time.

For a thorough analysis of the Fig.6 graph, the

trend of crisis beds during simulation has to be

considered (Fig.7).

Same line colors of Fig.6 have been used for all

the simulation graphs presented in this paper.

Analyzing Fig.6 and Fig.7 graphs at the same

time, the great impact of the hospitalization time on

the Hospital’s level of occupancy can be put in

evidence.

Figure 7: Crisis Beds Occupancy during time vs AvgLOS.

According to simulation results, currently (Average

Hospital LOS of 9,6 days) Hospital is almost always

working in bed capacity saturation conditions, and 5

additional crisis beds are necessary to face the

admission demand. It can be observed that if the

Avg.LOS grows up to 10 days, the demand for crisis

beds would rise up to 9 (on 13 available crisis beds).

Both these results are worrying because it has to

be noted that in this work the authors consider just

the ED admission flow related to yellow-coded

patients, and this doesn’t obviously represent the

total admission demand coming from such structure.

Other Fig.6’s curves (red and purple) show the

expected benefit from a possible decrease in the

average hospitalization time.

If the Hospital management could achieve a

6,25% decrease in the avgLOS (from 9,6 to 9 days),

the Hospital occupancy would stabilize around 380

beds (96% of total available beds) and thus no crisis

beds would be occupied.

The expected benefit in the fourth scenario

(purple line, 11,5% decrease in avgLOS) is even

greater, with an occupancy level of about 90,6% of

total capacity (360 occupied beds).

In order to complete the analysis, SS (Fig.7) and

OBI (Fig.8) behavior in the four scenarios has been

evaluated.

Figure 8: SS Occupancy during time vs HospitalLOS.

ASystemDynamicsStudyofanEmergencyDepartmentImpactontheManagementofHospital'sSurgeryActivities

601

By looking at both graphs it is possible to observe

how the demand for ordinary beds impact on OBI

and SS occupancy.

When the Hospital is not completely full (red and

purple lines), 7 Short Stay’s beds and 3 OBI’s beds

are required, respectively on 12 and 8 total available

beds.

Figure 9: OBI Occupancy during time vs Hospital LOS.

On the contrary, by looking at the blue and green

lines, when the Hospital’s capacity reaches the limit,

these two structures are affected by an increased

demand for beds. In current case (blue line) the

demand for SS beds increases of one unit, while the

OBI occupancy remains unchanged. In the worst

scenario (green line) the SS occupancy rises up to 9

beds, and the OBI demand increases by one unit.

Such a simulated behavior reproduces the reality

in a very accurate way; the ED decision makers, in

fact, use these two structures as a kind of “shock

absorber” for the Hospital in order to drain the

admission demand from ED. This practice could be

considered as a “bad behavior” of the system

because OBI and SS for their own nature should be

destined to a different kind of patients. They should

allow ED physicians to keep a certain percentage of

patients monitored for a limited period of time (24 or

72 hours) whether their conditions are not

completely clear.

Eventually, since only yellow-coded patients

have been considered in this study, it should be

noted once again that graphs shown in Fig.7 and

Fig.8 are not representative for the real occupancy

level of the structures. By completing the analysis

with other patients’ flows, is reasonable to expect a

saturation of capacity for both structures

5 CONCLUSIONS

This study points out the criticality of the impact of

yellow-coded patients on the ordinary surgery

structures.

In order to avoid such critical situations, two

strategies have been identified through the

simulation analysis:

 Increase the number of available beds without

change the LOS

 Decrease the avgLOS of 6,25%, passing from 9,6

to 9 days

However, the first strategy does not match with the

current Italian trend of Healthcare costs reduction in

which the decrease of beds is one of key points. This

could be true not only for Italy, but also for other

countries such as USA or England as well.

The second alternative, even if feasible from a

management point of view, would need a non trivial

change in some medical habits and it could be even

seen like an interference of engineers in the

physicians’ decisions. The pressure on Hospital

physicians to discharge patient in a shorter time, in

order to increase the assistance capacity, could bring

patients to revisit the ED and thus to increase the

demand for hospitalization (Baer et al., 2001); (Jack

et al., 2009).

Acting on their own capability in handling

complex systems, the DIME-MIT group suggested a

third strategy to slow down the problem at its

source: this approach consists into contain the

number of yellow-coded patients coming to the ED.

While the decentralization of some ED activities

to 24 hours clinics is taking place, as advanced by

actual government, it can be put in evidence that a

great number of yellow-coded patients are originated

by chronic ills (i.e. diabetic, heart patients) which do

not comply elementary healthcare rules. This

phenomenon in 2011 caused an overall LOS

estimated in about 5000 days (considering all the

hospitalization structures in the studied Hospital). A

strategy to contain this problem could be the

creation of dedicated outpatient clinics in order to

monitor such kind of patients in scheduled visits

such as happens for the precautionary screening of

other diseases (i.e. colon tumors, breast cancers).

By adopting this strategy, hospitals would incur

in almost negligible costs because these outpatient

clinics would have to be open just a few hours a

week, with scheduled visits carried out by ward’s

physicians in low workload moments. On the other

hand, the advantages in terms of social costs and

patients satisfaction would be significant.

The management of the Hospital appreciated

such a proposal and then declared that they will

seriously take into consideration the proposed

solution.

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

602

6 FUTURE DEVELOPMENTS

To face the problem discussed in this work, the

authors became aware of some problems affecting

the operational functioning of the Emergency

Department.

In particular it has come to light that the triage

phase is not carried out with an adequate accuracy.

In fact, a considerable percentage of hospital

admissions (37%) is ascribable to patients

previously identified with green code, while the

greatest part of such category is supposed to be

discharged, or in the worst cases, sent to OBI or SS.

On another hand, it has been pointed out that the

great pressure on ED physicians, caused by white

and green codes that usually represent the majority

of ED accesses, has no reasons to exist. It is a non

sense to wear out and divert such kind of emergency

specialists with high frequency visits forced by the

significant number of patients affected by low

critical diseases. This kind of patients could be

easily visited by young specializing doctors as

already happens in the US. For such a reason, the

authors are currently building a discrete event

simulator in order to evaluate a possible ED re-

organization. This re-organization will have to take

into consideration the creation of a different path for

white and green-coded patients among the hospital,

in order to allow emergency specialists to take care

of real urgent cases in a better way.

REFERENCES

Asplin, B. R., Magid, D. J., Rhodes, K. V., Solberg, L. I.,

Lurie, N., Camargo, C.A., 2003. A conceptual model

of emergency department crowding. In Annals of

Emergency Medicine, vol.42, Issue 2, pag. 173-180

Baer, R. B., Pasternack, J. S., et al. 2001. Recently

discharged inpatients as a source of emergency

department overcrowding. In Acad Emerg Med 8(11)

Briano, E., Caballini, C., Mosca, R., Revetria, R., Testa,

A., 2010. Proposing a system dynamic approach to

assess and improve Italian ports competitiveness.

Proceedings of the 12th WSEAS Conference on

Automatic Control, Modelling and Simulation

Cassettari L., Dagnino F., Mosca M., Revetria R., 2010.

Analysis of a urban route traffic flow exploiting the

system dynamic model. Proceedings of the 4th

WSEAS International Conference on Computer

Engineering and Applications (CEA’10), Cambridge,

USA, January 27-29, 2010.

Cassettari L., Mosca R., Revetria R. Rolando F., 2011.

Sizing of a 3,000,000t Bulk Cargo Port through

Discrete and Stochastic Simulation Integrated with

Response Surface Methodology Techniques.

Proceedings of 11th WSEAS International Conference

on Systems Theory And Scientific Computation

(ISTASC '11), Florence, Italy, August 23-25.

Cassettari, L., Mosca, R., Revetria, R., 2012. Monte Carlo

Simulation Models Evolving in Replicated Runs: A

Methodology to Choose the Optimal Experimental

Sample Size. In Mathematical Problems In

Engineering, 2012 Hindawi Publishing, Article

Number: 463873 DOI: 10.1155/2012/463873.

Frigato, A., Mosca, M., Schenone, M., 1999. Risk

management applied to project management and

project control. Proceedings of MIC 99- IASTED

Symposium on Modelling, Identification and Control,

Innsbruck (Austria).

Jack, B. W., Chetty, V. K., et al. 2009. A Reengineered

Hospital Discharge Program to Decrease

Rehospitalization: A Randomized Trial. In Ann Intern

Med. 150(3).

Homer, J. B. and Hirsch G. B., 2006. System Dynamics

Modelling for Public Health: Background and

Opportunities. In Am J Public Health 96(3).

Lattimer, V., Brailsford, S., Turnbull, J., Tarnaras, P.,

Smith, H., George, S., Gerard, K., Maslin-Prothero S.,

2004. Reviewing emergency care systems I: insights

from system dynamics modelling. In Emerg Med J

2004, n.21, 685-691.

Morrison, J. B., Rudolph, J. W., 2011. Learning from

Accident and Error: Avoiding the Hazards of

Workload, Stress, and Routine Interruptions in the

Emergency Department. Academic Emergency

Medicine, Vol.18, Issue 12, Dec. 2011.

Morrison, J. B., Wears, R. L., 2011. Emergency

Department Crowding: Vicious Cycles in the ED. 4

Mayo Clinic Conference on Systems Engineering &

Operations Research in Health Care Proceedings,

Rochester, MN.

Mosca, R., Giribone, P., 1982. Optimal lenght in O.R.

simulation experiments of large scale production

system. Proceedings of IASTED "Modelling,

Identification and Control", Davos (CH), 1982, pp.

78-82.

Mosca, R., 2002. Using HLA as a framework for supply

chain management: Project web-integrated logistics

designer. Simulation 78 (5 SPEC.) ,SCS, pp. 289-292.

Mosca, R., Bruzzone, A.G., Revetria R., 2002.

Cooperation in Maritime Training Process using

Virtual Reality Based and HLA Compliant Simulation.

Proceedings of XVII International Port Conference.

January 27-29, Alexandria Egypt.

Mosca, R., Cassettari, L., Revetria, R., Magro, L., 2005.

Simulation as Support for production planning in

Small & Medium Enterprise: A Case Study.

Proceedings of Winter Simulation Conference 2005,

Orlando (FL), 5-7 December 2005.

Mosca, R., Bruzzone, A. G., Cassettari, L., Mosca, M.

2009. Risk analysis for industrial plants projects: an

innovative approach based on simulation techniques

with experimental error control. Proceedings of the

European Modelling and Simulation Symposium

(EMSS’09).

ASystemDynamicsStudyofanEmergencyDepartmentImpactontheManagementofHospital'sSurgeryActivities

603

Mosca, R., Cassettari, L., Revetri,a R., 2010.

Experimental error mesaurement in Monte Carlo

Simulation. Handbook of Research on Discrete Event

Simulation: Technologies and Applications –

Chapter6, ISBN 978-1-60566-774-4 ( hardcover ),

ISBN 978-1-60566-775-1 ( ebook ) Evon M.O.Abu

Taieh and Asim Abdel Rahman El Sheikh,

Information Science Reference, New York, USA.

Mosca R., Mosca M., Cassettari L., Giribone P.G., 2010.

The Stochastic analysis of investments in industrial

plants by simulation models with control of

experimental error: theory and application to a real

business case. Applied Mathematical Sciences, Vol. 4,

2010, no. 76, 3823 – 3840.

Nawar, E. W., Niska R. W., et al. 2007. National Hospital

Ambulatory Medical Care Survey: 2005 Emergency

Department Summary. In Advance Data from Vital

and Healt Statistics, Hyattsville, MD, National Center

for Health Statistics.

O’Shea, J. S., 2007. The crisis in America’s Emergency

Rooms and what can be done. In Executive Summary

Backgrounder, n.2092, The Heritage Foundation.

Revetria, R., Testa, A., Cassettari, L., 2011. A generalized

simulation framework to manage logistics systems: a

case study in waste management and environmental

protection. Proceedings of the 2011 Winter Simulation

Conference , 943-952.

Sterman, J., 2000. Business Dynamics: Systems thinking

and modeling for a complex world, McGraw-

Hill/Iriwin.

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

604