
MOPED: An Agent-based Model for Peloton Dynamics in Competitive
Cycling
Erick Martins Ratamero
Erasmus Mundus Master in Complex Systems Science,
´
Ecole Polytechnique, Paris, France
Centre for Analytical Science, University of Warwick, Coventry, U.K.
Keywords:
Agent-based Modelling, Computer Simulation, Peloton Dynamics, Flocking, Emerging Complexity.
Abstract:
MOPED (an acronym for Model of Peloton Dynamics) is a proposed model for peloton dynamics in com-
petitive cycling. Using an agent-based approach, it aims to generate the very complex behaviour observed in
real-life competitive cycling from a collective of agents with very simple rules. Members of a peloton try to
minimize the average energy expenditure by riding behind other cyclists, in a behaviour known as drafting.
Drafting cyclists spend considerably less energy than frontrunners, making many different strategies possible.
We incorporate physiology concepts trying to quantify energy expenditure and recovery in different scenarios.
Starting from a very simple model of identical cyclists, multiple iterations with increasing complexity are pro-
posed, incorporating more and more aspects of the real physics involved in this sport. Finally, we analyse the
results and try to compare them to real-life behaviour to validate the model.
1 INTRODUCTION
Despite the appearance of a purely individual sport
where the strongest tends to win, professional cycling
is actually very strategical. A very simple fact gener-
ates complex behaviours and strategies: the fact that
air resistance dictates how much energy an athlete
spends. The drafting effect, thus, plays a big role on
peloton dynamics. The existence of a peloton itself
can be explained by this effect: energy expenditure
when drafting in a single line is reduced by approxi-
mately 18% at 32km/h, 27% at 40km/h, when drafting
a single rider, and by as much as 39% at 40km/h in a
group of eight riders (McCole et al., 1990).
Emerging from this fact is the behaviour observed
in a real-life cycling race: riders tend to group to-
gether and rotate in front of the peloton, trying to min-
imize the average spent energy. When a group tries
to break away from the pack of riders, the peloton de-
cides either to chase them or let them open a time gap.
If the group is deemed too dangerous, the typical be-
haviour is to chase it, and by having a bigger number
of athletes (and therefore a smaller average energy ex-
penditure for the same speed), they normally succeed
in this task. Only when a breakaway group is con-
sidered harmless enough a gap is established, and the
tired riders from this group are normally caught close
to the finish line.
Based on contributions (Olds, 1998) (Hoenigman
et al., 2011), we take a mathematical approach try-
ing to quantify energy expenditures based on different
factors as speed, gradient of the terrain, cross-section
area and weight of the cyclist, and specific physiolog-
ical characteristics of each individual. We regard the
rider basically as a static engine on the bike, and con-
sider the external factors that try to impede motion,
such as drag resistance, rolling resistance and changes
in the potential energy (such as when climbing a hill).
Based on these opposing forces and in physiological
data from professional cyclists, we establish an en-
ergy balance consistent with real-life values.
This is not the first agent-based approach for mod-
elling competitive cycling; another work (Hoenigman
et al., 2011) does this quite extensively. However,
their work has a focus on final results of a race and
a game-theoretical, best-response model for elaborat-
ing strategies. In this work, we focus not on the ac-
tual results of a race, but rather on simulating the be-
haviour of a peloton during a race, under different cir-
cumstances.
Also, we take the peloton as a complex dynamical
system. We establish general principles and rules for
the behaviour of each agent, roughly based on flock-
ing models already existing (Wilensky, 1998), calcu-
lating cohesive and separating forces for each agent,
so that they stay together as a group, but having spa-
134
Martins Ratamero E..
MOPED: An Agent-based Model for Peloton Dynamics in Competitive Cycling.
DOI: 10.5220/0004617501340143
In Proceedings of the International Congress on Sports Science Research and Technology Support (icSPORTS-2013), pages 134-143
ISBN: 978-989-8565-79-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

tial gaps between them. We alter this model so that it
makes sense in the context of this work and observe a
self-organizing pattern emerge, resembling other nat-
ural dynamical systems (Trenchard, 2012).
We develop a model proposal (MOPED - Model
of Peloton Dynamics) for the dynamic behaviour of a
competitive cycling peloton, in an agent-based fash-
ion, based on a small set of basic rules for each agent.
This rules are derived from the mathematical, phys-
iological and dynamical concepts presented, and the
emerging patterns are roughly similar to those ob-
served in real life and in other systems.
Finally, we discuss the results based on data gen-
erated during simulations for many different parame-
ters of the system. Starting from this data, we try to
establish similarities with real-life cycling behaviour
and validate the constructed model. We see this work
as a first step to possible further analysis of this sport
via computational simulation in the future, integrat-
ing even more parameters for natural influence and
specific behaviour of the agents. As in any complex
dynamical system, it is possible that, via simulation,
we can be able to study much more closely the in-
fluence of isolated parameters in the performance of
each cyclist and of the peloton as a whole.
2 THE MODEL
When constructing our model, we search for differ-
ent kinds of parameters in order to replicate and ex-
tend the real-life behaviour of cyclists in a peloton.
This work proposed an agent-based model for that.
Agent-based models are very well suited for situa-
tions where dynamics emerge from simple interac-
tions between different individuals, or agents (Wool-
ridge and Wooldridge, ).
When realizing an agent-based model, we search
for a set of parameters good enough for simulating the
expected behaviour of the system, but always keeping
in mind that an overcomplicated model becomescom-
putationally infeasible.
In this work, we model agents as cyclists, each of
them with three different kinds of parameters: me-
chanical, physiological and dynamical. Dynamical
parameters are the same for every cyclist, since they
regulate the way a rider behaves inside the peloton:
trying to keep group unity, but steering away from
nearby agents so that as not to cause a crash. We
choose to make mechanical parameters the same for
everyone, for the sake of simplicity. This way, all
cyclists have the same weight and cross-section. It
would be trivial, though, to extend this model to con-
template some variety in these parameters, so as to
accurately describe real cyclists.
Finally, we have physiological parameters. These
regulate the energy balance of each rider. We have
decided that, instead of having identical agents with
identical physical capacities, it would be more inter-
esting to have them normal-distributed around real-
life parameters from professional cyclists. This way,
we expect to see more interesting results, such as the
peloton whittling down during a long climb due to ex-
haustion from lesser riders. In the following sections,
we detail the approach taken for each set of parame-
ters in our model.
2.1 Dynamical Parameters
In this section, we describe the utilized dynamical pa-
rameters for our model; that is, the set of parame-
ters responsible for interaction between agents and the
peloton behaviour. This is a central part in our model,
arguably the most important. A non-desirable choice
of values here leads to unordered behaviour from the
agents, rendering our energy balance equations com-
pletely useless and turning the model away from the
dynamics it expects to simulate.
As a starting point for our dynamics, we take
a simple flocking model (Wilensky, 1998). In this
model, agents are subject to three different kinds of
forces: separating, aligning and cohesive forces. The
separating force is intended to make agents keep a
minimum separation between them, so that they do
not collapse to a single point. This is well-suited to
our model, since cyclists will try to steer away from
other fellow cyclists, to avoid crashes.
We have, then, an aligning force. This force is
applied to each agent to make it follow the direction
from their nearest neighbours. In our case, this seems
a bit out of place. Naturally, in a bicycle race, all com-
petitors are following the same direction, and steering
inside the peloton is a relatively small change in di-
rection. This way, we have decided to model intra-
peloton movement by purely lateral movement, with-
out change of heading direction. There is, then, no
aligning force in place.
Finally, we have a cohesion force. In the flock-
ing model, each agent turns in to become closer to
its flock-mates, making the group a coherent flock.
As we want to simulate a peloton behaviour, it makes
sense to port this kind of force to our model.
In the previous work, the resulting behaviour of
the agents is to move around freely when far from
other agents. However, when approaching other
agents, this group tends to become a coherent flock,
with agents exhibiting similar headings and staying
together, but with some spatial separation between
MOPED:AnAgent-basedModelforPelotonDynamicsinCompetitiveCycling
135

them.
As an improvement on this flocking model, we
take the Swarm Chemistry model (Sayama, 2007).
This time, different sets of agents have different
parameters for cohesive, separating and alignment
forces, making the proportion between those differ-
ent. This makes different sets behave in different
ways, and they tend to stay together in space, even
though they are not coupled together by anything
other than the similarity of their parameters.
From this work, we take the way of calculating
separating and cohesive forces, with minor adjust-
ments for our model. The original pseudo-code from
(Sayama, 2007) is presented as Algorithm 1.
Figure 1: Sayama’s algorithm for cohesive and separating
forces.
With Algorithm 1, we calculate an acceleration for
each agent, based on its relative position to the others.
However, this code calculates it taking into account
any other agent inside R
i
, a vision radius. This way,
agents actually look all around them when calculating
their new positions. As we are trying to model hu-
man behaviour, it is useful to slightly change this al-
gorithm, so that we only take into account agents that
could possibly be seen by a human, that is, contained
inside a visual cone. We also want to take different
scales of distance when calculating cohesive and sep-
arating forces. Cohesive force should be a long-range
calculation, taking into account pretty much any other
agent in the visual field, while separating force is
more local, with only close agents being taken into
account.
Based on these assumptions, we present a new
pseudo-code for these forces, defined here as Algo-
rithm 2.
In Algorithm 2, N
c
and N
s
are, respectively, the
neighbourhoods used for the calculation of cohesive
and separating forces. These neighbourhoods are
cones with an aperture angle of 140
o
, defined to
mimic a human visual cone, and different radii. The
neighbourhood for cohesive force is being used with
a radius of 20m, and the separating one with a radius
of 2m, so that the rider only tries to avoid contact with
other agents in the immediate neighbourhood.
Figure 2: MOPEDs algorithm for cohesive and separating
forces.
A last point to be addressed in this section is some
kind of bias to the center; real cyclists tend to be as
close to the center of the road as possible in the case
where no wind is blowing, so as to avoid danger on
the fringes of the road. A frontrunner would not try
to go too far to one side except if there is a sidewind
blowing, in which case optimal drafting is not directly
behind another rider, but rather in a diagonal. How-
ever, our model does not incorporate sidewinds, and
therefore we want our frontrunners to stay in the mid-
dle of the road. For that, a very small bias is put in
place.
As we also want some variety in the behaviour of
agents, a small, random acceleration is put into place.
With this, we finish our dynamical model of the pelo-
ton, and then we can move into energetic considera-
tions. A final pseudo-code algorithm for this dynami-
cal part would be similar to Algorithm 3.
Figure 3: MOPEDs complete algorithm for peloton dynam-
ics.
As a final addendum, we introduce the concept of
active riders: a rider is considered active if he is will-
icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport
136

ing to cooperate and be the frontrunner of the peloton,
being out of drafting positions in order to protect the
other cyclists. This is modelled by adding a small bias
to the front for active cyclists, as far as they are not
already the frontrunners. This way, the last statement
from the Algorithm 3 would be substituted by what is
presented as Algorithm 4.
Figure 4: Addendum for active cyclists.
We observe that this algorithm, with the right set
of parameters, yields a very life-like behaviour, with
a narrow peloton front giving place to a wider forma-
tion behind, as it can be seen at Figure 5.
Figure 5: View of a simulation of the peloton.
2.2 Energetic Parameters
We will now group together mechanical and physi-
ological parameters, since both sets of parameters af-
fect the energetic balance of the cyclist, making it eas-
ier to analyse them together.
Physiological data about cyclists is abundant; the
literature on how the human body behaves under these
circumstances is extensive and it is not our idea to
redefine anything on this domain, rather than to use
existing results and adjust our model to reflect them.
Many mathematical models for competitive cy-
cling exist already. For this model, we will use ele-
ments from (Olds, 1998), who has a validated, well-
behaved set of equations for energy expenditures.
We also use specific results from (Hoenigman et al.,
2011), who extended Olds’ results and applied it on
an agent-based model, and (Martin et al., 1998) for
the potential-energy equation. By taking an agent-
based approach and simulating both peloton dynam-
ics and energy expenditures, we believe it is possible
to have a more complete model and to have simula-
tions that yield results closer to real life.
Our first point is to calculate the drafting coeffi-
cient, that is, a correction factor relating the air resis-
tance when drafting and when not drafting. (KYLE,
1979) measured this coefficient experimentally and
affirms that the reduction in air resistance diminishes
when wheel spacing increases. This is a fairly intu-
itive result. He mentions that this reduction obeyed a
second-order polynomial, but he does not present the
equation. (Olds, 1998) reconstructs the equation from
the graphical data, arriving at
CF
dra ft
= 0.62− 0.0104d
w
+ 0.0452d
2
w
(1)
where d
w
is the wheel spacing (in meters) between
the bicycle and the preceding rider, and CF
dra ft
is the
correction coefficient. However, eq. 1 can be ap-
plied only when drafting happens in a paceline, that
is, when riders are exactly behind one another. In
a peloton, drafting occur also in other ways; riders
in a diagonal have a ”comet’s tail” effect, with draft-
ing bonuses decreasing when the rider behind moves
backwards or sideways. There is no extensive study
of drafting coefficients when a cyclist is not directly
behind another one, as there is no study about draft-
ing multiple riders; we only know that drafting behind
multiple riders is more beneficial than behind only
one (McCole et al., 1990). In this situation, we have
decided to assign weights depending on the angle of
view to the preceding rider. Riders inside a 10
o
cone
have weight 1; riders inside a 50
o
, 0.3, and the re-
maining riders inside a 90
o
cone have a weight of 0.1.
It is important to notice that drafting benefits are neg-
ligible in a distance over 3m, and therefore we limit
our calculations to this radius.
Having calculated CF
dra ft
, we can now go on to
the power equations. As we are using a scale of one
iteration per second of simulation, there is no need
to account for the difference between power and en-
ergy: they are numerically the same. From (Hoenig-
man et al., 2011), we have the following equations:
P
air
= kCF
dra ft
v
3
(2)
P
roll
= C
r
g(M + Mb)v (3)
On eq. 2, k is a lumped constant for aerodynamic
drag, dependant, between other things, on the cross-
section area of the cyclist. This constant is generally
reported with the value 0.185 kg/m, and we are fol-
lowing this value. Of course, v is wind speed (and,
as we are considering only a situation without wind,
is equal to ground speed). On eq. 3, C
r
is a lumped
constant for all frictional losses on a bike, and is gen-
erally reported with a value of 0.0053. Of course, g
is the usual gravitational constant (9.81 m/s
2
). The
variables M and M
b
represent, respectively, the mass
of the cyclist and of the bicycle. On this model, we are
using values of 63kg and 7kg, respectively, for these
variables, without any variation between cyclists.
MOPED:AnAgent-basedModelforPelotonDynamicsinCompetitiveCycling
137

These equations are enough for modelling the en-
ergy expenditure of a cyclist in a flat, non-windy situ-
ation. However, we want to model also the behaviour
of the peloton in uphills and downhills, and therefore
we need an extra equation for that. (Martin et al.,
1998) present this equation, for grades up to 10%
(where we consider sin(arctan(G
r
)) = G
r
) :
P
PE
= G
r
g(M + Mb)v (4)
and, therefore, we can introduce this on eq. 3, ob-
taining the following:
P
roll+PE
= (C
r
+ G
r
)g(M + Mb)v (5)
and a total energy expense of:
P
t
= E
t
= (C
r
+ G
r
)g(M + Mb)v+ kCF
dra ft
v
3
(6)
But this is only taking into account the energy ex-
penditure. We need to model how the cyclists react
to this and how much energy they can spend without
exhausting themselves. For that, we will introduce
the concept of lactate or anaerobic threshold, very
well-known in any endurance sport. Roughly speak-
ing, the lactate threshold is the power output an ath-
lete is capable of without accumulating lactic acid in
his muscles, that is, without getting tired (Vogt et al.,
2006). In this model, we will assess how tired a rider
is through a simple ”energy-left” variable, so that, at
lactate threshold, the value of this variable is roughly
unchanged.
As presented in (Hoenigman et al., 2011), a speed
of 0.7S
m
is slightly under the lactate threshold, where
S
m
is the speed at which a rider can travel at his Max
10
power output. The Max
10
represents the 10-minute
maximum power a rider can generate, and is gener-
ally regarded as an indicator of a rider’s skill level.
We are using, as in that work, a mean value for Max
10
µ = 7.1W/kg. That represents, for a rider with 63kg,
a Max
10
of approximately 450W. This is equivalent,
on flat ground, to S
m
= 12.96m/s. Therefore, 0.7S
m
is
approximately 9m/s, and this should be slightly under
lactate threshold. Finally, we take 10m/s as a repre-
sentative value for this threshold, and set a ”recovery”
variable, normally distributed with µ = 225W, that
will be deduced from the actual spent energy. Only
an energy expenditure over this limit will make the
rider grow tired.
We are still faced with the challenge of determin-
ing how long does it take for a rider over his anaer-
obic threshold to be exhausted. For that, we will use
the concept of time to exhaustion (T
lim
), as defined in
(Olds, 1998). The defining equation for T
lim
is
ln(T
lim
) = −6.351ln( fVO
2
max
) + 2.478 (7)
In this equation, fVO
2
max
is the fraction of the
VO
2
max
(maximum oxygen consumption) being used.
We can substitute that for Max
10
generating then:
ln(T
lim
) = −6.351ln(
P
tot
Max
10
) + 2.478 (8)
For establishing which would be the initial value
of ”energy-left” to each rider, we decided to take an
average situation: a sole rider at 45km/h (or 12m/s).
From that, with our typical Max
10
of 450W, we cal-
culate which would be the time to exhaustion. From
there, considering our average recovery of 225W, we
calculated how much reserves a cyclist should have at
the beginning of the simulation to achieve this typi-
cal time to exhaustion, arriving at the value of 760kJ.
With that, our modelling of the energy expenditure is
finished.
2.3 An Overview of the Model
We have presented the two parts of the model: the
dynamicalparameters and equations and the energetic
parameters and equations. Now, we present how these
two parts are interconnected.
It is clear that the position of an athlete inside
the peloton greatly affects his energy balance: if a
rider spends the whole time in front of the peloton,
he will certainly use more energy than another one
sitting safely in the middle of the group. This way,
the dynamical parameters and equations are influen-
tial on the energy balance. On the other hand, in our
model, the energy balance is, usually, not relevant for
the positioning of the cyclist: position calculation de-
pends only on neighbouring agents. However, when
the cyclist becomes tired, this is then relevant to his
position. We have postulated that a rider with less
than 100kJ of energy left is declared ”exhausted”. An
exhausted rider has a backward bias and is effectively
slower than the peloton average. This way, he tends to
hang at the back of the peloton, eventually letting the
group go altogether. A rider with 0 energy left quits
the peloton altogether. In our model, he is positioned
in the leftmost coordinate and becomes even slower.
However, if he can somehow recover energy enough
to get out of this condition altogether, he will rejoin
the peloton. We present figure 6, a small, schematic
flowchart representing the relation between the two
”sides” of our model.
3 RESULTS
In the following section, we summarize the results ob-
tained from the simulations using MOPED. These are
icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport
138

Figure 6: Schematic diagram showing the relation between
parts of the model.
divided between general behaviour, dynamical and
energetic results, for clarity purposes.
3.1 General Behaviour
In general, the emerging complex behaviour from the
agents is very promising; riders rotate back when they
feel they are under the average energy of the pelo-
ton. The peloton itself conforms to the general form
of real-life pelotons, with a very narrow front (usually
a 3-5 long single line of riders) and a widening profile
as we look backwards.
We rapidly see a convection dynamic settling in.
Riders at the back of the peloton wishing to move
forwards take the sides and dash forwards, since the
middle is cluttered with cyclists and going through is
virtually impossible. When they get to the front, they
normally settle down in the center of the road, and as
they stay there other riders coming from the back start
to overtake them. This way, the general dynamics
is: forward-moving cyclists take the sides, backward-
moving cyclists stay in the middle. Of course, to
move forwards through the sides, the athletes end up
spending more energy than those in the center of the
peloton.
(Trenchard, 2012) compares this dynamics to a
convection roll, dissipative dynamic, with ”warming”
riders in the peripheries and ”cooling” riders in the
middle. He then presents other natural systems with
similar dynamics, such as Rayleigh-Bernard cells and
penguin huddle rotations, and hints that this is the way
for achieving optimal energy dissipation in the whole
system. Even though our model does not take any en-
ergy considerations into account for the dynamics, we
still establish similar patterns, which is quite interest-
ing.
Independently of the number of active cyclists
chosen, they rapidly take over the head of the pelo-
ton. Even though not all active agents gather at the
front of the peloton at a single time, most of the time
the frontrunner will be an active cyclist.
When a sustained effort is maintained, cyclists
start to get exhausted and a sizeable group soon forms
at the back of the peloton. Not much after, the first
spent cyclists start to appear, giving up on the pelo-
ton. If this effort is maintained for long enough, only
the strongest riders stay in the peloton, with all the
rest giving up. This is consistent with long climbs in
professional races, where the front group is normally
smaller than ten cyclists. Also as in real life cycling,
a long descent after a climb has the effect of bringing
lots of cyclists back to the peloton, as they recover
energy.
3.2 Dynamical Parameters
Most of the results about the dynamics are difficult
to quantify. As commented in the section above, the
general behaviour of the peloton seems coherent with
real life, and furthermore, coherent with an optimal
energy dissipation.
As an addendum, we can show graphically the
convection dynamics. On figure 7, we have a graph
of average draft coefficient for agents moving forward
(blue) and backward (red). It is clear that, on average,
forward-moving cyclists on the periphery will have
less opportunities to draft behind another cyclists, and
the opposite happens with the central, backward mov-
ing agents.
Figure 7: Temporal distribution of draft coefficient for
backward and forward-moving agents.
MOPED:AnAgent-basedModelforPelotonDynamicsinCompetitiveCycling
139

3.3 Energetic Parameters
At first, for illustrating which kind of behaviour our
model generates, we start with an example. We sub-
mit 100 agents to a 3-hour race at a constant speed
of 45km/h. Of course this speed is too high for up-
hill parts, making them spend much more energy than
humanly possible, but we are only interested in the
qualitative behaviour that exhaustion generates. We
generate a profile for the race plotting the elevation at
each time. As we are at constant speed, it is the same
as plotting elevation per distance. The generated pro-
file is represented on figure 8.
Figure 8: Temporal profile of our test race.
Subjecting our cyclists to this profile, we generate
then a graph illustrating the amount of exhausted rid-
ers at any given time. The plot is shown as figure 9.
Figure 9: Exhausted riders (out of 100) at any given time.
We can now establish correlations between both
plots. In the very long initial uphill, relatively few
riders were exhausted. That is, of course, because at
the beginning of the race, every athlete is still fresh.
A slight downhill follows, enough to recover all cy-
clists. However, a second, steepest uphill follows, and
this time the exhaustion is much bigger in the pelo-
ton. Even during the shallow part close to the sum-
mit, the number of exhausted riders is still increasing
considerably. Another downhill follows and, again,
it is enough to recover all riders. Now, a short, not
too steep climb is presented, and the result is a big in-
crease again in exhaustion, this time much more due
to the accumulation of climbs than because of the dif-
ficulty of this one. A very long downhill is next, and
of course all riders arrive down there in conditions. A
false-flat (very shallow gradient) do not break them,
but as soon as the road gets steeper exhaustion in-
creases. Even a long, slight downhill after the climb is
not enough to recover, and exhaustion keeps increas-
ing even during this part. Finally, a relatively short,
but very steep climb to finish the race. This time, only
the very best stay in the front group at the top.
The whole behaviour of the peloton described on
the paragraph above will certainly sound familiar for
anyone who already watched a mountain stage in a
professional cycling race. The patterns are quite sim-
ilar, even if not identical, which indicates that the en-
ergy balance of the model is sound.
As a visual representation of what was described
here, we present figures 10 and 11. Figure 10 shows
what the peloton looks like at the summit of a long
climb. You can see a relatively small group of 14 rid-
ers in front, followed by a bigger group barely hang-
ing at the back, and many agents already at the left-
most coordinate, representing they have no more en-
ergy.
Figure 10: Peloton at the top of a climb.
Figure 11: Peloton during the descent.
As a comparison, figure 11 shows the peloton dur-
ing the descent, when the lesser riders havealready re-
covered. You can see the peloton shape is still longest
than normal due to the fact that the back riders are
icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport
140

still coming back, but there are no more riders with
no energy left and the group is unified again.
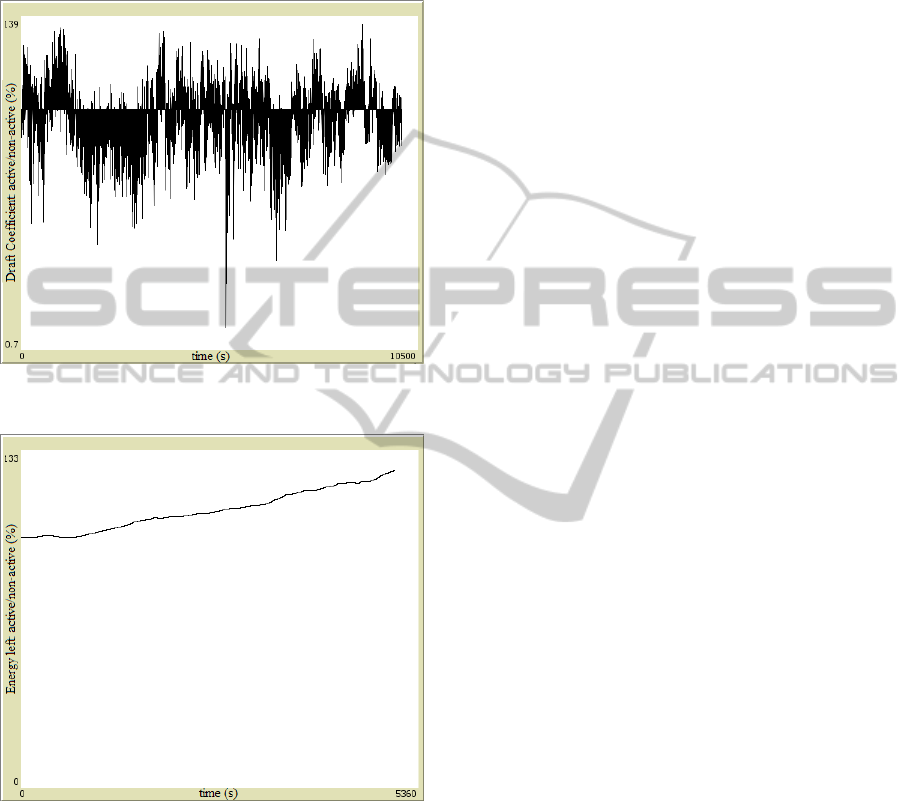
Finally, we present an interesting, counter-
intuitive result derived from the model. We start by
drawing, at figure 12, the average draft coefficient for
active riders (considering 20 out 100 to be active rid-
ers) compared to the average draft coefficient of non-
active ones.
Figure 12: Draft coefficient of active riders, as a percentage
of DC of non-active riders.
The horizontal reference level is 100%, which would
mean that, on average, active and non-active riders
have similar draft coefficients. However, that is not
what the graph shows: even if it is not that easy to
see on this plot, active riders have significantly lower
draft coefficients, which means they spend less en-
ergy. To confirm that, we plot a quocient between av-
erage energy for active and non-active cyclists, and,
even though it starts at 1 as expected, it undoubtedly
increases with time, indicating active riders are, in-
deed, spending less energy on average. This plot is
presented as figure 13.
This result is surprising, but there are reasons
for it: active riders spend more time on the well-
organized, single line part of the peloton. This way,
they have constantly medium-to-lowdraft coefficients
in these positions. Even if they do have to go to the
front more frequently than non-active riders, this if
offset by the fact that they are consistently drafting
some other cyclists. Non-active riders spend more
time in the convection-like part of the peloton, con-
stantly going back and forth and spending consider-
able amount of time in non-drafting positions at the
periphery of the peloton. Besides that, with much
more movement inside the peloton, they are not guar-
anteed to have another rider right in front of them at
Figure 13: Quocient of energy left between active and non-
active cyclists.
all times, as someone in the single-line part of the
peloton does. This way, their draft coefficient is much
more subject to variations.
This can also be shown by figure 14, where we
plot a quocient between average neighbourhood size
for active and non-active agents. At the beginning,
when the active agents are still organizingthemselves,
the plot goes under and over 1, but it quickly settles
under 1 as soon as the active riders organize them-
selves. This shows that they are getting smaller draft
coefficients in spite of drafting less cyclists, which is
coherent with the idea that they spend more time ex-
actly behind another cyclist.
Figure 14: Average size of active-agent neighborhood com-
pared to nonactive agents.
All results above are calculated with 20 active rid-
ers out of 100. We may wish to look at different
MOPED:AnAgent-basedModelforPelotonDynamicsinCompetitiveCycling
141
numbers to see if there is any qualitative difference
on these results. This way, we present, on figures 15
and 16, analogous plots to those at figures 12 and 13,
but this time calculated for only 5 active agents out of
100.
Figure 15: Draft coefficient of active riders, as a percentage
of DC of non-active riders - 5 active riders.
Figure 16: Quocient of energy left between active and non-
active cyclists - 5 active riders.
It is clear that the qualitative behaviour is exactly the
same, independently of the quantity of active agents.
4 DISCUSSION
This work presents a model for peloton dynamics in
competitive cycling, using an agent-based approach.
Based on a few simple rules for dynamics and energy
balance, we derived a rather complex pattern of con-
vection in the peloton, and coherent results in terms
of energy. Some interesting, counter-intuitive results
arised from the proposed model.
The result where active cyclists spent less energy
than non-active ones does not conform to general
knowledge in cycling, and it shows that there is room
for improvement and calibration in the model. For in-
stance, when moving around, agents do not look for
favourable positions in terms of drafting possibilities,
and the lack of data for drafting in diagonal positions
and behind multiple cyclists hinder the accuracy of
energy distributions.
Besides that, we do not account for many real-life
factors that affect competitive cyclists. An example is
wind, a factor that has major impact in many profes-
sional races. Frontal wind can be modelled as a dif-
ference in speed for the aerodynamical factor in our
energy expenditure equation, but sidewinds require a
whole new approach that was not within the scope of
this work. Of course, there is a different dimension
of cycling that was also not modelled here: the strate-
gic part. ”Intelligent” agents, who know what their
best response to the circumstances of a race is, could
create breakaways, become active or non-active mid-
way during a race, save as much energy as possible
for a final sprint. This is certainly feasible as a future
model.
This is probably the first time an agent-based ap-
proach is used to try and simulate large-scale cycling
peloton dynamics. Another work (Hoenigman et al.,
2011) take a similar approach, using an agent-based
model to simulate results of cyclingraces. Manyideas
between this work and their work are similar; in spe-
cial, the energy balance is probably quite similar, even
though they do not model uphills and downhills and
this work takes a different approach for modelling the
time to exhaustion of a cyclist. However, their fo-
cus is on obtaining final results of the races, while we
want to simulate the dynamics of a peloton during the
race. A different work (Trenchard, 2012) makes some
proto-simulations of pelotons with drafting, looking
for hysteresis on phase transitions. In spite of pre-
senting interesting results, his model is not interested
in simulating the complex dynamics of a peloton, but
only in illustrating a concept.
As the first work to explore simulation of such a
complex system as a cycling peloton, we do not ex-
pect this to be a complete work in any way, but rather
to be a first step on exploring this fascinating phe-
nomenon of collective behaviour. The results pre-
sented are certainly promising and show that a more
complete model of this system is feasible and can
even show similarities with other natural systems.
icSPORTS2013-InternationalCongressonSportsScienceResearchandTechnologySupport
142

ACKNOWLEDGEMENTS
Many thanks to Prof. Ren´e Doursat (Institut des
Syst`emes Complexes Paris
ˆ
Ile-de-France) for the
teachings about agent-based models and for support-
ing his students’ ideas. To James Newling, many
thanks for the insightful discussions during the devel-
opment of the model. This work was supported by an
Erasmus Mundus Masters scholarship.
REFERENCES
Hoenigman, R., Bradley, E., and Lim, A. (2011). Cooper-
ation in bike racing when to work together and when
to go it alone. Complexity, 17(2):39–44.
KYLE, C. R. (1979). Reduction of wind resistance and
power output of racing cyclists and runners travelling
in groups. Ergonomics, 22(4):387–397.
Martin, J. C., Milliken, D. L., Cobb, J. E., McFadden, K. L.,
and Coggan, A. R. (1998). Validation of a mathemat-
ical model for road cycling power. Journal of Applied
Biomechanics, 14:276–291.
McCole, S., Claney, K., Conte, J.-C., Anderson, R., and
Hagberg, J. (1990). Energy expenditure during bicy-
cling. Journal of Applied Physiology, 68(2):748–753.
Olds, T. (1998). The mathematics of breaking away and
chasing in cycling. European journal of applied phys-
iology and occupational physiology, 77(6):492–497.
Sayama, H. (2007). Decentralized control and interactive
design methods for large-scale heterogeneous self-
organizing swarms. In Advances in Artificial Life,
pages 675–684. Springer.
Trenchard, H. (2012). The complex dynamics of bicycle
pelotons. arXiv preprint arXiv:1206.0816.
Vogt, S., Heinrich, L., Schumacher, Y. O., Blum, A.,
Roecker, K., Dickhuth, H., and Schmid, A. (2006).
Power output during stage racing in professional road
cycling. Medicine and science in sports and exercise,
38(1):147.
Wilensky, U. (1998). Netlogo flocking model. Center for
Connected Learning and Computer-Based Modeling,
Northwestern University, Evanston, IL.
Woolridge, M. and Wooldridge, M. Introduction to multia-
gent systems. 2001.
MOPED:AnAgent-basedModelforPelotonDynamicsinCompetitiveCycling
143
