Modelling Transdermal Drug Delivery through a Two-layered System
Giuseppe Pontrelli
1
, Andrea Di Mascio
1
and Filippo de Monte
2
1
Istituto per le Applicazioni del Calcolo, CNR, Roma, Italy
2
Department of Industrial and Information Engineering and Economics, University of L’Aquila, L’Aquila, Italy
Keywords:
Diffusion-reaction Equation, Transdermal Drug Delivery, Percutaneous Absorption, Local Mass Non-
equilibrium.
Abstract:
One of the most promising frontiers of bioengineering is the controlled release of a therapeutic drug from
a vehicle across the skin (transdermal drug delivery). In order to study the complete process, a multiphase
mathematical model describing the dynamics of a substance between two porous coupled media of different
properties and extents is presented. A system of partial differential equation describes the diffusion and the
reversible binding and unbinding processes in both layers. Additional flux continuity at the interface and
clearance conditions into systemic circulation are imposed. A Sturm-Liouville problem is solved and an
analytical solution is given in the form of an infinite series expansion. The model points out the role of the
diffusion and reaction parameters, which control the complex transfer mechanism and the drug kinetics across
the two layers. Drug mass are given and their dependence on the physical parameters are discussed.
1 INTRODUCTION
Systemic delivery of drugs by percutaneous perme-
ation (transdermal drug delivery – TDD for short) of-
fers several advantages compared to oral release or
hypotermic injection, guarantees a controlled release
rate that can provide a constant concentration for a
long period of time, improves patient compliance, and
represents an attractive alternative to oral administra-
tion (Chien, 1992).
Drugs can be delivered across the skin to have an
effect on the tissues adjacent to the site of applica-
tion (topical delivery) or to be effective after distri-
bution through the circulatory system (systemic de-
livery). While there are many advantages to deliver
drugs through the skin, the barrier properties of it pro-
vide a significant challenge. To this aim, it is impor-
tant to understand the mechanism of drug permeation
from the delivery device (or vehicle, typically a trans-
dermal patch or medicated plaster, fig. 1) across the
skin (Mitragotri et al., 2011; George et al., 2004).
Mathematical modelling for TDD constitutes a
powerful predictive tool for fundamental understand-
ing of biotransport processes. In the absence of ex-
periments, many studies have been carried out about
TDD, on its efficacy, the optimal design of devices,
based on with mathematical models and numerical
simulations (Manitz et al., 1998; Addick et al., 1989;
Mitragotri et al., 2011). The transdermal release of
drug must be carefully tailored to achieve the optimal
therapeutic effect and to deliver the correct dose in the
required time (Prausniz and Langer, 2008). The phar-
macological effects of the drug, tissue accumulation,
duration and distribution could potentially have an ef-
fect on its efficacy and a delicate balance between an
adequate amount of drug delivered over an extended
period of time and the minimal local toxicity should
be found (Anissimov and Roberts, 2009). Although
a large number of mathematical models are available
nowadays for drug dynamics in the skin, there is a
limited effort to explain the drug delivery mechanism
from the vehicle platform. This is a very important
issue indeed, since the polymer matrix acts as a drug
reservoir, and a strategical design of its microstruc-
tural characteristics would improve the release per-
formances (Rim et al., 2005). It is worth to em-
phasize that the drug elution depends on the proper-
ties of the “vehicle-skin” system, taken as a whole,
and modelled as a coupled two-layered system. In
it, together with diffusive effects, local mass non-
equilibrium transfer processes are considered here,
due to the drug binding-unbinding phenomena. In
both layers these effects, usually neglected or under-
estimated, play an important role.
In this paper a “vehicle-skin” coupled model is
presented and a semi-analytical form is given for drug
concentration and mass in the vehicle and the skin at
various times. Our mathematical approach is similar
645
Pontrelli G., Di Mascio A. and de Monte F..
Modelling Transdermal Drug Delivery through a Two-layered System.
DOI: 10.5220/0004619706450651
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (BIOMED-2013), pages
645-651
ISBN: 978-989-8565-69-3
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The transdermal patch, a typical vehicle in trans-
dermal drug delivery.
to that used to describe drug dynamics from a drug-
eluting stent in arterial wall and is based on a two-
layer diffusion model (Pontrelli and de Monte, 2010).
The simulations, aimed at the design of technologi-
cally advanced vehicles, can be used to provide valu-
able insights into local TDD and to assess experimen-
tal procedures to evaluate drug efficacy. A major issue
in modelling drug penetration is the assessment of the
key parameters defining skin permeability, diffusion
coefficients and local mass non-equilibrium transfer
rates. A big challenge is the large number of param-
eters required for an advanced modelling, often not
readily available.
2 FORMULATION OF THE
PROBLEM
Let us consider a two-layered delivery system consti-
tuted by the vehicle (the transdermal patch or the film
of an ointment), and the skin (the stratum corneum
followed by the skin-receptor cells and the capillary
bed) (fig. 2). The first layer acts as a drug reser-
voir made of a thin substrate (generally a polymer
or a gel) containing a therapeutic drug to be deliv-
ered. Because of the small size of the vehicle, most
of the mass dynamics occurs along the direction nor-
mal to the flat skin surface, we restrict our study to a
simplified one-dimensional model. In particular, we
consider as x-axis the normal to the skin surface and
pointing outwards.
Without loss of generality, let x
0
= 0 be the
vehicle-skin interface and l
0
and l
1
the thicknesses of
the layers, respectively (fig. 2). Either the vehicle and
the skin are treated as macroscopically as two homo-
geneous porous media.
In the vehicle, at initial time, the drug is encapsu-
c
c
0 1
(skin)(vehicle)
l
1
l
x=0
0
x
(capillary bed)
Figure 2: Cross-section of the vehicle and the skin layers.
Due to an initial difference of unbounded concentrations c
0
and c
1
, a mass flux is established at the interface x = 0 and
drug diffuses through the skin. At x = l
1
the skin-receptor
(capillary) is set. Figure not to scale.
lated at maximum concentration in solid phase (e.g.
nanoparticles) (c
e
): in a such (bounded) state, it is un-
able to be delivered to the tissue. Nevertheless, when
the vehicle is applied over the skin, the “in situ” sys-
tem starts the release process: a fraction of the drug
mass is first transferred, in a finite time, to an un-
bounded – free, biologically available – phase (c
0
),
and diffuses into the biological tissue (c
1
). Similarly,
in the skin a part of the unbounded drug is metabo-
lized by the cells and transformed in a bounded state
(c
b
) (percutaneous absorption). Hence, the drug de-
livery process starts from the vehicle and ends to the
skin receptors, with a phase change in a cascade se-
quence, as schematically represented in fig. 3. Lo-
cal mass non-equilibrium processes, such as bidirec-
tional drug binding and unbinding phenomena, play a
key role in TDD, with characteristic times faster than
those of diffusion. A volume-averaged drug concen-
tration c(x,t) (mg/ml) is considered.
In the first layer the process is described by the
following equations:
∂c
e
∂t
= −β
0
c
e
+ δ
0
c
0
in(−l
0
,0)
∂c
0
∂t
= D
0
∂
2
c
0
∂x
2
+ β
0
c
e
− δ
0
c
0
in(−l
0
,0) (1)
where D
0
(cm
2
/s) is the diffusion coefficient of the
unbounded solute, β
0
≥ 0 and δ
0
≥ 0 are the unbind-
ing and binding rate constants in the vehicle, respec-
tively (s
−1
).
Similarly, in the second layer, the drug dynamics
is governed by a similar reaction-diffusion equation:
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
646

c
0
c
1
c
b
skin
c
e
vehicle
free drug diffusion
binding
unbinding
unbinding
binding
(δ
0
)
(β
0
)
(δ
1
)
(β
1
)
Figure 3: A diagram showing the schematic mechanism of
percutaneous drug absorption in the vehicle-skin system. A
unbinding (resp. binding) reaction occurs in the vehicle
(resp. in the skin). Reverse reactions are possible in both
layers. Diffusion occurs only in the free phases c
0
and c
1
.
∂c
1
∂t
= D
1
∂
2
c
1
∂x
2
− β
1
c
1
+ δ
1
c
b
in (0,l
1
)
∂c
b
∂t
= β
1
c
1
− δ
1
c
b
in (0,l
1
) (2)
where D
1
is the effective diffusivity of unbounded
drug, β
1
≥ 0 and δ
1
≥ 0 are the binding and unbinding
rate constants in the skin, respectively.
To close the previous bi-layered mass transfer sys-
tem of eqns. (1)-(2), flux and flux continuity condi-
tions have to be assigned at the vehicle-skin interface:
D
0
∂c
0
∂x
= D
1
∂c
1
∂x
− D
1
∂c
1
∂x
= P(c
0
− c
1
) at x = 0
with P the skin permeability coefficient (cm/s). No
mass flux passes between the vehicle and the sur-
rounding and we impose a no-flux condition:
D
0
∂c
0
∂x
= 0 at x = −l
0
Finally, a boundary condition has to be imposed at the
skin-receptor (capillary bed) boundary. At this point
the elimination of drug by capillary system follows
first-order kinetics:
K
cl
c
1
+ D
1
∂c
1
∂x
= 0 at x = l
1
where K
cl
is the skin-capillary clearance per unit area
(cm/s). The initial conditions are:
c
e
(x,0) = C
e
c
0
(x,0) = 0
c
1
(x,0) = 0 c
b
(x,0) = 0
2.1 Dimensionless Equations
All the variables and the parameters are now normal-
ized to get easily computable dimensionless quanti-
ties as follows:
¯x =
x
l
1
¯
t =
D
1
(l
1
)
2
t ¯c
i
=
c
i
C
e
γ =
D
D
1
φ =
Pl
1
D
1
K =
K
cl
l
1
D
1
¯
β =
β(l
1
)
2
D
1
¯
δ =
δ(l
1
)
2
D
1
By omitting the bar for simplicity, the mass transfer
problem (1)-(2) in the two-layered system can be now
written in dimensionless form as:
∂c
e
∂t
= −β
0
c
e
+ δ
0
c
0
in(− l
0
,0)
∂c
0
∂t
= γ
0
∂
2
c
0
∂x
2
+ β
0
c
e
− δ
0
c
0
in(− l
0
,0)
∂c
1
∂t
= γ
1
∂
2
c
1
∂x
2
− β
1
c
1
+ δ
1
c
b
in (0,1)
∂c
b
∂t
= β
1
c
1
− δ
1
c
b
in (0,1) (3)
and the following interface and B.C.’s:
∂c
0
∂x
= 0 at x = −l
0
γ
0
∂c
0
∂x
= γ
1
∂c
1
∂x
at x = 0
− γ
1
∂c
1
∂x
= φ(c
0
− c
1
) at x = 0
Kc
1
+ γ
1
∂c
1
∂x
= 0 at x = 1 (4)
supplemented with the initial condition:
c
e
(x,0) = 1 c
0
(x,0) = 0
c
1
(x,0) = 0 c
b
(x,0) = 0 (5)
3 METHOD OF SOLUTION
Preliminarily, we note that the solution of the linear
non-homogeneous ODE (3.1) is:
c
e
(x,t) = exp(−β
0
t)
+ exp(−β
0
t)
t
Z
0
exp(β
0
τ)δ
0
c
0
(x,τ)dτ
By considering the correspondent homogeneous
problem, it turns out that c
e
can be expressed as a
ModellingTransdermalDrugDeliverythroughaTwo-layeredSystem
647

function of c
0
. Similarly, from eqn. (3.4), c
b
can be
expressed as a function of c
1
c
b
(x,t) = exp(−δ
1
t)
t
Z
0
exp(δ
1
τ)β
1
c
1
(x,τ)dτ
Let us find a solution for c
0
and c
1
by separation
of variables
c
0
(x,t) = X
0
(x)G
0
(t) c
1
(x,t) = X
1
(x)G
1
(t)
As a consequence of the previous remark, the homo-
geneous part of c
e
and c
b
can be also separated by the
same eigenvector set as:
c
e
(x,t) = X
0
(x)G
e
(t) c
b
(x,t) = X
1
(x)G
b
(t)
If X
0
6= 0, X
1
6= 0, the previous problem becomes:







dG
e
dt
= −β
0
G
e
+ δ
0
G
0
1
γ
0
G
0

dG
0
dt
− (β
0
G
e
− δ
0
G
0
)

=
X
′′
0
X
0
= −λ
2
0
(6)







dG
b
dt
= −δ
1
G
b
+ β
1
G
1
1
γ
1
G
1

dG
1
dt
− (δ
1
G
b
− β
1
G
1
)

=
X
′′
1
X
1
= −λ
2
1
(7)
where λ
0
and λ
1
have to be computed. We have a
solution for X
i
in the form (Pontrelli and de Monte,
2010):
X
0
(x) = a
0
cos(λ
0
x) + b
0
sin(λ
0
x)
X
1
(x) = a
1
cos(λ
1
x) + b
1
sin(λ
1
x)
By enforcing the boundary-interface conditions (4):
a
0
sin(λ
0
l
0
) + b
0
cos(λ
0
l
0
) = 0
γ
0
λ
0
b
0
− γ
1
λ
1
b
1
= 0
φ(a
0
− a
1
) + γ
1
λ
1
b
1
= 0
[Kcos(λ
1
) − γ
1
λ
1
sin(λ
1
)]a
1
+[Ksin(λ
1
) + γ
1
λ
1
cos(λ
1
)]b
1
= 0
A non trivial solution exist only if the determinant of
the coefficient matrix is zero, i.e.:
γ
1
λ
1
(γ
1
λ
1
sin(λ
1
) − Kcos(λ
1
))
× [γ
0
λ
0
sin(λ
0
l
0
) − φcos(λ
0
l
0
)]
− γ
0
φλ
0
sin(λ
0
l
0
)(Ksin(λ
1
) + γ
1
λ
1
cos(λ
1
)) = 0
(8)
The four time dependent functions G
0
,G
1
,G
e
,G
b
have to be determined from
d
dt

G
e
G
0

=

−β
0
δ
0
β
0
−δ
0
− γ
0
λ
2
0

G
e
G
0

(9)
d
dt

G
b
G
1

=

−δ
1
β
1
δ
1
−β
1
− γ
1
λ
2
1

G
b
G
1

(10)
Denoting by µ
±
(resp. ν
±
) the eigenvalues of the
matrices in eqns. (9) and (10). The general solution
of the previous system is:
G
e
(t) = c
1
δ
0
β
0
+ µ
+
exp(µ
+
t) + c
2
δ
0
β
0
+ µ
−
exp(µ
−
t)
G
0
(t) = c
1
exp(µ
+
t) + c
2
exp(µ
−
t)
G
1
(t) = c
3
exp(ν
+
t) + c
4
exp(ν
−
t)
G
b
(t) = c
3
β
1
δ
1
+ ν
+
exp(ν
+
t) + c
4
β
1
δ
1
+ ν
−
exp(ν
−
t)
with:
µ
±
=
−(β
0
+ δ
0
+ γ
0
λ
2
0
) ±
q
(β
0
+ δ
0
+ γ
0
λ
2
0
)
2
− 4γ
0
β
0
λ
2
0
2
ν
±
=
−(β
1
+ δ
1
+ γ
1
λ
2
1
) ±
q
(β
1
+ δ
1
+ γ
1
λ
2
1
)
2
− 4γ
1
δ
1
λ
2
1
2
(11)
It is easily seen that µ
±
and ν
±
are real and nega-
tive. A necessary condition to guarantee continuity of
fluxes at x = 0 is that µ
±
= ν
±
.
4 A SPECIAL CASE
We develop here the solution for a particular combina-
tion of parameters, being the general case addressed
in a forthcoming paper. Under the assumption that
δ
1
= β
0
δ
0
= β
1
and
γ
0
λ
2
0
= γ
1
λ
2
1
(12)
we have, from eqn. (11):
µ
±
= ν
±
The nonlinear eqn. (8) is solved together with (12) to
get λ
k
0
and λ
k
1
, k = 1,2,..... Correspondingly, we have
a countable set of eigenfunctions X
k
0
,X
k
1
k = 1, 2, ... .
Finally, the solution of the our problem is given by the
linear superposition of the fundamental solution:
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
648

c
e
(x,t) =
∑
k
X
k
0
(x)

A
k
δ
0
β
0
+ µ
k
+
exp(µ
k
+
t)
+ B
k
δ
0
β
0
+ µ
k
−
exp(µ
k
−
t)

c
0
(x,t) =
∑
k
X
k
0
(x)

A
k
exp(µ
k
+
t) + B
k
exp(µ
k
−
t)

c
1
(x,t) =
∑
k
X
k
1
(x)

A
k
exp(µ
k
+
t) + B
k
exp(µ
k
−
t)

c
b
(x,t) =
∑
k
X
k
1
(x)

A
k
β
1
δ
1
+ µ
k
+
exp(µ
k
+
t)
+ B
k
β
1
δ
1
+ µ
k
−
exp(µ
k
−
t)

(13)
The constants A
k
, B
k
are found by applying the ini-
tial condition. First of all, from eqn (13.2) and (13.3)
it follows that B
k
= −A
k
. Let us impose the initial
condition on the (13.1) and (13.4), i.e:
∑
k
A
k
X
k
0
(x)

δ
0
β
0
+ µ
k
+
−
δ
0
β
0
+ µ
k
−

= 1
∑
k
A
k
X
k
1
(x)

β
1
δ
1
+ µ
k
+
−
β
1
δ
1
+ µ
k
−

= 0 (14)
By truncating the series to M terms, by collocating in
M points, we solve the system (14) is solved to get the
constants A
k
,k = 1, ..., M.
The analytical form of the solution given by eqns.
(13) allows an easy computation of the drug mass (per
unit of area) as integral of the concentration over the
correspondent layer:
M(t) =
Z
c(x,t)dx
5 NUMERICAL SIMULATIONS
AND RESULTS
A common difficulty in modelling physiological pro-
cesses is the identification of reliable estimates of
the model parameters. Experiments of TDD are pro-
hibitively expensive or impossible in vivo and the
only available source are data from literature. The
physical problem depends on a large number of pa-
rameters, each of them may vary in a finite range,
with a variety of combinations and limiting cases.
The model constants cannot be chosen independently
from each other and there is a compatibility range of
them. For simplicity, the following physical param-
eters are kept fixed for simulations in TDD (Simon
and Loney, 2005; Kubota et al., 2002; Anissimov and
Roberts, 2009):
0 2 4 6 8 10 12 14 16
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
time
M
e
0 2 4 6 8 10 12 14 16
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
time
M
0
β
0
= 10
−3
β
1
= 10
−4
β
0
= 2 ⋅ 10
−4
β
1
= 10
−4
β
0
= 8 ⋅ 10
−5
β
1
= 10
−4
Figure 4: Time histories of the drug mass M
e
and M
0
in the
vehicle for three values of β
0
(s
−1
).
D
0
= 10
−8
cm
2
/s D
1
= 10
−9
cm
2
/s
P = 10
−6
cm/s K
cl
= 10
3
cm/s
The thickness of the vehicle is set as: l
0
= 40µm,
whereas the limit of the skin layer (l
1
) is estimated by
the following considerations. Strictly speaking, in a
diffusion-reaction problem the concentration vanishes
asymptotically at infinite distance. However,for com-
putational purposes, the concentration is damped out
(within a given tolerance) over a finite distance at a
given time. Such a distance (“penetration length” d
∗
)
critically depends on the diffusive properties of the
two-layered medium, and in particular, is related to
the ratio
D
0
D
1
. By taking l
1
< d
∗
the condition (4.4) is
imposed erroneously before it should be. Any trunca-
tion of the domain before d
∗
is arbitrary and does not
ensure a conservative model. On the other hand, tak-
ModellingTransdermalDrugDeliverythroughaTwo-layeredSystem
649

ing l
1
> d
∗
the condition (4.4) is verified, but leads
to an overdetermined system. The precise concept
and the estimation of the penetration distance in two
and multiple layer systems is given in (Pontrelli and
de Monte, 2010). All series appearing in the eqn.
(13) and following have been truncated at a number
of terms M = 50.
The concentration is decreasing inside each layer,
being possibly discontinuousat the interface, and van-
ishes at a distance that is within the stratum corneum,
at all times. Due to the relatively large value of D
0
and to the small l
0
, the concentration profiles are al-
most flat in the vehicle, with levels reduced in time,
and have a decreasing behavior in the skin layer.
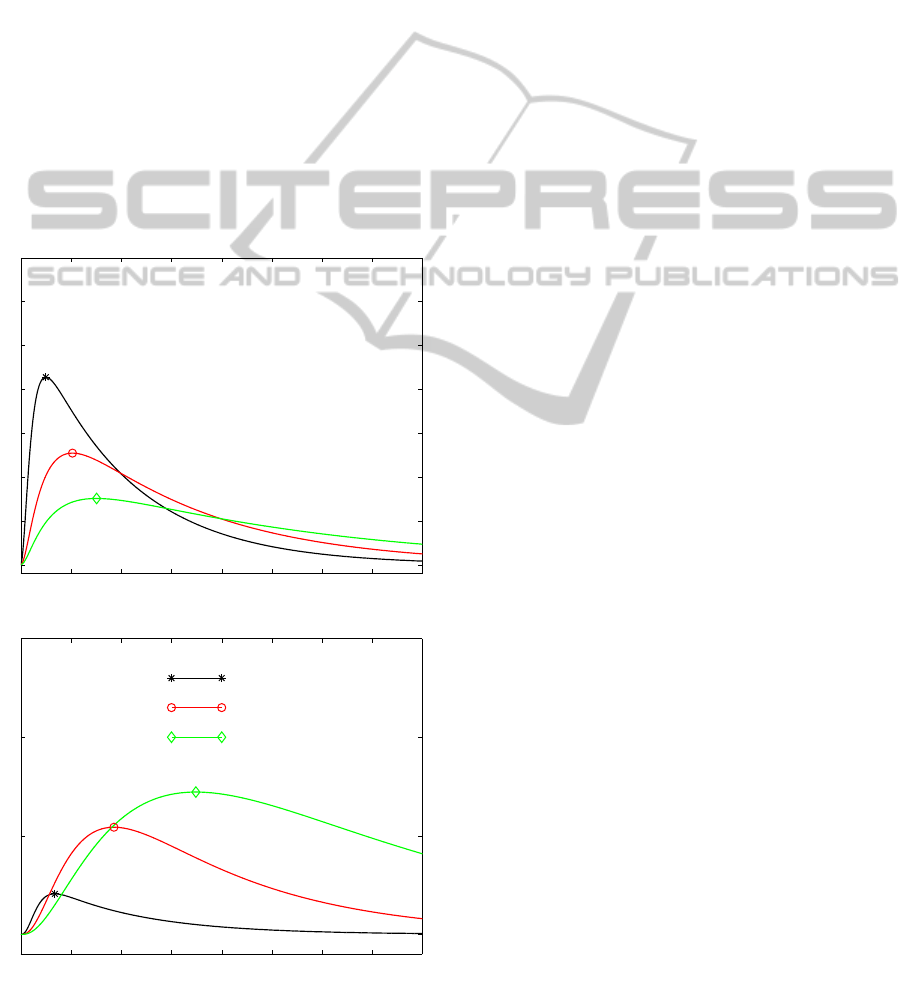
The effect of local mass non-equilibrium is stud-
ied by varying the values of the on-off reaction rates
β
0
and β
1
. The mass M
e
is exponentially decreasing
in the vehicle, and M
0
it is first increasing up to some
upper bound and then decaying asymptotically (fig.
0 2 4 6 8 10 12 14 16
0
0.05
0.1
0.15
0.2
0.25
0.3
time
M
1
0 2 4 6 8 10 12 14 16
0
0.05
0.1
time
M
b
β
0
= 10
−3
β
1
= 10
−4
β
0
= 2 ⋅ 10
−4
β
1
= 10
−4
β
0
= 8 ⋅ 10
−5
β
1
= 10
−4
Figure 5: Time histories of the drug mass M
1
and M
b
in the
vehicle for three values of β
0
(s
−1
).
4). The relative size of β
0
= δ
1
and β
1
= δ
0
affects
the transfer binding/unbinding processes, thus influ-
encing the mechanism of the whole dynamics. The
occurrence and the magnitude of the drug peak de-
pends on the combination and the relative extent of
the diffusive and reaction parameters. The outcomes
of the simulation provides valuable indicators to as-
sess whether drug reaches target tissue, and to opti-
mize the dose capacity in the vehicle. For example,
fig. 5 shows that a lower value of the unbinding pa-
rameter β
0
guarantees a more prolonged and uniform
release. On the other way around, a large value of
β
0
is responsible for a localized peaked distribution
followed by a faster decay.
The present TDD model constitutes a simple tool
that can help in designing and in manufacturing new
vehicle platforms that guarantee the optimal release
for an extended period of time.
6 CONCLUSIONS
In the last decades, transdermal delivery has emerged
as an attractive alternative and an efficient route for
drug administration. A mathematical model of drug
delivery by percutaneous permeation is presented in
this paper. To account the various aspects of drug dy-
namics from the vehicle across the skin, a multiphase
two-layered model is developed and a semi-analytic
solution for drug concentration is proposed.
The model incorporates the binding reversible
process and can be employed to study the effects of
the various parameters that control the vehicle-skin
delivery system. This can be of interest in the design
of smarter devices in order to get the optimal thera-
peutic effect by releasing the correct dose in the re-
quired time.
Although limited to a simple one-dimensional
case, the results of the numerical simulations can of-
fer a useful tool to estimate the performance of the
delivery devices.
ACKNOWLEDGEMENTS
The authors are grateful to the support of the Italian
project “Interomics”.
REFERENCES
Addick, W., Flynn, G., Weiner, N., and Curl, R. (1989). A
mathematical model to describe drug release from thin
topical applications. Int. J. Pharm., 56:243–248.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
650

Anissimov, Y. and Roberts, M. (2009). Diffusion modelling
of percutaneous absorption kinetics: effects of a slow
equilibration process within stratum corneum on ab-
sorption and desorption kinetics. J. Pharm. Science,
98:772–781.
Chien, Y. (1992). Novel drug delivery systems. M. Dekker
Inc.
George, K., Kubota, K., and Twizell, E. (2004). A
two-dimensional mathematical model of percutaneous
drug absorption. Biomed. Eng. Online, 3:18:567–578.
Kubota, K., Dey, F., Matar, S., and Twizell, E. (2002). A
repeated dose model of percutaneous drug absorption.
Appl. Math. Modell, 26:529–544.
Manitz, R., Lucht, W., Strehmel, K., Weiner, R., and Neu-
bert, R. (1998). On mathematical modeling of dermal
and transdermal drug delivery. J. Pharm. Sciences,
87:873–879.
Mitragotri, S., Anissimov, Y., Bunge, A., and al. (2011).
Mathematical models of skin permeability: an
overview. Int. J. Pharm., 418:115–129.
Pontrelli, G. and de Monte, F. (2010). A multi-layer porous
wall model for coronary drug-eluting stents. Int. J.
Heat Mass Transf., 53:3629–3637.
Prausniz, M. and Langer, R. (2008). Transdermal drug de-
livery. Nat. Biotechnol., 26 (11):1261–1268.
Rim, J. E., Pinsky, P., and van Osdol, W. (2005). Finite ele-
ment modeling of coupled diffusion with partitioning
in transdermal drug delivery. Ann. Biomed. Eng., 33
(10):1422–1438.
Simon, L. and Loney, N. (2005). An analytical solution
for percutaneous drug absorption: application and re-
moval of the vehicle. Math. Biosci., 197:119–139.
ModellingTransdermalDrugDeliverythroughaTwo-layeredSystem
651