
Tyre Footprint Reconstruction in the Vehicle Axle Weight-in-Motion
Measurement by Fibre-optic Sensors
Alexander Grakovski, Alexey Pilipovecs, Igor Kabashkin and Elmars Petersons
Transport and Telecommunication Institute, 1 Lomonosova Street, Riga, Latvia
Keywords: Transport Telematics, Weigh-in-Motion, Fibre-optic Sensor, Tyre Footprint.
Abstract: The problem of measuring road vehicle’s weight-in-motion (WIM) is important for overload enforcement,
road maintenance planning and cargo fleet managing, control of the legal use of the transport infrastructure,
road surface protection from the early destruction and for the safety on the roads. The fibre-optic sensors
(FOS) functionality is based on the changes in the parameters of the optical signal due to the deformation of
the optical fibre under the weight of the crossing vehicle. A fibre-optic sensor responds to the deformation,
therefore for WIM measurements it is necessary to estimate the impact area of a wheel on the working
surface of the sensor called tyre footprint. This information is used further for the estimation of the vehicle
wheel or axle weight while in motion. Recorded signals from a truck passing over a group of FOS with
various speeds and known weight are used as an input data. The results of the several laboratory and field
experiments with FOS, e.g. load characteristics according to the temperature, contact surface width and
loading speed impact, are provided here. The examples of the estimation of a truck tyre surface footprint
using FOS signals are discussed in this article.
1 INTRODUCTION
The worldwide problems and costs associated with
the road vehicles overloaded axles are being tackled
with the introduction of the new weigh-in-motion
(WIM) technologies. WIM offers a fast and accurate
measurement of the actual weights of the trucks
when entering and leaving the road infrastructure
facilities. Unlike the static weighbridges, WIM
systems are capable of measuring vehicles traveling
at a reduced or normal traffic speeds and do not
require the vehicle to come to a stop. This makes the
weighing process more efficient, and in the case of
the commercial vehicle allows the trucks under the
weight limit to bypass the enforcement.
There are four major types of sensors that have
been used today for a number of applications
comprising the traffic data collection and overloaded
truck enforcement: piezoelectric sensors, bending
plates, load cells and fibre-optic sensors (McCall et
al., 1997); (Teral, 1998). The fibre-optic sensors
(FOS), whose working principle is based on the
change of the optical signal parameters due to the
optic fibre deformation under the weight of the
crossing road vehicle (Batenko et al., 2011); (Malla
et al., 2008), have gained popularity in the last
decade.
Analysis of the WIM current trends indicates that
optical sensors are more reliable and durable in
comparison to the strain gauge and piezoelectric
sensors. Currently the two FOS types based on two
main principles are used:
Bragg grating (the change of diffraction in a
channel under deformations);
The fibre optical properties (transparency,
frequency, phase and polarization) change during
the deformations.
A lot of recent investigations are devoted to the
peculiarities of the construction and applications of
the sensors, using different physical properties. The
data presented in this publication have been received
using SENSOR LINE PUR experimental sensors
(SENSORLINE, 2010) based on the change of the
transparency (the intensity of the light signal) during
the deformation.
527
Grakovski A., Pilipovecs A., Kabashkin I. and Petersons E. (2013).
Tyre Footprint Reconstruction in the Vehicle Axle Weight-in-Motion Measurement by Fibre-optic Sensors.
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics, pages 527-536
DOI: 10.5220/0004620905270536
Copyright
c
SciTePress
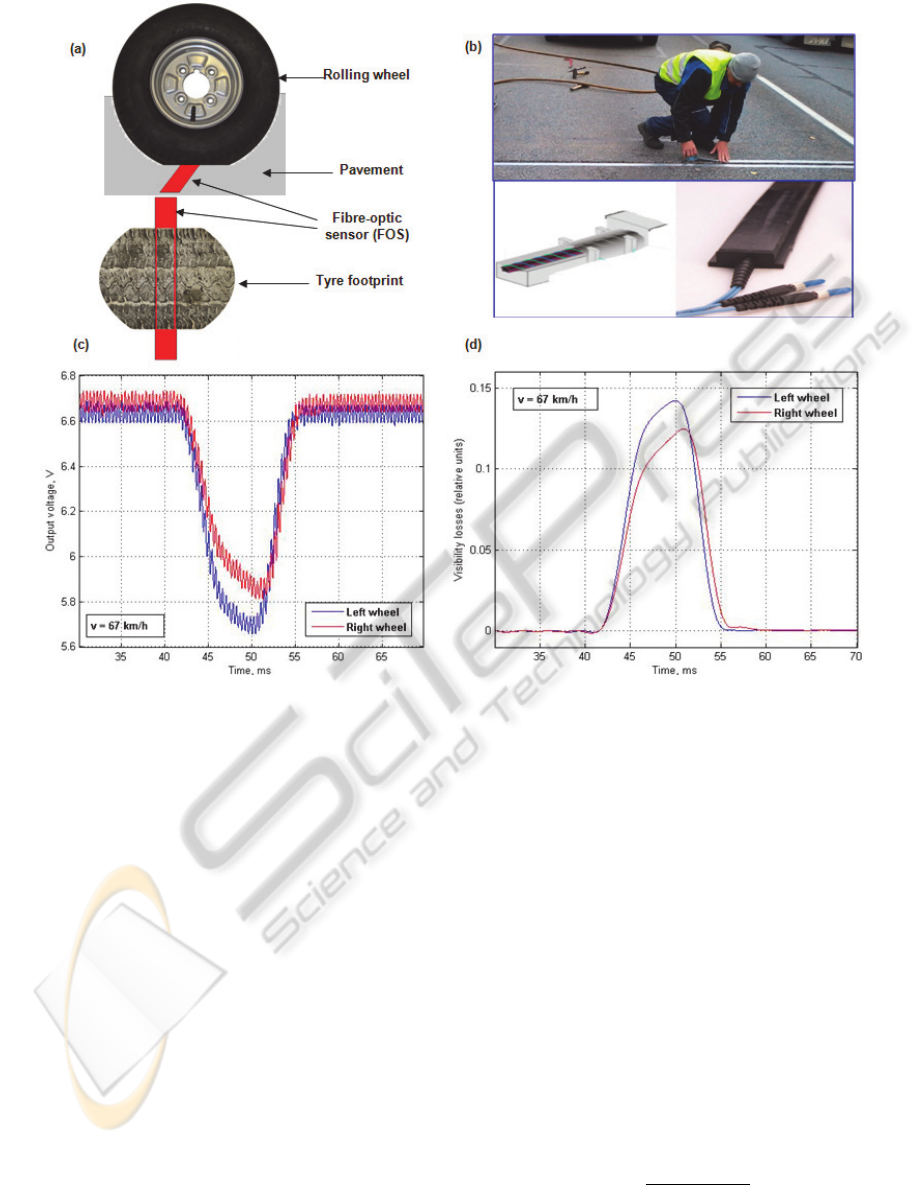
Figure 1: (a) Fibre optic sensor’s position against the wheel and tyre footprint, (b) SENSORLINE PUR installation and
construction of the sensor, (c) FOS output voltage, (d) Visibility losses as the function of pressure after pre-processing
(filtering).
2 AXLES
WEIGHING-IN-MOTION
PRINCIPLES
The fibre optic weight sensor is the cable consisting
of a photoconductive polymer fibres coated with a
thin light-reflective layer (Fig. 1(b)). A light
conductor is created in such a way that the light
cannot escape. If one directs a beam of light to one
end of the cable, it will come out from the other end
and in this case the cable can be twisted in any
manner. To measure the force acting on the cable,
the amplitude technology is more appropriated for
the measurements based on measuring of the optical
path intensity, which changes while pushing on the
light conductor along its points.
At these points the deflection of a light conductor
and reflective coating occurs, that is why the
conditions of light reflection inside are changed, and
some of it escapes. The greater the load the less light
comes from the second end of the light conductor.
Therefore the sensor has the unusual characteristic
for those, familiar with the strain gauges: the greater
the load the lower the output is. Apart from the fact
that it is reversed and in addition to this it is non-
linear.
In order to avoid the inaccuracy of zero load
level we need to exclude the high frequency
components from the voltage signal at the output of
the sensor’s transducer by filtering, as well as to
recalculate the voltage signal U(t) (Fig. 1(c)) into the
relative visibility losses signal V(t) (Fig. 1(d)),
directly related to the weight pressure on the FOS
surface. It can be done by the transformation (1):
0
0
U
tUU
tV
)(
)(
(1)
where U
0
is the voltage of sensor’s output with zero
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
528

Figure 2: Experimental truck “Volvo FH12” with full load 36900 kg.
Table 1: The reference static axle weights.
Date: 20.04.2012 (Air Temperature +12
о
С).
Reference axle weight (tons): 7.296 12.619 5.509 5.641 5.844
load. The signal transformation to the relative
visibility losses signal V(t) gives the possibility to
compare signals for different measurements in
different conditions.
Fibre optic load-measuring cables are placed in
the gap across the road, filled with resilient rubber
(Fig. 1(b)). The gap width is 30 mm. Since the
sensor width is smaller than the tyre footprint on the
surface, the sensor takes only part of the axle weight.
Two methods are used in the existing systems to
calculate the total weight of the axle [2, 3]: the
Basic Method and the Area Method. The following
formula is used to calculate the total weight of the
axis using the Basic Method:
ttha
PAW
(2)
where W
ha
– weight on half-axle, A
t
– area of the
tyre footprint, P
t
~ V(t) – air pressure inside the tyre
and, according to Newton’s 3
rd
law, it is proportional
to the axle weight.
As we can see the exact values of the formula
factors are unknown. The area of the tyre footprint is
calculated roughly by the length of the output
voltage impulse, which, in its turn, depends on the
vehicle speed. The Area Method uses the
assumption that the area under the recorded impulse
curve line, in other words – the integral,
characterizes the load on the axle. To calculate the
integral, the curve line is approximated by the
trapezoid. In this case the smaller the integral – the
greater the load. This method does not require
knowing the tyre pressure, but it requires the time-
consuming on-site calibration. Also, it has to be kept
in mind that the time of the tyre crossing the sensor
is too small to get an electrical signal of high quality
for its further mathematical processing. We use the
Area method only for the tyre footprint area
definition in (2), but the pressure is measured from
the signal amplitude.
3 EXPERIMENTAL VEHICLE
PARAMETERS
There was the set of measurement experiments with
the roadside FOS sensors on April, 2012 in Riga,
Latvia. Loaded truck (Fig.2) was preliminary
weighed on the weighbridge with the accuracy <
1%.
Reference weights of the separate axles are given
in the Table 1. The output signals from FOS sensors
for truck speeds 70 km/h and 90 km/h are
demonstrated on Fig.3. It is evident that the signals
for the different speeds have been changing by
amplitude and the proportion of amplitudes does not
fit the axle weights (Fig.3). The reason of this
behaviour may be explained by FOS properties such
as weight (pressure) distribution along the sensor
length as well as sensor non-linearity and
temperature dependence.
4 FIBRE OPTIC SENSOR
PROPERTIES
Fibre-optic sensor (SENSORLINE PUR) output
light intensity changes due to the applied external
vertical force were measured using of the optical
interface SL MA-110 that was developed by
SensorLine GmbH (SensorLine, 2010). Laboratory
experiments with varying parameters (temperature,
steel plate width and load speed) were made at
Latvian University Institute of Polymer Mechanics
with electronically controlled compression machine.
TyreFootprintReconstructionintheVehicleAxleWeight-in-MotionMeasurementbyFibre-opticSensors
529
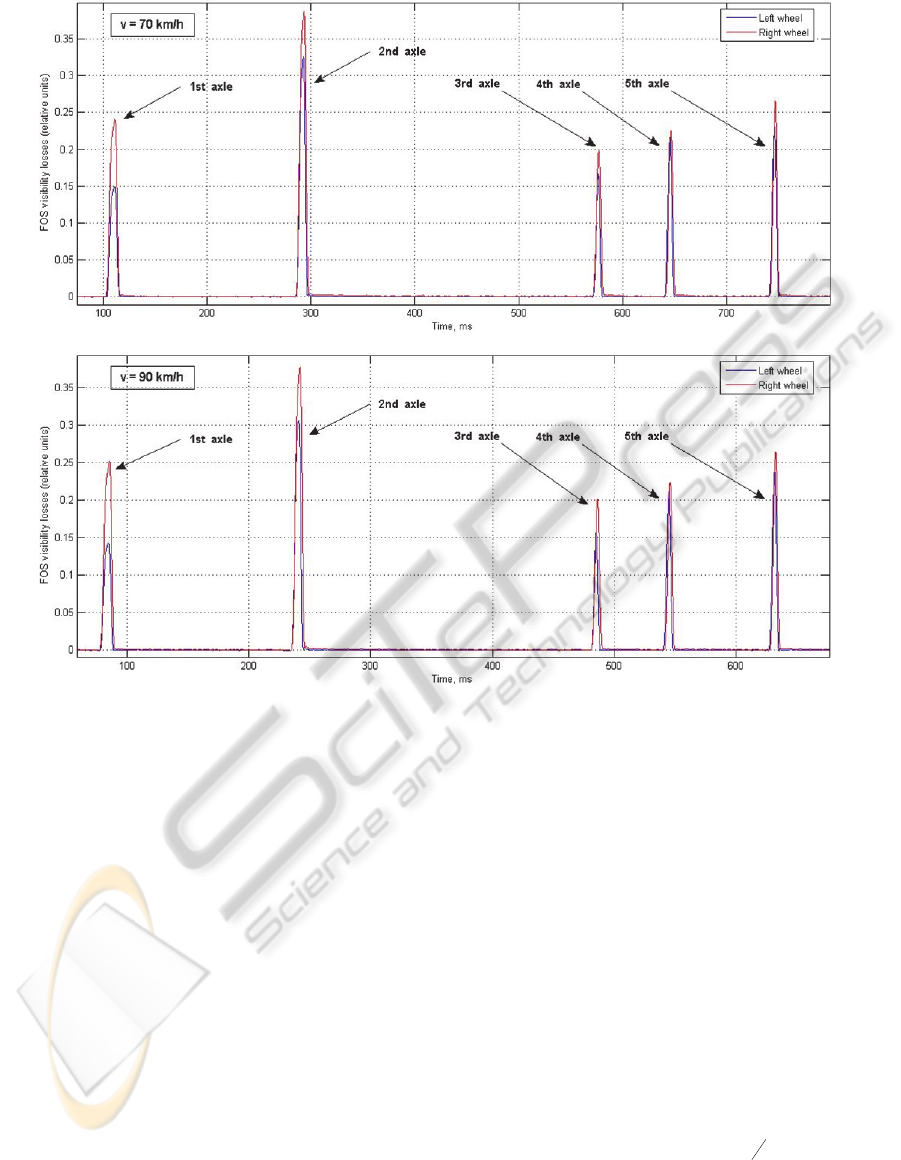
Figure 3: Examples of FOS signals of experimental truck for vehicle speeds 70 km/h and 90km/h respectively.
The first experiment examined the load
characteristic according to the temperature change:
FOS was placed into the tube of the soft thermal
insulation material in which chilled carbon dioxide
was circulating. The load from a compression
machine was applied to the sensor through the tube
and a 200 x 200 mm square steel plate (Figure 4(a)).
It was found during this experiment that the optical
response of the FOS was changing due to the
warming. And it is important to notice, that no
pressure was applied (Figure 4(b)).
FOS is permanently installed in the road surface,
therefore environment temperature changes affect
characteristics of the protective housing rubber
(stiffness) and the medium where the light
propagates. These changes introduce nonlinear
distortions which together with externally applied
pressure on a FOS are displayed at figure 4(c).
Relations between the load characteristics at the
different temperatures are displayed in the figure
4(d). These relations can be conditionally described
by polynomial approximation model:
),atata(LCLC
]C[]C[T 01
2
230
(3)
where LC
T[C]
is desired load characteristic at T
o
C
degrees, LC
30[C]
is load characteristic at 30
o
C
degrees and a
2,1,0
are coefficients of least square
optimisation calculated from figure 4(d).
In the real environment tyre footprint width may
vary depending on tyre size and inflation pressure,
which will result in the different force redistribution.
The second experiment shows this dependence
(figure 5(a)), these measurements were made at
constant temperature 14
o
C degrees and constant
loading speed 20 mm/s.
Relations between the load characteristics
obtained using the different steel plates are displayed
in figure 5(b). These relations can be conditionally
described by exponential approximation model:
),e(aLCLC
W
a
]mm[]mm[W
0
1
1200
(4)
where LC
W[mm]
is desired load characteristic with W
mm wide plate, LC
200[mm]
is load characteristic with
200 mm wide plate and a
1,2
are coefficients of least
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
530

Figure 4: (a) Experimental laboratory equipment scheme, (b) FOS temperature dependence without applying load, (c) FOS
load characteristics at different temperatures and (d) Fitted model of FOS various temperature load characteristic ratio
values relative to 30
o
C degrees.
square optimisation calculated from figure 5(b).
The vehicles are crossing the FOS at the different
speeds and the sensor reaction is different due to its
inertia properties. Therefore the third experiment
was dedicated to study FOS output signal
dependence on applied force at the different speeds
(figure 6(a)): these measurements were made at the
constant temperature 17
o
C degrees and the steel
plate size 200 mm. Relations between the load
characteristics at the different applied speeds are
displayed in figure 6(b). These relations can be
conditionally described by power approximation
model:
),Sa(LCLC
a
]s/mm[.]s/mm[S
0
10660
(5)
where LC
X[mm/s]
is desired load characteristic at S
mm/s, LC
0.066[mm/s]
is load characteristic at 0.066
mm/s and a
1,0
are coefficients of least square
optimisation calculated from figure 6(b).
5 TYRE FOOTPRINT AND
WEIGHT ESTIMATION
As it is clearly seen from the expression (2), the At
area of the tyre footprint should be known to
calculate the axle weight by the registered FOS
signal (Batenko et al., 2011). The form of the signal
is non-symmetric and sufficiently distorted by the
rolling process of the wheel on the road surface (see
Figure 7(a)).
TyreFootprintReconstructionintheVehicleAxleWeight-in-MotionMeasurementbyFibre-opticSensors
531

Figure 5: (a) FOS load characteristics with the different steel plate widths and (b) Fitted model of FOS various steel plate
width load characteristic ratio values relative to 200x200mm steel plate.
Figure 6: (a) FOS load characteristics at different load speeds and (b) Fitted model of FOS various load speed load
characteristic ratio values relative to 0.066 mm/s load speed.
One of the possible explanations of the signal
waveform distortion is the idea about the common
interaction of two factors (Krasnitsky, 2012):
vertical dead weight gravity of conditionally
immovable wheel (according to wheel geometry it
must be symmetric, see Figure 7(b)), and the force
of friction (it depends on the pavement and tyre
properties, wheel’s speed and weight, and its
expected waveform is asymmetric, see Figure 7(c)).
The problem of the decomposition of the non-
symmetric signal in two parts (symmetric and
asymmetric) can be solved by the polynomial
approximation using the least square method and the
further grouping of members with even and odd
powers separately or by standard even-odd
decomposition of the signal on finite window
(Mesco, 1984); (Vinay et al., 2006).
On the other hand, by assumption that the
vehicle moves uniformly and all forces maximally
compensate each other, we can accept that the
friction force is as minimal as possible (rolling
friction only without sliding friction). It is possible
to minimize the friction component magnitude
moving the axis of symmetry before the pulse (see
Figure 8(b)). It will be minimal at the position
conditionally named as the “mass centre” of the
pulse (see Figure 8(a)). The waveform of the friction
component on Figure 8(b)) sufficiently differs from
the same on Figure 7(c). Two maximums and two
minimums clearly locate the characteristic points for
the tire footprint estimation in the elliptic
approximation (see Figure 8(c)).
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
532
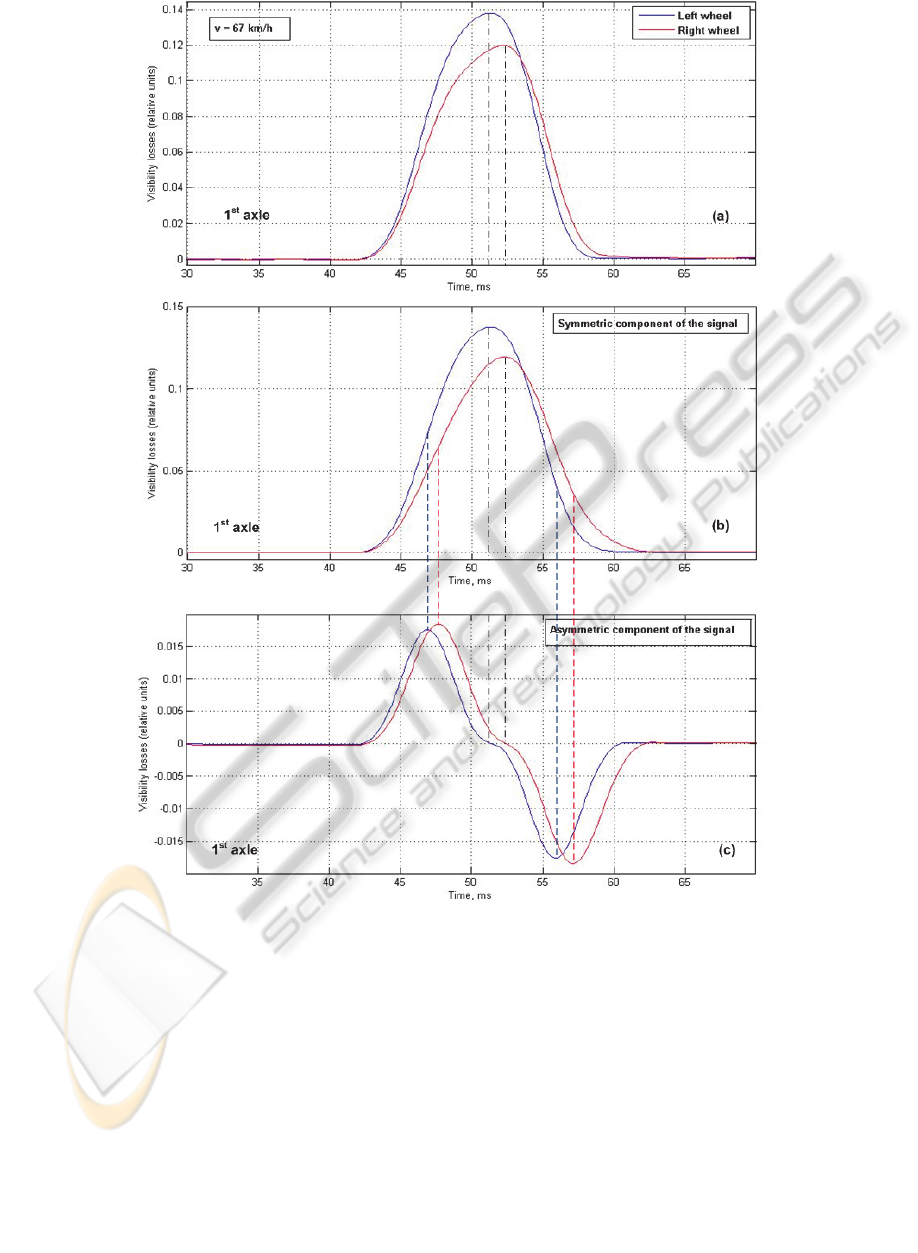
Figure 7: (a) FOS output signal in the form of visibility losses (formula 1), (b) Approximated vertical weight component
(symmetric), and (c) Approximated asymmetric component depending on horizontal velocity and friction (Krasnitsky, 2012).
Now the problem of the tyre footprint area
estimation may be solved. Multiplying the impulse
length by the speed of the wheel we can calculate
the length of the footprint. In the considered
examples (Figures 7 and 8) it is L
left
= 0.1905 m and
L
right
= 0.1976 m. It agrees with another data for the
wheel R22.5 and tyre width of 315 mm for the 1
st
axle. Full data of footprint lengths for experimental
cargo vehicle (see Figure 2 and Table 1) are the
following: left side wheels lengths are L
L12345
=
{0.1905 0.1652 0.1278 0.1354 0.1379}
meters, and right side wheels lengths are L
R12345
=
{0.1976 0.1799 0.1509 0.1449 0.1356} meters.
The difference between the lengths of each wheel
can be explained by the fact that the 2
nd
axle has the
double-wheel, the trailer tyres but (axles No 3-5)
width is 385 mm.
Applying the sensors signal processing algorithm
together with the of estimation of the tyre footprint
area and approximation of the nonlinear
characteristics of the FOS (Figures 4, 5 and 6) for
the suitable range of temperatures, it is possible to
estimate the following weights of axles (Table 2).
TyreFootprintReconstructionintheVehicleAxleWeight-in-MotionMeasurementbyFibre-opticSensors
533

Figure 8: (a) FOS output signal in the form of visibility losses in dimensionless units, (b) Approximated vertical weight
component (symmetric), (c) Approximated asymmetric component and tire footprint reconstruction in case of minimal
friction condition.
As it can be seen from the Table 2, the most
preferred for the measurements are the velocity
ranges from 50 km/h and above: the measurement
errors of the axle loads do not exceed 10%, which is
consistent with the problem of the pre-selection of
the overloaded vehicles. The dynamics of vehicle
breaking or acceleration is more visible at the low
velocities. It can seriously distort the waveform of
asymmetric friction component and change
characteristic points for tyre footprint estimation.
The source of the relatively big measurement errors
at the low velocities are the distortion and footprint
area reconstruction errors because of the vertical
oscillations of the dynamic motion of the vehicle,
whose amplitudes are smaller at the higher speeds.
Taking into account the properties of each
individual sensor, the calibration of FOS should be
conducted twice: at first in the laboratory (load
characteristics in the temperature range from -20
o
C
to +30
o
C), and, secondly, after installing the sensor
in the road surface using the vehicles with allowed
but known weight.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
534

Table 2: The results of the axle weight estimation and errors for the different measurements at the speeds 10-90 km/h (2-6
sets of measurements per speed bin).
Date: 20.04.2012 (Air Temperature +12
о
С)
Parameter: 1
s
t
axle 2nd axle 3rd axle 4th axle 5th axle
Reference axle’s weight (tons): 7.296 12.619 5.509 5.641 5.844
Group of speed: 10 km/h
1 Error for v=16 km/h 0.589% 0.855% -12.994% -10.317% -0.453%
2 Error for v=13 km/h -1.058% 10.985% -16.472% -8.316% 12.152%
Group of speed: 20 km/h
1 Error for v=19 km/h -2.176% 2.496% -3.417% 10.885% 11.251%
2 Error for v=20 km/h -0.046% 7.408% -18.445% -14.253% -3.248%
3 Error for v=17 km/h 0.104% 11.259% -24.200% -14.172% -9.916%
Group of speed: 50 km/h
1 Error for v=53 km/h 3.921% -4.982% -2.327% -3.582% -5.029%
2 Error for v=53 km/h 2.042% -1.114% -7.144% -4.676% -3.918%
3 Error for v=56 km/h -0.960% 0.278% -9.221% -0.203% -5.632%
4 Error for v=53 km/h 4.276% -0.762% -2.402% -1.905% -1.903%
5 Error for v=52 km/h -1.729% 1.864% -8.976% 2.880% -2.962%
Group of speed: 70 km/h
1 Error for v=73 km/h 2.969% -3.487% -4.746% 0.482% -2.497%
2 Error for v=74 km/h 2.455% -1.204% -4.474% 1.747% 0.183%
3 Error for v=72 km/h 4.699% -2.881% -1.259% -3.693% -1.093%
4 Error for v=74 km/h 4.879% -0.886% -0.923% 3.921% 1.865%
5 Error for v=75 km/h 4.314% -2.824% 3.493 1.918% 1.247%
6 Error for v=67 km/h -2.708% 2.749% 0.281% 4.664% 3.249%
Group of speed: 90 km/h
1 Error for v=86 km/h 0.499% 1.702% -8.152% -4.744% -3.859%
2 Error for v=85 km/h 4.149% -4.338% -5.907% 0.278% 0.094%
6 CONCLUSIONS
Fibre-optic sensors (FOS) are mainly used as the
vehicle detectors because of the complicated
dependence of a set of factors (sensor’s surface
temperature, area of impact (vehicle’s tyre width),
the speed of loading, and vehicle velocity). The set
of input parameters made relatively problematic the
task of weigh-in-motion using FOS. The results of
the present research demonstrate that the factors
mostly impacting the FOS measurement accuracy
can be investigated and included into the axle weight
calculations.
An idea to normalize the FOS output voltage by
the sensor visibility losses (changing from 1 to 0)
parameter helps to avoid the influence of the static
voltage source instability as well as the conditions of
sensor installation into the pavement. Each
instantaneous measured value of the rolling wheel is
independent here from the output voltage for the
unloaded sensor. Also, the static part of the
temperature dependence is compensated by this way.
A novel approach to decompose each wheel
response into the gravity (symmetric) and the rolling
friction (asymmetric) components near the “mass
center” of the pulse, leads to the possibility of tyre
footprint area estimation and weight calculation
based on mixed Basic and Area method. Preliminary
results of the proposed method for WIM using FOS
demonstrates the accuracy of measurements are in
range of less than 10% of the measured weight. It is
sufficient for the problem of overloaded vehicles
pre-selection. The experimental results show that the
range of the vehicles velocity from 50 to 90 km/h
seems more appropriate for WIM based on fibre-
optic sensors. From the authors point of view, using
the additional signal processing efforts, it is possible
to achieve the consistent accuracy level not only at
the high speeds (above 50 km/h), but also at the low
speeds (10-50 km/h). We mean B+(7) according to
COST 323 for the high speeds and D2 according to
OIML R134 for the low speeds (O’Brien et al.,
1998).
ACKNOWLEDGEMENTS
This research was granted by ERDF funding, project
“Fiber Optic Sensor Applications for Automatic
Measurement of the Weight of Vehicles in Motion:
TyreFootprintReconstructionintheVehicleAxleWeight-in-MotionMeasurementbyFibre-opticSensors
535

Research and Development (2010-2013)”, No.
2010/0280/2DP/2.1.1.1.0/10/APIA/VIAA/094,
19.12.2010.
REFERENCES
Batenko, A., Grakovski, A., Kabashkin, I., Petersons, E.,
Sikerzhicki, Y., 2011. Weight-in-Motion (WIM)
Measurements by Fiber Optic Sensor: Problems and
Solutions. Transport and Telecommunication, Riga,
TTI, 12(4), 27–33.
Krasnitsky, Y., 2012. Transient Response of a Small-
Buried Seismic Sensor. Computer Modelling and New
Technologies, Riga, TTI, 16 (4), 33–39.
Malla, R. B., Sen, A., Garrick, N.W., 2008. A Special
Fiber Optic Sensor for Measuring Wheel Loads of
Vehicles on Highways. Sensors, 8, 2551–2568.
McCall, B., Vodrazka, W.Jr., 1997. States’ successful
practices weigh-in-motion handbook. Federal
Highway Administration: Washington, DC.
Mesco A., 1984. Digital Filtering: Applications in
Geophysical Exploration for Oil, v.1-2, Academiai
Kiado, Budapest.
Mimbela, L.-E.Y., Pate, J., Copeland, S., Kent, P. M.,
Hamrick, J., 2003. Applications of Fiber Optic Sensors
in Weigh-in-Motion (WIM) Systems for monitoring
truck weights on pavements and structures. Final
report on research project (158 p.). Las Cruces, New
Mexico, USA: New Mexico State University.
O’Brien, E. J., Jacob, B., 1998. European Specification on
Vehicle Weigh-in-Motion of Road Vehicles. In
Proceedings of the 2nd European Conference on
Weigh-in-Motion of Road Vehicles, 171–183.
Luxembourg: Office for Official Publications of the
European Communities.
SENSORLINE GmbH.(© Sensor Line), 2010. SPT Short
Feeder Spliceless Fiber Optic Traffic Sensor: product
description. Retrieved January 7, 2011, from
http://sensorline.de/home/pages/downloads.php
Teral, S.R.., 1998. Fiber optic weigh-in-motion: looking
back and ahead. Optical Engineering, 3326, 129-137.
Vinay K. I., John G. Proakis., 2006. Digital Signal
Processing Using MATLAB, Thomson Learning.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
536
