
Cardiovascular Dynamics during Head-up Tilt assessed Via a Pulsatile
and Non-pulsatile Model
N. Williams, H. T. Tran and M. S. Olufsen
Department of Mathematics, NC State University, Raleigh, NC, U.S.A.
Keywords:
Cardiovascular Dynamics Modeling, Head-up Tilt, Pulsatile vs. Non-pulsatile Modeling, Parameter Estima-
tion.
Abstract:
This study compares a pulsatile and a non-pulsatile model for prediction of head-up tilt dynamics for healthy
young adults. Many people suffering from dizziness or light-headedness are often exposed to the head-up
tilt test to explore potential deficits within the autonomic control system, which is supposed to maintain the
cardiovascular system at homeostasis. However, this system is complex and difficult to study in vivo. This
study shows how mathematical modeling can be used to extract features of the system that cannot be measured
experimentally. More specifically, we show that it is possible to develop a mathematical model that can predict
changes in cardiac contractility and vascular resistance, quantities that cannot be measured directly, but which
can be useful to assess the state of the system. The cardiovascular system is pulsatile, yet predicting control in
response to head-up tilt for the complete system is computationally challenging, and limits the applicability of
the model. In this study we show how to develop a simpler non- pulsatile model that can be interchanged with
the pulsatile model, which is significantly easier to compute, yet it still is able to predict internal variables.
The models are validated using head-up tilt data from healthy young adults.
1 INTRODUCTION
Emergency rooms and syncope clinics see a large
number of people who have experienced lighthead-
edness or dizziness. These syndromes may be as-
sociated with orthostatic intolerance: the inability
to maintain blood pressure and flow in response to
active standing or head-up tilt. Orthostatic intoler-
ance (Lanier et al., 2011) is triggered by a number
of factors, the most important being dysautonomia, a
disorder associated with the autonomic nervous sys-
tem.
In this study we use mathematical modeling to
predict blood pressure and heart rate dynamics ob-
served during HUT. The HUT protocol starts with a
subject resting in supine position on a tilt-table, after
steady oscillating values for heart rate and blood pres-
sure have been recorded, the subject is tilted head up
to a 60-70 degree angle. The test typically lasts be-
tween 10-20 minutes after initiation of the tilt. At this
point most subjects feel light-headed and are tilted
back to supine position. Upon tilting blood is pooled
in the lower body causing a drop in blood pressure
in the upper body, while blood pressure in the lower
body is increased. In response (for healthy subjects),
the autonomic system causes an increase in heart
rate, cardiac contractility, and peripheral resistance
redistributing blood volume and thereby reestablish-
ing homeostasis. For patients suffering from dysau-
tonomia, these responses may be partly or completely
inhibited.
More specifically, this paper compares a pulsatile
and a non-pulsatile mathematical model that can pre-
dict cardiovasculardynamics during HUT. Although a
pulsatile model for the cardiovascular system is bene-
ficial, it enables analysis of dynamics within beats and
can be used to understand how modulation of the sys-
tem affects pulsatility (Williams et al., 2013), which
is useful in the study of the response immediately fol-
lowing HUT (within minutes of the tilt). However,
for numerous problems it is adequate to analyze the
system with the simpler non-pulsatile model. For ex-
ample, if the objective is to study dynamics associ-
ated with the entire procedure (10-20 min). In this
study we develop a non-pulsatile model for the car-
diovascular system that can predict HUT dynamics,
and show that parameters estimated with the non-
pulsatile model can be used within the pulsatile model
or possibly be combined with more complex models
including spatial information.
673
Williams N., T. Tran H. and S. Olufsen M..
Cardiovascular Dynamics during Head-up Tilt assessed Via a Pulsatile and Non-pulsatile Model.
DOI: 10.5220/0004624006730680
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (BIOMED-2013), pages
673-680
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Besides being able to interchange the non-
pulsatile and pulsatile models, in itself non-pulsatile
models have multiple advantages. First, since they
are less complex, coupling a non-pulsatile model with
more advanced models studying larger systems such
as the respiratory or renal systems becomes feasi-
ble. Moreover, with a simple model it becomes pos-
sible to study system dynamics over much longer
time-scales (hours-days). The respiratory cycle is
approximately a fourth of the cardiovascular cycle,
and control associated with respiratory dynamics take
min-hours (Hall, 2011). The renal system is one of
the most complex physiological feedback systems, it
interacts with the cardiovascular system, and feed-
back associated with this system is hours-days (Hall,
2011). Even if the objective is to study the impact of
fainting, often studied using HUT tests, it may be nec-
essary to use a simpler model. Typically, after HUT
it takes 10-20 minutes before the subject tilted ex-
periences light headedness (Lanier et al., 2011). Fi-
nally, it should be emphasized that computations with
the non-pulsatile are significantly faster, in particu-
lar, since it is no longer necessary to account for the
discrete events associated with opening and closing
of the heart valves. In the following we will present
both a pulsatile and a non-pulsatile model and show
that they can be used interchangably in the study of
HUT dynamics.
2 METHODS
This section describes both the pulsatile and non-
pulsatile models, as well as the model changes im-
posed to predict gravitational pooling and autonomic
regulation necessary to predict HUT dynamics. We
first describe the two models, we discuss HUT, and
methods needed for comparing model predictions.
2.1 Data
As a point of departure we use the model and model-
ing results presented in (Williams et al., 2013), which
develops and validates a pulsatile model predicting
HUT dynamics for five healthy young subjects. Since
our objective is to develop a non-pulsatile model us-
ing the same framework as the pulsatile model, we
modify the heart compartment, while the remaining
model compartments stay the same. To compare
the two models, we predict the moving average of
the pressures, cardiac output, and total blood volume
from the pulsatile model and compare results with
the non-pulsatile model. Comparisons are done using
sensitivity analysis, subset selection, and optimiza-
qvl
Cal
Vau
Cau
Up Body
Up Body
Vvu
Cvu
pvu
Vlh
plh
Rvl
pau
Raup
RavRmv
qavqmv
Elh(t)
Left Heart
qaup
Ralp
qalp
Val
Vvl
ArteriesVeins
Lower Extremities
Upper Body
qal Ral
Low Body
Low Body
pvl
pal
Cvl
Figure 1: Compartment model predicting HUT dynam-
ics. For each compartment an associated blood pressure p
(mmHg), volumeV (ml), and compliance C (ml/mmHg) are
defined. The compartments represent the upper body arter-
ies (subscript au), lower body arteries (subscript al), upper
body veins (subscript vu), lower body veins (subscript vl),
and the left heart (subscript lh). Resistances R (mmHg s/ml)
are placed between all compartments: R
al
denotes the resis-
tance between arteries in the upper and lower body, R
aup
and R
alp
denote resistance between arteries and veins in the
upper and lower body, respectively. For the pulsatile model,
the two heart valves, the mitral valve and the aortic valve,
are modeled as pressure dependent resistors R
mv
and R
av
.
Finally, the resistance between the lower and upper body
veins R
vl
is also modeled as pressure dependent to prevent
retrograde flow into the lower-body during the HUT.
tion. More specifically, we estimate a set of model pa-
rameters minimizing the least squares error between
states computed by the two models. Only parameters
that represented differences between the two models
(i.e., the heart component) are allowed to vary.
2.2 Lumped Cardiovascular Models
This section describes the pulsatile and non-pulsatile
cardiovascular models depicted in Figure 1. These
models are developed to estimate blood flow, volume,
and pressure in the systemic circulation during HUT
with and without a pulsating heart. Similar to the pul-
satile model (Williams et al., 2013), the non-pulsatile
model development is split into parts including devel-
opment of a lumped cardiovascular model estimating
dynamics while the subject is resting in supine posi-
tion; developing model components allowing predic-
tion of dynamic changes to HUT; and development of
methods for estimating the impact of cardiovascular
regulation on the model parameters.
Both models follow the same basic layout shown
in Figure 1, including four compartments represent-
ing arteries and veins in the upper and lower body
and a compartment representing the heart. The latter,
is the only compartment that differ between the two
models. Therefore, the general equations outlined be-
low are valid for both models.
For each compartment, a pressure-volume relation
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
674

can be defined as
V
i
−V
un
= C
i
(p
i
− p
ext
), (1)
where V
i
(ml) is the compartment volume, V
un
(ml)
is the unstressed volume, C
i
(ml/mmHg) is the com-
partment compliance, p
i
(mmHg) is the compartment
instantaneous blood pressure, and p
ext
(mmHg) (as-
sumed constant) is the pressure in the surrounding tis-
sue. Moreover, for each compartment, the change in
volume is given by
dV
i
dt
= q
in
− q
out
, (2)
where q (ml/s) denotes the volumetric flow. Using a
linear relationship analogous to Ohm’s law the vol-
umetric flow q (ml/s) between compartments can be
computed as
q =
p
in
− p
out
R
, (3)
where p
in
and p
out
are the pressure on either side of
the resistor R (mmHg s/ml). Differentiating (1), using
(2), and inserting (3) allows us to obtain a system of
differential equations in blood pressure of the form
dp
i
dt
=
1
C
i
dV
i
dt
=
1
C
i
p
i−1
− p
i
R
i−1
−
p
i
− p
i+1
R
i
,
where i refer to the compartment for which the pres-
sure p
i
is computed, while i− 1 and i + 1 refer to the
two neighboring compartments. For resistances that
appear between compartments, R
i−1
refer to the resis-
tance between compartments i− 1 and i, and R
i
refer
to the resistance between compartments i and i + 1.
The latter equation is valid since we assume that C
i
(ml/mmHg) is constant. This formulation is utilized
for the four arterial and venous compartments.
For the pulsatile model, (2) describes the change
in volume of the left heart. Using a relation similar to
(1) we get
p
lh
= E
lh
(V
lh
−V
un
), (4)
where E
lh
(mmHg/ml) is the left heart elastance (the
reciprocal of its compliance) and V
lh
is the left heart
volume. Pumping is achieved by introducing a vari-
able elastance function (Ellwein, 2008) of the form
E
lh
(
˜
t) = (5)
E
M
−E
m
2
(1− cos(
π
˜
t
T
M
) + E
m
),
˜
t ≤ T
M
E
M
−E
m
2
(cos(
π(
˜
t−T
M
)
T
R
) + 1) + E
m
,
˜
t ≤ T
M
+ T
R
E
m
,
˜
t ≤ T
where
˜
t is the time within a cardiac cycle T = 1/H.
E
m
and E
M
denote the minimum and maximum elas-
tance, respectively. For each cardiac cycle elastance
is increased for 0 <
˜
t < T
M
and decreased for T
M
<
˜
t < T
M
+ T
R
, while during diastole T
M
+ T
R
<
˜
t < T
elastance is kept constant at its minimum value. Val-
ues for T and T
M
are obtained from data, while T
R
is
a model parameter.
Finally, heart valves are modeled using pressure
dependent resistors for which a large resistance R
cl
represents a closed valve, while a small resistance
R
op
represents an open valve. These are modeled as
smooth sigmoidal functions of the form
R
v
= R
cl
−
R
cl
− R
op
1+ e
−β(p
in
−p
out
)
, (6)
where p
in
and p
out
denote the pressures in compart-
ments on either side of the valve. For p
in
> p
out
,
R
v
→ R
op
(the valve is open), and when p
out
> p
in
,
R
v
→ R
cl
(the valve closes).
The non-pulsatile heart model is adapted work
by Batzel et al. (Batzel et al., 2007), which fol-
lowed ideas originally proposed by Grodins (Grodins,
1959). This method does not explicitly model the
pumping of the heart, but predicts cardiac output Q
as a function of venous pressure p
v
. The original
model was used within a complete circulation. It pre-
dicted cardiac output as a function of pulmonary ve-
nous pressure, the current model only encompasses
the systemic circulation, consequently this study pre-
dicts cardiac output as a function of systemic venous
pressure p
vu
.
The basic assumption concerning cardiac output,
i.e., the outflow of blood from the heart, for non-
pulsatile flow states that: Given the heart rate H (in
strokes per minute) the flow of the left ventricle Q
generated by a ventricle is given by
Q = HV
str
, (7)
where V
str
is the stroke volume, i.e., the volume of
blood ejected during one stroke. As a result time vary-
ing quantities in the non-pusatile model are to be in-
terpreted as averages over the length of a pulse. The
stroke volume is given by
V
str
= V
ED
−V
ES
, (8)
where V
ED
is the end-diastolic volume and V
ES
is the
end-systolic volume of the heart.
Another assumption involves expressing stroke
volume V
str
as a function of the arterial and ve-
nous pressures acting on the ventricle. Concerning
the ejection phase of the heart cycle we have the
so called Frank-Starling mechanism (Burton, 1972),
which states that the stroke volume of the heart in-
creases in response to an increase in the volume of
blood filling the heart (the end diastolic volume) when
all other factors remain constant. Consequently, in-
creased filling of the ventricle during diastole, causes
an increased contraction force during the following
CardiovascularDynamicsduringHead-upTiltassessedViaaPulsatileandNon-pulsatileModel
675

systole.
V
str
=
S
p
a
(V
ED
−Vun), (9)
where p
a
is the arterial pressure against which the
ventricle has to eject (the afterload) and S denotes the
contractility of the left ventricle.
Using the previous two assumptions we express
the ventricular output Q (the cardiac output) as a func-
tion of blood pressure. To model the filling process of
the heart, when the mitral valve is open, we assume
that the inflow in to the ventricle depend on the differ-
ence between the filling pressure and the left ventricle
pressure, using an expression analogous to (3), we get
˙
V
lh
(t) =
1
R
lh
(p
v
− p
lh
), (10)
where V
lh
is the ventricular volume at time t after the
filling process has started, p
lh
is the ventricular pres-
sure, p
v
is the venous filling pressure assumed to be
constant, and R
lh
is the total ventricular resistance to
the inflow of blood.
For the relaxed ventricle, a similar volume-
pressure relation can be derived (e.g., as in (1)),
V(t) = C
lh
p
lh
(t) +V
un
, (11)
where V
un
denotes the unstressed volume of the re-
laxed ventricle and C
lh
denotes the heart compliance.
The initial value for (10) is given by V(0) = V
ES
. Us-
ing (11) in (10), integrating, and letting t = t
d
, the
time of end-diastole, we obtain
V
ED
= kV
ES
+ a(C
lh
p
v
+V
un
), (12)
where k = exp(−t
d
/C
lh
R
lh
) and a = 1− k.
Equations (8), (9), and (12) constitute a system of
linear equations for V
ED
, V
ES
, and V
str
. We obtain
V
ED
= C
lh
p
v
+V
un
−
C
lh
kp
v
S
ap
a
+ kS
, (13)
V
ES
= C
lh
p
v
+V
un
−
C
lh
p
v
S
ap
a
+ kS
, (14)
V
str
=
aC
lh
p
v
S
ap
a
+ kS
. (15)
Combining (7) and (15) gives the cardiac output
out of the ventricle
Q = H
aC
lh
p
v
S
ap
a
+ kS
, (16)
where H is heart rate,C
lh
heart compliance, p
v
venous
pressure, p
a
arterial pressure, and S contractility.
There are essentially two possibilities for a ventri-
cle to change the cardiac output: to change the heart
rate or the contractility. Heart rate and contractility
are related through the Bowditch effect (Klabunde,
1972), which states that contractility is proportional
to heart rate. The Bowditch effect can be accounted
for by introducing the second order ordinary differen-
tial equation, of the form
¨
S+ γ
˙
S+ αS = βH, (17)
where γ, α, and β are positive constants and H is heart
rate. For this study, we rewrite this second order ODE
as two first order equations.
Using these relations the pulsatile five differential
equations can be written as
dp
au
dt
= (q
av
− q
al
− q
aup
)/C
au
dp
al
dt
=
q
al
− q
alp
/C
al
dp
vl
dt
=
q
alp
− q
vl
/C
vl
dp
vu
dt
= (q
aup
+ q
vl
− q
mv
)/C
vu
dV
lh
dt
= q
mv
− q
av
and the non-pulsatile equations as
dp
au
dt
= (Q− q
al
− q
aup
)/C
au
dp
al
dt
=
q
al
− q
alp
/C
al
dp
vl
dt
=
q
alp
− q
vl
/C
vl
dp
vu
dt
= (q
aup
+ q
vl
− Q)/C
vu
,
dS
dt
= σ
dσ
dt
= −αS− γσ+ βH,
where
q
av
=
p
lh
− p
au
R
av
q
aup
=
p
au
− p
vu
R
aup
q
al
=
p
au
− p
al
R
al
q
alp
=
p
al
− p
vl
R
alp
q
vl
=
p
vl
− p
vu
R
vl
q
mv
=
p
vu
− p
lh
R
mv
.
In the last set of equations the left ventricular pressure
(p
lh
) is predicted using (4), the pressure dependent re-
sistances used to model the valves (R
av
,R
mv
) are pre-
dicted from (6), and the total blood volume can be
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
676

computed from pressures using (1). These equations
were solved in Matlab using the ODE15s differential
equations solver. Abbreviations (subscripts) are given
in Table 1.
2.2.1 Modeling HUT
As the subject is tilted (shown in Figure 2), blood is
pooled in the lower extremities leading to an increase
in pressure in the lower body, while pressure in the
upper body decreases. To account for gravity, the
pressure at the level of the carotid arteries are used
as a reference pressure, so an extra term is added to
the flow (q
al
) and subtracted from the flow (q
vl
) of the
lower body compartments. The gravitational effects
are calculated as described by Olufsen et al. (Olufsen
et al., 2005; Williams et al., 2013), giving the follow-
ing modified flow equations
q =
ρgh
tilt
sin(θ(t)) + p
in
− p
out
R
, (18)
θ(t) =
π
180
0 t < t
st
v
t
(t − t
st
) t
st
≤ t ≤ t
st
+ t
ed
60 t > t
st
+ t
ed
where ρ (g/ml) is blood density, g (cm/s
2
) is the con-
stant of gravitational acceleration, h
tilt
(cm) is the
absolute height between the upper body and lower
body compartments, θ(t) is the tilt angle (in radians),
v
t
= 15 degrees/s is the tilt speed, while t
st
and t
ed
denote the time at which HUT is started and ended,
respectively. The combined term ρgh
tilt
sin(θ(t)) de-
notes the hydrostatic pressure between the upper and
lower body compartments.
2.2.2 Modeling Effects of Cardiovascular
Regulation
Upon HUT firing of the baroreceptor nerves are mod-
ulated by the aortic and carotid sinus baroreceptors
sensing changes in the stretch of the arterial wall.
Typically, HUT leads to a decrease in blood pressure
mediating an increase in sympathetic outflow along
Table 1: Abbreviations (subscripts) used in the compart-
mental model.
Abbreviation Name
av aortic valve
au upper body arteries
al lower body arteries
aup upper body ”peripheral” vascular bed
alp lower body ”peripheral” vascular bed
vu upper body veins
vl lower body veins
lh the left heart (ventricle and atrium)
Figure 2: The HUT test: The subject depicted is tilted to
an angle of 60 degrees at a constant speed of 15 degrees
per second. Red and yellow circles indicate the locations
for the blood pressure sensors. Each sensor is mounted on
the index finger, one finger (red) is placed at the level of
the carotid artery, while the other (yellow) is placed at the
level of the heart. Upon HUT blood is pooled in the lower
extremities.
with parasympathetic withdrawal. Sympathetic stim-
ulation elicits changes in vascular resistance and car-
diac contractility, while parasympathetic withdrawal
primarily has an effect on heart rate and cardiac con-
tractility. Heart rate is used as an input, consequently,
parasympathetic heart rate regulation is implicitly ac-
counted for in the model. For the pulsatile model,
regulation of cardiac contractility is modeled by con-
trolling the minimum elastance of the left heart (E
m
)
and vascular resistance is regulated in both the up-
per and lower body. However, as the compartments
representing the upper and lower body arteries appear
in parallel, both resistances are not identifiable. We
controlled R
aup
directly, while we let R
alp
= kR
aup
,
where k is the ratio of the optimized supine values of
R
aup
and R
alp
. For the non-pulsatile model, we do not
have an explicit expression for E
m
, instead contrac-
tility is included via the Bowditch effect (Klabunde,
1972), and modeled as a function of heart rate as de-
scribed in (17). Hence, changes in contractility has
been modeled indirectly, via the 2’nd order ODE,
while parameters associated with autonomic control
of vascular resistance should be modeled. To so, sim-
ilar to (Williams et al., 2013) we predict R
aup
as a
piece-wise linear function given by
X(t) =
N
∑
i=1
γ
i
K(t), (19)
K(t) =
t − t
i−1
t
i
− t
i−1
, t
i−1
≤ t ≤ t
i
t
i+1
− t
t
i+1
− t
i
t
i
≤ t ≤ t
i+1
0, otherwise
where the unknown coefficients γ
i
, i = 1...N are the
new parameters that will be estimated to predict the
CardiovascularDynamicsduringHead-upTiltassessedViaaPulsatileandNon-pulsatileModel
677
control. N is the number of nodes along the time span
analyzed. The spread of the N nodes should be spec-
ified in the model. For simulations reflecting dynam-
ics observed in supine position we placed the nodes
with a frequency of 6-10 seconds, but during HUT,
where dynamics change, significantly more points are
added. It should be noted that the more points are
added to the time-span, the longer the simulations.
3 RESULTS
We first show results obtained for a subject in supine
position followed by results obtained when the same
subject is tilted upright to a 60 degree angle (see Fig-
ure 2). Results during supine position are included to
tune model parameters to the subject studied, while
during HUT we allow parameters regulated by the
autonomic control system to vary in time. For each
event we estimate parameters minimizing the least
squares error between the model output and data. To
develop two models (pulsatile and non-pulsatile) that
can be interchanged, we compute moving averages
for the quantities X = {p
m
au
, p
m
vu
, p
m
al
, p
m
vl
, CO
m
, V
m
tot
}
using pulsatile model outputs predicted in Williams
et al. (Williams et al., 2013), and use these as data for
the non-pulsatile model.
3.1 Optimization During Supine
Position
First we predict dynamics during supine position, as
stated above. These simulations are included to tune
the model to the subject studied. For these simu-
lations we estimate parameters in the non-pulsatile
heart model (R
lh
, C
lh
, α, β, γ, c) minimizing the least
squares error
J =
1
N
N
∑
i=1
X
d
i
− X
m
i
X
d
i
2
,
where X denotes the states listed above, super-
script d refers to the data (obtained from the pul-
satile model (Williams et al., 2013)), and superscript
m refers to results obtained with the non-pulsatile
model.
It should be noted that parameters ”not” associ-
ated with the heart compartment are kept constant,
since they represent components common for the two
models. Results comparing the pulsatile and non-
pulsatile model during steady state are shown in Fig-
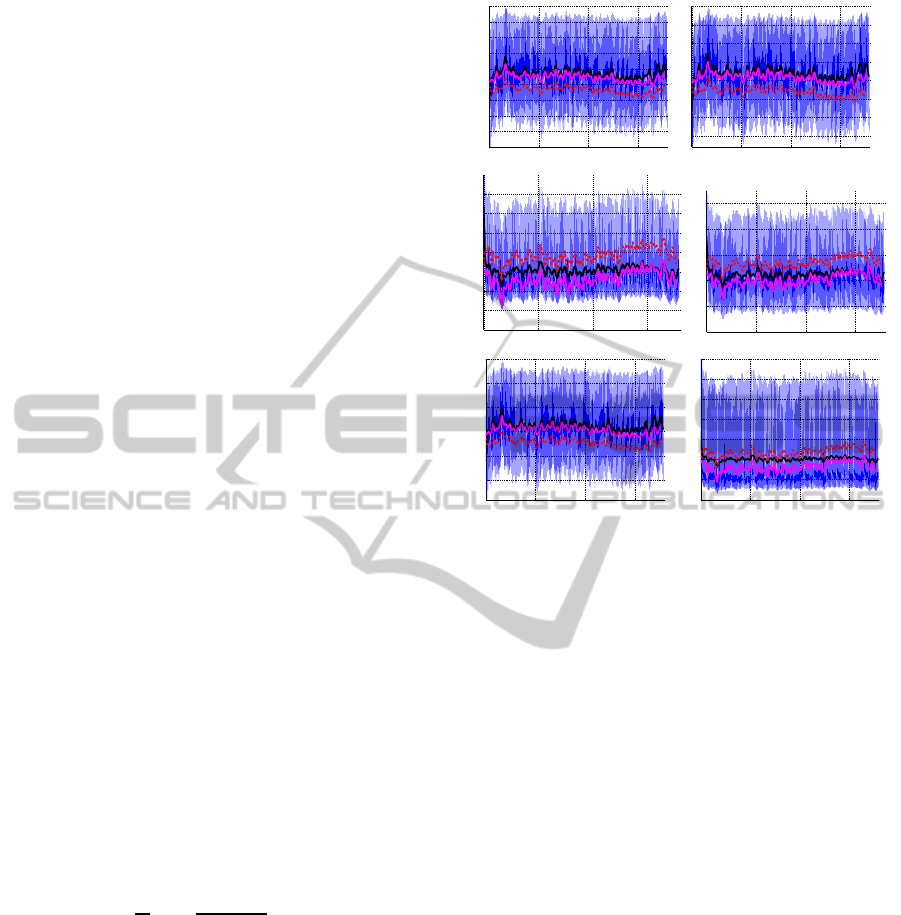
ure 3. This figure shows all pressures and cardiac
output. Each graph shows pulsatile model results
(from Williams et al. (Williams et al., 2013)), moving
0 50 100 150
50
55
60
65
70
75
80
85
90
95
pau (mmHg)
0 50 100 150
55
60
65
70
75
80
85
90
pal (mmHg
0 50 100 150
2.6
2.7
2.8
2.9
3
3.1
3.2
3.3
pvl (mmHg)
0 50 100 150
2.2
2.4
2.6
2.8
3
3.2
pvu (mmHg)
0 50 100 150
70
80
90
100
110
120
time (s)
CO (ml/s)
0 50 100 150
4400
4600
4800
5000
5200
5400
5600
5800
time (s)
Vtot (ml)
Figure 3: Predictions during supine position. All graphs in-
clude the pulsatile model output (blue), the mean of the pul-
satile model output (black), the non-optimized (red, dashed)
and optimized (magenta) non-pulsatile model output for the
upper and lower body arterial pressure p
au
and p
al
, upper
and lower body venous pressure p
vu
and p
vl
, cardiac output
CO, and total volume V
tot
.
averages predicted from the pulsatile model (black
line), computations with the non-pulsatile model us-
ing nominal parameters (red dashed line), and com-
putations with optimized parameters for the non-
pulsatile model (magenta line). Note that for all states
the two models agree well.
Initial parameters used for the arterial and venous
portions of the model (results not shown) were esti-
mated as described in previous studies Williams et
al. (Williams et al., 2013). In short, we used sen-
sitivity analysis and subset selection to obtain a set
of parameters that can be estimated given the model
and available data, and used nonlinear optimization
to estimate their value. For this study, we only es-
timated parameters associated with the heart com-
ponent within the non-pulsatile heart, assuming the
tuned arterial and venous parameters found within the
pulsatile model can be used within both formulations.
3.2 HUT Optimization
Once baseline parameters were obtained, we imposed
HUT, by modifying flows between the upper and
lower body as described in (18). For these simula-
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
678
tions, we only estimate the control parameters θ =
γ
Raup,i
used for computing R
aup
as stated in (19), i.e.,
we let the parameter R
sup
vary in time. In the pul-
satile model we also let contractility be time-varying,
via estimation of γ
Em,i
, yet the non-pulsatile model
directly accounts for this part of the control via the
Bowditch effect (17), predicting cardiac contractility
S as a function of heart rate H. For this portion of
the model, we only included p
au
in the cost function,
giving
J =
1
N
N
∑
i=1
p
d
au,i
− p
m
au,i
p
d
au,i
!
2
,
where superscript d refers to the data and superscript
m for the model.
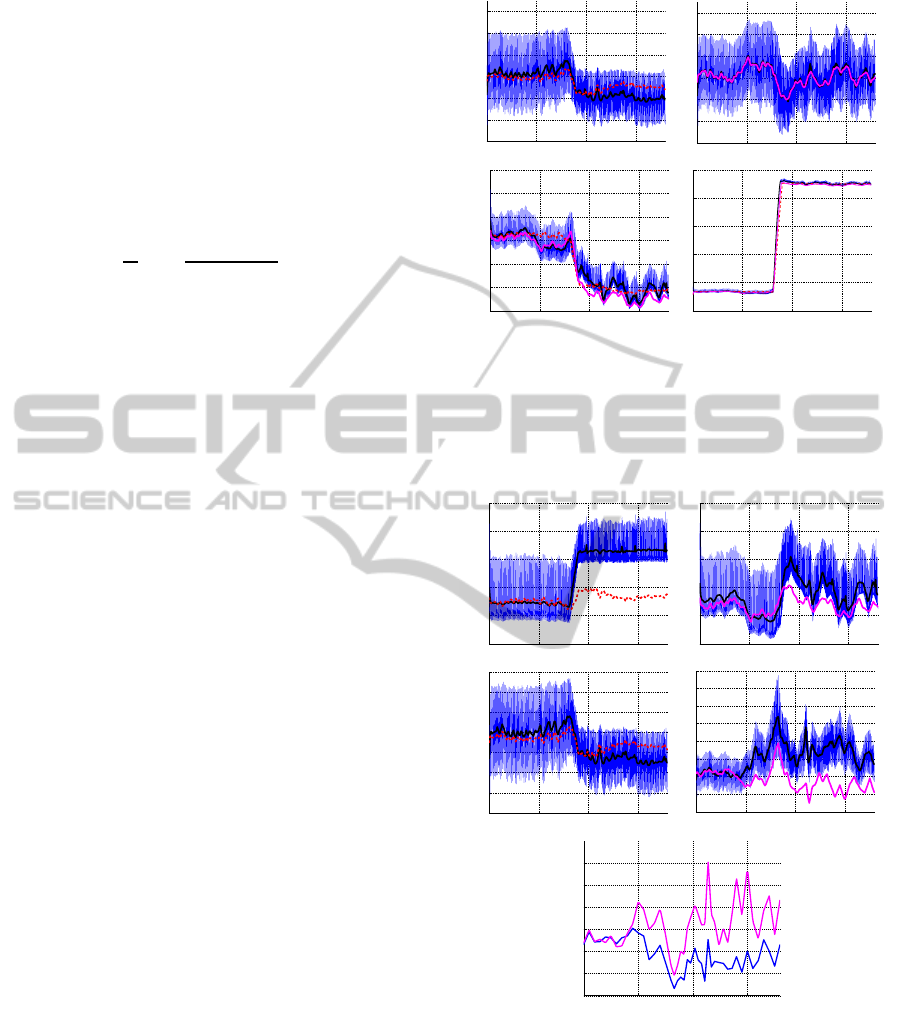
Figure 4 shows the pulsatile model output (blue),
the moving average data computed from the pulsatile
model (black), and results using nominal parameter
values (red dashed) during HUT. The subject is tilted
after 80 sec and remains upright for the duration of
the simulation. The top left graph in Figure 4 de-
picts dynamics without activating the control, i.e., for
this simulation R
aup
is kept at its baseline value. Note
that after about 100 sec, this part of the model devi-
ates slightly from results obtained with the pulsatile
model. This is likely due to the fact that the non-
pulsatile model results already incorporate control of
contractility (S), while the ”data” obtained from the
pulsatile model were obtained using constant contrac-
tility values E
m
. The following graphs show all model
predicted pressures obtained with the non-pulsatile
model using optimal parameter values. Note that pre-
dictions for p
au
are significantly closer than for the
other states, this is likely because for these simula-
tions, we only include p
au
in the cost function. In
other words, no effort was made to account for varia-
tion in the remaining states. Finally, Figure 5 shows
corresponding volumes and cardiac output, both are
shown with nominal and optimized parameter values.
This figure also shows time-varying prediction of pe-
ripheral vascular resistance R
sup
.
The significance of the relation between the pul-
satile and non-pulsatile models are corroborated fur-
ther by examining dynamics of quantities for which
data are not available, i.e., for p
vu
, p
al
, and p
vl
de-
picted in Figure 4. Finally, our model provides good
predictions of blood volume and cardiac output, de-
picted for a representative subject in Figure 5.
4 CONCLUSIONS
This study has shown that it is possible to develop
a pulsatile and a non-pulsatile model that can both
0 50 100 150
40
50
60
70
80
90
100
pau (mmHg)
time (s)
0 50 100 150
40
50
60
70
80
90
100
pau (mmHg)
0 50 100 150
1
1.5
2
2.5
3
3.5
4
pvu (mmHg)
0 50 100 150
0
5
10
15
20
25
pvl (mmHg)
Figure 4: Predictions during HUT. Pulsatile (blue), mov-
ing average from pulsatile model (magenta), non-pulsatile
model with nominal (red dashed) and optimized (magenta)
parameter values. The top graph shows p
au
predicted using
nominal parameter values. The following four panels com-
pares arterial and venous pressures in the upper and lower
body.
0 50 100 150
4000
4500
5000
5500
6000
6500
Vtot (ml)
0 50 100 150
4000
4500
5000
5500
6000
6500
Vtot (ml)
0 50 100 150
50
60
70
80
90
100
110
120
CO (ml/s)
0 50 100 150
40
60
80
100
120
140
160
180
200
time (s)
CO (ml/s)
0 50 100 150
0.4
0.6
0.8
1
1.2
1.4
1.6
time (s)
Raup (mmHg s/ml)
Figure 5: Volume and CO predictions during HUT. The top
two graphs depict the total blood volume during HUT with-
out (left) and with (right) cardiovascular regulation. The
following two graphs show cardiac output computed with-
out (left) and with (right) cardiovascular regulation. Again,
pulsatile (blue), pulsatile mean values (black), and non-
pulsatile (red, dashed) denote simulations with nominal and
(magenta) with estimated parameter values. The bottom
graph shows estimated values for R
aup
with pulsatile (ma-
genta) and non- pulsatile (blue) models.
CardiovascularDynamicsduringHead-upTiltassessedViaaPulsatileandNon-pulsatileModel
679

predict dynamics during HUT, and that time-varying
parameters (R
aup
) can be predicted by both models.
Moreover, we have shown (graph not included) that it
is possible to use parameter estimates obtained with
the non-pulsatile model within the pulsatile model.
This could be used in simulations done over long
time-scales (min-hours) where it may only be neces-
sary to study pulsatility intermittently, e.g., following
given events within the system. Finally, it should be
noted that compartments and parameters associated
with the arterial and venous subsystems are identical
for the two models. The only difference is the com-
partment predicting dynamics of the left heart.
In summary, we have developed a non-pulsatile
model and shown that it can be used to predict HUT
dynamics. These models (the pulsatile and non-
pulsatile models) have many potential benefits for the
study of complex models, which contain a cardiovas-
cular component. The advantage of results presented
here is that the non-pulsatile model has potential to
be included in for applications that require analysis of
data over large time-scales.
ACKNOWLEDGEMENTS
Williams and Olufsen were supported in part by
the virtual rat physiology project (VPR) supported
by NIH-NIGMS under grant #1P50GM094503-01A0
sub-award to NCSU. Tran and Olufsen were also sup-
ported by NSF under the grant NSF/DMS #1022688.
REFERENCES
Batzel, J., Kappel, F., Schneditz, D., and Tran, H. (2007).
Cardiovascular and respiratory systems: modeling,
analysis, and control. SIAM, Philadelphia, PA.
Burton, A. (1972). Physiology and biophysics of the cir-
culation: an introductory text. Year Book Medical
Publishers Inc, Chicago, IL.
Ellwein, L. (2008). Cardiovascular and respiratory mod-
eling. PhD thesis, Department of Mathematics, NC
State University, Raleigh, NC.
Grodins, F. (1959). Integrative cardiovascular physiology:
a mathematical synthesis of cardiac and blood vessel
hemodynamics. Q Rev Biol, 34:93–116.
Hall, J. (2011). Guyton and Hall Textbook of Medical Phys-
iology. Saunders, Philadelphia, PA, 12th edition.
Klabunde, R. (1972). Physiology and biophysics of the cir-
culation: an introductory text. Lippincott Williams
and Wilkins, Philadelphia, PA.
Lanier, J., Mote, M., and Clay, E. (2011). Evaluation
and management of orthostatic hypotension. Am Fam
Physician, 84:527–536.
Olufsen, M., Ottesen, J., Tran, H., Ellwein, L., Lipsitz, L.,
and Novak, V. (2005). Blood pressure and blood flow
variation during postural change from sitting to stand-
ing: model development and validation. J Appl Phys-
iol, 99:1523–1537.
Williams, N., Wind-Willassen, O., Program, R., Mehlsen,
J., Ottesen, J., and Olufsen, M. (2013). Patient specific
modeling of head-up tilt. Math Med Biol, In press.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
680
