On the Extension of k-Means for Overlapping Clustering

Average or Sum of Clusters’ Representatives?

Chiheb-Eddine Ben N’Cir

and Nadia Essoussi

LARODEC, ISG Tunis, University of Tunis, Bardo, Tunis, Tunisia

LARODEC, FSEG Nabeul, University of Carthage, Nabeul, Tunisia

Keywords:

Overlapping Clustering, Multi-labels, Non disjoint Clusters, Additive Clustering.

Abstract:

Clustering is an unsupervised learning technique which aims to ﬁt structures for unlabeled data sets. Iden-

tifying non disjoint groups is an important issue in clustering. This issue arises naturally because many real

life applications need to assign each observation to one or several clusters. To deal with this problem, recent

proposed methods are based on theoretical, rather than heuristic, model and introduce overlaps in their opti-

mized criteria. In order to model overlaps between clusters, some of these methods use the average of clusters’

prototypes while other methods are based on the sum of clusters’ prototypes. The use of SUM or AVERAGE

can have signiﬁcant impact on the theoretical validity of the method and affects induced patterns. Therefore,

we study in this paper patterns induced by these approaches through the comparison of patterns induced by

Overlapping k-means (OKM) and Alternating Least Square (ALS) methods which generalize k-means for

overlapping clustering and are based on AVERAGE and SUM approaches respectively.

1 INTRODUCTION

Clustering is an important task in data mining. It

aims to divide data into groups where similar obser-

vations are assigned to the same group called cluster.

It has been applied successfully in manyﬁelds such as

marketing that ﬁnds groups of customers with similar

purchasing behaviors, biology that groups unlabeled

plants or animals into species and document classi-

ﬁcation that groups related documents into clusters.

Many applications of clustering require assigning ob-

servations to several clusters. This kind of prob-

lematic is referred as overlapping clustering (Diday,

1984; Banerjee et al., 2005; Cleuziou, 2008; Fellows

et al., 2011).

Overlapping clustering is based on the assumption

that an observation can really belong to several clus-

ters. In this cluster conﬁguration, an observation may

belong to one or several clusters without any member-

ship coefﬁcient and the resulting clustering is a cover.

The resolution of this problem contributes to solve

many real life problems that require to ﬁnd overlap-

ping clusters in order to ﬁt the data set structure. For

example, in social network analysis, community ex-

traction algorithms should be able to detect overlap-

ping clusters because an actor can belong to multiple

communities (Tang and Liu, 2009; Wang et al., 2010;

Fellows et al., 2011). In video classiﬁcation, overlap-

ping clustering is a necessary requirementwhile video

can potentially have multiple genres (Snoek et al.,

2006). In emotion detection, overlapping clustering

methods should be able to detect several emotions

for a speciﬁc piece of music (Wieczorkowska et al.,

2006), etc.

Many methods have been focused on detecting

non-disjoint groups in data. First methods modify re-

sults of fuzzy classiﬁcation to produce overlapping

clusters such as the extension of clusters obtained

with Fuzzy c-means method by thresholding clus-

ters memberships (Deodhar and Ghosh, 2006; Lin-

gras and West, 2004; Zhang et al., 2007). The main

issue in these methods is the learning of prior thresh-

old which is a difﬁcult task. In addition, criteria to

be optimized iteratively look for optimal partitions

without introducing overlaps between data in the op-

timization step. These contributions, which are not

based on theoretical approaches, can lead to suitable

results in some contexts but their extensions or im-

provements are limited (Banerjee et al., 2005).

Recent methods look for overlapping clusters

based on theoretical approaches. The most important

advantage of these methods is their ability to produce

non-disjoint clusters where overlaps are introduced in

their optimized criteria. These recent methods can be

208

Ben N’Cir C. and Essoussi N..

On the Extension of k-Means for Overlapping Clustering - Average or Sum of Clusters’ Representatives?.

DOI: 10.5220/0004626502080213

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval and the International Conference on Knowledge

Management and Information Sharing (KDIR-2013), pages 208-213

ISBN: 978-989-8565-75-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

categorized into two main approches: SUM and AV-

ERAGE. We denoted by SUM methods which group

observations into overlapping clusters while minimiz-

ing the sum of distances between each observation

and the sum of clusters’ representatives (prototypes

or centroids) to which the observation belongs to. Ex-

amples of these methods are Principal Cluster Anal-

ysis (PCL) (Mirkin, 1987b) with its variants (Mirkin,

1987a; Mirkin, 1990), the Alternating Least Square

algorithms (ALS) (Depril et al., 2008; Wilderjans

et al., 2012) and the Lowdimensional Additive Over-

lapping Clustering (Depril et al., 2012).

Conversely, methods based on AVERAGE ap-

proach group observations into overlapping clusters

while minimizing the sum of distances between each

observation and the average, instead of the sum, of

clusters’ representatives to which the observation be-

longs to. Examples of these methods are the Over-

lapping k-means (OKM) (Cleuziou, 2008), Kernel

Overlapping k-means (KOKM) (N’cir et al., 2010),

Overlapping k-Medoid (OKMED) (Cleuziou, 2009),

the Evidential c-means (ECM) (Masson and Denux,

2008) and Overlapping Clustering with Sparseness

Constraint (Lu et al., 2012).

All these methods extend k-means to take into ac-

count that an observation belongs to several clusters.

Despite different approaches are used by these meth-

ods, they are considered as generalization of k-means

to overlapping clustering (Cleuziou, 2008; Mirkin,

1990; Depril et al., 2008). If each observation is as-

signed to only one cluster, objectivecriteria optimized

by these methods exactly match with the objectivecri-

terion of k-means. The aim of this paper is to study

patterns induced by AVERAGE and SUM approaches

used to model overlapping clustering. We compare

effectiveness of OKM (AVERAGE based method) and

ALS (SUM based method) to identify overlapping

groups. We discuss cases in which these models can

be applied in real life applications.

This paper is organized as follows: Section 2 and

Section 3 describe respectively OKM and ALS meth-

ods. Then, Section 4 presents discussions on pat-

terns induced by OKM and ALS and describes clus-

tering applications in which these methods were ap-

plied. Section 5 presents experiments performed on

real overlapping data sets to check effectiveness of

OKM and ALS in detecting overlapping clusters. Fi-

nally Section 6 presents conclusion and future works.

2 OVERLAPPING k-Means (OKM)

OKM introduces the overlapping constraint (an ob-

servation can belong to more than one cluster) in the

usual squared error objective function. The function

models a local error on each observation x deﬁned

by the squared Euclidean distance between x and it’s

representative in the clustering, denoted as “image”

(im(x)). Given a dataset X with N data over R

and a

number K of expected clusters, the aim of OKM is to

ﬁnd the binary assignment matrix Π(N × K) and the

cluster representatives (prototypes) C = {c

,...,c

}

such that the following objective function is mini-

mized:

OKM

(Π,C) =

∑

∈X

k x

− im

Π,C

) k

, (1)

where im

Π,C

) is the average combination of cluster

representatives. Let Π

the set of clusters to which

belongs and |Π

| the number of clusters for x

, the

Π,C

) is described by:

Π,C

) =

∑

k∈Π

|Π

. (2)

The minimization of the objective function is per-

formed by iterating two principal steps:

1. computation of cluster representatives (C).

2. multi assignment of observationsto one or several

clusters (Π).

The update of representatives is performed locally for

each cluster. For the multiple assignment step, the

OKM method uses an heuristic to explore part of

the combinatorial set of possible assignments. The

heuristic consists, for each observation, in sorting

clusters from closest to the farthest, then assigning

the observation in the order deﬁned while assignment

minimizes the distance between the observation and

its image. The stopping rule of algorithm is charac-

terized by two criteria: the maximum number of iter-

ations or the minimum improvement of the objective

function between two iterations.

3 ALTERNATING LEAST

SQUARE (ALS)

ALS is based on the Additive Overlapping Clustering

model (Mirkin, 1990). This model introduces the pos-

sibility that an observation belongs to more than one

cluster by considering variable values of an observa-

tion equals to the sum of the clusters’ proﬁles (pro-

totypes) to which the observation belongs to. Given

a dataset X with N data over R

and a number K of

expected clusters, a model matrix M = ΠC is looked

for to optimally approximate X. The matrix M can be

estimated by minimizing the least squares loss func-

tion:

OntheExtensionofk-MeansforOverlappingClustering-AverageorSumofClusters'Representatives?

209

ALS

(Π,C) =k X −ΠC k

∑

∈X

k x

−

∑

k∈Π

, (3)

where k . k

is the Frobenius norm of a matrix. For

the minimization of the loss function, ALS starts from

an initial binary membership matrix Π

, then it will

estimate the conditionally optimal proﬁles C upon Π;

subsequently it will estimate the conditionally opti-

mal memberships Π upon C, and this process will

be repeated until convergence. The advantage of this

method consists of its ability to take into account all

possible assignments for each observation by explor-

ing 2

assignments. The optimal assignments for each

observation are the assignments which minimize the

local error between the observation and the sum of

clusters’ proﬁles to which this observation belongs to.

4 DISCUSSION

We note that both OKM and ALS tolerate overlaps be-

tween clusters leading to non disjoint clusters. If we

add the constraint that each observation is assigned

to only one group |Π

| = 1, the optimized criteria by

these methods match with the objective criterion of k-

means. The main difference between OKM and ALS

consists on how the overlaps are introduced in the ob-

jective criterion: for OKM, each observation is repre-

sented by the average of clusters’ prototypes to which

the observation belongs to, however for ALS each ob-

servation is represented by the sum of clusters’ proto-

types.

To study the inﬂuence of this fact on the induced

patterns, we visualize partitioning of OKM (AVER-

AGE based method) and ALS (SUM based method)

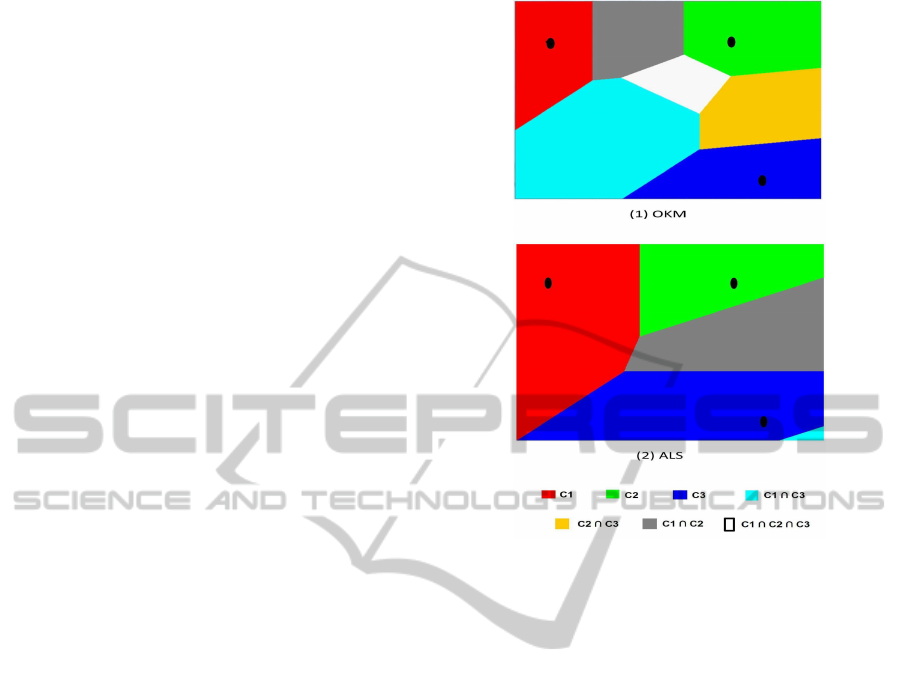
through Vorono¨ı cells obtained for three clusters over

a two dimensional space as deﬁned by the objec-

tive criterion optimized by these methods. Figure ??

shows an example of these Vorono¨ı cells: the rep-

resentation space is divided into several cells where

each possible combination of clusters is associated to

one cell. For OKM, we show seven cells (all pos-

sible combinations of clusters except the empty set)

where each cell is centered on a prototype or a com-

bination (average) of prototypes. For ALS, we notice

that overlaps between clusters are not recovered, we

show only overlaps between cluster1∩ cluster2 and

between cluster2 ∩ cluster3 . We can easily remark

that the gray cell is deﬁned by the combination (sum)

of representatives of cluster 1 (red cell) and cluster 2

(green cell).

Methods based on SUM and AVERAGE ap-

proaches can lead to non disjoint groups. The adop-

tion of these approaches are motivated by require-

ments of real life applications. Methods based on

Figure 1: Vorono¨ı cells obtained with OKM (AVERAGE

based Approach) and ALS (SUM based Approach) for three

clusters.

SUM have been well applied in grouping patients into

diseases. Each patient may suffer from more than one

disease and therefore could be assigned to multiple

syndrome clusters. Thus, the ﬁnal symptom proﬁle

of a patient is the sum of the symptom proﬁles of all

syndromes he is suffering from. However, this type of

methods needs sometimes to prepare data to have zero

mean to avoid false analysis. For example, if symp-

tom variable represents the body temperature, then

when a patient simultaneously suffers from two dis-

eases, it is not realistic to assume that his body tem-

perature equals to the sum of body temperatures as

associated with two diseases.

Methods based on AVERAGE approach have

been well applied to group music signals into dif-

ferent emotions and ﬁlms into several genres. These

methods consider that overlapping observations must

appear in the extremity surface between overlapping

clusters. For example, if a ﬁlm belongs to action and

horror genres, it should have some shared properties

with these categories of ﬁlms but it can neither be a

full action ﬁlm neither a full horror one. So, overleap-

ing ﬁlms belonging to action and horror categories

may appear in the limit surface between full horror

and full action ﬁlms.

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

210

Table 1: Statistics of used data sets.

Data set Domain N Dimension Labels Cardinality

EachMovie Video 75 3 3 1.14

Music emotion Music 593 72 6 1.86

Scene Images 2407 192 6 1.07

5 EXPERIMENTS

In this section, we check effectiveness of OKM and

ALS in detecting overlapping groups through an ex-

perimental study on real overlapping data sets.

5.1 Data Sets Description and

Evaluation Measures

Experiments are performed on Eachmovie

, Music

emotion

and Scene

data sets. For each data set, the

number of clusters K was set to the number of un-

derlying categories in the data set. Table 1 shows the

statistics for each data set. “Labels” is the number of

categories and “Cardinality” (natural overlaps) is the

average number of categories for the observations.

Cardinality = 1/N

∑

∈X

, (4)

where N is the number of observations and L

is the

number of labels of observation x

Results are compared using four validation mea-

sures: Precision, Recall, F-measure and Overlap size.

The ﬁrst three validation measures estimate whether

the prediction of categories is correct with respect to

the underlying true categories in the data. Precision

is calculated as the fraction of observations correctly

labeled as belonging to class c

divided by the total

number of observations labeled as belonging to class

. Recall is the fraction of observations correctly

labeled as belonging to class c

divided by the total

number of observations that really belong to class c

The F-measure is the harmonic mean of Precision and

Recall.

Precision(c

) = NCLO/TNLO

Recall(c

) = NCLO/TNAC

F-measure(c

) = 2*Precision(c

)*Recall(c

) /

(Precision(c

)+Recall(c

))

where NCLO, TNLO and TNAC are respectively the

number of correctly labeled observations, the total

number of labeled observations and the total number

cf. http://www.grouplens.org/node/76.

cf.http://mlkd.csd.auth.gr/multilabel.html

of observations that really belong to the correct class.

All these measures are performed separately on each

cluster, then the average value of all clusters is re-

ported. The fourth measure, Overlap size, evaluates

the size of overlaps builded by the learning method.

This measure can be determined by the average num-

ber of labels of each observation in the data set as

follows:

Overlapsize =

∑

∈X

|X|

, (5)

where |X| is the total number of observations and |c

is the number of clusters to which observation x

be-

longs.

5.2 Empirical Results

Table 2 reports the average of precision (P), recall (R)

and F-measure (F) on ten runs on Eachmovie, Music

Emotion and Scene data sets. For each run, all meth-

ods have the same initialization of prototypes. Re-

sults of ALS in Scene data set are not reported be-

cause of computational problem

. We notice that av-

erage of F-measures obtained with overlapping meth-

ods outperform F-measures obtained with k-means.

For example F-measures obtained with OKM and

ALS in Music Emotion data set are equal to 0.362

and 0.388 respectively, while using k-means the ob-

tained F-measure is 0.288. However, in Scene data set

F-measure obtained with k-means outperforms those

obtained with OKM and ALS. This result is explained

by the fact that actual overlaps in Scene data set are

not large (overlaps=1.07). Compared to k-means, re-

sults obtained with OKM and ALS are more impor-

tant as well as the size of overlaps in the data set in-

creases.

Results obtained with fuzzy c-means using differ-

ent thresholding membership are characterized by law

values and are much sensitive to the used threshold:

for example, in the Scene data set, using a threshold

equal to 0.3, all observations are not assigned to any

cluster which explain the null values of fuzzy c-means

in this data set. However, in Eachmovie data set using

execution needs more than 24 hours

OntheExtensionofk-MeansforOverlappingClustering-AverageorSumofClusters'Representatives?

211

Table 2: Comparison of the performance of OKM and ALS versus other existing methods in overlapping data sets.

Data set Label Eachmovie Music Scene

P R F P R F P R F

k-means 0.731 0.544 0.623 0.501 0.203 0.288 0.503 0.515 0.508

Fuzzy c-means (threshold=0.3) 0.523 0.847 0.647 0.441 0.251 0.310 0.000 0.000 0.000

Fuzzy c-means (threshold=0.4) 0.691 0.523 0.596 0.490 0.205 0.288 0.000 0.000 0.000

OKM 0.582 0.827 0.687 0.397 0.332 0.362 0.338 0.887 0.482

ALS 0.515 0.779 0.620 0.299 0.555 0.388 - - -

Table 3: Size of overlaps obtained with ALS, OKM and other methods in overlapping data sets.

Size of Overlap

Eachmovie data set Music data set Scene data set

Real overlap size (1.14) (1.81) (1.08)

k-means 1 1 1

Fuzzy c-means (threshold=0.3) 1.26 1.22 0.00

Fuzzy c-means (threshold=0.4) 0.93 0.97 0.00

OKM 1.40 2.35 2.85

ALS 1.73 3.46 -

fuzzy c-means with the same threshold’ value gives

0.647 of F-measure. These results show the limit of

fuzzy c-means to detect overlapping groups and show

the sensitivity of ﬁxing the threshold.

For all experiments, the obtained size of overlaps

affects the value of obtained F-measure: as well as

the size of overlaps increases, the value of Precision

decreases and the value of Recall increases. We no-

tice that OKM and ALS have the best values of Re-

call because they build clusters with large overlapping

boundaries and k-means has the best values of Preci-

sion because overlaps are null.

Therefore, knowing the actual overlaps in each

data set, sizes of overlaps built by each method are

discussed. Table 3 summarizes overlaps obtained

with OKM and ALS compared to K-means and Fuzzy

c-means. All built size of overlaps with k-means

are equal to 1 since this method builds non disjoint

clusters and ignores the possibility that an observa-

tion belongs to more than one cluster. Fuzzy c-means

builds acceptable overlaps if the threshold is well de-

termined, elsewhere we can obtain an overlap size less

than 1. For all data sets, we notice the large over-

laps built by ALS compared to overlaps obtained with

OKM. For example, in music emotion data set, the

size of overlaps obtained with ALS is 3.46 while us-

ing OKM the size of overlaps is 2.35.

6 CONCLUSIONS

In order to extend k-means to take into account that

each observation may be assigned to several clusters,

many methods have been proposed based on SUM

and AVERAGE approaches to model the overlaps be-

tween clusters in the objectivecriterion. We studied in

this paper patterns induced buy two existing methods

which are OKM and ALS. We show that the adoption

of one of these approaches can lead to non disjoint

clusters, however it depends on the deﬁnition of over-

laps in the target application.

To improve the comparison of SUM and AVER-

AGE approaches we plan to compare others existing

methods based on these approaches. We plan to con-

duct experiments on others real and artiﬁcial overlap-

ping data sets.

REFERENCES

Banerjee, A., Krumpelman, C., Basu, S., Mooney, R. J., and

Ghosh, J. (2005). Model based overlapping cluster-

ing. In International Conference on Knowledge Dis-

covery and Data Mining, pages 532–537, Chicago,

USA. SciTePress.

Cleuziou, G. (2008). An extended version of the k-means

method for overlapping clustering. In International

Conference on Pattern Recognition ICPR, pages 1–4,

Florida, USA. IEEE.

Cleuziou, G. (2009). Two variants of the okm for overlap-

ping clustering. In Advances in Knowledge Discovery

and Management, pages 149–166.

Deodhar, M. and Ghosh, J. (2006). Consensus cluster-

ing for detection of overlapping clusters in microarray

data.workshop on data mining in bioinformatics. In

International Conference on data mining, pages 104–

108, Los Alamitos, CA, USA. IEEE Computer Soci-

ety.

Depril, D., Mechelen, I. V., and Wilderjans, T. F.

(2012). Lowdimensional additive overlapping clus-

tering. Journal of Classiﬁcation, 29(3):297–320.

Depril, D., Van Mechelen, I., and Mirkin, B. (2008). Al-

gorithms for additive clustering of rectangular data

tables. Computational Statistics and Data Analysis,

52(11):4923–4938.

KDIR2013-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval

212

Diday, E. (1984). Orders and overlapping clusters by pyra-

mids. Technical Report 730, INRIA, France.

Fellows, M. R., Guo, J., Komusiewicz, C., Niedermeier, R.,

and Uhlmann, J. (2011). Graph-based data clustering

with overlaps. Discrete Optimization, 8(1):2–17.

Lingras, P. and West, C. (2004). Interval set clustering of

web users with rough k-means. J. Intell. Inf. Syst.,

23(1):5–16.

Lu, H., Hong, Y., Street, W., Wang, F., and Tong, H. (2012).

Overlapping clustering with sparseness constraints. In

IEEE 12th International Conference on Data Mining

Workshops (ICDMW), pages 486–494.

Masson, M.-H. and Denux, T. (2008). Ecm: An eviden-

tial version of the fuzzy c-means algorithm. Pattern

Recognition, 41(4):1384 – 1397.

Mirkin, B. G. (1987a). Additive clustering and qualitative

factor analysis methods for similarity matrices. Jour-

nal of Classiﬁcation, 4(1):7–31.

Mirkin, B. G. (1987b). Method of principal cluster analysis.

Automation and Remote Control, 48:1379–1386.

Mirkin, B. G. (1990). A sequential ﬁtting procedure for

linear data analysis models. Journal of Classiﬁcation,

7(2):167–195.

N’cir, C.-E. B., Essoussi, N., and Bertrand, P. (2010).

Kernel overlapping k-means for clustering in feature

space. In KDIR, pages 250–255.

Snoek, C. G. M., Worring, M., van Gemert, J. C., Geuse-

broek, J.-M., and Smeulders, A. W. M. (2006). The

challenge problem for automated detection of 101 se-

mantic concepts in multimedia. In Proceedings of the

14th annual ACM international conference on Mul-

timedia, MULTIMEDIA ’06, pages 421–430, New

York, USA. ACM.

Tang, L. and Liu, H. (2009). Scalable learning of collective

behavior based on sparse social dimensions. In Pro-

ceedings of the 18th ACM conference on Information

and knowledge management, pages 1107–1116.

Wang, X., Tang, L., Gao, H., and Liu, H. (2010). Discov-

ering overlapping groups in social media. In Proceed-

ings of the 2010 IEEE International Conference on

Data Mining, pages 569–578.

Wieczorkowska, A., Synak, P., and Ras, Z. (2006). Multi-

label classiﬁcation of emotions in music. In Intelligent

Information Processing and Web Mining, volume 35

of Advances in Soft Computing, pages 307–315.

Wilderjans, T. F., Depril, D., and Mechelen, I. V. (2012).

Additive biclustering: A comparison of one new and

two existing als algorithms. Journal of Classiﬁcation,

30(1):56–74.

Zhang, S., Wang, R.-S., and Zhang, X.-S. (2007). Identi-

ﬁcation of overlapping community structure in com-

plex networks using fuzzy c-means clustering. Phys-

ica A: Statistical Mechanics and its Applications,

374(1):483–490.

OntheExtensionofk-MeansforOverlappingClustering-AverageorSumofClusters'Representatives?

213