A Framework for Optimizing the Supply Chain Performance of a

Steel Producer

Ali Diabat

, Raid Al-Aomar

, Mahmoud Alrefaei

, Ameen Alawneh

and Mohd Nishat Faisal

Masdar Institute, Abu Dhabi, U.A.E.

Abu Dhabi University, Abu Dhabi, U.A.E.

Jordan University of Science and Technology, Irbid, Jordan

Qatar University, Doha, Qatar

Keywords: Supply Chain Management, Linear Programming, Simulation, Simulated Annealing, Steel Industry.

Abstract: Supply Chain Management (SCM) is focused on developing, optimizing, and operating efficient supply

chains. Efficient supply chains are characterized by cost effective decisions, lean flow and structure, high

degree of integration, and well-chosen Key Performance Indicators (KPIs). Although there exists a large

body of literature on optimizing individual supply chain elements (transportation, distribution, inventory,

location, etc.), the literature does not provide an effective methodology that can address the complexity of

the supply chain of a large scale industry such as steel producers. This paper, therefore, builds on existing

research methods of supply chain modeling and optimization to propose a framework for optimizing supply

chain performance of a steel producer. The framework combines deterministic modeling using Linear

Programming (LP) with stochastic simulation modeling and optimization. A holistic LP deterministic

optimization model is first used to characterize and optimize the supply chain variables. The model

minimizes the annual operating cost of the steel company’s supply chain. Simulation-based optimization

with Simulated Annealing is then used to determine the operational levels of the supply chain drivers that

meet a desired level of customer satisfaction. The proposed approach is applied to the supply chain of a

major steel producer in the Arabian Gulf.

1 INTRODUCTION

Supply chain management (SCM) has attracted ever

increasing attention over the last two decades in

response to a highly competitive and globalized

marketplace and the pressure to cut the cost of

creating and delivering value to customers. As

discussed in (Min and Zhou, 2002), a supply chain is

an integrated system which synchronizes a series of

inter-related business processes in order to. (1)

Acquire raw materials and parts; (2) transform these

raw materials and parts into finished products; (3)

add value to these products; (4) distribute and

promote these products to either retailers or

customers; (5) facilitate information exchange

among various business entities, e.g. suppliers,

manufacturers, distributors, third-party logistics

providers, and retailers. Figure 1 shows the main

elements/stages in a supply chain network from raw

materials’ sources to customers.

Figure 1: A generic framework for a supply chain

network.

Cost effective supply chain management under

various market, logistics and production

uncertainties is a critical issue for companies in

554

Diabat A., Al-Aomar R., Alrefaei M., Alawneh A. and Faisal M..

A Framework for Optimizing the Supply Chain Performance of a Steel Producer.

DOI: 10.5220/0004628405540562

In Proceedings of the 15th International Conference on Enterprise Information Systems (SSOS-2013), pages 554-562

ISBN: 978-989-8565-59-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

general and for steel industry in particular. Such

uncertainties often result in multiple planning and

operational issues that challenge planners and

potentially lead to bad decisions. In order to

optimize the performance of a supply chain, it must

be first modeled using deterministic mathematical

models that maximize/minimize some or all supply

chain costs or using stochastic simulation-based

models. Mula et al. (Mula et al., 2010) presented a

review of mathematical programming models for

supply chain production and transport planning.

However, the assumptions used when developing

such models may not be realistic resulting in exact

solutions that may be infeasible for problems of any

reasonable size. Heuristic global optimization

methods such as Tabu Search (TS), Simulated

Annealing (SA), and Genetic Algorithms (GA) can

escape some of these assumptions and can often

yield good (near-optimal) solutions (Arostegui et al.,

2006).

Another issue is the fact that optimizing the

supply chain performance is a multi-attribute

decision. Altiparmak et al. (Altiparmak et al., 2006)

formulated supply chain design as a multi-objective

optimization problem in which the objective is not

only to minimize supply chain costs, but also to

maximize customer service while at the same time

maximizing the capacity utilization balance at the

distribution centers. Finally, the complexity of the

supply chain network largely contributes to the

difficulty of optimizing supply chain performance.

Jayaraman and Ross (Jayaraman and Ross, 2003)

described the PLOT (Production, Logistics,

Outbound, Transportation) system to address

network design problems involving a central

manufacturing plant, multiple distribution centers

and cross-docking sites, and retail outlets stocking

multiple products.

In the context of steel industry, however, little

research is directed at optimizing the supply chain

using deterministic or stochastic methods. Some

literature is focused on optimizing individual supply

chain elements (transportation, distribution,

inventory, location, etc.) but it does not provide an

effective methodology that can address the

complexity of the supply chain of a steel producer.

While optimizing the performance of each supply

chain element is important, steel industry is focused

on improving the overall performance of the supply

chain network. This requires a comprehensive and

dynamic modeling and optimization approach.

Thus, this research intends to build on the current

research methods of supply chain modeling and

optimization for a steel company. To this end, the

proposed research method combines deterministic

modeling with LP with stochastic simulation

modeling and optimization. The proposed approach

develops a comprehensive deterministic LP model to

minimize the annual cost of the steel company’s

supply chain including transportation, inventory, and

distribution. The viability of decision variables

resulted from the solution of the LP model is

verified in a dynamic and stochastic Discrete Event

Simulation (DES) model of the supply chain. The

model is set to produce a specific set of Key

Performance Indicators (KPIs) that are developed to

characterize the supply chain performance in terms

of responsiveness, efficiency, and utilization.

Finally, simulated annealing is used to set values to

model variables that achieve a multi-criteria tradeoff

of the defined supply chain KPIs. The proposed

approach will be applied to the supply chain of Qatar

Steel (QS) which is a main steel producer in Qatar

and the Arabian Gulf.

2 LITERATURE SURVEY

Many case studies have appeared in the literature

documenting the effectiveness of SCM in reducing

costs and increasing customer satisfaction. Sharma

et al. (Sharma et al., 2008) analyze the results of a

survey to assess the effect SCM practices have had

on the Indian automobile industry, and conclude that

SCM practices have had a positive impact on design

quality, and on the quality of conformance, the

degree to which a product's operating characteristics

meet its design specifications. Walker (Walker,

2009) discusses the implementation of a SCM

system at a manufacturing company, focusing on the

experiences and lessons learned from a management

perspective; the resulting system led to a cost

savings of $8.8 million, with an internal rate of

return of 32%. Scarsi (Scarsi, 2007) reports on a

case study in the steel industry, logistics challenges

were dealt with successfully.

Efficient supply chains are characterized by a

high degree of integration and well-chosen Key

Performance Indicators (KPIs) to provide feedback

and to rapidly diagnose potential problems. Stevens

(Stevens, 1989) proposed a four-stage evolutionary

model for supply chain integration. Potter et al.

(Potter et al., 2004) discussed the benefits achieved

through integration of a steel supply chain. These

include a halving in cycle times for many of the

more popular products, reducing the levels of safety

stock required, and reducing the lead times, resulting

in significant cost savings. Chae (Chae, 2009)

AFrameworkforOptimizingtheSupplyChainPerformanceofaSteelProducer

555

emphasizes the role of KPIs in closing the gap

between planning and execution of supply chain

operations, and offers guidelines for developing such

indicators. KPIs are suggested for four of the

processes in the Supply Chains Operations-

Reference (SCOR) framework; Plan, Source, Make,

and Deliver.

Simulated Annealing, in particular, plays a

critical role in keeping the time required to optimize

the model manageable for practical problems.

Ulungu et al. (Ulungu et al., 1995) conceived a

Multi-Objective Simulated Annealing (MO-SA)

algorithm for solving combinatorial optimization

problems. Alrefaei and Diabat (Alrefaei et al., 2009)

also proposed a simulated annealing for solving a

multi-objective optimization problem and

implemented it on an inventory problem. Another

example of using SA for SCM optimization can be

found in (Yanling et al., 2009). There has been also

an increasing interest in the use of simulation to

model the performance of supply chains. Jahangirian

et al. (Jahangirian et al., 2010) provide a

comprehensive review of the simulation literature as

it relates to manufacturing and business. Terzi and

Cavalieri (Terzi and Cavalieri, 2004) survey the

literature on the use of simulation in a supply chain

context. Other examples of simulation-based supply

chain management applications can be found in

(Longo and Mirabelli, 2008; Jung et al., 2004; Yoo

et al., 2010). A complete list of advantages and

disadvantages in using simulation approach for

supply chain modeling can be found in (Ingalls,

1998).

Existing analytical methods, however, are not

able to handle all the dynamically changing supply

chain variables. A dynamic simulation approach is a

better tool for managing the stochastic behavior of

supply chains. Effective supply chain management,

therefore, requires the integration of deterministic

and stochastic optimization the supply chain based

on a dynamic simulation platform. To this end, we

propose the integration of LP, DES, and SA. A

holistic LP deterministic optimization model is first

used to characterize and optimize the supply chain

variables. The problem of determining the

operational levels of supply chain drivers to meet a

desired level of customer satisfaction is then

approached using a simulation-based optimization

method based on simulated annealing. An industrial-

scale case study (i.e., Qatar Steel) is presented to

demonstrate the utility of the proposed approach.

This includes modeling and analyzing the supply

chain of the steel company, verifying the results of

deterministic LP using DES, developing a specific

set of KPIs to measure the performance of QS

supply chain, and optimizing such performance with

simulated annealing.

LP model is solved with GAMS software tool.

Supply chain simulation is carried out in general

purpose simulation software. The SA module is

developed to function with simulation in an integral

mode. Anticipated results include developing a total

cost model using key elements of QS supply chain,

recommending optimal settings to critical decision

variables in the cost model, and recommending a set

of operational KPIs to maintain a high level of QS

supply chain performance.

In addition to industry contributions, research

contributions to existing literature include

developing a comprehensive LP model of key

supply chain components (supply, warehouse,

production, inventory, and distribution), combining

LP optimization (a classical supply chain

deterministic optimization method) and simulation-

based optimization (a stochastic optimization

method), and optimizing the supply chain

performance using multiple KPIs. The approach can

be adapted to other steel industries and will be

generalized to a flexible company structure.

3 RESEARCH DESIGN AND

METHOD

This research proposal consists of three major

phases; Phase I is data collection and network

development for Qatar Steel supply chain. Phase II

is formulating and solving a LP that minimizes the

total cost of QS supply chain subject to supply,

demand, and operational constraints. Phase III is the

developing of DES model of QS supply chain

including a set of KPIs. Finally, Phase IV is

optimizing the supply chain using Simulated

Annealing. Figure 2 summarizes the four stages of

the research method.

As this is an ongoing research project, further

details of the research methods will be specified

later. The functionality of the proposed research

method is depicted in Figure 3. Once QS supply

chain (QS-SC) is analyzed and pertinent data is

collected, a LP model is developed so the total cost

constraints at the company. A DES model of QS-SC

is also developed to include other stochastic

variables that impact the supply chain performance.

The resulting set of decision variables (X) is used in

the DES model and the model is set to generate the

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

556

Figure 2: Research method plan.

Figure 3: Prototype of the proposed SC optimization

framework.

defined set of KPIs. The Simulated Annealing (SA)

module is used to optimize similar or enhanced set

of decision variables (X’) using the DES model as a

multi-criteria objective function. Iteration of SA

search and simulation evaluation of KPIs will

eventually lead to an efficient tradeoff of the defined

KPIs of QS-SC. The QS-SC performance will be

monitored using the SA-set levels of KPIs.

3.1 The LP Module

A LP model is developed and will be later

customized to the SC of the application case study.

The theoretical background of LP method is

assumed to be well known to readers. In this

research, the LP model formulation includes the

following:

 Objective function: Minimize total yearly

cost of inbound transportation, inventory,

and distribution

 Decision Variables: Pricing, inventory

policies, quantity shipped from each

supplier, and quantity shipped to traders

(distributors)

 Constraints: Capacity, demand, and budget

Based on the preliminary analysis of the supply

chain optimization problem, a generic LP

optimization model is developed for the supply

chain. The data, variables, objective function, and

constraints of the proposed LP model are not

presented here for the sake of efficiency.

3.2 The DES Module

In the proposed method, simulation is used as an

overall representation of the supply chain. The DES

model incorporates variability in terms of demand,

lead time, process reliability, etc., into the supply

chain model and it is used to assess supply chain

performance based on multiple KPIs. The

preliminary plan for the DES model of the supply

chain can be described as follows:

Model Structure

A simulation module is developed to represent each

component in the underlying supply chain including

supply, warehouse, production, Inventory, and

Shipping. The details of each module (in terms of

structure, logic, and data) will be developed during

Phase III of the project.

Model Variables

The variables defined in the LP model will be

included in the DES model. This includes material

supplies, inventory, and processing in addition to

facility activities and capacity. However, time-based

variables and probabilistic variables will be

dynamically changed during run time to mimic the

actual behavior of the supply chain.

Model Data

The data elements defined in the LP model will be

included in the DES model. Pertinent data will be

collected from the five modules; supply, warehouse,

production, inventory, and shipping. Collected data

will also include supply chain constraints (facility,

AFrameworkforOptimizingtheSupplyChainPerformanceofaSteelProducer

557

capacity, etc.) as well as supply and demand

requirements.

Model Logic

The flow logic of materials, information, and money

throughout the supply chain will be developed using

the flexibility of DES software tool. This includes

material flow from suppliers (local and

international) to the company’s warehouse, through

production, finished items inventory, and shipping to

customers.

Model Outcomes

The DES model will be set to produce relevant

statistics that are essential to optimize the

performance of the supply chain. For the case study

application, the developed KPIs of QS-SC can be

categorized as follows:

 Responsiveness:

o Average yield time: order-to-

delivery time.

o Fill rate: Fraction of

orders/demand met on time from

inventory.

 Efficiency:

o Average inventory measured in

units, days of demand, and

financial value.

o Average inbound transportation

cost as % of sales or cost of each

ton of steel.

 Utilization: Four KPIs are developed; one

for each of the four main operations in steel

production including Direct Reduction,

Electrical Furnace, Continuous Casting,

and Rolling Mill.

3.3 The SA Module

SA is an optimization method that is based on the

structural properties of materials (mainly metals)

undergoing the annealing process, where materials

are melted down and then cooled slowly in a

controlled manner (Metropolis et al., 1953). Such

process resembles the SA search in seeking global

optima while avoiding being trapped at local optima.

As a global search engine, SA has become a popular

tool for solving problems where mathematical

programming formulations become intractable. This

includes solving various combinatorial optimization

problems in circuit design, scheduling, path

generation, and many others. Further descriptions of

SA and its applications can be found in (Eglese,

1990; Laarhoven and Aarts, 1987).

SA algorithm starts by setting SA control

parameters; initial temperature (T), cooling

parameter (), number of T decrement steps (S), and

the maximum number of iterations (n) at each T

step. The temperature T, which is modulated by a

predetermined cooling schedule, controls the degree

of randomness presents within the search.

Determining the initial T value is a problem-specific

that depends on the scaling of the objective function.

Generally speaking, T must be high enough to allow

the search to move to almost any neighbourhood

state in order to avoid being trapped in local optima.

The search will seek convergence to the local optima

toward the end of the computation, when the

temperature T is nearly zero.

The cooling parameter   [0,1] controls the rate

at which the temperature is reduced, where large

values (typically between 0.70 and 0.99) will

produce better results through slow cooling

schedules. Longer temperature steps (large number

of iterations n) will also produce slower cooling rate

at a fixed  by allowing the system to stabilize at

that temperature step. The combination of cooling

rate () and the length of temperature step (or

cooling time) in terms of n establishes the SA

cooling schedule. Such schedule is highly problem-

dependent and has a considerable impact on the

quality of the solution found. Slow SA cooling

results in longer computation time and higher chance

of finding the optimum solution.

After setting SA parameters, an initial solution is

generated randomly and used as the first current

solution. The initial solution, as well as future

solutions, is evaluated using some objective function

(the MCS-based estimation of NP in this case).

When employed with SA search, a modification to

the simple Monte Carlo method is made so that a

new point in search space is sampled by making a

slight change to the current point and unrealistic

samples are not placed into the ensemble. This

modified procedure, which is known as a Metropolis

MCS or Metropolis annealing, was proposed by

Kirkpatrick in 1983 to find the lowest energy (most

stable) orientation of a system.

The SA module will interact with the DES model

during search iterations. The DES model will serve

as an evaluation mechanism of the supply chain

objective function under stochastic and dynamic

conditions. Model KPIs will be assessed using

multiple simulation runs and fed into the SA

“evaluate solution” step. A mechanism will be

developed to combine KPIs into a multi-criteria

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

558

utility function. The plan is to translate supply chain

KPIs into an overall cost/revenue model that can be

used in the SA search method. An excel sheet

interface will be used to implement the

communication between SA module and the DES

model. An alternative is to use a built-in SA module

that comes with some of the new simulation

packages such as WITNESS™ (Lanner Group Inc.,

2011).

4 APPLICATION CASE STUDY

The proposed framework will be applied to optimize

the performance of supply chain at Qatar Steel (QS).

Qatar Steel (QS) is one of the leading companies in

the region that has impact on the growth of Qatar

economy. With the price of steel declining over the

past year, due to recession in the shrinkage in

construction sector, steel companies face tight

margins and fierce competition. Therefore, steel

companies are increasingly looking for methods to

cut costs in their production and business operations

and provide extra value to their customers

throughout the supply chain. To stay competitive,

QS is increasing its focus on cutting cost and adding

more value to customers rather than increasing

prices. A major cost element is contributed by the

company’s supply chain.

Steel manufacturing at Qatar Steel (QS)

comprised of four integrated primary units: Direct

Reduction (DR), Electric Arc Furnace (EAF) for

molten steel production, continuous casting, and

rolling mill. DR plant produces solid iron using Iron

ore pellets. The reformer converts natural gas into

hydrogen and carbon monoxide. These gases remove

oxygen from the heated ore in the furnace,

converting the ore into metallic iron. Cool gas/water

circulates through the lower part of the furnace and

cools the iron. The process produces what is called

Directly Reduced Iron (DRI), and is fed into the

Electric Arc Furnace (EAF). The EAF is used to

produce molten steel from DRI. The furnace, with

its roof swung aside, is charged with scrap using

powerful electric current arcs (jumps) between the

electrodes and the charge. This action produces

intense heat, which melts the charge and promotes

chemical reactions that produce steel.

Workers turn off the power to the electrodes at

the end of the refining process. Then they tilt the

furnace, which is mounted on rockers, to pour out

the slag. After the slag has been poured off, the

electric arc furnace is tilted in the opposite direction.

The liquid steel rushes out through the tap hole and

is collected in a ladle. The molten steel produced in

the electric furnace is poured into the continuous

casting unit, which shapes molten steel into billets.

The steel flows through a specially shaped mold.

Cold water quickly cools the steel, causing it to

harden as it moves through the rolls of the caster.

These billets are one type of QS products. This is

another unit which shapes molten steel. Rolling

Steel bars takes place in a bar mill, which resembles

a hot-rolling mill. A bar mill has rolls that are

grooved to roll hot billets into square, round, oval or

hexagonal. Figure 4 depicts the steel manufacturing

process at QS.

Figure 4: QS manufacturing process.

The main functions of Qatar Steel’s supply chain

include procurement, logistics, warehousing, and

distribution. Procurement focuses raw materials,

equipment, spares and consumables, and supply

contracts. Logistics is focused on customs and

transportation. Warehousing is focused on inventory

control, warehouse operations (receiving and

shipping), and item management. Bulk materials do

not enter the warehouse. They are stored in the

outside yard. Finished items are not also entered to

the warehouse and stored in the plant’s internal

storage bays prior to shipping. Bays can host items

up to 14 days of production. Distribution is a

AFrameworkforOptimizingtheSupplyChainPerformanceofaSteelProducer

559

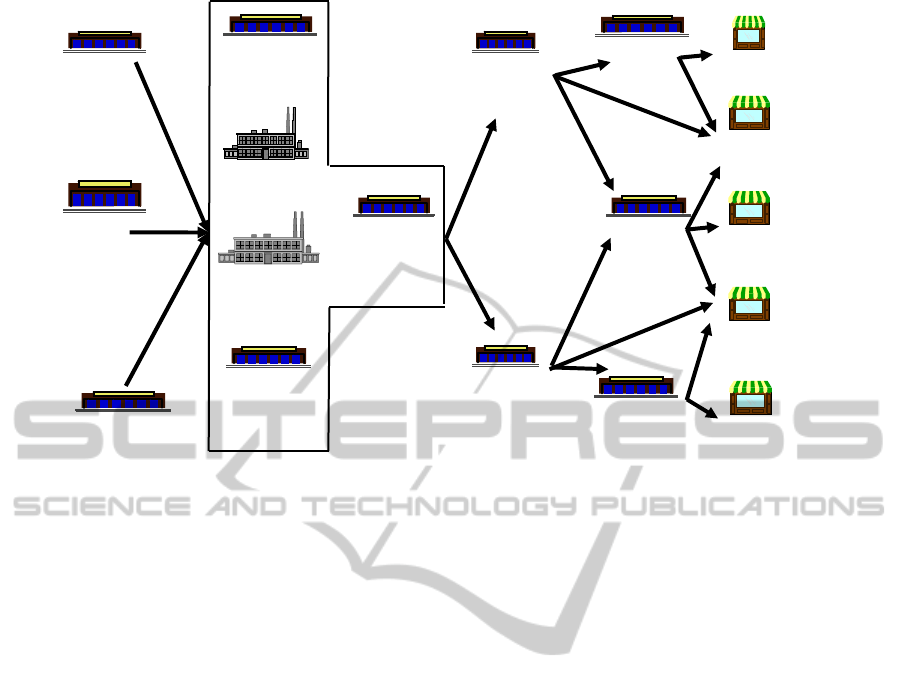
Figure 5: QS supply chain.

function controlled by the domestic and regional

traders (dealers) who order steel products and pick

up their orders from the plant. Figure 5 depicts the

generic structure of QS supply chain network.

5 ANTICIPATED RESULTS

This is still an ongoing research project so results are

not ready yet. However, preliminary data collected

from QS company indicates some operational and

coordination problems with the supply chain. This

resulted in increased cost at various elements of the

supply chain including inbound transportation,

inventory, and distribution. Anticipated results

include the QS-SC KPIs, decision variables, total

cost, and pull framework. Several other useful

findings and results are expected from analyzing the

supply chain of steel industry. Few researchers have

approached this before including (Potter et al., 2004;

Heidrich, 2002). In particular key results will be

specified when developing an Integrated Supply

Chain Network (ISCN) for QS Company and

developing DES to model a dynamic and stochastic

network.

Developing a set of informative KPIs for QS-SC.

Measuring the supply chain performance using a

specific set of KPIs is imperative to quantify

improvement, monitor progress, identify potential

problems, and reveal gaps between planning and

execution. As discussed in (Chae, 2009), KPIs can

be developed to cover each stage of the Supply

Chain Operations Reference (SCOR) model which

includes Planning, Sourcing, Making, and Delivery.

Alternatively, and as discussed in (Chopra and

Meindl, 2007), KPIs can be developed for each

supply chain driver including facilities, inventory,

transportation, sourcing, pricing, and Information

Technology (IT). In this research, KPIs will be

developed based on what is essential for the success

of QS supply chain in terms of responsiveness,

efficiency, and utilization. The final form of the

proposed KPIs will be set after collecting further

information on QS supply chain stages and drivers.

As a starting point, however, the following set of

KPIs will be developed for QS supply chain:

 Average yield time: order-to-delivery time

 Fill rate: Fraction of orders/demand met on

time from inventory

 Average inventory measured in units, days

of demand, and financial value

 Average inbound transportation cost as %

of sales or cost of each ton of steel

 The utilization of the four main operations

in QS steel production: Direct Reduction,

Electrical Furnace, Continuous Casting,

and Rolling Mill

Measuring and validating the values of these

KPIs will be used to evaluate the research results as

well as for monitoring the QS-SC performance. To

validate project results, these KPIs will be first

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

560

measured for previous year of supply chain

operation and then used for planning the coming

year. The flexibility of DES model will facilitate the

validation of current performance and the prediction

of the future performance. The total cost results from

the LP model will be more meaningful to company’s

management and can be used to validate the project

results. The total cost of supply chain using last year

data will be first computed from the LP model. The

result will be compared to the actual values as

reported in the company’s book.

The values of defined decision variables in the

QS-SC will be also produced as project outcomes.

These variables will be identified during the project,

approved by management, and used to formulate the

LP total cost model. The DES model will be used to

test the QS-SC performance under other stochastic

variables and the SA algorithm will be used to

develop robust settings for these variables under

similar-to-real-world conditions. The proposed

solution is expected to result in a reduced total cost

of the supply chain. Finally, a pull framework for the

QS-SC case study is also expected from this

research to reduce the waste and costs and develop a

lean supply chain. This result can be evaluated by

implementing the proposed framework and

reassessing the developed KPIs. Other issues that

would make this research significant to QS include:

 The accuracy of demand forecasting

including market traders orders, sales, and

marketing. This forces the company to keep

14 days’ worth of finished products in

inventory.

 Currently, the company adopts a push

system for the supply chain. As a result,

staged inventory is increasing across the

facilities due to production fluctuation.

 Difficulties in monthly plan translation into

RM requirements and weekly production

plan. Estimated variability of mismatch is

5-10%.

 Long order lead time of 1-2 months for

inbound shipments. This results in keeping

1-3 months safety stock of raw material:

Overseas suppliers use ships to deliver RM

through company operated port and

additives from Doha port.

 Material management: bar-coding project is

still in progress for items excluding bulk

materials. Along with that, better material

handling equipment and methods are in

need.

 MRP module is not effective when linked

to company’s Enterprise Resources

Planning (ERP) system

6 CONCLUSIONS

This paper presented a framework for optimizing the

supply chain of a major steel producer. This

framework integrates mathematical programming

with simulation and simulated annealing. This

includes modeling and analyzing the supply chain of

the steel company, verifying the results of

deterministic models using simulation, developing a

specific set of KPIs to measure the performance of

the supply chain, and optimizing such performance

with simulated annealing. The framework defines

specific set of Key Performance Indicators (KPIs)

that are developed to characterize the supply chain

performance in terms of responsiveness, efficiency,

and utilization. The framework is part of an ongoing

research project. Further details and results will be

presented at the conference.

ACKNOWLEDGEMENTS

The researchers would like to acknowledge Qatar

National research Fund (QNRF) of Qatar

Foundation for funding this research.

REFERENCES

Min, H., and Zhou, G., 2002. “Supply chain modeling:

Past, present and future,” Computers & Industrial

Engineering, 43, 231–249.

Mula, J., Peidro, D., Diaz-Madronero, M., and Vicens, E.,

2010. “Mathematical programming models for supply

chain production and transport planning,” European

Journal of Operational Research 204, 377–390.

Arostegui, M. A., Kadipasaoglu, S. N., Khumawala, B.

M., 2006. “An empirical comparison of Tabu Search,

Simulated Annealing, and Genetic Algorithms for

facilities location problems,” International Journal of

Production Economics 103, 742 - 754.

Altiparmak, F., Gen, M., Lin, L., Paksoy, T., 2006. “A

genetic algorithm approach for multi-objective

optimization of supply chain networks,” Computers &

Industrial Engineering 51, 196 - 215.

Jayaraman, V., Ross, A., 2003. “A simulated annealing

methodology to distribution network design and

management,” European Journal of Operational

Research 144, 629 - 645.

AFrameworkforOptimizingtheSupplyChainPerformanceofaSteelProducer

561

Sharma, V., Sahay, B. S., Sardana, G. D., 2008. “An

Empirical Assessment of the Impact of SCM Practices

on Quality Performance: A Case in the Indian

Automobile Industry,” Supply Chain Forum 9(1), 28 -

40.

Walker, K., 2009. “Ingredients for a Successful Supply

Chain Management System Implementation,” Supply

Chain Forum 10(1), 44 - 50.

Scarsi, R., 2007. “Recovering Supply Chain Cost

Efficiency Through Original Logistics Solutions: A

Case in the Steel Industry,” Supply Chain Forum 8(1),

74 - 82.

Stevens, G. C., 1989. “Integrating the Supply Chain,”

International Journal of Physical Distribution &

Logistics Management 19(8), 3-8.

Potter, A., Mason, R., Naim, M., Lalwani, C., 2004. “The

evolution towards an integrated steel supply chain: A

case study from the UK,” International Journal of

Production Economics 89, 207-216.

Chae, B. K., 2009. “Developing key performance

indicators for the supply chain: and industry

perspective,” Supply Chain Management: An

International Journal 14(6), 422-428.

Ulungu, E.L., Teghem, J., and Fortemps, Ph., 1995.

“Heuristic for multi-objective combinatorial

optimization problems by simulated annealing,” in: J.

Gu, G. Chen, Q. Wei, S. Wang (Eds), MCDM: Theory

and Applications, Sci-Tech, 229–238.

Alrefaei, M. H., and Ali Diabat., 2009. “A Simulated

Annealing Technique for Multi-Objective Simulation

Optimization,” Applied Mathematics and

Computation, 215, 3029-3035.

Yanling, W., Deli, Y., Guoqing, Y., 2010. “Logistics

supply chain management based on multi-constrained

combinatorial optimization and extended simulated

annealing,” 2010 International Conference on

Logistics Systems and Intelligent Management, 188-

192.

Jahangirian, M., Eldabi, T., Naseer, A., Stergiouslas, L.

K., Young, T., 2010. “Simulation in manufacturing

and business: A review,” European Journal of

Operational Research 203, 1-13.

Terzi, S., Cavalieri, S., 2004. “Simulation in the supply

chain context: a survey,” Computers in Industry 53, 3-

16.

Longo, F., Mirabelli, G., 2008. “An advanced supply

chain management tool based on modeling and

simulation,” Computers & Industrial Engineering 54,

570–588.

Diabat, A., Richard, J. P., Codrington, C. W., 2013. “A

Lagrangian relaxation approach to simultaneous

strategic and tactical planning in supply chain

design,” Annals of Operations Research, 203(1), 55-

80.

Jung, J. Y., Blau, G., Pekny, J. F., Reklaitis, G. V.,

Eversdyk, D., 2004. “A simulation based optimization

approach to supply chain management under demand

uncertainty,” Computers & Chemical Engineering 28,

2087-2106.

Yoo, T., Cho, H., Yücesan, E., 2010. “Hybrid algorithm

for discrete event simulation based supply chain

optimization,” Expert Systems with Applications 37,

2354-2361.

Ingalls, R. G., 1998. “The value of simulation in modeling

supply cha

in,” In Proceedings of the 1998 winter

simulation conference, Washington DC, 1371–1375.

Metropolis, N., A. Rosenbluth, M. Rosenbluth, A., Teller,

E., 1953. “Equation of state calculations by fast

computing machines,” Journal of Chemical Physics,

21, 1087-1092.

Eglese, R. W., 1990. “Simulated annealing: a tool for

operational research,” European Journal of

Operational Research 46(3), 271- 279.

Laarhoven, P. J. M. and E. Aarts, 1987. “Simulated

Annealing: Theory and Applications,” D. Reidel

Publishing Company, Holland.

Lanner Group Inc., 2011. http://www.lanner.com/

Heidrich, J., 2002. “Implementation of supply chain

management systems in steel industry,” Industry

Management, 18(5), 46-49.

Chopra, S. and Meindl, P. 2007. Supply Chain

management; Strategy, Planning, and Operations.

Prentice Hall, New Jersey.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

562