
Damaged Letter Recognition Methodology
A Comparison Study
Eva Volna
1
, Vaclav Kocian
1
, Michal Janosek
1
, Hashim Habiballa
2
and Vilem Novak
2
1
Department of Informatics and Computers, University of Ostrava, 30 dubna 22, Ostrava, Czech Republic
2
Centre of Excellence IT4Innovations, University of Ostrava, 30 dubna 22, Ostrava, Czech Republic
Keywords: Hebb Network, Adaline, Backpropagation Network, Fuzzy Logic, Pattern Recognition, Classifiers.
Abstract: The problem of optical character recognition is often solved, not only in the field of artificial intelligence
itself, but also in everyday computer usage. We encountered this problem within the industrial project
solved for real-life application. Best solver of such a task still remains human brain. Human beings are
capable of character recognition even for damaged and highly incomplete images. In this paper, we present
alternative softcomputing methods based on application of neural networks and fuzzy logic with evaluated
syntax. We proposed a methodology of damaged letters recognition, which was experimentally verified. All
experimental results were mutually compared in conclusion. Training and test sets were provided by
Company KMC Group, s.r.o.
1 INTRODUCTION
The main obstacle in the task of character
recognition lies in damaged or incomplete graphical
information. The input of the task includes an image
with the presence of a symbolic element. Our goal is
to recognize this symbolic element (character or
other pattern) from a picture, which we can assume
as raw pixel matrix. Computer science and its
branch, Artificial intelligence, study an
automatization of the recognition for a long time.
There are many methods how to recognize patterns,
but we focus on neural networks and fuzzy logic
analysis in the article.
In this paper we present two approaches to the
character recognition. One of them is a software tool
called PRErecogniton of PICtures (PREPIC) based
on mathematical fuzzy logic calculus with evaluated
syntax. Second one is a neural network based
classifiers approach. We have generalised
algorithms for wide usage of the method the
PREPIC uses. The method has been already
presented in detail (Novak 2012). This calculus was
initiated in (Pavelka 1979) in propositional version
and further developed in first order version. The
pattern recognition method was originally described
in (Novak 1997). The original method was modified
accordingly and proved to be quite effective in the
task. The recognition rate, of course, depends on the
image pre-processing but once the letter is somehow
extracted from the image, the recognition rate is
close to 100%.
Neural network based classifiers represent three
different types of neural networks based on Hebb,
Adaline and backpropagation training rules (Fausett
1994). Each of these networks has been embedded
into a uniform framework which managed the
following sub-tasks:
1. Binarization
2. Learning
3. Testing
4. Performance evaluation
All experimental results were mutually compared
in conclusion.
2 DATASETS
The company KMC Group, s.r.o.
(http://www.kmcgroup.cz) offers the supplies of
marking equipment manufactured by American
company InfoSight Corp. for metallurgical materials
identification. InfoSight equipment use for marking
various technologies: Stamping, Paint marking,
Laser marking directly on material, and Tagging.
Method of stamping is one of the most extended
methods whose main advantage is creating of
535
Volna E., Kocian V., Janosek M., Habiballa H. and Novak V..
Damaged Letter Recognition Methodology - A Comparison Study.
DOI: 10.5220/0004631005350541
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 535-541
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

indelible marking that is very good legible also on
considerably rough surface of marked material.
Alphanumeric characters in dot matrix form are
created by impact of air shoot pins from hard-metal
on material (see Fig. 1). Character creation is
controlled by electronics what offers big flexibility
of free programming of marked text.
Figure 1: Samples of marking by stamping.
Unfortunately, the letters become badly visible over
time because of the hot background and, moreover,
they can be damaged already in the stamping
moment. We had to solve the problem of
recognizing letters stamped on hot iron. We
proposed a methodology of damaged letters
recognition based on application of neural networks
and fuzzy logic with evaluated syntax. The company
KMC Group, s.r.o. has provided two sets of patterns
- the training and the testing one. The training set
T_0 consists of 10 “ideal samples” of particular
digits (see Fig. 2). The testing set T
_
T consists of
106 real digits samples. Some of the testing samples
were severely distorted and badly readable even for
a human reader. (see Fig. 3). The distribution of
particular digits in the testing set is not uniform.
Figure 2: Define training set T_0.
Figure 3: Examples of badly corrupted samples from the
testing set T_T.
Figure 4: Training set T_1.
During testing, we have found that neural networks
do not reach satisfactory results with the original
training set (Fig.2). Therefore we have created
Figure 5: Training set T_2.
two more additional training sets of randomly
selected test samples labelled as T
_
1 (Fig. 4) and
T
_
2 (Fig. 5). With this two test sets we’ve managed
to achieve significantly better results. Further, for
reference purposes, we have created a training set
T
_
T which was identical to the test set.
In fuzzy logic the situation is different which
follows of the nature of the method. We don’t have
training set, although we can create patterns set for
comparison from ideal samples as described from
previous chapter. We used the same samples and
tuned up pattern set as it can be seen from software
tool for fuzzy logic analysis pre-recognition
Software tool – PREPIC (Novak and Habiballa,
2012).
3 NEURAL NETWORK
CLASSIFIERS
Neural network classifiers have used three different
methods of patterns’ “binarization” (features
extraction):
Copy - the original image was encoded as a
bitmap, only adapted to the size.
Vertical histogram - the “Copy” bitmap was
transferred to a new bitmap of the same size so that
number of "1" bits in each column stayed the
same, only their line positions were changed so the
bits were "stacked" (Trier et al., 1996), see Fig.
6
.
Horizontal histogram - the “Copy” bitmap was
transferred to a new bitmap of the same size so that
number of "1" bits in each row stayed the same,
only their line positions were changed so the bits
were lying "side by side" (Trier et al., 1996), see
Fig.
6
.
These three basic ways of binarization were
tested in three combinations:
b-simple - only the copy binarization was used.
The size of the resulting pattern was n = copy
bitmap size.
b-histogram - vertical and horizontal histogram
were used (Fig.
6
). The size of the resulting pattern
was 2n (n = bitmap size).
b-histogram - vertical and horizontal histogram
were used (Fig.
6
). The size of the resulting pattern
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
536

was 2n (n = bitmap size).
Figure 6: Vertical and horizontal binarization principle.
The classification phase. The winner-take-all
strategy has been used for output neurons
(Y
1
,.....,Y
n
). Y
i
is considered as the winner if and only
if
)(: jiyyyyj
ijij
, i.e. the
winner is the neuron with the highest output value y
i
.
In the case that more neurons have the same output
value, the classification result is considered to be
fault.
The learning phase. The learning process works
in the following phases:
Learning phase - do one learning epoch (process
all training patterns and modify weights according
to the network adaptation rule).
Checking phase - switch the network to an active
mode, process all the training patterns. If all the
patterns were classified properly, the network is
ready. Stop the learning.
Repeat the process, if e < e
max
, where e is the actual
number of learning epoch and e
max
is the
maximum number of learning epochs - termination
criterion.
4 FUZZY CLASSIFIER
The method of pre-recognition of pictures based on
fuzzy logic analysis works with patterns set (file).
These files can be obtained from provided templates
using same procedure as for classification itself.
Figure 7: Threshold computation.
Initial action upon recognition is to create matrix
of formulae according to the image with pattern
(Fig. 7). We use standard method of threshold,
where its value is computed from segmented image
histogram. In this histogram we search for global
maximum segment and then after the maximal
segment local maximal segment with higher
intensity. Resulting automatically generated
threshold then should be intensity corresponding to
index of minimal segment between these two
maxima. It follows from natural deduction that
background pixels will be the most frequent and the
pattern pixels will be the second most frequent
intensity in an image with recognized symbol. Then,
we can compute the best matching pattern.
Figure 8: Matrix of formulae creation.
The theoretical background of the proposed method
is the following. First, we consider a special
language J of first-order Lukasiewicz algebra. We
suppose that it contains a sufficient number of terms
(constants) t
i,j
which will represent locations in the
two-dimensional space (i.e., selected parts of the
image). Each location can be whatever part of the
image, including a single pixel or a larger region of
the image. The two-dimensional space will be
represented by matrices of terms taken from the set
of closed terms (1):
mnm
n
Jj
Iiji
tt
tt
tM
1
111
,
)(
(1)
where I = {1,..., m} and J = {1,..., n} are some index
sets. The matrix (1) will be called the frame of the
pattern. The pattern itself is the letter which we
suppose to be contained in the image and which is to
DamagedLetterRecognitionMethodology-AComparisonStudy
537

be recognized. A vector
),...,(
1 ini
L
i
ttt
is a line
of the frame M and
),...,(
1 mjj
C
i
ttt
is a column of
the frame M. The simplest content of the location is
the pixel since pixels are points of which images are
formed. A pixel is represented by a certain
designated (and fixed) atomic formula P(x) where
the variable x can be replaced by terms from (1).
Another special designated formula is N(x). It will
represent “nothing” or also “empty space”. We put
N(x) = 0. Formulas of the language J are properties
of the given location (its content) in the space. They
can represent whatever shape, e.g., circles,
rectangles, hand-drawn curves, etc. As mentioned,
the main concept in the formal theory is that of
evaluated formula. It is a couple a / A where A is a
formula and a [0, 1] is a syntactic truth value. In
connection with the analysis of images, we will
usually call a intensity of the formula A.
Let M
be a frame. The pattern
is a matrix of
evaluated formulas (2), where A(x) (x), t
ij
M
and
M
I
,
M
J
are index sets of terms taken from the
frame M
.
M
M
Jj
Iiijxij
tAa ])[/(
(2)
A horizontal component of the pattern
is (3),
where
L
i
t
is a line of M
. Similarly, a vertical
component of the pattern
is (4), where
C
j
t
is a
column of M
.
M
L
iijijxij
H
i
JjtttAa )][/(
(3)
M
C
jijijxij
V
j
IitttAa )][/(
(4)
When the direction does not matter, we will simply
talk about component. Hence, a component is a
vertical or horizontal line selected in the picture
which consists of some well defined elements
represented by formulas. Let two components,
= (a
1
/A
1
,..., a
n
/A
n
) and ’ = (a’
1
/A’
1
,..., a’
n
/A’
n
) be
given. Put K
1
and K
2
the left-most and right-most
indices of some nonempty place which occurs in
either of the two compared patterns in the direction
of the given components. Then, we can compare two
patterns
and
‘(9) by two different views (5):
(5)
First one (n
C
) can be characterized as content
comparison (depends on provability degrees for
pixels). Second one (n
I
) describes comparison of
pixel intensity equivalence. The components
,
’
are said to tally in the degree q (average of n
C
and
n
I
), if
.1
01
)1(2
12
12
othervise
KKif
KK
nn
q
IC
(6)
We will write
q
’ to denote that two
components
and
’ tally in the degree q. When
q = 1 then the subscript q will be omitted. We can
also differentiate vertical and horizontal comparison
of patterns. In fact, we distinguish horizontal or
vertical dimensions of the pattern depending on
whether a pattern is viewed horizontally or
vertically. Note that both dimensions are, in general,
different.
5 EXPERIMENTAL STUDY
5.1 Experimental Settings
With respect to neural networks, we use the
following nomenclature:
x is input value.
t is required (expected) output value.
y
in
is input of neuron y.
y
out
is output of neuron y.
α is a learning rate – this parameter can adjust
adaptation speed in some types of networks.
φ is a formula for calculating the neuron output
value (activation function) y
out
= φ(y
in
).
∆w is a formula for calculating the change of the
weight value.
In our experimental study we have used three
different types of neural networks. Hebb network,
Adaline and Back Propagation network. All
simulation models were constructed in the same way
as in (Kocian and Volná, 2012). All classifiers work
with the same set of inputs. Details about initial
configurations of the used networks are shown in
tables 1 - 3. All neural networks used the winner-
takes-all algorithm when they work in the active
mode. The Hebb network initial configuration is
shown in table 1. The Hebb network contains
minimum parameters and it is adapted during one
cycle. Just as in our previous work (Volna et al.,
2013), we have used a slightly modified Hebb rule
with identity activation function y
out
= y
in
, i.e. input
value to the neuron is considered as its output value.
This simple modification allows using the winner-
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
538

take-all strategy without losing information about
the input to the neuron. Back Propagation network is
a two-layer network, which is adapted by a
backpropagation rule, as described in (Volna et al.,
2013). Setting up this type of network requires more
testing. Finally, the following parameters were
chosen for our experiments, see table 2. Adaline
network contain 10 adaline neurons in output layer
with an identical input layer. The initial
configuration is shown in table 3. Adaline uses the
same simplified (identity) activation function as the
Hebb network, e.g. y
out
= y
in
(Kocian and Volná,
2012).
Table 1: Hebb network initial configuration.
Network
topology
Input layer: x=100, 200 or 300 neurons,
according to the binarization way
Output layer: 10 neurons
Interconnection: fully
φ
∆w
I/O values
identity
x
t
bipolar
Table 2: Back Propagation initial configuration.
Network
topology
Input layer: x=100, 200 or 300 neurons,
according to the binarization way
Hidden layer: 20 neurons
Output layer: 10 neurons
Interconnection: fully
α
φ
∆w
0.4
Sigmoid (slope = 1.0)
)1()(
outoutout
yytyx
Table 3: Adaline initial configuration.
Network
topology
Input layer: x=100, 200 or 300 neurons,
according to the binarization way
Output layer: 10 neurons
Interconnection: fully
α
φ
∆w
0.3
identity
)/(
lenghtout
xytx
With respect to fuzzy logic, we used for comparison
T_0 and T_1 sets since T_2 has no sense in fuzzy
logic analysis (we have only comparison pattern for
specific character, not set of patterns). There is also
possibility to set up global required match level for
specific character. This allows making the method
flexible. As the level lowers the algorithm becomes
more tolerant to partial differences on two compared
patterns. As the level rises it becomes stricter,
requiring partial comparisons to be almost exact.
5.2 Analysis of Experimental Results
Three different neural networks (Hebb, Adaline and
Back propagation) were tested during the
experiment. Each neural network was tested with
four training sets (T_O, T_1, T_2 and T_T) and
three binarization combinations (b_simple,
b_histogram a b_combine). According to the
binarization way (Fig. 6), the input layer contains
different number of neurons. There are 100 neurons
(size of bitmap is 10x10) in the case of b_simple
binarization way or 200 neurons (size of bitmap is
10x20) in the case of b_histogram binarization way
or 300 neurons (size of bitmap is 10x30) in the case
of b_combine binarization way. Input layer contains
the same number of neurons in all used neural
networks. 1000 instances of neural network were
created, learned and tested for each combination of
neural network, training set and binarization. Thanks
to this we could assess the results statistically
(min/max/avg) and eliminate the wrong conclusions
which could occur as a result of the random nature
of the Adaline and Back propagation algorithms.
As we can see in Fig. 9, the best results were
achieved with the b_simple binarization. Regarding
the binarization way, Back propagation network
detected the least impact. The chart in Fig 9 was
created for the training set T_1.
Figure 9: Effect of a binarization on the quality
classification.
As we can see in Fig.10, there was a dramatic
improvement the quality of classification when we
used training data derived from test data. Moreover,
some "intelligence" of Adaline and Back
propagation networks is highlighted if poorly chosen
training set T_0 and the training sets with more
elements were applied. It is worth noting that all the
networks were able to learn and recognize all
patterns from the training set T_T without errors. It
means that the capacity of all three networks was
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
b_simple b_histogram b_combine
Hebb
Adaline
Backpropagation
DamagedLetterRecognitionMethodology-AComparisonStudy
539
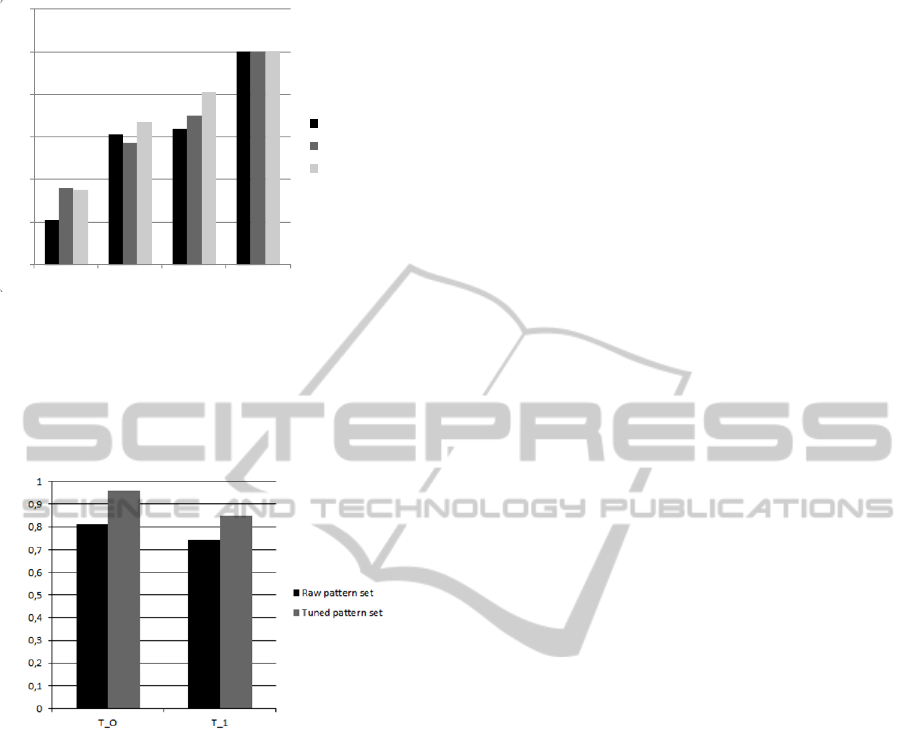
Figure 10: Effect of a training set on the quality
classification.
sufficient to deal with the present task. It was not
possible to demonstrate the ability experimentally
due to small numbers of sample that we received
from the company KMC Group, s.r.o.
Figure 11: Fuzzy logic analysis recognition results.
Fuzzy logic analysis is completely different in its
nature. We do not have any training set, since we
compare all patterns with particular matrix of
formulae of images. Best results were obtained using
tuned pattern set created from T_0. In contrast with
neural network T_1 has weaker recognition rate,
Fig. 11.
6 CONCLUSIONS
This paper describes an experimental study based on
the application of neural networks for pattern
recognition of numbers stamped into ingots. This
task was also solved using fuzzy logic (Novak and
Habiballa,2012). Our experimental study confirmed
that for the given class of tasks can be acceptable
simple classifiers. The advantage of simple neural
networks is their very easy implementation and
quick adaptation. Unfortunately, the company KMC
Group, s.r.o. provided only two sets of patterns.
Artificially created training set T_0 included only 10
patterns of "master" examples of individual digits
(see Fig. 2). Test set consists of 106 real patterns.
During our experimental study, we reached the
following conclusions:
Using randomly chosen patterns from the test set,
we achieved success rate approx 30-60% with the
test set according to the choosen binarization way.
Neural networks need a sufficient number of
training patterns (real data, not artificially created)
so the pattern recognition is successful.
All the three tested neural networks have managed
to learn the whole test set T_T. It can be
interpreted as prove that capabilities of the
networks are suitable for this task.
Fuzzy logic analysis proved to be very suitable for
the situation where limited number of training
cases is present. We can have only ideal cases and
the recognition rate for tuned set is close to 100%
(96%).
Fuzzy logic analysis is also computationally
simpler (time consumption) since it has not any
“learning” phase.
ACKNOWLEDGEMENTS
The paper has been financially supported by
University of Ostrava grant SGS23/PřF/2013 and by
the European Regional Development Fund in the
IT4 Innovations Centre of Excellence project
(CZ.1.05/1.1.00/02.0070).
REFERENCES
Fausett, L. V., 1994. Fundamentals of Neural Networks.
Prentice-Hall, Inc., Englewood Cliffs, New Jersey.
Kocian, V. and Volná, E., 2012. Ensembles of neural-
networks-based classifiers. In R. Matoušek (ed.):
Proceedings of the 18th International Conference on
Soft Computing, Mendel 2012, Brno, pp. 256-261.
Novak, V., Zorat, A., Fedrizzi, M., 1997. A simple
procedure for pattern prerecognition based on fuzzy
logic analysis. Int. J. of Uncertainty, Fuzziness and
Knowledge-Based systems 5, pp. 31-45
Novak, V., Habiballa, H., 2012. Recognition of Damaged
Letters Based on Mathematical Fuzzy Logic Analysis.
International Joint Conference CISIS´12-ICEUTE´12-
SOCO´12 Special Sessions. Berlin: Springer Berlin
Heidelberg, pp. 497-506.
Pavelka, J., 1979. On fuzzy logic {I}, {II}, {III}.
Zeitschrift fur Mathematische Logik und Grundlagen
der Mathematik 25, pp. 45-52, 119-134, 447-464
0
0,2
0,4
0,6
0,8
1
1,2
T_O T_1 T_2 T_T
Hebb
Adaline
Backpropagation
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
540

Trier, O. D., Jain, A.K. and Taxt, T., 1996. Feature
Extraction methods for Character recognition – A
Survey, Pattern Recognition, Vol. 29, No. 4, ,
pp.641-662
Volna, E., Janošek, M., Kotyrba, M., and Kocian, V. 2013.
Pattern recognition algorithm optimization. In Zelinka,
I., Snášel, V., Rössler, O.E., Abraham, A., and
Corchado E.S. (Eds.): Nostradamus: Modern Methods
of Prediction, Modeling and Analysis of Nonlinear
Systems, AISC 192. Springer-Verlag Berlin
Heidelberg, pp. 251-260.
DamagedLetterRecognitionMethodology-AComparisonStudy
541
