Macroscopic Simulation of Multi-axis Machining Processes

Meysam Minoufekr

, Lothar Glasmacher

and Oliver Adams

CAx-Technologies, Fraunhofer-Insitute for Production Technology, Steinbachstr. 17, 52074 Aachen, Germany

Chair of Manufacturing Technology, WZL, RWTH Aachen University, Steinbachstr. 19, 52074 Aachen, Germany

Keywords: Geometric Modelling, NC Machining Simulation, Tool/Workpiece Engagement.

Abstract: The machining of safety-critical components, e.g. turbine disks and blades, is expected to meet highest

demands regarding functionality and quality. At the same time, a fast and affordable process design for the

production is a major driver for the economic development of these components. Effective increase in

productivity requires in addition to the development of machining technologies, new approaches in process

design and planning. The integration of simulation into computer aided design of multi-axis processes

provides a great potential for further optimisation of the processes. By using the macro simulation model

introduced in this paper, the computational complexity to gain relevant process information is reduced and

hence made accessible more easily. Through the presented macro simulation, detailed tool-workpiece

engagement is calculated which co-relates to mechanical and thermal stresses on the tool. Based on the

calculations the process can be designed by reducing the tool load in the course of the process. This way, the

tool life of the used milling cutters can be significantly increased resulting in an increase of process

robustness and efficiency, thereby reducing used resources.

1 INTRODUCTION

The process sequence for milling of free-form

surfaces can be divided into roughing, pre-finishing

and finishing. When roughing, the goal is often to

achieve a high performance cutting process (HPC)

by driving the process at maximal feed rates and

depth of cut resulting in a high material removal rate

(MRR). However, in HPC processes high feed rates

lead to increasing cutting forces and tool loads

which have to be controlled in order to avoid a large

tool wear or even tool breakage during the process.

The workpiece resulting from the roughing

operation is usually characterized by a macroscopic

surface roughness on the surface contour, (Arntz,

2013). In pre-finishing, a uniform surface is

achieved by removing the rest material generated in

the rough machining. The goal of pre-finishing is a

constant material distribution on the entire

workpiece, so that in the following finishing

operation, requirements of accuracy and surface

quality can be achieved. As the last process,

finishing is critical since the final surface of the part

is generated. Failures in finish milling lead to

expensive rework or even to scrap generation. Both,

in pre-finishing and in the subsequent finishing

processes, often a high speed cutting (HSC)

approach is applied by using extremely high spindle

speed and feed rates. In the course of HSC

processes, the engagement conditions, e.g. the

contact angle and the resulting chip thickness, have

to be controlled since, in combination with the

cutting speeds, the mechanical and thermal loads on

the tool may result in low surface quality on the final

part. Consequently, in HPC as well as in HSC

processes, methods are needed for a careful process

design to drive the processes to their limits but also

to avoid critical situations along the value chain of

the processes.

Especially in the transition from roughing to pre-

finishing, the analysis and evaluation of the

engagement conditions plays an important role, as

the contact situation between cutter and workpiece

becomes unpredictable. The residual material

geometry on the workpiece, which results from

roughing, usually cannot be determined in advance

for parts with free-form geometry. Contact situations

of the tool and the workpiece leading to unknown

and possibly undesirable engagement conditions

seem to be unavoidable during the process. Due to

the continuously changing machining allowance and

contact situation, it is important for the process

505

Minoufekr M., Glasmacher L. and Adams O..

Macroscopic Simulation of Multi-axis Machining Processes.

DOI: 10.5220/0004631905050516

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 505-516

ISBN: 978-989-8565-71-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

planner to understand the interaction between the

tool and the workpiece and evaluate the same

against significant process parameters. In particular,

the engagement conditions during simultaneous five-

axis milling have to be observed in this context.

The simulation approach introduced in this work

helps to understand the geometrical engagement

situation occurring in the milling process. Thus,

critical regions in the process where engagement

condtions exceed the tolerances can be automatically

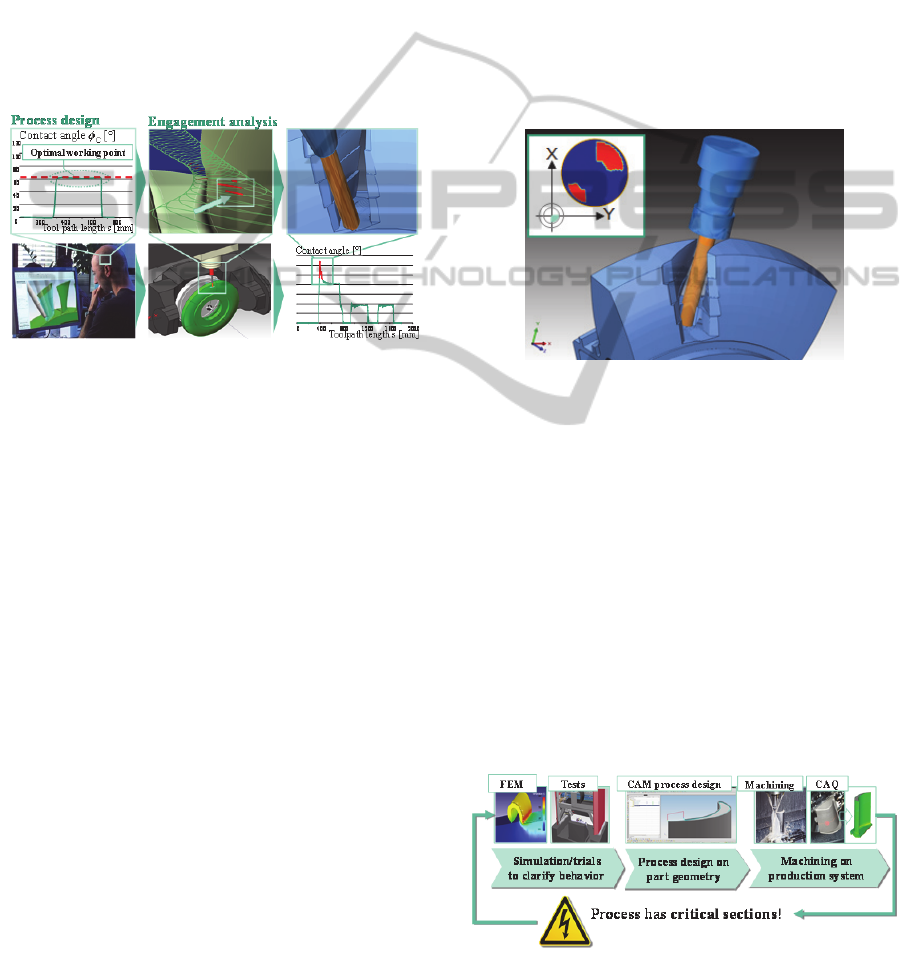
identified, Figure 1. This is the basis for a process

analysis, since process parameters directly related to

the geometrical engagement conditions are evaluated

and optimised in advance.

Figure 1: General idea for simulation of critical sections

on the toolpath.

So, this paper suggests the macro simulation

model for multi-axis machining processes. It is

structured as follows. In section 2, problems in

current multi-axis machining are described.

Furthermore, the engagement and fundamental

parameters defining the cutter-workpiece contact are

analysed. In section 3, the macroscopic simulation

model for machining processes is introduced. Based

on this concept, the calculation models for discrete

engagement conditions are explained in-depth. Then,

in section 4 the macro simulation is discussed by a

roughing example, where engagement conditions are

calculated. The paper is finally concluded in

section 5.

2 BACKGROUND AND

PROBLEM DEFINITION

Almost any complex part can be produced using

simultaneous multi-axis machining. Here, the

simultaneous multi-axis milling is characterized by

suddenly changing the tool orientation and the

transient contact conditions between tool and

workpiece. The manufacturing of the parts is carried

out on NC controlled machine tools. Here, the

process is loaded as a series of NC commands, i.e.

the "NC program", on the machine tool and

executed. Depending on the NC command in the NC

program, up to three translational and two rotational

axes are controlled simultaneously during the

machining. Accurate NC programs are crucial for

manufacturing without interruption and potential

machine breakdowns. Due to the complex

kinematics, milling processes are not verifiable

without supporting process design tools because it is

difficult to visualise the location of the cutting tool

due to the complex axis control. The consequences

are unpredictable and probably critical to cutting

conditions, Figure 2.

Figure 2: Example of a BLISK manufacturing with a

critical engagement due to collision of the workpiece with

the non-cutting part of the cutter.

Nowadays, the development of machining

processes is characterized by a sequential iterative

approach, which has to be followed in a few

optimization loops before reaching stable

production, (Schug, 2012). Therefore, computer

based technologies (CAx technologies) are involved

in planning and verification of the entire milling

process in advance, Figure 3. The parameter

windows and the acquired technology knowledge

gained from machining trials are used to determine

the process-specific, optimal parameter

combinations which are essential in the design and

planning of the manufacturing.

Figure 3: Sequential CAx process chain for machining.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

506

The planning in CAM is dedicated to the design

of the machining operation where the milling

toolpath is parameterized by process variables such

as cutting speed and depth of cut to manufacture the

real part geometry. The designed process is

transferred to the production system by an

appropriate output data format for machining.

Potential errors that are identified at the end of the

process design stage, or during the process carried

out on the machine tool, cause expensive iteration

steps. According to (Zabel, 2010), the costs to

eliminate an error increase with the progress of the

process design stages. Consequently, an

identification of process parameters leading to

undesired cutting conditions is considered necessary

at an early stage in the process planning.

2.1 Simulation-based Design of

Multi-axis Processes

The main application of process simulation is in the

area of computer-based process planning and design,

Figure 4. By using the process simulation, it is

possible to locate errors and fix problems faster, than

it is achievable through trial-and-error methods. The

starting point for using the process simulation

system is between the NC data generation by the

CAx system and the loading of NC data on the

machine tool. Unlike the sequential CAx process

chain, the NC data is not transferred directly to the

machine tool, but passed to the simulation system.

Especially requirements referring to the efficiency of

the used simulation tool process play a role because

the simulation increases the CAx process design

chain length, (Zabel, 2010). In this context, the

simulation model with affordable complexity of

computation time and space is desirable.

Figure 4: Evaluation of the process behaviour by the

presented simulation approach.

2.2 State of the Art in the Simulation of

Machining Processes

Numerous simulation approaches have been

developed in the last decades with the objective of

determining the important parameters of the

machining process which can be classified as FE-

based models, analytical models and geometrical

models, Figure 5. The group of geometrical models

can be further subdivided into approaches using

constructive solid geometries (CSG) and spatial

space partitioning schemes. Zabel gives a detailed

overview of these models and their application in

(Zabel, 2010).

Figure 5: Overview of existing simulation models for

machining processes.

Although many physical effects can be modeled

by using FEM and analytical model equations,

however, the predictive capabilities of available

approaches are still limited and thus cannot be

applied for planning the entire multi-axis operation.

A complete analysis of five-axis milling processes,

i.e. simulation of every instant of the process is

expensive due to limitations on available computing

capacity and hardly practical. On the other hand,

geometric models focus on the determination of

visual properties such as the shape of the workpiece

during the milling operation by efficient real-time

methods for updating the workpiece.

Simulation techniques based on the discretization

of the workpiece vary according to the geometric

design, (Glaeser, 1997), (Jerard, 1989), (Robert,

1987). Milling simulation methods based on the

voxel or dexel model are presented in (Ayasse,

2001) and (Stautner, 2005). The consideration of

physical properties is of minor importance. Systems

like Vericut offer simulation methods for collision

detection in three and five axis milling, (CGTech,

2013). The adjustment of the NC programs is often

based on parameters, wherein the simulated residual

material on the finished part is used to increase the

material removal rate. However, only the feed rates

are adjusted, the geometry of the toolpath remains

unchanged. In these systems, assumptions in the

modeling approaches are highly simplified. Hence,

MacroscopicSimulationofMulti-axisMachiningProcesses

507

results obtained are insufficient for a qualitative

statement about the geometrical engagement

situation in the course of the milling process.

2.3 Macroscopic Engagement

Conditions for Process Evaluation

The mechanical and thermal tool load is primarily

dependent on the combination of three factors: the

chip thickness h

the contact angle ϕ

and the

contact length l

, Figure 4.

Figure 6: Engagement of cutting tool at instant t.

Optimal cutting conditions can be maintained

easily in straight cuts by constant cutting width a

However, engagement situations change rapidly in a

multi-axis process. In machining of free-form

surfaces, the contact angle ϕ

increases, whenever

the tool enters a turn causing a longer contact length

between the cutting edges and the workpiece,

Figure 7. In fact, cutting-edge temperature increases

significantly as the contact length l

increases,

which results in a decrease of tool life. This relation

has been proven by Meinecke in (Meinecke, 2009).

Figure 7: Straight vs. corner cuts result in different

engagement despite equal cutting depth, (Diehl, 2011).

The relevance of the contact angle ϕ

can also be

seen in cutting theory, as the chip thickness h

increases with increasing ϕ

and thus leads to higher

cutting forces, (Klocke, 2011). According to Ståhl,

(Ståhl, 2012), the approximate chip thickness h

and

the chip width b

are expressed by the contact angle

and the axial depth of cut a

, respectively:











∙



(1)











sin

(2)

where κ is the major cutting edge angle of the

cutting tool, f

the feed per tooth and a

the cutting

depth. Specifically, the the machining forces in

radial (F

), tangential (F

) and axial direction (F

) are

related to the contact angle ϕ

. This can be seen by

substituting h

and b

in the Kienzle equation,

(KLocke, 2011):

sin

·k

i1.1

·(f

·sinϕ

)



1-m



(3)

where k

i1.1

and m

are material specific constants and

i ∈ {a,r,t}. Hence, the contact angle and the contact

length play a major role in the evaluation of

machining processes. For the calculation of the

contact angle ϕ

, it is necessary to regard the cutter-

workpiece engagement at each point in time in the

course of the process. However, the contact angle

can be determined by considering the interaction of

the tool bounding geometry with the workpiece,

where the angular contact area on the tool is referred

as ϕ

= ϕ

- ϕ

, i.e. defined as the difference of the

exiting angle ϕ

and the starting angle ϕ

, Figure 8.

In accordance to (Meinecke, 2009), quantities as ϕ

and ϕ

are referred to as macro conditions, since

their calculation is abstracted from the exact tool

geometry and the tool cutting edges are not taken

into account.

Figure 8: Macro engagement of cutting tool.

2.4 Influence of the Tool Geometry and

Tool Kinematic

In addition to the suddenly changing contact

situation in the course of the multi-axis milling, two

further aspects complicate the calculation of macro

conditions at each instant of the process; the tool

geometry and tool orientation. During the machining

Engagement on the tool

=r·ϕ

=60°

=12%

=24°

=12%

·r

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

508

of freeform surfaces many constellations of the

engagement may arise from the material removal

leading to sudden changes of engagement conditions

along the tool.

To capture the engagement situation in multi-

axis machining, an extended definition of process

parameters and engagement conditions is needed

considering the tool geometry and the tool

orientation. Hence, the engagement conditions are

parameterized by their axial location k ∈ [0,l] on the

tool axis at an instant in the course of the process.

Thus, the starting and exiting angle are defined as

(k)

and ϕ

(k), respectively. Also the radial depth

of cut is referred to the current location of the tool

axis and is deifined as a

(k). Since the tool radius is

also variable along the tool axis it is also

parameterized as r(k),

Figure

Figure 9: Parameterization of the engagement conditions

in reference to the tool length l.

When machining with ball end mills, for

instance, every cutter point undergoes a different

load during the engagement. The altering contact

along the tool axis has consequences for the

determination of the chip length l

, since it depends

on the contact angle ϕ

and tool radius r(k) which is

varying according to the tool shape along the tool

axis,

Figure

10.

The calculation of the engagement condition is

further complicated by the orientation of the tool

relative to the workpiece and the feed direction. In

context of NC machining, the position of the tool is

defined by a local tool coordinate system TCS which

has its origin at the tool center point O

TCS

and is

determined by the current feed direction v

, the tool

orientation n and the bi-normal b=n × v

Figure

11.

The orientation of the tool vector n is determined by

the lead and tilt angle β

and β

, respectively.

Figure 10: Influence of the tool geometry on the

calculation of engagement conditions.

Figure 11: Definition of the Tool coordinate system.

Figure 12: Influence of the tool orientation on the

engagement conditions.

During the machining of freeform surfaces, the

tool may be tilted to the surface normal, i.e. β

≠0

and β

≠0, respectively. Since the contact situation

depends on the lead angle β

and tilt angle β

describing the angular situation of the tool normal

vector n to the surface of the workpiece,

(k)

r(k)

MacroscopicSimulationofMulti-axisMachiningProcesses

509

(Arntz, 2013), the starting and exiting angles ϕ

(k)

and ϕ

(k) vary along the tool axis resulting from the

kinematic situation of the tool and the workpiece.

Hence, at each individual tool height, there is a

different contact angle ϕ

(k), Figure 12. Depending

on the tool orientation to the workpiece, the contact

angle ϕ

(k) varies along the tool axis at a discrete

instant t.

2.5 Problem Definition and Research

Question

On one hand, the engagement situation depends on

the orientation resulting in altering contact angles

(k) along the tool axis. This affects also the course

of h

, which is followed by equation (2). On the

other hand, the tool geometry, in particular the

variable tool radius along the tool axis leads to

changing contact lengths during the engagement.

Additionally, the contact situation changes in the

course of the cutting process at each instant t. Thus,

the contact angle on the tool is defined as ϕ

(t,k)

specifying the angular contact on point k ∈0,



along the tool axis and at an arbitrary point in time t.

Furthermore, the contact length can be expressed as

(t,k)= ϕ

(t,k) ⋅ r(k)

(4)

In this context, the following assumption can be

formulated:

A discretized simulation model allows a sufficiently

accurate approximation of macroscopic engagement

conditions in the course of multi-axis machining

processes.

To verify this key assumption, the following

research question has to be investigated:

Can the geometrical contact situation of multi-axis

machining processes be described as a sequence of

discrete states, where engagement conditions vary

on each discrete point k on the tool axis and at each

discrete instant t?

Answering this question involves the realization of a

simulation model which allows a sufficiently

accurate approximation of geometrical engagement

conditions, in particular macroscopic engagement

conditions, between the cutting tool and the

workpiece in simultaneous multi-axis machining.

3 SOLUTION AND METHOD

The geometrical simulation approach introduced in

this paper, determines macroscopic engagement

conditions by regarding the cutter-workpiece

engagement area based on a discretized geometry

model. The macro simulation is based on a

hierarchical simulation approach which allows the

prediction of engagement conditions on the tool over

a sufficiently long period of time by purely

geometrical modelling, Figure 13. Based on the

macroscopic simulation, critical process areas can be

identified or can be investigated for sub-optimal

process performance.

Figure 13: Hierarchical structure of the simulation system

for macroscopic engagement conditions.

Therefore, the toolpath is divided into discrete

segments. At each discrete point on the toolpath, the

contact between the tool and the workpiece

geometry is determined and then used for calculating

the engagement conditions,

Figure

14. Between two

points on the toolpath, the intersection of the

bounding geometry of the tool and the workpiece

model is determined. The set of intersecting points

can be used directly for the calculation of removed

material on the workpiece model. The removed

material data resulting from the tool position and

orientation on the current toolpath point is used to

derive the macro conditions, i.e. the contact angle

(t,k) and the chip length l

(t,k). At a discrete

instant t of the process, the profile of macroscopic

quantities can be determined along the tool axis by

subdividing the tool in m+1 tool discs, resulting in a

particular value ϕ

(t,k) at each tool disc k, where

k=0,1,2,… m.

Since the calculation of macro conditions is

abstracted from the exact cutting geometry, the

computational effort is drastically reduced. So,

macroscopic conditions are calculable throughout

the entire process by avoiding expensive calculation

steps. Both aspects, namely sufficient reliability of

the model as well as demands on efficiency are

achieved. In this regard, efficient techniques for

workpiece update with special consideration of a

sufficiently precise engagement modeling are

indispensable. Especially complex workpiece

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

510

geometries with machining operations consisting of

several 100,000 NC blocks need to be verified in the

macro simulation with the reasonable response

times.

Figure 14: Geometric approach for macroscopic

engagement simulation of multi-axis processes.

3.1 Calculation Models for Macro

Simulation

The calculation of engagement conditions is based

on the geometrical contact of the cutter and the

workpiece. Accurate predictions on the contact

between the tool and workpiece are the basis for

further calculations and therefore essential in the

simulation approach. Both the tool and the

workpiece can be modeled in the context of

geometrical simulation in various ways. Highly

dimensioned and complex workpiece geometries

require a large memory usage and fast methods for

the update during machining. So, the choice of

appropriate “modeling schemes”, i.e. how a

workpiece is discretized, (Stifter, 1995) affects the

simulation accuracy and space complexity greatly,

Figure 15.

A further focus is on the introduction of

modeling schemes with special consideration of a

sufficiently accurate mapping of engagement

conditions since engagement calculations are

directly derived from the discretized elements of the

workpiece model and hence influence the quality of

the simulation results. Practical tests have shown

that the dexel and the multi-dexel scheme provide a

high accuracy for engagement calculation operations

while allowing an efficient dynamic update of the

workpiece, Figure 16.

The workpiece model representation used in this

work is based on the multi-dexel scheme introduced

by Stautner, (Stautner, 2005). Furthermore, the

boundary model of the milling tool, given as a CSG

model, is used to determine the contact area, i.e. the

cutting edges of the tool are neglected. The dexel

scheme is an instance of spatial enumeration

techniques with desired requirements referring

accuracy and performance, (Stifter, 1995).

Figure 15: Space complexity of the modelling schemes

and their memory usage for a cube geometry.

Figure 16: Accuracy of the modelling schemes for

engagement calculation.

The dexel model of the workpiece is determined

by a set of parallel and equidistant rays intersected

with the original workpiece geometry,

Figure

17. By

intersecting each ray with the workpiece, two points

on a line segment, which is totally inside the

workpiece, are determined. A dexel is defined by

these two points on the line segment. The

intersection points can be calculated with a high

Nominal Δ Z-Fiels Δ Voxel Δ Multidexel

Max. Error

137.54° 10.64° 14.83° 4.23°

Ø Error 0.00° 6.77° 8.23° 2.7°

120

Contact angle ϕ

[ ]

150

180

Tool path length in y-direction [mm]

50 100 100 150 200

Analytical

Voxel

Z-

Field

Multi dexel

MacroscopicSimulationofMulti-axisMachiningProcesses

511

accuracy since the dexel grid provides float

precision parallel to the ray direction. However, a

single dexel model leads to deviations in

representing the original workpiece if the shape is

sampled parallel to the projection plane of the dexel

grid. Here, the determination of intersection is

depending on the grid interval.

Figure 17: Dexel based representation of the workpiece.

To overcome this insufficiency, the multi-dexel

scheme is used which can be regarded as an

extension of the dexel model. As shown in Figure

18, the multi-dexel model consists of three

overlapping orthogonal dexel grids. Compared to the

single direction dexel model, the multi-dexel scheme

expresses a model more precisely since the

computation of each coordinate of an intersection

point can be performed with float precision. The

multi-dexel model is defined as a set of {d

i,j,k

}, by a

constant grid distance δ relative to the origin point

O, (Ren, 2008). Each dexel d

i,j,k

has two nodes ξ

i,j,k

and ξ

i,j,k

as the lower and the upper bound of the

dexel segments, Figure 18. The space complexity is

estimated by O(N

⋅

+ N

⋅

+ N

⋅

)

⋅

∈ O(N²),

where N

are the cell numbers along principal axes

and M

is the maximum number of dexel nodes.

Figure 18: Logical structure of the dexel model,

(Ren, 2008).

To simulate the material removal by machining,

the contact area between the tool and dexels that are

involved in the cutting are calculated at a given

instant. This means a rearranging of the dexel data at

region of tool-workpiece interaction, while the entire

material removal requires a sequential update of the

dexel elements. These steps are repeated at each

discrete point of the machining toolpath until the

machining process is completed, Figure 19.

Figure 19: Intersection of the tool with the workpiece.

3.2 Calculation of Macroscopic

Engagement Conditions

The contact between the tool and the workpiece can

be calculated by the intersection of the tool

boundary geometry and the dexels. This requires

determining the area of the tool that is in contact

with each dexel and then identifying the

corresponding ξ

i,j,k

and ξ

i,j,k

for each d

i,j,k

involved

during a cut. Hence, let S

Tool

and S

Workpiece

be defined

as the tool domain and the workpiece domain,

respectively. Further, let p=(p

) ∈ S

Tool

be a

discrete point of S

Tool

and q=(q

) ∈ S

Workpiece

a point on the workpiece. If the condition

∃ α,β,γ ∈ {i,j,k} with p

≤ q

, p

(5)

is satisfied at a discrete point in time t, the tool and

the workpiece are considered to be in engagement

and lead to the engagement domain D(t), which is

defined as follows:

D(t) = {(s

, s

) | s

∈³, s

∈³},

(6)

where s

=(s

) and s

=(s

) fulfill (5) for

a q ∈

Tool

. The set D(t) consists of point pairs

describing the line segments which are cut by the

tool at t. The corresponding points of the 2-tupels in

D(t) can be expressed as s

=(i,j,ξ

i,j,k

) and

=(i,j,ξ

i,j,k

), respectively by regarding the

intersection of the cut dexel d

i,j,k

and S

Tool

in the

nodes ξ

i,j,k

and ξ

i,j,k

Figure

20.

i,j,1

i,j,0

i+1,j,1

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

512

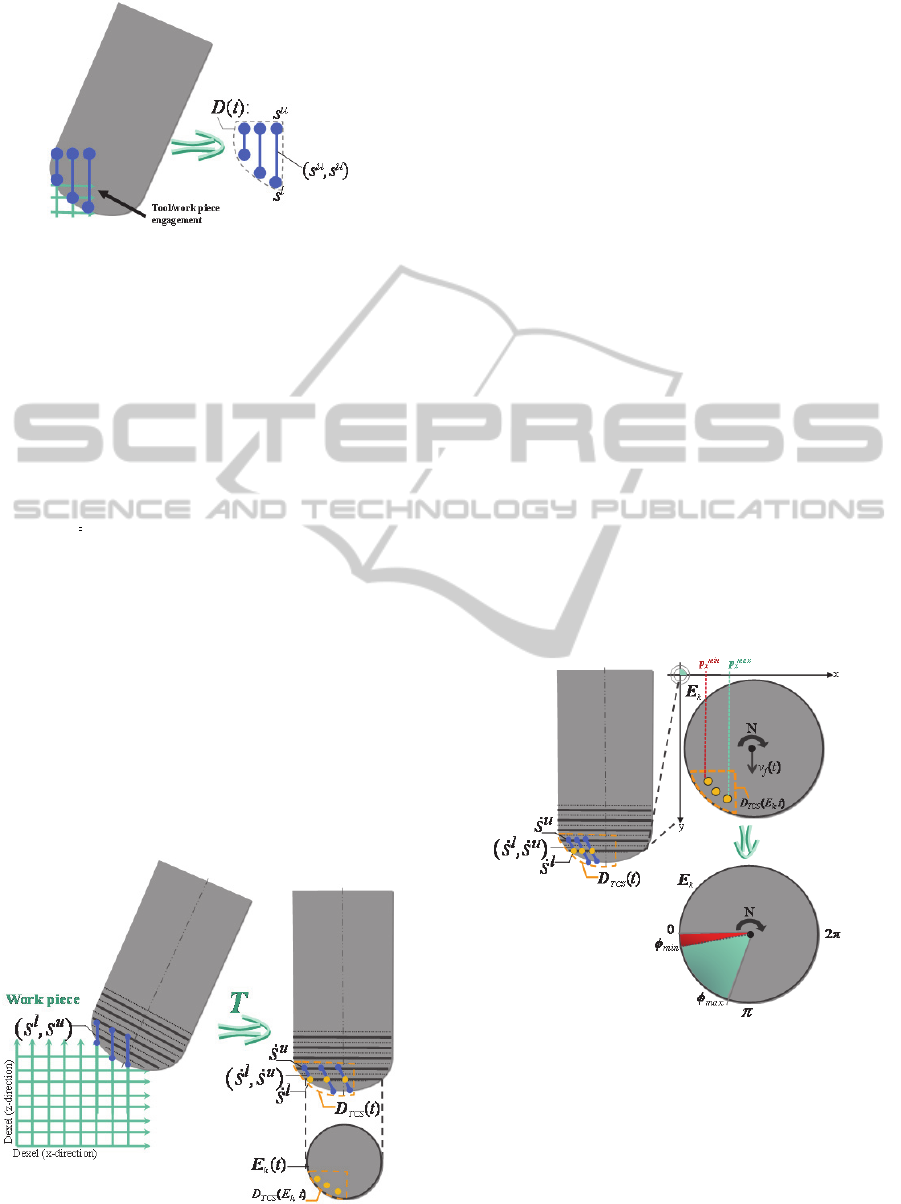
Figure 20: Set of the the intersecting dexel segements with

the tool during the engagement.

To express the contact conditions referring to the

cutting area on the tool, each element of D(t) is

transformed into the coordinate system of the tool

TCS, see section 2.4. Thus, the engagement domain

TCS

(t) is defined as

TCS

(t) = {(ṡ

, ṡ

) | ṡ

⋅

-v, ṡ

⋅

-v},

(7)

where s

∈ D(t), s

∈ D(t) and T ∈ 

3×3

defined as the

basis transformation matrix build up by the three

vectors n, v

, b ∈ ³. The vector v ∈ 

describes the

offset between O and O

TCS.

Furthermore, it can be

easily seen that D

TCS

(t) is bounded by the bounding

geometry of the tool, i.e.

∀(ṡ

ṡ

) ∈ D

TCS

(t): (ṡ

ṡ

) ⊆ S’

Tool

(8)

where S’

Tool

:={T

⋅

q – v | q ∈ S

Tool

}. The macroscopic

engagement conditions are derived by using the

engagement domain D

TCS

(t) at each instant t. As

described in section 2.5, the contact conditions may

vary along the tool axis. In order to estimate the

course of engagement conditions depending on the

tool axis, the engagement area is evaluated by

discretizing the tool along its length in m+1 discs,

Figure

21.

Figure 21: Material removal mapped on the discrete tool

disc along the tool axis.

Each disc has a position and an orientation on the

tool that defines the oblique cutting performed by

that disc segment. For a defined tool orientation

n=(n

), the tool discs can be defined as a set of

planes originated in O

TCS:



={E

⊂



³| E

={p ∈E

⋅

Δz}}

(9)

where k=0, 1, 2,…, m. The contact area for each tool

disc E

is determined by finding the intersection of a

line segments (ṡ

,ṡ

) ∈D

TCS

(t) with E

. Hence, the

engagement area of E

at a discrete instant t can be

described as

TCS

,t)={p| ∃(ṡ

,ṡ

) ∈D

TCS

(t): p∈

∩(ṡ

,ṡ

)}.

(10)

For each E

and (ṡ

,ṡ

), it is true that ǁE

∩(ṡ

,ṡ

)ǁ = 1,

i.e. E

and (ṡ

,ṡ

) intersect only in p, except (ṡ

,ṡ

)

completely lies in E

. By recalling (6), for every

p ∈ (ṡ

ṡ

) it is also true that p ∈S’

Tool

since p lies on

the line segment limited by ṡ

and ṡ

. It follows that

TCS

,t) ⊆ S’

Tool

for some E

∈ . Looking closer

to D

TCS

,t), it can be seen that

∀ p ∈ D

TCS

,t): ǁp - O

TCS

ǁ ≤ r(k)

(11)

for r(k) ∈  and k=0,1,…m, i.e. the contact points in

TCS

,t) are bounded by the corresponding tool

radius at the tool disc E

Figure 22: Estimation of the minimal and maximal angles

on a tool disc E

The particular angular engagement area for a

given disc E

is given by the minimal angle ϕ

min

(k)

and the exit angle ϕ

max

(k) on E

. These two

parameters provide a compact form to describe the

tool-workpiece engagement at a particular region

along the tool axis at the tool length l=(m+1)

⋅

Δz,

Figure

23. The minimal angle ϕ

min

(k) and

MacroscopicSimulationofMulti-axisMachiningProcesses

513

maximal angle ϕ

max

(k) to each respective disc E

are

assigned by finding the point with minimal and

maximal coordinates in x-direction on E

. Thus, let

min

=(p

min

) be the corresponding point to

the minimal x-value in D

TCS

,t) and

max

=(p

max

) the maximal, respectively.

The angular values of ϕ

max

(k) and ϕ

min

(k) are

determined by





:































,for





0



















,for





0

(12)

and





:































,for





0



















,for





0

(13)

and ϕ

min/max

(k)≔0

for p

min/max

=0. In case of

clockwise rotating tool, it is ϕ

(k)=ϕ

max

(k) and

(k)=ϕ

min

(k). In case of a counterclockwise rotating

tool, ϕ

(k) and ϕ

(k)

are swapped. The contact angle

(k) at E

is estimated by ϕ

(k):=ϕ

(k)-ϕ

(k),

Figure

23.

Figure 23: Calculation of contact angle on a tool disc.

4 RESULTS AND DISCUSSION

The main advantage of process simulation is that

process behaviour can be evaluated before cost

expensive trials are conducted. The link between the

simulation with data from the process monitoring

results in a higher knowledge base about the process

interdependencies in the milling process, Figure 24.

Therefore, a synchronisation between both data

sources has to be developed. As a synchronisation

over time scale is not reliable, because the machine

tool’s acceleration behaviour has to be known

exactly, here an approach using synchronisation over

position is chosen.

Figure 24: Link between offline and online process

analysis.

4.1 Use of the Macro Simulation to

Evaluate Processes

In order to prove the concept of linking simulation

data with process monitoring data, test geometry is

defined and manufactured. The test geometry

consists of simple geometric features. A cuboid, a

cylinder and a triangle are placed on a rectangular

base, Figure 25. As workpiece material Aluminum is

used and the tool is a standard 10 mm diameter shaft

mill with two cutting edges. The workpiece is

mounted on a Kistler 9255B force measurement

platform to acquire the process forces. A Mazak

Variaxis 630-5X II t, which is a 5-axis machining

centre, is used to carry out the experiments.

Table 1: Process setup details and process parameters.

Workpiece

Aluminum

140 mm x 150 mm

Tool 10 mm diameter shaft mill

Cutting parameter

= 0.1 mm

= 280 m/min

= 5 mm

Figure 25: Test setup on Mazak Variaxis 630-5X II t.

Δa

(k)

(t)

(k)



ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

514

The toolpath and CAM operations are conducted

in the PLM software Siemens NX 8.5. A standard

contour parallel milling strategy is used in

combination with conventional cutting, Figure 26.

Figure 26: Generated toolpath.

A macro simulation of the engagement condition

is carried out and shows the contact angle between

workpiece and tool over time, Figure 27. The macro

conditions were calculated in 3 sec. 430 ms at a

laptop computer (Dell Precision M4600@4x2.2GHz

and 8GB RAM). The toolpath was segmented in

2027 discrete points. The workpiece was discretised

by a precision δ = 0.3mm. From the simulation it can

be seen that the created toolpath leads to frequently

changing engagement situations. As the contact

angle correlates with the process forces the resulting

tool load is varying as well. Critical sections with

high contact angle are identified and can be

optimized through either changing the toolpath or by

reducing the feed rate in the NC program.

Furthermore, sections with rather low contact angles

can be optimized in order to reduce process time. In

addition to optimizing the milling process itself,

process monitoring strategies can be applied.

Integrating and linking geometric information from

macro process simulation with process monitoring

tools opens new ways for online-monitoring of

multi-axis milling processes.

Figure 27: Contact angle over time t.

Using the Kienzle equation, Equation (3), the

expected force depending on the local engagement

situation is calculated. This allows a process

monitoring system to compare online, the expected

force with the current force and decide whether the

milling process is in a stable situation. Compared to

standard monitoring systems no teaching activities

are necessary. The result of calculated monitoring

force and real process force is evaluated in time

domain, Figure 28.

Figure 28: Process monitoring solution for milling

process.

5 CONCLUSIONS AND FURTHER

RESEARCH

Due to frequently changing manufacturing tasks, it

is difficult to control the complexity of machining

processes. However, the parts have to be machined

with high accuracy, robustness and efficiency. Thus,

the shop floors are under strong pressure to deliver

optimal results in shorter times.

In order to efficiently find optimal process

parameters, the level of production automation for

developing processes is important. A simulation

approach that allows the determination and

evaluation of the actual status of the machine and the

process at any time contributes to realize a

systematic optimization of machining operations.

However, complex calculations are used for the

simulation of multi-axis milling processes which are

not yet appropriately controllable despite improved

hardware technologies and parallelization of

algorithms. Important as the use of powerful

hardware and parallel algorithms may be, novel

concepts are needed to minimize the complexity of

the problems to be analysed on the essential level of

120 125 130 135

100

150

Contact angle  / °

Time t / s

120 125 130 135

100

200

300

400

500

Active Force F / N

Time t / s

F_calculate

F_measured

MacroscopicSimulationofMulti-axisMachiningProcesses

515

abstraction.

In this paper, the macro simulation for multi-axis

machining processes has been introduced which

focusses on significant parameters in the process. It

enables the reliable detection of disturbances such as

process instabilities or overloads of tool and/or

machine which lead to an excess of tolerances and

hence undesired process deviations. Thus, the

presented work contributes to a significant reduction

of expensive damages and system failures in

production. Apart from the prediction of engagement

conditions, further research is needed to modify

process parameters based on the simulation.

Complex toolpaths in particular can be optimized

regarding the manufacturing and design parameters.

The adjustment of feed rates, the toolpath trajectory

and the tool definition offer a potential for reducing

the process time and creating a more robust

machining process. Hence, future research will focus

on optimizing these parameters based on

macroscopic engagement conditions.

ACKNOWLEDGEMENTS

The authors would like to thank the German

Research Foundation DFG for the support of the

depicted research within the Cluster of Excellence

"Integrative Production Technology for High-Wage

Countries".

REFERENCES

Arntz, K., 2013, Technologie des Mehrachsfräsens von

vergütetem Schnellarbeitsstahl, Aachen

Schug, P. et al, 2012, Durchgängige CAx-Prozessketten,

Forschung an der Werkzeugbau Akademie, Apprimus,

Aachen

Zabel, A., 2010, Prozesssimulation in der Zerspanung,

Vulkan-Verlag, Dortmund

Glaeser, G., 1997, Efficient volume-generation during the

simulation of NC-milling, Proceedings of the

international workshop on visualization and

mathematics’97, pp 89-106 Springer, Heidelberg

Jerard, R., 1989, Approximate methods for simulation and

verification of numerically controlled machining

programs. Visual Computer 5, pp 329-348

Robert, L., 1987, Discrete simulation of NC machining,

Proceedings of the third Annual Symposium on

Computational Geometry, Ontario

Ayasse, J., 2001, Interactive manipulation of voxel

volumes with free-formed voxel tools, VM 2001,

Stuttgart

Stautner, M., 2005, Simulation und Optimierung der

mehrachsigen Fräsbearbeitung, Vulkan Verlag Essen.

CGTech [Online], 2013, http://cgtech.com

Meinecke, M., 2009, Prozessauslegung zum fünfachsigen

zirkularen Schruppfräsen von Titanlegierungen,

Aachen

Diehl A., 2011, Increasing Productivity with Engagement-

Generated Toolpaths, CNC Machining, Vol 14, Iss 47

Klocke F., 2011, Manufacturing Processes 1, Springer,

Berlin,

Ståhl, E., 2012, Metal Cutting. Theories and Models,

Elanders, Lund,

Stifter S., 1995, Simulation of NC Machining Based on

the Dexel Model: A Critical Analysis, Int. Journal for

Advanced Manufacturing Technology, Springer,

London

Ren, Y., 2008, Feature Conservation and Conversion of

Tri-dexel Volumetric Models to Polyhedral Surface

Models for Product Prototyping, Computer-Aided

Design and Application, CAD Solutions,

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

516