A Discrete Simulation Framework for Part Replenishment

Optimization

David Alfred Ostrowski

, Bradley Graham

and Oleg Gusikhin

Ford Resarch and Engineering, Ford Motor Company, Dearborn, U.S.A.

Ford Part Supplies and Logistics, Ford Motor Company, Dearborn, U.S.A.

Keywords: Supply Chain Optimization, Discrete Simulation.

Abstract: Supply Chains are difficult to plan as they involve complex relations and maintain dynamically changing

variables that influence them. In this paper, we present a discrete event simulation framework for purpose of

decision making in a replacement auto parts Supply Chain. Ford Motor’s Parts, Supply and Logistics

(PS&L) department supports a Supply Chain that represents a trade-off where parts are either maintained at

a central distribution facility or sent directly to local distribution center. This represents a compromise

between inventory transportation costs and accessibility in parts distribution. To support decisions within

this environment, we present a framework to characterize this scenario as a discrete simulation problem

allowing for the means to evaluate controls for the determination of optimal inventory (on-hand inventory

dollars), fill rate and labor costs. Our case study results demonstrate the necessary dynamics to support this

decision making process.

1 INTRODUCTION

To support a competitive advantage, Supply Chains

are continually faced with challenges of process

improvement to support adaptation to customer

demand. Effective Supply Chains are those designed

to deliver products and services in a reliable fashion

with low cost and high quality. Fluctuations in

demand and production change dynamically making

Supply Chains difficult to grasp (Shapiro and

Jeremy, 2001) (Sabri et al., 2000). One approach is

to develop Supply Chain models for analysing

operational, tactical and strategic decisions in order

to improve performance (Seppala and Holmstrom,

1997).

Supply Chain Management (SCM) can be

divided into two levels: strategic and operational

(Cooper et al., 1997) (Gunther and Meyr, 2009). The

primary objective of strategic optimization models is

to determine the most cost-effective location of

facilities (plants and distribution), flow of goods

throughout the Supply Chain and assignment of

customers to distribution centers. These types of

models do not seek to determine required inventory

levels and customer service levels. The main

purpose of optimization at the operational level is to

determine safety stock for each product at each

location, size and frequency of product batches that

are replenished or assemble, replenishment transport

and production lead times and the customer service

levels (Mentzer et al., 2001).

Uncertainty is one of the most challenging

problems in SCM making it difficult in the practical

analysis of performance (Mason-Jones and Towill,

1998) (Van der Vorst and Beulens, 2002). In the

absence of randomness, the problems of material

and product supply are eliminated. As a result, all

demands, production and transportation behaviour

would be completely resolved and therefore,

predictable. Our goal in this work is to support both

strategic and operational analysis to a Supply Chain

in light of uncertainty through the means of a

discrete simulation.

Ford Motor Parts, Supplies and Logistics

department (PS&L) maintains a Supply Chain

network that is responsible for the purchase and

distribution of Ford and Motorcraft branded service

parts for over 3000 Ford and Lincoln dealers. The

distribution network is referred to as Ford

Authorized Distribution (FAD) representing sales of

2.4B parts annually. To service dealers, Ford

Customer Service Division (FCSD) maintains 20

High Volume Distribution Centers (HVC) for high

volume parts.

467

Alfred Ostrowski D., Graham B. and Gusikhin O..

A Discrete Simulation Framework for Part Replenishment Optimization.

DOI: 10.5220/0004633004670473

In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),

pages 467-473

ISBN: 978-989-8565-69-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Among parameters to be considered in this

Supply Chain includes the categories of demand,

allocation and controls. Each of the given scenarios

are guided by the forecast of demand with the ability

to measure true demand to determine their

performance. Many business decisions are

considered around the dynamics of this Supply

Chain, including the appropriate intervals and levels

of replenishment. When these parameters are

changed, it is difficult to understand and analyze

how they can affect customer service levels (fill),

labor, inventory levels and total inventory over time.

Viewing the Supply Chain across the entire

production process, each component is

interconnected, by materials in one direction, the

flow of orders in the other and flow of information

in both. Changes in any one of these components

usually create waves of influence that propagate

through the Supply Chain. Such waves are reflected

in inventory levels.

This paper describes the construction of a

discrete simulation framework that allows for the

exploration of scenarios across a range of forecasts.

A simulation-based program is created using a

historical demand, forecast, and inventory plan to

determine a time series output representing

inventory, fill rate and labor. The eventual goal of

this framework is to support a complete system-level

optimization. In the next section, we present a

survey of related work. Section three continues with

the discussion of our proposed methodology. Section

Four presents our test cases demonstrating the

framework and Section Five presents our

conclusions.

2 CURRENT RESEARCH

Simulation is a well-known technique for

investigating line-dependent behaviors in complex

and uncertain systems (Cooper et al., 1997). This

allows a distinct advantage over static models as

they do not incorporate dynamic aspects of the

Supply Chain that are important for it to perform.

Discrete Event Simulations (DES) are effective

techniques in Supply Chain planning by enabling

evaluation of dynamic aspects as well as influence

of variance on Supply Chains, which can be used to

support decision making (Angerhofer and

Angelides, 2000), (Kleijnen, 2005). A number of

variations of DES have been leveraged to real world

problems. One example is (Hellström and Johnsson,

2002) who applied DES to simulate the effects of

wireless identification technology as applied to unit

loads throughout a retail Supply Chain without

disrupting the actual system being modelled

(Hellström and Johnsson, 2002). (Almeder et al.,

2009) demonstrated the utility of integrating discrete

event simulation and mixed-integer linear

programming into a general framework to support

operational decisions for Supply Chain networks

(Almeder et al., 2009). Based on initial simulation

runs, cost parameters, production and transportation

times were estimated for an optimization model.

This problem was applied iteratively until the

difference between subsequent solutions were

determined. (Lee et al.,) proposed an architecture of

combined discrete-event and continuous modeling

for supply chain, which included an equation of

continuous proportion in the supply chain, thus

demonstrating the effectiveness of a combined

approach (Lee et al., 2002).

(Sabri and Beamon, 2000) supported a multi-

objective Supply Chain model to use in

simultaneous and operational planning. They were

able to incorporate production, delivery and demand

uncertainty, thus providing a multi-objective

performance vector for the entire network (Sabri and

Beamon, 2000). (Chopra and Sodhi, 2004) identified

categories of risk within the Supply Chain including

effects that include how actions that mitigate one

risk and exacerbating others. Examples include

where low inventory levels decrease the impact of

over-forecasting demand, thus simultaneously

increasing the impact of a Supply Chain disruption

(Chopra and Sodhi, 2004). Additional examples

include genetic algorithms (Altiparmak et al., 2006),

fuzzy sets (Chen and Lee, 2004), pre-emptive goal

programming (Wang et al., 2004) visual interactive

goal programming (Karpak et al., 2001) as well as

hybrid models (Aburto and Weber, 2007)

(Sarjoughian et al., 2005).

Supply Chain simulations have also explored the

affect of information flows within the supply chain

and it’s effect on the dynamics. Among this area,

(Chen et al., 2000) identified demand forecasting

and order lead times as contributing to what was

determined as the bullwhip effect. By extending

their models to multiple-stage Supply Chains with

centralized customer demand information they were

able to demonstrate that the bullwhip effect can be

reduced, but not completely eliminated, by

centralizing demand information (Chen et al.,

2000.). (Lee and Hau, 2000) also quantified the

benefits of information sharing between a simple

two-level supply chain with non-stationary end

demands. Their results suggested that the value of

demand information sharing can be quite high,

SIMULTECH 2013 - 3rd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

468

especially when demands are significantly correlated

over time (Lee et al., 2000).

3 METHODOLOGY

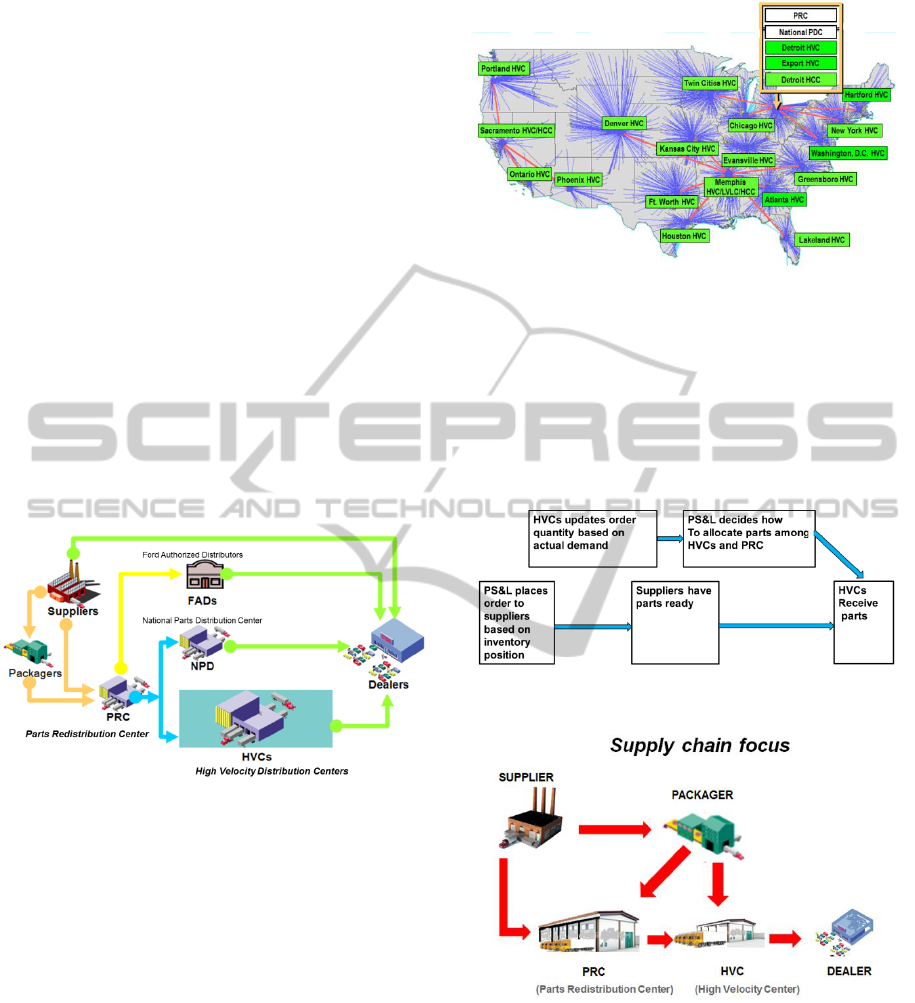
Figure 1 below details the paths in Ford PS&L’s

Supply Chain that are to be considered for our

framework. The starting points for all parts are at a

manufacturer. Each producer may either send a part

first to a packager or directly to the main

(centralized – PRC) facility. In case of emergencies,

a direct delivery may be performed, thus bypassing

the PRC or HVC locations and delivered directly to

a dealer. At the PRC, parts are either maintained in

inventory or sorted for the each of the HVCs. After

delivery to the respected centers, they are delivered

to dealers to satisfy the consumer demand.

Additional routes exist in this path including three

(low-volume) High Cube Centers (HCCs) for large

size parts as well as Ford Authorized Distributors

(retailers).

Figure 1: Overview of Supply Chain.

Figure 2. presents the main HVCs along with

associated paths for the continental US. Each dealer

has an associated sequence of HVC locations to

consider for each individual part. Also, in

conjunction with each part/dealer reference is a

described referral pattern that support the selection

process across the sequence allowing each dealer to

have a separate methodology of how to search for a

potential part through all 27 locations if necessary.

Figure 3. presents the order process along a time

line. The PS&L department maintains the inventory

positions in both the PRC and local HVCs. Order for

replenishment are executed at the PRC level and are

influenced by inventory positions as well as

forecasted demand. Suppliers have the parts ready

for the distribution network along a specified lead

time. During the lead time the HVC’s observe the

central demand and consequently updates the

Figure 2: HVC.

appropriate quantity. The PS&L department decides

how many parts to push to the HVCs and how many

parts to store at the PRC for future pull deployment.

Risk pooling is obtained by storing parts in the PRC

which is balanced with the extra cost of inventory,

storage and labor. The following figure 4. defines

the focus of our Supply chain framework

Figure 3: Order Process.

Figure 4: Supply Chain Focus.

3.1 Problem Definition

Optimization of our Supply Chain is assisted

through evaluation of past forecasts as well as

comparisons between alternative configurations. The

three primary parameters of interest in this case are

the fill rate (capability to meet demand), labor

(transportation costs) and inventory (storage costs).

A Discrete Simulation Framework for Part Replenishment Optimization

469

Two strategies exist in this problem identified as

either a “pull” or centralized inventory or a “push”

or decentralized inventory. A pull strategy may be

beneficial in scenarios in which a specific HVC

experiences a lower demand as compared to the

forecast during a suppliers production lead time. In

this case it may be beneficial to send less parts to the

HVC and store the remaining at the PRC (central

facility) The parts stored would then be able to

satisfy demand at any HVC in the future (due to the

effect of risk pooling). On the other hand if the

PS&L department decides to push parts to the HVC

regardless of the observed demand, the inventory

costs would be lower at the PRC while increasing

risk of possible redistribution costs. For the

description of our implemented framework, we first

consider the initial terms:

ltd = Lead Time Demand

fr = Fill Rate

l = Labor

OH = On-Hand Inventory

I = In-transition Inventory

T = Total Inventory

Where lead time demand is calculated as the

estimated (forecasted) demand (as a function of lead

time between the PRC to corresponding HVCs). Fill

Rate represents the ratio of backorder to demand and

is calculated as (1 – b/d). Labor is expressed as a

unit of cost of transportation from between all noted

locations. In-transition inventory is designed as the

future expected inventory of a location and T as the

total (onHand and InTransition).

3.2 Part Ordering Policy

PS&L applies a variation of the Standard Economic

Ordering Model (EOQ) for inventory level

maintenance at each local HVC. At the end of each

period, the manager checks the inventory level

(inventory on hand plus inventory in transition) for

each part in each building (HVC). If the level is

lower than a predetermined amount (SS plus one

month forecast demand) the manager will place an

order with a predetermined amount for that part.

Within the HVC all orders are aggregated from

which they are counted against the current

inventory. Orders are also influenced by external

factors including production lot size and quantity

discount. Following is a breakdown of the formulas

that are to be applied in the context of each DRP day

of operation:

tgd = total gross demand (forecast)

tgr = total gross receipt

ps = projected stock

rnd = rounded net demand (constrained)

und = unrounded net demand (adapted)

t = time

ps = 



+ tgd + rnd

Considering the following condensed spreadsheets

as an example, each day at an HVC location must

consider updated inventory positions and weight

them against the necessary forecasts. After the

dealer demand has been satisfied, updated inventory

will serve as a starting point as net demand

calculation will be utilized to influence the

allocation tiers as described in the following section.

Figure 5: PRC, HVC daily deployment.

3.3 Supplier Order

Supplier order is considered at the end of every

inventory calculation at the PRC. An order to a

supplier will only occur after a set ‘freeze period’

determined as the interval by which orders may be

made to a supplier. A potential order to a supplier is

determined as the supplier shortage amount, total

gross demand of the PRC inventory, total supplier

EOQ demand subtracted by projected stock and total

gross demand

Net demand is calculated as:

min(0, D

+ Inv

i-1

–ss

+ R

)

The shipping quantity is an Economic order

quantity, calculated as:

EOQ



, where

K – order cost



- forecasted annual volume for part I

SIMULTECH 2013 - 3rd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

470

– cost of part i

I – annual interest rate (19-21%)

The safety stock is calculated based on the service

type II model.



standard deviation of demand is

equal to 1.25 multiplied by the MAD that is the

difference between the actual and the forecasted

demand. From EOQ, fill rate, and standard deviation

of the demand over the lead time L we find:

L(z) =





)1( EOQ

Then we find z, and calculate safety stock as: ss = z



3.4 Part Replenishment Policy

When parts have been received at the PRC, there are

four separate tiers of allocation that are applied. The

following sequence is followed: 1) residual

backorders, 2) regular demand 3) safety stock 4)

sum of net demand. Backorders are calculated as

previous projected stock subtracted by current total

gross demand. This is the highest level of priority as

it indicates a shortage in inventory. The LeadTime is

determined as the amount of projected demand that

is accumulated over the associated Lead Time days.

Safety Stock coverage calculated from historical

safety stock evaluations. The EOQ formula is

identified as the sum of the rounded net demand for

the next end of order quantity data. Each of these

levels are calculated on the HVC independent of the

events then an incremental building level is

designated by eliminating both the higher priority

tiers as well as current inventory (physical) position.

The value is then rounded and added among the

other tiers, to determine an upper limit for the tiers.

For extra inventory considered between the tiers of

allocation, the following calculations are applied to

allow for ameans of proportionate allocation.

Identified as the fairshare algorithm each HVC will

receive allocations based on the following

calculations:

4 SIMULATION

Our simulation considers each part independently

within our reduced configuration (supplier,

packager, PRC, MVC, dealer). This process is

detailed in eight steps as presented in the following

diagram. The system considering a single part along

with a standing inventory begins with step one in

which the HVC receives an order that has been

ordered in the past. In step two, considering the

future (forecasted) demand, an HVC will place an

order. In step three, the business day then begins in

which customers arrive and HVCs in turn satisfy a

given demand. In step four if the given demand is

short of the current inventory, an HVC will place it

on backorder. Following in step five, the PRC

aggregates orders for the HVCs then places them as

a single order to a supplier. At step six, Parts are

then ready at the suppliers at t + SUPLT (supplier

lead time). Next, in step seven the PRC’s will

allocate parts according to five separate tiers of

allocation. Finally (step eight) the day ends (where

each process begins as parts ordered arrive and then

are ready to be considered against next business day)

Figure 6: Simulation Timeline pt1.

Figure 7: Simulation Timeline pt2.

The overall simulation process description is

A Discrete Simulation Framework for Part Replenishment Optimization

471

presented in Figure 7. Four major points are

illustrated in the flow of inventory stating with the

beginning stock (1), continuing with the net demand

determining the planned amount to sell (2). Next the

supplier order is presented (3) from which the day is

wrapped up with the consideration of exactly what

amount sold (4).

5 CASE STUDY

We examine the application of our model to support

the characterization of a Supply Chain. We examine

a single part AA5Z16138A towards these attributes.

Part AA5Z16138A maintains service to five separate

HVC centers in which each are characterized along a

historical demand for the business days between

June-4-2012 to Aug-4-2012 for each simulation run.

Considering an individual simulation, the in-transit

and total inventory levels and corresponding fill

rates are presented as a function of the established

lead times and EOQ (figure 8). Following, we

Figure 8: Simulation Overview.

Figure 9: PRC time series inventory, FL for EOQ = 3.

examine a characterization of the effect of lead time

on service levels. This is characterized along a 60

day month interval (figure 9). As noted in the

following diagram the same scenario was explored

across ranges of Economic Order Quantity (EOQ) in

which all other variables were fixed (figure 10). In

our part description – there was an issue with

regards to the demand forecast producing an

overcapacity – the demand was lowered to one part

per HVC in order to produce this effect.

Figure 10: PRC Inventory Time Series and Fill Rate

(EOQ= 6).

6 CONCLUSIONS

We have presented a framework so support a

discrete event simulation for part replenishment

optimization. Our framework considers the

interaction between a centralized facility and local

distribution centers for a parts distribution Supply

Chain. Our simulation accounts for forecast-driven

allocations to be evaluated within set configurations

including specified order intervals and lead time

demands. Supplier Orders are modelled after an

EOQ model and service replenishments are driven

by a proprietary algorithm to allow for a

proportional replenishment. Considering our

framework with an individual part, we can generate

the effects of Lead Time and EOQ over a specified

range and determine associated fill rates which may

be compared against corresponding labor and

inventory costs for a means of comparison. Future

work includes the scaling of parts evaluations as

well as incorporation of optimization methods into

this framework.

SIMULTECH 2013 - 3rd International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

472

REFERENCES

Shapiro, Jeremy F. 2001. Modeling the supply chain. Vol.

971. Pacific Grove, CA: Duxbury

Sabri, Ehap H., and Benita M. Beamon. 2000. "A multi

objective approach to simultaneous strategic and

operational planning in supply chain design." Omega

28.5: 581-598.

Seppala, U, Holmstrom, J. 1997. “Rough modelling of

logistics networks”, Integrated Manufacturing

Systems, vol 6. No . 5, pp 13-20,1995

Cooper, Martha C., Douglas M. Lambert, and Janus D.

Pagh. 1997. "Supply chain management: more than a

new name for logistics." International Journal of

Logistics Management, The 8, no. 1: 1-14.

H. O. Gunther, H. Meyr. 2009. Supply Chain Planning ,

Springer-Verlag Berlin Heideberb

Mentzer, John T., William DeWitt, James S. Keebler,

Soonhong Min, Nancy W. Nix, Carlo D. Smith, and

Zach G. Zacharia. 2001."Defining supply chain

management." Journal of Business logistics 22, no. 2:

1-25.

Mason-Jones, Rachel, and Denis R. Towill. 1998.

"Shrinking the supply chain uncertainty circle." IOM

Control 24.7: 17-22.

Van der Vorst, Jack GAJ, and Adrie JM Beulens. 2002.

"Identifying sources of uncertainty to generate supply

chain redesign strategies." International Journal of

Physical Distribution & Logistics Management 32, no.

6: 409-430

Angerhofer, Bernhard J., and Marios C. Angelides. 2000.

"System dynamics modelling in supply chain

management: research review." In Simulation

Conference, 2000. Proceedings. Winter, vol. 1, pp.

342-351. IEEE

Kleijnen, Jack PC. 2005."Supply chain simulation tools

and techniques: a survey."International Journal of

Simulation and Process Modelling 1, no. 1: 82-89.

Hellström, D., and M. Johnsson. 2002. "Using discrete-

event simulation in supply chain planning." 14th

Annual Conference for Nordic Researchers in

Logistics.

Almeder, Christian, Margaretha Preusser, and Richard F.

Hartl. 2009. "Simulation and optimization of supply

chains: alternative or complementary

approaches?."Supply Chain Planning. Springer Berlin

Heidelberg, 1-25.

Lee, Young Hae, et al. 2002. "Supply chain simulation

with discrete–continuous combined

modeling." Computers & Industrial Engineering 43.1:

375-392.

Sabri, Ehap H., and Benita M. Beamon. 2000. "A multi-

objective approach to simultaneous strategic and

operational planning in supply chain

design."Omega 28.5: 581-598.

Chopra, Sunil, and ManMohan S. Sodhi. 2004. "Supply-

chain breakdown." MIT Sloan management review

(2004).

Altiparmak, Fulya, Mitsuo Gen, Lin Lin, and Turan

Paksoy. 2006. "A genetic algorithm approach for

multi-objective optimization of supply chain

networks."Computers & Industrial Engineering 51,

no. 1: 196-215.

Chen, Cheng-Liang, and Wen-Cheng Lee. 2004. "Multi-

objective optimization of multi-echelon supply chain

networks with uncertain product demands and

prices."Computers & Chemical Engineering 28, no. 6 :

1131-1144.

Wang, Ge, Samuel H. Huang, and John P. Dismukes.

2004. "Product-driven supply chain selection using

integrated multi-criteria decision-making

methodology."International journal of production

economics 91, no. 1 (2004): 1-15.

Karpak, Birsen, Erdoğan Kumcu, and Rammohan R.

Kasuganti. 2001. "Purchasing materials in the supply

chain: managing a multi-objective task." European

Journal of Purchasing & Supply Management 7, no. 3:

209-216.

Aburto, Luis, and Richard Weber. 2007. "Improved supply

chain management based on hybrid demand forecasts."

Applied Soft Computing 7, no. 1: 136-144.

Sarjoughian, Hessam S., Dongping Huang, Gary W.

Godding, Karl G. Kempf, Wenlin Wang, Daniel E.

Rivera, and Hans D. Mittelmann. 2005. "Hybrid

discrete event simulation with model predictive

control for semiconductor supply-chain

manufacturing." In Proceedings of the 37th conference

on Winter simulation, pp. 256-266. Winter Simulation

Conference

Chen, Frank, et al. 2000. "Quantifying the bullwhip effect

in a simple supply chain: The impact of forecasting,

lead times, and information." Management

science46.3 (2000): 436-443.

Lee, Hau L., Kut C. So, and Christopher S. Tang. "The

value of information sharing in a two-level supply

chain." Management science 46, no. 5 (2000): 626-643

A Discrete Simulation Framework for Part Replenishment Optimization

473