
An Investigation on the Simulation Horizon Requirement for Agent
based Models Estimation by the Method of Simulated Moments
Ricardo Giglio
Department of Ecomomics, University of Kiel, Kiel, Germany
Keywords: Agent based Models, Method of Simulated Moments, Simulation Horizon, Inactive Traders.
Abstract: The accurate estimation of Agent Based Models (ABM) by the method of simulated moments is possibly
affected by the simulation horizon one allows the model to run due to sample variability. This work presents
an investigation on the effects of this kind of variability on the distribution of the values of the objective
function subject to optimization. It is intended to shown that, if the simulation horizon is not sufficiently
large, the resulting distribution may present frequent extreme points, which can lead to inaccurate results
when one tries to compare different models. For doing so, a model contest is carried out using different
simulation horizons to assess the difference in goodness of fit when inactive traders are introduced in one of
the Structural Stochastic Volatility models proposed by Franke (2009).
1 STAGE OF THE RESEARCH
This is the report of an on-going investigation.
Although some experiments have been already
performed, and the necessary computational infra-
structure is built, the project still lacks important
methodological improvements, especially with
regard to model comparison.
2 OUTLINE OF OBJECTIVES
The accurate estimation of Agent Based Models
(ABM) by the method of simulated moments is
possibly affected by the simulation horizon one
allows the model to run due to sample variability.
The main objective is to investigate the effects of
this kind of variability on the distribution of the
values of the objective function subject to
optimization.
A second objective concerns the improvements
in goodness of fit brought by the inclusion of
inactive traders in one of the Structural Stochastic
Volatility models proposed by Franke (2009).
3 RESEARCH PROBLEM
As a working hypothesis, the following statement is
considered: if the simulation horizon is not
sufficiently large, the resulting distribution may
present frequent extreme points, which can lead to
inaccurate results when one tries to compare
different models.
In an attempt to answer to this quesiton, a model
contest is carried out using different simulation
horizons to assess the difference in goodness of fit
when inactive traders are introduced in one of the
Structural Stochastic Volatility models proposed by
Franke (2009).
4 STATE OF THE ART
The objective of this introduction is to briefly
overview Agent Based Model (ABM) methodology,
which is claimed to take into account the so-called
stylized facts to a great extent, and, thus, could be
viewed as an alternative to the Efficient Market
Hypothesis theoretical background (Lux, 2008).
In doing so, selected recent empirical findings
are highlighted, and a brief taxonomy for ABMs is
presented. Then, three specific ABMs are discussed
in greater detail while focusing on their ability to
explain some of the stylized facts.
The second section deals explicitly with the
estimation of ABMs by the method of simulated
moments, focusing on practical concerns one has to
20
Giglio R. (2013).
An Investigation on the Simulation Horizon Requirement for Agent based Models Estimation by the Method of Simulated Moments.
In Doctoral Consortium, pages 20-28
DOI: 10.5220/0004637600200028
Copyright
c
SciTePress

deal with when using derivative-free methods (in
particular, the Nelder-Mead Simplex Algorithm).
Finally, the last section presents an investigation on
the simulation horizon requirements by means of an
example of model contest assessing the difference in
goodness of fit of allowing inactive traders in one of
the Structural Stochastic Volatility models proposed
by Franke (2009).
4.1 Stylized Facts
Apart from the theoretical critiques developed by
Grossman et al. (1980), the Efficient Market
Hypothesis (EMH) seems to be misaligned with
some empirical features of financial markets. This
debate is presented by Lux (2008) by portraying
how various lines of research refer to these empirical
findings, each in its own different way. On the EMH
side, these findings were referred to as anomalies,
that is, there should be at least a few strange
empirical results in disagreement with the
established theoretical foundation. On the other
hand, recent studies have referred to these empirical
results as stylized facts, meaning that they can be
found quite regularly in financial markets and, thus,
they deserve proper theoretical explanation.
An extensive list of these stylized facts is
presented by Chen (2008) concerning several data
natures (such as returns and trading volume) and
frequencies (ranging from tick-by-tick order book
data to annual seasonality). Here, attention is only
focused on some of those data concerning daily
price returns, namely the absence of autocorrelation
in raw returns, fat tails of absolute returns, and
volatility clustering.
The absence of autocorrelation in raw returns has
never been referred to as an anomaly, because it is
an empirical finding in total agreement with the
EMH theoretical background. It is related to the
martingale property (Mandelbrot, 1966), which
states that markets behave similar to a random walk.
According to Lux (2008), this is the EMH’s most
important empirical finding, but the author also
points that a lot of attention was paid to it, thus
neglecting in consequence other relevant stylized
facts.
With regard to the tails of returns distributions, it
is expected by the EMH that they would behave
normally due to the arrival of purely random
information. However, even old empirical findings
(Mandelbrot, 1966) suggested that the normal
distribution is not well suited to financial returns,
because it has probability mass more concentrated
on its mean and extreme values than is expected in a
normally distributed process.
Since it is seen that kurtosis is not well suited for
evaluating such a statistical property, it is then
common to deal with the Hill estimator of tail index
α, calculated as follows: first, absolute daily returns
are sorted in a descending order so that a threshold
value which defines a tail
can be calculated as the
correspondent first (usually 5) returns, and
is defined as the number of returns labeled as
belonging to the tail. Finally, the Hill estimator is
given by the equation 1.
∑
ln
ln
(1)
Finally, volatility clustering deals with the fact that
directions of returns are hard to predict, but not their
magnitude. There seem to exist alternate moments of
financial fury and relaxation, printing clusters of
high and low volatility on empirical data that are not
at all accounted for by the EMH background. As
pointed out by Lux (2008), even though a great deal
of research on econometrics is focused on modelling
this fact (the ARCH methodology), very little
research has been done to explain it.
4.2 Taxonomy
According to an extensive survey conducted on the
topic dealt with by Chen (2008), during the 1990s,
the first attempts were made to explain some
observed regularities in financial data by means of
ABM. The main concern of these early works was to
artificially reproduce some of the so-called stylized
facts observed in real financial data. Hence, the
objective of the authors just mentioned was to
simulate and calibrate parameters of an artificial
financial market by ABM, and then apply standard
econometric techniques to evaluate how much of the
stylized facts (both quantitatively and qualitatively)
could be reproduced by their artificial generated
data.
Even though these early works share the goal of
matching stylized facts, their ABM formulations
may vary dramatically. For this reason, a taxonomy
was developed by Chen (2008) in an attempt to
classify recent work on ABM with regard to specific
aspects, namely agent heterogeneity, learning, and
interactions.
With regard to heterogeneity, agents can
basically be divided into two groups: N-types and
autonomous agents. In the former, all possible types
of behaviour are pre-defined in some sense by the
designer; whereas in the latter, new strategies (that
is, agent types) can emerge autonomously. We can
AnInvestigationontheSimulationHorizonRequirementforAgentbasedModelsEstimationbytheMethodofSimulated
Moments
21

consider the model by Lux et al. (1999) as an
example of N-type design, in which agents can be
fundamentalists (that is, their demands respond
proportionally to the current deviation from
fundamental price) or chartists (who try to
extrapolate the last trend observed).
Chartists’ strategy is also determined by a
sentiment index (pessimism or optimism) which
determines whether chartists believe that the last
trend observed will be maintained or reversed. On
the other hand, we can consider the Santa Fe
Artificial Stock Market (Arthur et al., 1997) as an
example of autonomous agent design. In this
context, agents are allowed to autonomously search
for profitable strategies that were usually not pre-
defined by the designer by means of genetic search
algorithms.
With regard to learning, Lux (2008) points out to
a branch of literature called Adaptive Belief Systems
(ABS), which, unlike some of the other less flexible
models, allows agents to dynamically switch
between different strategies. With regard to the N-
type models, this feature is most commonly
introduced by means of two approaches, namely
transition probabilities and discrete choice.
Following the transition probability approach, a
majority index is defined as representing how much
one group dominates (or is dominated by) the other.
Each agent switches from one group to the other
according to time-varying transition probabilities
,
and
,
, which are functions of the current
state of the system, which is generally defined here
as
. According to Franke et al. (2009), it can be
demonstrated under some assumptions, that at the
macroscopic level, population shares are depicted by
and
1
whereas the transition probabilities are
given by
1,
, and
1,
can be viewed as a
flexibility parameter.
On the other hand, there is the discrete-choice
approach proposed by Brock et al. (1998), in which
the adjustment happens directly on the population
shares (and not on its rate of change) according to
the following equation
,
,
(2)
where is the intensity of choice, and the state of
the system is allowed to be different for each group.
The way the state of the system influences agent
choice significantly varies in literature. As
examples, one can consider the specification of a
herding
or a misalignment
component
∗
where
∗
is the
fundamental price. This will be pursued in greater
detail in the next section.
Finally, the way agents interact defines the
structure of the artificial financial market and its
price determination. When considering N-type
models, it is common to sum up demand of both
groups and to assume a market maker who holds a
sufficiently large inventory to supply any excess of
demand and to absorb any excess of supply. Then,
this market maker adjusts the price in the next period
to reflect this excess demand or supply. However, as
stated by LeBaron (2006), this is not a very realistic
assumption in the way that no actual market clearing
is taking place. In addition, a true market clearing
mechanism would be easier to be implemented in an
autonomous agent design by means of direct
numerical cleaning.
5 METHODOLOGY
In the remaining part of the section, two specific
agent-based models are described in greater detail,
namely the trading inactivity model proposed by
Westerhoff (2008) and the structural stochastic
volatility model proposed by Franke et al. (2009).
The idea is to present some practical issues
concerning the development of an agent-based
model, and also to introduce the task of estimating
its parameters that is the objective of the next
section.
5.1 Trading Inactivity Model
In an attempt to use simple agent based models to
illustrate the potential effects of regulatory policies
on financial markets, Westerhoff (2008) introduces a
modification on the chartists-fundamentalists
traditional scheme by allowing agents also to be
absent from markets, that is, they can be inactive.
This innovation may imprint models with more
reality and also is important for using agent based
models in the analyses of regulatory and taxing
policies. This section outlines this model by
focusing on this new device of trading inactivity and
also on the model’s power to reproduce some of the
stylized facts.
As it is common practice, the demands of
chartists and fundamentalists are respectively given
by
SIMULTECH2013-DoctoralConsortium
22

(3a)
(3b)
where stands for demand, the superscripts and
represents chartists and fundamentalists respectively,
is the time unit, is the log of price, is the log
of fundamental price, and are positive reaction
parameters for chartists and fundamentalists
respectively, and are I.I.D. random normal
process with zero mean and
and
are standard
deviations that capture intra-group heterogeneity
respectively for chartists and fundamentalists.
In this context, price formation is given by the
following price impact function
(4)
where denote population shares, is a positive
price adjustment coefficient and is an I.I.D.
random normal process with zero mean and standard
deviation
.
The determination of , that is, the choice
between the three available strategies, depends on
past performance and is given by the following
equations in the spirit of the discrete choice
approach:
(5a)
(5b)
0
(5c)
where the superscript stands for inactivity,
denotes each strategy attractiveness and is composed
by the sum a short run capital gain term and an
accumulated profits term which is weighted by the
memory parameter . is a percentage tax
applied both when buying and selling the asset.
Finally, defining as the so called intensity of
choice, population shares are represented by
1
(6a)
1
(6b)
1
1
(6c)
Even though the author does not carry on a
systematic estimation procedure, a set of benchmark
input parameters are presented and thus the
calibrated model is claimed to reproduce some of the
stylized facts (mainly volatility clustering and fat
tails) when no is applied. Figure 1 presents a
single simulation of the model with the following set
of input parameters presented by the author (1,
0.04, 0.04, 0.975, 300,
0.01,
0.05, and
0.01).
5.2 Structural Stochastic Volatility
Model
With regard to agent design, this is a two-group
model where agents can be fundamentalists or
chartists. The main difference is that fundamentalists
respond to deviations from fundamental price, and
chartists extrapolate the returns they just observed in
the previous period. Thus, their demand functions
,
are given by
Figure 1: Upper panel shows the log of price, middle panel
its percentage returns, and lower panel the shares of
fundamentalists (gray), chartists (black) and inactive
(white) traders.
∗
~0,
, 0
(7a)
~
0,
,0
(7b)
where the superscripts and denote agent
affiliation (fundamentalists and chartists,
respectively); the subscript represents time unit;
is the log of the price;
∗
is the log of the (fixed)
fundamental price;
,
are group-specific random
terms (with zero mean and
,
standard deviations)
that account for intra-group heterogeneity;
corresponds to the responsiveness of the
fundamentalists to the deviation from fundamental
price; and corresponds to the responsiveness of the
chartists to the last trend observed.
However, this model also accounts for learning,
in the sense that agents can dynamically change their
minds and move to the other group. Therefore, the
AnInvestigationontheSimulationHorizonRequirementforAgentbasedModelsEstimationbytheMethodofSimulated
Moments
23
shares of each group in the total population are
allowed to vary over time. Considering that
,
denotes their respective population shares, total
excess demand can be written as
. Seen
that this equation may not balance, a market maker
is assumed to hold a sufficiently large inventory for
supplying any excess of demand and for absorbing
any excess of supply. This is done by adjusting the
price in the next period by a fixed coefficient that is
inversely related to market liquidity. Considering
these specifications, price determination at each time
unit is given by
∗
(8)
where
~
0,
,
(9)
summarizes what the authors coined as Stochastic
Structural Volatility (SSV), and can be viewed as a
structural modelling approach to time-varying
variance.
What remains to be explained is the learning
mechanism that yields the dynamics of the
population shares. Even though the authors
presented two different technical approaches for this,
namely transition probabilities and discrete choice,
only the latter will be considered here, given its best
performance in a comparative study conducted by
the same authors Franke et al. (2011). It is worth
beginning with the definition of a switching index
, which attempts to measure the relative
attractiveness of the fundamentalist’s strategy in
comparison to that of the chartist, given by
∗
(10)
where
is a predisposition parameter to switch to
fundamentalism;
captures the idea of herding
behaviour; and
can be understood as a measure
of the influence of price misalignment (that is, the
larger the gap, the higher the attractiveness of
switching to fundamentalism). Thus, in the spirit of
the discrete-choice approach, the shares of the total
population in each group can be written as
11
⁄
and
1
where is the
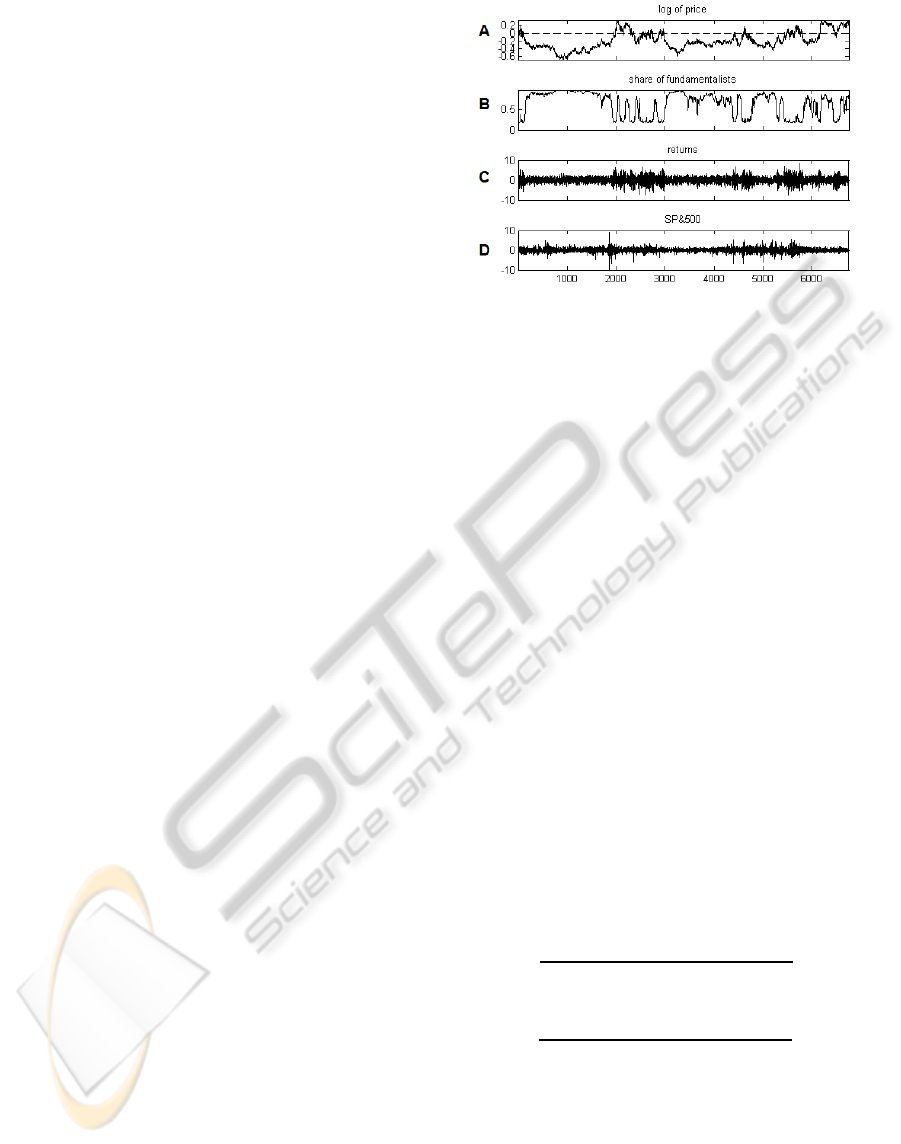
intensity of choice. Figure 2 compares outputs from
a single run of the model with returns of S&P500 as
a benchmark.
Figure 2: 6750 observations of (A) log of price, (B)
share of fundamentalists, and (C) returns from a simple
run of the model and (D) daily returns from S&P500 from
January 1980 to March 2007. Inputs to the model are as
follows: 0.0728, 0.0896, 0.01,
0.327,
1.815,
9.6511,
1.0557,
2.9526,
∗
0, and 1.
5.3 Introducing Inactivity to SSV
Models
This section described the exact same model from
last section, but augmented to allow agents to be
absent (inactive) from the market. Hence, it is now a
three-group model (fundamentalists, chartists, and
inactive), with demand functions
,,
given by
∗
(11a)
(11b)
0
(11c)
where the subscript denotes the inactive group, and
all the other variables remain the same from
equation 7. Another modification required from the
two-group model described in the last section
concerns the shares of the total population in each of
the three group, which is now described as
1
1
(12a)
1
1
(12b)
1
(12c)
5.4 Estimation
In this section, the Method of Simulated Moments is
applied to the model (SSV augmented with inactive
traders) just described. In order to follow this
SIMULTECH2013-DoctoralConsortium
24

method of estimation, one has to first select the
moments of interest. Following the approach
developed by the authors just mentioned (Franke and
Westerhoff, 2011), only four stylized facts that have
received more attention in the literature are
considered here, namely the absence of
autocorrelation in raw returns, fat tails of returns
distribution, volatility clustering, and long memory.
Therefore, it is argued that the following set of nine
moments is enough to account for these four stylized
facts, namely the Hill estimator of tail index of
absolute returns , mean of the absolute returns
̅, first-order autocorrelation of the raw returns
, and six different lags from the
autocorrelation function of the absolute returns
,
,
,
,
,
and
. Each single run of the model will then
be compared with a specific empirical data set with
regard to this vector of selected moments.
The distance between the moments vector
generated by a single run of the model (with set of
inputs , sample size , and random seed ) and the
vector of empirical moments
is defined by a
weighted quadratic loss function in the following
form
,,
,,
,,
(13)
where is a weighting matrix that intends to
capture both correlation between individual
moments and sampling variability.
Among several options for choosing a proper
weighting matrix , here the inverse of the
estimated variance-covariance matrix of the
moments Σ
is used. In order to estimate such a
matrix, the following bootstrapping method was
applied. For the two first moments ( and ̅),
10
random resamples with replacement were
constructed from the original series, and the
respective moments were calculated. However, since
the other moments deal with autocorrelations, such a
procedure would be inadequate due to the
destruction of long-term dependencies by the
sampling procedure. Therefore, for these moments,
an index-bootstrapping method was used by
randomly selecting (with replacement) set of time
indexes
,
,…,
from indexes and then
calculating the correlation coefficient regarding time
lag as
1/
∑
̅
̅
∈
where ̅ is the mean value of
over , and
̅ if 0.
Considering
as the vector of moments of
each of these bootstrapped resamples and as the
vector of their moment specific means, the variance-
covariance matrix was, thus, estimated as Σ
∶ 1/
∑
.
5.4.1 Avoiding Local Minima
Finally, the minimization problem
,,
min
! was performed by the Nelder-Mead simplex
algorithm to estimate the set of parameters that
minimizes the loss function . Here, only seven
parameters were allowed to vary, namely , ,
,
,
,
, and where the remaining were fixed at
0.01,
0.327, and 1. Starting from
an initial set of parameters
, the algorithm returns
an estimated set of parameters and a value for the
objective function . To avoid getting trapped in a
local minima, this obtained set of estimated
parameters was re-introduced in the algorithm
here as the initial set of parameters (that is,
),
and this procedure was carried out as many times it
was necessary until no improvement higher than
0.001 was achieved in the objective function.
5.4.2 Experiment on Simulation Horizon
Requirements
In order to reduce sample variability, Franke et al.
(2011) points that a model simulation horizon ten
times bigger than the empirical size (that is,
10) was considered sufficient for their model
comparison purposes. The main objective of this
study is to assess how such results change when one
increases simulation horizon beyond this value. For
doing so, first it will be described in more detail how
a model specific p-value is calculated by means of
Monte Carlos runs, and then the comparison of these
p-values calculated using both 10 and
100 will be presented.
5.4.2.1 Definition of a Model Specific
P-value
Apart from providing the variance-covariance
matrix, the bootstrap procedure of empirical data
described in the previous section can also be used to
assess the fit of different model simulations to real
data. This idea, presented by Franke et al. (2011),
consists of calculating the value of the objective
function for each of the vector of moments
obtained by bootstrapping empirical data 5000
times, and then finding a critical value
which
represents the 95% quantile of the distribution of the
AnInvestigationontheSimulationHorizonRequirementforAgentbasedModelsEstimationbytheMethodofSimulated
Moments
25

objective function values. This critical value was
found to be
.
17.228. In this sense, if a
simulation run from a given model presents a value
of the objective function higher than
.
, this run
cannot be said to have a good fit to empirical data.
Finally, the p-value of a model is given by the
proportion of Monte Carlo runs which lies below
this critical value. Figure 3 presents the distribution
of objective function values obtained by
bootstrapping empirical data, and its correspondent
critical value.
5.4.3 Model Fit for Different Simulation
Horizons
To begin with, table 1 shows, for a given random
seed, and considering the simulation horizon of
10, the set optimal parameters obtained by a
single run of the model, and their correspondent
value of .
Table 2 shows the moments obtained with this
optimized set of parameters in this specific run of
the model, and compares them with the empirical
moments for S&P500 and their bootstrapped
statistics. It can be seen that, at least with regard to
this specific random seed, the moments obtained
with the optimal set of inputs rely inside the bands
provided by bootstrapping empirical data.
Figure 3: Distribution of objective function values
obtained by bootstrapping empirical data, and its
correspondent critical value.
Table 1: Estimated parameters for a given random seed,
considering a simulation horizon of 10.
11.744 0.914 2.077 0.992 0.89 1.359 2.049 0.548
In order to check whether these results depend on
the given pseudo-random number sequence, a
similar estimation procedure to the one just
described was carried on while considering 1,000
Table 2: Moments obtained with optimized parameters for
10, the empirical moments for S&P500 and their
bootstrapped bound values.
run 2.5% mean 97.5%
3.448 3.155 3.484 3.891
̅
0.706 0.690 0.706 0.723
0.006 -0.018 0.006 0.030
0.154 0.128 0.154 0.182
0.184 0.163 0.184 0.205
0.166 0.148 0.166 0.185
0.142 0.125 0.143 0.161
0.126 0.107 0.126 0.147
0.089 0.075 0.090 0.106
different random seeds. Table 3 summarizes this
Monte Carlo experiment by presenting the average
and 5% bounds for the obtained optimized
parameters and values of the objective function .
The p-value for this model and simulation horizon,
calculated as described previously, is 0.290.
Table 3: Mean and bound values for parameters estimated
for 1,000 different random seeds, considering a simulation
horizon of 10.
6.210 0.750 1.759 0.988 0.711 1.212 1.885 0.491
18.833 0.948 1.962 0.993 0.964 1.328 2.075 0.538
62.944 1.160 2.184 0.998 1.098 1.538 2.178 0.597
Similarly, table 4 presents the same statistics as table
3, but now considering a longer simulation horizon
of 100. It can be seen that, although there is a
larger variability for some of the estimated
parameters, the resulting distribution of the values of
the objective function presents much less extreme
values. Figure 4 depicts this result, by showing the
distribution of both for a simulation horizon of
10 (solid) and of 100 (dashed). The
obtained p-value for the longer case is 0.021, which
is significantly smaller than for the shorter.
Table 4: Mean and bound values for parameters estimated
for 1,000 different random seeds, considering a simulation
horizon of 100.
7.595 0.597 1.559 0.990 0.669 1.116 1.871 0.474
10.702 0.961 1.952 0.991 0.928 1.379 2.030 0.546
16.268 1.301 2.217 0.992 1.184 1.642 2.218 0.609
5.4.4 Assessing the Introduction of Inactive
Traders
It was shown in the last section that a great extent of
the inability of the model to reproduce the stylized
facts (that is, large values o ) was in fact a sort of
SIMULTECH2013-DoctoralConsortium
26

noise introduced by a not sufficiently large
simulation horizon. Then, the present section
introduces a p-value based model contest, as
proposed by Franke et al. (2011), in order to check
whether the introduction of inactive traders improve
or not the goodness of fit of this class of models to
empirical data.
Table 5 presents two versions of a model contest,
one for each simulation horizon 10 and
100. It can be seen that the introduction of
inactive traders improve the goodness of fit in both
versions. Figure 5 depicts this result, by showing the
distribution of for each pair model-horizon.
Although a significant reduction sample variability
is obtained by using larger simulation horizons, it
can be seen that the central tendencies of each
distribution of do not change widely in respect to
.
Figure 4: Comparison of the distributions of objective
function values for simulation horizons of 10 and
100.
Table 5: Model contest to asses the improvement in
goodness of fit when allowing inactive traders in SSV
models using different simulation horizons.
p-value
DCA
10
2.5% 10.175
0.349
mean 16.451
97.5% 27.151
DCA
100
2.5% 13.362
0.051
mean 15.518
97.5% 17.530
DCA-I
10
2.5% 6.210
0.290
mean 18.833
97.5% 62.944
DCA-I
100
2.5% 7.595
0.021
mean 10.702
97.5% 16.268
6 EXPECTED OUTCOME
There are two main expected outcomes from the
PhD thesis. First, and most important, is to shed
light on the simulation horizon requirements one
allows a model to run when performing estimations
by the method of simulated moments.
The current stage of the research has already
shown that a great deal of sample variability can be
avoided by longer simulation horizons, but it is still
an open question whether this implies major
problems when performing estimations.
Figure 5: Comparison of the distributions of objective
function values for simulation horizons of 10 and
100, and for inclusion/exclusion of inactive traders.
A second expected outcome is the definition of a
model contest procedure able to determine goodness
of fit of different models, hence allowing one to
compare models and decide for the best performing
one. In addition to this second objective, it is also an
expected outcome to assess the improvement in
goodness of fit when allowing inactive traders in one
of the Structural Stochastic Volatility models
proposed by Franke (2009).
7 CONCLUSIONS
From the current stage of the research, two initial
conclusions can be drawn. First, the introduction of
inactive traders in the Structural Stochastic
Volatility (SSV) model proposed by Franke (2009)
yields better goodness of fit when compared to the
standard two agent types model, as pointed by the
smaller values of the objective function shown in
figure 5. By allowing agents to be inactive for some
periods of time, the model gains a more realistic
feature, and, hence, is able to better reproduce the
AnInvestigationontheSimulationHorizonRequirementforAgentbasedModelsEstimationbytheMethodofSimulated
Moments
27

stylized facts represented by the selected moments
of interest.
The second conclusion deals with the simulation
horizon requirements one allows the model to be
run. From figure 5 it is clear that a great deal of
sample variability is reduced when the simulation
horizon is extended from 10 to 100 times the size of
the empirical time series used as reference in the
estimations. However, it can also be seen in figure 5
that the centroids of the distributions do not change
(that is, the mean locations remain the same) when
the model is simulated for a longer time horizon. In
this sense, the relevance of the longer simulation
horizon with respect to the estimation procedure still
requires further investigation.
REFERENCES
Arthur, W., Holland, J., LeBaron, B., Palmer, R., and
Tyler, P., 1997. Asset Pricing Under Endogenous
Expectations in an Artificial Stock Market. In Arthur,
W., Durlauf, S., and Lane, D. (eds.), The Economy as
an Evolving Complex System. Reading, Mass.:
Addison-Wesley, 15-44, 1997.
Brock, W., and Hommes, C., 1998. Heterogeneous beliefs
and routes to chaos in a simple asset pricing model.
Journal of Economic dynamics and Control,
22.89:1235-1274.
Chen, S., 2008. Computational intelligence in agent-based
computational economics. In: Fulcher, J., Jain. L.
(eds.), Computational intelligence: a compendium,
Springer, 517-594.
Franke, R., and Westerhoff, F., 2008. Validation of a
Structural Stochastic volatility Model of Asset Pricing.
Christian-Albrechts-Universitat zu Kiel, Department
of Economics, Working Paper.
Franke, R., and Westerhoff, F., 2011. Structural Stochastic
Volatility in Asset Pricing Dynamics: Estimation and
Model Contest. Christian-Albrechts-Universitat zu
Kiel, Department of Economics, Working Paper.
Grossman, S., and Stiglitz, J., 1980. On the impossibility
of informationally efficient markets. The American
Economic Review, 70.3:393-408.
LeBaron, B., 2006. Agent-based Computational Finance.
Handbook of Computational Economics, 2:1187-1233.
Lux, T., and Marchesi, M., 1999. Scaling and criticality in
a stochastic multi-agent model of a financial market.
Nature, 387:498-500.
Lux, T., 2008. Stochastic Behavioral Asset Pricing Models
and the Stylized Facts. Christian-Albrechts-Universitat
zu Kiel, Department of Economics, Working Paper N.
1426.
Mandelbrot, B., 1966. Forecasts of future prices, unbiased
markets, and martingale models. Journal of Business,
1:242-25.
Westerhoff, F., 2008. The use of agent-based financial
markets to test the effectiveness of regulatory policies.
Journal of Economics and Statistics, 228:195-227.
SIMULTECH2013-DoctoralConsortium
28
