Human-like Sensor Fusion Mechanisms in a Postural Control Robot

Georg Hettich, Vittorio Lippi and Thomas Mergner

Neurocenter, Neurological University Clinic, Breisacher Str. 64, 79106 Freiburg, Germany

Keywords: Sensor Fusion, Postural Control, Sensory Feedback, Humanoid Robot.

Abstract: In humans, maintaining body posture is a basis for many activities such as standing, walking or reaching.

Human posture control involves multi-sensory integration mainly of joint angle, joint torque, vestibular and

visual inputs. This integration provides humans with high flexibility and with robustness in terms of fail-

safety. Roboticists may draw inspirations from the human control methods when building devices that

interact with humans, such as prostheses or exoskeletons. This study presents a multisensory control method

derived from human experiments, which is re-embodied in a biped postural control robot. The robot uses

ankle and hip joints for balancing in the sagittal plane during external disturbances such as support surface

motion. For the balancing, the robot estimates the external disturbances that have impact on its body by

fusing the sensory signals. It then uses these estimates in negative feedback to command the local joint

controls to compensate for the disturbances. This study describes the human sensor fusion mechanisms and

their implementation into the robot, and it compares robot and human responses to support surface tilt.

Measured balancing responses of the robot resemble in the main characteristics those of the human subjects,

suggesting that the described sensor fusion mechanisms capture important aspects of human balancing.

1 INTRODUCTION

Sensors play a fundamental role in the sensorimotor

behaviors of animals and humans. Use of sensors

offloads computational burdens to the periphery and

early processing stages of the central nervous system

(CNS; e.g. Wehner, 1987). Furthermore, fusion of

sensory data represents an important step in the

perceptual reconstruction of the external world

events having impact on the body (Mergner, 2002).

Motion control of mechatronic systems, such as

humanoid robots, still face many unsolved research

problems, therefore roboticists show an increasing

interest to unravel the human sensorimotor control,

together with neuroscientists. This research aims to

adopt principles from biological signal processing

and sensorimotor control in humanoid robots, so that

these can (i) show more human-like characteristics

such as robustness in terms of fail-safety, versatility,

and energy efficiency; (ii) show mechanical

compliance to ensure safety in human-robot

interactions; and (iii) serve as guidelines for

constructing medical devices such as neural

prostheses and exoskeletons.

Neuroscientists often distinguish between

proactive and reactive sensorimotor control. The

term proactive refers to feed forward control of

voluntary actions, dealing with foreseen or self-

produced disturbances. The term reactive refers to

sensory feedback control in response to unforeseen

disturbances. A prototype of reactive control is

balancing of upright posture during unforeseen

external disturbances. Human control of this posture

involves sensory feedback mainly from joint

proprioception, vestibular system and vision (see

Horak and MacPherson, 1996). The underlying

neural sensor fusion mechanisms, often called multi-

sensory integration, allow humans to adapt posture

control to changes in the environment and to the

availability of sensory information. Depending on

the external conditions, the relative contributions of

sensors to balance vary considerably, which has

been called ‘sensory reweighting’ (Nashner and

Berthoz, 1978); (Peterka, 2002); (Mergner et al.,

2003); (Maurer et al., 2006); (van der Kooij and

Peterka, 2011). The sensory integration and

reweighting mechanisms are still the topic of on-

going research. This paper presents a novel posture

control concept that builds mainly on sensor fusion

mechanisms and is currently implemented in a

humanoid robot that balances even when subjected

to changing external disturbances.

Previous bipedal robots that perform sensor

152

Hettich G., Lippi V. and Mergner T..

Human-like Sensor Fusion Mechanisms in a Postural Control Robot.

DOI: 10.5220/0004642701520160

In Proceedings of the International Congress on Neurotechnology, Electronics and Informatics (SensoryFusion-2013), pages 152-160

ISBN: 978-989-8565-80-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

fusion often used Kalman filters for multisensory

integration (Tahboub and Mergner, 2007);

(Mahboobin et al., 2008); (Klein et al., 2011).

Corresponding simulation models of sensor fusion in

the postural control also used Kalman filters (van

der Kooij et al., 1999); (Kuo, 2005). Common to

these models is a ‘sensory integration center’ in

which multiple sensory signals are combined with

centrally generated information (‘efference copy’).

The aim of combining this information is to find the

most accurate sensory representation for a given

environmental situation. These solutions were

primarily inspired by the technical evolution rather

than the biological evolution.

A different approach was used by Mergner and

colleagues (Mergner et al., 2003); (Maurer et al.,

2006); (Mergner, 2010). These authors investigated

fusion of vestibular and proprioceptive sensory

signals in human psychophysical experiments on

self-motion perception using an open loop systems

analysis approach. They found that humans use

several processing steps to combine the signals,

which originate from several sensory transducers

and finally result in a few estimates of the external

disturbances that have an impact on body posture.

The underlying fusion mechanisms are rather

simple, in that they don’t require use of a full

dynamic model of human biomechanics and of

iterative processing.

The inferred fusion mechanisms were then

implemented into a stance control model, having in

mind that normally a high congruency between

perception and action exists (Mergner, 2002). In

model simulation, a close correspondence between

simulated and experimentally observed postural

responses to external disturbances has then been

observed (Mergner et al., 2003); (Maurer et al.,

2006). Noticeably, the implemented sensor fusion

mechanisms provide a means for automatic sensory

re-weightings and for reducing effects of sensory

noise. The model was implemented and successfully

tested so far on a 1 degree of freedom (DOF) robot

with ankle joint actuation (Posturob I; Mergner et

al., 2009).

The implementation of human-inspired posture

control concepts in this robot mimics to a large

extent the human balancing of moderate external

disturbances in the sagittal plane, which uses mainly

the ankle joints (‘ankle strategy’; Nashner and

McCollum, 1985); (Horak and Nashner, 1986). The

simplification of human biomechanics as a single

inverted pendulum (SIP) was also helpful in

modeling studies (e.g. Peterka, 2002). However, the

SIP simplification is no longer applicable when

humans use other joints in addition to the ankle

joints, such as the hip joints, as one typically

observes when strong transient disturbances are

applied (‘hip strategy’; Nashner and McCollum,

1985); (Horak and Nashner, 1986).

In this study we extend the human-inspired

postural control model to deal with the double

inverted pendulum (DIP) biomechanics of humans

and a 2 DOF robot (hip and ankle joint). The focus

is here, however, not so much on involving the hip

joints during strong disturbances, but rather another

aspect. During many activities such as walking, the

secondary task ‘head stabilization in space’ is

superimposed on the primary task of maintaining

equilibrium using the ankle joints. This secondary

task uses the hip joint to maintain a given trunk (and

head) orientation in space to stabilize the

workspaces of gaze, arms and hands and is thought

to improve under dynamic conditions sensory

feedback from the vestibular and visual cues arising

in the head (Bronstein, 1988); (Pozzo et al. 1991).

In the following, a model of sensorimotor control

is explained, which was used to interpret human SIP

balancing responses around the ankle joints. Then

the concept is extended to control a DIP by

including the hip joints. The implementation of the

control model into a humanoid robot and the

comparison between robot and human subjects is

described. In the final section, it is concluded that

the human-inspired sensorimotor control concept

can be used in the form of a modular control

architecture for humanoid robots that are expected to

show human-like characteristics when interacting

with humans behaviorally or in the form of

prostheses or exoskeletons.

2 METHODS

A model for controlling hip and ankle joint torques

during balancing of external disturbances was

developed using human-inspired sensor fusion

mechanisms. These fusion mechanisms provide

estimates of the external disturbances, which are

used for disturbance compensation by feeding back

the estimates rather than the raw sensory signals

(disturbance estimation and compensation, DEC,

concept). First, the sensor fusion underlying the

DEC concept will be briefly reviewed.

2.1 Basic Aspects of Sensor Fusion in

the DEC Concept

The DEC concept involves essentially two steps of

Human-likeSensorFusionMechanismsinaPosturalControlRobot

153

fusion. In the first step, information from several

sensory transducers is fused to obtain measures of

physical kinematic and kinetic variables. In the

second step, these physical variables are combined

to yield estimates of the external disturbances.

2.1.1 Sensory Transducer Data Fusion

An example of the first step is the human sense of

joint angle proprioception. It combines information

from several sensory transducers such as muscle

spindles, Golgi Tendon organs and cutaneous

receptors (Gandevia et al., 2002). Also the human

perception of head on trunk rotation is derived from

such combinations, even with rotations across

several segments of the cervical vertebral column.

The result is a sense of angular head-on-trunk

velocity and position, as if a rate sensor and a

goniometer were measuring head-trunk rotation and

speed about a single joint (Mergner et al., 1983);

(Mergner et al., 1991).

Another example for the first step, better known

to engineers, is the fusion of angular and linear

accelerometers in an inertial measuring unit (IMU).

There is a problem with linear accelerometers, as

they do not distinguish between inertial and

gravitational forces (i.e. between linear acceleration

and tilt of the sensor). There is also a problem with

angular accelerometers (often used in the form of

gyroscopes that measure angular velocity), as they

show signal drifts over time. Both problems can be

solved for the earth vertical planes by fusing the

inputs from the two sensors in an appropriate way.

This has an analogy in the human vestibular system

that is located in the inner ears. Its otholith organs

and canal systems represent biological equivalents

of linear and angular accelerometers, respectively

(Mergner et al., 2009). The canal-otolith and gyro-

accelerometer fusions require information of the

gravitational vector, however. Therefore, spatial

orientation in the horizontal translational and

rotational planes requires further information. In

technical systems, often a Global Positioning System

(GPS) is used. Humans usually use the visual system

for this specific purpose.

In the following we will speak of joint angle and

angular velocity sensors and mean corresponding

virtual sensors that result from step one. The same

applies when we refer to the vestibular sensor and its

three output measures, i.e. 3D angular velocity and

linear acceleration in space and orientation with

respect to the gravitational vertical. It is known from

animal studies that neural signals coding local and

global physical variables already exist in low

processing levels of the CNS such as the spinal cord

(Bosco and Poppele, 1997; Poppele et al., 2002).

The measures of the physical variables represent the

inputs to the second step of sensor fusion.

2.1.2 Disturbance Estimation

In the second step, the signals of these variables are

combined to reconstruct disturbances that have

impact on the body. This step was motivated by

reports of human subjects in the psychophysical

experiments and by simple plausibility related to

mechanics. An example from the psychophysical

experiments is that a subject, asked to report his

percept when passively turned on a rotation chair, is

typically not reporting a sensation of head in space

rotation stemming from the vestibular system, but a

rotation of the chair, which is the underlying cause

of the head rotation. Without being aware of it, the

subject internally reconstructs the physical cause by

using the vestibular head-in-space signal and

combines it with proprioceptive information on the

trunk rotation relative to the head, thereby obtaining

the percept of trunk in space rotation, which during

sitting is in haptic connection with the chair. This

percept can formally be described in terms of a

coordinate transformation by which the trunk is

referenced to the vestibular derived notion of space

(Mergner et al., 1997).

Another intuitive example of a reconstruction of

an external disturbance by sensor fusion in step two

concerns gravity as a field force. For field forces in

general, it is known that subjects presented with a

new aspect of a field force perceive and readily learn

to counteract its impact on the body and then no

longer perceive it consciously (Lackner and DiZio,

1994). Considering specifically gravity, during body

lean it tends to accelerate the body away from the

vertical. Stabilizing the body posture then requires a

compensatory ankle torque. With small body

excursions, this torque is proportional to the body

COM angle in space. On the sensory side, the body

lean is directly measured by the vestibular system.

Knowing the vestibular signal, the body mass and

the COM height, the gravitational ankle torque can

be estimated and directly compensated. As before

with the estimation of a rotation of the chair (support

surface), neck proprioceptive signals allow to

reference the body lean to the vestibular notion of

space.

Interestingly, it suffices to add to the just

described two disturbances, i.e. to (a) support

surface rotation and (b) field forces such as gravity,

two more disturbances, which are (c) support surface

NEUROTECHNIX2013-InternationalCongressonNeurotechnology,ElectronicsandInformatics

154

translational acceleration and (d) contact forces such

as a push or pull, in order to cover all the external

disturbances that may have impact on the body

during balancing. The latter two external

disturbances also can be estimated by sensor fusion

in simple, non-iterative ways (Mergner, 2010).

Furthermore, it was shown that the four estimates

may be implemented in a feedback control to

compensate for the disturbances.

Implementation of both steps of sensory fusion

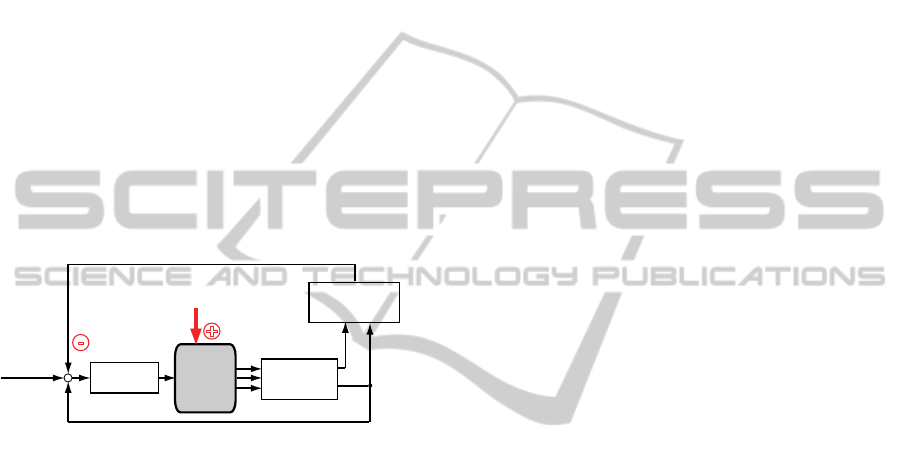
into a feedback model is shown schematically in

Figure 1. The figure shows that the first fusion step

(Transducer Fusion) applies to two distinct feedback

loop systems. In the lower loop of the scheme, it

provides a kind of local state feedback in the form of

a proprioceptive signal of joint angle. In addition,

the first fusion step provides inputs to the upper loop

system where the external disturbances are estimated

using the second fusion step (Disturbance

Estimation).

Figure 1: Simplified scheme of the Disturbance Estimation

and Compensation (DEC) concept.

The lower loop in Figure 1 represents a short-

latency local mechanism for regulating a joint in the

form of a simple ‘servo control’. It receives a

voluntary input signal (Set Point Signal) of the

desired joint position. The controller (with a

proportional and a derivative factor; PD controller)

provides the motor command that is transformed by

the muscles (not shown) into joint torque. Passive

stiffness and viscosity, stemming from intrinsic

properties of the musculoskeletal system contribute

a minor part to the joint torque (also not shown).

Proprioceptive feedback, biomechanics, and

controller values are adjusted to account for the

moment of inertia of the plant such that the actual

displacement trajectory corresponds to the desired

trajectory. Therefore, no feed forward of plant

dynamics (e.g. through an inverse of plant

dynamics) is required.

Noticeably, the P and D factors identified in

human stance control experiments (Peterka, 2002;

Alexandrov et al., 2005; Maurer et al., 2006) are

surprisingly low. In a SIP scenario, they appear to be

geared to the body mass m of the pendulum, the

height h of the mass and gravitational acceleration g

(mgh; P ≈ mgh; D ≈ mgh/4). The human identified

values are only slightly higher than these values.

The upper loop in Figure 1 stands for a more

time consuming feedback loop from the disturbance

estimates (identified lumped time delay of both loop

systems, ≈180 ms; Peterka, 2002); (Maurer et al.,

2006). The upper loop commands the servo loop to

compensate the effects that the external disturbances

have on the body (note that sign of upper loop is

opposite to that of the disturbances). By this, for

example, the gravitational torque in the SIP joint is

compensated for, in that the corresponding estimate

commands the servo accordingly. The loop gain (at

the level of the controller) is raised by this additional

feedback. However, this increase occurs only at the

time of the disturbance and to the extent of its

impact. Interestingly, the compensation applies even

with superposition of several disturbances as well as

with superposition of the disturbances with

voluntary movements (Mergner et al., 2009).

It has been shown by comparisons between

human data and model simulations that the DEC

concept describes the human balancing in a variety

of disturbance scenarios. This even applied when the

model was implemented in a 1 DOF humanoid robot

(PostuRob I), including human time delays, and was

tested in the human laboratory (overview Mergner,

2010). These testings demonstrated that the control

method is robust against real world problems such as

inaccurate and noisy sensors, mechanical dead

zones, etc.

2.2 Sensor Fusion in Hip and Ankle

Joints

Current work on the DEC concept, described below,

deals with the questions (1) how the disturbance

estimates and their compensation might deal with

the DIP biomechanics, (2) how the head/trunk

stabilization task is achieved, (3) how inter-

segmental coupling torques are dealt with, and (4)

how movement synergies are generated in the DEC

control. The approach proceeds from the assumption

that the DEC concept is realized in a multi-

segmental system in the form of a modular control

architecture. By controlling each DOF with one

DEC module, the whole control would be easily

scalable to changes in the number of DOFs.

2.2.1 Dip Biomechanics

The DIP biomechanical model is shown in Figure 2.

Disturbance Compensation

External

Disturbances

Proprioceptive Feedback

Controller

Plant

Disturbance

Estimation

Set Point

Signal

Transducer

Fusion

Human-likeSensorFusionMechanismsinaPosturalControlRobot

155

In Figure 2A, COM

, COM

and COM

stand for the

COM of the trunk, leg and whole body, respectively.

Leg length is given by l

, the trunk and leg COM

heights are given by h

and h

, respectively. Figure

2B shows the angular excursion of the trunk and leg

segments with respect to earth vertical (trunk-space

angle α

, leg-space angle α

). Angular excursion of

COM

is defined as body-space angle α

. The foot

has firm contact with the support surface, therefore

platform tilt angle equals foot angle with respect to

earth horizontal (foot-space angle α

). The trunk-

leg joint angle is α

and the leg-foot joint angle is

. In perfectly erect position all angles are 0°.

Angular speed during reactive human balancing can

be assumed to be slow enough such that the Coriolis

and centrifugal forces can be neglected; the model

can be linearized using the small angle

approximation, assuming that the subject is

maintaining his upright position close to the vertical.

Figure 2: DIP biomechanics.

Maintaining upright stance in the situation of a

support surface tilt in the sagittal plane requires

corrective joint torque in the ankle and hip joints.

This torque can be expressed by the following

equations for hip torque T

























∝



















∝





 









∝



(1)

and for ankle torque T

























∝





 





























∝







































∝













∝



 









∝



(2)

where ∝





, ∝





and ∝





represent angular

accelerations, g is the gravitational acceleration, m

and m

are the segment masses, and J

and J

the

segment moments of inertia (details in AlBakri,

2008).

In the DEC concept for the DIP, the hip joint is

used for balancing the head-trunk segment and the

ankle joint for balancing the whole-body using two

separate controls. The co-operation between the two

joint controls is achieved by extending the afore-

mentioned second step of sensory fusion in a form

that the control of the lower segments benefits from

the fusion in the upper control and, vice versa, the

upper control benefits from the fusion in the lower

control.

The vestibular signals used for controlling the

DIP are: the trunk-space angle ∝



, trunk-space

angular velocity ∝





and head translational

acceleration 



. The proprioceptive signals are:

the trunk-leg angle ∝



and the trunk-leg angular

velocity ∝





; the leg-foot angle ∝



and the leg-foot

angular velocity ∝





. Uppercase letters in the angle

subscripts were used to indicate physical angles,

while lowercase letters were used to indicate sensory

derived representations of the same angles.

2.2.2 Hip Joint Control

The control of the trunk segment at the hip joint

reflects a DEC control as described above for the

SIP biomechanics. In the considered support surface

tilt scenario, the leg segment is not perfectly

stabilized in space, but rotates somewhat with the

platform. Because the legs represent the support

base for the trunk, their rotation causes the following

disturbances in the hip joint:

(a) Tilt of the support base for the trunk during leg

rotation, 



. Intrinsic properties of the

musculoskeletal system (passive stiffness and

viscosity) then generate a hip torque that tends to

move the trunk along with the legs (

_

(b) Hip translational acceleration x



during the leg

rotation. This tangential acceleration produces a

hip torque in relation to the trunk’s moment of

inertia (T

_

). Here treated as if it were an

external disturbance rather than an inter-

segmental coupling effect.

_

) arises when the

trunk is rotated off the vertical.

The three disturbances are estimated by the sensor

fusion mechanisms in the DEC-based module of the

hip (Figure 3) in the following form:

(i) Estimation of leg tilt ∝





. This estimate is

derived from fusing the vestibular velocity signal

∝





with the proprioceptive velocity signal ∝





in the

form of ∝





∝





∝





. (Assumption: such

NEUROTECHNIX2013-InternationalCongressonNeurotechnology,ElectronicsandInformatics

156

coordinate transformations are performed as vector

summations separately for the three body planes).

The estimate ∝





is obtained by applying to the

signal a detection threshold and a mathematical

integration.

(ii) Estimation of hip translational acceleration







. The estimate is derived from fusing vestibular

signals ∝





and 



in the form













∝













(3)

This kinematic estimate 





is, in turn, used to

estimate the inertial disturbance torque in the form























(4)

(iii) Estimation of gravitational hip torque





_

. Using the vestibular signal ∝



,the third

term of equation (1) becomes

















∝



(5)

2.2.3 Ankle Joint Control

This balance control stabilizes the whole body above

the ankle joint, which includes the leg and the trunk

segments. Correspondingly, the ankle DEC-based

module combines the leg and trunk angular

excursions in the form of whole-body COM

excursion in space, ∝



. In this respect, also the

DEC module for the ankle joint can be viewed as

dealing with a SIP. The three disturbances that have

impact on the ankle torque during support surface

tilts are:

(a) The support surface tilt 



. It evokes the passive

ankle torque 

_

(b) The gravitational ankle torque 

_

. It arises

from COM

angular excursion in space ∝





_

. It arises through angular acceleration of

the trunk segment.

For disturbance estimation, the ankle joint DEC

module fuses sensory signals from the vestibular

system and the hip and ankle joint proprioception.

To this end, sensory signals from the hip DEC

module are transmitted (“down-channeled”) to the

ankle joint DEC module. This leads to the following

disturbance estimates:

(i) Estimation of foot-space rotation ∝





. This

estimate uses a down-channeled version of ∝





and

combines it with the ankle joint velocity signal ∝





in the form

∝





∝





∝





(6)

Analogous to the hip module, the estimate ∝





obtained by applying to the signal a detection

threshold and a mathematical integration.

(ii) Estimation of gravitational ankle torque





_

. This estimate relates to the fourth and fifth

terms of equation (2), which are mathematically

combined in the COM

excursion ∝



. From this,

the gravitational torque is obtained as follow

















∝



(7)

where m

represents whole-body mass and h

COM

height. Small angular excursions allow

approximating h

by a constant value.

(iii) Estimation of the inter-segmental coupling

torque 



_

. This torque arises upon rotational

acceleration of the trunk and evokes a leg counter-

motion. It may be estimated on the basis of the first

three terms of equation (2). Previous work showed,

however, that leg motion in the same direction

already results from stabilizing the COM

, often

referred to as trunk-leg synergy (compare

Alexandrov et al., 2005). This suggests, and model

and robot simulation confirm that one can refrain

from compensating this torque, at least in the

framework of the human balancing (Hettich et al.,

2011).

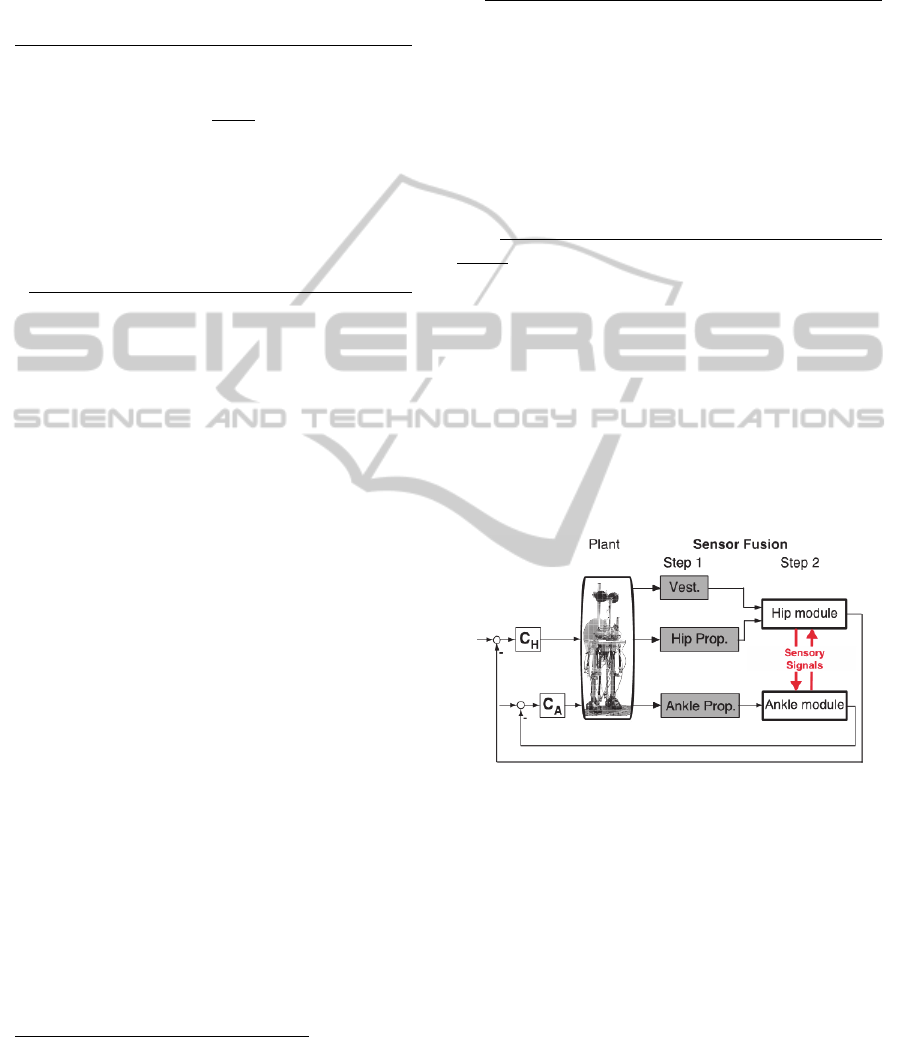
Figure 3: Basic aspects of control concept of PostuRob II.

and C

are hip and ankle controllers, Vest. is the

vestibular input while Hip Prop. and Ankle Prop. are the

proprioceptive inputs.

The combination of the hip and ankle control

modules and the mutual exchange of sensory

information are shown schematically in Figure 3.

Details of the “up-channeled” sensory information

will be given in a forthcoming publication.

2.3 PostuRob II

The two-module control concept was implemented

in PostuRob II. This robot consists of mechanical,

mechatronic, and computer control parts. The

mechanical part comprises one trunk segment, two

Human-likeSensorFusionMechanismsinaPosturalControlRobot

157

legs and two feet, with a total mass of 59 kg and a

total height of 1.78 m. Two hip joints and two ankle

joints connect the segments (4 DOF in the sagittal

plane; Figure 4). The mechatronic part comprises an

artificial vestibular sensor (see Mergner et al., 2009)

that is fixed to the trunk segment. Artificial

pneumatic ‘muscles’ (FESTO, Esslingen, Germany;

Typ MAS20) connected with serial springs (spring

rate 25 N/mm) are used for actuation. An electronic

inner torque control loop ensures that actual torque

equals approximately desired torque. Sensory

signals are sampled at 200 Hz via an acquisition

board. Computer control is performed through a real

time PC that executes a compiled Simulink model

using Real-Time Windows Target (The Math Works

Inc., Natick, USA).

Figure 4: PostuRob II. The robot consists of trunk, leg,

and foot segments interconnected by the hip joints (a) and

ankle joints (b). Sensory information stems from artificial

vestibular system (c) and ankle and hip joint angle sensors.

Actuation is through pneumatic ‘muscles’ (d). PostuRob II

stands freely on a motion platform (e).

2.4 Human and Robot Experiments

The two-module control concept was tested by

comparing human responses with robot responses to

support surface tilt in the sagittal plane in a human

posturography laboratory. For this study, seven

healthy human subjects (3 female; mean age, 28 ± 3

years) gave their informed consent. The subjects

(with eyes closed) and the robot stood freely on a

motion platform (see Figure 4). The experiment

consisted of six successive pseudorandom ternary

tilt sequences, each 60.5 s long, with peak-to-peak

amplitude of 4° (PRTS stimulus; frequency range

0.017 – 2.2 Hz; Peterka, 2002). The first rows in

Figure 5A,B shows one 60.5 s long tilt stimulus

sequence.

Figure 5: Tilt stimulus and angular excursion responses of

one representative subject (A) and of PostuRob II (B).

Trunk, leg, and COM

angular excursions in

space were calculated on the basis of opto-

electronically measured markers (Optotrak 3020®;

Waterloo, Canada) that were recorded with a

sampling frequency of 100 Hz. Data analysis took

into account human anthropometric measures

(Winter, 1990) and was performed using custom-

made software programmed in Matlab (The

MathWorks, Natick, USA). The responses were

expressed as gain and phase from the frequency

response function (Peterka, 2002) in a form where

zero gain means no body excursion and unity gain

means that body angular excursion equals platform

tilt. Phase represents the temporal relationship

between stimulus and response. Variability of

averaged values was expressed as 95% confidence

limits (Otnes and Enochson, 1972).

3 RESULTS

Subjects and PostuRob II balance the support

surface tilts in similar way. Time series of the

responses of one subject and the robot are shown in

Figure 5. Note that their responses are similar both

for the body (COM

) and the trunk angles. The

mean gain and phase curves are also very similar

between the human subjects and the robot as it is

shown in Fig. 6. The gain and phase values vary

NEUROTECHNIX2013-InternationalCongressonNeurotechnology,ElectronicsandInformatics

158

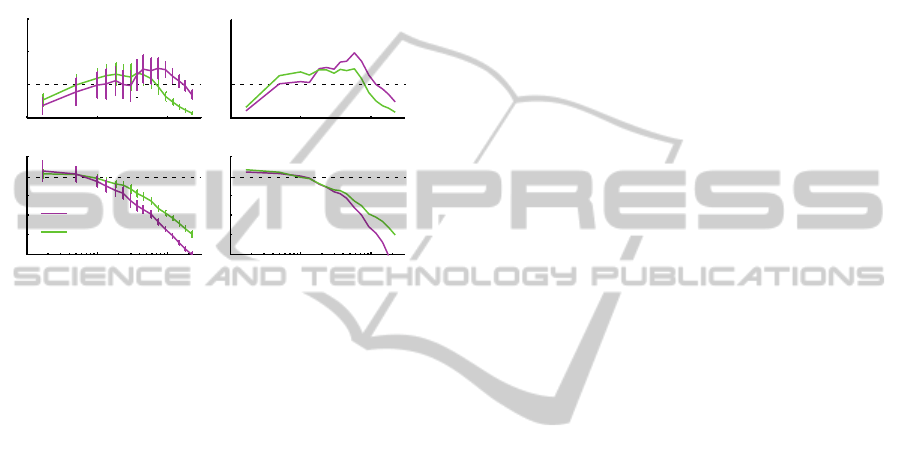
with stimulus frequency. In the low frequency range

(< 0.3 Hz) trunk in space (TS) gain is lower than

body in space (BS) gain. In the high frequency range

(> 0.3 Hz) TS gain exceeds BS gain, while the phase

shows a larger phase lag.

The good match of the data between the human

subjects and PostuRob II suggests that the proposed

sensor fusion mechanisms capture important aspects

of human balancing.

Figure 6: Tilt responses in terms of gain, phase and

coherence of human subjects (A) and PostuRob II (B).

4 CONCLUSIONS

The presented posture control system takes

advantage of sensor fusion mechanisms derived

from findings in human experiments. The sensor

fusion proceeds in two steps. In the first step,

sensory transducer signals are fused to obtain

physical variables. In the second step, the physical

variables are combined to estimate external

disturbances. This is performed without integrating

any dynamic model of the whole body in the control

architecture.

Balancing upright stance using hip and ankle

joints in terms of a DIP requires the integration of

sensory signals from the whole body. For instance,

to estimate a support surface tilt, the vestibular

information of head-space angular velocity (here in

the absence of head-trunk excursions equivalent to

trunk-space velocity ∝





) is fused with co-planar

proprioceptive signals to obtain the angular speed of

foot in space ∝





. This value is then integrated to

obtain ∝



. Before the integration, ∝





is filtered

through a nonlinear operation, which is a deadband

threshold. This works as a filtering system

stabilizing the estimate ∝





based on the noisy

vestibular signal (Mergner et al., 2009). The

threshold also explains the nonlinear responses of

human subjects upon increase of the external

disturbances (Maurer et al., 2006), which reflects an

important aspect of the automatic sensory re-

weighting. Another aspect is that the control

automatically adjusts to changes in disturbance type

and sensor availability (Mergner, 2010).

The presented sensor fusion system proved to be

efficient enough to stabilize a humanoid robot in the

presence of external disturbances. The control

system based on this approach is modular in that it

controls every joint as a SIP. Although optimizing

the control parameters of the DEC concept is still a

topic under research, the concept proved to have

several promising features. These include: (i) a

computationally very simple implementation, since

almost all sensor fusions are based on algebraic

operations; (ii) the control complexity scales linearly

with the number of joints, since every joint is

controlled as a SIP; (iii) noise rejection makes it

possible to fuse the input of an high number of

sensors; and lastly (iv) the system, originally

proposed for its predictive power of human

behaviour, can be employed to control actuated

prostheses and exoskeletons to preserve a natural

feeling in the user.

Future work comprises fusion of sensor-derived

disturbance estimates with expected disturbance

estimates and further validation of the concept by

implementing it in a robot with a higher number of

DOF.

ACKNOWLEDGEMENTS

Supported by the European Commission (FP7-ICT-

600698 H2R).

REFERENCES

AlBakri, M. (2008). Development of a mathematical

model and simulation environment for the postural

robot (PostuRob II). Retrieved June 12, 2013, from

http://www.posturob.uniklinik-freiburg.de.

Alexandrov, A. V., Frolov, A. A., Horak, F. B., Carlson-

Kuhta, P. and Park, S. (2005). Feedback equilibrium

control during human standing. Biol Cybern, 93, 309–

322.

Bosco, G. and Poppele, R. E. (1997). Representation of

multiple kinematic parameters of the cat hindlimb in

spinocerebellar activity. J Neurophysiol, 78, 1421–

1432.

Bronstein, A. M. (1988). Evidence for a vestibular input

contributing to dynamic head stabilization in man.

Acta Otolaryngol, 105, 1–6.

Gain

200

Phase (°)

Frequency (Hz)

0.01 0.1 1

-200

Frequency (Hz)

0.01 0.1 1

Human subjects PostuRob II

Human-likeSensorFusionMechanismsinaPosturalControlRobot

159

Gandevia, S. C., Refshauge, K. M. and Collins, D. F.

(2002) Proprioception: peripheral inputs and

perceptual interactions. Adv Exp Med Biol, 508, 61-8.

Hettich, G., Fennell, L. and Mergner, T. (2011). Double

inverted pendulum model of reactive human stance

control. Multibody Dynamics Conference 2011

(available http://www.posturob.uniklinik-freiburg.de).

Horak, F. B. and Nashner, L. M. (1986). Central

programming of postural movements: adaptation to

altered support-surface configurations, J Neurophysiol,

55, 1369–1381.

Horak, F. B. and Macpherson, J. M. (1996). Postural

Orientation and Equilibrium. Rowell, L., & Shepherd,

J., Handbook of physiology. Vol. 1. New York: Oxford

University Press.

Klein, T. J., Jeka, J., Kiemel, T. and Lewis, M. A. (2011).

Navigating sensory conflict in dynamic environments

using adaptive state estimation. Biol Cybern, 105, 291-

304.

Kuo, A. D. (2005). An optimal state estimation model of

sensory integration in human postural balance. J

Neural Eng, 2, 235–249.

Lackner, J. R. and DiZio, P. (1994). Rapid adaptation to

Coriolis force perturbations of arm trajectories. J

Neurophysiol, 72, 299–313.

Mahboobin, A., Loughlin, P. J., Redfern, M. S., Anderson,

S. O., Atkeson, C. G. and Hodgkins, J. K. (2008)

Sensory adaptation in balance control: lessons for

biomimetic robotic bipeds. Neural Netw, 21(4), 621–

627.

Maurer, C., Mergner, T. and Peterka, R. J. (2006).

Multisensory control of human upright stance, Exp

Brain Res, 171, 231–250.

Mergner, T., Nardi, G. L., Becker, W. and Deecke, L.

(1983). The role of canal-neck interaction for the

perception of horizontal trunk and head rotation. Exp

Brain Res, 49, 198-208.

Mergner, T., Siebold, C., Schweigart, G. and Becker, W.

(1991). Human perception of horizontal trunk and

head rotation in space during vestibular and neck

stimulation. Exp Brain Res, 85, 389-404.

Mergner, T., Huber, W. and Becker, W. (1997).

Vestibular-neck interaction and transformations of

sensory coordinates. J Vestibul Res-Equil, 7, 119–135.

Mergner, T. (2002). The Matryoshka Dolls principle in

human dynamic behavior in space—A theory of linked

references for multisensory perception and control of

action. Curr Psychol Cogn, 21, 129–212.

Mergner, T., Maurer, C. and Peterka R. J. (2003). A

multisensory posture control model of human upright

stance, Prog Brain Res, 142, 189-201.

Mergner, T., Schweigart, G. and Fennell, L. (2009).

Vestibular humanoid postural control. J Physiol

(Paris), 103, 178–194.

Mergner, T. (2010). A neurological view on reactive

human stance control. Annu Rev Control, 34, 177-198,

2010.

Nashner, L. M. and Berthoz, A. (1978). Visual

contribution to rapid responses during postural control.

Exp Brain Res, 150, 403–407.

Nashner, L. and McCollum, G. (1985). The organization

of human postural movements: a formal basis and

experimental synthesis. Behav Brain Sci, 8, 135–172.

Otnes, R. K. and Enochson, L. D. (1972) Digital Time

Series Analysis. New York: Wiley.

Peterka, R. J. (2002). Sensorimotor integration in human

postural control. J Neurophysiol, 88, 1097–1118.

Poppele, R. E., Bosco, G. and Rankin, A. M. (2002).

Independent representations of limb axis length and

orientation in spinocerebellar response components. J

Neurophysiol, 87, 409–422.

Pozzo, T., Berthoz, A., Lefort, L. and Vitte, E. (1991).

Head stabilization during various locomotor tasks in

humans. II. Patients with bilateral peripheral vestibular

deficits. Exp Brain Res, 85, 208– 217.

Tahboub, K. A. and Mergner, T. (2007) Biological and

engineering approaches to human postural control.

Integ. Comput Aid Eng, 13, 1–17.

van der Kooij, H., Jacobs, R., Koopman, B. and

Grootenboer, H. (1999). A multisensory integration

model of human stance control. Biol Cybern, 80, 299–

308.

van der Kooij, H. and Peterka R.J. (2011) Non-linear

stimulus-response behavior of the human stance

control system is predicted by optimization of a

system with sensory and motor noise. J Comput

Neurosci, 30(3), 759-778.

Wehner, R. (1987). Matched Filters - Neural models of the

external world, J Comp Physiol A, 161, 511-531.

Winter, D. A. (1990). Biomechanics and motor control of

human movement (2nd ed.). New York: Wiley.

NEUROTECHNIX2013-InternationalCongressonNeurotechnology,ElectronicsandInformatics

160