
Fuzzy Optimization Models for Seaside Port Logistics
Bel
´
en Meli
´
an-Batista
1
, Christopher Exp
´
osito-Izquierdo
1
, Eduardo Lalla-Ruiz
1
, Mar
´
ıa Teresa Lamata
2
and J. Marcos Moreno-Vega
1
1
Department of Statistics, Operations Research and Computing, University of La Laguna, La Laguna, Spain
2
Department of Computer Science and Artificial Intelligence, University of Granada, Granada, Spain
Keywords:
Fuzzy Optimization Model, Seaside Operations, Maritime Container Terminal, Variable Neighbourhood
Search.
Abstract:
The main goal of maritime container terminals is to serve the container vessels arriving at port. This means
that they must be berthed in a position along the quay, a subset of quay cranes must be assigned to them and
work schedules have to be planned for unloading the import containers and loading the export containers onto
each container vessel. This work addresses the Tactical Berth Allocation Problem, in which the vessels are
assigned to a given berth, and the Quay Crane Scheduling Problem, for which the work schedules of the quay
cranes are determined. Due to the fact that the nature of this environment gives rise to inaccurate knowledge
about the information related to the incoming vessels, the aforementioned optimization problems are tackled
considering fuzzy arrival times for the vessels and fuzzy processing times for the loading/unloading operations.
1 INTRODUCTION
The global container trade has grown over the
decades
1
. The maritime container terminals are high-
lighted infrastructures built with the goal of facing
the technical requirements arising from the increasing
volume of containers in the international sea freight
trade. They are aimed at transferring and storing con-
tainers within multimodal transportation networks.
The main transport modes found at a maritime con-
tainer terminal are container vessels, trucks and trains.
In this regard, a maritime container terminal can be
considered as an open system that brings together dif-
ferent container flows, those stemming from freight
sources to destinations (Stahlbock and Voβ, 2008).
The layout of a maritime container terminal is usu-
ally split into three different functional areas: seaside,
yard and landside (Petering, 2011). Firstly, the sea-
side is the area of the terminal where the container
vessels arriving at port are berthed in order to be
loaded or unloaded. An exhaustive analysis concern-
ing the seaside operations planning problems is pro-
vided in the book by (Meisel, 2010). The yard is the
part of the terminal in which the containers are tem-
porarily stored until their later retrieval (Kim et al.,
2008). Finally, the landside is the area which connects
1
United Nations Conference on Trade And Develop-
ment, http://unctad.org
the container terminal with the land transport modes,
that is, trains and trucks (Froyland et al., 2008).
The main goal of a maritime container terminal
is to serve appropriately those container vessels that
arrive at port. In this regard, the service of a con-
tainer vessel can be modeled through a well-defined
sequence of steps. Firstly, it is required to provide a
specific berthing position along the quay and berthing
time for each container vessel according to its particu-
lar characteristics (dimensions, expected service time,
draft, arrival time, etc.) and contractual agreements
(Lalla-Ruiz et al., 2012). Afterwards, a subset of the
available quay cranes at the terminal is allocated to
each container vessel for performing the loading and
unloading tasks established by its stowage plan (Bier-
wirth and Meisel, 2010). Finally, the work schedules
associated with the allocated quay cranes are deter-
mined (Bierwirth and Meisel, 2009).
The aforementioned planning decisions can be
modeled by means of several optimization problems
in maritime container terminals. The Tactical Berth
Allocation Problem (TBAP) pursues to define the
berthing position, berthing time and quay cranes al-
located to each container vessel over a given planning
horizon. On the other hand, the Quay Crane Schedul-
ing Problem (QCSP) is aimed at determining the work
schedules for the quay cranes allocated to a container
vessel. It is worth mentioning that solving the TBAP
289
Melián-Batista B., Expósito-Izquierdo C., Lalla-Ruiz E., Teresa Lamata M. and Moreno-Vega J..
Fuzzy Optimization Models for Seaside Port Logistics.
DOI: 10.5220/0004652202890299
In Proceedings of the 5th International Joint Conference on Computational Intelligence (SCA-2013), pages 289-299
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

and the QCSP for each container vessel provides an
overall service planning for a container terminal.
Algorithms and model formulations to solve the
TBAP and QCSP have usually assumed that the data
are known accurately. However, this is not true in
real-world applications and it is particularly problem-
atic for data representing the arrival times of vessels
and processing times that cannot be precisely esti-
mated, but that need to be taken into account in order
to provide the decision makers with real solutions.
The inherent imprecision that appears in the data
involved in real-world problems can have different
natures: randomness, subjectivity, vagueness, etc. If
the goal is to tackle the problems at hand without al-
tering their nature, what seems more desirable is to
consider the approach that fits the best to the origin
of the imprecision, either stochastic, interval-based
or fuzzy. Among these possibilities, the imprecision
considered in this work is not random but linguisti-
cal and therefore vague (for instance, “the processing
time will be large”). Although vague information ap-
pears in these real-world applications, to the best of
our knowledge, this is the first work that considers this
nature of imprecision in maritime container terminals
when solving the TBAP and QCSP. Other imprecision
natures are out of the scope of this paper.
In those scenarios in which subjectivity in the in-
terpretation of the data is related to randomness, the
fuzzy sets provide us a theoretical framework to solve
a wide range of problems in different research areas
(Tiwari et al., 2006) (Verdegay, 2003) with a high
degree of efficacy and efficiency. In this paper, we
are particularly interested in solving the TBAP with
fuzzy arrival times for the vessels and the QCSP with
fuzzy processing times for the loading/unloading op-
erations. With the purpose of solving these problems,
we propose mathematical models in which some co-
efficients in the constraints are not known accurately.
In both cases, in order to solve the optimization prob-
lems derived from these situations, we will make use
of models which are well known in the area of Fuzzy
Mathematical Programming (Cadenas and Verdegay,
2006) (Herrera and Verdegay, 1995) (Sancho-Royo
et al., 2006).
The remainder of this paper is structured as fol-
lows. Section 2 describes the main logistic problems
arising in the seaside. Section 3 describes the fuzzy
coefficients used in the mathematical formulations of
the TBAP and QCSP. Section 4 proposes two Variable
Neighbourhood Searches for the TBAP and QCSP.
Section 5 shows the computational experiments per-
formed in this work. Finally, Section 6 presents the
main conclusions extracted from the work and indi-
cates several directions for further research.
2 SEASIDE OPERATIONS
The seaside operations are those concerning the ser-
vice of container vessels that arrive at port. As indi-
cated by (Wiegmans et al., 2001), the turnaround time
of container vessels constitutes the main indicator of
the competitiveness of maritime container terminals.
With this fact in mind, terminal managers are particu-
larly interested in reducing the service times and max-
imizing the usage of the available resources: berths
and quay cranes.
2.1 Tactical Berth Allocation Problem
The Tactical Berth Allocation Problem (TBAP) pur-
sues to determine the berthing position, berthing time
and allocation of quay cranes for the container vessels
arriving at port over a well-defined time horizon.
In the TBAP we are given a set of incoming ves-
sels N, a set of berths M, and a set of quay crane
profiles p ∈ P
i
per each vessel i ∈ N. Each container
vessel i ∈ N must be assigned to an available berth
k ∈ M within the vessel and berth time window [a
i
,b
i
]
and [a
k
,b
k
], respectively. The berthing position of a
vessel should be close to the departure position of
its containers. In this regard, the housekeeping cost
represents the cost derived from moving a given con-
tainer among different berthing positions of the quay.
Moreover, for each vessel i ∈ N, a quay crane profile,
p ∈ P
i
, determines the distribution of quay cranes used
for serving it. Q denotes the number of quay cranes at
the terminal. The service time of a vessel depends on
the quay crane profile associated with it. Each profile,
p ∈ P
i
, has an associated value v
p
i
, which reflects the
usage of quay cranes.
The goal of the TBAP is to maximize the value
of the quay crane profiles used to serve the vessels
and minimize the housekeeping costs derived from
the transshipment of containers among vessels.
An example of the TBAP is depicted in Figure
1. The example shows 3 container vessels, 3 berths
and a maximum number of 8 quay cranes. For each
container vessel i ∈ N, the number of QC hours re-
quired to perform its loading and unloading opera-
tions is termed as m
i
. The profiles assigned to the
vessels determine the distribution of quay cranes and
their service time. For instance, the vessel 3 is served
by 2, 3, 3, and 2 quay cranes and its service time is
4 hours. It is worth pointing out that, despite ves-
sels 1 and 3 require the same number of quay crane
hours, their service times are different because they
have assigned different profiles. In this regard, the
quay crane profile assigned to vessel 1 is more expen-
sive than that assigned to vessel 3.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
290

Vessel 3
2 3 3 2
m
3
= 10
Vessel 2
2 2 3 4
m
2
= 11
Vessel 1
3 3 4
m
1
= 10
0 2 6 8 8 3 4
QCs:
0 1 2 3 4 5 6 7
Time (h.)
Quay
Berth 3 Berth 2 Berth 1
Figure 1: Example of TBAP with 3 container vessels and 3 berths.
In order to make this work self-contained, this
subsection describes the mixed integer linear program
formulation for the TBAP proposed by (Giallombardo
et al., 2010).
The following notations are used in the model:
• N Set of container vessels
• M Set of berths
• H Set of time steps
• P
i
Set of feasible quay crane profiles for the
container vessel i ∈ N
• t
p
i
Service time of container vessel i ∈ N under
QC profile p ∈ P
i
• v
p
i
The value of serving the container vessel i ∈
N with the QC profile p ∈ P
i
• Q
h
Maximum number of quay cranes available
at the time step h ∈ H
• q
pu
i
Number of quay cranes assigned to the con-
tainer vessel i ∈ N in profile p ∈ P
i
at the time step
u ∈ H
• f
i j
Flow of containers exchanged between con-
tainer vessels i, j ∈ N
• d
kw
Housekeeping cost per unit of container be-
tween yard slots in berths k,w ∈ M
• [a
i
,b
i
] [earliest, latest] arrival time of container
vessel i ∈ N
• [a
k
,b
k
] [start, end] of the availability time of the
berth k ∈ M
• [a
h
,b
h
] [start, end] of the time step h ∈ H
A graph G
k
= (V
k
,A
k
) ∀ k ∈ M, where V
k
= N ∪
{o(k), d(k)}, with o(k) and d(k) additional vertices
representing berth k and A
k
⊆ V
k
×V
k
is generated.
The decision variables are shown below.
• x
k
i j
∈
{
0,1
}
, ∀ k ∈ M, ∀ (i, j) ∈ A
k
, set to 1 if con-
tainer vessel j is scheduled after container vessel
i in berth k, and 0 otherwise.
• y
k
i
∈
{
0,1
}
, ∀ k ∈ M, ∀ i ∈ N, set to 1 if container
vessel i is assigned to berth k, and 0 otherwise.
• z
kw
i j
∈
{
0,1
}
, ∀ k, w ∈ M, ∀ i, j ∈ N, set to 1 if
y
k
i
= y
w
j
, and 0 otherwise.
• γ
h
i
∈
{
0,1
}
, ∀ h ∈ H, ∀ i∈ N, set to 1 if the con-
tainer vessel i arrives in time step h, and 0 other-
wise.
FuzzyOptimizationModelsforSeasidePortLogistics
291

• λ
i
p
∈
{
0,1
}
, ∀ p ∈ P
i
, ∀ i∈ N, set to 1 if container
vessel i is served under profile p, and 0 otherwise.
• ρ
ph
i
∈
{
0,1
}
, ∀ p ∈ P
i
, ∀ h ∈ H, ∀ i∈ N, set to 1
if container vessel i is served under profile p and
arrives at time step h, and 0 otherwise.
• T
k
i
≥0, ∀ k ∈ M, ∀ i∈ N, berthing time of con-
tainer vessel i at berth k.
• T
k
o(k)
≥0, ∀ k ∈ M, ∀ i∈ N, starting operation time
of berth k.
• T
k
d(k)
≥0, ∀ k ∈ M, ∀ i∈ N, ending operation time
of berth k.
The corresponding MILP formulation for the TBAP
is stated as follows:
max
∑
i∈N
∑
p∈P
i
λ
p
i
ν
p
i
−
1
2
∑
i∈N
∑
j∈N
∑
k∈M
∑
w∈M
f
i j
d
kw
z
kw
i j
(1)
∑
k∈M
y
k
i
= 1 ∀i ∈ N (2)
∑
j∈N∪{d(k)}
x
k
o(k) j
= 1 ∀k ∈ M (3)
∑
i∈N∪{o(k)}
x
k
id(k)
= 1 ∀k ∈ M (4)
∑
j∈N∪{d(k)}
x
k
i j
−
∑
j∈N∪{o(k)}
x
k
ji
= 0 ∀k ∈ M, ∀i ∈ N
(5)
∑
j∈N∪{d(k)}
x
k
i j
= y
k
i
∀k ∈ M, ∀i ∈ N (6)
T
k
i
+
∑
p∈P
i
t
p
i
λ
p
i
− T
k
j
≤ (1 − x
k
i j
)M1
∀k ∈ M∀i ∈ N,
∀ j ∈ N ∪ {d(k)}
(7)
T
k
o(k)
− T
k
j
≤ (1 −x
k
o(k) j
)M2 ∀k ∈ M, ∀ j ∈ N (8)
a
i
y
k
i
≤ T
k
i
∀k ∈ M,∀i ∈ N (9)
T
k
i
≤ b
i
y
k
i
∀k ∈ M,∀i ∈ N (10)
a
k
≤ T
k
o(k)
∀k ∈ M (11)
T
k
d(k)
≤ b
k
∀k ∈ M (12)
∑
p∈P
i
λ
p
i
= 1 ∀i ∈ N (13)
∑
h∈H
s
γ
i
h
=
∑
p∈P
s
i
λ
p
i
∀i ∈ N, ∀s ∈ S (14)
∑
k∈M
T
k
i
− b
h
≤ (1 − γ
h
i
)M3 ∀h ∈ H, ∀i ∈ N (15)
a
h
−
∑
k∈M
T
k
i
≤ (1 − γ
h
i
)M4 ∀h ∈ H, ∀i ∈ N (16)
ρ
ph
i
≥ λ
p
i
+ γ
h
i
− 1 ∀h ∈ H, ∀i ∈ N, ∀p ∈ P
i
(17)
∑
i∈N
∑
p∈P
i
h
∑
u=max(h−t
p
i
+1;1)
ρ
pu
i
q
p(h−u+1)
i
≤ Q
h
∀h ∈ H
¯s
(18)
∑
k∈M
∑
w∈M
z
kw
i j
= g
i j
∀i, j ∈ N (19)
z
kw
i j
≤ y
k
i
∀i, j ∈ N ∀k,w ∈ M (20)
z
kw
i j
≤ y
w
j
∀i, j ∈ N ∀k,w ∈ M (21)
In this model M1, M2, M3 and M4 represent
sufficiently large constants. The objective function
(1) maximizes the sum of the values of the chosen
quay crane assignment profiles over all the container
vessels and, at the same time, minimizes the house-
keeping cost generated by the flows of containers ex-
changed between container vessels. Constraints (2)
establish that every container vessel must be assigned
to one and only one berth. Constraints (3) and (4) de-
fine the outcoming and incoming flows to the berths,
whereas flow conservation for the remaining vertices
is ensured by constraints (5). Constraints (6) establish
the link between variables x
k
i j
, whereas precedences
in every sequence are ensured by constraints (7) and
(8). The time windows of the container vessels are de-
fined by the constraints (9) and (10), whereas berths
time windows are defined by constraints (11) and
(12). Constraints (13) ensure that one and only one
QC profile is assigned to every container vessel. Con-
straints (14) define the link between variables γ
h
i
and
λ
p
i
, whereas constraints (15) and (16) link binary vari-
ables γ
h
i
and T
k
i
. Variables ρ
ph
i
are linked to variables
λ
p
i
and γ
h
i
by constraints (17). Finally, constraints (18)
ensure that, at every time step, the total number of as-
signed QCs does not exceed the number of maximum
QCs available in the terminal. Constraints (19), (20)
and (21) are included to linearize the quadratic objec-
tive function.
2.2 Quay Crane Scheduling Problem
The QCSP pursues to define the sequences of trans-
shipment operations performed by a set of quay
cranes in order to load and unload the containers as-
sociated with a given vessel berthed at the container
terminal.
The input data for the QCSP are composed by the
set of tasks Ω = {1,..., n} and the set of quay cranes
Q = {1,...,m} allocated to the vessel. Each task t ∈ Ω
represents a set of containers with similar character-
istics (weight, dimensions, destination port, etc.) lo-
cated adjacent to each other in the same bay, l
t
. The
processing time of the task t ∈ Ω is denoted by p
t
.
Two dummy tasks 0 and T with p
0
= p
T
= 0 are con-
sidered with the goal of representing the beginning
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
292

0 1 2 3 4 5 6 7 8 9
1
2
3 4 5
6
7
8
QC
1
QC
2
Task, t
Position, l
t
Processing Time, p
t
1 2 3 4 5 6 7 8
1 1 3 4 6 6 6 8
10 8 10 15 7 6 5 10
Figure 2: Example of QCSP instance composed of 8 tasks.
and the ending of the vessel service, respectively. In
addition, we define the set
¯
Ω = Ω∪{0,T }. The struc-
ture of the vessel imposes limitations in the transship-
ment operations order (Kim and Park, 2004). For in-
stance, unloading operations have to be performed be-
fore loading operations. The precedence relationships
among tasks located in the same bay are defined by
the set Φ, in such a way that, (i, j) ∈ Φ if and only if
task i has to be finished before the starting of task j.
On the other hand, each quay crane q ∈ Q is located
in the bay l
q
0
and it is available after time r
q
. The time
required by the quay crane q ∈ Q to move between the
bays in which the tasks i, j ∈ Ω are currently located
is denoted by t
q
i j
. For safety reasons, the quay cranes
must keep a minimum distance between them, δ, and
measured in bay units. The safety distance gives rise
to that same pairs of tasks cannot be performed simul-
taneously due to the fact that they are close. These
pairs of tasks are gathered into the set Ψ.
The optimization criterion of the QCSP is to mini-
mize the makespan of the schedule, that is, the finish-
ing time of the last task performed by the quay cranes,
c
T
. The QCSP is already known to be an NP-hard
problem (Sammarra et al., 2007).
An example of the QCSP is depicted in Figure 2.
The example represents a vessel berthed at the quay
with 10 bays, ranged from the bay 0 up to the bay 9,
for which the bays 1, 3, 4, 6 and 8 have at least one
task to perform by a quay crane. For each bay, the
tasks are sorted according to their precedence rela-
tionships. For instance, the task 1 has to be performed
before the starting of task 2 in the bay 1. The location
and processing time of each task are reported in the
associated table. A schedule with 2 quay cranes for
this example is shown in Figure 3. The quay crane
1 performs the tasks 1, 2, 3, 5, 6 and 7, whereas the
quay crane 2 performs the tasks 4 and 8. As can be
seen, the quay cranes keep a safety distance of at least
2 bays and move with a speed of 1 bay per time unit.
In this case, the makespan is 52 time units.
0
1
2
3
4
5
6
7
8
9
0 10 20 30 40 50
Time
Bays
1 (10) 2 (8)
3 (10)
4 (15)
5 (7) 6 (6) 7 (5)
8 (10)
Figure 3: Schedule with 2 quay cranes for the example de-
picted in Figure 2.
In the following, we present the mathematical formu-
lation proposed by (Bierwirth and Meisel, 2009) for
the QCSP. The following notation is used by the for-
mulation:
• ∆
vw
i j
. Minimum temporal span to elapse between
the processing of the tasks i and j if they are pro-
cessed by the quay cranes v and w, respectively.
• Θ. Set of all combinations of tasks and quay
cranes that potentially lead to quay crane interfer-
ence.
The decision variables of the model are:
• x
k
i j
∈ {0,1}, set to 1 if tasks i and j are processed
consecutively by quay crane k, 0 otherwise.
• z
i j
∈ {0,1}, set to 1 if task j starts after the com-
pletion of task i, 0 otherwise.
The mathematical formulation is as follows:
minc
T
(22)
Subject to:
∑
j∈Ω
T
x
k
0 j
= 1,∀k ∈ Q (23)
∑
j∈Ω
0
x
k
jT
= 1,∀k ∈ Q (24)
∑
k∈Q
∑
j∈Ω
T
x
k
i j
= 1, ∀i ∈ Ω (25)
∑
j∈Ω
0
x
k
ji
−
∑
i∈Ω
T
x
k
i j
= 0, ∀i ∈ Ω,∀ ∈ Q (26)
c
i
+t
i j
+ p
j
−c
j
≤ M(1− x
k
i j
),∀i, j ∈
¯
Ω,∀k ∈ Q (27)
c
i
+ p
j
− c
j
≤ 0 , ∀(i, j) ∈ Φ (28)
c
i
+ p
j
− c
j
≤ M(1 − z
i j
),∀i, j ∈ Ω (29)
c
j
− p
j
− c
i
≤ Mz
i j
,∀i, j ∈ Ω (30)
z
i j
+ z
ji
= 1 , ∀(i, j) ∈ Ψ (31)
∑
u∈Ω
0
x
v
ui
+
∑
u∈Ω
0
x
w
u j
≤ 1 + z
i j
+ z
ji
,∀(i, j,v,w) ∈ Θ
(32)
FuzzyOptimizationModelsforSeasidePortLogistics
293

c
i
+ ∆
v
i j
w + p
j
− c
j
≤ M(3 − z
i j
−
∑
u∈Ω
0
x
v
ui
−
∑
u∈Ω
0
x
w
u j
),
∀(i, j,v,w) ∈ Θ (33)
c
j
+ ∆
v
i j
w + p
i
− c
i
≤ M(3 − z
ji
−
∑
u∈Ω
0
x
v
ui
−
∑
u∈Ω
0
x
w
u j
),
∀(i, j,v,w) ∈ Θ (34)
r +t
k
0 j
+ p
j
− c
j
≤ M(1 − x
k
0 j
),∀ j ∈ Ω,∀k ∈ Q (35)
c
i
≥ 0,∀i ∈
¯
Ω (36)
The minimization of the makespan is modeled by
(22). Each quay crane starts performing the task 0
and finishes performing the task T. This is mod-
eled by constraints (23) and (24). All the non-dummy
tasks have to be performed exactly once as set by con-
straints (25) and have a previous task and a succeed-
ing task, constraint (26). Constraints (27) set the fin-
ishing time of each task. Constraints (28) ensure the
precedence relationships among tasks. The values of
variables z
i j
are established by constraints (29) and
(30). Constraints (31) ensure the non-simultaneity
of tasks. The interference between quay cranes are
avoided by constraints (32)-(34). The ready times of
the quay cranes are handled by constraints (35). Fi-
nally, the domain of the finishing times of each task is
defined by constraints (36).
3 FUZZY COEFFICIENTS IN THE
CONSTRAINTS FOR THE TBAP
AND QCSP
In the TBAP, the arrival times of the vessels a
i
,i ∈ N,
are considered to be uncertain values. In the QCSP,
the processing times of the loading/unloading opera-
tions, p
t
, of the different tasks t ∈ Ω are also consid-
ered to be uncertain values. Even though the number
of quay cranes assigned to carry out the loading and
unloading operations of a container vessel is fixed, the
real service time, will depend on several factors, such
as interferences or breaks of the quay cranes assigned
to that container vessel.
Modeling the uncertainty in the values of the pa-
rameters can be tackled by considering that they are
fuzzy numbers. In this sense, independently of the
wide range of different models that may be used, the
problems above can be addressed by the following
model.
max{cx/A
f
x ≤
I
b
f
,x ≥ 0},
where A
f
and b
f
refer to the fact that we are consid-
ering fuzzy numbers in the coefficients that define the
restrictions (thereby allowing, as a trivial case, them
to also be real numbers when there are no ambigui-
ties), and the symbol ≤
I
means that the way of com-
paring both members in the inequality, due to formal
coherence, must be done by using a relationship for
ordering the fuzzy numbers. This comparison rela-
tion ≤
I
may be any one from the extensive list avail-
able (Wang and Kerre, 1996), which in turn would
also allow the decision-maker to have a greater de-
gree of freedom when it comes to establish prefer-
ences. In more specific terms, in order to provide
that theoretical model with a way for operating, let
us briefly refer back to the different indices for com-
paring fuzzy numbers that have been described in the
literature (Wang and Kerre, 1996). Amongst the dif-
ferent approaches described for comparing them, for
the sake of simplicity, in this paper we shall only deal
with the one that is derived from the use of indices
for comparison. Hence, by denoting as F(R) the set of
fuzzy numbers, if
I : F(R) → [0, 1]
is a comparison index for this kind of numbers, then
∀P
f
,Q
f
∈ F(R),P
f
≤
I
Q
f
⇔ I(P
f
) ≤ I(Q
f
)
whereby, according to the index I that is used, differ-
ent auxiliary models may be obtained for effectively
solving the problems described above from the prac-
tical point of view. Therefore, in general, the auxil-
iary models that are used to solve the problems de-
scribed above from the practical viewpoint, would be
approached as follows.
max{cx/I(A
f
x) ≤ I(b
f
),x ≥ 0 }
Using an index I or another depends on each
decision-maker, and hence what index I to choose to
be used is not the matter here. In order to illustrate the
approach, and as a trivial example, let us consider two
triangular fuzzy numbers P
f
,Q
f
∈ F(R), denoted as
usually as P
f
= (P,P
i
,P
d
) and Q
f
= (Q, Q
i
,Q
d
), and
as form of comparison, the one given by Yager’s First
Index (Wang and Kerre, 1996),
P
f
≤
I
Q
f
⇔ (1/3)(P+P
i
+P
d
) ≤ (1/3)(Q+Q
i
+Q
d
)
The membership function corresponding to a tri-
angular fuzzy number A
f
= (A,A
i
,A
d
) is stated as fol-
lows:
µ
A
f
(x) =
0, x ≤ A
i
x−A
i
A−A
i
, A
i
< x ≤ A
A
d
−x
A
d
−A
, A < x ≤ A
d
0, x ≥ A
d
Then, the previous model takes the following op-
erating form,
max{cx/(A +A
i
+ A
d
)x ≤ (b + b
i
+ b
d
),x ≥ 0}
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
294

from which we can obtain a solution for the previous
models in a straightforward way.
Since in the TBAP model described above, the ar-
rival times of the vessels, a
i
,i ∈ N, which cannot be
estimated accurately, appear as coefficients in the con-
straints, the methodology explained in this section can
be used to provide the decision makers with adequate
solutions. The same fact happens in the QCSP for-
mulation, in which the processing times of the load-
ing/unloading operations, p
t
, of the different tasks
t ∈ Ω, appear as coefficients in the constraints. When
applying this methodology with the Yager’s First In-
dex as a simple example, the original fuzzy models
can be converted into mixed integer linear models that
can be solved using any effective optimization tech-
nique from the literature.
4 OPTIMIZATION TECHNIQUES
In order to generate suitable solutions for the fuzzy
considerations of the TBAP and QCSP, the solution
approaches proposed by (Lalla-Ruiz et al., 2013) are
considered. These approaches are based on the Vari-
able Neighbourhood Search (VNS) which has demon-
strated to be a high competitive metaheuristic when
solving combinatorial and global optimization prob-
lems (Hansen et al., 2010). In general terms, the foun-
dation of a VNS is to perform a systematic change of
neighbourhood structures within a local search algo-
rithm.
With the goal of providing a self-contained paper,
in the following subsections we present the VNS ap-
proaches used for solving the TBAP and QCSP, re-
spectively. For further details the interested reader is
referred to (Lalla-Ruiz et al., 2013).
4.1 VNS for Solving the TBAP
Algorithm 1 depicts the pseudocode of the VNS used
for solving the TBAP. Given a solution ω, it considers
two neighbourhood structures based upon the reinser-
tion movement, N
a
(ω,λ), in which λ vessels and their
assigned profiles are removed from the berth b ∈ B
and reinserted into another berth b
′
, where b ̸= b
′
, and
the interchange movement, N
b
(ω), which consists of
exchanging a vessel v ∈ V assigned to berth b ∈ B with
another vessel v
′
assigned to berth b
′
, where b ̸= b
′
.
The starting solution of the VNS, ω, is generated
by assigning the profile p ∈ P with the highest usage
cost to each container vessel. The berthing position of
each vessel is selected at random, whereas the start-
ing of its service time is selected as the earliest pos-
sible within its time window (line 1). The value of
Algorithm 1: VNS for the TBAP.
1: ω ← Generate initial solution
2: k ← 1
3: repeat
4: ω
′
← Shake(ω,k)
5: k
1
← 1
6: repeat
7: ω
′′
← Local Search(ω
′
,k
1
)
8: if f (ω
′′
) > f (ω
′
) then
9: ω
′
← ω
′′
10: k
1
← 1
11: else
12: k
1
← k
1
+ 1
13: end if
14: until k
1
= k
1max
15: if f (ω
′
) > f (ω) then
16: ω ← ω
′
17: k ← 1
18: else
19: k ← k + 1
20: end if
21: until k = k
max
the parameter k is set to 1 (line 2). The shaking pro-
cess (line 4) allows to escape from those local optima
found along the search by using the neighbourhood
structure N
a
. The solution exploitation phase of the
VNS is based on a Variable Neighbourhood Descent
Search (VND) (lines 6 − 14). Given a solution ω
′
,
it explores one neighbourhood at a time until a local
optimum with respect to the neighbourhood structures
N
a
and N
b
is found. The application of the neighbour-
hoods structures in the VND is carried out according
to the value of the parameter k
1
, initially set to 1 (line
5). The first neighbourhood structure explored is N
a
and later N
b
. The best solution found by means of the
VND is denoted by ω
′
. The objective function value
of ω
′
allows to update the best solution found along
the search (denoted by ω) and restart the value of k
(lines 15 − 17). Otherwise, the value of k is increased
(line 19). These steps are carried out until k = k
max
(line 21).
4.2 VNS for Solving the QCSP
The pseudocode of the proposed VNS for solving the
QCSP is depicted in Algorithm 2. It is based upon
two neighbourhood structures, the reassignment (N
1
)
and interchange of tasks (N
2
). The search starts gen-
erating an initial schedule, σ, by assigning each task
t ∈ Ω to its nearest quay crane (line 1). The value
of the parameter k is also set to 1 (line 4). A shak-
ing procedure allows to reach unexplored regions of
FuzzyOptimizationModelsforSeasidePortLogistics
295

Algorithm 2: VNS for the QCSP.
1: σ ← Generate initial solution
2: ES ←
/
0
3: repeat
4: k ← 1
5: repeat
6: σ
′
← Shake(σ,k)
7: σ
′′
← Local Search(σ
′
)
8: Update ES
9: if f (σ
′′
) < f (σ) then
10: σ ← σ
′′
11: k ← 1
12: else
13: k ← k + 1
14: end if
15: until k = k
max
16: σ
′
,σ
′′
← Select schedules from ES
17: σ ← Combine(σ
′
,σ
′′
)
18: until Stopping Criteria
the search space by means of the reassignment of k
tasks to another quay crane. The reassigned tasks are
selected on the basis of a frequency memory. In this
way, at each step, a neighbour schedule, σ
′
, is gen-
erated at random from σ within the neighbourhood
structure N
k
(line 6). A local optimum, σ
′′
, is reached
through a local search based on the proposed neigh-
bourhood structures (line 7). An improvement in the
value of σ
′′
allows to update σ and restart k (lines 9,
10 and 11). Otherwise, the value of k is increased
(line 13). These steps are carried out until k = k
max
(line 15).
An elite set, ES, is included into the VNS with
the goal of collecting the promising schedules found
during the search process. It is composed of those
schedules with the lowest objective function value
and those local optima with the highest diversity in
the ES. The diversity of two schedules is measured
as the number of tasks performed by different quay
cranes. At each step, ES provides a pair of sched-
ules σ and σ
′
selected at random (line 16) in order
to be combined (line 17) and restart the search. The
combination process keeps those tasks performed by
the same quay crane, whereas the remaining ones are
randomly assigned to one quay crane on the basis of
the objective function values of σ and σ
′
.
5 COMPUTATIONAL
EXPERIMENTS
This section is devoted to assess and analyze the per-
formance of the VNSs described in the Section 4 for
solving the TBAP and the QCSP under imprecise sce-
narios. All the computational experiments described
along the present section have been carried out on a
computer equipped with a CPU Intel 3.16 GHz and 4
GB of RAM.
5.1 Computational Experiments for
the TBAP
The computational tests aimed at evaluating the be-
haviour of the VNS introduced in the Subsection 4.1
for the TBAP were conducted by using the prob-
lem instances proposed in the work by (Giallombardo
et al., 2010). These instances are based upon real
data provided by the Medcenter Container Terminal
of Gioia Tauro located in Italy. In this case, only
a subset of 9 of these instances are used during this
computational experiment. The size of the problem
instances ranges from 20 up to 40 container vessels
that must be located in 5 berths over a time horizon of
one week.
The Table 1 reports the computational results ob-
tained by means of the VNS over the group of in-
stances taken up from the benchmark suite described
above. The first column (Instance) shows the in-
stances to solve. For each instance, the name (Name),
the number of container vessels (N), the number of
berths (M) and the maximum number of quay crane
profiles per each vessel (P) are presented. The sec-
ond column (CPLEX) shows the upper bound (UB)
obtained by the CPLEX Optimizer with a maximum
computational time of 2 hours. The column VNS
shows the results obtained when the arrival time of
the vessels is deterministic. Under this heading, it is
reported the objective value of the best solution found
by the VNS ( f
V NS
), the execution time (t. (s.)) and the
relative error ((Gap (%)) regarding the upper bound.
Lastly, the next columns (V NS
S−I
and V NS
S−II
) show
the results by considering scenarios with fuzzy num-
bers to model the arrival times of the container ves-
sels. In this context, we have evaluated the perfor-
mance of the VNS concerning the following fuzzy
numbers:
• S-I = (a
i
, a
i
− 1, a
i
+ 4)
• S-II = (a
i
, a
i
− 2, a
i
+ 8)
These fuzzy scenarios (S-I and S-II) model, on one
hand, the anticipation or delay of the arrival time of
the container vessel arrived at port regarding their
expected times. These scenarios represent a com-
mon problem in maritime container terminals, since
the vessels are subject to tidal, traffic or contractual
changes. In this regard, these issues are frequently
translated into a delay of the expected arrival time of
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
296

the container vessel, due to that, the fuzzy numbers
of both scenarios S-I and S-II consider a higher de-
lay than anticipation of their arrival time. For each
scenario, the best solution value found by the VNS
( f
V NS
) and its required computational time (t. (s.)),
measured in seconds, are reported.
In spite of the change of scenario there is not a
clear trend in the target values, as it is reported in Ta-
ble 1. It is expected that the uncertainty in the ar-
rival times of the container vessels has a direct impact
on the feasibility of the solutions due to the reduc-
tion in the time window constraints and the availabil-
ity of quay cranes. Moreover, it may implicitly affect
to the objective function value if the late arrival of the
container vessel forces to allocate it in another berth
than the expected one. The reason is found in that
this fact would increase the housekeeping cost derived
from the transshipment operations. In this regard, the
anticipation or delay of the arrival time of the ves-
sels may also impact on the assignment of quay crane
profiles, namely, early arrival times would allow to
assign longer quay cranes profiles, whereas late ar-
rival times would require shorter quay crane profiles
if one is willing to keep the vessels assigned to their
initial assigned berth. These facts and further analy-
sis of the structure of the final solutions would be a
topic of future work. It is worth mentioning that for
the instances from the literature are obtained feasi-
ble solutions for fuzzy arrival times considered in this
computational experiment.
5.2 Computational Experiments for
the QCSP
In order to check the suitability of the VNS introduced
in the Subsection 4.2 for solving the QCSP, we have
considered a representative subset of the problem in-
stances proposed by (Bierwirth and Meisel, 2009).
The original set of instances is composed of 90 in-
stances grouped into 9 groups with 10 instances each
one. Each group of instances has different number of
tasks (from 10 up to 50) and quay cranes (from 2 up to
6) which allows to cover real-world scenarios. In this
case, we have selected one instance from each origi-
nal group in such a way that our benchmark suite is
composed of 9 instances. It is worth mentioning that,
as done in previous works, we have established in this
experiment that the quay cranes are available from the
starting of the service time (r
q
,∀q ∈ Q) and they have
to keep a safety distance of one bay (δ = 1) among
them.
Table 2 shows the computational results we have
obtained by means of the proposed VNS when solv-
ing the aforementioned instances. The first column
(Instance) reports the characteristics of the instances
used during the experiment: name (Name), number of
tasks (n) and number of quay cranes (m). The second
column (Optimal) shows the objective function value
of the optima schedules for the instances at hand re-
ported in the work by (Bierwirth and Meisel, 2009).
The third column (VNS) show the computational re-
sults obtained by means of the VNS described in the
Subsection 4.2 under deterministic scenarios. In this
case the objective function value of the best schedule
found during the search ( f
V NS
) and the computational
time (t. (m.)), measured in minutes, are reported. Fi-
nally, as described in the Section 3, we consider fuzzy
numbers to model the processing times of the tasks.
In this context we have evaluated the performance of
the VNS under the following fuzzy numbers:
• S-III = (p
t
, p
t
− 25%p
t
, p
t
+ 10%p
t
)
• S-IV = (p
t
, p
t
− 10%p
t
, p
t
+ 25%p
t
)
• S-V = (p
t
, p
t
− 10%p
t
, p
t
+ 50%p
t
)
The first fuzzy number (S-III) models that scenario in
which reductions in the processing time of the tasks
associated with a given container vessel are more
likely than delays. On the other hand, due to the
fact that delays in the processing time of the tasks are
the most common in maritime container terminals, we
have proposed the numbers S-IV and S-V considering
a higher delay than reduction. In this regard, Table 2
has one column (V NS
S−III
, V NS
S−IV
and V NS
S−V
)
with the computational results reported by the VNS
when the previous fuzzy numbers are taken into ac-
count. In each case, the objective function value of
the best schedule found during the search ( f
V NS
) and
the computational time (t. (m.)), measured in minutes,
are reported.
In spite of the fact that analyzing the performance
of the VNS under deterministic scenarios is not a ma-
jor goal of this work, with the aim of providing an
overall study we firstly focus on this issue. In this re-
gard, the computational results reported in the Table
2 indicate that the proposed VNS is highly effective
at finding optimal or near-optimal schedules for the
QCSP under deterministic scenarios (column VNS).
As can be seen, it provides the optima schedules for 7
instances from the benchmark suite at hand, whereas
the gap is below 1.2% in the worst case (k94). More-
over, below 4.5 minutes have been required for finish-
ing the search process in all the cases. An exhaustive
analysis of the performance of the VNS under deter-
ministic scenarios is described in the original work by
(Lalla-Ruiz et al., 2013). Additionally, the efficiency
of our optimization technique has allowed to apply it
successfully to integrated approach as that described
in the same work.
FuzzyOptimizationModelsforSeasidePortLogistics
297
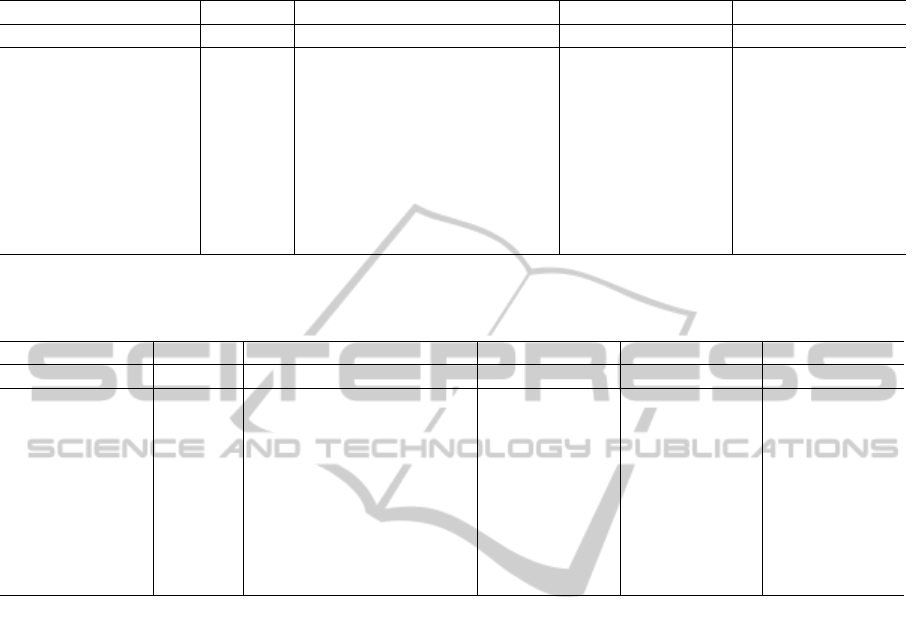
Table 1: Computational results obtained by means of the Variable Neighbourhood Search described in the Subsection 4.1
considering different fuzzy numbers.
Instance CPLEX VNS V NS
S−I
V NS
S−II
Name N M P UB f
V NS
t. (s.) Gap (%) f
V NS
t. (s.) f
V NS
t. (s.)
A
p10
20 5 10 1383614 1344035 8.70 2.86 1348244 16.70 1345272 71.87
A
p20
20 5 20 1384765 1349455 18.67 2.55 1344308 11.62 1346265 24.81
A
p30
20 5 30 1385119 1343119 13.09 3.03 1344374 10.56 1342836 13.14
B
p10
30 5 10 1613252 1546878 64.78 4.11 1557261 80.69 1542448 21.39
B
p20
30 5 20 1613769 1550839 26.26 3.90 1551015 27.90 1546422 28.03
B
p30
30 5 30 1613805 1553673 36.73 3.73 1550520 13.12 1548215 27.67
C
p10
40 5 10 2289660 2229807 195.76 2.61 2231800 170.91 2235877 176.04
C
p20
40 5 20 2290662 2234516 330.21 2.45 2231730 263.82 2229076 310.01
C
p30
40 5 30 2291301 2232260 228.64 2.58 2227989 221.56 2226721 134.12
Table 2: Computational results obtained by means of the Variable Neighbourhood Search described in the Subsection 4.2
considering different fuzzy numbers.
Instance Optimal VNS V NS
S−III
V NS
S−IV
V NS
S−V
Name n m Obj. f
V NS
t. (m.) Gap (%) f
V NS
t. (m.) f
V NS
t. (m.) f
V NS
t. (m.)
k13 10 2 453 453 < 0.01 0.00 423 < 0.01 468 < 0.01 504 < 0.01
k27 15 2 657 657 0.02 0.00 612 0.02 681 0.01 729 < 0.01
k42 20 3 573 573 0.11 0.00 540 0.08 591 0.04 639 0.04
k48 25 3 639 639 0.23 0.00 600 0.18 657 0.14 708 0.13
k53 30 4 717 717 0.64 0.00 675 0.50 741 0.48 804 0.47
k69 35 4 807 807 0.99 0.00 756 0.85 837 0.84 900 0.83
k82 40 5 717 723 2.22 0.84 678 2.29 747 2.30 807 2.46
k89 45 5 843 843 2.83 0.00 792 2.94 867 2.67 942 2.76
k94 50 6 786 795 4.42 1.15 768 4.05 828 4.26 903 4.07
On the other hand, as might be expected, the uncer-
tainty on the processing times of the tasks defined by
the stowage plan of a given container vessel has a di-
rect impact on its service time (makespan). This is
evidenced in particular by a decrease in the objective
function value of the schedules obtained by the VNS
over those scenarios in which the processing times
tend to be shorter than the original ones. That is, when
the fuzzy number S-III is considered. For instance,
we have obtained a reduction of 51 time units in the
makespan of the schedule reported by the VNS for
the instance k89 in comparison with the deterministic
version of the problem. A similar reasoning should
be applied to the scenarios in which the processing
times of the tasks tend to be larger than the original
ones, that is, under the fuzzy numbers S-IV and S-V.
In these cases, the makespan of the schedules reported
by the VNS are larger than those of the schedules
found under the deterministic scenarios. For example,
an increase of 108 times units in the makespan of the
schedule reported by the VNS has been obtained for
the instance k94 when the fuzzy number S-V is con-
sidered in comparison with the deterministic version
of the problem. Finally, it is worth mentioning that
the makespan of the schedules found when the fuzzy
number S-V is considered are larger that those of the
schedules obtained under the fuzzy number S-IV. This
fact is derived from the higher increase produced in
the former case.
6 CONCLUSIONS
The maritime container terminals are large infrastruc-
tures aimed at serving the container vessels arrived at
port. In this regard, a berthing time and berthing po-
sition along the quay is assigned to each vessel. For
loading and unloading its containers, a subset of quay
cranes is allocated to it. These quay cranes perform
the loading and unloading operations associated with
the containers of the vessel. In this context, two rele-
vant logistical problems should be highlighted: Tacti-
cal Berth Allocation Problem (TBAP) and the Quay
Crane Scheduling Problem (QCSP). Unfortunately,
due to the inherent imprecision that appears in the
data involved in this environment, terminal managers
are particularly interested in solving these problems
by considering the uncertainty arising in the termi-
nals.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
298

In this paper the TBAP and the QCSP are tack-
led under imprecise scenarios. For this purpose, two
fuzzy models that consider the uncertainty of the
arrival time of the vessels and the processing time
of the quay cranes are proposed. Moreover, in or-
der to effectively solve these models, two solutions
approaches based on the Variable Neighbourhood
Search metaheuristic are introduced. Both methods
are able to provide feasible solutions with reasonable
computational times.
ACKNOWLEDGEMENTS
This work has been partially funded by the Spanish
Ministry of Economy and Competitiveness (project
TIN2012-32608). Christopher Exp
´
osito Izquierdo
and Eduardo Lalla-Ruiz thank CajaCanarias and the
Canary Government the financial support they receive
through their post-graduate grants, respectively.
REFERENCES
Bierwirth, C. and Meisel, F. (2009). A fast heuristic for
quay crane scheduling with interference constraints.
Journal of Scheduling, 12(4):345–360.
Bierwirth, C. and Meisel, F. (2010). A survey of berth al-
location and quay crane scheduling problems in con-
tainer terminals. European Journal of Operational Re-
search, 202(3):615 – 627.
Cadenas, J. and Verdegay, J. (2006). A primer on fuzzy
optimization models and methods. Iranian Journal of
Fuzzy Systems, 3(1):1–21.
Froyland, G., Koch, T., Megow, N., Duane, E., and Wren,
H. (2008). Optimizing the landside operation of a con-
tainer terminal. OR Spectrum, 30(1):53–75.
Giallombardo, G., Moccia, L., Salani, M., and Vacca, I.
(2010). Modeling and solving the tactical berth al-
location problem. Transportation Research Part B:
Methodological, 44(2):232–245.
Hansen, P., Mladenovi
´
c, N., and P
´
erez, J. A. M. (2010).
Variable neighbourhood search: methods and appli-
cations. Annals of Operations Research, 175(1):367–
407.
Herrera, F. and Verdegay, J. (1995). Three models of fuzzy
integer linear programming. European J. of Opera-
tional Research, 83(3):581 – 593.
Kim, K., Park, Y.-M., and Jin, M.-J. (2008). An optimal
layout of container yards. OR Spectrum, 30(4):675–
695.
Kim, K. H. and Park, Y.-M. (2004). A crane scheduling
method for port container terminals. European Jour-
nal of Operational Research, 156(3):752–768.
Lalla-Ruiz, E., Exp
´
osito-Izquierdo, C., Meli
´
an-Batista, B.,
and Moreno-Vega, J. M. (2013). A metaheuristic ap-
proach for the seaside operations in maritime con-
tainer terminals. In IWANN (Part II), volume 7903
of Lecture Notes in Computer Science. Springer.
Lalla-Ruiz, E., Meli
´
an-Batista, B., and Moreno-Vega, J. M.
(2012). Artificial intelligence hybrid heuristic based
on tabu search for the dynamic berth allocation prob-
lem. Engineering Applications of Artificial Intelli-
gence, 25(6):1132 – 1141.
Meisel, F. (2010). Seaside Operations Planning in Con-
tainer Terminals. Contributions to Management Sci-
ence. Physica-Verlag HD.
Petering, M. E. (2011). Decision support for yard capac-
ity, fleet composition, truck substitutability, and scal-
ability issues at seaport container terminals. Trans-
portation Research Part E: Logistics and Transporta-
tion Review, 47(1):85 – 103.
Sammarra, M., Cordeau, J.-F., Laporte, G., and Monaco,
M. F. (2007). A tabu search heuristic for the quay
crane scheduling problem. Journal of Scheduling,
10(4-5):327–336.
Sancho-Royo, A., Pelta, D., and Verdegay, J. (2006). A pro-
posal of metaheuristics based in the cooperation be-
tween operators in combinatorial optimization prob-
lems. In Proceedings of the IEEE 20-th Interna-
tional Parallel and Distributed Processing Sympo-
sium, Rhodes, Greece.
Stahlbock, R. and Voβ, S. (2008). Operations research at
container terminals: a literature update. OR Spectrum,
30:1–52.
Tiwari, A., Knowles, J., Avineri, E., Dahal, K., and Roy,
R. (2006). Applications of Soft Computing : Recent
Trends (Advances in Soft Computing Series). Springer.
Verdegay, J. (2003). Fuzzy Sets based Heuristics for Op-
timization. Studies in Fuzziness and Soft Computing.
Springer.
Wang, X. and Kerre, E. (1996). On the classification and the
dependencies of the ordering methods. In Ruan, D.,
editor, Fuzzy Logic Foundation and Industrial Appli-
cations. International Series in Intelligent Technolo-
gies, pages 73–90. Kluwer.
Wiegmans, B. W., Rietveld, P., and Nijkamp, P. (2001).
Container terminal services and quality. Serie Re-
search Memoranda 0040, VU University Amsterdam,
Faculty of Economics, Business Administration and
Econometrics.
FuzzyOptimizationModelsforSeasidePortLogistics
299
