Decision Support Systems to Obtain Decision Criteria by Fuzzy AHP

for Location of Renewable Energy Facilities

Juan M. Sánchez-Lozano

, Jose Angel Jiménez-Pérez

M. Socorro García-Cascales

and M. Teresa Lamata

Depto de Expresión Gráfica, Universidad Politécnica de Cartagena, Cartagena, Spain

Depto de Electrónica, Tecnología de Computadoras y Proyectos, Universidad Politécnica de Cartagena, Cartagena, Spain

Depto de Ciencias de la Computación e Inteligencia Artificial, CITIC, Universidad de Granada, 18071 Granada, Spain

Keywords: Decision Support Systems (DSS), Optimal Location, Renewable Energy Facilities, Fuzzy AHP.

Abstract: Location of Renewable Energy Facilities will depend on various factors such as environmental, orography

location and climatology criteria, which in turn are broken down into sub-criteria that will depend on the

technology to locate. The objective of the present paper is to obtain the weights of the decision criteria

which influence in the problem of location of renewable energy facilities, especially in wind farms and solar

plants (photovoltaic and thermoelectric). To that end a Decision Support System (DSS) has been designed

to help the decision-maker to obtain the weights of the criteria involved in this decision. Fuzzy AHP

methodology is used with that DSS for the extraction of expert knowledge and to model the vague and

imprecise data by triangular fuzzy numbers.

1 INTRODUCTION

Renewable energy is the energy obtained from

virtually inexhaustible natural sources, either due to

the vast amount of energy they contain, or because

they are able to regenerate by natural media. One of

the great problems of humanity’s dependence on

fossil fuels is their depletion and the environmental

impact they cause (Intergovernmental Panel on

Climate Change IPCC, 1992; United Nations, 1997).

When implementing renewable energy facilities,

the promoter must find and select the best location in

order to obtain a better use of energy and reduce the

risks that, in facilities of this size, can cause serious

economic and environmental damage (Kahraman et

al., 2009). It is, however, not unusual that in

choosing the right site among various sites, there is a

degree of uncertainty. If the knowledge and

experience of the decision group are combined with

methodologies and tools to assist in decision making

(Ramirez- Rosado et al., 2008), this uncertainty

could be avoided.

Decision Support Systems DSS (Turban et al.,

2006) appeared in the 1970s as solutions which

could be used to help with complex decision-making

and problem solving in a structured manner. The

DSS are particularly suitable for solving the same

complex problem several times. Location problems

in industrial plants and specifically in the problems

of locating renewable energy facilities there is a set

of decision criteria which affect the decision on the

location of these facilities and that will depend on

the type of technology (solar, wind ...) to be installed

on the facilities. Therefore it is of great interest to

have a DSS to help obtain the weights of criteria to

decide the optimal locations for renewable energy

installations.

Thus, this article focuses on the design of a DSS

that facilitates the decision maker to obtain the

weights of the criteria in a location problem of

renewable energy facilities.

The paper will be structured as follows: Section

2 will focus on the hierarchical structure of decision

criteria for the case of wind facilities and solar

photovoltaic and thermoelectric plants. Section 3

will focus on the design of the DSS algorithms to

work with and the data entry into the system.

Section 4 presents the results of the DSS output for

different renewable technologies and finally in

section 5 we present the main conclusions of the

paper.

300

Sanchez-Lozano J., Jimenez-Pérez J., Garcia-Cascales M. and Lamata M..

Decision Support Systems to Obtain Decision Criteria by Fuzzy AHP for Location of Renewable Energy Facilities.

DOI: 10.5220/0004655603000308

In Proceedings of the 5th International Joint Conference on Computational Intelligence (SCA-2013), pages 300-308

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 DECISION CRITERIA FOR

THE OPTIMAL LOCATION OF

RENEWABLE ENERGY

FACILITIES

It is necessary to know which criteria influence (and

to what extent), the decision-making problem

proposed. Although previous studies have been

conducted indicating the features that these criteria

should meet (Janke, 2010; Al-Yahyai et al., 2012),

the fact of using one or another will depend mainly

on the study area. However, it is possible to establish

common generic criteria that subsequently may be

decomposed into specific criteria of sub-criteria,

which will depend on the characteristics and nature

of the area to be analyzed.

Therefore, following the guidelines established

in (Aran Carrión et al., 2008), four groups of main

criteria will be established:

 Environment criterion

 Location criteria

 Orography criteria

 Climatology criteria

Through environment criterion it is not intended

to assess the impact that these facilities cause of

renewable energy plants in certain sites, the

description of this criterion is based on the

suitability of installing renewable energy plants

depending on the capacity that it presents a land to

host them. Location criteria will be compose on the

one hand by those criteria that allow to evaluate the

distances that it would have the future renewable

plants regarding infrastructures or areas in which

they cannot be implemented (cities, airports, masts,

etc) and, on the other hand by those criteria that will

not only allow to reduce the installation costs but

also will favour its performance (distance to main

roads, power lines, etc). Orography criteria are based

on both the extension and the orographic features

that it presents a land to implement this type of

facilities in order to minimize the installation costs

and increase efficiency, for example, to implement

solar facilities will not only be appropriate that the

land has sufficient area but it must also have low

slopes and a correct orientation. Finally climatology

criteria will allow evaluating the production capacity

of the renewable energy plants. It should be chosen

sites where these criteria present appropriate values

because these criteria are essential not only for the

correct operation of the plant but also to optimize the

production.

These criteria are common to the main renewable

energy facilities, and especially to those which this

paper is focused on: wind farms, solar photovoltaic

plants and thermoelectric plants.

The difference between the different

technologies exists in the definition of the sub-

criteria to be considered in the location, based on the

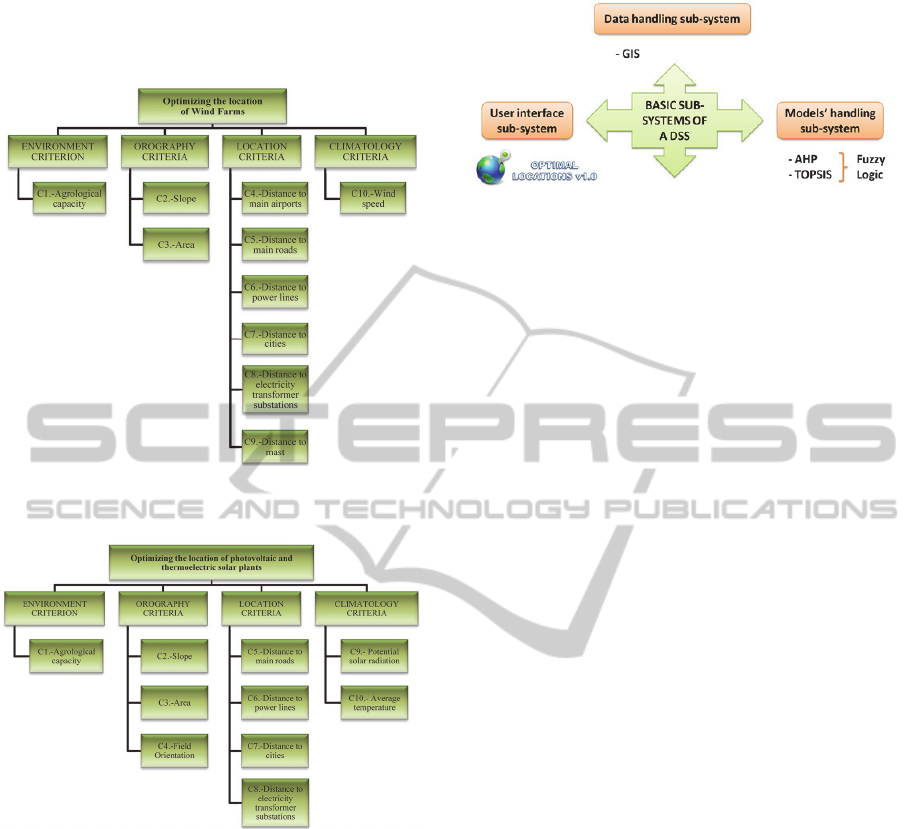
type of technology used. So for wind farms the

hierarchy of criteria is that shown in Figure 1 when

(Sanchez-Lozano et al., 2013b):

 C

: Agrological capacity (Classes): Suitability

of land for agricultural development, if the land

presents excellent agrological capacity it will

not be suitable to implement the renewable

facility and vice versa.

 C

: Slope (%): Inclination of the land, the

higher the percentage of surface inclination, the

worse fitness it will have to implement a wind

farm.

 C

: Area (m²): Surface contained within a

perimeter of land that can accommodate a

renewable energy facility.

 C

: Distance to main airports (m): Space of

interval between the nearest airport and the

different possible sites.

 C

: Distance to main roads (m): Space of

interval between the nearest main road and the

different possible sites.

 C

: Distance to power lines (m): Space of

interval between the nearest power line and the

different possible sites.

 C

: Distance to cities (m): Space of interval

between the population centres (cities and

towns) and the different possible sites.

 C

: Distance to electricity transformer

substations (m): Space of interval between the

nearest electricity transformer substation and

the different possible sites.

 C

: Distance to mast (m): Space of interval

between the nearest mast and the different

possible sites.

 C

: Wind speed (m/s): It corresponds to the

wind speed at an elevation of 80 meters in the

different possible sites.

In the case of solar photovoltaic and

thermoelectric plants the criteria tree is as in Figure

2 where we have some similar criteria (C

, C

, and C

) but others which are different

due to the technology used (Sanchez-Lozano et al.

2013a):

 C

: Field Orientation (Cardinal points): Position

or direction of the ground to a cardinal point.

 C

: Potential solar radiation (kJ·m²/day): It

corresponds to the amount of solar energy a

ground surface receives over a period of time

(day).

DecisionSupportSystemstoObtainDecisionCriteriabyFuzzyAHPforLocationofRenewableEnergyFacilities

301

 C

: Average temperature (ºC): Average

temperatures measured on ground in the course

of one year.

Figure 1: Criteria tree for optimizing the location of wind

farms.

Figure 2: Criteria tree for optimizing the location of

photovoltaic and thermoelectric plants.

3 DECISION SUPPORT SYSTEM

FOR LOCATION OF

RENEWABLE ENERGY

FACILITIES

We have developed a Decision Support System DSS

for the location of renewable energy facilities with

the structure shown in Figure 3 and called Optimal

Location v1.0.

Optimal Location v1.0 is formed by three sub-

systems (Turban et al., 2006):

 Data handling sub-system: Contains

information about the problem. In this case,

Figure 3: Structure of DSS.

the Data Base is obtained by means of a

Geographical Information Systems (GIS)

 Models’ handling sub-system: Mathematical

models that are used to solve the problem.

Optimal Location v1.0 uses AHP and the

TOPSIS method with or without fuzzy logic.

By means of AHP we obtain the weights of the

criteria.

AHP estimates the impact of each one of the

alternatives on the overall objective of the hierarchy.

In this method the quantified judgements provided

by experts in the field on pairs of criteria (Ci, Cj) are

represented in an nxn matrix expressed by the

following expression (1).

 C

C 



 c



 c













(1)

The c

value is supposed to be an approximation of

the relative importance of C

to C

, i.e., c

≈

). The statements below can be concluded:

≈ (w

) i, j = 1, 2, …, n

= 1, i=1, 2, …, n

If c

=α, α≠0, then c

=1/α , i=1,2,…, n

If C

is more important than C

then c



)

> 1

Matrix C should be a positive and reciprocal matrix

with 1´s in the main diagonal so; the expert needs

only to provide value judgments in the upper

triangle of the matrix.

TOPSIS method is applied to obtain the ranking

of the alternatives. Nevertheless, this paper has been

carried out with the aim of obtaining the weight of

the criteria.

 User interface sub-system: It is the

environment in which the user controls the

DSS. By means of this interface, on the one

hand we are able to introduce the input data in

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

302

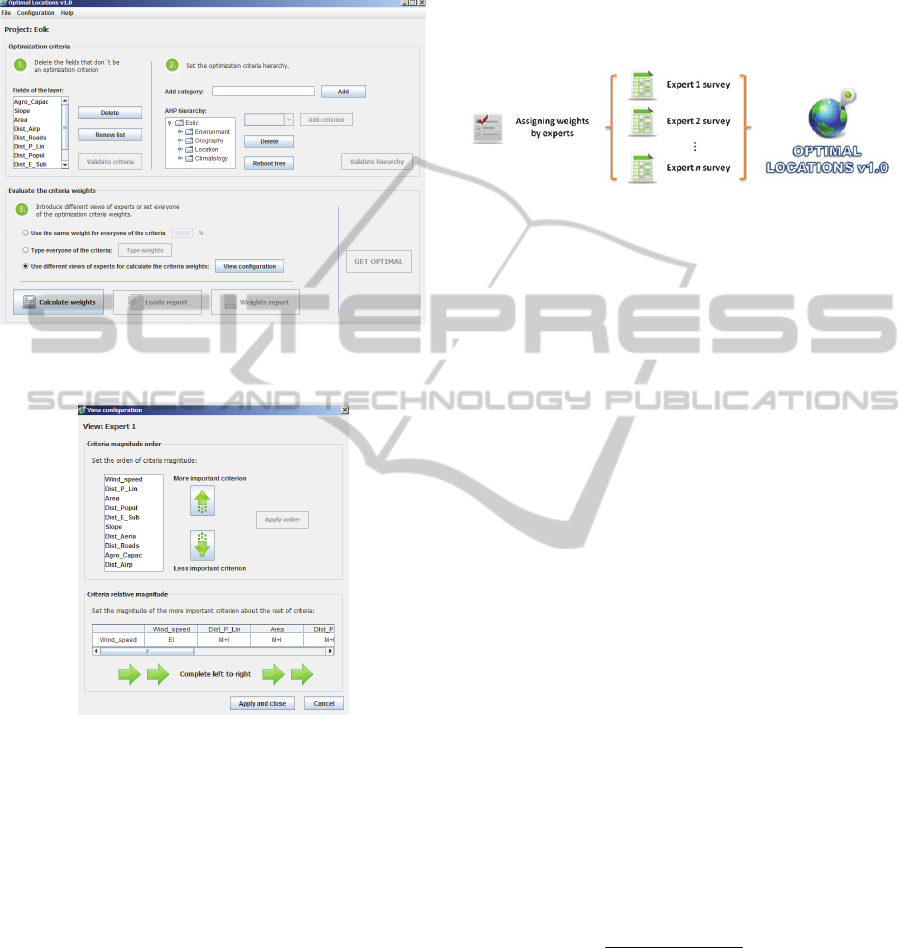
order to apply the AHP method (see Figures 4,

5) and on the other, we are able to show the

results (output of the DSS), these results are

shown in figs 8-13.

Figure 4: Insertion the criteria and categories in Optimal

Location v1.0.

Figure 5: Insertion the order of importance for each

criterion in Optimal Location v1.0.

3.1 Data Input to the DSS

The DSS starts with a file format ESRI Shape file

(.Shp.) (Zeiler, 2010) to perform its functions. This

file must have been previously published and

analysed on professional GIS software. In this

particular case, the gvSIG tool has been used

because it is free software.

For optimisation calculations it is necessary to

establish the relative importance of each decision

criterion. To do that, the DSS uses the AHP method

(Saaty, 1980, 1989).

This seeks to establish the pairwise comparisons

required by this method by conducting surveys to

different experts in the field. It is a pseudo-Delphi

technique, in which different independent experts

without mutual interaction value judgments made

for pairwise comparison. In this way, we aim to

obtain a vector of weights of the criteria from each

expert and then to produce a single weight vector by

performing an arithmetic mean between them, see

Figure 6.

Figure 6: Group Decision Making with Optimal Location

v1.0.

The information provided by the experts is

qualitative in character or is very vague since is has

been obtained through linguistic terms; because of

this the data obtained should be set modelled so that

further handling is feasible and easy.

Among the various options for representing

information and because, on the one hand the data is

grouped perfectly, and on the other, handling is

simple and effective, fuzzy numbers will be chosen

to represent information (Delgado et al., 1992;

Herrera et al., 2009).

In the case studied, the data provided shall be

represented by triangular fuzzy numbers (Zadeh

1965, Klir and Yuan, 1995; Dubois and Prade,

1980).

3.2 Treatment of the Data

For that purpose, a questionnaire similar to that

made by (Garcia-Cascales et al., 2012) was

developed, which was given to experts with the aim

of reducing uncertainty and imprecision of the

proposed problem. The Linguistic labels used in the

Fuzzy AHP model are shown in Table 1.

In AHP problems, where the values are fuzzy,

we will use the geometric normalized average,

expressed by the following expression (2):



ij ij ij

abc









(2)

where



ij ij ij

abc

is a fuzzy number

The group of experts involved in the decision

process answer a survey based in the Fuzzy AHP

model. In this case the way to obtain the weighted

criteria is type bottom to top (see Figure 7), this

DecisionSupportSystemstoObtainDecisionCriteriabyFuzzyAHPforLocationofRenewableEnergyFacilities

303

Table 1: Linguistic labels used in fuzzy AHP.

Verbal judgments of preferences between criterion i and criterion j Triangular fuzzy scale and reciprocals

Ci and Cj are equally important (II) (1, 1, 1) /(1,1,1)

Ci is slightly more/less important than Cj (S+I/S-I) (2, 3, 4)/(1/4,1/3,1/2)

Ci is strongly more/less important than Cj (+I/-I) (4, 5, 6)/ (1/6,1/5,1/4)

Ci is very strongly more/less important than Cj (VS+I/VS-I) (6, 7, 8)/ (1/8,1/7,1/6)

Ci is extremely more/less important than Cj (Ex+I/Ex-I) (8, 9, 9)/ (1/9,1/9,1/8)

is to calculate all the weights of the sub-criteria at

the second level by comparing all the sub- criteria

with each other. Subsequently, the sub-criteria are

aggregates to their main criterion.

The survey is divided into two parts:

The decision problem is explained indicating

what the goal to achieve is (optimal location of

sites for renewable energy facilities), the

methodology used and the criteria that

influence the decision making process. Thus,

the basic elements of the decision problem are

described through a hierarchical structure, as

shown in the criteria trees (Figures 1 and 2).

It is based on the hierarchical structure

described and its purpose is to gather data to

obtain the weight or coefficient of importance

of criteria. The survey consists of a block of

three questions:



: Do you believe that all the sub-criteria have

the same weight?

If the answer is yes, it will not be necessary to

apply any MCDM to obtain the weights of the

criteria, as these will have the same value.

Otherwise, i.e., if experts consider that not all

the criteria have equal importance, the second

question in the survey will be posed:



: List the criteria in descending importance.



: Compare the approach to be considered

first with respect to that considered secondly

and successively, using the linguistic labels in

Table 1.

Figure 7: AHP method Bottom to Top.

In the particular case of wind farms, the answers for

each of the sub-criteria indicated in fig. 2 were the

followings.

Answer Q1: NO

Answer Q2: The orders of importance for each of

the experts are shown in table 2.

Table 2: Order of importance of the sub-criteria for each

of the experts for the case of location of wind farms.

Criteria Expert 1 Expert 2 Expert 3

9º 10º 10º

6º 3º 5º

3º 8º 6º

10º 7º 9º

8º 5º 3º

2º 2º 7º

4º 6º 2º

5º 4º 4º

7º 9º 8º

1º 1º 1º

Answer Q3: The pair comparisons among sub-

criteria by the experts are shown in Table 3.

Table 3: Pair comparison among sub-criteria for the case

of location of wind farms by linguistic labels.

Expert 1 Expert 2 Expert 3

1º → 2º S+

VS+

S+

1º → 8º VS+

Ex+

1º → 5º S+

VS+

1º → 3º S+

VS+

1º → 9º Ex+

Ex+

1º →

º +

Ex+

VS+

1º → 4º S+

VS+

1º → 6º +

VS+

1º → 10º Ex+

Ex+

So, the weights of the criteria will be determined

by pair-wise comparison among criteria. As a result

of the data collection used, a total of (n-1)

comparisons will be required against the complete

AHP method n(n-1)/2 comparisons.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

304

3.3 Weights of the Criteria in Wind,

Photovoltaic and Thermoelectric

Plants

The results of the DSS output are discussed for the

three types of technologies and with the hierarchical

structure criteria according to figures 1 and 2, both

for the sub-criteria as well as for the principal

criteria.

3.3.1 Data Results for the Sub-criteria

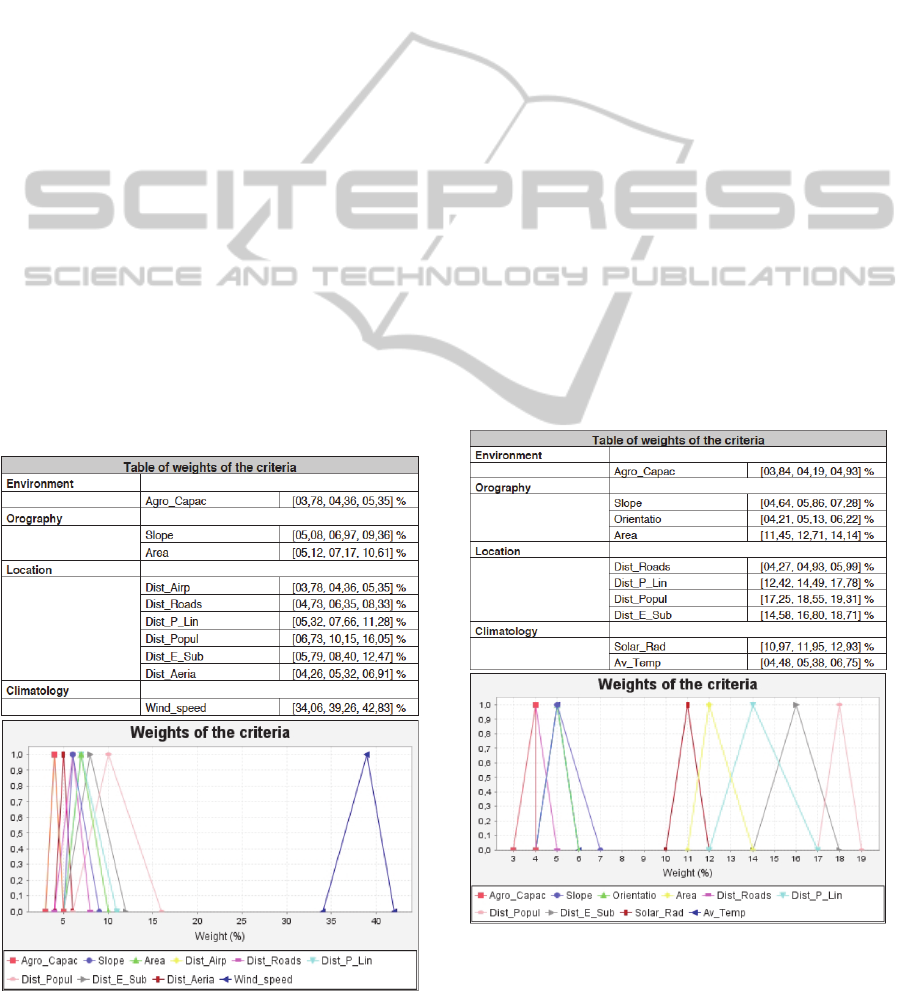
DSS provides the results for the sub-criteria as seen

in Figure 8, in the case of the decision sub-criteria

for the location of wind farms, Figure 9 for the case

of the decision sub-criteria for the location of solar

photovoltaic plants, and Figure 10 in the case of

decision sub-criteria for locating thermoelectric

plants.

In the case of wind farms the sub-criteria (Figure

8) which clearly stands out above the other sub-

criteria is the wind speed (C

) with almost 40% of

total weights. This result is logical since to

implement a wind farm, the wind speed plays a

crucial role, and if this is not enough in a given area,

that area is removed by any promoter of these

facilities. The remainder of these sub-criteria are

further apart and grouped around a weight between 5

and 10% of the total.

Figure 8: Weights of the sub-criteria criteria for wind farms.

This does not happen in the case of solar

technologies where there is not a single criterion

whose weight or importance coefficient is so high

that it allows to discard the rest. Analysing Figure 9

sub-criteria for photovoltaic plants it is shown that

the three best sub-criteria for the location problem

for solar plants are the distance to power lines (C

);

distance to electricity transformer substations (C

);

and distance to cities (C

), with the latter being the

highest rated. By contrast, the criteria that less

influence the decision, that is to say, those with the

lowest values, correspond to the sub-criterion of

agrological capacity (C

) and to the sub-criterion of

distance to main roads (C

The results are consistent since in the

implementation of a photovoltaic solar plant, the fact

of having a pour point to the nearest grid greatly

reduces the initial investment costs thus reducing the

payback period of the facility. However, it should

also be highlighted that the most important criterion

presented corresponds to the distance to centers of

population, the justification for this high weight can

be found in both the potential environmental impact

that this type of facility can generate and in growth

and expansion of cities because, given the useful life

of photovoltaic solar plants, implementing these

facilities in close proximity to centers of population

can condition their expansion.

Figure 9: Weights of the sub-criteria for photovoltaic plants.

DecisionSupportSystemstoObtainDecisionCriteriabyFuzzyAHPforLocationofRenewableEnergyFacilities

305

Analysing Figure 10, the sub-criteria

forthermoelectric plants it is shown that the three

best sub-criteria for the location problem for solar

thermoelectric plants are potential solar radiation

); distance to electricity transformer substations

); and area (C

), with the latter being the highest

rated. By contrast the sub-criteria that have less

influence in the decision in this case are distance to

cities (C

) and distance to roads (C

The results are consistent as solar thermoelectric

plants are facilities that not only require a territory

covering a large area, but also, the installed capacity

of them is usually very high (with the aim of

reducing the period of payback) therefore there is a

need to have nearby transformer substations that

allow to directly pour the electricity generated

because, if not, the promoter himself should meet

the additional cost of building a transformer

substation to discharge the energy generated in the

thermoelectric plant.

Figure 10: Weights of the sub-criteria for thermoelectric

plants.

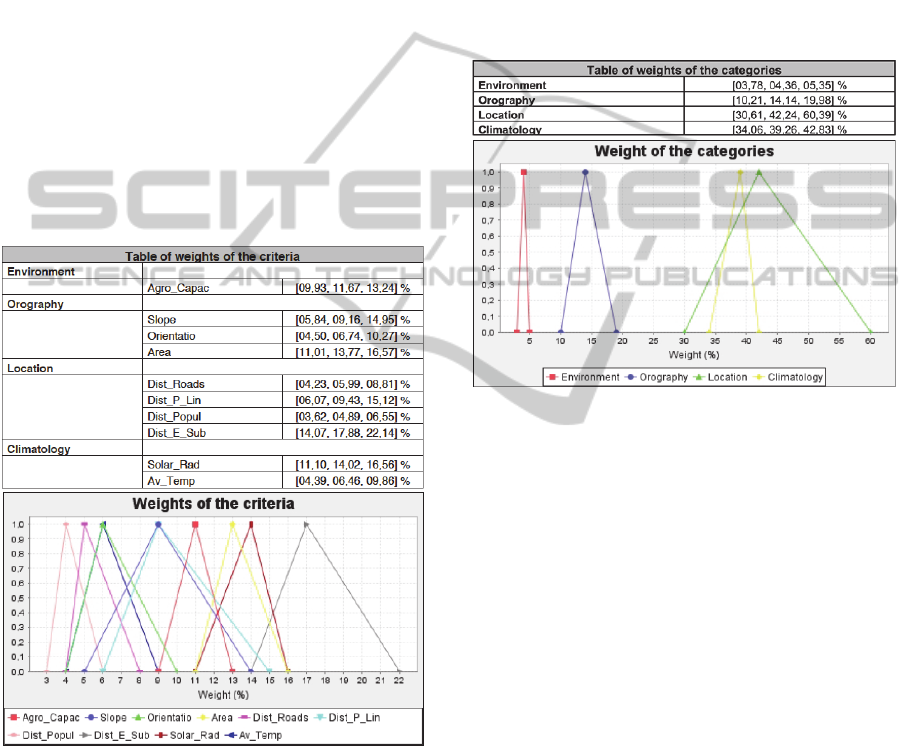
3.3.2 Data Results for the Main Criteria

The output results for the three technologies

considered and the inclusion of data from at least

three experts for each technology provides the

following DSS data: weights of the main criteria for

the location of wind farms (Figure 11); weights of

the main criteria for the location of photovoltaic

plants (Figure 12); and finally the weights of the

main criteria for the location of thermoelectric plants

(Figure 13). The results for the main criteria are

obtained from the aggregation bottom to top (Figure

7) of different sub-criteria grouped into each main

criterion, as can be seen in figures 1 and 2.

It seems clear that in general for all the primary

technologies the criterion which has more weight in

the decision is that of the location rather than

environmental criteria which have less weight in the

decision in all the technologies, wind, photovoltaic

and thermoelectric, see Figures 11, 12 and 13.

Figure 11: Weights of the main criteria for the location of

wind farms.

However, the second criterion by weight is not

the same for all the technologies: in the case of the

location of wind farms the climatology criteria,

Figure 11. This is to a certain extent a logical result

since it is the only criterion in which humankind

cannot intervene to improve it, that is to say that

although a site may offer excellent conditions to

implant a wind farm, if there is hardly any wind or

the wind is very slight, then it cannot be an optimal

site for such an installation. While in the case of

solar, both photovoltaic, Figure 12, and

thermoelectric, Figure 13, it is the orography

criteria. The fact that this criterion is in second

position is principally due to the fact that the

proximity to or distance from population nuclei or

infrastructures which influence the decision are of

great importance when including if a zone is optimal

to implant this type of facilities.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

306

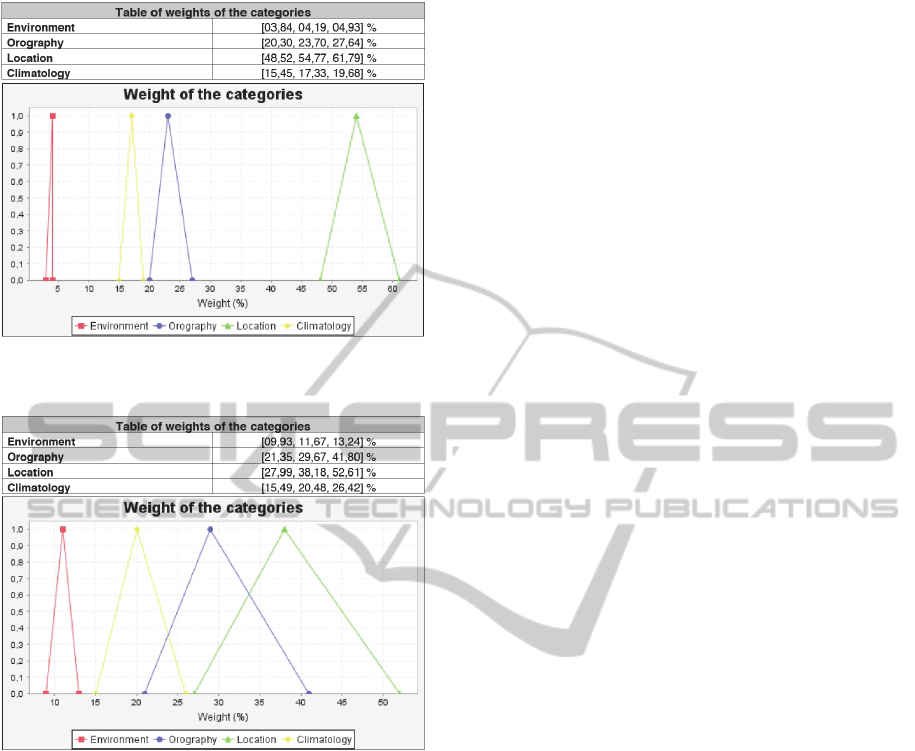
Figure 12: Weights of the main criteria for the location of

photovoltaic plants.

Figure 13: Weights of the main criteria for the location of

thermoelectric plants.

5 CONCLUSIONS

The study has shown that we must take into account

a number of criteria to select which is the best

location for renewable energy facilities (wind farms,

solar photovoltaic plants and solar thermoelectric

plants). Moreover, such criteria do not equally

influence in decision making so it is very important

to know beforehand the weights of these criteria for

each technology when implementing such facilities.

So it is interesting to show that there are

important differences among Eolic and Solar

technologies, and between the two solar

technologies there is a greater similarity.

It is of great interest for the promoters of

renewable energy facilities to have a tool such as

this, a DSS to model the importance of the decision

criteria when locating renewable energy installations

that aggregates all the information by different

experts to be involved in decision making.

This DSS is simple and intuitive to manage for

any expert in the field of renewable energy without

any knowledge of soft computing, when experts

only have to answer three simple questions to obtain

the weights of the criteria of sub-criteria involved in

the decision making of the optimal location for

renewable energy facilities.

ACKNOWLEDGEMENTS

This work is partially supported by FEDER

funds, the DGICYT and Junta de Andalucía

under projects TIN2011-27696-C02-01 and

P11-TIC-8001, respectively.

REFERENCES

Al-Yahyai, S., Charabi, Y., Gastli, A. & Al-Badi, A.,

(2012). Wind farm land suitability indexing using

multi-criteria analysis. Renewable Energy, 44, 80-87.

Arán-Carrión, J., Espín-Estrella, A., Aznar-Dols, F.,

Zamorano-Toro, M., Rodríguez, M., & Ramos-Ridao,

A., (2008). Environmental decision-support systems

for evaluating the carrying capacity of land areas:

Optimal site selection for grid-connected photovoltaic

power plants. Renewable and sustainable energy

reviews, 12, 2358-2380.

Delgado, M., Verdegay, J.L & Vila, M.A., 1992.

Linguistic Decision Making Models. International

Journal of Intelligent Systems. 7, pp. 479-492.

Dubois, D. & Prade, H., 1980. Fuzzy sets and systems:

theory and applications. New York, Academic Press

Inc.

García-Cascales M. S., Lamata M. T, J. M. Sánchez-

Lozano (2012). Evaluation of photovoltaic cells in a

multi-criteria decision making process, Annals of

Operations Research, 199, 373-391.

Herrera, F., Alonso, S. Chiclana, F. & Herrera-Viedma,

E., 2009. Computing with words in decision making:

foundations, trends and prospects. Fuzzy Optimization

Decision Making. 8. pp.337–364.

Intergovernmental Panel on Climate Change (1992)

Climate Change: The IPCC 1990 and 1992

assessments. World Meteorological Organization /

United Nations Environment Program. Canada.

Janke, J.R., (2010). Multicriteria GIS modeling of wind

and solar farms in Colorado. Renewable Energy, 35,

2228-2234.

Kahraman, C., Kaya, I. & Cebi, S., (2009). A comparative

analysis for multiattribute selection among renewable

energy alternatives using fuzzy axiomatic design and

DecisionSupportSystemstoObtainDecisionCriteriabyFuzzyAHPforLocationofRenewableEnergyFacilities

307

fuzzy analytic hierarchy process. Energy, 34, 1603–

1616.

Klir, G. J. & Yuan, B., 1995. Fuzzy sets and fuzzy logic:

theory and applications. Prentice Hall

Ramírez-Rosado, I. J., García-Garrido, E. G., Fernández-

Jiménez, L. A., Zorzano-Santamaría, P. J., Monteiro,

C. & Miranda, V., (2008). Promotion of new wind

farms based on a decision support system. Renewable

Energy, 33, 558–566.

Saaty, T. L., (1980). The Analytic Hierarchy Process.

McGraw-Hill, New York.

Saaty T. L. (1989) Group Decision Making and the AHP.

New York: Springer Verlag.

Sánchez-Lozano J. M., García-Cascales M.S., Lamata M.

T, (2013a). Decision Criteria for Optimal Location of

Solar Plants: Photovoltaic and Thermoelectric, F.

Cavallaro (ed.), Assessment and Simulation Tools for

Sustainable Energy Systems, Green Energy and

Technology 129, Springer-Verlag London.

Sánchez-Lozano J.M. García-Cascales M. S., Lamata M.

T, Sierra C. (2013b). Decision Criteria for Optimal

Location of Wind Farms. Exploring Innovative and

Successful Applications of Soft Computing IGI-

Global Editorial (In press).

Turban E., Aronson J. E., Liang T.-P. and Sharda R.

(2006). Decision Support and Business Intelligence

Systems (9

Edition)

United Nations, (1997). Framework convention on

climatic change: Report of the conference of the

parties on its third session. Adoption of the Kyoto

Protocol, Kyoto

Zadeh L. A. (1965). Fuzzy sets. Information and Control,

8. Pp. 338-353.

Zeiler M. (2010). Modeling Our World. The ESRI Guide

to Geodatabase Design. Second edition, Esri Press.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

308