
Hierarchical Qualitative Descriptions of Perceptions for Robotic
Environments
E. Mu
˜
noz, T. Nakama and E. Ruspini
Collaborative intelligent agents Lab, European Centre for Soft Computing, C/ Gonzalo Guti
´
errez Quir
´
os, Mieres, Spain
Keywords:
Human-robot Teams, Information Abstraction, Precisiated Natural Language.
Abstract:
The development and uptake of robotic technologies, outside the research community, has been hindered by
the fact that robotic systems are notably lacking in flexibility. Introducing humans in robot teams promises
to improve their flexibility. However, the major underlying difficulty in the development of human-robot
teams is the inability of robots to emulate important cognitive capabilities of human beings due to the lack
of approaches to generate and effectively abstract salient semantic aspects of information and big data sets.
In this paper we develop a general framework for information abstraction that allows robots to obtain high
level descriptions of their perceptions. These descriptions are represented using a formal predicate logic that
emulates natural language structures, facilitating human understanding while it remains easy to interpret by
robots. In addition, the proposed formal logic constitutes a precisiation language that generalizes Zadeh’s
Precisiated Natural Language, providing new tools for the computation with perceptions.
1 INTRODUCTION
Multi-robot teams are successfully employed in a
broadening range of application areas. However,
purely robotic systems are rather unflexible and have
difficulties adapting to unexpected changes in the en-
vironment. Introducing humans in robotic teams can
alleviate these problems, adding the required flexi-
bility and adaptability. Especially when humans and
robots collaborate as peers, in contrast to scenarios
where humans use robots as mere tools.
Despite the advantages offered by human-robot
teams, some challenging problems need to be ad-
dressed to favor their development and uptake, pri-
marily concerning human-robot interaction and coor-
dination. Humans can easily share information and
coordinate due to their ability to abstract and aggre-
gate salient information about complex objects and
events. Nonetheless, these abilities have not been
matched by robots yet. It is necessary to provide
robots with these capacities to support their integra-
tion in human-robot teams.
To a large extent robotic limitations are caused by
an unsuitable choice of tools to represent knowledge.
In most cases robots rely on technologies that empha-
size precision and detail, failing to recognize major
features, themes and motifs (“not seeing the forest
because of the trees”). These techniques have been
designed historically for computational convenience
rather than to facilitate understanding of the nature
and behavior of complex systems. Employing per-
ceptions, as defined by Zadeh (Zadeh, 2001), we can
overcome this problem, favoring the abstraction and
summarization of information at various levels.
Perceptions can be considered clumps of values
drawn together by some similarity measure, whose
boundaries are unsharp or fuzzy (Zadeh, 2001). Con-
ceiving perceptions as fuzzy-granules, or f-granules,
helps to avoid emphasis on detail and precision that
is detrimental to the obtaining of high-level abstrac-
tions, and makes it possible to imitate the ways in
which human concepts are created, organized and ma-
nipulated (Dubois and Prade, 1996; Zadeh, 1997).
In this paper we establish a framework that, em-
ploying perceptions as a base, permits the abstraction
of the information obtained by robots, and its commu-
nication through a quasi-natural language. We define
a formal logic to effectively define perceptions. In
formal logic each sentence is assigned a truth value
(in two valued logic, for example, it is either true or
false). In our framework a multi-valued logic is used,
and sentences can be assigned a truth value in the in-
terval [0, 1]. These truth values are computed using
what we have called perception functions, which are
inspired by f-granular definition of perceptions. This
paper is an extension of our previous work (Nakama
309
Muñoz E., Nakama T. and Ruspini E..
Hierarchical Qualitative Descriptions of Perceptions for Robotic Environments.
DOI: 10.5220/0004657703090319
In Proceedings of the 5th International Joint Conference on Computational Intelligence (SCA-2013), pages 309-319
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2013b), which introduced a formal logic to de-
scribe and specify robotic tasks. More details about
this framework can be also found in the companion
article (Nakama et al., 2013a), which discusses the
semantics of the formal logic.
We have chosen a formal logic as a middle-ground
between natural language used by humans and low
level data and instructions used by robots. A formal
logic can produce an indefinite number of sentences,
but avoids natural language ambiguity, and can be
easily interpreted and produced by robots. In addi-
tion, humans can also easily understand this logic,
since we adapt its syntax to the syntactic structures
frequently observed in natural language (Halliday and
Matthiessen, 2004). In particular, we aim to make it
accessible for naive users with a limited experience in
robotics.
The framework is organized following a hierarchy
of perception functions, where higher-level functions
are built combining lower-level ones. Using a simple
procedure, perception functions can be easily trans-
lated into sentences from the formal logic.
The proposed formal logic is also a first step to-
wards the establishing of an operative precisiation
language. A precisiation language (Zadeh, 2001;
Zadeh, 2004) is a subset of natural language that con-
sists of propositions that can be precisiated through
translation into a formal language, whose proposi-
tions can be used to compute and deduce with per-
ceptions.
The remainder of this paper is organized as fol-
lows. Section 2 discusses related work. The proposed
approach is presented in Section 3. Section 4 presents
a formal predicate logic to describe perceptions. A
methodology for defining perception functions is de-
fined in Section 5. A mechanism to translate percep-
tion functions into logic sentences is shown in Section
6. Section 7 presents the research conclusions.
2 RELATED WORK
In human robot interactions, humans have tradition-
ally played the role of teleoperators or supervisors
(Tang and Parker, 2006). Nonetheless, the improve-
ment in the capabilities of robots has favored the de-
velopment of teams where humans and robots collab-
orate as true peers. This kind of teams, in contrast to
human supervised teams and fully autonomous teams,
allow humans and robots to support each other in dif-
ferent ways as needs and capabilities change through-
out a task (Marble et al., 2004), overcoming the dif-
ferent disadvantages of the other approaches.
However, the development of this kind of teams
has been hindered by robotic limitations that prevent
a fluent communication between humans and robots.
In particular, robots’ inability to successfully abstract
salient information from perceived data is a flaw that
should be overcome to improve such communication.
This problem has been frequently studied in other
fields, particularly in computational intelligence, but
consistently ignored in robotics.
Notable among the approaches dealing with infor-
mation abstraction are Qualitative Object Description
methods (Zwir and Ruspini, 1999), which summa-
rize and abstract key qualitative features in a complex
computational object. These methods rely on combi-
nations of fuzzy logic, evolutionary computation, and
data mining techniques. They have been successfully
applied in a variety of fields, notably in molecular
biology (Romero-Zaliz et al., 2008) and time series
analysis (Zwir and Ruspini, 1999).
This problem has been also addressed in the field
of linguistic summarization (Yager, 1982). This ap-
proach, based upon the theory of fuzzy sets, uses tem-
plates to summarize big sets of data, and has been suc-
cesfully employed in time series (Wilbik, 2010) and
assistive environments (Anderson et al., 2008). Other
approaches include that of Fogel (Fogel, 2002), us-
ing methods for the learning and detection of seman-
tic features in complex systems, or the one proposed
by Martin et al. (Martin et al., 2006), who generated
fuzzy summaries by means of fuzzy associative rules.
However, the approaches above mainly proposed
ad-hoc methods particularly developed to address
concrete problems. In contrast, in this paper we pro-
pose a general framework that facilitates the creation
of summaries and abstractions.
In addition, the introduced predicate logic can
work as a precisiation language, allowing compu-
tation, manipulation and deduction using percep-
tions. We extend and generalize precisiation lan-
guage, which has been initially defined to represent
relations in the form
X isr R,
where X denotes a constrained variable, R denotes the
constraining relation, and r identifies the modality of
the constraint (Zadeh, 2001; Zadeh, 2004). The for-
mal logic introduced in this paper extends these re-
lations to include more complex sentences. Further-
more, we illustrate how to implement computation
with perceptions, which has not been previously done.
3 THE APPROACH
In this Section we introduce a framework that facil-
itates the expression of perceptions in a way easily
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
310

Figure 1: An example of the hierarchy.
comprehensible for both humans and robots. Percep-
tions are employed to describe an object or set of ob-
jects. We define object as any element relevant to
the problem being addressed, whose characteristics
need to be described. Some examples of objects, in
a robotic environment, may include: boxes, reports of
the state of a patient, people or other robots.
Perception descriptions abstract raw data obtained
by robot sensors using perception functions, which
are based on fuzzy set theory. Fuzzy sets are a natu-
ral choice to represent perceptions as f-granules. Em-
ploying this tool we can define high level concepts as
functions that evaluate the raw observations that de-
scribe an object, and indicate to what degree the ob-
ject is represented by the concept. Perception func-
tions are defined and described using a formal pred-
icate logic. Utilizing predicate logic we can con-
struct well formed sentences that have an unambigu-
ous meaning, facilitating robot interpretation, and a
structure similar to natural language, easing human
understanding. Furthermore, the degree of member-
ship obtained from the perception function represents
the truth value associated to a sentence, and allows
computing with them.
Perception functions are organized following a
double hierarchy, with a first hierarchy, called local
hierarchy, that describes single objects and a second
one, named global hierarchy, that characterizes sets
of objects. In both hierarchies, high-level perception
functions are built combining lower level perception
functions. Using a hierarchical structure we can pro-
duce abstract concepts at an appropriate level for the
targeted listener, for example depending on its back-
ground, or on the amount of information she prefers
to deal with. In addition, we can easily explain high
level perceptions using those perceptions that were
used to define them.
At the bottom of the local hierarchy we find de-
scriptions of individual objects that can be directly ob-
tained from observations. Their meaning is grounded,
because they can be directly mapped into measure-
ments of the perceived objects. Combining them
we can obtain more elaborated local perception func-
tions, conforming the second level of the hierarchy,
which can be combined analogously obtaining third
level, and so on.
If the number of objects is high, descriptions that
concern just one object may not be sufficient. For this
reason, It is necessary to define perception functions
that describe groups of objects aggregated according
to a significant grouping, the so-called global percep-
tion functions. Global perception functions that con-
stitute the first level of the global hierarchy are ob-
tained combining local perception functions from the
top-most level of the local hierarchy. Successively,
second level global perception functions are created
combining global perception functions from the first
one. This process can be iteratively applied until an
adequate level of aggregation is reached.
Figure 1 shows an example of the proposed idea,
where a robot monitors the state of a patient at pe-
riodic intervals of one minute. Using its sensors the
robot can measure the values of certain attributes, like
blood pressure, body temperature or pulse rate. As
a first level of abstraction we define fuzzy sets that
partition and describe those attributes. Next we com-
bine those simple concepts to create more elaborated
concepts that describe each time interval. These per-
ception functions represent the local hierarchy. Since
the patient is monitored for a long period of time it
is necessary to aggregate the obtained descriptions.
This is done aggregating observations at intervals of
HierarchicalQualitativeDescriptionsofPerceptionsforRoboticEnvironments
311

one hour, and defining perception functions that de-
scribe those intervals. This process can be repeated,
for instance, joining hour observations in eight hours
intervals, as shown in the example.
4 A FORMAL LOGIC TO
DESCRIBE PERCEPTIONS
In this section we introduce the predicate logic em-
ployed to describe perception functions in quasi-
natural language. To facilitate naive users’ under-
standing, sentences follow a syntax that seems closer
to propositional logic, where predicates are repre-
sented using quasi-natural language syntactic expres-
sions (box is red), instead of functions (is(box, red)).
It should be noted, however, that sentences belong to
a predicate logic, where the predicate is the verb and
the rest of components of the sentence are constants,
variables, quantifiers, qualifiers or operators. Instead
of propositional logic, we chose predicate logic be-
cause of its ability to deal with more complex sen-
tences that include quantifiers and variables, which,
in our opinion, are necessary to describe perceptions.
Due to space restrictions we cannot fully formal-
ize the predicate logic, but we will introduce its syn-
tax. In a previous work (Nakama et al., 2013b) we
fully characterized a propositional logic to describe
robotic tasks. The formal logic introduced here ex-
tends that approach to deal with perceptual informa-
tion.
4.1 Components of Well formed
Sentences
We start by defining the sets of components that can
compose a sentence. Such sets are called component
sets. We consider the following sets:
• Q denotes the set of quantifiers that can bound
a variable. For instance, we can consider Q =
{
All, Most, Some
}
.
• N indicates the set of object constants that can
be described using perceptions, where constant
is defined as a term that has a well determined
meaning that remains invariable (traditional def-
inition of constant in formal logic). For example,
N =
{
Box 1, Minute 1
}
.
• R denotes the set of object variables that can be
described using perceptions, with a variable be-
ing a term with no meaning by itself and whose
value can be substituted by any constant (tradi-
tional definition of variable in formal logic). For
example, R =
{
Boxes, Minutes
}
.
• A denotes the set of aggregation sets, which rep-
resent boundaries for variables. For instance, we
can consider A =
{
Room 1, Hour 1
}
.
• P specifies the set of prepositions that can be used
to link variables to aggregation sets. For instance,
P =
{
in
}
.
• S denotes the set of objects and aggregations of
objects that can be described using perceptions, it
can include constants, variables and bounded vari-
ables. Hence S = N ∪ R ∪ (R × P × A). Members
of this set constitute the subjects of well formed
sentences.
• V denotes the set of verbs or predicates em-
ployed to characterize objects. For instance, V =
{
be, have
}
.
• C specifies the set of complements that can de-
scribe objects, being these complements typically
perception functions. For instance, we can have
C =
{
red, blue, big, small, high, low
}
.
• T denotes the set of object attributes. For exam-
ple, T =
{
Color, Size, Pulse rate
}
.
• O indicates the set of available operators to com-
bine perceptions. As a first step, we will just
keep basic logic operators. Hence, we have O =
{
and, or, not
}
.
These elements are combined in a specific way to
form valid sentences. Table 1 summarizes the types
of sentences allowed in the framework.
4.2 Atomic Valid Sentences
An atomic valid sentence is defined to be a tuple that
consists of elements in the component sets. Each ad-
missible tuple structure is specified in the form of
a cartesian product of component sets. To develop
linguistic object descriptions, we employ tuple struc-
tures that reflect syntactic structures observed in nat-
ural language. We can distinguish two different types
of atomic valid sentences, copulative sentences and
attribute sentences.
4.2.1 Copulative Sentences
In linguistics a copulative sentence is a sentence
where the verb acts as a nexus between two meanings.
Such verbs are called copulative verbs, and have prac-
tically no meaning, acting as a copula between subject
and complement. The complement is the most impor-
tant word in the sentence, while the verb expresses
time, mode and aspect. In English, the most common
copulative verb is the verb to be. Other examples in-
clude to appear or to become.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
312

Table 1: Summary of sentence types.
Atomic Sentence (AS) Compound Sentence
Type Copulative Attribute
Basic Structure Q ×S ×V ×C Q ×S ×V ×C × T AS × O × AS
Example Some Minutes in Hour 1 Most Minutes in Hour 1 Minute 1 has Low Pulse rate and
are Normal have Low Pulse rate Minute 1 has High Temperature
Our framework emulates copulative sentences as
QSVC clauses, meaning that they can take values
from the cartesian product Q × S ×V ×C (where Q, S,
V , C, stand for quantifier, subject, verb and comple-
ment). Adding a “null element” to Q, we can also
have sentences in the form SVC. Bellow we show
some examples:
•
null
Q
Min 1
S
is
V
Normal
C
.
•
Most
Q
Hours
S
are
V
Abnormal
C
.
•
Some
Q
Minutes
R
in
P
Hour 1
A
S
are
V
Normal
C
.
4.2.2 Attribute Sentences
While copulative sentences describe objects charac-
teristics, we sometimes need to describe a specific
attribute. For example, Most Minutes have Normal
Heart rate. In some occasions this expressions can be
transformed into a copulative sentence. However, in
some others such transformation is not natural. For
that reason, we introduce attribute sentences. These
sentences are QSVCT clauses (where Q, S, V , C ,
T , stand for quantifier, subject, verb, complement
and attribute), with an admissible sentence structure
Q × S ×V × C × T . Q includes the “null element” in
order to allow the creation of SVCT clauses. The fol-
lowing examples show valid attribute sentences:
•
null
Q
Minute 1
S
has
V
High
C
Pulse rate
T
.To simplify
the notation we will omit instances of the null el-
ement. Thus, this sentence will be expressed as
Minute 1
S
has
V
High
C
Pulse rate
T
.
•
All
Q
Minutes
S
have
V
High
C
Temperature
T
.
•
Some
Q
Minutes
R
in
P
Hour 1
A
S
have
V
Low
C
Pulse rate
T
.
4.3 Compound Sentences
Copulative and attribute sentences constitute what we
call atomic sentences. Employing them we can create
many sentences, which are easy to specify and un-
derstand for humans. Meanwhile, the structural and
lexical constraints substantially limit the diversity and
flexibility of everyday language, ensuring that the re-
sulting summaries can be effectively interpreted and
created by robots.
However, in certain occasions, particularly when
it is necessary to define complex perception functions,
we may need to combine atomic sentences obtain-
ing more complex sentences, called compound sen-
tences. A compound sentence consists of multiple
atomic sentences combined using operators from the
set O. Some examples may include:
•
M inute 1
S
has
V
Low
C
Pulse rate
T
Atomic sentence
and
O
M inute 1
S
has
V
High
C
Temperature
T
Atomic sentence
.
•
Some
Q
Minutes
R
in
P
Hour 1
A
S
have
V
Low
C
Pulse rate
T
Atomic sentence
and
O
M ost
Q
Minutes
R
in
P
Hour 1
A
S
have
V
High
C
Temperature
T
Atomic sentence
.
compound sentences are the key mechanism that
allows the combination of perceptions to build the
double hierarchy.
5 PERCEPTION FUNCTIONS
5.1 Example
Before formalizing perception functions we illustrate
them by means of an example, where a robot rec-
ognizes boxes while navigating through a building.
Using its sensors the robot obtains a set of measure-
ments concerning some relevant attributes. In partic-
ular, each box has six attributes, height, width, length
and the three RGB color coordinates. For each at-
tribute we define fuzzy sets identifying level-0 local
perception functions. In this example we focus on
size attributes and employ the partitions shown in Fig-
ure 2, where low and high refer to height, narrow and
broad to width, and short and long to length. These
partitions were specifically designed for this example
in a subjective way. However, in many cases, in or-
der to design these partitions the help of an expert
or the use of more sophisticated tools will be neces-
sary, as explained in Section 5.5. To obtain a more
sophisticated description we can combine these three
HierarchicalQualitativeDescriptionsofPerceptionsforRoboticEnvironments
313
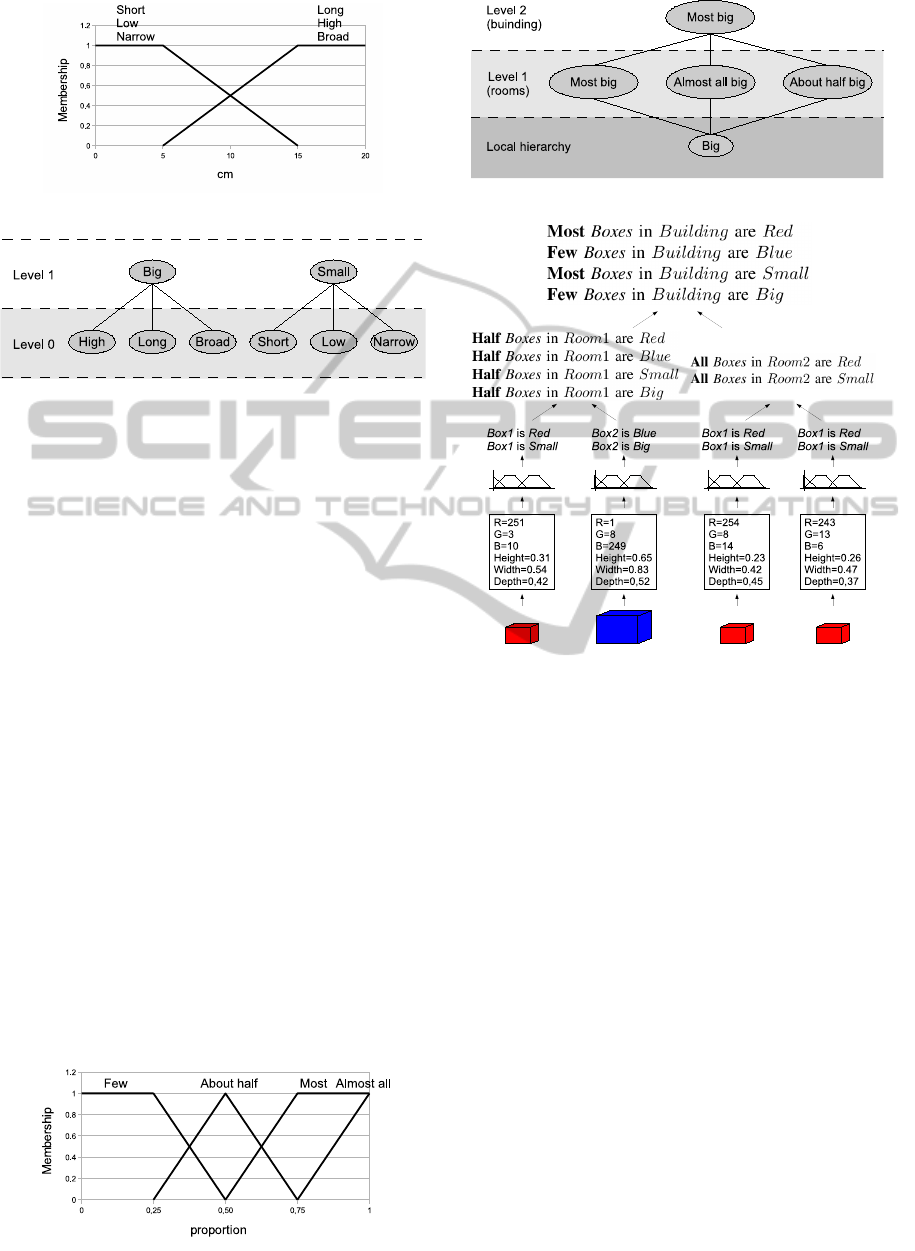
Figure 2: Fuzzy sets describing height, width and length.
Figure 3: Simple hierarchy of local perceptions.
attributes, creating the concept of size, and the per-
ceptions big and small. box is big could be defined as
box is high and box is broad and box is long, on the
other hand, box is small could be defined as box is low
and box is narrow and box is short. In this way we
have created a simple hierarchy of local perceptions
as the one showed in Figure 3.
Using these local perception functions we start
building the global hierarchy, which defines concepts
concerning more than one object. We group boxes
depending on their location and define global percep-
tions that describe sets of boxes present in a room.
Such perceptions are obtained combining top-most
perceptions from the local hierarchy. For instance, us-
ing fuzzy quantifiers we define Most boxes in Room
are Big, where most is a proportional quantifier as
shown in Figure 4. These fuzzy quantifiers were sub-
jectively defined trying to be as general as possible.
However, these concepts can be application depen-
dent and it could be necessary to use techniques as
those shown in Section 5.5 to define them. Follow-
ing the same procedure we can describe other global
perceptions functions as Few boxes in Room are Big,
About half boxes in Room are Small, and so on.
At a higher level it can be necessary to regroup
boxes, for example joining all boxes found in the
Figure 4: Fuzzy sets describing quantifiers.
Figure 5: Simple hierarchy of global perceptions.
Figure 6: An example of the obtained perceptions.
same building. If the building is just composed of
Room 1 and Room 2, this is the same as joining the
boxes from Room 1 and Room 2. For instance, we
can define more elaborated global perceptions as Most
boxes in building are big as a combination of percep-
tions from the first level. In particular, we can define
it as (Most Boxes in Room1 are Big and Most Boxes
in Room2 are big) or (Almost all Boxes in Room1 are
Big and About half Boxes in Room2 are Big). In a
similar way we can characterize other global percep-
tion functions as Few Boxes in building are big, About
half boxes in building are Big, Almost all boxes in
building are Big, and so on. Figure 5 shows the part
of the global hierarchy concerning the global percep-
tion function Most boxes in building are Big.
Figure 6 shows an example of the kind of abstrac-
tions obtained by a robot. In particular, the robot
observes four boxes present on a building with two
rooms, and employs the previously defined perception
functions to abstract data. Only those abstractions
that obtained a high membership value are shown.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
314

5.2 Fuzzy Sets, Fuzzy Quantifiers and
Perceptions
In this section we introduce some common concepts
used in fuzzy sets theory and necessary to fully un-
derstand this paper.
Let X be the universal set, or the set of all elements
of concern in a given context. In traditional crisp sets,
the function that defines a crisp set assigns each ele-
ment in the universal set a membership value of either
0 or 1, therefore discriminating between members and
nonmembers. In contrast, fuzzy sets generalize this
function in such a way that the values assigned to the
elements of the universal set fall within a specified
range and indicate the membership grade of these el-
ements in the set in question (Klir and Yuan, 1995).
Larger values denote higher degrees of set member-
ship. Such a function is called membership function.
Nonetheless, in order to obtain functions that rep-
resent complex concepts, single fuzzy sets are not
enough. Therefore it is necessary to combine different
fuzzy sets. This can be done using fuzzy operations
of complement, union and intersection.
The complement of a fuzzy set is specified in gen-
eral as c : [0, 1] → [0, 1], and represents the degree to
what an element does not belong to a fuzzy set. The
complement has to satisfy the following axioms (Klir
and Yuan, 1995):
• c(0) = 1 and c(1) = 0.
• ∀a, b ∈ [0, 1], i f a ≤ b, then c(a) ≥ c(b).
And it is desirable that satisfies these axioms:
• c is a continuous function.
• c is involutive, which means that c(c(a)) = a for
each a ∈ [0, 1].
Sugeno class complements (Sugeno, 1977) are a
widely used family of involutive complements.
The union of two fuzzy sets is specified in gen-
eral as u : [0, 1] × [0,1] → [0, 1], and has to satisfy the
following axioms:
• u(0, 0) = 0;u(0, 1) = u(1, 0) = u(1, 1) = 1;
• u(a, b) = u(b, a);
• If a ≤ a
′
and b ≤ b
′
, then u(a, b) ≤ u(a
′
, b
′
);
• u(u(a, b), c) = u(a, u(b, c)).
A function that satisfies these axioms is usually called
a triangular conorm or t-conorm. One of the most
commonly used t-conorms is max, however, many
others have been proposed (Klir and Yuan, 1995).
On the other hand, the intersection of two fuzzy
sets is specified in general as i : [0, 1] × [0, 1] → [0, 1],
and has to satisfy the following axioms:
• i(1, 1) = 1;i(0, 1) = i(1, 0) = i(0, 0) = 0;
• i(a, b) = i(b, a);
• If a ≤ a
′
and b ≤ b
′
, then i(a, b) ≤ i(a
′
, b
′
);
• i(i(a, b), c) = i(a, i(b, c)).
A function that satisfies these axioms is usually called
a triangular norm or t-norm. One of the most com-
monly used t-norms is min, however, many others
have been proposed (Klir and Yuan, 1995).
Along with these fuzzy operators it is necessary to
use linguistic or fuzzy quantifiers to define complex
functions. A quantifier is a logic operator that lim-
its a variable specifying its quantity. Zadeh (Zadeh,
1983) introduced fuzzy quantifiers, representing them
as fuzzy sets. We can distinguish two general classes
of quantifiers: absolute and relative. Absolute quan-
tifiers are defined as fuzzy subsets of [0, +∞] and can
be used to represent statements like, about six or less
than twenty. Relative quantifiers are defined as fuzzy
subsets of the interval [0, 1] and can express concepts
like most, about half or almost all.
5.3 Formalizing Perception Functions
Let us suppose that we are observing a set of objects
O =
{
1, 2, . . .
}
, where every object is described by
a set attributes A =
{
a
1
, . . . , a
n
}
, whose domains are
A
1
, . . . , A
n
, being n the number of attributes.
After observing an object o ∈ O we obtain a mea-
surement m
o
∈ ×A
i
, which specifies the values mea-
sured in the object for each attribute. We call M =
{
m
o
: o ∈ O
}
the set of all measurements, where for
each object o ∈ O we have exactly one measurement.
5.3.1 Local Perception Functions
We define local perception functions as functions
L
k
j
: ×
n
i=1
A
i
→ [0, 1] that describe individual objects,
where k indicates the level of the function in the hi-
erarchy, and j is an index to identify each function.
If k = 0, then L
k
j
(M
o
) represents a fuzzy membership
function. On the other hand, when k > 0 L
k
j
(m
o
) is de-
fined as a combination of local perception functions
from level k − 1, using fuzzy union (∧), intersection
(∨) and negation (¬). For example, L
1
1
can be defined
as L
1
1
(m
o
) = (L
0
1
(m
o
) ∧ L
0
2
(m
o
)) ∨ ¬L
0
5
(m
o
). This is a
process analogous to that followed in the example to
define function Big.
Note that we can take advantage of the fact that
every L
k
j
(M
o
) is defined as a function of local percep-
tion functions from level k − 1 to save computational
effort, by calculating truth values in ascending order.
HierarchicalQualitativeDescriptionsofPerceptionsforRoboticEnvironments
315

5.3.2 Global Perception Functions
Global perception functions describe groups of ob-
jects called aggregations. At each level of the global
hierarchy the set of measurements is partitioned ob-
taining a set of aggregations, or aggregation set, that
will be recursively defined. We will use a super-
script to specify the level of the aggregation set in
the global hierarchy. Let S
0
= M, then for each
level v ≥ 1 we define a partition S
v
of S
v−1
; S
v
=
{
s
v
1
, s
v
2
, ...
}
, ∀i, j ; i ̸= j; s
v
i
∩ s
v
j
=
/
0,
∪
s
v
l
= S
v−1
.
These partitions are used to group measurements in
sets from which we will obtain global perceptions. In
the example shown in Section 5.1, aggregation sets
correspond to the groupings of boxes, for instance,
boxes in room 1.
The domain induced by an aggregation set S
v
is
referred to as D
v
=
(
×
n
i=1
A
i
)
|
s
v
l
|
max
. Where
|
·
|
max
in-
dicates the maximum number of measurements m
o
that a s
v
l
∈ S
v
can contain. We characterize the r − th
global perception function from v − th level of the
global hierarchy as G
v
r
: D
v
→ [0, 1]. Such functions
describe groups of objects, indicating to which degree
they present a given characteristic. When k ≥ 1, the
r −th global perception function, G
v
r
, is obtained as a
combination of global perception functions from level
v−1, using ∧, ∨, ¬ and fuzzy quantifiers. When k = 0
G
v−1
r
are substituted by local perception functions of
the top-most level of the local hierarchy. For instance,
we can define G
3
1
(s
3
) = Q s
2
i
in s
3
j
are G
2
1
(s
2
i
), where
Q is a fuzzy quantifier.
In the example proposed in Section 5.1, percep-
tions Most Big (level 1 and 2), Almost all Big, About
half Big are examples of global perception functions,
which use diverse fuzzy quantifiers.
Since global perception functions are organized as
a hierarchy, where functions in the higher levels are
obtained as combinations of functions of lower levels,
we can easily simplify their domains. In this way,
the domain of G
v
r
can be reduced to [0, 1]
x
, where x
represents the number of perception functions from
level v − 1 that compose G
v
r
.
5.4 Partition of the Set of
Measurements
In order to create global perception functions it is nec-
essary to define adequate partitions of the set of mea-
surements M. In particular, one partition per hierar-
chy level. These partitions are crucial to obtain mean-
ingful descriptions of the data, and consequently, it
is necessary to define them carefully. We distinguish
two methods to define partitions, space-driven and
data-driven.
Sometimes the space where observed objects can
be found induces partitions in an intuitive or natural
way. For instance, in the example of the robot moni-
toring a patient, it was natural to group measurements
indicating activity in minutes, hours, and so on. Anal-
ogously, in the example of the robot exploring a build-
ing, observations where intuitively grouped depend-
ing on where they took place, a room, or a building.
We call these partitions space-driven partitions.
In certain occasions, however, the partition of the
set of measurements is not so immediate. Particu-
larly when perception functions are designed to find
specific or special structures among objects. In such
cases it is necessary to analyze data looking for those
specific patterns, and we cannot arbitrarily partition
the set of objects according to the structure of the
space. We need to group objects taking into account
the information they present and the defined percep-
tion functions. This process can be complex and may
require the use of approximate tools like genetic algo-
rithms. For instance, Zwir (Zwir and Ruspini, 1999)
and Romero-Zaliz (Romero-Zaliz et al., 2008), used
genetic algorithms together with fuzzy definitions of
structures to describe time series and DNA sequences,
respectively. Since these partitioning processes de-
pend on the actual data and perception functions, we
call them data-driven partitions.
5.5 Defining Perception Functions
Perception functions are the core of the proposed
framework, and thus, they have to be carefully speci-
fied. In most cases they can be defined with the help
of domain experts, who know which features are more
interesting or relevant. For example, in the medical
scenario previously introduced, experts like doctors
or nurses can indicate which information is more rel-
evant to detect potential problems. Many previous ef-
forts use this approach (Zwir and Ruspini, 1999; Mar-
tin et al., 2006; Anderson et al., 2008).
In other areas, however, defining perception func-
tions is not so automatic and it is necessary to discover
them from historical data. For instance, a robot used
for elder care may need to learn what can be consid-
ered the normal behavior of its owner, in order to dis-
cover uncommon behavior patterns that may indicate
health problems. In these cases the use of unsuper-
vised learning strategies, as fuzzy clustering, can be
very helpful. This approach has been used by Wilbik
et al. (Wilbik et al., 2012) and by Romero-Zaliz et al.
(Romero-Zaliz et al., 2008).
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
316

6 FROM PERCEPTION
FUNCTIONS TO SENTENCES
In this section we specify how perception functions
can be translated into valid sentences from the for-
mal logic and vice versa. To explain the process we
establish a mapping between component sets and the
elements used to build perception functions.
We assume that each object is represented by a
logic constant and has a unique identifier or name,
being all object names included in component set N.
Each attribute is also given a unique name and com-
ponent set T contains all attribute names. Each lo-
cal perception function is also given a unique name,
the set of all names of local perceptions is added to
component set C. In addition, for each local percep-
tion function it is necessary to indicate if it should be
worded as a copulative or an attribute sentence.
Local perception functions worded as attribute
sentences need one more step when their level is 1 or
more. In particular, a new artificial attribute has to be
created and added to T . For example, when we recog-
nize objects, the color is perceived with three different
attributes R, G, and B, and the attribute color is artifi-
cial, as it is obtained combining these three attributes.
Furthermore, the fact that level n, with n > 0, local
perception functions are obtained using fuzzy opera-
tors makes it possible to explain the meaning of the
perception function, obtaining a compound sentence
that includes all the level n − 1 local perception func-
tions that compose it. Such sentences are combined
using the operators in O =
{
and, or, not
}
.
When local perception functions are combined to
obtain global perception functions, the process to ob-
tain sentences is slightly different. First, in this case
the unique name is optional, since some of the func-
tions may only specify aggregations with no individ-
ual meaning. For instance, in the patient monitoring
example, we can specify that a night in which Most
hours in night are quiet can be also explained as night
is quiet . However, in the box aggregation example,
a sentence Some boxes in Room 1 are Blue, has no
equivalent copulative sentence. In any case, if they
are given a name, they follow a treatment similar to
level n local perception functions, where we have to
specify if they are copulative or attribute sentences. In
the last case, it is also necessary to indicate the name
of the artificial attribute and add it to T .
Obtaining an explanation for global perception
functions is a bit more complicated than for local,
given the fact that they may include quantifiers and
variables, in addition to logic operators. Quantifiers
treatment requires the definition of a unique name for
each quantifier. The set of all names of the available
quantifiers constitutes component set Q. Regarding
variables, it is necessary to define one variable name
per level in the hierarchy. Starting in level 1 with a
variable name for the domain of the objects, and con-
tinuing with each subsequent level. For instance, in
the patient monitoring example, since minutes consti-
tute the objects in level 1, we have minutes as level
1 variable name, hours as level 2 variable name, and
so on. On the other hand, in the boxes example, the
variable name for every level is boxes. Component set
R includes all variable names. In addition, all the ele-
ments included in aggregation sets need unique iden-
tifiers to allow their use as a subject or as a bound for
variables, and each one of these names has to be in-
cluded in component sets N and A. For instance, we
may obtain the following summaries,
Hour 1 is quiet
and Most minutes in Hour 1 are quiet, in which Hour
1 is the name of an element of level 2 aggregation
set that is used as a subject, in the first sentence, and
as a bound, in the second. With respect to combina-
tions of perception functions using logical operators
the process is equivalent to that used for local percep-
tion functions.
Once this mapping has been established we can
easily translate perception functions into sentences
and vice versa, obtaining a language that is both eas-
ily interpretable for humans and robots. Table 2 sum-
marizes the mapping between component sets and the
elements used to define perception functions.
7 CONCLUSIONS
In this paper we present a general framework to pro-
vide robots with information abstraction and aggre-
gation capabilities. This framework allows robots to
obtain high-level summaries and descriptions of com-
plex objects, events, and relations in terms that are
easy to comprehend by both humans and robots.
In order to obtain such abstractions we rely on
what Zadeh has described as perceptions (Zadeh,
2001), which group observations into fuzzy gran-
ules. This approach changes the traditional stand-
point, which emphasizes detail and precision. By do-
ing so we expect to overcome the problems shown
by traditional methods, which fail to recognize major
features, themes and motifs.
In addition, perceptions are translated into expres-
sions easy to interpret by humans and robots. We have
defined a predicate logic that acts as a middle-ground
between natural language and low-level commands,
which limits the diversity and flexibility of everyday
language. Nonetheless, logic sentences syntax emu-
lates syntactic structures frequently observed in nat-
HierarchicalQualitativeDescriptionsofPerceptionsforRoboticEnvironments
317

Table 2: Mapping between component sets and perception functions.
Component set Perception function element
Q Fuzzy quantifiers
N Object names, names of elements in aggregation sets
R variable names defined per level
A names of elements in aggregation sets
P purely linguistic, it does not depend on the perception function, initially we will only use in
S N ∪ R ∪ (R × P ×A)
V verbs that can be used, initially to be and to have
C local and global perception functions names (for those global that have a name)
T names of objects attributes and artificial attributes
O and, or, not
ural language, facilitating human interpretation, even
for naive users.
Perception functions, and their associated linguis-
tic descriptions, are organized following a hierar-
chy. This structure permits the creation of appropriate
summaries that change the level of detail depending
on the targeted user. It also provides an easy way to
explain high-level perceptions, navigating through the
hierarchy, and favors computational efficiency.
In addition this framework is a first step towards
obtaining an operative precisiation language that al-
lows us to compute with perceptions. Such language
makes it possible to represent the meaning of a propo-
sition drawn from a natural language. And conse-
quently, provides a basis for a significant enlargement
of the role of natural languages in scientific theories.
As future work we plan to extend the frame-
work, incrementing the number of available struc-
tures. Some possibilities include:
• The use of linguistic hedges to annotate comple-
ments/perception functions.
• The introduction of new types of declarative sen-
tences.
• Permitting the qualification of subjects. Like in
the sentence Most Red boxes are Big.
• Allowing the use of compound complements.
Like in the sentence Most boxes in Room 1 are
Red and Big.
ACKNOWLEDGEMENTS
This work is partially supported by the Spanish Min-
istry of Economy and Competitiveness through AB-
SYNTHE project (TIN2011-29824-C02-02).
REFERENCES
Anderson, D., Luke, R. H., Keller, J. M., and Skubic,
M. (2008). Extension of a soft-computing frame-
work for activity analysis from linguistic summariza-
tions of video. In Fuzzy Systems, 2008. FUZZ-IEEE
2008.(IEEE World Congress on Computational In-
telligence). IEEE International Conference on, pages
1404–1410.
Dubois, D. and Prade, H. (1996). Approximate and com-
monsense reasoning: From theory to practice. In Pro-
ceedings of the 9th International Symposium on Foun-
dations of Intelligent Systems, ISMIS ’96, pages 19–
33, London, UK, UK. Springer-Verlag.
Fogel, D. B. (2002). Blondie24: playing at the edge of
AI. Morgan Kaufmann Publishers Inc., San Francisco,
CA, USA.
Halliday, M. A. K. and Matthiessen, C. M. I. M. (2004). An
introduction to functional grammar / M.A.K. Halliday.
Hodder Arnold, London :, 3rd ed. / rev. by christian
M.I.M. matthiessen. edition.
Klir, G. J. and Yuan, B. (1995). Fuzzy sets and fuzzy logic:
theory and applications. Prentice-Hall, Inc., Upper
Saddle River, NJ, USA.
Marble, J. L., Bruemmer, D. J., Few, D. A., and Duden-
hoeffer, D. D. (2004). Evaluation of supervisory vs.
peer-peer interaction with human-robot teams. In
Proceedings of the Proceedings of the 37th Annual
Hawaii International Conference on System Sciences
(HICSS’04) - Track 5 - Volume 5.
Martin, T., Majeed, B., Lee, B.-S., and Clarke, N. (2006).
Fuzzy ambient intelligence for next generation tele-
care. In Fuzzy Systems, 2006 IEEE International Con-
ference on, pages 894–901.
Nakama, T., Mu
˜
noz, E., and Ruspini, E. (2013a). Gen-
eralization and formalization of precisiation language
with applications to human-robot interaction. To ap-
pear in Proceedings of the 5th International Confer-
ence on Fuzzy Computation Theory and Applications,
FCTA 2013.
Nakama, T., Mu
˜
noz, E., and Ruspini, E. (2013b). General-
izing precisiated natural language: A formal logic as
a precisiation language. To appear in Proceedings of
the 8th conference of the European Society for Fuzzy
Logic and Technology, EUSFLAT-2013.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
318

Romero-Zaliz, R., Rubio-Escudero, C., Cobb, J., Herrera,
F., Cordon, O., and Zwir, I. (2008). A multiobjective
evolutionary conceptual clustering methodology for
gene annotation within structural databases: A case
of study on the gene ontology database. Evolutionary
Computation, IEEE Transactions on, 12(6):679 –701.
Sugeno, M. (1977). Fuzzy measures and fuzzy integrals:
a survey. In Gupta, M., Saridis, G., and Gains, B.,
editors, Fuzzy automata and decision processes, pages
89–102. North Holland, Amsterdam.
Tang, F. and Parker, L. E. (2006). Peer-to-peer human-robot
teaming through reconfigurable schemas. In AAAI
Spring Symposium: To Boldly Go Where No Human-
Robot Team Has Gone Before, pages 26–29. AAAI.
Wilbik, A. (2010). Linguistic summaries of time series us-
ing fuzzy sets and their application for performance
analysis of mutual funds. PhD thesis, Polish Academy
of Sciences.
Wilbik, A., Keller, J., and Bezdek, J. (2012). Generation
of prototypes from sets of linguistic summaries. In
2012 IEEE International Conference on Fuzzy Sys-
tems (FUZZ-IEEE), pages 1 –8.
Yager, R. R. (1982). A new approach to the summarization
of data. Information Sciences, 28(1):69–86.
Zadeh, L. A. (1983). A computational approach to fuzzy
quantifiers in natural languages. Computers & Math-
ematics with Applications, 9(1):149–184.
Zadeh, L. A. (1997). Toward a theory of fuzzy information
granulation and its centrality in human reasoning and
fuzzy logic. Fuzzy Sets Syst., 90(2):111–127.
Zadeh, L. A. (2001). A new direction in AI: toward a
computational theory of perceptions. AI magazine,
22(1):73.
Zadeh, L. A. (2004). Precisiated natural language (PNL).
AI magazine, 25(3):74.
Zwir, I. S. and Ruspini, E. H. (1999). Qualitative object de-
scription: Initial reports of the exploration of the fron-
tier. In proceedings of the Joint EUROFUSE-SIC’99
International Conference.
HierarchicalQualitativeDescriptionsofPerceptionsforRoboticEnvironments
319
