Using a Fuzzy Decision Tree Ensemble for Tumor Classiﬁcation from

Gene Expression Data

Jos

e M. Cadenas

, M. Carmen Garrido

, Raquel Mart

ınez

, David A. Pelta

and Piero P. Bonissone

Dept. of Information Engineering and Communications, Computer Faculty, University of Murcia, Murcia, Spain

Dept. of Computer Science and Artiﬁcial Intelligence, University of Granada, Granada, Spain

General Electric Global Research, One Research Circle, Niskayuna, New York, U.S.A.

Keywords:

Fuzzy Random Forest, Gene Selection, Gene Expression Data, Tumor Datasets.

Abstract:

Machine learning techniques are useful tools that can help us in the knowledge extraction from gene expression

data in biological systems. In this paper two machine learning techniques are applied to tumor datasets based

on gene expression data. Both techniques are based on a fuzzy decision tree ensemble and are used to carry

out the classiﬁcation and selection of features on datasets. The classiﬁcation accuracies obtained both when

we use all genes to classify and when we only use the selected genes are high. However, in this second case

the result also increases the interpretability of the solution provided by the technique. Additionally, the feature

selection technique provides a ranking of importance of genes and a partitioning of the domains of the genes.

1 TUMOR CLASSIFICATION

FROM GENE EXPRESSION

DATA

The challenge of cancer treatment has been to tar-

get speciﬁc therapies to pathogenetically distinct tu-

mor types, to maximize efﬁcacy and minimize toxic-

ity. Improvements in cancer classiﬁcation have thus

been central to advances in cancer treatment. Can-

cer classiﬁcation is divided into two challenges: class

discovery and class prediction. Class discovery refers

to deﬁning previously unrecognized tumor subtypes.

Class prediction refers to the assignment of particu-

lar tumor examples to already-deﬁned classes. In the

early days, cancer classiﬁcation has been relying on

subjective judgment from experienced pathologists.

When microarray technology was discovered began

to be applied to cancer diagnosis. The most important

application of the microarray technique is to discrimi-

nate the normal and cancerous tissue samples accord-

ing to their expression levels, identify a small subset

of genes that are responsible for the disease and to

discover potential drugs, (Ghoraia et al., 2012).

Experimental techniques based on oligonu-

cleotide or cDNA arrays now allow the expression

level of thousands of genes to be monitored in par-

allel (Alon et al., 1999). To use the full potential of

such experiments, it is important to develop the ability

to process and extract useful information from large

gene expression datasets.

Constantly improving gene expression proﬁling

technologies are expected to provide understanding

and insight into cancer related cellular processes.

Gene expression data is also expected to signiﬁcantly

aid in the development of efﬁcient cancer diagnosis

and classiﬁcation platforms. Gene expression data

can help in better understanding of cancer. Normal

cells can evolve into malignant cancer cells through a

series of mutations in genes that control the cell cy-

cle, apoptosis, and genome integrity, to name only a

few. As determination of cancer type and stage is of-

ten crucial to the assignment of appropriate treatment

(Golub et al., 1999), a central goal of the analysis of

gene expression data is the identiﬁcation of sets of

genes that can serve, via expression proﬁling assays,

as classiﬁcation or diagnosis platforms.

Another important purpose of gene expression

studies is to improve understanding of cellular re-

sponses to drug treatment. Expression proﬁling as-

says performed before, during and after treatment, are

aimed at identifying drug responsive genes, indica-

tions of treatment outcomes, and at identifying poten-

tial drug targets (Clarke et al., 1999). More generally,

complete proﬁles can be considered as a potential ba-

sis for classiﬁcation of treatment progression or other

trends in the evolution of the treated cells.

320

Cadenas J., Garrido M., Martínez R., A. Pelta D. and P. Bonissone P..

Using a Fuzzy Decision Tree Ensemble for Tumor Classiﬁcation from Gene Expression Data.

DOI: 10.5220/0004658203200331

In Proceedings of the 5th International Joint Conference on Computational Intelligence (SCA-2013), pages 320-331

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Data obtained from cancer related gene expression

studies typically consists of expression level mea-

surements of thousands of genes. This complexity

calls for data analysis methodologies that will efﬁ-

ciently aid in extracting relevant biological informa-

tion. Previous gene expression analysis work em-

phasizes clustering techniques (nonsupervised classi-

ﬁcation), which aim at partitioning the set of genes

into subsets that are expressed similarly across differ-

ent conditions. On the other hand, supervised clas-

siﬁcation techniques (also called class prediction or

class discrimination) with the aim to assign examples

to predeﬁned categories, (Golub et al., 1999; Diaz-

Uriarte and de Andr

es, 2006; Nitsch et al., 2010).

The objectives of supervised classiﬁcation tech-

niques are: 1) to build accurate classiﬁers that enable

the reliable discrimination between different cancer

classes, 2) to identify biomarkers of diseases, i.e. a

small set of genes that leads to the correct discrimi-

nation between different cancer states. This second

purpose of supervised classiﬁcation can be achieved

by classiﬁers that provide understandable results and

indicate which genes contribute to the discrimination.

Following this line, in this paper the goal is to

apply two techniques to classify and select features

to tumor datasets in order to carry out an analysis of

these datasets and to obtain the information that pro-

vide understandable results. We use the Fuzzy Ran-

dom Forest method (FRF) proposed in (Bonissone

et al., 2010; Cadenas et al., 2012a) and the Feature Se-

lection Fuzzy Random Forest method (FRF-fs) pro-

posed in (Cadenas et al., 2013).

This paper is organized as follows. First, in Sec-

tion 2 some techniques applied to gene expression

data reported in literature are brieﬂy described. Next,

in Section 3, the applied methods are described. Then,

in Section 4 we perform an analysis of two tumor

datasets using these methods. Finally, in Section 5

remarks and conclusions are presented.

2 MACHINE LEARNING AND

GENE EXPRESSION DATA

In this section, we describe some of the machine

learning techniques used for the management of gene

expression data.

2.1 Cluster Analysis based Techniques

Clustering is one of the primary approaches to ana-

lyze such large amount of data to discover the groups

of co-expressed genes. In (Mukhopadhyaya and

Maulikb, 2009) an attempt to improve a fuzzy clus-

tering solution by using SVM classiﬁer is presented.

In this regard, two fuzzy clustering algorithm, VGA

and IFCM have been used.

In (Alon et al., 1999) a clustering algorithm to or-

ganize the data in a binary tree is used. The algorithm

was applied to both the genes and the tissues, reveal-

ing broad coherent patterns that suggest a high degree

of organization underlying gene expression in these

tissues. Coregulated families of genes clustered to-

gether. Clustering also separated cancerous from non-

cancerous tissue.

In (Golub et al., 1999) a SOM to divide the

leukemia examples into cluster is used. First, they

applied a two-cluster SOM to automatically discov-

ering the two types of leukemia. Next, they applied

a four-cluster SOM. They subsequently obtained im-

munophenotype data on the examples and found that

the four classes largely corresponded to AML, T-

lineage ALL, B-lineage ALL, and B-lineage ALL, re-

spectively. The four-cluster SOM thus divided the ex-

amples along another key biological distinction.

In (Ben-Dor et al., 2000) a clustering based clas-

siﬁer is built. The clustering algorithm on which the

classiﬁer is constructed is the CAST algorithm that

takes as input a threshold parameter t, which controls

the granularity of the resulting cluster structure, and

a similarity measure between the tissues. To classify

a example they cluster the training data and example,

maximizing compatibility to the labeling of the train-

ing data. Then they examine the labels of all elements

of the cluster the example belongs to and use a simple

majority rule to determine the unknown label.

2.2 Techniques for Feature Selection

and Supervised Classiﬁcation

Discovering novel disease genes is still challenging

for constitutional genetic diseases (a disease involv-

ing the entire body or having a widespread array of

symptoms) for which no prior knowledge is available.

Performing genetic studies frequently result in large

lists of candidate genes of which only few can be fol-

lowed up for further investigation. Gene prioritiza-

tion establishes the ranking of candidate genes based

on their relevance with respect to a biological process

of interest, from which the most promising genes can

be selected for further analysis, (Nitsch et al., 2010).

This is a special case of feature selection, a well-

known problem in machine learning.

In (Golub et al., 1999) a procedure that uses

a ﬁxed subset of “informative genes” is developed.

These “informative genes” are chosen based on their

correlation with the class distinction.

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

321

In (Diaz-Uriarte and de Andr

es, 2006), a Random

Forest ensemble is used to carry out the feature selec-

tion process for classiﬁcation from gene expression

data. The technique calculates a measure of impor-

tance for each feature based on how the permutation

of the values of that feature in the dataset affects to

the classiﬁcation of the out-of-bag (OOB) dataset of

each decision tree of ensemble (Breiman, 2001). Fol-

lowing this study, in (Genuer et al., 2010), a Random

forest ensemble which solves the problems existing in

(Diaz-Uriarte and de Andr

es, 2006) is proposed.

In (Duval and Hao, 2010) a study of classiﬁcation

of gene expression data using metaheuristics is pre-

sented. The authors show that gene selection can be

casted as a combinatorial search problem, and conse-

quently be handled by these optimization techniques.

In (Nitsch et al., 2010), four different strategies to

prioritize candidate genes are proposed. These strate-

gies are based on network analysis of differential ex-

pression using distinct machine learning approaches

to determine whether a gene is surrounded by highly

differentially expressed genes in a functional associa-

tion or protein-protein interaction network.

Another work to select genes is proposed in

(Dagliyan et al., 2011). This paper shows that a sys-

tematic and efﬁcient algorithm, mixed integer linear

programming based hyper-box enclosure (HBE) ap-

proach, can be applied to classiﬁcation of different

cancer types efﬁciently.

3 CLASSIFICATION AND

FEATURE SELECTION BY

FUZZY RANDOM FOREST

In this section, we describe the methods that we will

use in this paper.

3.1 Fuzzy Random Forest for

Classiﬁcation

We brieﬂy describe the Fuzzy Random Forest (FRF)

ensemble proposed in (Bonissone et al., 2010; Cade-

nas et al., 2012a). FRF ensemble was originally pre-

sented in (Bonissone et al., 2010), and then extended

in (Cadenas et al., 2012a), to handle imprecise and

uncertain data. We describe the basic elements that

compose this FRF ensemble and the types of data that

are supported by this ensemble in both learning and

classiﬁcation phases.

Fuzzy Random Forest Learning: Let E be a dataset.

FRF learning phase uses Algorithm 1 to generate the

FRF ensemble whose base classiﬁer is a Fuzzy Deci-

sion Tree (FDT). Algorithm 2 shows the FDT learning

algorithm, (Cadenas et al., 2012b).

Algorithm 1: FRFlearning.

1: Input: E, Fuzzy Partition; Output: FRF

2: begin

3: repeat

4: Take a random sample of |E| examples with replace-

ment from the dataset E

5: Apply Algorithm 2 to the subset of examples ob-

tained in the previous step to construct a FDT

6: until all FDTs are built to constitute the FRF ensemble

7: end

Algorithm 2: FDecisionTree.

1: Input: E, Fuzzy Partition; Output: FDT

2: begin

3: Start with the examples in E with values

Fuzzy Tree,root

(e) = 1 to all examples with a sin-

gle class and replicate the examples with set-valued

class and initialize their weight according to the

available knowledge about their class

4: Let A be the feature set (all numerical features are par-

titioned according to the Fuzzy Partition)

5: repeat

6: Choose a feature to the split at the node N

7: loop

8: Make a random selection of features from the set A

9: Compute the information gain for each selected

feature using the values χ

Fuzzy Tree,N

(e) of each e

in node N taking into account the function µ

simil(e)

for the cases required

10: Choose the feature such that information gain is

maximal

11: end loop

12: Divide N in children nodes according to possible se-

lected feature outputs in the previous step and re-

move it from the set A. Let E

be the dataset of each

child node

13: until the stopping criteria is satisﬁed

14: end

Algorithm 2 has been designed so that the FDTs

can be constructed without considering all the fea-

tures to split the nodes. Algorithm 2 is an algorithm

to construct FDTs where the numerical features have

been discretized by a fuzzy partition. The domain of

each numerical feature is represented by trapezoidal

fuzzy sets, F

, . . . , F

so each internal node of the

FDTs, whose division is based on a numerical feature,

generates a child node for each fuzzy set of the parti-

tion. Moreover, Algorithm 2 uses a function, denoted

by χ

t,N

(e), that indicates the degree with which the

example e satisﬁes the conditions that lead to node N

of FDT t. Each example e is composed of features

which can be crisp, missing, interval, fuzzy values

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

322

belonging (or not) to the fuzzy partition of the fea-

ture. Furthermore, we allow the class feature to be

set-valued. These examples (according to the value

of their features) have the following treatment:

• Each example e used in the training of the FDT t

has assigned an initial value χ

t,root

(e). If an ex-

ample has a single class this value is 1. If an

example has a set-valued class, it is replicated

with a weight according to the available knowl-

edge about the classes.

• According to the membership degree of the exam-

ple e to different fuzzy sets of partition of a split

based on a numerical feature:

– If the value of e is crisp, the example e

may belong to one or two children nodes,

i.e., µ

f uzzy set partition

(e) > 0. In this case

t,childnode

(e) = χ

t,node

(e) · µ

f uzzy set partition

(e).

– If the value of e is a fuzzy value matching with

one of the sets of the fuzzy partition of the fea-

ture, e will descend to the child node associ-

ated. In this case, χ

t,childnode

(e) = χ

t,node

(e).

– If the value of e is a fuzzy value different from

the sets of the fuzzy partition of the feature, or

the value of e is an interval value, we use a sim-

ilarity measure, µ

simil

(·), that, given the feature

“Attr” to be used to split a node, measures the

similarity between the values of the fuzzy par-

tition of the feature and fuzzy values or inter-

vals of the example in that feature. In this case,

childnode

(e) = χ

node

· µ

simil

(e).

– When the example e has a missing value, the

example descends to each child node node

h = 1, . . . , H

with a modiﬁed value proportion-

ately to the weight of each child node. The

modiﬁed value for each node

is calculate as

node

(e) = χ

node

(e) ·

T χ

node

T χ

node

where T χ

node

the sum of the weights of the examples with

known value in the feature i at node node and

T χ

node

is the sum of the weights of the exam-

ples with known value in the feature i that de-

scend to the child node node

Fuzzy Random Forest Classiﬁcation

The fuzzy classiﬁer module operates on FDTs of the

FRF ensemble using one of these two possible strate-

gies: Strategy 1 - Combining the information from the

different leaves reached in each FDT to obtain the de-

cision of each individual FDT and then applying the

same or another combination method to generate the

global decision of the FRF ensemble; and Strategy 2

- Combining the information from all leaves reached

from all FDTs to generate the global decision of the

3.2 Fuzzy Random Forest for Feature

Selection

The FRF-fs method (Cadenas et al., 2013) is classi-

ﬁed as a hybrid method that combines the ﬁlter and

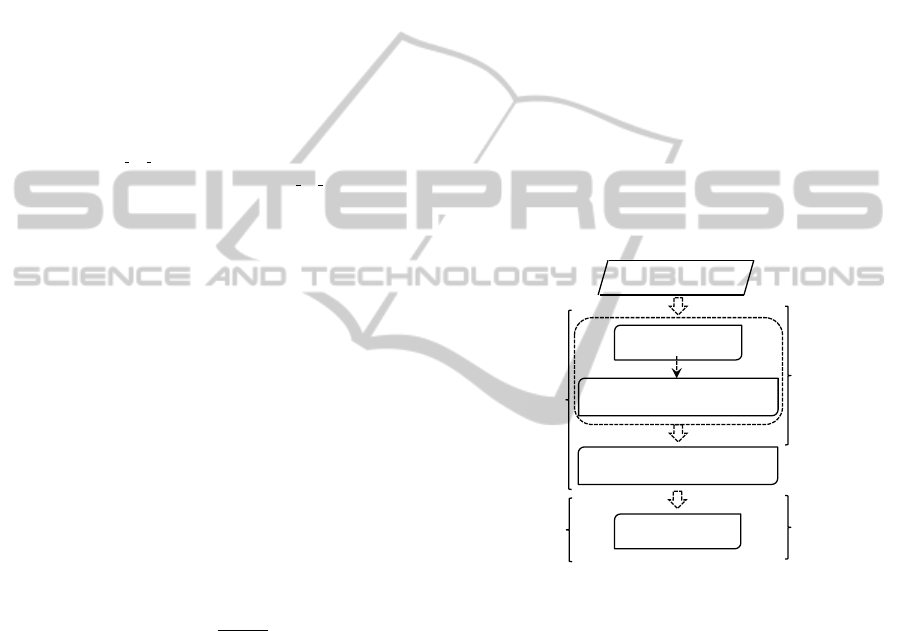
wrapper methods. The framework (Fig. 1) consists

of main steps: (1) Scaling and discretization process

of the feature set; and feature pre-selection using the

discretization process; (2) The feature pre-selection

ranking process using information given by Fuzzy

Random Forest ensemble; and (3) Wrapper feature se-

lection using a classiﬁcation technique. Starting from

the ordered features, this wrapper method constructs

an ascending sequence of sets of candidate features,

by invoking and testing the features stepwise. The

different feature subsets obtained by this process are

evaluated by a machine learning method. In each step,

the method obtains information useful to the user:

pre-selected feature subset, feature subsets ranking

and optimal feature subset.

Dataset Feature set

Ranking process of features

Feature subsets

Data preprocess

Obtaining subset of features

Preselection and Ranking

Optimal feature

subset

WRAPPER METHOD

FILTER METHOD

Figure 1:: Framework of FRF-fs.

In the ﬁlter method, we use the method proposed

in (Cadenas et al., 2012b). From the feature subset

and the dataset obtained with the ﬁlter method, we

apply FRF method. Once FRF ensemble has been ob-

tained, we have all the information about each FDT.

Algorithm 3 describes how information provided for

each FDT of the ensemble is compiled and used to

measure the importance of each feature.

More speciﬁcally, the information we get from

each FDT t for each feature a is the following:

• Information gain of node N for the feature a

(IG

) where the feature a has been selected as

the best candidate to split it.

• Depth level of node N (P

) where feature a has

been selected as the best candidate to split it.

• Classiﬁcation accuracy Acc

of FDT t when clas-

sifying the dataset OOB

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

323

Algorithm 3: INFFRF Information of the FRF.

1: Input: E, Fuzzy Partition, T N; Output: INF

2: begin

3: Building a Fuzzy Random Forest (Algorithm 1 - 3.1)

4: for each FDT t=1 to T N of the FRF ensemble do

5: Save the feature a chosen to split each node N, in-

formation gain of node, IG

, and the depth of that

node P

, in INF

6: Obtain the classiﬁcation accuracy Acc

of the FDT t

with its corresponding OOB

dataset.

7: end for

8: end

Algorithm 4 details how the information INF ob-

tained from the FRF ensemble is combined to obtain

an importance measure of the features where p

is the

weight we assign to feature a depending on the place

where it appears in the FDT t. After the information

is combined, the output of this algorithm is a matrix

(IMP) where for each FDT t and for each feature a,

the importance value obtained in the FDT t for the

feature a is stored.

Algorithm 4: IMPFRF Combining information INF.

1: Input: INF, T N; Output: IMP

2: begin

3: for each FDT t=1 to T N do

4: for each feature a=1 to |Attr| do

5: for all nodes N where feature a appears do

6: if P

= i then

7: IMP

= IMP

+ p

· IG

with i ≥ 0 and

rootnode

= 0

8: end if

9: end for

10: for each feature a=1 to |Attr| do

11: IMP

(

IMP

−min(IMP

)

max(IMP

)−min(IMP

)

· OOB

12: end for

13: The vector IMP

is ordered in descending or-

der, IMP

, where σ

is the permutation obtained

when ordering IMP

14: end for

15: end for

16: end

The idea behind the measure of importance of

each feature is that it uses the features of the FDTs

obtained and the decision nodes built with them in

the following way. The importance of a feature is de-

termined by its depth in a FDT. Therefore a feature

that appears on the top of a FDT is more important

in that FDT than another feature that appears in the

lower nodes. And, a FDT that has a classiﬁcation ac-

curacy greater than another to classify the correspond-

ing OOB (dataset independent of the training dataset)

is a better FDT. The ﬁnal decision is agreed by the

information obtained for all FDTs.

As a result of Algorithm 4, we obtain for each

FDT of FRF ensemble an importance ranking of fea-

tures. Speciﬁcally, we will have T N importance rank-

ings for each feature a. Applying an operator OWA,

we add them into one ranking. This ﬁnal ranking in-

dicates the deﬁnitive importance of the features.

OWA operators (Ordered Weighted Averaging)

were introduced by Yager in 1988, (Yager, 1988).

OWA operators are known as compensation opera-

tors. They are aggregation operators of numerical in-

formation that consider the order of the assessments

that will be added. In our case, we have T N ordered

sets. Given a weight vector W , the vector RANK rep-

resents the ranking of the pre-selected feature subset

and is obtained as follows (the vector RANK is or-

dered in descending order: RANK

OWAIMP

= W ·IMP

, for t = 1, . . . , T N

RANK

T N

∑

t=1

OWAIMP

tσ

(a)

, for a = 1, . . . , |A|

3.3 Wrapper for Feature Final Selection

Once the ranking of the pre-selected feature subset,

RANK

, is obtained, we have to ﬁnd an optimal sub-

set of features. One option to search the optimal sub-

set is by adding a single feature at a time following a

process that uses RANK

. The several feature subsets

obtained by this process are evaluated by a machine

learning method that supports low quality data (called

Classi f ier

LQD

) with a process of cross-validation.

The detailed process of the proposed wrapper method

is shown in Algorithm 5.

Starting from the ordered feature pre-selected,

construct an ascending sequence of FRF models, by

invoking and testing the features stepwise. We per-

form a sequential feature introduction in two phases:

• In the ﬁrst phase two feature subsets are built: the

feature subsets CF

base

and CF

comp

. A feature f

added to the CF

base

subset only if the decrease of

the error rate using the features of CF

base

∪ { f

}

subset exceeds a threshold δ

. The idea is that the

error decrease by adding f

must be signiﬁcant for

that feature to belong to the CF

base

subset. If when

we classify using the subset CF

base

∪{ f

}, an error

decrease smaller than a threshold δ

or an error

increase smaller than a threshold δ

is obtained,

becomes part of the subset CF

comp

• The second phase starts with both CF

base

and

comp

sets. We ﬁx CF

base

and add feature sub-

groups from CF

comp

to build several FRF mod-

els. This phase determines the ﬁnal feature set

with minimum error according to the conditions

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

324

reﬂected on line 22 of Algorithm 5. These con-

ditions are interpreted as “select the subset that

decrements the error in an amount over threshold

or decrements the error in an amount below δ

but using a smaller number of features.”

Algorithm 5: Wrapper method.

1: Input: E, candidate feature set C F and information

system RANK

; Output: C F

opt

selected feature set

2: begin

3: CF

comp

= {} and CF

base

= { f

} where f

is the ﬁrst

feature of RANK

4: ERR

= Classi f ier(E,CF

base

) using cross-validation,

BE = ERR

5: for each f

∈ CF, with i = 2, . . . , |CF| in the order de-

termined by RANK

6: ERR

= Classi f ier

LQD

(E,CF

base

∪ { f

}) using

cross-validation

7: if (BE − ERR

) > δ

then

8: CF

base

= CF

base

∪ { f

}

9: else

10: if (ERR

− BE) < δ

then

11: CF

comp

= CF

comp

∪ { f

}

12: end if

13: end if

14: end for

15: CF

aux

= CF

base

16: for each f

∈ CF

comp

, with i = 1, . . . , |CF

comp

| in the

order determined by RANK

17: B = CF

base

, ST OP = 0, j = i

18: while (STOP < δ

) and ( j ≤ |CF

comp

|) do

19: B = B ∪ { f

}

20: ERR

= Classi f ier

LQD

(D, B) using cross-

validation

21: if ((BE −ERR

) ≥ δ

) or (0 ≤ (BE −ERR

) < δ

and |CF

aux

| > |B|) then

22: CF

aux

= B, BE = ERR

23: else

24: if (ERR

− BE) > δ

then

25: ST OP = (ERR

− BE)

26: end if

27: end if

28: j = j + 1

29: end while

30: end for

31: Return: CF

opt

= CF

aux

32: end

4 FRF AND TUMOR

CLASSIFICATION

In this section we examine the performance of the

FRF ensemble for classiﬁcation and feature selection

from gene expression data.

4.1 Gene Expression Data

In this section, we describe the two datasets that we

will analyze. The ﬁrst dataset involves comparing tu-

mor and normal examples of the same tissue, while

the second dataset involves examples from two vari-

ants of the same disease.

4.1.1 Colon Cancer and Leukemia Datasets

Colon tumor is a disease in which cancerous growths

are found in the tissues of the colon epithelial cells.

The Colon dataset contains 62 examples. Among

them, 40 tumor biopsies are from tumors (labeled

as “negative”) and 22 normal (labeled as “positive”)

biopsies are from healthy parts of the colons of the

same patients. The ﬁnal assignments of the status of

biopsy examples were made by pathological exami-

nation. The total number of genes to be tested is 2000

(Alon et al., 1999).

In the 1960s was provided the ﬁrst basis for clas-

siﬁcation of acute leukemias into those arising from

lymphoid precursors (acute lymphoblastic leukemia,

ALL) or from myeloid precursors (acute myeloid

leukemia, AML). The Leukemia dataset is a collec-

tion of expression measurements reported by (Golub

et al., 1999). The dataset contains 72 examples. These

examples are divided to two variants of leukemia:

25 examples of acute myeloid leukemia (AML) and

47 examples of acute lymphoblastic leukemia (ALL).

The source of the gene expression measurements was

taken from 63 bone marrow examples and 9 pe-

ripheral blood examples. Gene expression levels in

these 72 examples were measured using high density

oligonucleotide microarrays. The expression levels of

7129 genes are reported.

4.2 Estimating Prediction Errors

We apply the cross-validation method to evaluate the

prediction accuracy of the classiﬁcation method. To

apply this method, we partition the dataset E into k

sets of examples, C

, . . . ,C

. Then, we construct a

data set D

= E −C

, and test the accuracy of a model

obtained from D

on the examples in C

. We estimate

the accuracy of the method by averaging the accuracy

over the k cross-validation trials.

There are several possible choices of k. A com-

mon approach is to set k =number of examples. This

method is known as leave one out cross validation

(LOOCV). We will use the LOOCV method.

Although our purpose is not to compare the results

with other methods, as a sample, in Tables

1 and 2 we

The results marked with A, B and C are obtained from

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

325

show the accuracy estimates for the different meth-

ods applied to the two datasets. The results obtained

in (Diaz-Uriarte and de Andr

es, 2006; Genuer et al.,

2010) are calculated with the .632+bootstrap method,

and the Leukemia dataset has 38 examples and 3051

features.

Table 1: Accuracy of different methods on Colon dataset.

Correct Unclassiﬁed

Clustering

88.70 0.00

Nearest Neighbor

80.60 0.00

SVM, linear kernel

77.40 9.70

SVM, quad. kernel

74.20 11.30

Boosting, 100 iter.

72.60 9.70

NN.vs

84.20 0.00

RF.du (s.e.=0)

84.10 0.00

RF.ge

91.70 0.00

FRF 91.94 0.00

Table 2: Acc. of different methods on Leukemia dataset.

Correct Unclassiﬁed

Nearest Neighbor

91.60 0.00

SVM, linear kernel

93.00 5.60

SVM, quad. kernel

94.40 4.20

Boosting, 100 iter.

95.80 1.40

NN.vs

44.40 0.00

RF.du (s.e.=1)

92.30 0.00

RF.ge

99.00 0.00

FRF 98.61 0.00

Estimates of classiﬁcation accuracy give only a

partial insight on the performance of a method. Also,

we treat all errors as having equal penalty. In the

problems we handle, however, errors have asymmet-

ric weights. We distinguish false positive error - nor-

mal tissues classiﬁed as tumor, and false negative er-

rors - tumor tissues classiﬁed as normal. In diagnostic

applications, false negative errors can be detrimental,

while false positives may be tolerated.

ROC curves are used to evaluate the “power”

of a classiﬁcation method for different asymmetric

weights (Brandley, 1997; Hanley and McNeil, 1982).

Since the area under the ROC curve (denoted by

AUC) is a portion of the area of the unit square, its

value will always be between 0.0 and 1.0. A real-

istic classiﬁer should not have an AUC less than 0.5

(area under the diagonal line between (0,0) and (1,1)).

The AUC has an important statistical property: the

AUC of a classiﬁer is equivalent to the probability

that the classiﬁer will rank a randomly chosen posi-

tive instance higher than a randomly chosen negative

(Ben-Dor et al., 2000; Diaz-Uriarte and de Andr

es, 2006;

Genuer et al., 2010), respectively

instance. This is equivalent to the Wilcoxon test of

ranks (Hanley and McNeil, 1982).

The confusion matrixes obtained by applying FRF

to the two datasets are shown in Table 3.

Table 3: Confusion Matrixes obtained with FRF.

Colon Leukemia

actual value actual value

1 0 ALL AML

prediction 1 37 2 ALL 46 0

outcome 0 3 20 AML 1 25

Confusion matrix of Colon dataset shows ﬁve er-

rors, and a Speciﬁcity of 0.9091 and Sensibility of

0.9250. Confusion matrix of Leukemia dataset shows

one error, and a Speciﬁcity of 1.0 and Sensibility of

0.9787.

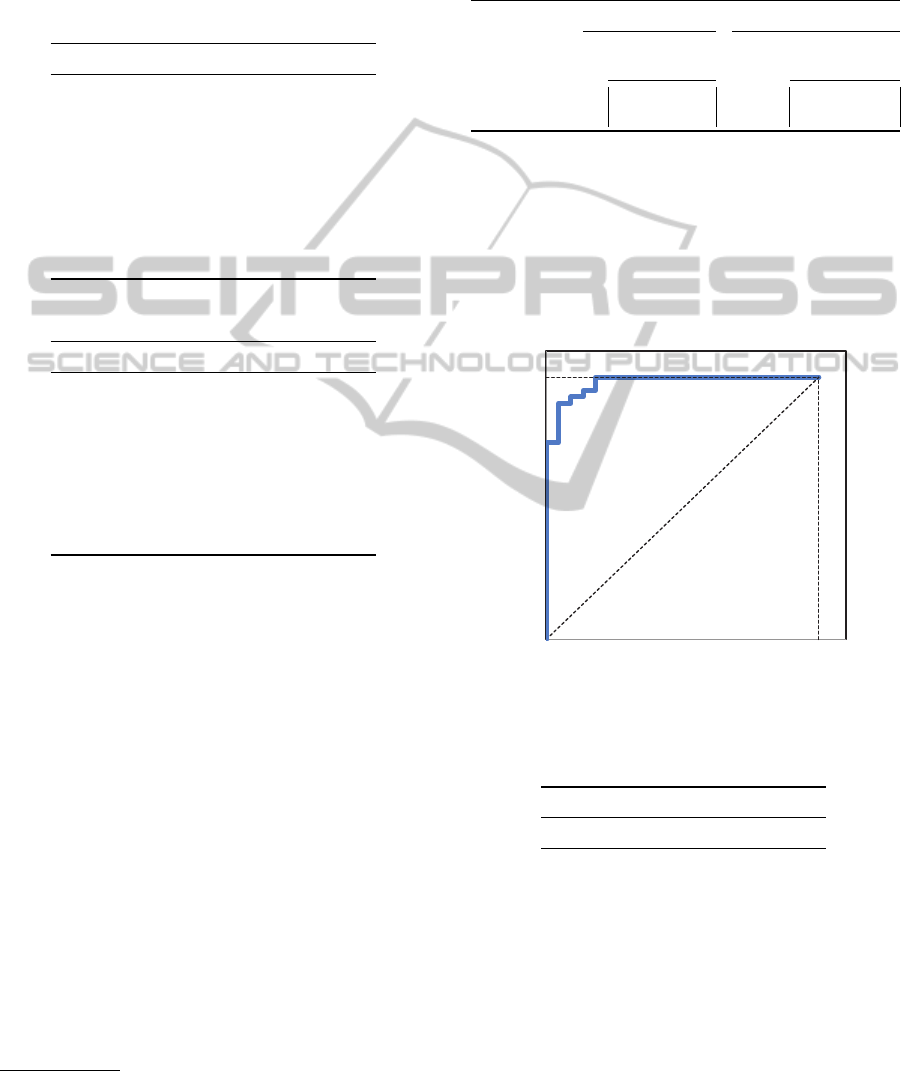
ROC curves are shown in Figures 2 and 3 and

AUC values in Table 4.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

sensitivity

1-specificity

Figure 2: Colon: ROC curve with all features.

Table 4: AUC values for Colon and Leukemia datasets.

Colon Leukemia

AUC values 0.9761 0.9991

4.3 Gene Selection

It is clear that the expression levels of many of the

genes in our datasets are irrelevant to the distinction

between tumors. Taking such genes into account dur-

ing classiﬁcation increases the dimensionality of the

classiﬁcation problem, presents computational difﬁ-

culties, and introduces noise to the process. Another

issue with a large number of genes is the interpretabil-

ity of the results. If our methods to distinguish tumor

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

326

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

sensitivity

1-specificity

Figure 3: Leukemia: ROC curve with all features.

from normal tissues is encoded in the expression lev-

els of few genes, then we might be able to understand

the biological signiﬁcance of these genes.

Thus, it is crucial to recognize whether a small

number of genes can sufﬁce for good classiﬁcation.

The gene expression datasets are problematic in that

they contain a large number of genes (features) and

thus methods that search over subsets of features can

be expensive. Moreover, these datasets contain only a

small number of examples, so the detection of irrele-

vant genes can suffer from statistical instabilities.

4.3.1 Signiﬁcance of a Gene and Ranking

The FRF-fs method (Cadenas et al., 2013) to feature

selection obtains a feature ranking based on an im-

portance measurement of each feature, and from that

ranking, an optimal feature subset. The vector RANK

(see Subsection 3.2) contains the importance measure

of the features. In Tables 9 and 10 (in Appendix 5)

a portion of that ranking of features and their impor-

tance values is shown.

4.3.2 Gene Prioritization in Cancer Data

In the ﬁnal phase of the FRF-fs method (Cadenas

et al., 2013) an optimal feature subset is obtained.

In the Colon dataset the optimal feature subset is

{419, 765, 824, 1168, 513, 1772, 571, 1546, 1423,

1761, 1939, 1990, 377, 1668, 1346, 1586, 548, 474,

802, 1867}. In addition, to give more interpretability,

FRF-fs method obtains a feature partition. In Table

11 (in Appendix 5) we show the partition obtained for

this optimal features subset. The ﬁrst column shows

the gene number while the second one shows the dif-

ferent partitions for this gene.

In the Leukemia dataset the optimal feature subset

is {3252, 4847, 2288, 2354, 6041, 6376, 4644}. In

Table 12 (in Appendix 5) we show the partition ob-

tained for this optimal features subset.

In Tables 13 and 14 (in Appendix 5) we show a

description of the selected genes (features) by FRF-fs

method. The ﬁrst column shows the importance value

of each gene, the second one the gene number and the

third the description of it.

4.3.3 Classifying with Selected Subsets

Now, the classiﬁcation procedure is applied using the

training data restricted to the subset of selected genes.

In Tables 5 and 6 we show the accuracy estimates

for the different methods applied to the two datasets

with the selected features.

Table 5: Accuracy with/without selected features for Colon

dataset.

FRF

All features Sel. features

Correct Unclassiﬁed Correct Unclassiﬁed

91.40 0.00 93.55 0.00

Table 6: Accuracy with/without selected features for

Leukemia dataset.

FRF

All features Sel. features

Correct Unclassiﬁed Correct Unclassiﬁed

98.61 0.00 98.61 0.00

The confusion matrixes obtained by applying FRF to

the two datasets with the selected features are shown

in Table 7.

Table 7: Confusion Matrixes obtained with FRF using se-

lected features.

Colon Leukemia

actual value actual value

1 0 ALL AML

prediction 1 38 2 ALL 46 1

outcome 0 2 20 AML 0 25

Confusion matrix of Colon dataset shows four er-

rors, and a Speciﬁcity of 0.9091 and Sensibility of

0.9500. Confusion matrix of Leukemia dataset shows

one error, and a Speciﬁcity of 0.9600 and Sensibility

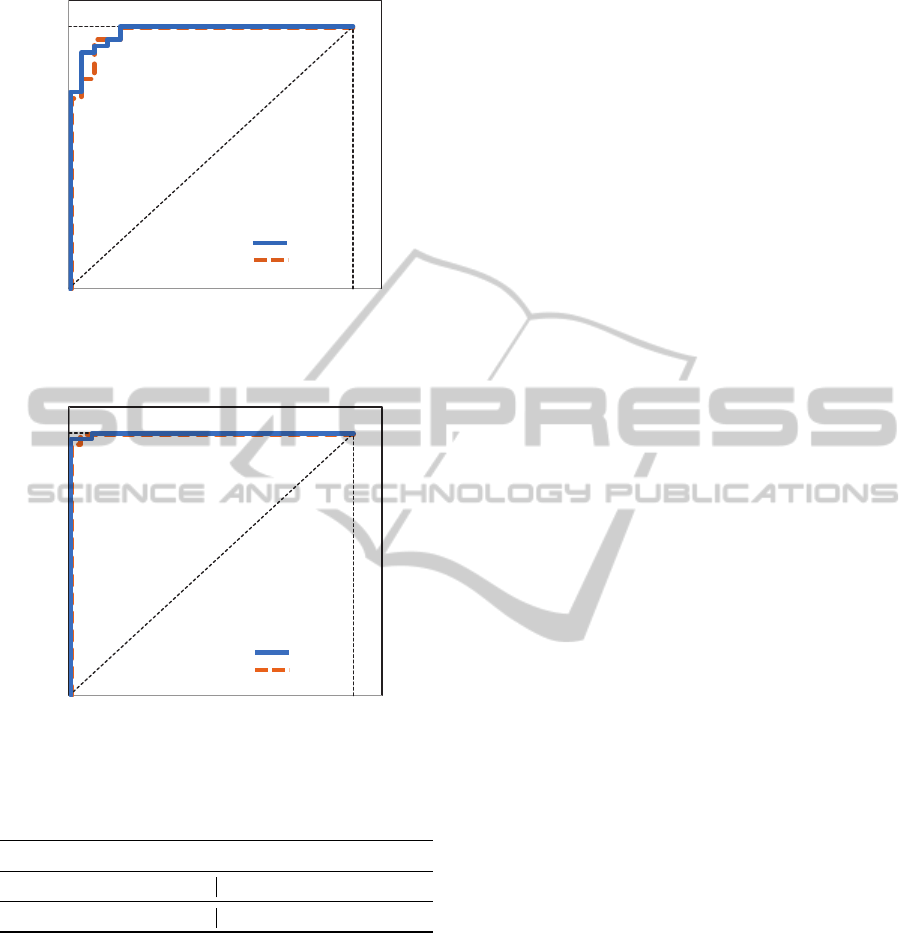
of 1.0. ROC curves are shown in Figures 4 and 5.

AUC values (Table 8) are compared with the obtained

when using all features.

Following the methods proposed in (Hanley and

McNeil, 1982; DeLong et al., 1988), we conclude that

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

327

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

sensitivity

1-specificity

all

selec.

Figure 4: Colon: ROC curve with all/selected features.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1

sensitivity

1-specificity

all

selec.

Figure 5: Leukemia: ROC curve with all/selected features.

Table 8: AUC values.

Colon Leukemia

all features sel. features all features sel. features

0.9761 0.9710 0.9991 0.9987

there are no signiﬁcant differences between the results

obtained when using all features or the selected ones.

We can therefore conclude that the selection of

features does not cause loss of accuracy but signiﬁ-

cantly decreases the number of features.

5 CONCLUSIONS

In this paper we have applied a fuzzy decision tree en-

semble to tumor datasets with gene expression data.

On the one hand, we have applied the ensemble to

the classiﬁcation of examples described by the set of

all features. On the other hand, we have applied the

ensemble to select a gene subset and to classify exam-

ples only described with the selected genes. The clas-

siﬁcation accuracies, in both cases, are high. These

results are validated statistically by the ROC curve

and AUC area.

When we work with a fuzzy decision tree ensem-

ble, in addition to achieve good results, these one are

provided in a highly interpretable way.

As part of the solution, the method provides a par-

tition of numerical features of the problem and a rank-

ing of importance of these features which permits the

identiﬁcation of sets of genes that can serve as classi-

ﬁcation or diagnosis platforms.

ACKNOWLEDGEMENTS

Supported by the projects TIN2011-27696-C02-01

and TIN2011-27696-C02-02 of the Ministry of Econ-

omy and Competitiveness of Spain. Thanks also

to “Agencia de Ciencia y Tecnolog

ıa de la Regi

de Murcia” (Spain) for the support given to Raquel

Mart

ınez by the scholarship program FPI.

REFERENCES

Alon, U., Barkai, N., Notterman, D. A., Gish, K., Ybarra,

S., Mack, D., and Levine, A. J. (1999). Broad patterns

of gene expression revealed by clustering analysis of

tumor and normal colon tissues probed by oligonu-

cleotide arrays. Proc Natl Acad Sci U S A., 96:6745–

6750.

Ben-Dor, A., Bruhn, L., Friedman, N., Nachman, I.,

Schummer, M., and Yakhini, Z. (2000). Tissue clas-

siﬁcation with gene expression proﬁles. Journal of

Computational Biology, 7:559–583.

Bonissone, P. P., Cadenas, J. M., Garrido, M. C., and

ıaz-Valladares, R. A. (2010). A fuzzy random for-

est. International Journal of Approximate Reasoning,

51(7):729–747.

Brandley, A. P. (1997). The use of the area under the

roc curve in the evaluation of machine learning algo-

rithms. Pattern Recognition, 30(7):1145–1159.

Breiman, L. (2001). Random forests. Machine Learning,

43:5–32.

Cadenas, J. M., Garrido, M. C., and Mart

ınez, R. (2013).

Feature subset selection ﬁlter-wrapper based on low

quality data. Expert Systems with Applications, 40:1–

10. doi:10.1016/j.eswa.2013.05.051.

Cadenas, J. M., Garrido, M. C., Mart

ınez, R., and Bonis-

sone, P. P. (2012a). Extending information processing

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

328

in a fuzzy random forest ensemble. Soft Computing,

16(5):845–861.

Cadenas, J. M., Garrido, M. C., Mart

ınez, R., and Bonis-

sone, P. P. (2012b). Ofp class: a hybrid method to

generate optimized fuzzy partitions for classiﬁcation.

Soft Computing, 16:667–682.

Clarke, P., George, M., Cunningham, D., Swift, I., and

Workman, P. (1999). Analysis of tumor gene expres-

sion following chemotherapeutic treatment of patients

with bowel cancer. In Proc. Nature Genetics Microar-

ray Meeting, pages 39–39, Scottsdale, Arizona.

Dagliyan, O., Uney-Yuksektepe, F., Kavakli, I. H., and

Turkay, M. (2011). Optimization based tumor classi-

ﬁcation from microarray gene expression data. PLoS

One, 6:e14579.

DeLong, E. R., DeLong, D. M., and Clarke-Pearson, D. L.

(1988). Comparing the areas under two or more corre-

lated receiver operating characteristic curves: A non-

parametric approach. Biometrics, 44:837–845.

Diaz-Uriarte, R. and de Andr

es, S. A. (2006). Gene selec-

tion and classiﬁcation of microarray data using ran-

dom forest. BMC Bioinformatics, 7(3).

Duval, B. and Hao, J.-K. (2010). Advances in metaheuris-

tics for gene selection and classiﬁcation of microarray

data. Brieﬁngs in Bioinformatics, 11(1):127–141.

Genuer, R., Poggi, J.-M., and Tuleau-Malot, C. (2010).

Variable selecting using random forest. Pattern

Recognition Letters, 31(14):2225–2236.

Ghoraia, S., Mukherjeeb, A., and Duttab, P. K. (2012).

Gene expression data classiﬁcation by vvrkfa. Pro-

cedia Technology, 4:330–335.

Golub, T. R., Slonim, D. K., Tamayo, P., Huard, C., Gaasen-

beek, M., Mesirov, J. P., Coller, H., Loh, M., Down-

ing, J., Caligiuri, M., Bloomﬁeld, C., and Lander, E.

(1999). Molecular classiﬁcation of cancer: Class dis-

covery and class prediction by gene expression moni-

toring. Science, 286:531–537.

Hanley, J. A. and McNeil, B. J. (1982). The meaning and

use of the area under a receiver operating characteris-

tic (roc) curve. Radiology, 143:29–36.

Mukhopadhyaya, A. and Maulikb, U. (2009). Towards

improving fuzzy clustering using support vector ma-

chine: Application to gene expression data. Pattern

Recognition Pattern Recognition, 42:2744–2763.

Nitsch, D., Gonzalves, J. P., Ojeda, F., de Moor, B., and

Moreau, Y. (2010). Candidate gene prioritization

by network analysis of differential expression using

machine learning approaches. BMC Bioinformatics,

11:460.

Yager, R. R. (1988). On ordered weighted averaging ag-

gregation operators in multicriteria decision making.

IEEE transactions on Systems, Man and Cybernetics,

18:183–190.

APPENDIX

Ranking and Partitions of Datasets

Table 9: Features Ranking in Colon dataset.

Ranking Fe. n.

1 35.6266 419

2 17.0359 765

3 15.6419 1635

4 13.5216 824

5 13.4986 1168

6 13.4898 513

7 9.6363 1772

8 7.2361 571

9 7.0409 1546

10 6.8134 1423

11 6.7085 1761

12 6.6085 1939

13 6.4989 1990

14 5.9908 377

15 4.6654 1668

16 4.0917 1346

17 3.1929 1586

18 2.3743 548

19 2.0175 474

20 1.8373 802

21 1.7315 1867

.. ..... ...

Table 10: Features Ranking in Leukemia dataset.

Ranking Fe. n.

1 31.2849 3252

2 30.1804 1882

3 30.1763 1834

4 26.5833 4847

5 23.9430 2288

6 13.5707 2354

7 13.1465 6041

8 9.8707 6376

9 4.8665 4644

10 1.4004 3623

.. ..... ...

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

329

Table 11: Features Partition in Colon dataset.

Fe.n. Partitions

377 (0,0,0.4046,0.5246) (0.4046,0.5246,1,1)

419 (0,0,0.6981,0.7140) (0.6981,0.7140,0.7241,0.7256) (0.7241,0.7256,1,1)

474 (0,0,0.8360,0.9194) (0.8360,0.9194,1,1)

513 (0,0,0.5625,0.5657) (0.5625,0.5657,1,1)

548 (0,0,0.7852,0.9132) (0.7852,0.9132,1,1)

571 (0,0,0.3579,0.4168) (0.3579,0.4168,1,1)

765 (0,0,0.4869,0.5655) (0.4869,0.5655,0.6270,0.6286) (0.6270,0.6286,0.6293,0.6294) (0.6293,0.6294,0.6543,0.6769)

(0.6543,0.6769,0.7320,0.7667) (0.7320,0.7677,1,1)

802 (0,0,0.4227,0.7499) (0.4227,0.7499,1,1)

824 (0,0,0.6009,0.6017) (0.6009,0.6017,0.6026,0.6033) (0.6026,0.6033,1,1)

1168 (0,0,0.5665,0.5793) (0.5665,0.5793,1,1)

1346 (0,0,0.4839,0.5456) (0.4839,0.5456,1,1)

1423 (0,0,0.8269,0.8730) (0.8269,0.8730,1,1)

1546 (0,0,0.0792,0.3206) (0.0792,0.3206,0.4904,0.5156) (0.4904,0.5156,1,1)

1586 (0,0,0.9168,0.9753) (0.9168,0.9753,1,1)

1668 (0,0,0.2804,0.6472) (0.2804,0.6472,1,1)

1761 (0,0,0.5641,0.5764) (0.5641,0.5764,0.5784,0.5902) (0.5784,0.5902,1,1)

1772 (0,0,0.5156,0.5172) (0.5156,0.5172,1,1)

1867 (0,0,0.5292,0.6251) (0.5292,0.6251,1,1)

1939 (0,0,0.8908,0.8934) (0.8908,0.8934,1,1)

1990 (0,0,0.1022,0.3066) (0.1022,0.3066,0.4484,0.5811) (0.4484,0.5811,1,1)

Table 12: Features Partition in Leukemia dataset.

Fe.n. Partitions

2288 (0,0,0.0733,0.0835) (0.0733,0.0835,1,1)

2354 (0,0,0.1451,0.1931) (0.1451,0.1931,1,1)

3252 (0,0,0.0681,0.0706) (0.0681,0.0706,0.0738,0.0747) (0.0738,0.0747,1,1)

4644 (0,0,0.2425,0.2427) (0.2425,0.2427,1,1)

4847 (0,0,0.2116,0.2157) (0.2116,0.2157,0.3479,0.3531) (0.3479,0.3531,1,1)

6041 (0,0,0.1937,0.1963) (0.1937,0.1963,0.2001,0.2037) (0.2001,0.2037,1,1)

6376 (0,0,0.1408,0.1422) (0.1408,0.1422,1,1)

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

330

Describing Selected Features

Table 13: Description of selected genes of the Colon dataset by FRF-fs method.

Imp. V. n gene Gene Description

35.6266 419 R44418 EBNA-2 Nuclear protein (Epstein-barr virus)

17.0359 765 M76378 Human cysteine-rich protein (CRP) gene, exons 5 and 6

15.6419 1635 M36634 Human vasoactive intestinal peptide (VIP) mRNA, complete cds

13.5216 824 Z49269 H.sapiens gene for chemokine HCC-1

13.4986 1168 U04953 Human isoleucyl-tRNA synthetase mRNA, complete cds

13.4898 513 M22382 Mitochondrial matrix protein P1 precursor (HUMAN)

9.63634 1772 H08393 Collagen alpha 2(XI) CHAIN (Homo sapiens)

7.23607 571 R42501 Inosine-5’-Monophosphate Dehydrogenase 2 (HUMAN)

7.04094 1546 T51493 Homo sapiens PP2A B56-gamma1 mRNA, 3’ end of cds

6.81338 1423 J02854 Myosin regulatory light chain 2, Smooth muscle isoform (HUMAN);

contains element TAR1 repetitive element

6.70853 1761 T94350 Peripheral myelin protein 22 (Homo sapiens)

6.60851 1939 X70297 Neuronal acetylcholine receptor protein, alpha-7 chain (HUMAN)

6.49896 1990 U15212 Human caudal-type homeobox protein (CDX1) mRNA, partial cds

5.99079 377 Z50753 H.sapiens mRNA for GCAP-II/uroguanylin precursor.

4.66543 1668 M82919 Human gamma amino butyric acid (GABAA) receptor beta-3 subunit mRNA,

complete cds.

4.09169 1346 T62947 60S RIBOSOMAL PROTEIN L24 (Arabidopsis thaliana)

3.19286 1586 L14848 Human MHC class I-related protein mRNA, complete cds.

2.37430 548 T40645 Human Wiskott-Aldrich syndrome (WAS) mRNA, complete cds.

2.01753 474 T70046 Endothelial actin-binding protein (Homo sapiens)

1.83728 802 X70326 H.sapiens MacMarcks mRNA

1.73155 1867 U32519 Human GAP SH3 binding protein mRNA, complete cds.

1.71548 1724 H16991 Nucleolysin tiar (HUMAN)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Table 14: Description of selected genes of the Leukemia dataset by FRF-fs method.

Imp. V. n gene Gene Description

31.2849 3252 U46499 Glutathione S-transferase, Microsomal

30.1804 1882 M27891 CST3 Cystatin C (amyloid angiopathy and cerebral hemorrhage)

30.1763 1834 M23197 CD33 CD33 antigen (differentiation antigen)

26.5833 4847 X95735 Zyxin

23.9430 2288 M84526 DF D component of complement (adipsin)

13.5707 2354 M92287 CCND3 Cyclin D3

13.1465 6041 L09209 s APLP2 Amyloid beta (A4) precursor-like protein 2

9.87071 6376 M83652 s PFC Properdin P factor, complement

4.86655 4644 X80230 mRNA (clone C-2k) mRNA for serine/threonine protein kinase

1.4004 3623 U68727 Homeobox-containing protein mRNA

1.2354 4708 X84002 TAFII20 mRNA for transcription factor TFIID

1.1158 5691 D89377 Adult tooth pulp of third molar ﬁbroblast mRNA for MSX-2

0.9525 6855 M31523 TCF3 Transcription factor 3 (E2A immunoglobulin enhancer binding factors

E12/E47)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

UsingaFuzzyDecisionTreeEnsembleforTumorClassificationfromGeneExpressionData

331