
Generalization and Formalization of Precisiation Language with
Applications to Human-Robot Interaction
Takehiko Nakama, Enrique Mu
˜
noz and Enrique Ruspini
European Center for Soft Computing, c/Gonzalo Guti
´
errez Quir
´
os, s/n, 33600 Mieres, Spain
Keywords:
Precisiated Natural Language, Precisiation Language, Formal Logic, Propositional Logic, Predicate Logic,
Quantificational Logic, Fuzzy Logic, Fuzzy Relation, Human-Robot Interaction.
Abstract:
We generalize and formalize precisiation language by establishing a formal logic as a generalized precisiation
language. Various syntactic structures in natural language are incorporated in the syntax of the formal logic so
that it can serve as a middle ground between the natural-language-based mode of human communication and
the low-level mode of machine communication. As regards the semantics, we establish the formal logic as a
many-valued logic, and fuzzy relations are employed to determine the truth values of propositions efficiently.
We discuss how the generalized precisiation language can facilitate human-robot interaction.
1 INTRODUCTION AND
SUMMARY
In his computational theory of perceptions (e.g.,
(Zadeh, 2001), (Zadeh, 2002), (Zadeh, 2004)), Zadeh
introduced the concept of precisiated natural lan-
guage (PNL), which refers to a set of natural-language
propositions that can be treated as objects of compu-
tation and deduction. The propositions in PNL are as-
sumed to describe human perceptions, and they allow
artificial intelligence to operate on and reason with
perception-based information, which is intrinsically
imprecise, uncertain, or vague.
Precisiation language is an integral part of this
framework. Each proposition in PNL is translated
into a precisiation language, which then expresses
it as a set or a sequence of computational ob-
jects that can be effectively processed by machines
(e.g., (Zadeh, 2001), (Zadeh, 2002), (Zadeh, 2004)).
Zadeh proposed a precisiation language in which each
proposition is a generalized constraint on a variable.
This precisation language is called a generalized-
constraint language.
Zadeh considered the primary function of natural
language as describing human perceptions, and his
PNL and precisiation language only deal with per-
ceptual propositions ((Zadeh, 2001), (Zadeh, 2002),
(Zadeh, 2004)). However, the importance of natu-
ral language is not limited to describing human per-
ceptions. For instance, using a natural language, we
describe not only perceptions but also actions. There-
fore, it is important, both theoretically and practically,
to extend PNL and precisiaton language to other types
of proposition. Generalized constraints in Zadeh’s
precisiation language are suitable for precisiating per-
ceptual propositions but not for precisiating action-
related propositions (See Section 3).
One of the major fields that require the precisi-
ation of action-related propositions in natural lan-
guage is robotics. Recently, many studies (e.g.,
(Marble et al., 2004), (Dias et al., 2006), (Dias
et al., 2008b), (Johnson et al., 2008), (Johnson and
Intlekofer, 2008)) have been conducted to develop
robotic systems in which humans and robots work
as true team members, requiring peer-to-peer human-
robot interaction. Such systems can be highly ef-
fective and efficient in performing a wide range of
practical tasks—assistance to people with disabili-
ties (e.g., (Lacey and Dawson-Howe, 1998), (Shim
et al., 2004), (Feil-Seifer and Mataric, 2008),(Ku-
lyukin et al., 2006)), search and rescue (e.g., (Kitano
et al., 1999), (Casper and Murphy, 2003), (Dias et al.,
2008a), (Norbakhsh et al., 2005)), and space explo-
ration (e.g., (Wilcox and Nguyen, 1998), (Fong and
Thorpe, 2001), (Fong et al., 2005), (Ferketic et al.,
2006)), for instance. One of the major challenges
of developing these robotic systems is the increased
complexity of the human-robot interactions (e.g.,
(Goodrich and Schultz, 2007)). Although humans
prefer natural language as a communication medium,
it presents several major problems when used for
332
Nakama T., Muñoz E. and Ruspini E..
Generalization and Formalization of Precisiation Language with Applications to Human-Robot Interaction.
DOI: 10.5220/0004660703320343
In Proceedings of the 5th International Joint Conference on Computational Intelligence (SCA-2013), pages 332-343
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

human-robot communications; natural-language ex-
pressions tend to be notoriously underspecified, di-
verse, vague, or ambiguous, so they often lead to
errors that are hard to overcome (e.g., (Winograd
and Flores, 1986), (Tomassi, 1999), (Shneiderman,
2000), (Forsberg, 2003), (Gieselmann and Stenneken,
2006)). Low-level sensory and motor signals and ex-
ecutable code are easy for machines to interpret, but
they are cumbersome for humans and thus cannot,
on their own, create an effective human-robot inter-
face. Task descriptions or specifications for robotic
systems typically involve action-related propositions,
such as “bring the box to the room” and “keep the
robot in the building if it rains.” A generalized pre-
cisiation language that can precisiate not only per-
ceptual propositions but also action-related proposi-
tions can effectively mediate human-robot interaction
in robotic systems that employ a peer-to-peer commu-
nication mode.
Recently, Nakama et al. (Nakama et al., 2013)
have taken a first step toward generalizing and formal-
izing precisiation language by establishing a formal
logic as a generalized precisiation language. Their
formal logic can generate infinitely many precisiated
propositions, just as infinitely many propositions can
be generated in natural language, while ensuring that
every proposition in the formal logic is precisiated.
In this paper, we further develop and elaborate on the
framework proposed in (Nakama et al., 2013).
The remainder of this paper is organized as fol-
lows. In Section 2, we examine the properties of for-
mal logic that are desirable for precisiating natural-
language expressions. The syntax of our formal logic
is explained in Section 3. In Section 4, we discuss
the generality of our framework. In Section 5, we ex-
amine how to add a deductive apparatus to our for-
mal logic so that we can infer and reason in it. In
Section 6, we develop a hierarchy of propositions that
enhances the expressive power and the interactivity of
our formal logic. The semantics of the formal logic is
explained in Section 7.
Since the precisiation of perceptual propositions
has been examined (e.g., (Zadeh, 2001), (Zadeh,
2004)), we focus on examining how to precisiate
action-related propositions in this paper. In (Mu
˜
noz
et al., 2013), we provide details on how to extend
our generalized precisiation language to perceptual
propositions. To explain our formal scheme, we will
first appeal to ordinary practices and then move on
to formal considerations so that the reader can under-
stand it intuitively. To generate examples of ordinary
practice, we consider establishing task descriptions
for human-robot interaction. As mentioned earlier,
task descriptions inherently involve actions, so the
precisiation of task descriptions is an important step
toward generalizing precisiation language and PNL.
2 PROPERTIES OF FORMAL
LOGIC SUITABLE FOR
PRECISIATION OF
NATURAL-LANGUAGE
EXPRESSIONS
The application of formal logic to natural language
is a paradigm of logical analysis (Tomassi, 1999); it
provides genuine insight into the syntactic structures
of natural-language sentences and the consequential
characters of assertions expressed by them. This anal-
ysis is important for precisiating propositions in natu-
ral language.
In order for PNL to have high expressive power,
it is desirable that precisiation language can generate
infinitely many precisiated propositions while ensur-
ing that every proposition in it is precisiated. Formal
logic achieves these properties by a recursive defini-
tion of its syntax; it can generate infinitely many well-
formed formulas while ensuring that every formula in
it is well-formed.
As in other formal logics, we can reason logically
in our formal logic by adding a deductive apparatus
to it; the resulting analytical machinery allows us to
determine when one sentence in the formal language
follows logically from other sentences. Thus our for-
mal logic precisiates the inference and the reasoning
in which humans engage using a natural language.
See Section 5.
Our scheme also reflects the theory of descrip-
tions in formal logic, which was introduced by Rus-
sell (Russell, 1984). He claimed that the reality con-
sists of logical atoms, which can be considered in-
decomposable, self-contained building blocks of all
propositions in formal logic, and that logical anal-
ysis ends when we arrive at logical atoms. In our
precisiation language, precisiation ends when we ar-
rive at logical atoms, which will be represented by
atomic propositions at the lowest level of a hierarchy
of propositions. See Section 6.
3 SYNTAX OF THE FORMAL
LOGIC
In this section, we describe how to form proposi-
tions in our formal language. To explain our scheme,
we will first appeal to ordinary practices and then
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
333

move on to formal considerations so that the reader
can understand it intuitively. To generate examples
of ordinary practice, we consider establishing task
descriptions for human-robot interaction, but keep
in mind that our scheme is not limited to precisi-
ating propositions that describe tasks. (Also notice
that, since tasks typically involve actions, we will be
extending PNL and precisiation language to action-
related propositions.) We will discuss the general-
ity of our formal logic in Section 4. In this for-
mal logic, each proposition has a syntactic form ob-
served in natural language. Our formal logic gen-
eralizes Zadeh’s generalized-constraint language by
incorporating multiple syntactic forms so that it can
deal with not only perceptual propositions but also
action-related propositions.
In Section 3.1, we describe the components of
such propositions. In Section 3.2, we describe how
to form an atomic proposition. In Section 3.3, we
describe how to form a compound proposition. In
Section 3.4, we provide a recursive definition of well-
formed formulas that allows our formal logic to gen-
erate infinitely many well-formed formulas while en-
suring that every formula in it is well-formed.
In these sections, we will provide examples of
rather simple task descriptions, but our scheme can
be easily applied to robotic systems that require more
intricate task descriptions. See Section 4.
3.1 Component Sets
In our formal logic, we generate propositions using
elements in component sets. To provide concrete ex-
amples, we consider the sets S, V , O, A and C shown
in Table 1 as component sets.
In Section 3.2, we will explain how to generate
atomic propositions using elements in S, V , O, and
A. In this example, the elements in S are also in O
because they can not only perform a task but also re-
ceive an action in V . The element labeled as “null,”
called the null element, is included in O and A. In
Section 3.2, we will explain how the null element is
used in forming atomic propositions. In Section 3.3,
we will explain how to form compound propositions
using the connectives in C.
Although the component sets in Table 1 are rather
simple, they can be made as rich as necessary, and
other types of component sets can be incorporated in
our formal logic. See Section 4.
3.2 Atomic Propositions
In our formal logic, an atomic proposition is defined
to be a tuple in the Cartesian product of component
Table 1: Examples of component sets.
set elements
S agents that can perform tasks
e.g., S = {robot1, robot2, user}
V verbs that characterize actions required by
tasks
e.g., V = { f ind, deliver, go, move, press}
O objects that may receive an action in V or
compose an adverbial phrase
e.g., O =
{
box, button, table, room1,
room2, robot1, robot2, user, null
}
A adverbial phrases that can be included in
task descriptions
e.g., A =
{
in γ, f rom γ, f rom γ
1
to γ
2
,
to γ, null | γ, γ
1
, γ
2
∈ O
}
C connectives that can be used to com-
bine multiple propositions in forming com-
pound propositions
e.g., C = {and, i f , or, then}
sets, and the Cartesian product specifies each admis-
sible tuple structure. To develop formal propositions
that can be easily identified with natural-language
sentences, we employ tuple structures that reflect syn-
tactic structures observed in natural languages such
as English. For instance, using the component sets
described in Section 3.1, we can define each atomic
proposition in our formal logic to be an SVOA clause
(The S, V, O, and A in SVOA stand for subject, verb,
object, and adverbial phrase, respectively) by setting
the admissible tuple structure to S ×V × O × A. The
SVOA structure is observed in many languages, in-
cluding English, Russian, and Mandarin. Using the
null element in O and A, we can also generate SVO,
SVA, and SV clauses. See the following examples
of atomic propositions resulting from the component
sets in Table 1:
•
robot1
S
move
V
. (The actual form of this proposition
is
robot1
S
move
V
null
O
null
A
, but we will omit instances
of the null element to simplify the resulting
expressions.)
•
robot2
S
move
V
to room1
A
robot1
S
move
V
null
O
to room1
A
.
•
robot2
S
f ind
V
ball
O
.
•
robot1
S
deliver
V
box
O
f rom room1 to room2
A
.
For humans, these propositions (task descriptions)
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
334

are easy to specify and understand. Meanwhile, the
structural and lexical constraints noticeably limit the
diversity and flexibility of everyday language to en-
sure that robots can unambiguously interpret the re-
sulting propositions (i.e., the specified tasks can be
precisely interpreted and executed by robots).
Atomic propositions can be considered building
blocks of all propositions. As will be explained in
Section 6, we establish a hierarchy of propositions. At
the lowest level of the hierarchy, each atomic propo-
sition is directly associated with an indecomposable,
self-contained executable code, and atomic proposi-
tions at each level compose propositions at higher lev-
els.
There are several ways to deal with the undesir-
able or nonsensical atomic propositions that can be
formed in S × V × O × A. (Note that in formal log-
ics, there can be well-formed formulas that are self-
contradictory.) We can remove all such propositions
from the cartesian product to ensure that each re-
sulting atomic proposition is a precisiated proposi-
tion. (In this case, we abuse the notation and let
S × V × O × A denote the “cleaned” cartesian prod-
uct.) Also, we can consider them as always false so
that they will never be executed in practice (see Sec-
tion 7).
In our formal logic, the atomic propositions need
not be expressed as generalized constraints on vari-
ables. By incorporating the SV, SVO, SVA, and
SVOA structures in the syntax, we can precisiate
action-related propositions rather naturally and effec-
tively. Clearly, other syntactic structures can be incor-
porated in our formal logic; see Section 4.
3.3 Compound Propositions
In our formal logic, we generate each compound
proposition by combining multiple atomic proposi-
tions using one or more connectives in the component
set C. With the component sets in Table 1, we can
form the following compound propositions:
•
robot2
S
go
V
to room1
A
atomic proposition
i f
C
user
S
press
V
button
O
atomic proposition
.
•
robot1
S
go
V
to room1
A
atomic proposition
i f
C
user
S
call
V
robot1
O
atomic proposition
or
C
user
S
press
V
button
O
atomic proposition
!
. (1)
In formal logic, parentheses are used to indicate the
scope of each connective. In our examples, parenthe-
ses disambiguate the manner in which atomic tasks
are performed.
These compound propositions are still quite easy
for humans to specify and understand, and the syntac-
tic structures imposed on the clauses and the compo-
sitions ensure effective interpretation and execution
by robots. Note that these compound propositions
are precisiated propositions although they are not ex-
pressed as generalized constraints on variables. In
fact, it can be quite difficult or ineffective to translate
them into generalized constraints.
In (1), the clause “user call robot1” or “user press
button” represents a condition that must be checked
in determining whether to send the robot to room1,
and the clause “robot1 go to room1” is an imperative.
There are many task descriptions that can be effec-
tively expressed as compound propositions consisting
of conditions and imperatives. In our scheme, task
descriptions consist of atomic propositions described
in Section 3.2, and each atomic proposition is either a
condition or an imperative. The type of each atomic
proposition in a compound task description is unam-
biguously determined by the logical connective that
connects it and by the location of the atomic propo-
sition relative to the connective. An atomic proposi-
tion that forms a subordinate clause immediately fol-
lowing the connective “if” is considered a condition,
whereas an atomic proposition that forms a clause
immediately preceding the connective is considered
an imperative. If the proposition is a condition, the
robotic system monitors the described condition. If it
is an imperative, the system executes the described ac-
tion provided that all the required conditions are sat-
isfied.
3.4 Recursive Definition of
Well-Formed Formulas
In order for a precisiation language to have high ex-
pressive power observed in natural language, it should
be able to generate infinitely many precisiated propo-
sitions while ensuring that every proposition in it is
precisiated. As described in Section 2, we can attain
these properties in formal logic by recursively defin-
ing its syntax; formally, our formal logic can generate
infinitely many well-formed formulas while ensuring
that every formula in it is well-formed.
The syntax of the formal logic described in Sec-
tions 3.1–3.3 can be recursively defined as follows:
1. Any x ∈ S ×V × O × A is an atomic well-formed
formula.
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
335

2. If α and β are well-formed formulas, then α c β,
where c ∈ C, is also a well-formed formula.
3. Nothing else is a well-formed formula.
This recursive definition allows our formal logic
to generate infinitely many precisiated propositions
while ensuring that every proposition in it is pre-
cisiated. As regards the examples described in Sec-
tions 3.1–3.3, with sufficiently rich component sets,
we can describe any task that must be performed by
the robotic system, and, using the syntax, we can
ensure that the robotic system does not operate on
any ill-formed task descriptions (i.e., task descriptions
that are not interpretable).
4 GENERALITY OF THE
FORMAL LOGIC
In Sections 3–3.4, we facilitated the exposition of our
formal logic by explaining it with rather simple com-
ponent sets and syntactic structures. Obviously, we
can easily extend our scheme to more sophisticated
component sets and syntactic structures so that our
formal logic can deal with highly complex actions
and perceptions. Each component set can be made as
large as necessary, and other component sets or clause
structures can be incorporated in the formal logic. For
instance, in addition to the SV, SVO, SVA, and SVOA
structures described and used in Sections 3–3.4 (and
in Section 6), we can also incorporate other com-
monly observed clause structures (see, for instance,
(Biber et al., 2002)), such as the SVC, SVOC, and
SVOO structures, in the syntax of atomic proposi-
tions. Furthermore, we can extend the clause struc-
tures so that a phrase can be used as the subject or the
object in an atomic proposition. Negation, a unary
logical connective, can certainly be incorporated in
the formal logic. We can also include Zadeh’s gen-
eralized constraints, which are suitable for express-
ing perceptual propositions, in our formal logic; each
generalized constraint can be considered an atomic
proposition that has the SVC structure, and it can be
combined with other propositions by connectives to
form a compound proposition.
We can establish not only a propositional logic
but also a quantificational logic, which fully incorpo-
rates quantifiers and predicates in well-formed formu-
las. Since propositions that describe perceptions often
include quantifiers (see, for instance, (Zadeh, 2002),
(Zadeh, 2004)), it is desirable to develop a quantifica-
tional logic as a precisiation language that covers both
actions and perceptions.
5 INFERENCE AND REASONING
IN THE FORMAL LOGIC
As in other formal logics, we can infer and reason in
our formal logic by adding a deductive apparatus to
it. Syntactically, a set of inference rules can be con-
structed, and axioms can also be established. (The hi-
erarchy described in Section 6 represents non-logical,
domain-dependent axioms.) Typical induction- and
elimination-rules in formal logics, such as modus po-
nens and modus tollens, can be easily incorporated in
our formal logic. Consequently, we can form a se-
quent, which consists of a finite (possibly empty) set
of well-formed formulas (the premises) and a single
well-formed formula (the conclusion), and we can ex-
amine its provability (derivability) using proof theory;
we can determine if a conclusion follows logically
from a set of premises by examining whether there
is a proof of that conclusion from just those premises
in the formal logic.
As will be described in Section 7, we can employ
fuzzy relations to establish the semantics of our for-
mal logic. This semantics allows us to investigate
the truth conditions and the semantic validity of each
proposition or sequent. As in other formal logics,
comparative truth tables can be used to determine se-
mantic validity.
6 HIERARCHY OF
PROPOSITIONS
The importance of the hierarchy of propositions de-
scribed in this section is threefold. First, it enhances
the expressive power of the formal logic by build-
ing up its vocabulary while ensuring the precisiabil-
ity of each resulting proposition. Second, it fortifies
the high interactivity of our formal logic by allowing
human-robot communications to take place at various
levels of detail. Third, it strengthens the deductive
apparatus of the formal logic by establishing domain-
dependent axioms that can be used for inference and
reasoning.
We will first explain the hierarchy intuitively using
the task description scheme described in Section 3. A
complex task can be described rather concisely, i.e., it
can be expressed by an atomic proposition. In many
cases, naive users will prefer specifying a complex
task using an atomic proposition as opposed to a more
lengthy compound proposition. On the other hand, in
order for a robotic system to actually execute a com-
plex task, the task must be broken down into sim-
pler subtasks, and the manner in which the subtasks
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
336

are performed must be specified. Consequently, the
atomic proposition describing a complex task can be
reexpressed as a compound proposition that consists
of atomic propositions describing the required sub-
tasks. Some of the subtasks may have to be further
decomposed in order to fully specify how to execute
them. Expert users may want to establish and com-
bine these subtasks carefully so that the robotic sys-
tem can perform the task effectively and efficiently.
Thus, we can precisiate an atomic proposition by
reexpressing it as a compound proposition consisting
of atomic propositions that precisiate it. This pro-
cess also leads to flexibility in the level of detail.
In the task description example, the flexibility gives
naive users an efficient, user-friendly interface with
robots while giving expert users the power to cus-
tomize tasks. As a result, the hierarchy allows human-
robot interactions to take place at various levels of de-
tail, and it also helps determine the appropriate level
of detail for each human-robot interaction; the hierar-
chy determines whether, from the point of view of a
given user, a given task is “atomic” or “compound.”
Consider the following task description:
robot1
S
examine
V
patient1
O
in room1
A
. (2)
This atomic proposition can be reexpressed as a com-
pound proposition that consists of three atomic propo-
sitions representing subtasks that must be performed
to accomplish the task:
robot1
S
f ind
V
patient1
O
in room1
A
atomic proposition 1
then
C
robot1
S
check
V
patient1
O
atomic proposition 2
then
C
robot1
S
send
V
data
O
atomic proposition 3
. (3)
Atomic propositions 1 and 2 in (3) can also be re-
expressed as compound propositions that clarify how
they are performed; atomic proposition 1 in (3) can be
defined as
robot1
S
go
V
to room1
A
atomic proposition
then
C
robot1
S
search
V
patient1
O
atomic proposition
,
(4)
and atomic proposition 2 in (3) can be defined as
robot1
S
go
V
to patient1
A
atomic proposition
then
C
robot1
S
measure
V
heart rate
O
atomic proposition
and
C
robot1
S
measure
V
blood pressure
O
atomic proposition
!
. (5)
Therefore, using (4)–(5) and atomic proposition 3 in
(3), we can reexpress (2) as
robot1
S
go
V
to room1
A
atomic proposition
then
C
robot1
S
search
V
patient1
O
atomic proposition
then
C
robot1
S
go
V
to patient1
A
atomic proposition
then
C
robot1
S
measure
V
heart rate
O
atomic proposition
and
C
robot1
S
measure
V
blood pressure
O
atomic proposition
!
then
C
robot1
S
send
V
data
O
atomic proposition
. (6)
Figure 1 visualizes this hierarchy, which consists of
three levels (levels 0, 1, and 2). For simplicity,
each atomic proposition is represented by its verb;
for instance, the atomic proposition at the highest
level (level 2), “Robot1 examine patient1 in room1,”
is represented by “examine.” The task expressed
by the atomic proposition at level 2 is described in
more detail at the intermediate level (level 1), where
the atomic propositions that involve the verbs “find,”
“check,” and “send” describe the subtasks that consti-
tute the task. These subtasks are described in more
detail at the lowest level (level 0), where they are ex-
pressed by the atomic propositions that involve the
verbs “go,” “search,” “measure,” and “send.”
The hierarchy clearly shows how atomic proposi-
tion (2) at level 2 is precisiated. At level 0, we have
atomic propositions that are not decomposable; each
of them is directly associated with a self-contained ex-
ecutable code that is run to perform the corresponding
task. Thus, atomic propositions at level 0 can be con-
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
337

Find Check Send
Examine
Level 2
Level 1
Level 0
MeasureGoSearch Send
Figure 1: Hierarchical task description. At the highest level
(level 2), the task is expressed as atomic proposition (2),
represented by “examine.” At the intermediate level (level
1), the task is expressed as compound proposition (3),
which consists of atomic propositions represented by “find,”
“check,” and “send.” At the lowest level (level 0), the task
is expressed as compound proposition (6), which consists
of atomic propositions represented by “go,” “search,” “mea-
sure,” and “send.”
sidered logical atoms described in Section 2, and they
precisiate each proposition at higher levels.
The suitability of a given proposition depends on
the level of granularity required for it. As regards the
task description scheme, naive users will most likely
prefer describing tasks at level 2, thus preferring (2).
For expert users, there may be situations where they
prefer specifying a given task step by step or reconfig-
uring its subtasks according to various circumstances;
in such cases, interacting with robots at level 1 using
(3) or at level 0 using (6) will be desirable. Thus,
the hierarchy allows a variety of users to interact with
robots at various levels of detail.
The hierarchy of propositions can be characterized
more formally as follows. Let S
i
, V
i
, O
i
, A
i
, and C
i
denote the component sets for level i of the hierarchy
(i ≥ 0). The elements in these sets reflect the degree
of detail suitable for level i. Then at level i, we estab-
lish a formal logic with these component sets, as de-
scribed in Section 3. Atomic propositions in S
0
×V
0
×
O
0
× A
0
are the logical atoms and the building blocks
of all propositions; each of them is indecomposable
and directly associated with a self-contained compu-
tational unit. We will call such a computational unit as
a computational atom. For each i ≥ 1, every atomic
proposition in S
i
× V
i
× O
i
× A
i
can be decomposed
into atomic propositions in S
i−1
×V
i−1
×O
i−1
×A
i−1
.
Figure 2 visualizes a typical form of this hierarchy.
For each i and j, p
(i)
j
denotes an atomic proposition at
level i, and e
j
denotes a computational atom associ-
ated with p
(0)
j
. In the figure, p
(0)
j
is connected to e
j
for
each j, and for each i ≥ 1 and j, p
(i)
j
is connected to
atomic propositions at level i − 1 that precisiate p
(i)
j
.
The figure shows that, for instance, p
(2)
2
can be ex-
pressed as a compound proposition consisting of two
Computational atoms
Figure 2: Hierarchy of propositions. At level i, the formal
logic described in Sections 3–3.4 is established with com-
ponent sets S
i
, V
i
, O
i
, A
i
, and C
i
. Atomic propositions in
S
0
× V
0
× O
0
× A
0
are the logical atoms and the building
blocks of all propositions, and each of them is directly as-
sociated with a computational atom. For each i ≥ 1, every
atomic proposition at level i is connected to atomic propo-
sitions at level i − 1 that precisiate it.
atomic propositions (p
(1)
1
and p
(1)
4
) at level 1 and also
as a compound proposition consisting of four atomic
propositions (p
(0)
1
, p
(0)
2
, p
(0)
3
, and p
(0)
4
) at level 0.
The hierarchy clearly shows the definition of
each proposition by expressing it in terms of precisi-
ated propositions at lower levels. Thus, non-logical,
domain-dependent axioms result from the hierarchy,
and they can be used for inference and reasoning in
the formal logic.
Different levels of granularity may require differ-
ent component sets, but the same syntactic structure
is enforced at all levels. Using the hierarchy, we can
ensure that all the resulting propositions remain pre-
cisiated at each level, and we can attain flexibility in
the level of detail.
7 SEMANTICS OF THE FORMAL
LOGIC
The semantics of formal logic specifies how to de-
termine the truth value of each proposition. In two-
valued logics, for instance, the truth value is either
1 (true) or 0 (false). As described by Zadeh (e.g.,
(Zadeh, 2001), (Zadeh, 2004)), this bivalence is not
suitable for PNL, so we develop a many-valued se-
mantics for our formal logic. The meaning of the truth
value depends on the context. For the task description
scheme described in Sections 3–6, for instance, one
can evaluate each proposition and let its truth value
reflect the feasibility of the corresponding task speci-
fication; 1 indicates that the task certainly can be car-
ried out whereas 0 indicates that it certainly cannot
be. In this case, it is more realistic and practical to let
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
338

the degree of feasibility take on not only the values 0
and 1 but also other values between 0 and 1. In real-
world problems, it can be highly practical to evaluate
the feasibility of a task description before any seri-
ous attempt is made to execute it. If robotic systems
interact with a variety of users, including users who
have no knowledge of these systems, some users may
describe tasks that are virtually impossible to accom-
plish. It is more desirable to disregard such highly in-
feasible tasks immediately than to waste resources by
attempting to realize them. Also, the user may want to
be informed of the degree of feasibility of the task that
he specifies before the system attempts to perform it.
When multiple options are available for performing a
specified task, the user may want to compare their de-
grees of feasibility before determining which option
to take.
To determine the truth value of each proposition
in our formal logic systematically and effectively, we
use fuzzy relations. A fuzzy relation is a generaliza-
tion of a classical (“crisp”) relation (see, for instance,
(Klir and Folger, 1988)). It is a mapping from a Carte-
sian product to the set of real numbers between 0 and
1. While a classical relation only expresses the pres-
ence or absence of some form of association between
the elements of factors in a Cartesian product, a fuzzy
relation can express various degrees or strengths of
association between them. (Hence a classical rela-
tion can be considered a “crisp” case of a fuzzy rela-
tion.) In our formal logic, each proposition consists of
pre-specified components, so a function that assigns a
truth value to each proposition can be represented by a
fuzzy relation on the Cartesian product of the compo-
nents. Using some of the operations defined on fuzzy
relations (they are described in Appendix), we can
systematically and economically determine the truth
value of each proposition.
We will explain the semantics of our formal
logic using concrete examples of task descriptions for
human-robot interaction so that the reader can under-
stand it intuitively. To facilitate our exposition, we
consider very simple task descriptions resulting from
atomic propositions in S ×V × O. Notice that even in
this rather simple case, we need an efficient scheme
for determining the truth value of each proposition.
For instance, if each of the component sets S, V , and
O contains ten elements, then there are 10
3
atomic
propositions in S ×V × O, and it may be impractical
to determine the truth values of all the atomic propo-
sitions individually. Moreover, if the component set C
consists of three connectives, then we can generate a
total of 3 · 10
6
compound propositions that consist of
two atomic propositions. In practice, it may be neces-
sary to promptly evaluate and compare the truth val-
ues of a large number of task descriptions represented
by such compound propositions in order to determine
which option to execute, so even this simple case re-
quires an efficient, systematic scheme for examining
the truth conditions of propositions. (Also note that
infinitely many propositions can be generated from
these component sets.)
In Section 7.1, we explain how to determine the
truth values of atomic propositions. In Section 7.2,
we explain how to determine the truth values of com-
pound propositions.
7.1 Truth Conditions of Atomic
Propositions
For concreteness, we consider establishing a fuzzy
relation on S × V × O, which is a mapping from
the Cartesian product to a totally ordered set called
a valuation set. In our formulation of many-
valued logic, the valuation set is the unit interval
[0, 1]. We consider the following component sets:
S = {robot1, robot2}, V = {recognize, hold}, O =
{ball, pen}. Table 2 shows the atomic propositions in
S ×V × O. Since the component sets considered here
Table 2: Atomic propositions resulting from
S = {robot1, robot2}, V = {recognize, hold}, and
O = {ball, pen}.
s ∈ S v ∈ V o ∈ O
robot1 recognize ball
robot1 recognize pen
robot1 hold ball
robot1 hold pen
robot2 recognize ball
robot2 recognize pen
robot2 hold ball
robot2 hold pen
are small, we only have eight atomic propositions in
the Cartesian product. However, as mentioned ear-
lier, the total number of atomic propositions becomes
quite large with large component sets, and we need
an efficient, systematic scheme for determining the
truth conditions of these propositions. We establish
our scheme using three operations on fuzzy relations:
projection, cylindric extension, and cylindric closure.
These operations are explained in Appendix.
Suppose that the truth conditions (for concrete-
ness, we assume that they represent degrees of fea-
sibility) of these atomic propositions are determined
for a robotic system under the following conditions:
(a) Robot1 is equipped with a high-resolution cam-
era that enables it to recognize various objects, in-
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
339

cluding a ball and a pen. However, it does not
have any arm, so it cannot hold any object.
(b) Robot2 has an arm that enables it to hold various
objects, including a ball and a pen. However, it is
not equipped with a high-resolution camera, so it
is not fully capable of identifying objects.
(c) With the high-resolution camera, a ball is easier to
recognize compared to a pen.
(d) With the arm, a pen is easier to hold compared to
a ball.
Our strategy is to derive a fuzzy relation on S ×
V × O from fuzzy relations on S × V and on V × O.
Hence, we first establish fuzzy relations on S ×V and
on V × O. Let R
S×V
: S ×V → [0, 1] denote a fuzzy
relation on S ×V . Based on conditions (a) and (b), we
set the values of R
S×V
as shown in Table 3. Recall
Table 3: Fuzzy relation R
S×V
on S ×V based on conditions
(a) and (b).
s ∈ S v ∈ V R
S×V
(s, v)
robot1 recognize .9
robot1 hold 0
robot2 recognize .2
robot2 hold .8
that a fuzzy relation expresses various degrees or
strengths of association between elements in compo-
nent sets. The value assigned to (robot1, recognize)
is relatively large (.9) because robot1 is equipped
with a high-resolution camera and is thus suitable for
recognizing objects, whereas the value assigned to
(robot1, hold) is zero because robot1 is not equipped
with an arm and is thus incapable of holding objects.
Similarly, the value assigned to (robot2, recognize) is
relatively small (.2) because robot2 is not equipped
with a high-resolution camera and is thus unsuitable
for recognizing objects, whereas the value assigned to
(robot2, hold) is relatively large (.8) because robot2
is equipped with an arm and is thus suitable for hold-
ing objects. Technically, the fuzzy relation R
S×V
is
considered the underlying fuzzy relation on S ×V ×O
projected onto S ×V (see Appendix for the operation
of projection).
Analogously, based on conditions (c) and (d), we
set the values of a fuzzy relation R
V ×O
: V × O →
[0, 1] as shown in Table 4. The value assigned
to (recognize, ball) is larger than that assigned to
(recognize, pen) because with a high-resolution cam-
era, a ball is easier to recognize compared to a pen.
Similarly, the value assigned to (hold, pen) is larger
than that assigned to (hold, ball) because with an
arm, a pen is easier to hold compared to a ball. Tech-
nically, the fuzzy relation R
V ×O
is considered the un-
Table 4: Fuzzy relation R
V ×O
on V ×O based on conditions
(c) and (d).
v ∈ V o ∈ O R
V ×O
(v, o)
recognize ball .9
recognize pen .8
hold ball .7
hold pen .8
derlying fuzzy relation on S ×V × O projected onto
V × O (see Appendix for the operation of projection).
We establish a fuzzy relation R
S×V ×O
: S × V ×
O → [0, 1] by combining the fuzzy relations R
S×V
and R
V ×O
. Formally, we obtain R
S×V ×O
by first ob-
taining the cylindric extensions of R
S×V
and R
V ×O
to S × V × O and then computing the cylindric clo-
sure of the two cylindric extensions (see Appendix
for cylindric extension and cylindric closure). First,
we obtain the cylindric extensions of R
S×V
and R
V ×O
to S ×V ×O. Table 5 shows the cylindric extension of
R
S×V
to S ×V ×O, which we denote by R
S×V ↑S×V×O
.
Table 5: Cylindric extension R
S×V ↑S×V×O
.
s ∈ S v ∈ V o ∈ O R
S×V ↑S×V ×O
(s, v, o)
robot1 recognize ball .9
robot1 recognize pen .9
robot1 hold ball 0
robot1 hold pen 0
robot2 recognize ball .2
robot2 recognize pen .2
robot2 hold ball .8
robot2 hold pen .8
This cylindric extension can be characterized as
maximizing nonspecificity in deriving a fuzzy rela-
tion on S ×V × O from a fuzzy relation on S ×V (see
Appendix). Similarly, Table 6 shows the cylindric ex-
tension of R
V ×O
to S × V × O, which we denote by
R
V ×O↑S×V ×O
.
Table 6: Cylindric extension R
V ×O↑S×V ×O
.
s ∈ S v ∈ V o ∈ O R
V ×O↑S×V ×O
(s, v, o)
robot1 recognize ball .9
robot1 recognize pen .8
robot1 hold ball .7
robot1 hold pen .8
robot2 recognize ball .9
robot2 recognize pen .8
robot2 hold ball .7
robot2 hold pen .8
This cylindric extension can be characterized as
maximizing nonspecificity in deriving a fuzzy relation
on S ×V ×O from a fuzzy relation on V ×O (see Ap-
pendix). Finally, we set R
S×V ×O
to the cylindric clo-
sure of R
S×V ↑S×V×O
and R
V ×O↑S×V ×O
on S × V × O
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
340
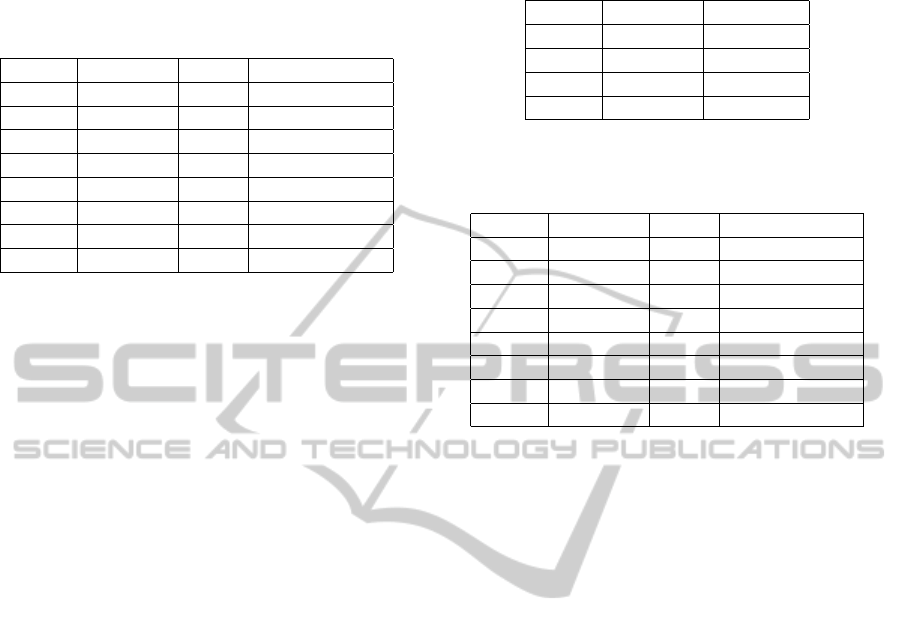
(see Appendix for the operation of cylindric closure),
which is shown in Table 7.
Table 7: Cylindric closure R
S×V ×O
of R
S×V ↑S×V×O
and
R
V ×O↑S×V ×O
on S ×V ×O.
s ∈ S v ∈ V o ∈ O R
S×V ×O
(s, v, o)
robot1 recognize ball .9
robot1 recognize pen .8
robot1 hold ball 0
robot1 hold pen 0
robot2 recognize ball .2
robot2 recognize pen .2
robot2 hold ball .7
robot2 hold pen .8
Notice that the resulting truth values (degrees of
feasibility) assigned to the eight atomic propositions
reflect the conditions (a)–(d). For example, the truth
values clearly indicate that robot1 is highly capable
of recognizing objects (because it is equipped with a
high-resolution camera) but is incapable of holding
objects (because it does not have any arm). Sim-
ilarly, the truth values clearly indicate that robot2
is highly capable of holding objects (because it is
equipped with an arm) but is rather incapable of rec-
ognizing objects (because it is not equipped with a
high-resolution camera).
It is efficient to derive a fuzzy relation on S ×V ×
O from fuzzy relations on S ×V and on V ×O. Again,
suppose that each of these component sets consists
of ten elements. Then a total of 10
3
atomic proposi-
tions result from them, and it may be time-consuming
to determine 10
3
truth values individually. With our
scheme, we can derive the 10
3
truth values by deter-
mining 2 · 10
2
values of the fuzzy relations R
S×V
and
R
V ×O
. This efficiency of the scheme becomes more
notable as the size of each component set or the num-
ber of component sets increases.
Another important strength of our scheme lies in
updating the truth values of the atomic propositions.
In practice, the values shown in Tables 3–4 will be
determined dynamically based on the conditions of
the robots. For instance, if the high-resolution camera
of robot1 becomes dysfunctional, then we will use the
fuzzy relation R
0
S×V
shown in Table 8 instead of the
fuzzy relation R
S×V
in Table 3 in computing the truth
values of the atomic propositions.
Notice that the value of R
0
(robot1, recognize) is
.2, reflecting the fact that robot1 can no longer use
its high-resolution camera to recognize objects. It is
easy to verify that Table 9 shows the cylindric closure
R
0
S×V ×O
of the cylindric extensions R
0
S×V ↑S×V×O
and
R
V ×O↑S×V ×O
.
Comparing Tables 7 and 9, we can see that the up-
Table 8: Fuzzy relation R
0
S×V
on S ×V (reflecting a damage
to robot1’s high-resolution camera).
s ∈ S v ∈ V R
0
S×V
(s, v)
robot1 recognize .2
robot1 hold 0
robot2 recognize .2
robot2 hold .8
Table 9: Cylindric closure R
0
S×V ×O
of R
0
S×V ↑S×V×O
and
R
V ×O↑S×V ×O
on S×V ×O (reflecting a damage to robot1’s
high-resolution camera).
s ∈ S v ∈ V o ∈ O R
0
S×V ×O
(s, v, o)
robot1 recognize ball .2
robot1 recognize pen .2
robot1 hold ball 0
robot1 hold pen 0
robot2 recognize ball .2
robot2 recognize pen .2
robot2 hold ball .7
robot2 hold pen .8
dated truth values (shown in Table 9) reflect the con-
dition that the high-resolution camera of robot1 has
become dysfunctional. Notice that we have efficiently
updated the fuzzy relation on S×V ×O by just updat-
ing the fuzzy relation on S ×V . With our scheme, it
is possible to keep the truth values of a large number
of atomic propositions updated continually.
7.2 Truth Conditions of Compound
Propositions
Since we establish our formal logic as a many-valued
logic, we treat the connectives in C as logic primitives
of many-valued logic or fuzzy logic. Here we exam-
ine thee typical logical primitives: conjunction (rep-
resented by ”and” in C), disjunction (represented by
”or” in C), and implication (also called conditional,
represented by “if” in C).
In evaluating the truth value of a compound propo-
sition, conjunction is often implemented as a t-norm,
whereas disjunction is often implemented as a t-
conorm (e.g., (Klir and Folger, 1988), (H
´
ajek, 1998)).
Various forms of t-norm and t-conorm have been
proposed. Some of the frequently used t-norms are
the minimum t-norm, the product t-norm, and the
Łukasiewicz t-norm, and some of the frequently used
t-conorms are the maximum t-conorm, the probabilis-
tic sum, and the Łukasiewicz t-conorm. In practice,
the suitability of each of these t-norms or t-conorms
depends on what the truth value represents. Also,
there are various ways to implement implication in
evaluating the truth value of a compound proposition
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
341

(e.g., (Trillas and Alsina, 2012)). Some of the main
forms of implication are the material implication, the
conjunctive conditional, the residuated conditional
Sasaki hook, the Dishkant hook, and the Mamdani-
Larsen conditional. Again, in practice, the suitability
of each conditional depends on what the truth value
represents.
8 CONCLUSIONS
We have taken a first step toward establishing a formal
logic as a generalized precisiation language, which
is essential for generalizing PNL. Various syntactic
structures in natural language can be incorporated in
our formal logic so that it precisiates not only percep-
tual propositions but also action-related propositions.
The syntax of the formal logic allows us to create in-
finitely many precisiated propositions while ensuring
that every proposition in it is precisiated. As in other
formal logics, we can infer and reason in our for-
mal logic. The resulting generalized precisiation lan-
guage serves as a middle ground between the natural-
language-based mode of human communication and
the low-level mode of machine communication and
thus significantly facilitates human-machine interac-
tion.
ACKNOWLEDGEMENTS
This research is supported by the Spanish Ministry
of Economy and Competitiveness through the project
TIN2011-29824-C02-02 (ABSYNTHE).
REFERENCES
Biber, D., Conrad, S., and Leech, G. (2002). A student
grammar of spoken and written English. Pearson ESL.
Casper, J. and Murphy, R. R. (2003). Human-robot interac-
tions during the robot-assisted urban search and res-
cue response at the World Trade Center. IEEE Trans-
actions on Systems, Man, and Cybernetics, Part B,
33:367–385.
Dias, M. B., Harris, T. K., Browning, B., Jones, E. G., Ar-
gall, B., Veloso, M. M., Stentz, A., and Rudnicky, A. I.
(2006). Dynamically formed human-robot teams per-
forming coordinated tasks. In AAAI Spring Sympo-
sium: To Boldly Go Where No Human-Robot Team
Has Gone Before, pages 30–38.
Dias, M. B., Kannan, B., Browning, B., Jones, E. G., Argall,
B., Dias, M. F., Zinck, M., Veloso, M. M., and Stentz,
A. J. (2008a). Evaluation of human-robot interaction
awareness in search and rescue. In Proceedings of the
IEEE International Conference on Robotics and Au-
tomation, pages 2327–2332.
Dias, M. B., Kannan, B., Browning, B., Jones, E. G., Ar-
gall, B., Dias, M. F., Zinck, M., Veloso, M. M., and
Stentz, A. J. (2008b). Sliding autonomy for peer-to-
peer human-robot teams. In Proceedings of the 10th
International Conference on Intelligent Autonomous
Systems.
Feil-Seifer, D. and Mataric, M. J. (2008). Defining socially
assistive robotics. In Proceedings of the International
Conference on Rehabilitation Robotics, pages 465–
468.
Ferketic, J., Goldblatt, L., Hodgson, E., Murray, S., Wi-
chowski, R., Bradley, A., Chun, W., Evans, J., Fong,
T., Goodrich, M., Steinfeld, A., and Stiles, R. (2006).
Toward human-robot interface standards: Use of stan-
dardization and intelligent subsystems for advancing
human-robotic competency in space exploration. In
Proceedings of the SAE 36th International Conference
on Environmental Systems.
Fong, T., Nourbakhsh, I., Kunz, C., Fl
¨
uckiger, L., Schreiner,
J., Ambrose, R., Burridge, R., Simmons, R., Hiatt, L.,
and Schultz, A. (2005). The peer-to-peer human-robot
interaction project. Space, 6750.
Fong, T. and Thorpe, C. (2001). Vehicle teleoperation inter-
faces,. Autonomous Robots, 11:9–18.
Forsberg, M. (2003). Why is speech recognition difficult.
Chalmers University of Technology.
Gieselmann, P. and Stenneken, P. (2006). How to talk
to robots: Evidence from user studies on human-
robot communication. How People Talk to Computers,
Robots, and Other Artificial Communication Partners,
page 68.
Goodrich, M. A. and Schultz, A. C. (2007). Human-robot
interaction: a survey. Found. Trends Hum.-Comput.
Interact., 1:203–275.
H
´
ajek, P. (1998). Metamathematics of Fuzzy Logic, vol-
ume 4. Kluwer Academic.
Johnson, M., Feltovich, P. J., Bradshaw, J. M., and Bunch,
L. (2008). Human-robot coordination through dy-
namic regulation. In Robotics and Automation, 2008.
ICRA 2008. IEEE International Conference on, pages
2159–2164.
Johnson, M. and Intlekofer, K. (2008). Coordinated op-
erations in mixed teams of humans and robots. In
Proceedings of the IEEE International Conference on
Distributed human-Machine Systems.
Kitano, H., Tadokoro, S., Noda, I., Matsubara, H., Takah-
sahi, T., Shinjou, A., and Shimada, S. (1999).
RoboCup rescue: Search and rescue in large-scale dis-
asters as a domain for autonomous agents research. In
Proceedings of the IEEE International Conference on
Systems, Man, and Cybernetics, pages 739–743.
Klir, G. J. and Folger, T. A. (1988). Fuzzy sets, uncertainty,
and information. Prentice Hall.
Kulyukin, V., Gharpure, C., Nicholson, J., and Osborne,
G. (2006). Robot-assisted wayfinding for the visu-
ally impaired in structured indoor environments. Au-
tonomous Robots, 21:29–41.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
342

Lacey, G. and Dawson-Howe, K. M. (1998). The applica-
tion of robotics to a mobility aid for the elderly blind.
Robotics and Autonomous Systems, 23:245–252.
Marble, J., Bruemmer, D., Few, D., and Dudenhoeffer, D.
(2004). Evaluation of supervisory vs. peer-peer inter-
action with human-robot teams. In Proceedings of the
Hawaii International Conference on System Sciences.
Mu
˜
noz, E., Nakama, T., and Ruspini, E. (2013). Hierarchi-
cal qualitative descriptions of perceptions for robotic
environments. To appear in the Proceedings of the
Fifth International Conference on Fuzzy Computation
Theory and Application (FCTA).
Nakama, T., Mu
˜
noz, E., and Ruspini, E. (2013). Generaliz-
ing precisiated natural language: A formal logic as a
precisiation language. To appear in the Proceedings of
the Eighth Conference of European Society for Fuzzy
Logic and Technology (EUSFLAT).
Norbakhsh, I. R., Sycara, K., Koes, M., Yong, M., Lewis,
M., and Burion, S. (2005). Human-robot teaming for
search and rescue. Pervasive Computing, pages 72–
79.
Russell, B. (1984). Lectures on the philosophy of log-
ical atomism. In Marsh, R. C., editor, Logic and
Knowledge Essays 1901–1950. George Allen & Un-
win, London.
Shim, I., Yoon, J., and Yoh, M. (2004). A human robot
interactive system “RoJi”. International Journal of
Control, Automation, and Systems, 2:398–405.
Shneiderman, B. (2000). The limits of speech recognition.
Communications of the ACM, 43(9):63–65.
Tomassi, P. (1999). Logic. Routledge.
Trillas, E. and Alsina, C. (2012). From Leibnizs shinning
theorem to the synthesis of rules through Mamdani-
Larsen conditionals. In Combining Experimentation
and Theory, pages 247–258. Springer.
Wilcox, B. and Nguyen, T. (1998). Sojourner on mars and
lessons learned for future planetary rovers. In Pro-
ceedings of the SAE International Conference on En-
vironmental Systems.
Winograd, T. and Flores, F. (1986). Understanding com-
puters and cognition: A new foundation for design.
Ablex Pub.
Zadeh, L. A. (2001). A new direction in ai: Toward a
computational theory of perceptions. AI magazine,
22(1):73.
Zadeh, L. A. (2002). Some reflections on information gran-
ulation and its centrality in granular computing, com-
puting with words, the computational theory of per-
ceptions and precisiated natural language. Studies in
Fuzziness And Soft Computing, 95:3–22.
Zadeh, L. A. (2004). Precisiated natural language (PNL).
AI Magazine, 25(3):74–92.
APPENDIX
We describe three operations on fuzzy relations that
are used in determining the truth conditions of atomic
propositions in our formal logic: projection, cylin-
dric extension, and cylindric closure. First, we es-
tablish notation. Let X
1
, X
2
, . . . , X
n
be sets, and let
X
1
× X
2
× ·· · × X
n
denote their Cartesian product. We
will also denote the Cartesian product by ×
i∈N
n
X
i
,
where N
n
denotes the set of integers 1 through n.
A fuzzy relation on ×
i∈N
n
X
i
is a function from the
Cartesian product to a totally ordered set, which is
called a valuation set. In our formulation, the unit in-
terval [0, 1] is used as a valuation set. Each n-tuple
(x
1
, x
2
, . . . , x
n
) in X
1
× X
2
× ·· · × X
n
(thus x
i
∈ X
i
for
each i ∈ N
n
) will also be denoted by (x
i
| i ∈ N
n
). Let
I ⊂ N
n
. A tuple y := (y
i
| i ∈ I) in Y := ×
i∈I
X
i
is said
to be a sub-tuple of x := (x
i
| i ∈ N
n
) in ×
i∈N
n
X
i
if
y
i
= x
i
for each i ∈ I, and we write y ≺ x to indicate
that y is a sub-tuple of x.
Let X := ×
i∈N
n
X
i
and Y := ×
i∈I
X
i
for some I ⊂
N
n
. Suppose that R : X → [0, 1] is a fuzzy relation on
X. Then a fuzzy relation R
0
: Y → [0, 1] is called the
projection of R on Y if for each y ∈ Y , we have
R
0
(y) = max
x∈X : y≺x
R(x).
We let R
↓Y
denote the projection of R on Y .
We continue with X := ×
i∈N
n
X
i
and Y := ×
i∈I
X
i
(I ⊂ N
n
). Let F : Y → [0, 1] be a fuzzy relation on
Y . A fuzzy relation F
0
: X → [0, 1] is said to be the
cylindric extension of F to X if for all x ∈ X , we have
F
0
(x) = F(y),
where y is the tuple in Y such that y ≺ x. We let F
↑X
denote the cylindric extension of F to X. The cylin-
dric extension F
↑X
of a fuzzy relation F : Y → [0, 1] is
the “largest” fuzzy relation on X such that its projec-
tion on Y equals F; if we let R denote the set of all
fuzzy relations R
0
: X → [0, 1] such that R
0
↓Y
= F, then
for all x ∈ X, we have
F
↑X
(x) = max{R
0
(x) | R
0
∈ R}.
For each j, let Y
j
:= ×
i∈I
j
X
i
, where I
j
⊂ N
n
. Let
R
( j)
: Y
j
→ [0, 1] denote a fuzzy relation on Y
j
. Then
a fuzzy relation F : X → [0, 1] is called the cylindric
closure of R
(1)
, R
(2)
, . . . , R
(m)
on X if for each x ∈ X,
F(x) = min
1≤ j≤m
R
( j)
↑X
(x).
GeneralizationandFormalizationofPrecisiationLanguagewithApplicationstoHuman-RobotInteraction
343
