Heart Rate Variability

Knowing More about HRV Analysis and Fatigue in Transport Studies

Jesús Murgoitio Larrauri

, José Luis Gutierrez Temiño

and María José Gil Larrea

Fundación Tecnalia Research & Innovation, Ibaizabal Bidea 202 - Parque Tecnológico de Bizkaia, Zamudio, Spain

ESIDE, University of Deusto, Avenida de las Universidades 24, Bilbao, Spain

Keywords: Heart Rate Variability, HRV, Fatigue, Transport Applications.

Abstract: The use of ECG signal and derived HRV (Heart Rate Variability) analysis is a well-known technique for

detecting different levels of fatigue for objective evaluation in human activities (e.g. car-driver state

monitoring). This work takes a step further in detecting the first signals of fatigue without any hard methods

(usually car-drivers are forced not to rest for many hours). So, based on data coming from the ECG signal

for 24 experiments and the same number of different car-drivers driving for 3 hours starting in good

conditions, some correlations between fatigue and heart physiology has been explored through data mining

methods. Finally, one classifier based on a particular entropy evaluation has been used due to its very good

behaviour (True-Positives > 75 % and ROC area > 90 %). This work, using not the classifier itself but its

behaviour when the parameter known as “blending” (“blending” defines a different “neighbour” concept) is

changed, shows how the entropy between the computed “five minutes” driving windows (each window is

defined by a group of 15 previously selected variables) is more independent of the neighbour when these

time-windows are near to two hours driving. The work concludes that the entropy is more stable when

drivers reach two hours driving and this way will be promising. Consequently, it is proposed further studies

in the future based on this entropy concept too, but now integrating additional factors, e.g. age and circadian

cycles, which can complete and improve the HRV analysis, including different scenarios or applications out

of the safety in the transport studies.

1 INTRODUCTION

All studies about drivers state monitoring agree on

the detection of the first signals of fatigue around the

second hour driving. This is the reason why many

driving associations and public authorities

recommend taking a rest at least every two hours

driving. The figure 1 (RACE, 2011) obtained from

the 2011 report about fatigue is an example and

shows once again this aspect.

Thus, trying to find an objective method based

on physiological activity which is easy to use in

driving experiments when drivers drive a car,

TECNALIA Research & Innovation and the

University of Deusto has been working on using

ECG signal mainly focused on detection of the first

signals of fatigue. Furthermore, the reason for

considering it to be of interest to integrate the driver

ECG signal within the car system is closely related

to the “driver mental workload” measurement and

the relation with some physiological indices.

Figure 1: Evolution of the risk of fatigue when driving

(RACE).

Furthermore, most of the studies about driver

monitoring using ECG signal analyse this

information through the HRV (Heart Rate

Variability) but force drivers not to sleep for hours.

These previous experiences showed the influence of

fatigue in heart activity but it is not the most real

situation because the usual scenario is to start

driving in normal conditions. Besides, the part of

information coming from the ECG signal and

closely related to fatigue is very low and is

frequently only detected when fatigue is really

107

Murgoitio Larrauri J., Gutierrez Temiño J. and Gil Larrea M..

Heart Rate Variability - Knowing More about HRV Analysis and Fatigue in Transport Studies.

DOI: 10.5220/0004666501070114

In Proceedings of the International Congress on Cardiovascular Technologies (IWoPE-2013), pages 107-114

ISBN: 978-989-8565-78-5

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

evident or high. On the other hand it is clear that

other physiological signals like EEG are better but

more difficult to analyse and need more expensive

devices and methods.

In the following lines we will introduce you to

the reasons why only a small part of the data coming

from the heart activity has information we are

interested in.

1.1 Heart Activity

Two anatomically different structures are used as

physiological indicators of workload measures:

Central Nervous System (CNS, it includes the brain,

brain stem, and spinal cord cells), and Peripheral

Nervous System (PNS) measures. The PNS can be

divided into the Somatic Nervous System (SoNS,

concerned with the activation of voluntary muscles)

and Autonomic Nervous System (AuNS, controls

internal organs and is autonomous because AuNS

innervated muscles are not under voluntary control).

The AuNS is further subdivided into the

Parasympathetic Nervous System (PaNS, to

maintain bodily functions) and the Sympathetic

Nervous System (SyNS, for emergency reactions):

Figure 2: Anatomical structures.

Most organs are dually innervated both by SyNS

and PaNS, and both can be coactive, reciprocally

active, or independently active. Heart rate is an

example of AuNS measures. So, the heart is

innervated both by the PaNS and SyNS. Each heart

contraction is produced by electrical impulses that

can be measured in the form of the ECG

(Electrocardiogram). The following figure shows the

well-known and typical register of heart electrical

activity:

Figure 3: Heart electrical activity.

Based on the information coming from this heart

electrical activity, time domain, frequency and

amplitude measures can be derived.

1.2 Time Domain

In the time domain usually the R-Waves of the ECG

are detected, and the time between these peaks (IBI:

Inter Beat Interval) is calculated. IBI is directly

related to Heart Rate (HR). However, this relation is

no linear and IBI is more normally distributed in

samples compared with HR. Thus, IBI scores should

be used for detection and testing of differences

between mean HR. IBI scales are less influenced by

trends than the HR scale.

According to some scientific works, average

heart rate during task performance compared to rest-

baseline measurement is a fairly accurate measure of

metabolic activity, and not only physical effort

affects heart rate level; emotional factors, such high

responsibility or the fear of failing a test, also

influence mean heart rate.

In the time domain, HRV is also used as a

measure of mental load. HRV provides additional

information to average HR about the feedback

between the cardiovascular systems and CNS

structures. In general HRV decrease is more

sensitive to increases in workload than HR increase.

Some works showed that an increase in physical

load decreased HRV and increased HR, while an

increase in mental load was accompanied by a

reduced HRV and no effect on HR (Lee and Park,

1990). Fatigue is reported to increase HRV

(Mascord and Heath, 1992) while low amounts of

alcohol decrease HRV (González González et al.,

1992).

1.3 Frequency Domain

In frequency domain, HRV is decomposed into

components that are associated with biological

control mechanisms (Kramer, 1991); (Porges and

Byrne, 1992). Three frequency bands have been

identified (Mulder, 1988; 1992): a low frequency

band (0.02-0.06 Hz) believed to be related to the

regulation of the body temperature, a mid frequency

band (0.07-0.14 Hz) related to the short term blood-

pressure regulation and a high frequency band (0.15-

0.50 Hz) believed to be influenced by respiratory-

related fluctuations (vagal, PaNS influenced –

(Kramer, 1991)):

CARDIOTECHNIX2013-InternationalCongressonCardiovascularTechnologies

108

Figure 4: HRV: frequency analysis (PSD=Power Spectral

Density, VLF= Very Low Frequencies, LF= Low

Frequencies, HF= High Frequencies).

A decrease in power in the mid frequency band

(“0,10 Hz” component) and in the high frequency

band have been shown to be related to mental effort

and task demands (Jorna, 1992); (Backs and Seljos,

1994); (Paas et al., 1994).

1.4 Amplitude Domain

Finally, amplitude information from the ECG signal

can be used to obtain information about workload.

The amplitude of the T-wave (TWA) is said to

mainly reflect SyNS (Furedy, 1996) and decreases

with increases in effort.

Driving is a very dynamic task in a changing

environment. Moreover, the driving task is large

influenced by drivers themselves. Nowadays, there

are factors that may even lead to increased human

failure in traffic:

 The number of vehicles on the road is increasing,

so increased road intensity leads to higher

demands on the human information processing

system and an increased likelihood of vehicles

colliding.

 People continue to drive well into old age.

Elderly people suffer from specific problems in

terms of divided attention performance, a task

that is more and more required in traffic. One of

the causes of these increased demands is the

introduction of new technology into the vehicle.

 Drivers in a diminished state endanger safety on

the road (longer journeys, night time driving, and

so on). Driver fatigue is currently an important

factor in the cause of accidents.

The above mentioned factors and situations have

in common that in all cases driver workload is

affected. Although there are several definitions and

models to explain it, “mental workload” could be

defined as a relative concept; it would be the ratio of

demand to allocated resources. From this point of

view, several scientific works have demonstrated

that some parameters obtained from physiological

measures (pupil diameter, heart rate and respiratory,

electro dermal activity, EEG, electro-oculography

etc.) could help to ascertain the driver’s mental

workload and one of them is the ECG. Due to its

low level invasive characteristic, ECG information

seems very interesting information to increase safety

in driving tasks. The main idea is to use laboratory

methods considered in traffic research and based on

ECG signal.

From this point of view, as is explained in the

next section, several experiments have been carried

out to acquire data from ECG together with other

interesting information, but now focusing on

detecting specific patterns for the first signals of

fatigue around the second hour driving for normal

users in normal scenarios.

2 METHODS

In order to have significant data the methodology

followed can be structured in the following phases:

Experiments definition, data collection, and analysis.

The analysis includes one preliminary analysis for

classifier selection including attribute selection, and

a final analysis.

Anyway, although this work is focussed on the

HRV analysis and its application to the safety within

road transport scenarios, it can be considered as the

starting point to be extensible to any environment

related to the measurement of the working

conditions, e.g. other situations of risk of fatigue -

like working long-time periods in a hospital or in a

factory with a machine.

2.1 Experiment & Data Collection

Up to 24 experiments were carried out for 24

different drivers, all of them males and between 18

and 70 years old. Each driver was informed before

starting about it and the corresponding authorization

was also signed by them.

Every driver drove along one clear defined route

(always the same for every driver) completing

around three hours driving. The route had different

types of roads which were classified in five different

ways as is shown in the following table.

HeartRateVariability-KnowingMoreaboutHRVAnalysisandFatigueinTransportStudies

109

Table 1: Route description.

KM Code Type ofRoad

Start 0,0

0,5 C5 Urban

3,0 C1 Highway

44,0 C2 National (1 lane)

83,5 C1 Highway

97,1 C2 National (1 lane)

115,3 C3 Local

138,1 C4 Local - Mountain

151,5 C3 Local

158,0 C5 Urban

169,4 C1 Highway

210,0 C2 National (1 lane)

212,8 C1 Highway

End 213,3 C5 Urban

As the main information to be considered was

the ECG signal the following devices were designed

and used to collect ECG signal (three electrodes

based):

Figure 5: Three electrodes based ECG data acquisition

system (1=Amplifier, 2=NI USB 6009, 3=Laptop,

4=Regulator, 5=battery).

Additionally data such as distance and time for

each five minutes driving were collected too.

Finally, up to 41 parameters were considered and

computed to assign for each five-minutes windows

with 50 % overlapping, e.g. circadian cycle (M in

the morning and T in the afternoon), age, mean and

standard deviation of RR intervals, and the

following 16 parameters from the frequency domain

(see figure 4).

Additionally, based on the Poincaré plot (Kitlas,

2005) the following two measures were also

calculated in the time domain: SD1 (instantaneous

beat-to-beat variability of the data), SD2 (continuous

beat-to-beat variability). The ratio SD1/SD2 is used

as a measure of heart activity too.

Table 2: Frequency domain parameters.

Description

1 X coordinate of peak in VLF

2 Y coordinate of peak in VLF

3 X coordinate of peak in LF

4 Y coordinate of peak in LF

5 X coordinate of peak in HF

6 Y coordinate of peak in HF

7 X coordinate of centroid in VLF

8 Y coordinate of centroid in VLF

9 X coordinate of centroid in LF

10 Y coordinate of centroid in LF

11 X coordinate of centroid in HF

12 Y coordinate of centroid in HF

13 Area of VLF (PSD)

14 Area of LF (PSD)

15 Area of HF (PSD)

16 Ratio of LF/HF areas

Figure 6: Poincaré plot: SD1 & SD2 graphical.

So, SD1, SD2 and the corresponding ratio are

considered as some of the most summarized and

complete information about the heart no linear

behaviour.

2.2 Analysis

2.2.1 Classifier: Instance-based Learners

The task of classifying objects is one to which

researchers in artificial intelligence have devoted

much time and effort and many different approaches

CARDIOTECHNIX2013-InternationalCongressonCardiovascularTechnologies

110

have been tried with varying success. Some well-

known schemes and their representations include:

ID3 which uses decision trees (Quinlan, 1986),

FOIL which uses rules (Quinlan, 1990), PROTOS

which is a case-based classifier (Porter et al., 1990),

and the instance-based learners IB1-IB5 (Aha et al.,

1991); (Aha, 1992). These schemes have

demonstrated excellent classification accuracy over

a large range of domains.

In this work we will use the entropy as a distance

measure which provides a unified approach to

dealing with these problems. Specifically we will

use the K-Star (Cleary and Trigg, 1995), an

instance-based learner which uses such a measure.

Instance-based learners classify an instance by

comparing it to a database of pre-classified

examples. The fundamental assumption is that

similar instances will have similar classifications.

The question lies in how to define “similar instance”

and “similar classification”.

Nearest neighbour algorithms (Cover and Hart,

1967) are the simplest of instance-based learners.

They use certain domain specific distance functions

to retrieve the single most similar instance from the

training set. The classification of the retrieved

instance is given as the classification for the new

instance. Edited nearest neighbour algorithms (Hart,

1968); (Gates, 1972) are selective and in these

instances are stored in the database and used in

classification. The k nearest neighbours of the new

instance are retrieved and whichever class is

predominant amongst them is given as the new

instance's classification. A standard nearest

neighbour classification is the same as a k-nearest

neighbour classifier for which k=1.

One of the advantages of the approach we are

following here is that both real attributes and

symbolic attributes can be dealt with together within

the same framework.

For K-Star we have to choose values for the

blending parameter. The behaviour of the distance

measure as these parameters change is very

interesting. Consider the probability function for

symbolic attributes as “s” changes. With a value of

“s” close to 1, instances with a symbol different to

the current one will have a very low transformation

probability, while instances with the same symbol

will have a high transformation probability. Thus the

distance function will exhibit nearest neighbour

behaviour. As “s” approaches 0, the transformation

probability directly reflects the probability

distribution of the symbols, thus favouring symbols

which occur more frequently. This behaviour is

similar to the default rule for many learning schemes

which is simply to take whichever classification is

most likely (regardless of the new instance's attribute

values). As “s” changes, the behaviour of the

function varies smoothly between these two

extremes. The distance measure for real valued

attributes exhibits the same properties.

So, the K-Star algorithm chooses a value for

“blending” (mentioned “s” parameter) by selecting a

number between n0 and N. Thus selecting n0 gives a

nearest neighbour algorithm and choosing N gives

equally weighted instances. For convenience the

number is specified by using the “blending

parameter” b, which varies from b= 0% (for n0) and

b=100% for N, with intermediate values interpolated

linearly.

We think of the selected number as a “sphere of

influence”, specifying how many of the neighbours

should be considered important (although there is

not a harsh cut off at the edge of the sphere—more

of a gradual decreasing in importance).

The underlying technique solves the smoothness

problem and we believe contributes strongly to its

good overall performance. The underlying theory

also allows clean integration of both symbolic and

real valued attributes and a principled way of

dealing with missing values (in this case symbolic

attributes were used).

2.2.2 Attribute Selection

For attribute selection, all five minutes windows

were labelled to defined six groups: “A” for the first

30 minutes driving, “B” for the next 30 minutes, and

so on until “F” for the last 30 minutes.

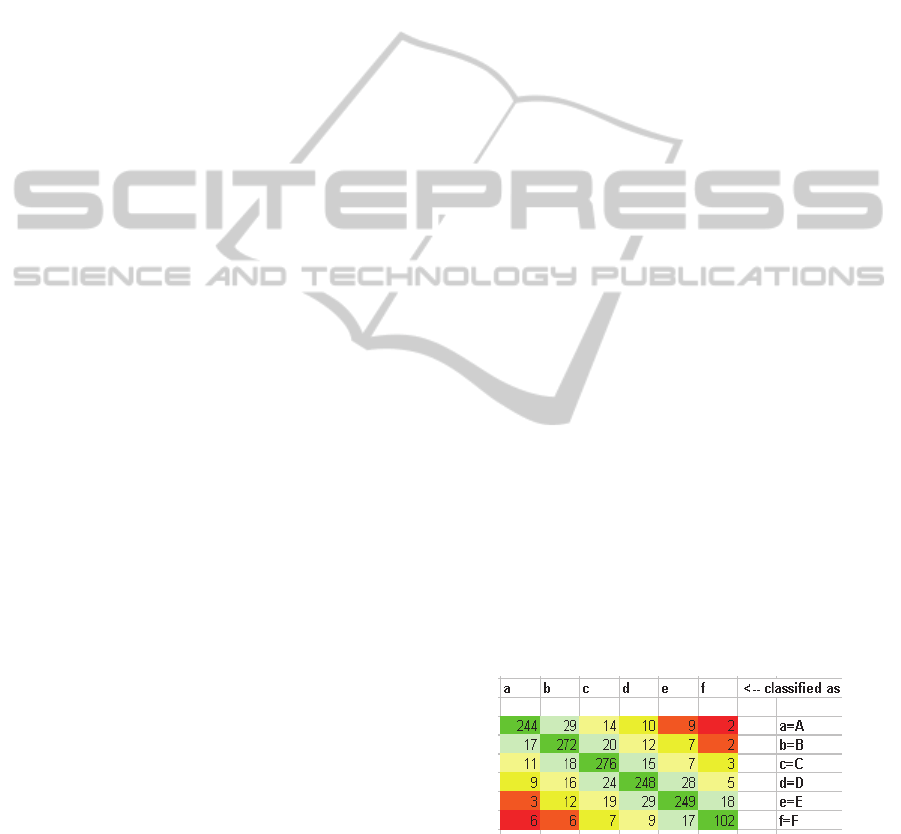
So, based on the WEKA (Waikato Environment

for Knowledge Analysis, version 3.6.6) tool and the

previously mentioned K-Star classifier, 15

parameters are shown to have the best confusion

matrix to classify all five minutes windows:

Figure 7: Confusion matrix.

The following figure shows the summary and the

detailed accuracy for each group, using “10-fold

cross validation” method for validation:

HeartRateVariability-KnowingMoreaboutHRVAnalysisandFatigueinTransportStudies

111

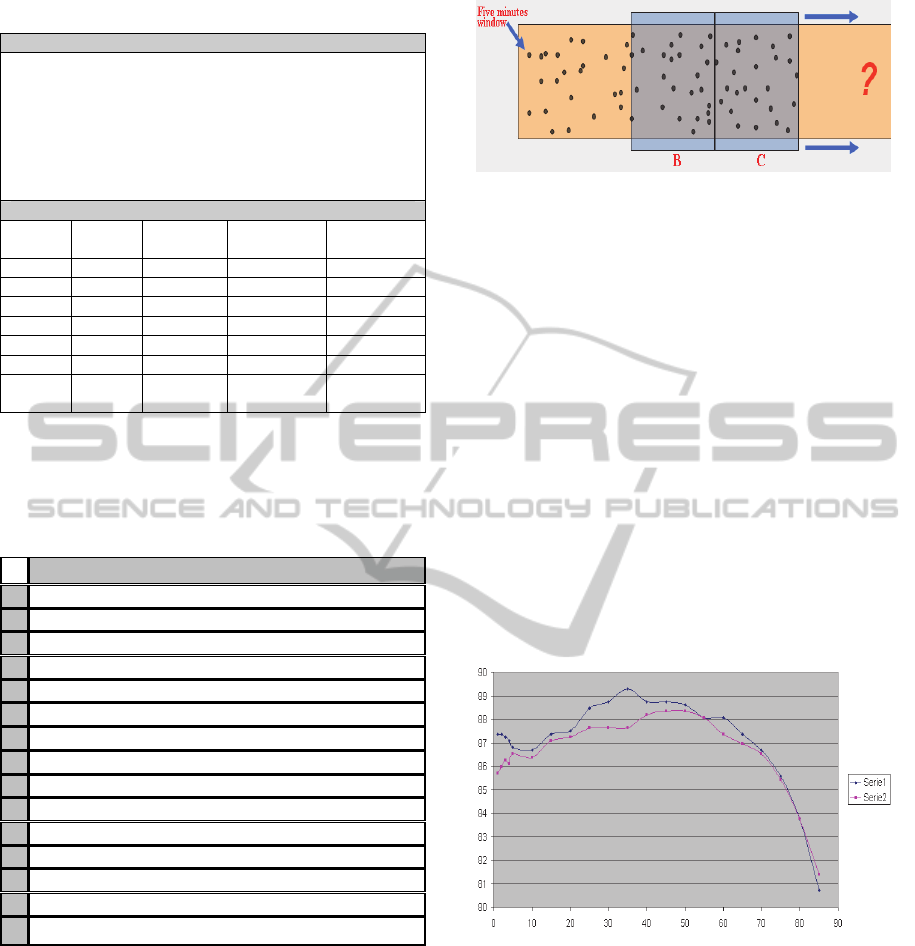
Table 3: Summary and Detailed Accuracy by class.

=== Summary ===

Correctly Classified Instances: 1.391 (78,3662 %)

Incorrectly Classified Instances: 384 (21,6338)

Kappa statistic: 0,7374

Mean absolute error: 0,0923

Root mean squared error: 0,235

Relative absolute error: 33,5625 %

Root relative squared error: 63,3865 %

Total Number of Instances: 1.775

=== Detailed Accuracy By Class ===

Rate

Precision ROC Area Class

0,792 0,031 0,841 0,963 A

0,824 0,056 0,771 0,958 B

0,836 0,058 0,767 0,955 C

0,752 0,052 0,768 0,939 D

0,755 0,047 0,785 0,938 E

0,694 0,018 0,773 0,958 F

0,784 0,047 0,785 0,951

Weighted

Avg.

The 15 parameters finally selected (assigned to

each five minutes window) to go further on the final

analysis were the following:

Table 4: Parameters selected.

Description

1 Circadian cycle (M=morning/T=afternoon)

2 Standard deviation of RR intervals (ms)

3 Mean of RR intervals (ms)

4 X coordinate of peak in LF (Hz)

5 X coordinate of peak in HF (Hz)

6 % of PSD for VLF

7 % of PSD for LF

8 % of PSD for HF

9 SD1: Improved standard deviation

10 SD2: Improved standard deviation

11 Ratio of PSD between LF/HF

12 X coordinate of centroid in VLF

13 X coordinate of centroid in LF

14 X coordinate of centroid in HF

15 Label of section in the route (A, B, C, D, E, F)

2.2.3 Final Analysis

Based on the preliminary analysis and results, a new

study was carried out considering only sections B

and C (each section = 30 minutes) when the border

between B and C sections was moved 5 to 5

minutes. It is graphically shown in the following

figure where each “dot” represents each of the five

minutes driving for one driver defined by the values

for the 15 parameters mentioned previously:

Figure 8: Two closed “30 minutes” windows moving

along the time.

Thus, the K-Star classifier behaviour to classify

B and C sections for different “blending”

(neighbour) values was analyzed for the border fixed

in each of the “t” instant.

3 RESULTS

The following figure shows this behaviour for two

different borders (series 1 and series 2) defined in

the route when the blending parameter is going from

0 to 100 %. It means that K-Star classifier behaviour

for “series 1” is improving from blending = 0 to 35

(until 89,3 % of correctly classified instances) and

then starts losing accuracy. So, this behaviour was

analyzed for different borders defined from 100

minutes to 135 all around the 2 hours (120 minutes):

Figure 9: Behaviour of the K-Star classifier for different

“blending” values (X=“blending”, Y=”accuracy”).

The final analysis of the behaviour of K-Star

classifier for each of the previously defined borders

(100-135) when the blending is changing showed

very interesting results about the entropy when the

first signals of fatigue are starting. It is graphically

documented in the following figure where e.g.

“Series 120” means the K-Star behaviour when the

border between B and C sections is defined in 120

minutes of the overall route. This analysis was

focused only on blending values between 15 % and

55 %, when the accuracy is the best and more stable.

CARDIOTECHNIX2013-InternationalCongressonCardiovascularTechnologies

112

Figure 10: Behavior of the K-Star classifier during

different moments near the second hour guiding

(X=“blending”, Y=”accuracy”).

The conclusion, based on the above results over

24 drivers driving during three hours, is that the

entropy starts being more stable (classification is not

significantly better) at around the two hours driving

point while the neighbourhood (blending) changes

from 15 to 55 %. It could be explained because the

five minutes windows defined by the selected 15

parameters are more equally distributed and the

variability is decreasing when the first phase of

fatigue appears. This would be because the heart

variability starts losing elasticity (decreasing of

general alertness due to fatigue).

In any case, as is shown in the above figure,

some changes are detected through the entropy

analysis based on several time and frequency

domain parameters derived from the heart rate

variability (HRV) near to the first 120 minutes

driving.

4 DISCUSSION

The analysis of the entropy behaviour based on data

derived from the heart activity is a promising way to

detect first signals of different human factors (e.g.

fatigue, alertness etc.) which would be related to

some physiological mechanisms.

This entropy should be analyzed further to know

how different factors can influence it, i.e. how does

the age of the drivers affect the defined entropy

concept? Is it affected in the same way for women

and men? What about the behaviour during different

weather conditions? And the road type, related to the

different alertness levels needed to drive the car, is it

really better detected by the entropy within the HRV

behaviour? How much is the circadian cycle

influencing the heart activity and then the HRV?

Could the distance function of the “instances based”

classifier be improved in order to optimize and

detect the first signals of fatigue?

Since the entropy analysis of heart physiology

and HRV has been so promising, more questions

have appeared motivating us to go further in the

research carried out up to now, mainly oriented to

know better the physiology of the heart, and

correlative effects on some human behaviour.

Besides, although the results obtained has been

focussed on the safety in road transport scenarios,

this specific HRV analysis is the appropriate starting

point to be applied for the measurement of the

working conditions, i.e. different situations where

the risk of fatigue exists (long-time periods working

in a hospital or in a factory with a machine,…).

ACKNOWLEDGEMENTS

The authors wish to express their gratitude to the

group of researchers of the Transport unit in

TECNALIA Research & Innovation. Deepest

gratitude is also due to the support of Prof. Dr.

Dionisio Del Pozo Rojo and Prof. Dr. Jesús María

López González whose were extremely helpful and

offered invaluable assistance and guidance.

The authors would also like to convey thanks to

the Spanish Ministry of Industry, Tourism and

Commerce for providing the financial means and

ESIDE Faculty of University of Deusto (Bilbao) for

laboratory facilities.

REFERENCES

Aha, D. W., Kibler, D. & Albert, M. K. (1991) "Instance-

based Learning Algorithms." Machine Learning 6, pp.

37-66.

Aha, D. W. (1992) “Tolerating Noisy, Irrelevant and

Novel Attributes in Instance-based Learning

Algorithms.” International Journal of Man Machine

Studies 36, pp. 267-287.

Backs, R. W.; Seljos, K. A. (1994). Metabolic and cardio

respiratory measures of mental effort: the effects of

level of difficulty in a working memory task.

International journal of Psychophysiology, 16, 57-68.

Cleary John G., Trigg Leonard E (1995). “K*: An

Instance-based Learner Using an Entropic Distance

Measure”. 12th International Conference on Machine

Learning.

Cover, T. T. & Hart, P. E. (1967) "Nearest Neighbour

Pattern Classification." IEEE Transactions on

Information Theory 13, pp. 21-27.

Furedy, J.; Szabo A.; Péronnet, F. (1996). Effects of

0 1020 30405060

Seri e 10

Seri e 11

Seri e 12

Seri e 13

HeartRateVariability-KnowingMoreaboutHRVAnalysisandFatigueinTransportStudies

113

psychological and physiological challenges on heart

rate, T-wave amplitude, and pulse-transit time.

International Journal of Psychophysiology, vol 22,

173-183.

Gates, G. W. (1972) "The Reduced Nearest Neighbour

Rule." IEEE Transactions on Information Theory 18,

pp. 431-433.

González González, J.; Mendez Llorens, A.; Mendez

Novoa, A.; Cordero Valeriano, J. J. (1992) Effect of

acute alcohol ingestion short term heart rate

fluctuations. Journal of studies on Alcohol, 53, 86-90.

Hart, P. E. (1968) "The Condensed Nearest Neighbour

Rule." IEEE Transactions on Information Theory 14,

pp. 515-516.

Jorna, P. G. A. M. (1992). Spectral analysis of heart rate

and psychological state: a review of its validity as a

workload index. Biological Psychology, 34, 237-257.

Kitlas A., Oczeretko E., Kowalewski M., Urban M. (2005)

"Nonlinear dynamics methods in the analysis of the

heart rate variability". Roczniki Akademii Medycznej

w Bialymstoku-Vol.50, 2005 – Suppl. 2. Annales

Academiae Medicae Bialostocensis.

Kramer, A. F. (1991). Physiological metrics of mental

workload: a review of recent progress. In D. L. Damos

(Ed.), Multiple-task performance. (pp 279-328).

Lee, D. H.; Park, K. S. (1990). Multivariate analysis of

mental and physical load components in synus

arrhythmia scores. Ergonomics, 33, 35-47.

Mascord D. J.; Heath (1992). Behavioural and

physiological indices of fatigue in a visual tracking

task. Journal of safety research, 23, 19-25.

Mulder, L. J. M. (1988). Assessment of cardiovascular

reactivity by means of spectral analysis. PhD Thesis.

Groningen: University of Groningen.

Mulder, L. J. M. (1992). Measurement and analysis

methods of heart rate and respiration for use in applied

environments. Biological Psychology, 34, 205-236.

Paas, F. G. W. C.; Van Merrienboer, J. G. J; & Adam, J. J.

(1994). Measurement of cognitive load in instructional

research. Perceptual and motor skills, 79, 419-430.

Porges, S. W.; Byrnes, E. A. (1992). Research methods for

measurement of heart rate and respiration. Biological

Psychology, 34, 93-130.

Porter, B. W., Bareiss, R. & Holte, R. C. (1990) "Concept

Learning and Heuristic Classification in Weak-theory

Domains." Artificial Intelligence 45, pp. 229-263.

Quinlan, J. R. (1986) "Induction of Decision Trees."

Machine Learning 1, pp. 81-106.

Quinlan, J. R. (1990) "Learning Logical Definitions from

Relations." Machine Learning 5, pp 239-266.

RACE (Real Automóvil Club de España). (2011). Informe

2011: La fatiga en la conducción.

CARDIOTECHNIX2013-InternationalCongressonCardiovascularTechnologies

114