
Abstracting Imperative Workflow to Declarative Business Rules
Preparation of Camera-Ready Contributions to INSTICC Proceedings
Lex Wedemeijer
Department of Computer Science, Open University, Valkenburgerweg 177, Heerlen, The Netherlands
Lex.Wedemeijer@ou.nl
Keywords: Business Rules, Requirements Engineering, Workflow Model, Controlflow Pattern, Relation Algebra.
Abstract: Large business administrations rely on workflow systems to coordinate their business processes. In practice,
workflow models are the blob-and-arc diagrams that outline required activities for dealing with an incoming
event. In general however, user understanding is served better by the business rules approach. The Business
Rules Manifesto advocates to express in declarative business rules what should be complied with, but to
abstract from how to accomplish that by way of procedures. In this paper, we transform the main procedural
components of imperative workflows to declarative business rules. The transformation results in two rules
that still reflect the procedural nature of workflow, but more abstract than the corresponding workflow
model. Once a workflow is transformed to declarative rules, these rules can be merged with other, content-
aware business rules or pruned for unnecessary restrictions. The declarative rules and relations may capture
business requirements about work processing better than blob-and-arc diagrams of imperative workflows.
1 INTRODUCTION
Have you ever done a Sudoku puzzle? Its rules are
surprisingly simple, yet the challenge of Sudoku is
that there is no simple workflow how to solve the
puzzle. The same applies to workflow models in
business: the rules governing the day-to-day work
are rather simple, yet the implemented workflows
and procedures that prescribe how business workers
and applications should execute the work, are much
more complicated.
Our point is that work should be done to comply
to the rules set by the business, but an operational
workflow may impose additional restrictions for
implementational reasons having little business rele-
vance. In keeping with the Business Rules Manifesto
(2003), we believe that business rules should be
expressed as explicit constraints on behavior,
independent of how the rules may currently be
implemented in process descriptions or workflow
diagrams. In practice, users regard workflow models
often just as blob-and-arc diagrams that depict how
an incoming event should be dealt with. Such
diagrams tell the users what to do and when, but not
why. Transforming the imperative workflow model
into the format of declarative business rules opens
the road to identify the rules based on legitimate
business requirements, and to eliminate the ones that
were added for implementational reasons.
Using the Relation Algebra approach for rules
coined by (Joosten, 2007), restrictions of the
workflow are captured in a single declarative rule
(section 5) which builds upon binary relations
corresponding to the various structural components
of common workflow models. Next, we express the
business goal of the workflow by a second rule
(section 6). Thus, the imperative constraints and the
goal reached by the workflow are exposed at the
same level of abstraction, and in a format compatible
to other business rules. The workflow rules,
previously encapsulated in descriptions or diagrams,
become amenable for practicable validation by the
user community, and for conflict analysis and
optimization by rule designers.
The paper outline is as follows. Section 2 sets the
stage for basic workflow models. Section 3 outlines
declarative business rules and notions used in the
paper. Sections 4 and 5 explain how the basic
constructs of workflow models are transformed to
assertions of Relation Algebra. Section 6 outlines
how the workflow process is driven by way of the
Control Principle. Section 7 discusses elaborations.
Section 8 concludes the paper and indicates some
directions for further research.
74
Wedemeijer L.
Abstracting Imperative Workflow to Declarative Business Rules.
DOI: 10.5220/0004774200740085
In Proceedings of the Third International Symposium on Business Modeling and Software Design (BMSD 2013), pages 74-85
ISBN: 978-989-8565-56-3
Copyright
c
2013 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 BASIC WORKFLOW MODELS
We outline features of conventional workflows, and
explain the core notion of imperative workflow.
2.1 Basic Workflow Models
The Workflow Management Coalition (1999)
defines a workflow process as a formalised view of a
business process. It is presented as a coordinated set
of process activities aimed to achieve a common
business goal. Figure 1 depicts a typical workflow
model as a blob-and-arc diagram. The example,
adapted from the WMC'99 technical report, contains
the four components of typical workflows: sequence,
parallel flow, selective flow, and iterative loop
(Aalst, Hofstede, et al., 2003). Sections 4 and 5
discuss how to transform each to relations and
declarative rules.
Figure 1: A typical workflow model.
A workflow model may be read in several ways.
The more usual interpretation is of the flow as a
kind of roadmap. Once an activity is completed, the
roadmap is consulted to answer the 'now what,
where to go next' type of question. The answer is
what may be called a 'statement of advice' (Witt,
2012). Upon completion of activities, it indicates
which activities in the processing chain may be
executed next. Typical wordings of this kind are 'you
may now start activity A', or 'activity B is now
enabled'. This interpretation of workflow is forward-
looking in time: what may come next, and we will
refer to it as the indicative view of workflow.
We prefer a more rigorous interpretation: the
flow specifies compulsory precedence. Prior to com-
pleting an activity, all of the preceding activities
should also have completed, out of necessity. The
question here is 'what must have come before', and
the answer takes the form of a business rule. The
rule has 'immediate' enforcement, i.e. the preceding
activities must have completed, and this may never
be violated. This interpretation looks backward in
time: what must have come before. We will refer to
this as the imperative view of workflow.
In this paper, we are only interested whether an
activity has completed or not. The timestamp of its
completion or duration of the activity are not recor-
ded. We abstract from details such as activity life
cycle (Russell, Aalst et al., 2006) comprising steps
like enabling, allocation to resource, work initiation,
data transacting or recording the data outputs. We
also abstract from issues such as resource respon-
sible for enactment, execution cost, etc.
2.2 Case Management
A workflow models how an incoming case is
processed. Therefore, it always features some trigger
(sometimes even more than one) where a new case
may enter the business process. Successive activities
are then executed for the case (in parallel and/or in
series) until all work is done and, by assumption, the
intended business goal is achieved. Spontaneous
generation of new cases somewhere along the line is
prohibited in the imperative view of workflow. Inte-
restingly, the indicative view of workflow allows
new cases to suddenly emerge, but it is a tacit
assumption that cases should start only at a trigger.
The notion of 'case' or 'workflow instance'
constitutes an essential difference between workflow
models and business rules in general. A declarative
business rules model specifies rules that should be
complied with, but it does not require the notion of
any particular 'case' being managed. If any rule is
violated, there is work to do, regardless how or what
caused the violation.
Hence, in order to transform the imperative
workflow model into declarative rules, we need to
include the concept of 'case' or 'working instance'
into our models. Surprisingly, we find that just this
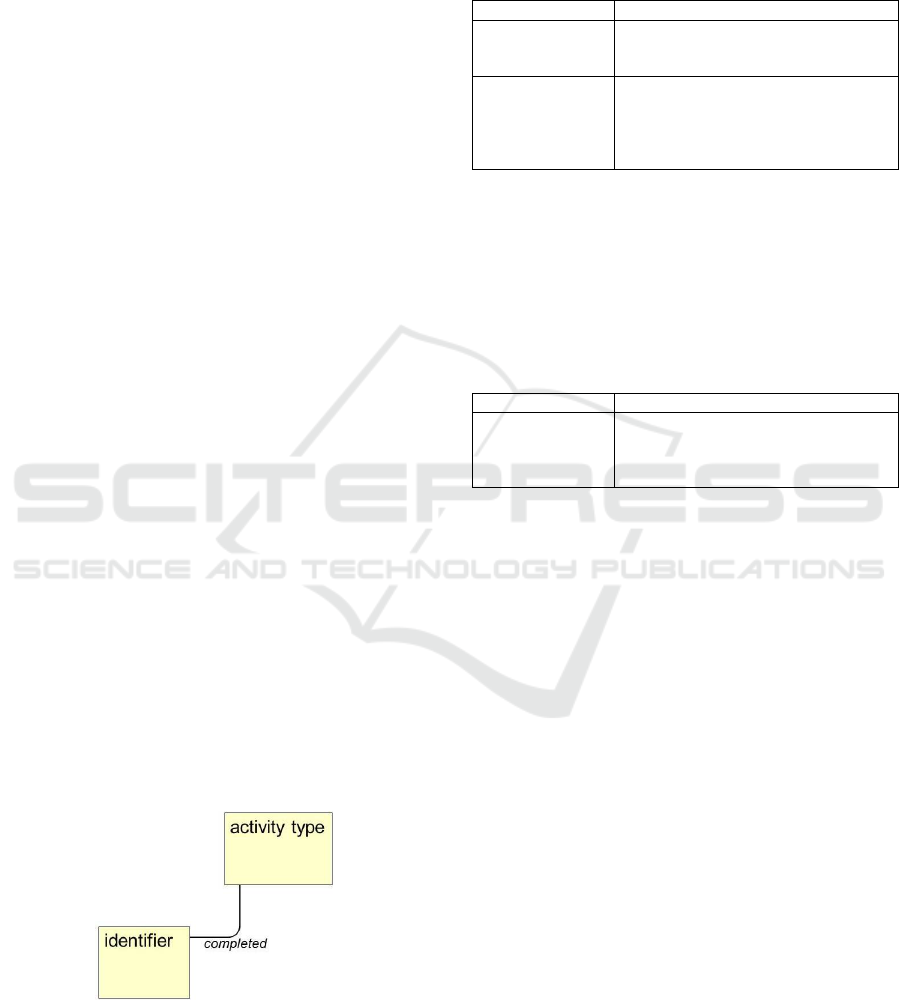
concept, together with the concept of 'activity type',
provide a basic structure (figure 2) that is sufficient
to transform an imperative workflow model into its
equivalent declarative rule model.
3 DECLARATIVE RULES
This section outlines features of declarative business
rules, and the structural components of the approach
for business rules that we will be using in the paper.
3.1 Relation Algebra
We use binary Relation Algebra (Maddux, 2005) to
specify and formulate our declarative rules. For
readers familiar with relational database modeling, a
few major differences may be mentioned. The
notion of concept as we use it, is comparable to enti-
ties, but our concept is just a single column which is
key, and has no attributes. Binary relations as we use
them, are not foreign-key pointers, but are defined as
Abstracting Imperative Workflow to Declarative Business Rules
75
subsets of the Cartesian Product. They have many-
to-many cardinality, unless specified otherwise.
Time is not a native notion of binary Relation
Algebras. Indeed, none of the formulas and rules
that we discuss in this paper will refer to timestamps
or intervals. For this reason, some authors call rules
formulated in binary Relation Algebra 'invariant'.
3.2 Related Approaches
Our terms declarative and imperative are interpreted
differently in (Mendling et al., 2009). Their
understanding of 'declarative' is simply that the
given behavior satisfies all requirements. The basic
workflow models that we consider will satisfy all
requirements, perhaps not instantly but eventually,
still we do not consider them to be declarative.
Linear Temporal Logic (LTL) is an excellent
approach to study workflows in great detail (Maggi
et al., 2011). LTL extends first-order logic with a
linear, discrete model of time. A workflow suite,
called Declare, uses LTL to model and execute
business processes. A main difference with our
approach is again the notion of time, which is a
prominent feature in LTL, but absent from ours. For
example, precedence is sometimes interpreted to
mean that an activity should not be started prior to
the completion of the preceding one. This would
imply that activities have a certain duration, but as
noted before, time is irrelevant to our approach and
we do not follow this interpretation.
Protocol modelling (McNeile and Simons, 2006)
also does away with temporal aspects and the notion
of cases. Aspect oriented models enable state transi-
tions while taking multiple crosscutting concerns
and business constraints into account. This approach
takes the indicative view of workflow when it labels
state transitions as 'desired' (Wedemeijer, 2012).
3.3 Structure of the declarative model
Figure 2: Basic structure of the declarative model.
To transform imperative flows to declarative rules of
Relation Algebra, we must first specify a suitable
structure to capture the terms, facts and rules of
imperative workflows. The basic structure of our
declarative model (figure 2) is attractively simple,
containing just two concepts as defined below. We
will expand this basic structure with other features
as needed:
concept semantics
[identifier]
is: (a pool of) available case identifiers,
each associated to a particular workflow
case, e.g. a case 'customer request 123'
[activity type]
is: (the set of) activity types. Each
activity type may be executed
(instantiated) any number of times, in
order to achieve the goal of the business
process
The declarative model for workflows specifies a
number of binary relations on these concepts. The
most important one, called completed, records
workflow progress. A tuple (i,A) in this relation
completed, sometimes called a transition, records
that this particular case identifier, i, has successfully
been processed by the particular activity type, A. For
ease of reading, we write relation names in italics:
relation semantics
[identifier]
completed
[activity type]
is: (the recording that) all work of the
activity type has been successfully
completed for (the case associated with)
identifier i.
The completed relation represents the audit trail
of the work done on a particular case. In accordance
with compliance regulations and good records-
keeping (McKemmish et al., 2006), tuples may be
added into this relation, but they may never be
altered or deleted thereafter: an activity cannot be
un-completed. And to safeguard referential integrity,
we cannot delete an identifier or activity type once it
is recorded in the completed relation.
Notice that we abstract from a lot of attributes
commonly included in audit trails, such at deadlines
being set, the exact times of start and completion,
business resource that executed the work, or the
actor taking responsibility for the work done.
We assume the completed relation to be total, i.e.
a case identifier is recorded only if it completed at
least one activity. This is because we are interested
only in identifiers associated with actual work done,
not in possible future work. The reverse is not
required: an activity type may exist even if no case
has ever completed that activity.
Instead of completed, an started relation might
have been modeled. Again, we are interested only in
actual work done, not in ongoing execution of activi-
ties. A similar argument is used in Petrinet theories,
the formal foundation of most workflow models.
Third International Symposium on Business Modeling and Software Design
76

4 TRANSFORMING FORWARD
FLOW
Many business processes can be represented in sim-
ple workflow models where activities are executed
in sequence, or perhaps in parallel. This section
outlines how common components are transformed:
sequence, synchronize (AND-join), and selective
OR-splits (disable, exclusive split), as in figure 3.
Figure 3: Common components in workflow.
4.1 Sequence / Precedence
4.1.1 Sequencing in Workflows
This is the most common pattern in workflows. Most
workflow diagrams depict sequencing by an arc
from one blob, representing some activity type A
0, to
some next blob labelled type A
1.
The indicative interpretation of such sequencing
is: after A
0 is completed, then A1 should be executed
next. Not having completed activity A
1 after A0
means that the rule for sequencing is temporarily vi-
olated. There is work to do while the violation lasts.
In the imperative interpretation of workflow, the
arc from A
0 to A1 represents strict precedence: if the
second activity A1 is completed for some case
instance, then A
0 must have already been completed
for that case instance. Or: if completion of A0 is not
on record, then the rule says that completion of A1 is
impossible. Not having completed A
0 prior to A1
means that the imperative workflow rule is violated,
and this violation is never permitted.
4.1.2 Rule for Precedence
To capture precedence as a declarative rule, the
precedes relation on activity types is used (see
table).
relation semantics
[activity type]
precedes
[activity type]
is: the precedence relation among
activity types. A tuple (A0,A1) in this
relation means that only if an activity of
type A0 has completed, may a
corresponding activity of type A1 also
be completed.
The precedence rule can be formulated in first-order
logic by way of the precedes relation:
for any i∈[identifier], and A1∈[activity type], we
have: if i completed A
1 then there must exist
some activity type A
0 such that i completed A0
and A0 precedes A1.
which in Relation Algebra reads:
completed ⊂ completed ○ precedes
(1)
4.1.3 Precedence for Triggers
A problem with the sequencing rule is that not every
activity type is preceded by another. Such activity
types are customarily called triggers, or initial
activities, and they are important because they set
the workflow in motion.
At first glance, triggers invalidate assertion (1),
as completion of an identifier cannot be recorded for
an initial activity type because a proper tuple in the
precedes relation is absent. We solve this by adjus-
ting the definition of relation precedes: initial
activity types are recorded by way of self-referring
tuples (A
0,A0). By recording such tuples in precedes,
assertion (1) also covers initial activities.
4.1.4 About the Precedes Relation
Basic properties of the binary precedes relation
correspond nicely to important features of
imperative workflows. As we are merely concerned
with transforming the workflow to declarative rules,
we refrain from a deeper analysis of this and other
relations to be defined. We take quality issues for
granted, such as the workflow being well-designed
with respect to liveness, deadlock etc.
The precedes relation is not univalent, and an
activity type may well precede several others,
corresponding to a so-called split in the workflow. It
establishes what may be called a multiple-instance
pattern (Aalst et al., 2003). The subsequent activities
may be executed and completed in parallel along
separate branches of the flow.
It is not total. An activity type may be a last one,
a terminating activity in the workflow. Nor is prece-
des an injective relation, as more than one activity
type may precede an activity type A
X. Assertion (1)
will ensure that at least one precedent is completed
prior to the completion of A
X. This is the common
OR-join of workflow models.
We explained above that self-referring tuples are
recorded to capture triggering (initial) activities. As
a result, the binary precedes relation is surjective.
Abstracting Imperative Workflow to Declarative Business Rules
77
4.2 Synchronizing AND-Joins
4.2.1 Synchronization in Workflows
Sometimes an activity may only be completed after
completion of more than one activity. Known as
AND-join or more formally as synchronization point
in workflow models, it is not captured by rule (1).
4.2.2 Rule for Multiple Precedence
To capture AND-joins in a declarative rule, we in-
troduce a relation multi_precedes for activity types.
relation semantics
[activity type]
multi-precedes
[activity type]
is: activity type precedes the next
activity type and executions must be
synchronized. A tuple (AM,AN) means
that only if the activity of type AM and
certain others too have completed, may a
corresponding activity of type AN also
be completed.
The synchronization rule is that no compulsory
precedent has not completed. In first-order logic:
for any i∈[identifier] and AY∈[activity type], we
have: if i completed A
Y, then it holds that never
an activity type AX multi_precedes AY and the
identifier i has not completed activity type AX.
In Relation Algebra, such a double negation is
known as left demonic composition operator (Back-
house, van der Woude, 1993). We can denote it as:
completed⊂ ¬(¬completed○multi_precedes)
(2)
4.2.3 About the Multi-precedes Relation
This relation looks a lot like the regular precedes
relation. In fact, the only difference is at the join-
points in a workflow. Whereas the precedes relation
captures OR-join behavior, multi-precedes models
AND-join behavior. As workflows can display both
types of behavior, both relations are needed.
The multi-precedes relation constitutes a partitio-
ning of activity types. Most partitions are uninteres-
ting, consisting of just a single activity type. Just a
few partitions, that correspond to the AND-joins,
contain more than one activity type, meaning that
those must synchronize: the workflow may only
continue once all of them have completed.
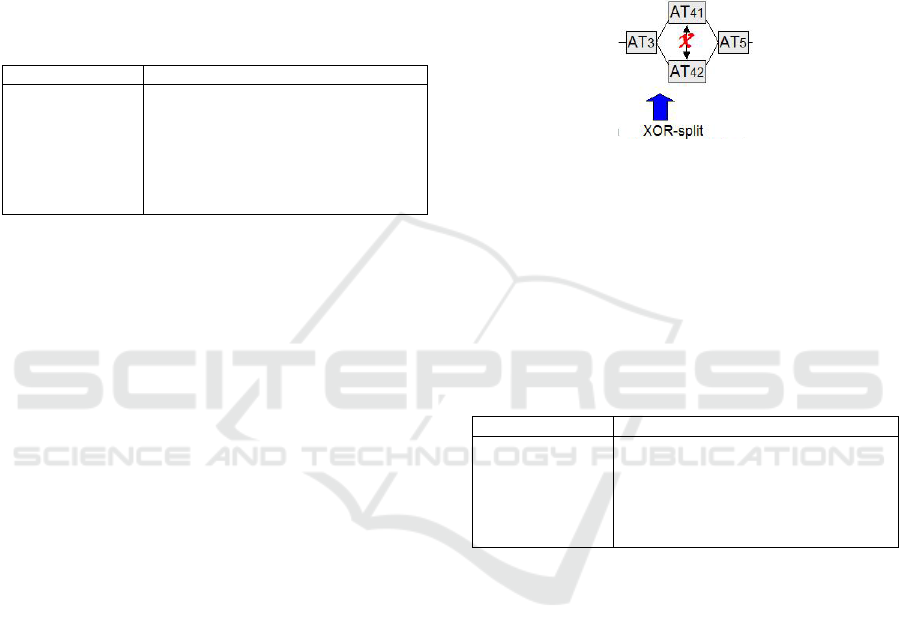
4.3 Selective OR-Splits and Disabling
4.3.1 Selections in Workflow
Selective flow, also known as conditional branching,
means that one activity precedes two (or more)
activities that are placed in parallel but not all of
these succeeding activities are allowed to complete.
Select in a workflow diagram is depicted by a so-
called XOR-split: two (or more) arcs go out from a
single point. Also, a business condition that
determines which arc should be enacted (or not) is
often indicated, but as we are concerned only with
transforming the imperative flow into declarative
rules, we abstract from such business knowledge.
Figure 4: Mutual exclusion of activity types.
4.3.2 Rule for Selective / Disabling Activities
Consider the XOR-split after activity type A3 which
is the precedent for both A41 and A42, but only one of
them is allowed to complete (figure 4). The first
consideration is normal sequencing, as has been
dealt with before. We cover the new restriction of
mutual exclusion by way of a new relation disables
on activity types:
relation semantics
[activity type]
disables
[activity type]
is: the disabling relation among activity
types. A tuple (AX,AY) in this relation
means that never if an activity of type
AX has completed, may an activity of
type AY be completed by the same
identifier.
The rule for selective flow can now be
formulated in first-order logic:
for any i∈[identifier] and AX,AY∈[activity type]
we have: if i completed A
Y then it is never true
that i completed AX and AX disables AY.
Denoted as a Relation Algebra assertion it reads:
completed ⊂ ¬ ( completed ○ disables )
(3)
4.3.3 About the Disables Relation
Most activities are not involved in disablings, and
therefore the disables relation is neither total nor
surjective. One activity type may disable, or be dis-
abled by several others, hence the relation is neither
univalent nor injective. Evidently, the homogeneous
disables relation is irreflexive, while nothing can be
said about its being transitive or not.
The important point however is that, in our
Third International Symposium on Business Modeling and Software Design
78
context, the disables relation is symmetric by nature.
A tuple (A
X,AY) in the disables relation means that
never if an activity of type A
X has completed, may a
corresponding activity of type AY also be completed.
The reverse is then automatic: if an activity of type
A
Y is recorded as completed, then no corresponding
activity of type AX may be completed.
Imperative workflows also know a disabling
feature, which however is not symmetric by nature.
A workflow may model that activity type A
3 is
disabling for activity type A2, meaning that
completion of A
2 is allowed prior to, but not after
A3. This allows a sequence of activities a1-a2-a3, but
not a sequence like a1-a3-a2. The exact sequencing
is determined by the actual timestamps of completi-
on, an attribute that we have explicitly omitted from
our declarative rules.
4.4 Forward-flow Rule
The three basic patterns of workflow analyzed so far
all ensure a forward flow, in contrast to the flow that
we will be analyzing in the next section. The three
Relation Algebra assertions (1), (2) and (3) acquired
so far, easily combine into a single assertion:
rule forward_flow as
completed must imply
( ( completed ○ precedes )
∪ ¬( ¬completed ○ multi_precedes ))
\ ( completed ○ disables )
For later reference, we will refer to the righthand
side of this assertion as the forward-flow relation:
relation semantics
[identifier]
forward-flow
[activity type]
is: the relation with a tuple (i,A)
indicating that at least one (regular)
precedent or all of its multi-precedents
are completed, and none of its disabling
activities has completed.
Using this relation, a forward flow rule may be
stated: 'if identifier i completed activity type A, then
tuple (i,A) must be in relation forward-flow'.
The rule has immediate enforcement: completion
is always prohibited if the tuple is absent from the
forward-flow relation. But, as the naming suggests,
the rule holds for forward flows only, and does not
apply for loops or 'backward' flows.
5 TRANSFORMING ITERATIVE
FLOW
The previous section transformed forward flows. this
section, we deal with the transformation of iterative
loops, which slightly more complicated.
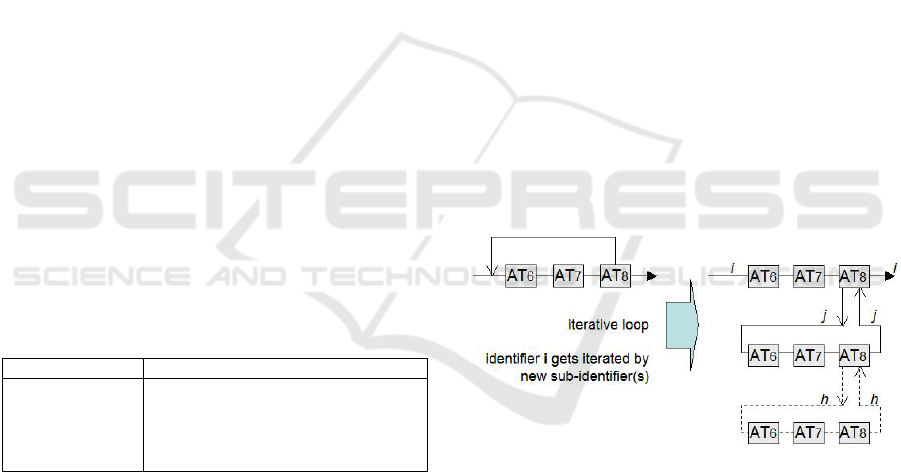
5.1 Iterative Looping in Workflows
Handling a workflow case may sometimes involve
the repeated execution of a series of activity types
until some condition is met. But the forward-flow
rule described above cannot deal with a flow that
loops back onto itself, so we must adjust the rule. A
peculiarity is that binary relations may record a tuple
once, but not several times over. Hence, completed,
as a binary relation, cannot record iterations as
required. Our solution is to employ a new identifier
for each iteration of the loop. By expanding the
definition of the identifier concept in this way, our
forward-flow condition remains valid.
5.1.1 Relations for Modeling Iterations
We capture iterations by imagining the execution of
the workflow-case to pause at the looping activity
where it may fire zero, one or more iterations, as
depicted in figure 5. Execution of the looping acti-
vity by the the workflow-case can be thought of as
being suspended, and only when all iteration(s) have
been dealt with, can it complete the looping activity,
and proceed in the normal way.
Figure 5: Iterating by way of sub-identifiers.
But this image cannot be taken literally, as our
approach has abstracted from duration of an activity
and we record only its completion. Instead, we just
prohibit the activity to complete if iterations are run-
ning. This is somewhat different from the standard
understanding of iterations, where a loop starts after
completion of the looping activity, and not during its
execution. As far as we could assess, this detail has
no consequences for validity of the transformation.
Several new relations are needed to help us
capture iteration loops as declarative rules.
First, relation loops_to records the iteration loop
as drawn in the workflow diagram. To keep things
Abstracting Imperative Workflow to Declarative Business Rules
79
simple, we will assume that this relation on activity
types is univalent and injective. Moreover, the target
activity type (where it loops to) is assumed to be a
precedent for the source activity type. This is to
ensure that a case looping back, will eventually
return to the activity type that fired it.
relation semantics
[activity type]
loops_to
[activity type]
is: the iterative-loop relation of activity
types. A tuple (AN,AK) in this relation
means that an activity of type AN,
before its completion, may invoke no,
one or more iterations of the loop
starting from AK.
As pointed out before, a binary relation such as
completed cannot record that the same activity type
is repeatedly completed by a single identifier. We
solve this by assigning a new identifier for every
loop iteration, in the same way as used in audit
trailing tools, activity logging and process mining
(van Dongen, van der Aalst, 2005). To track which
iterative loops are running for what workflow cases,
we coin two more relations, fired_from and iterates:
relation semantics
[identifier]
fired_from
[activity type]
is: which subordinate case identifier has
started from the activity type. A tuple
(j,AM) in this relation means that
identifier j is fired from the activity type
AM.
[identifier]
iterates
[identifier]
is: the iteration of identifiers. A tuple (j,i)
in this relation means that the identifier j
is fired for the identifier i, which is
deemed necessary as an activity executes
for the workflow case associated with
identifier i. The identifier that iterates
another is referred to as subordinate or
sub; the other identifier is called the main
case.
The iterates relation actually is a function.
Remark that a sub may again fire its own sub-
subordinates, and a stack of arbitrary depth can be
created. Moreover, the iterates relation allows to fire
several subordinates at once, for instance if a
complex scheduling problem is broken down into
several smaller scheduling alternatives, to be
analyzed in parallel. Still, an identifier cannot iterate
itself, so the iterates relation and its transitive
closure must be irreflexive.
The fired_from relation, which is also a function,
prevents possible confusion about which identifier
originates where, in case a workflow contains more
than one loop. For the sake of consistency, activity
types recorded in the fired_from relation must also
be present in the loops_to relation, but here again,
we take this quality issue for granted.
Firing-from an activity type can occur when the
case at hand has not completed the activity yet, and
some business worker or condition determines that
iteration is required. In this paper, we abstract from
the specific conditions or business knowledge that
controls invocation of the iterative loop.
5.1.2 Rules for Iteration
To model iterations in imperative workflow, three
restrictions regarding (the identifier of) the iteration
must be considered:
− allow the completion of its first activity,
− ensure completion of subsequent forward-flow
activities, and
− constrain the sub-identifier to stop at precisely
the activity type where it was fired-from, and no
further activities are to be completed.
Regarding the main case, we must ensure that:
− the main case identifier must wait for all of its
iterations to complete, prior to continuing.
First, remark that the activity type where an iteration
begins, is rarely marked as a trigger. Hence, the
forward-flow condition would normally prohibit that
the activity type is completed by this sub, as it lacks
its proper precedent, and spontaneous generation of
new cases is explicitly forbidden in the imperative
view. The solution of course is that another identifier
acts as a substitute for predecessor, viz. the main
case that is firing this iteration. The proper condition
for the starting activity of the subordinate case is
captured in first-order logic as:
for any j∈[sub] and AK∈[activity type] we have:
if j completed A
K, and AM loops_to AK, and j
iterates the identifier i, then the tuple (i,A
M) is in
the forward-flow relation.
Rephrased in Relation Algebra, it reads:
completed ⊂
iterates ○ forward_flow ○ loops_to
(4)
In rephrasing the first-order logic, we used that both
relations, iterates and loops_to, are functions. Also
remember that formula (4) applies only for the initial
activity to be completed by the subordinate
identifier.
Once an iteration has completed its initial
activity, it has to go forward through the entire loop,
up to the activity type where it was fired. This is
already described by the forward-flow condition,
and no additional rules are needed.
Third, we must ensure that the iteration termina
Third International Symposium on Business Modeling and Software Design
80

tes at its point of origin, where it is fired from. It
may never go beyond that point and complete some
activity further down the flow. In particular, the
firing activity type never precedes an activity type
that is being completed by a subordinate identifier.
In first-order logic:
for any j∈[sub] and AP∈[activity type], we have:
if j completed A
P, then it cannot be that j is
fired_from some activity type AM preceding AP.
Rephrased in Relation Algebra, it reads:
completed ⊂ - ( fired_from ○ precedes )
(5)
Finally, we need to consider the main case. That
main case must wait at exactly the activity type
where it fired subordinate identifier(s). Which is to
say that this main case might have completed this
activity under normal circumstances, but if some
iteration(s) are running then must wait for them to
complete. Otherwise, a running iteration becomes
orphaned, executing activities to no avail. Thus, at
the looping activity may be completed by the main
case only if all of the iterations that it fired from
there, have all run their course to completion. This
condition to wait for iterations can be formulated in
first-order logic:
for any i∈[identifier] and AM∈[activity type] we
have: if i completed A
M, then it is never true that
some sub exists that iterates this identifier i, and
that sub was actually fired_from A
M (remind that
a workflow may contain other loops), while it
has not yet completed the activity type A
M
(which is to say: that sub is still running).
Using double negation again, we can write this as a
Relation Algebra assertion:
completed ⊂
¬( iterates~ ; ( fired_from ∩ ¬completed ) )
(6)
The assertion is trivially satisfied if no iterations are
fired (Backhouse and van der Woude 1993). The
assertion is also satisfied if iterations for a case exist,
but were fired from other activity types in the
workflow than the one about to be completed by the
case. Notice how assertion (6) applies recursively,
i.e. nesting is allowed. If a subordinate identifier
fires sub-subordinates of its own, it too will wait for
its own sub-subordinates before completing.
5.2 Imperative Workflow Rule
5.2.1 Forward-Flow and Subordinates
Conditions (4) and (5) determine a scope for a sub
ordinate identifier. They govern the inception and
termination of each subordinate, i.e. the activity type
where it starts, and where it terminates. Evidently,
these two activity types coincide exactly with one
corresponding tuple in the loops_to relation. Condi-
tions (4) and (5) plus the forward-flow condition
describe behavior of the subordinate, which is
expressed in a Relation Algebra assertion as follows:
rule subordinate_workflow as
completed must imply
( forward_flow
∪ iterates ○ forward_flow ○ loops_to )
/ ( fired_from ○ precedes )
Notice how for main workflow cases this subor-
dinate_workflow rule coincides with the regular for-
ward-flow behavior, except at activity types where
looping may occur. Hence, we only need to merge
condition (6) that controls behavior at looping
activities into the rule above. The declarative
business rule for imperative workflow becomes:
rule imperative_workflow as
completed must imply
¬ ( iterates~ ; ( fired_from ∩ ¬completed ) )
∩ ( ( forward_flow
∪ iterates ○ forward_flow ○ loops_to )
/ ( fired_from ○ precedes ) )
Remarkably, this rule, although we produced it in
accordance to the imperative view of workflow,
provides us with an indicative view. The righthand
side of the rule assertion indicates for a case iden-
tifier i which activity types either have completed, or
are allowed to complete, always in full compliance
to the imperative workflow constraints. It is fairly
easy to deduce from this rule an is_enabled relation
that, for a given identifier, will determine exactly
which activity types are allowed to complete, but
have not completed yet.
6 CONTROL PRINCIPLE
The previous sections detailed how to capture the
various aspects of imperative workflow. This section
outlines how the workflow process is driven by way
of the Control Principle.
6.1 Completing the Flow
A general assumption is that a workflow case, to
fulfil the intended business goal, will always and
automatically run from start to finish. A recorded
Abstracting Imperative Workflow to Declarative Business Rules
81
trigger will always progress to its final tasks, or
terminal activities. Likewise, we assumed that any
subordinate iteration fired from some looping
activity type will always return to its point of origin.
The indicative view of workflow states what
should come after by way of enabling activities. By
assumption, every activity that is enabled, ought to
complete in due course, unless its completion is no
longer desired or disabled (McNeile, Roubtsova,
2008). By another assumption, the terminating acti-
vity of the workflow will be enabled and completed
eventually, and so the process goal is achieved.
In the imperative view of workflow, the goal of
the process is not achieved as a matter of course. If a
process halts in mid-term, nothing goes wrong. No
rule is violated, there is no signal that there is work
to do, or that a deadline has expired. The imperative
workflow rule dictates what must come before, but
not what ought to come after. Nothing controls that a
case shall be handled start to finish. To remedy this
situation, a new rule called the Control Principle is
formulated.
6.2 About the Progresses_to Relation
Whereas the imperative workflow rule has imme-
diate enforcement (it may never be violated), the
Control Principle does allow deferred enforcement:
violations are allowed but only temporarily so.
Every violation should be remedied sooner or later,
and work should proceed until there are no more
violations. The Control Principle reasons that every
workflow trigger should always progress to all of its
terminal activities:
for any i∈[identifier], and A0,AZ∈[activity type]:
if i completed A
0, with A0 trigger and AZ termi-
nating activity type for the workflow, then i must
(eventually) also have completed all such A
Z.
We coin a relation progresses_to from trigger to
terminating activity types. In fact, this relation
applies to not just one, but to all workflows that an
engineer may consider. We define it as follows:
relation semantics
[activity type]
progresses_to
[activity type]
is: the relation that describes the overall
start-to-finish structure of workflows. A
tuple (A0,AZ) in this relation means that
A0 is a triggering activity type and AZ is
a corresponding terminating activity type
in the workflow.
The Control Principle in Relation Algebra reads:
rule control_principle as
completed ○ progresses_to must imply
completed
Under this rule, work continues as long as any one
the final tasks has not yet been completed. All
outcomes must always be produced eventually; the
Control Principle does not allow to disregard or skip
some of the final tasks.
Inspecting the derived relation is_enabled, it will
be clear which activities may be completed in com-
pliance to the imperative workflow rule. Thus, work-
to-do can be allocated to available actors, human or
machine. In due course, activities are recorded as
completed, and the rules can once again be inspected
to determine violations and appropriate actions.
6.3 Workflow Execution
The Control Principle and the imperative workflow
rule act independently and in harmony to realize the
behavior as described in WMC'99 report.
Separate, each rule is valuable as a means to
understand and interpret workflow.
The imperative workflow rule dictates that work
must always be done in compliance to the workflow,
and specifies in exact detail how. Violation of this
rule is never tolerated. Applying this rule in a
business environment without the Control Principle
means that the work will certainly be performed in
the correct order, but there is no guarantee that the
process goals will be realized.
The Control Principle dictates that every work-
flow trigger should always progress to its terminal
activity or activities. Violation of this rule is
permitted, and it means that there is work to do.
Applying this rule in a business environment without
the imperative workflow rule means that business
workers know that there is work to do, but there is
no guidance as to the correct order of their activities.
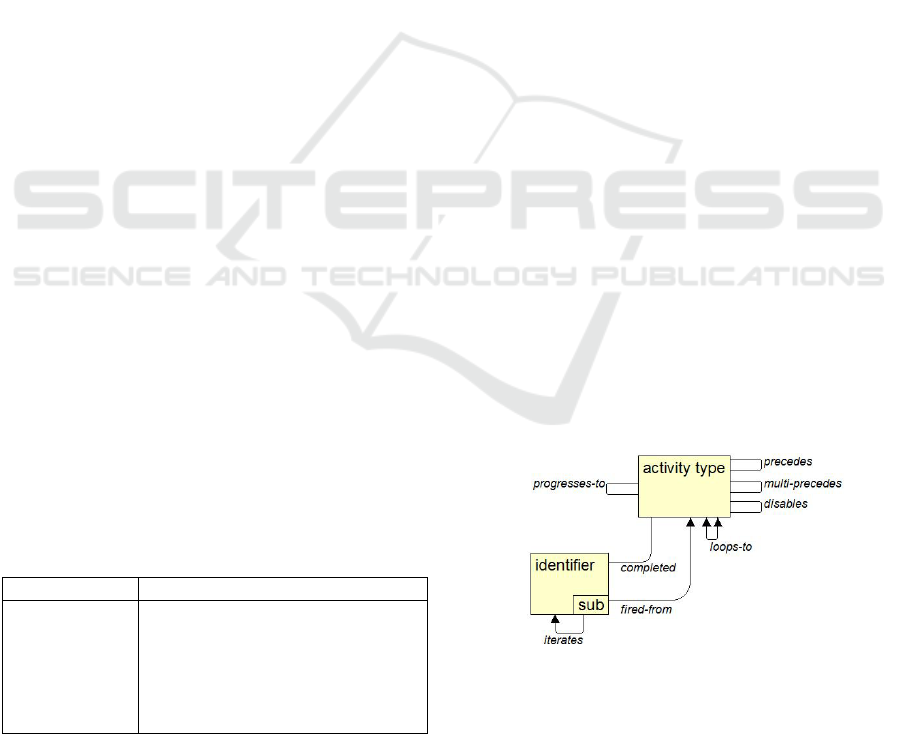
Figure 6: Elaborated structure of the declarative business
rules model.
The real benefit of our approach emerges when
the two rules are combined. Together, the rules
ensure that the process activities execute in a well-
co-ordinated fashion, exactly as pictured by the
Third International Symposium on Business Modeling and Software Design
82

workflow diagram. In the end, all violations are
resolved, all terminating activities have completed,
and the process goal is achieved.
Figure 6 is a diagram of the concepts and relati-
ons used to formulate our declarative business rules
for imperative workflow. An important observation
is that this declarative structure is not restricted to a
single workflow only. Other workflow models are
readily captured in the same declarative structure,
merely by populating the various binary relations
with the structural knowledge encapsulated in the
workflow models.
More details about the model, scripted in the
Ampersand toolset, will be available at the site
http://wiki.tarski.nl/index.php/Research_hub. There,
a realistic example will be available to show and
explore the benefits and issues of our approach. It
lists the binary relations, the exact formulas, and the
violations of the declarative business rules of a
workflow model fashioned like figure 1.
7 DISCUSSION
7.1 Advanced Flow Structures
This paper covered only the principal structures as
seen in workflows. We are convinced that other,
more advanced structures can also be transformed.
How, requires further analysis.
For instance, an 'empty' activity type may show
up in a workflow diagram. As we abstracted from
the actual work executed by an activity, the empty
activity type is treated like any other: it has
precedents, it may be the precedent of other activity
types, it turns up in the completed relation etc.
In practice other exceptions exist that operational
workflows must deal with, such as lack of resources,
user-initiated aborts, and crosscutting events (e.g. a
client dies, or an order is cancelled). Likewise,
quality problems may arise in workflows, such as
deadlock, irregular termination, or loops that never
terminate. Merely transforming to a declarative rules
model cannot be expected to solve the quality
problems. This area of research is beyond the scope
of this paper.
7.2 Limitations of Our Approach
The sequencing of activities in a workflow is the
outcome not only of business requirements, but also
of design decisions and implementation choices. An-
other designer may propose a different sequence that
also complies with the essential business rules.
Hence, precedence analysis is required to bring out
what aspects of the flow is due to design choices,
and which are based on actual business needs. To
some extend, is a matter of opinion whether a
workflow constitutes legitimate business rules, or
whether it is just a way to implement underlying,
more fundamental business rules (Hofstede, Aalst, et
al., 2003). It can also be debated with users which
flow features must have immediate enforcement, and
which ones may be relaxed to allow temporary
violations.
Moreover, flow rules such as precedence,
disabling and the like, are just one of the many kinds
of business rules. Business rules in general support
not only the consecutive steps of process flows but
also the rules to assess the business conditions and
facts as activities are being executed. For instance, a
workflow diagram often specifies the business rules
that determine whether iteration is required, or
which branch in an XOR-split to follow, but our
relations cannot records such business conditions.
In our approach, iterative loops are dealt with in
a slightly different way. The usual interpretation is
that an iteration branches off immediately after
completing a looping activity. Our interpretation is
that iterations are recorded by way of subordinate
identifiers, prior to completion of the looping
activity by the main case identifier.
Furthermore, our approach was found to be
limited in dealing with a disable, when there is time-
dependence involved. An example is a workflow
model with a constraint that 'an activity of type C3
may complete, but not before an activity of type C2'.
Such a non-coexistence rule would allow to record
the sequence of activities c1-c2-c3-c4, but disallow
the sequence c1-c3-c2-c4. Like all of the declarative
rules, our disabling rule is time-independent, and
therefore must be symmetric. It cannot distinguish
between the allowed sequence, c1-c2-c3-c4, and the
forbidden sequence, c1-c3-c2-c4. Hence, transfor-
ming this into declarative format is not possible. A
work-around may be to adjust the original workflow
model to capture the precedences in another way.
7.3 Lack of Temporal Features
Our approach is founded on Relation Algebra, which
does not provide temporal capabilities. Therefore, a
main limitation of our approach is the lack of time in
all of our formulas. This is not a drawback, instead
we regard it as a major advantage. Indeed, we
demonstrated how main components of workflow
can well be captured without referring to time.
Abstracting Imperative Workflow to Declarative Business Rules
83

Still, deadlines or deadline expiry are not
handled in our approach. Having abstracted from
time altogether, we do not record whether an activity
has begun, nor the time when its execution started.
Additional binary relation such as Identifier started
Activity_Type might be added, but it will require
extra constraints, such as: completed must imply
started. Furthermore, Relation Algebra provides no
clock mechanism that allows to inspect which activi-
ties have started but did not complete within the
allotted time. In all, we think that this paper is not
the place to investigate these aspects and how to deal
with them within the context of Relation Algebra.
Finally, it must be pointed out that time is also not a
native feature of Petrinets, the formal foundation of
most workflow models.
7.4 Transforming Rules to Workflow
We conducted one-way analysis: from implemented
workflow structure to more abstract business rules.
The workflow was transformed without information
loss, and reverse transformation will not prove to be
hard. However, this is not true in general. Once the
users edit, improve and rephrase the abstracted busi-
ness rules, there is no guarantee that reverse trans-
formation is easy, or that it produces a compatible
flow structure. Engineering a given set of abstract
business rules into a corresponding workflow model
involves implementation choices, and design skills.
8 CONCLUSIONS
AND OUTLOOK
The research in this paper covers the main structural
components of imperative workflows. We outlined
how to transform a workflow into just two rules.
The first one, called imperative-workflow rule,
captures the structure of the imperative workflow,
and it allows no violations at any time (immediate
enforcement). This comprehensive rule comprises
two parts. The easy part is called the forward-flow
rule, and it adequately captures normal and parallel
sequence, multiple precedence, and exclusions
(selection). The more complicated part captures the
iterative loops.
The second rule is called the Control Principle,
which drives the workflow through to its end. This
rule does allow violations, but while violations exist,
there is work to do resolving them (deferred
enforcement). Case handling is finished when there
are no more violations, and the goal of the business
process is reached.
The 8 binary relations and 2 rules that we
describe can be characterized as follows:
− they capture all the knowledge about the
workflow (sequencing, precedence, etc.),
− they are declarative, not procedural in character,
and involve only (persistent) states, not the
volatile events or transitions,
− the notion of time is not needed, the rules and
relations are time-invariant, and do not refer to
'before' or 'after'
− the imperative-workflow rule and the Control
Principle apply independently and simultane-
ously, there is no priority among the two.
We conclude that imperative workflows can be
transformed into declarative business rules following
the format of binary Relation Algebra. We demon-
strated in detail how to do this for each of the four
basic flow structures.
To accomplish the transformation of imperative
workflows to declarative rules, two concepts suffice.
One is the identifier concept, representing the work-
flow cases to be handled, and possibly the
subordinates when cases trace iterative loops in the
workflow. The other concept is activity type,
representing the 'blobs' of workflows. The various
types of 'arc' in workflow models are captured in a
number of binary relations, the majority being
homogeneous relations on the activity type concept.
We have shown how the procedures of workflow
may be mapped into declarative business rules. This
constitutes tangible evidence that the way of doing
business may indeed be captured in a business rules
model that meets all the demands of the Business
Rules Manifesto. On the other hand, the business
rules and relations that we describe are basically
procedural in character, while the Business Rules
Manifesto encourages to capture the business rules
in a non-procedural format.
Future work is to augment our two declarative
workflow rules with content-aware rules, such as the
criteria for iterations and OR-splits, and also the
implicit decision rules in activities encapsulated in
automated services or applied by knowledge
workers.
The Control Principle in its current formulation
requires that all final tasks must eventually be
completed. In practice, a workflow process may
finish even if not all outcomes have been produced.
For instance, when a customer order is rejected, then
the workflow produces only a rejection message,
and not the intended order delivery. The Control
Principle should be adapted and improved to cover
such practical circumstances. Furthermore, the
Third International Symposium on Business Modeling and Software Design
84

connections between the progresses_to relation of
the Control Principle, and the various relations that
capture the details of the imperative-workflow rule,
need to be analyzed and clarified.
As a result, we envision a ruleset that is
consistent and comprehensive, that reflects the
processing needs of the business, but without the
restrictions of workflow models. A next step is to
check with business users how the workflow
precedences and the like, now captured in binary
tables and declarative rules, correspond to the
requirements of the business.
We expect that declarative rules, developed
along these ideas, will capture the business require-
ments about the processing of incoming work better
than rigid rules of imperative workflows do. The
ruleset will provide an essential basis for improved
models to coordinate business processes. Indeed, the
reverse exercise, to derive an imperative workflow
compliant to even a small set of declarative rules,
may not be as straightforward, as may be illustrated
by your next Sudoku puzzle.
REFERENCES
Aalst W van der, Hofstede A ter, et al., 2003. Workflow
Patterns. In: Distributed and Parallel Databases 14(1)
p.5-51.
Ampersand. At: http://wiki.tarski.nl
Backhouse R, van der Woude J, 1993. Demonic operators
and monotype factors. In: Mathematical Structures in
Computer Science 3(4) p.417-433.
Business Rules Manifesto, 2003. At: www.business
rulesgroup.org/brmanifesto.htm. Version 2.0. Edited
R.G. Ross. Last accessed 24 march 2013.
van Dongen B, Aalst W van der, 2005. A meta model for
process mining data. CAiSE Conference Proceedings.
Joosten S, 2007. Deriving Functional Specification from
Business Requirements with Ampersand. Available at
http://icommas.ou.nl/wikiowi/images/e/e0/
Fahland D, Mendling J, et al., 2009. Declarative versus
Imperative Process Modeling Languages: The Issue of
Maintainability. In ER BPM.
Hofstede A ter, Aalst W van der, et al., 2003. Business
Process Management: A Survey. In: Business Process
Management. M. Weske, Springer Notes 2678.
Maddux R, 2006. Relation Algebras. Studies in Logic and
the Foundations of Mathematics, vol. 150. Elsevier
Science.
Maggi FM, Westergaard M, et al., 2011. Runtime
Verification of LTL-Based Declarative Process
Models. In: RV 2011, Khurshid and Sen (editors)
LNCS 7186, p.131–146.
McKemmish S, Acland G, et al., 2006. Describing records
in context in the continuum: the Australian
Recordkeeping Metadata Schema Archivaria 1(48).
McNeile A, Simons N, 2006. Protocol modelling: A
modelling approach that supports reusable behaviour
abstractions. In: Software and Systems Modeling 5(1)
p.91-107.
McNeile A, Roubtsova E, 2008. CSP parallel composition
of aspect models. In: Proceedings of the 2008 AOSD
workshop on Aspect-oriented modeling. Brussels,
Belgium, ACM p.13-18.
Russell N, Hofstede A ter, et al., 2006. Workflow Control-
Flow Patterns: A Revised View. At:
www.workflowpatterns.com/patterns
Russell N, Aalst W van der, et al., 2005. Workflow
Resource Patterns: Identification, representation and
tool support. Advanced Information Systems
Engineering, Springer.
Wedemeijer L, 2012. A comparison of two business rules
engineering approaches. In: BMSD 2012, p.113-121
Witt G, 2012. Writing Effective Business Rules. Morgan
Kaufmann. ISBN 978012-385051-5.
Workflow Management Coalition, 1999. Terminology &
Glossary. Tech.Report WFMC-TC-1011 issue 3.0.
Abstracting Imperative Workflow to Declarative Business Rules
85
