Innovation Cycles Control through Markov Decision Processes
Vassil S. Sgurev, Stanislav T. Drangajov, Lyubka A. Doukovska and Vassil G. Nikov
Institute of Information and Communication Technologies, Bulgarian Academy of Sciences,
Acad. G. Bonchev Str., Bl. 2, 1113 Sofia, Bulgaria
Keywords: Innovation Introduction, Markov Decision Processes.
Abstract: Innovations are introduced in several cycles, or steps which are of stochastic character. Successful
completion of each cycle results in the beginning of the next one. Initial stages are connected with expenses
of risk (venture) capital and the investments are returned in the final stages, usually with quite big profit. A
helpful approach for control of the innovation process is the use of Markov decision processes which have
proved to be an efficient tool for control of multi state stochastic processes. Those stages may be
summarizes as: 1 – prestart stage; 2 – start stage; 3 – initial expansion stage; 4 – quick expansion stage; 5 –
stage of reaching liquidity of venture investments; 6 – stage of project failure and its cancelling. The
transition from state to state may be controlled through control techniques of Markov Decision Processes so
that maximum profit is achieved in shortest time. The stages are conditional and some of them may be
united, e.g. 1 and 2, or 3 and 4.
1 INTRODUCTION
It is known that the innovations’ introduction
through the respective innovation cycles as a rule is
accompanied with considerable uncertainty and it is
of definitely expressed stochastic character. As the
successful completion of each innovation project
very often results in considerable profit this
stimulates the investment of considerable venture
(risk) means. A very important task arises for
preliminary careful considering and calculating the
stochastic character of the on going processes.
A multi step discrete Markov decision process
with mixed policies is proposed in the present work,
for the innovation risks interpretation. The
innovation process is accomplished, and probably
finished, as a rule, in a cycle of the following 6
stages: 1 – prestart and start stage; 2 – initial
expansion stage; 3 – quick expansion stage; 4 –
preparatory stage; 5 – stage of reaching liquidity of
the venture investment; 6 – stage of project failure
and its liquidation (Grossi, 1990, Cormican, 2004,
Bernsteina, 2006). Besides, the process at each stage
may be in different states where the decision maker
may undertake different actions which result in the
transition to a new state with respective profits and
losses. The first three stages are connected with
initial investments and respective losses. The
objective is they to be minimized. The last three
stages may generate profit and ensure full return of
the investments and considerable gains, but it may
also result in considerable loss if the innovation
product is a failure. It is to be clearly noticed that the
innovation introduction is a risky enterprise and not
each attempt is successful and winning.
It should be explicitly noticed that the innovation
process may only pass from a given stage to the next
one and can never return to a previous stage. No
other stages except the last ones – success or failure,
are absorbing - i.e. the innovation process may not
stay for ever in any of the initial stages or it fails.
The process may stay in a given stage for some time.
It is a responsibility of the decision maker to
undertake such control actions that the process
leaves as soon as possible the first three stages,
which generate expenses, with min losses and
reaches the final stage, which generate profit.
It is to be also noted, that depending on the
decision makers actions a stage may be omitted, e.g.
to pass directly from stage r to stage r+2. I.e. stages
so described are to some degree conditional but
nonetheless the process may develop in only forward
direction.
286
S. Sgurev V., T. Drangajov S., Doukovska L. and G. Nikov V.
Innovation Cycles Control through Markov Decision Processes.
DOI: 10.5220/0004776602860291
In Proceedings of the Third International Symposium on Business Modeling and Software Design (BMSD 2013), pages 286-291
ISBN: 978-989-8565-56-3
Copyright
c
 2013 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 MARKOV DECISION MODEL
FOR THE INNOVATION
PROCESS
We consider an innovation process, which might be
at any of the six stages of implementation of a new
product. Of course this is for purposes of
methodology. In fact one should begin from the first
stage and reach the last one.
We introduce the following denotation:
1

jj
N where the right hand part of the upper
equation is a reverse mapping of node j of the graph
from Figure 1.
k
ij
P denotes the transition probability
of the innovation process to pass from state
Ni

to state
Nj  when using control
i
Kk  , where
i
K is the set of possible policies from state i. As
leaping across or going back to stages of the
innovation process is impossible, then:






;,0
;;;,0
otherwise
KkNjNi
P
ij
k
ij
.;;1;10
i
Nj
k
ij
k
ij
KkNiPP 


By
k
i
x
will be denoted the probability the
innovation process to fall in state
i , at using control
i
Kk  from this state.
An important feature of the innovation process is
that at transition from one stage to the next one in
the first three stages resources are spent, and the
transition from stage to the other in the last three
stages increasing profit is gained, i.e.:






.
};6,5,4{;0
;};3,2,1{;0
i
i
k
i
Kki
Kki
r
(1)
Then the maximum restoration of the venture funds
initially invested will be obtained at optimal choice
of control actions from each possible state of the
process, i.e.:
}/*{
ri
NiKk 
.
This optimal control selection from the separate
states corresponds to maximization of the objective
function:




NjKk
k
j
k
j
j
xr max (2)
Different methods of linear and dynamic
programming (Mine, 1975) may be used for finding
the optimal solution of the objective function above
with the existing linear probability constraints.
The specific structure of the proposed here multi
step discrete Markov decision process corresponds
to a sufficient degree to the processes of realization
of innovations and provides possibilities for efficient
control of venture financing of innovations at their
realization.
3 NUMERICAL EXAMPLES
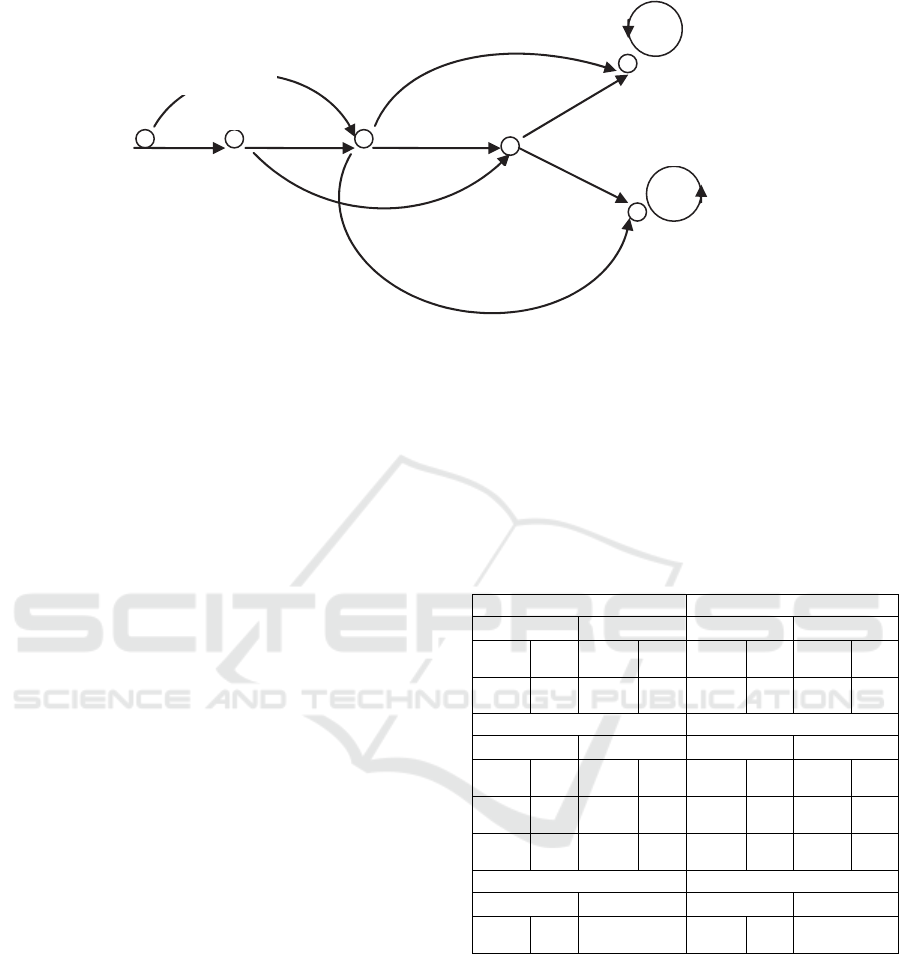
Next Figure 1 illustrates a Markov Decision Process
for control of the development of an innovation
through the 6 stages. The set of arcs U show the
possible transition from one stage (state) of the
innovation process to another one. The denotations
on the arcs of the decision graph should be decoded
as follows:
l
k
ji
P
,
- the probability for transition from stage i to
stage j using control action k
l
in state i.
In the final two stages, 5 and 6, which are
ergodic there is one only possible action. At the
other stages we accept for illustration that there are
two possible control actions with the respective
transition probabilities.
Formally this means that the possible actions
{k
j
} in each state
Nj

are defined in the
following way:






}6,5{\},2,1{
};6,5{},1{
Nj
j
k
j
The initial probability the process to be in state
Ni

is equal to:





.,0
;1,1
otherwise
i
a
i
The problem for finding optimal policies for the
Markov Decision Process shown in Figure 1 may be
reduced to the following linear programming
problem with objective function (2) and constraints:



j
Kk
k
i
x 1
, if i = 1 (3)
Innovation Cycles Control through Markov Decision Processes
287

)(
2
3,1
1
3,1
PP 
)(
2
2,1
1
2,1
PP
2
P
1
2,3
(P
2
23
)
3
P
1
3,5
(P
2
3,5
)
P
1
3,4
(P
2
3,4
)
4
P
1
4
,5
(P
2
4
,5
)
5
P
1
2,4
(P
2
2,4
)
6
P
1
3,
6
(P
2
3,
6
)
P
1
4,
6
(P
2
4,
6
)
P
1
5,5
=1
P
1
6,
6
=1
Figure 1: Exemplary transition graph for an innovation process.



jji
KkNjKk
k
i
k
ij
k
j
xPx 0
, if Nj  (4)
0
k
j
x , if NjKk
j


; (5)
If we take as a base the graph in Figure 1, then the
equations (2) and (3) to (5) will acquire the
following form:

1
4
1
4
2
3
2
3
1
3
1
3
2
2
2
2
1
2
1
2
2
1
2
1
1
1
1
1
xrxrxrxrxrxrxr
max
1
6
1
6
1
5
1
5
2
4
2
4
 xrxrxr
(6)
under the constraints:
1
2
1
1
1
 xx (7)
0
2
1
1
2,1
1
1
1
2,1
2
2
1
2
 xPxPxx (8)
0
2
2
2
3,2
1
2
1
3,2
2
1
1
3,1
1
1
1
2,1
2
3
1
3
 xPxPxPxPxx (9)
0
2
3
2
4,3
1
3
1
4,3
2
2
2
4,2
1
2
1
4,2
2
4
1
4
 xPxPxPxPxx
(10)
0
2
4
2
5,4
1
4
1
5,4
2
3
2
5,3
1
3
1
5,3
1
5
 xPxPxPxPx (11)
0
2
4
2
6,4
1
4
1
6,4
2
3
2
6,3
1
3
1
6,3
1
6
 xPxPxPxPx (12)
1
1
6
1
5
 xx
(13)
NjKkx
j
k
j
 ;;0
(14)
Let the profits (expenses) }{
k
i
r have the following
values:
.0;0
;12;10;8;7
;6;5;11;10
1
6
1
5
2
4
1
4
2
3
1
3
2
2
1
2
2
1
1
1



rr
rrrr
rrrr
The transition probability values are defined in the
following table:
Table 1: Transition probabilities.
STATE 1 STATE 2
Policy 1
Policy 2 Policy 1 Policy 2
1
2,1
P
0,8
2
2,1
P
0,9
1
3,2
P
0,7
2
3,2
P
0,8
1
3,1
P
0,2
2
3,1
P
0,1
1
4,2
P
0,3
1
4,2
P
0,2
STATE 3 STATE 4
Policy 1
Policy 2 Policy 1 Policy 2
1
4,3
P
0,6
2
4,3
P
0,5
1
5,4
P
0,8
2
5,4
P
0,7
1
5,3
P
0,3
2
5,3
P
0,3
1
6,4
P
0,2
2
6,4
P
0,3
1
6,3
P
0,1
2
6,3
P
0,2
STATE 5 STATE 6
Policy 1
- Policy 1 -
1
5,5
P
1
-
1
6,6
P
1 -
The respective transition probabilities are shown
above the arcs of the graph shown in Figure 1, when
using different possible policies. If only policy 1 or
respectively – only policy 2 is used, then the
transition probabilities tables will have the following
form:
1
Third International Symposium on Business Modeling and Software Design
288

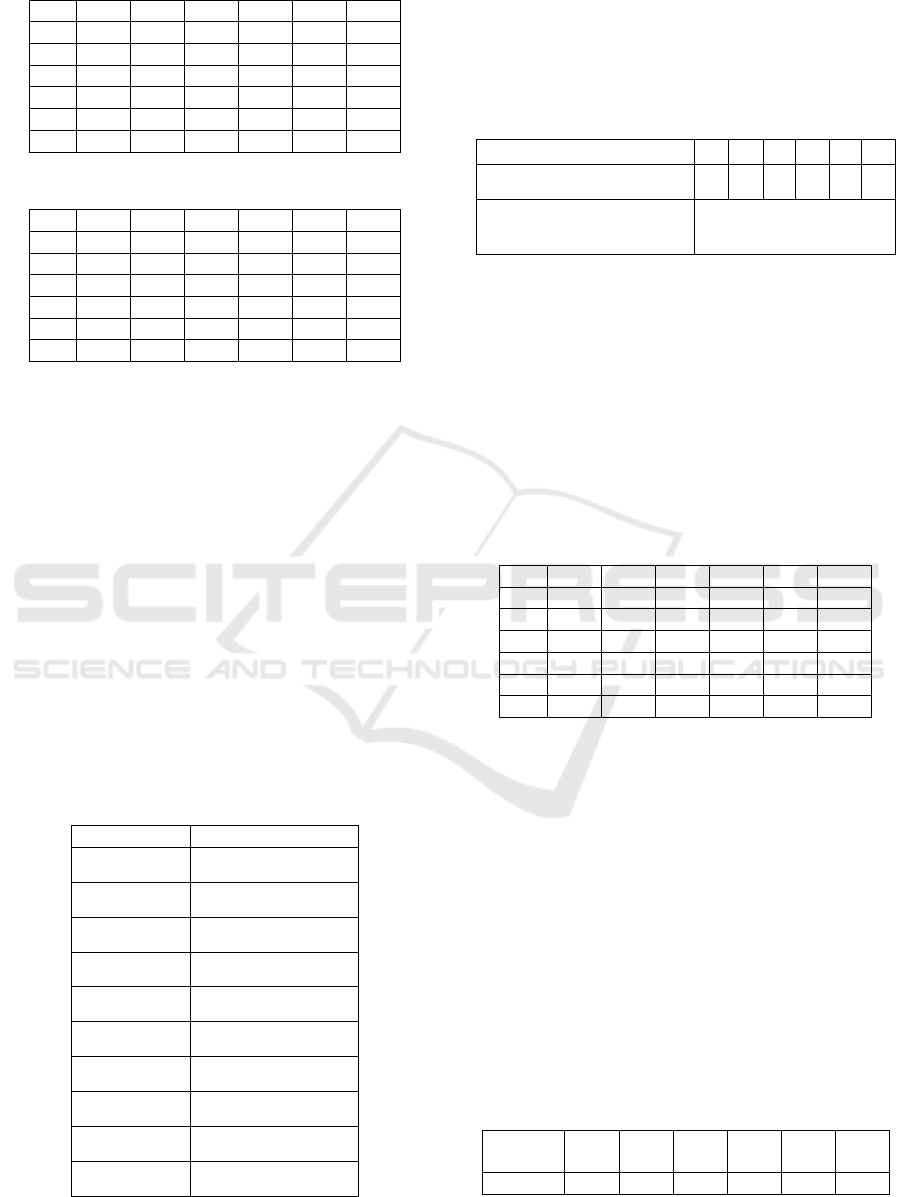
Table 2: Transition probabilities for policy 1.
1 2 3 4 5 6
1.
0 0,8 0,2 0 0 0
2.
0 0 0,7 0,3 0 0
3.
0 0 0 0,6 0,3 0,1
4.
0 0 0 0 0,8 0,2
5.
0 0 0 0 1 0
6.
0 0 0 0 0 1
Table 3: Transition probabilities for policy 2.
1 2 3 4 5 6
1.
0 0,9 0,1 0 0 0
2.
0 0 0,8 0,2 0 0
3.
0 0 0 0,5 0,3 0,2
4.
0 0 0 0 0,7 0,3
5.
0 0 0 0 1 0
6.
0 0 0 0 0 1
Table 2 reflects transition probabilities for policy
1 and Table 3 – for policy 2 respectively.
At least two classes may be distinguished in this
matrix – one quasi block diagonal ergodic, and one
absorbing, corresponding to states 5 and 6. When the
process being controlled falls in one of the latter
states it remains there for ever.
At defining the optimal control through relations
(5) to (13) in the rows of both matrices #3 and #4
will be used, in general with different probabilities,
i.e. both pure and mixed policies will be used, as
seen in the solving of the particular problem.
The linear programming problem (6) to (14)
includes 10 variables
}{
k
j
x and 8 constraints. Its
solution results in the following optimal values of
the variables:
Table 4: Linear programming problem solution.
Variables Optimal values
1
1
x
1
2
1
x
0
1
2
x
0,8
2
2
x
0
1
3
x
0,76
2
3
x
0
1
4
x
0
2
4
x
0,696
1
5
x
0,7152
1
6
x
0,248
It is seen from the table above, that in the
example considered the optimal solution leads to
pure optimal policies of both types – 1 or 2. Next
table shows the optimal pure policy and the
respective optimal strategy.
Table 5: Optimal pure policy and respective strategy.
State
Ni

1 2 3 4 5 6
Optimal policy
i
Kk 
*
1 1 1 2 1 1
Optimal strategy
}/{
*
NiKk
i

{1, 1, 1, 2, 1, 1}
The following matrix of the achieved optimal
transition probabilities of the Markov process may
be drawn up on the base of the optimal policies.
The new (optimal) transition probabilities matrix
thus constructed also consists of a quasi diagonal
ergodic class and an absorbing class of two states. In
it one row (the fourth) of Table 4 is used,
corresponding to policies 2. The remaining rows are
from Table 3, corresponding to policies 1. In this
sense it is mixed by using both policies – 1 and 2.
Table 6: Optimal transition probabilities matrix.
1 2 3 4 5 6
1.
0 0,8 0,2 0 0 0
2.
0 0 0,7 0,3 0 0
3.
0 0 0 0,6 0,3 0,1
4.
0 0 0 0 0,7 0,3
5.
0 0 0 0 1 0
6.
0 0 0 0 0 1
The Markov process thus constructed will flow
step by step according to the transition probabilities
from Table 6. In the next Figure 2 its stochastic
parameters are shown for the purpose of clearness –
on the arcs the respective probabilities
}{
ij
P
are
shown for falling from the initial state 1 into state
Nj

at passing through the previous state Ni

,
and in squares next to the vertices the final
probabilities
}/{
,
Nj
ji
 
are shown for the
process to fall from the initial state 1 into the
corresponding state
.Nj

The final probabilities are also shown in the
following table:
Table 7: Final probabilities.
Final
prob.
π
1,1
π
1,2
π
1,3
π
1,4
π
1,5
π
1,6
Values 1 0,8 0,76 0,69 0,72 0,28
Innovation Cycles Control through Markov Decision Processes
289

1
0,8
0,8
0,56
3 0,456
4
0,2
0,7
6
0,69
6
0,228
5
0,076
6
0,7152
0,4872
0,2088
0,2848
2
Figure 2: Markov process stochastic parameters from state to state and in the states.
On the base of the optimal values of the variables
}{
k
j
x of Table 4 through (6) the maximum value of
the objective function is computed to be - 0,328.
The results obtained provide the possibility some
conclusions to be made:
I. When teaching one of the two final states – 5
or 6 the investment made is not paid off in full as
0,328 units remain to be paid off. If the process has
fallen in state 5, then the project is successful and in
may go on further to pay off the investments made
and to produce profit. In case that the process fell in
state 6, the project is a failure and it is almost sure it
will be cancelled. The amount of 0,328 units should
be registered as a loss in this case.
II. Even at optimal decisions for leading the
stochastic innovation process, the end the end of the
project cannot be certainly predicted – a
considerable probability (in the case considered
almost 0,3) exists it to end as a failure. This reflects
the real conditions in similar class of processes,
which are always of explicitly expressed stochastic
character.
III. The method proposed for innovation
processes control on the base of Markov decision
processes has another important advantage - optimal
policies and strategies may be recomputed on the
base of new and more refined data after each step
completed step of the process and the state it falls
into. This may result in better final result by
improving the strategy initially computed.
IV. It is possible to use more precise classes of
Markov decision, e.g. by using profit discount at
each step at each step, with constrained capacity or
through Markov flows or Markov games (Sgurev,
1993).
4 CONCLUSIONS
In conclusion the following general inferences may
be drawn:
1. The innovation processes are highly stochastic
and uncertain, which results to highly imprecise
prognostication of their completion. And this is
connected with a big risk at the venture financing of
such processes.
2. The method proposed in the present work for
using multistep Markov decision processes for
description of the innovation processes provides a
possibility their stochastic character to be recognized
to a considerable degree and an effective procedure
to be proposed for their behavior control.
ACKNOWLEDGEMENTS
The research work reported in the paper is partly
supported by the project AComIn “Advanced
Computing for Innovation”, grant 316087, funded
by the FP7 Capacity Programme (Research Potential
of Convergence Regions) and partially supported by
the European Social Fund and Republic of Bulgaria,
Operational Programme “Development of Human
Resources” 2007-2013, Grant № BG051PO001-
3.3.06-0048.
REFERENCES
Grossi G., Promoting Innovations in a Big Business, Long
Range Planning, vol. 23, #1, 1990.
Mine H., S. Osaki, Markovian Decision Processes, Amer.
Elsevier Publ. Comp., Inc, N.Y., 1975.
1
Third International Symposium on Business Modeling and Software Design
290

Cormican K., D. O’Sullivan, Auditing best practice for
effective product innovation management,
Technovation, Volume 24, Issue 10, pp. 761-851,
Elsevier, 2004.
Bernsteina B., P. J. Singhb, An integrated innovation
process model based on practices of Australian
biotechnology firms, Volume 26, Issues 5–6, pp. 561–
572, Elsevier, 2006.
Sgurev V., Markov Flows, Publishing House of the
Bulgarian Academy of Sciences, Sofia, 1993 (in
Russian).
Innovation Cycles Control through Markov Decision Processes
291