
ANALYTICAL DESCRIPTION OF THE PRODUCTION OF
FORMATS IN HUMAN SPEECH
Damyan Damyanov
Technical University of Sofia, Faculty of Automation, Department for Industrial Automation,
Bulgaria, Sofia, Darvenitsa 1756,Bul. Kliment Ohridksi 8, block 9,room 9420
damyan_damyanov@tu-sofia.bg
Keywords: model of speech production, man-machine systems.
Abstract: For the purposes. of speech synthesis, biometrics , medical and psychological diagnosis, the functioning of
the glottis during phonation has been studied many times. At present, a relatively trivial solution proposed
by Fant has established itself, regardless of the actual purpose of the system, using the "pusle source - filter"
model. The model of Fant allows the linear prediction method to perform reconstruction of the current form
of the vocal tract and the excitation of glottal volume velocity. But the practice shows that the fluctuations
of the speech tract due to psycho-physiological effect on the functioning of the facial muscles in most cases
are negligible. Thus, they are below the accuracy, which the linear model allows, using approximation with
a cascade of coaxial cylindrical sections of equal length and constant cross-section. This requires more
complex algorithms, and thus additional information is extracted from the pattern of air volume velocity
after glottis. In this study, it is to be shown, that the model of Fant actually allows depiction of the psycho-
physiological changes in the spectral features of the speech signal without the use of additional models. For
this purpose it is sufficient to analyze the relationships of the main parameters of the excitation pulse of the
source with the frequency response of the filter. In the current practice, these correlations are not considered
and the source and the filter are examined separately.
1 INTRODUCTION
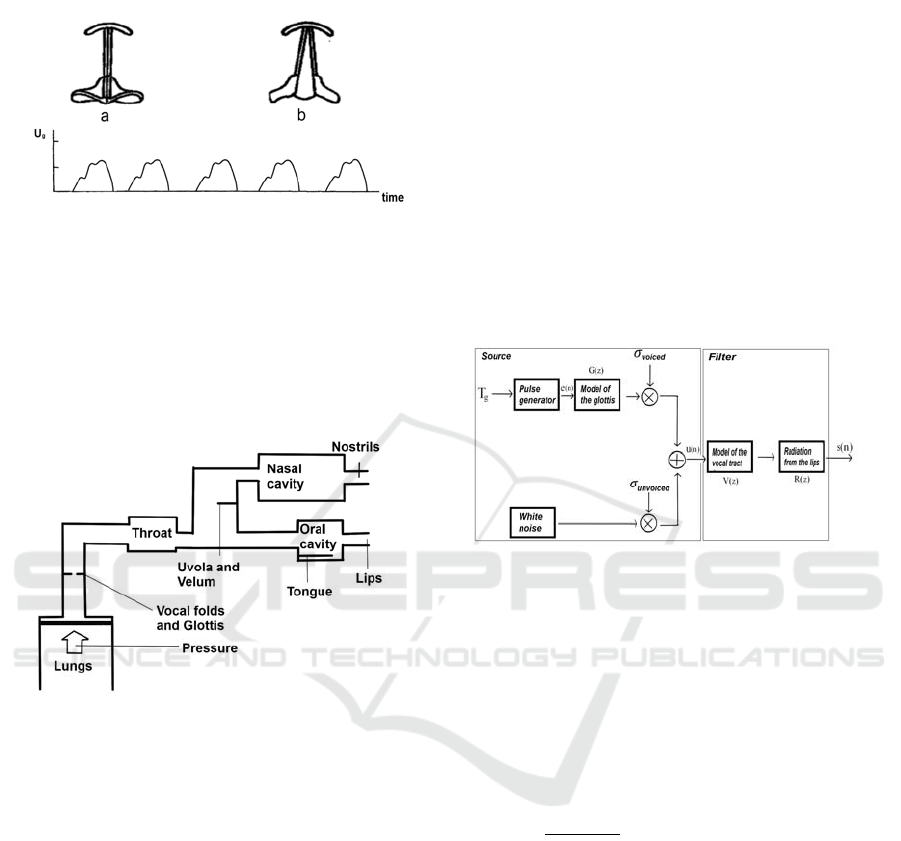
Phonation is a process which takes place in the
middle part of the larynx and sets up vibrations to
the exhaled airstream. As a consequence of this
process the air volume velocity after the glottis
immediately shows vibrational patterns (Figure 1),
which determines the pitch frequency of the speech
signal (Тилков, Д., Бояджиев., Т 1990). Changing
the tension of the vocal folds and the pressure during
the speech production process, one gets the desired
pitch frequency, needed for phonation of vowels and
voiced consonants. In the formation of non-voiced
consonants the vocal folds do not come near each
other and their constellation is like at physiological
breathing (Pickett J.M, 1982). In this case, the
incoming air pressure from the lungs is modulated
by the formation of turbulence and closure of the
vocal tract. The spectra of the resulting sound
sources are modified by resonances, the frequency
of which depends on the time-varying shape of the
throat and mouth, the location of the tongue and
many more.
Modern study of acoustic phenomena in the oral-
pharyngeal tract began in 1941 with the work of
Chiba and Kajiyama (Chiba, T., Kajiyama M.,
1941). The fundament of the present theory and
practice is shaped in 1960 by Fant (Fant, G., 1960),
and others. The systems for processing, transmitting
and storing of speech signals use various methods
and techniques, but they are all based on a model of
the functioning of articulatory tract and the air
volume velocity after the glottis. The purpose of the
modelling process of speech production is not only
to study its properties and specifics, but also to solve
problems for its effective coding and transmission ,
79
Damyanov D.
ANALYTICAL DESCRIPTION OF THE PRODUCTION OF FORMATS IN HUMAN SPEECH.
DOI: 10.5220/0004785600790084
In Proceedings of the Second International Conference on Telecommunications and Remote Sensing (ICTRS 2013), pages 79-84
ISBN: 978-989-8565-57-0
Copyright
c
2013 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
the automatic synthesis of speech and speech
recognition, for biometrical applications and others.
Figure 1: Air volume velocity immediately after the glottis
for vowels and voiced consonants. Position of the vocal
folds: a - phonation of vowels and voiced consonants, b -
physiological breathing.
In every such model (Proakis, J.,2000), in one
degree of another, the main components of
articulatory tract in terms of the laws of acoustics are
reflected (Figure 2)
Figure 2: Main components of the acoustic articulatory
tract.
These components include the excitation of the
vocal cords, the time-varying shape of the vocal
tract, radiation from the lips etc. Resonant
phenomena in the speech production process are
actually affected by losses in the walls of the tract,
depending on the thermal conductivity, elasticity and
friction. Significant influence is done by the nasal
cavity with the absorption of certain frequency
components of the spectrum (antiresonant
phenomena). This complex nature of the process
allows the development of many models, differing in
structure and degree of relevance. Interestingly,
despite the apparent complexity of the problem, it
found a relatively trivial solution proposed by Fant
(Fant, G., 1960), which has established itself in
practice regardless of the actual purpose of the
system.
The classical model of Fant separates the
excitation from the shaping of individual sound
components of speech, allowing approximately
treatment of speech sounds as a linear system.
Lungs, which provide air volume velocity, are
presented as direct current power source. Their
output is divided, corresponding respectively to the
voiced and unvoiced parts of the signal. The pulse
generator modulates the air volume velocity from
periodical excitation of the vocal folds, and the noise
generator models the formation of turbulence in the
places, where the vocal tract changes its cross-
section. The final speech signal is obtained after the
components are added together and passed through a
filter with linear transfer function, which models the
articulatory tract.
In modern systems, this model has found its
discrete implementation (Figure 3).
Figure 3: Digitalized model of Fant.
Generating a voiced speech segment after the z-
transform of a sampled speech signal is described by
the equation:
() () () ()
g
Sz U zVzLz
=
(1)
)(
1
)()()(
0
zG
z
zGzzU
K
son
son
n
nK
g
−
∞
=
−
−
=
=
∑
σ
σ
(2)
It is assumed, that the sampling period is T=1,
and the period of the pitch frequency is a multiple of
it Tp = KT (Damyanov, D., Galabov, V., 2012a).
The transfer function of the model of the glottis, the
model of the vocal tract and the lips radiation can be
combined in a common transfer function:
)()()()( zLzVzGzH
=
(3)
And the speech production process can be
written as
)()()( zHzEzS
=
(4)
Second International Conference on Telecommunications and Remote Sensing
80

{}
nTt
tsnTsnTsZzS
=
== )()(,)()(
(5)
Where E(z) is the z-transformed pulse excitation
of the glottis. Adoption of certain hypothesis about
the spectral properties of the glottis, of the vocal
tract and the lips radiation (Fant, G., 1960) allows
the use of an all-pole filter:
∑
=
−
+
=
M
i
i
i
za
zH
1
1
1
)(
(6)
Finding the coefficients of this filter is a task,
successfully solved in theory and practice. (Proakis,
J.,2000, Trashlieva, V., Puleva, T., 2011)
2 MOTIVATION
Using a process of speech production of type source-
filter, based on the model of Fant, many of the tasks,
associated with the processing of speech signals are
successfully solved. In this study, it is to be shown,
that despite their simplicity, these models are able to
explain some phenomena of the speech production,
observed in the changes of current psycho-
physiological state of humans. These include
changed rations of the amplitudes of formant
frequencies (less harsh or ringing voice), impaired
understandability, etc. For their description and
analysis of the functioning of the glottis during
phonation has been studied many times, in order to
create relevant model, especially for the purposes of
speech synthesis, medical and psychological
diagnosis, and biometrics. Much of the testing
methods are borrowed from medicine in order to
achieve greater accuracy, or to make measuring
easier. All of the above methods do not work
directly with the desired variable, but with some
other, depending on the desired one. Given the
complexity of making laryngoscopic and
laryngoendoscopic studies, and especially the need
for medical intervention, and because of the
significant impact of these methods on the overall
process of speech production, a great number of
indirect methods have been developed. These
include methods, base on electromyography -
registering the signals of muscle activity in the
throat while speaking, glottography - working with
the impedance of the neck in the plane of the glottis,
which largely depends on the cross-section of the air
volume velocity after the glottis. Despite numerous
studies, currently there is no unified theory that
explains the process of these changes in the spectral
characteristics of the speech signal. Most authors
seek the cause of these phenomena in the psycho-
physiological change in current form of the
articulatory tract. The model of Fant allows the
linear prediction method to perform reconstruction
(with some degree of approximation) of the current
form of the tract and the excitation of acoustic
volume velocity after the glottis. It is expected, that
the modelling of the speech tract provides conditions
for obtaining relevant information about the
functioning of the facial muscles and the
corresponding parts of the nervous system, which
are extremely sensitive to current psycho-
physiological state of the individual (Ekman, P,
Friesen, W., 1978 ). But the practice shows, that the
fluctuations of the speech tract due to psycho-
physiological effect on the functioning of the facial
muscles in most cases are too small . Thus they are
below the accuracy, which the linear model allows,
using approximation with a cascade of coaxial
cylindrical sections of equal length and constant
cross-section (Pfister, B., Kaufmann, T., 2008).
This requires more complex algorithms and
thus additional information is extracted from the
pattern of air volume velocity after glottis. The air
volume velocity gives information about the current
psycho-physiological condition in two ways - first,
through the entire process of speech production,
concerning the higher nervous activity, and the
second by the functional state of the autonomic
nervous system, including the overall muscular
tonus (Reuter-Lorenz, Patricia A., et.al., 2010, Kalat,
James W. 2012). For the extraction of this
information, the use of relatively complex models is
required, describing the tension on the vocal folds,
the mechanism of stretching and vibrating, the
pressure of the incoming air flow from the lungs,
etc. In this study, it is to be shown, that the model of
Fant actually allows depiction of the psycho-
physiological changes in the spectral features of the
speech signal without the use of additional models.
For this purpose, it is sufficient to analyze the
relationships of the main parameters of the
excitation pulse of the source with the frequency
response of the filter. In the current practice, these
correlations are not considered and the source and
the filter are examined separately. For readability
purposes, the following simplifications will be made
that do not change the generality of the study:
• The influence of the transfer function of
the glottis and the lips radiation will be
neglected, since they don't affect the
Analytical Description of the Production of Formats in Human Speech
81

formant frequencies, but only their
decay ;
• The excitation of the source will be
considered as a sequence of rectangular
pulses;
• The attenuation of formant frequencies
will be ignored, i.e. poles of the filter of
the vocal tract will lie of the unit circle;
3 PRODUCTION OF FORMANTS
IN HUMAN SPEECH
In this study, it is assumed, that the model of the
vocal tract is of second order:
2
1
2
2
11
)(
ω
ω
+
=
s
k
sH
(7)
i.e. the signal will contain only one formant with
circular frequency
1
ω
. The excitation pulses are of
type (Damyanov, D., Galabov, V., 2012b):
1,1
)1(,0
)1()1(,1
)(
_
_
−=
<≤−+
−+<≤−
=
⎪
⎩
⎪
⎨
⎧
imp
ggglottisopen
gglottisopeng
Nm
mTtTmt
TmttTm
te
(8)
where
g
T
is the period of the pitch frequency , and
glottisopen
t
_
is the duration of the phase of open
glottis. The output signal for the period of the pitch
frequency (m=1) is:
)
1
_1
(
1
_
1
_
)(
1
_
sin
F
glottisopen
F
glottisopen
A
F
glottisopen
AOt
F
glottisopen
ts
ϕω
+−=
(9)
for
glottisopen
t
_
, i.e. in the phase of open
glottis, and:
)
1
_1
(
1
_
)(
1
_
sin
F
glottisclosed
F
glottisclosed
At
F
glottisclosed
ts
ϕω
+=
(10)
for
glottisopen
tt
_
≥
, i.e. in the phase of closed
glottis, where:
1
1
_
k
F
glottisopen
AO =
is the DC component of the
signal in the phase of open glottis
1
1
_
k
F
glottisopen
A =
and
)
2
_1
(
1
2
1
_
sin
glottisopen
F
glottisclosed
A
t
k
ω
=
are the
amplitudes of the signal in the phases of open and
closed glottis
2
1
_
π
ϕ
=
F
glottisopen
and
2
_1
2
1
_
glottisopen
F
glottisclosed
t
ω
πϕ
−=
are the
angular phases of the signal in the phases of open
and closed glottis
11
2 f
π
ω
=
are the circular frequency, which
corresponds to the formant frequency
1
f
.
We can observe the following important features:
In the two phases - of open and closed glottis
- the formant frequency is determined only
on the coefficient of plain gain of the filter
The amplitude of the signal in the phase of
closed glottis depends again on this
coefficient, but also in a complicated way
on the ratio of duration of the preceding
phase of open glottis to the period of the
formant frequency.
The phase shift of the signal depends in a
similar way on the above stated variables.
Practically, this means that without changes in
the filter parameters, i.e. the geometry of the vocal
tract, changes in length of the phase of open glottis
can increase or decrease the formant frequencies of
the speech signal (Damyanov, D., Galabov, V.,
2012a). For better understanding of the paradigm, a
dimensionless coefficient is introduced, which is
proportional to the duration of the phase of open
glottis to the period of the formant frequency:
glottisopen
glottisopen
t
tr
_1
_1
ω
ω
=
(11)
In terms of amplitude of the signal before and
after closure of the glottis the coefficient can be
defined:
F
glottisclosed
A
F
glottisopen
A
F
glottisclosed
A
F
glottisopen
A
r
1
_
1
_
1
_
1
_
=
(12)
where the
glottisopen
tT
glottisclosed
t
g
__
−
=
is the
duration of the phase of closed glottis during the
period of the pitch frequency (Damyanov, D.,
Galabov, V., 2012b). The functional relationship
between these two coefficients is:
Second International Conference on Telecommunications and Remote Sensing
82

)
2
_1
(2
_1
1
_
1
_
sin
glottisopen
glottisopen
F
glottisclosed
A
F
glottisopen
A
t
t
rf
r
ω
ω
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
(13)
It can be seen, that varying the duration of the
phase of open glottis, without changing the filter
parameters, i.e. the geometry of the vocal tract, for a
given amplitude of the generated signal in the phase
of closed glottis can take any value from zero to two
times the amplitude in the phase of open glottis
(Damyanov, D., Galabov, V., 2012c).
This effect becomes more interesting, if the
speech segment contains several periods of the pitch
frequency. Then, besides the coefficient
glottisopen
t
glottisopen
t
r
_1
_1
ω
ω
=
, the ratio of the
amplitudes will be affected by the ratio of the length
phase of closed glottis during the period of pitch
frequency:
g
glottisopen
impfull
T
t
k
_
_
=
(14)
In this case one can obtain relatively complex
analytical dependencies. For example the
relationship of the amplitudes of the signal in the
phase of closed glottis to the phase of open glottis in
the second period of the pitch frequency is given by
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
==
)
_
2
_1
cos()
2
_1
sin(
1
4
)
_1
(
1
_
1
_
impfull
k
glottisopen
t
r
glottisopen
t
r
k
glottisopen
t
rf
F
glottisclosed
A
F
glottisopen
A
r
ωω
ω
(15)
2
1
2
2
)
2
_
_1
sin(
1
)
2
_1
(
2
sin
1
2
)
_
_1
2sin(
1
)
_1
sin(
1
−
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−+−
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−+
π
ωω
ω
π
ω
impfull
k
glottisopen
t
r
k
glottisopen
t
r
k
impfull
k
glottisopen
t
r
k
glottisopen
t
rk
If we assume that:
Nofonpresentatibinarythefrom
bitsofnumbertotalnumbits =
(16)
Then, for the N-th period of the pitch frequency
the dependencies are as follows:
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
+−+−+
+
+
+−
=
∑
∑
∏
∑
<+
+=
+−
=
=
−
−
=
BSBBBS
t
t
impfull
k
t
BFBBSB
impfull
k
t
t
t
k
F
glottisclosed
A
numbits
numbitssab
sabsub
sabsab
glottisopen
numbits
sab
sab
ampl
ampl
glottisopen
numbits
sab
numbits
glottisopen
glottisopen
))))(
222(1(
2
sin(
))2
_
cos(2(
))22
_
1
1(
2
sin(
)
2
sin(2
1
_
1
1
101
_1
1
2
2
)3(
_1
1
2
2
_1
1
_1
'
1
ω
ω
ω
ω
ω
ω
(17)
where
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
=
else
equalis
Nofonpresentatibinarythefrom
bittsignificanthsabtheif
BSB
,1
0
,0
(18)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
else
equalis
Nofonpresentatibinarythefrom
bitfirsttheif
BFB
,1
0
,0
(19)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
=
else
equalis
Nofonpresentatibinarythefrom
bittsignificansubthef
BSS
,1
0
,0
(20)
⎩
⎨
⎧
−−+
=
=
elsesabnumbitsBSB
numbitssabifBSS
BBS
,1
,
(21)
and
)
2
_
sin(
))1((
1
_
1
_
_1
1
'
1
π
ω
ω
+−−
−+=
impfull
k
Nt
t
TN
F
glottisclosed
Ak
F
glottisopen
A
glottisopen
g
(22)
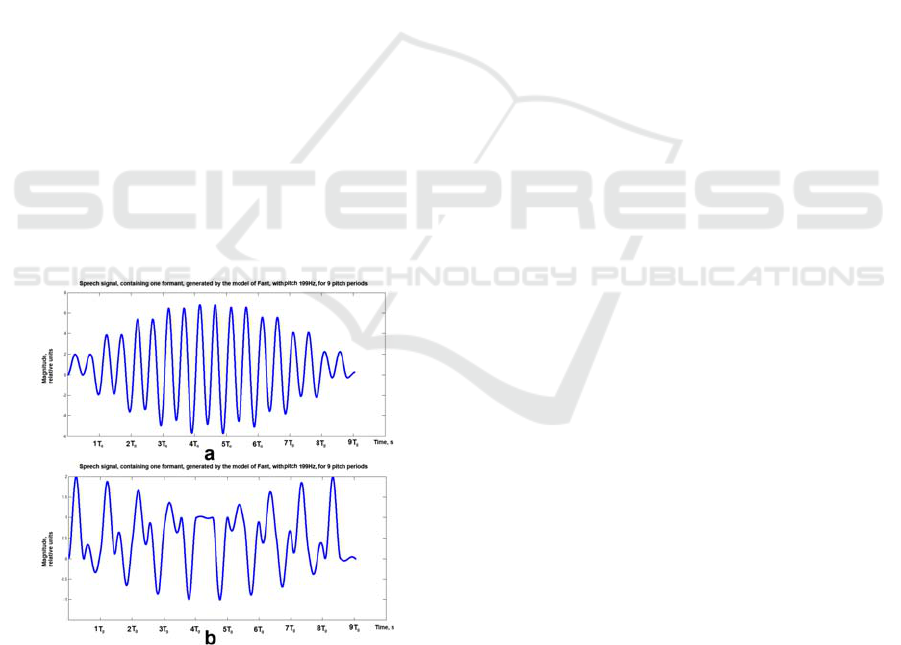
One can make the following conclusion:
By changing the ratio of the duration of the
phase of close glottis to the length of the pitch
frequency and without changing the geometry of the
vocal tract, one can generate speech segments, in
which the formant amplitude for each subsequent
period increases, decreases, or does not change
much. This can be seen in the two parts of figure 4.
In the figure, a speech signal, generated with the
model of Fant is resented. It contains one formant,
which has frequency 420 Hz. The pitch is 199 Hz,
and the plot contains 9 pitch periods. The signal in
the first part has
ms
glottisopen
t 39
_
=
, and the
second part has
ms
glottisopen
t 25
_
=
.
Analytical Description of the Production of Formats in Human Speech
83
4 CONCLUSIONS
The study shows that the model of Fant adequately
describes many phenomena of the speech production
process, that are known form theory and practice.
The reason for this probably lies in the genesis of the
model. A "pulse source-filter" model is created for
simplification of the process of analysis and
parameterization of a specific implementation. This
is accomplished, with the assumption, that the filter
is practically independent of the source of excitation.
This allows the implementation of effective methods
and techniques for the evaluation of the filter. This
approach gives excellent results in most cases -
mainly in speech analysis, synthesis, coding and
transmission. When the speech signals are used for
medical, psycho-physiological, biometrical purposes
however, it is customary to consider that the model
of Fant is not sufficiently relevant. This requires the
use of much more complex models and additional
information sources. Recently, the problem becomes
even more acute with the ever increasing demands
on quality of processing and transmission of speech
signals and their use in mobile devices. This paper
shows, that the model can be made much more
efficient without further complication. This is
achieved, using the cumulative effect of some of the
processes, that can be found in source and in the
filter.
Figure 4: Speech signal, generated with the model of Fant,
containing one formant, with pitch 199 Hz, 9 pitch
periods, with formant frequency 420 Hz, and duration of
the phase of open glottis 39 ms for a) and 25 ms for b).
REFERENCES
Chiba, T., Kajiyama, M.1995,The vowel, Its Nature and
Structure. Tokyo-Kaiseikan, Tokyo 1995
Damyanov, D., Galabov, V., 2012a, Characteristics of the
model of Fant of second order on speech production,
Proceedings of the Technical University - Sofia,
Volume 62, Issue 2, pp. 181-188, ISSN 1311-0829 ,
Sofia, 2012,
Damyanov, D., Galabov, V., 2012b, On the Impact of
duration of the phase of open glottis on the spectral
characteristics of the phonation process, Proceedings
of the Technical University - Sofia, Volume 62, Issue
2, pp. 173-180, ISSN 1311-0829 , Sofia, 2012,
Damyanov, D., Galabov, V., 2012c, Some effects of the
assumption of an all-pole filter, used to describe
processes of type "pulse source, 1-st International
Conference on Telecommunications and Remote
Sensing, August, 29-30, pp. 139-145, ISBN 978-989-
8565-28-0 , Sofia, 2012,
Ekman, P., Friesen W., 1978, The Facial Action Coding
System, Consulting Psychologist Press, San Francisco.
CA, 1978
Fant, G., 1990, Acoustic Theory of Speech Production,
Mouton&Co, Hauge
Flannagan, J., 1992, Speech analysis, Synthesis and
Perception, Springer, Berlin, 1992
Hayes, M., 1999, Schaum's Outline of Theory and
Problems of Digital Signal Processing, Singapore,
McGraw-Hill, 1999
Kalat, James W. 2012, Biological Psychology, Wadswoth.
Cengage Learning, 10-th edition, Belmont, 2009
Pfister, B., Kaufmann, T., 2008, Sprachverarbeitung -
Grundlagen und Methoden der Sprachsynthese und
Spracherkennung, Springer Verlag, Heidelberg, 2008
Pickett, J.M. 1982, The sounds of speech communication ,
Univercity Park Press, Baltimore, 1982
Proakis, J.,2000, Discrete Time Processing of Speech
Signals, New Jersey, JohnWiley&Sons, IEEE Press,
2000
Rabiner, L., Schafer R. 1992, Digital processing of speech
signals, Prentice-Hall Inc, Engelwood Cliffs, New
Jersey, 1992
Reuter-Lorenz, Patricia A., et.al., 2010, The Cognitive
neuroscience of mind: A tribute to Michael S.
Gazzaniga, MIT Press, April, London, 2010
Trashlieva, V., Puleva, T., 2011, Model building for
optimal administrative process management,
International Conference Automatics and
Informatics'11, Bulgaria, 3-7.10.2011, pp B-263-B-
266, ISSN 1313-1850, Sofia, 2011
Тилков, Д., Бояджиев., Т 1990, Българска Фонетика,
Наука и изкуство София 1990
Second International Conference on Telecommunications and Remote Sensing
84
