SOUND SOURCE LOCALIZATION IN A SECURITY SYSTEM

USING A MICROPHONE ARRAY

Vera Behar

, Hristo Kabakchiev

and Ivan Garvanov

Institute of Information & Communication Technologie, BAS, 25-A Acad. G.Bonchev Str., Sofia, Bulgaria

Faculty of Mathematics & Informatics,Sofia University, 15 Tsar Osvoboditel Blvd., Sofia, Bulgaria

University of Library Studies & Information Technologies, Sofia, Bulgaria

behar@bas.bg, ckabakchiev@yahoo.com, igarvanov@yahoo.com

Keywords: Adaptive array processing, microphone arrays, sound signal processing, DOA estimation

Abstract: A possible algorithm for sound source localization in a security system that is based on

beamforming of a microphone array is described in this paper. It is shown that the adaptive

beamforming algorithm, Minimum Variance Distortionless Response (MVDR), can be a part of

the signal processing implemented in a security system. This signal processing includes the

following stages: sound source localization, signal parameter estimation, signal priority analysis

and, finally, control of protective and warning means (for example, video camera). The adaptive

beamforming method MVDR is used for estimating the direction-of arrival (DOA) of signals

generated by different sound sources, which arrive at the microphone array from different

directions of the protected area. The scenario, in which four sound sources located at different

points of the protected area generate different sound signals (warning, alarm, emergency and

natural noise), is simulated in order to verify the algorithm for DOA estimation. The simulation

results show that an adaptive microphone array can be successfully used for accurate localization

of all sound sources in the observation area. The parallel version of the described algorithm is

tested in Blue Gene environment using the interface MPI.

1 INTRODUCTION

The security system is a standard part of any

building in the city. In most sensors used by a

security system for protection of a limited space

(home, parking) are mounted sound sirens that are

activated in the event of an adverse situation in the

protected space. Usually, in case of such a situation

(fire, smoke, vibration, and breakage of glass or

opening the car) the sirens of sensors give a loud

beep for a few minutes. The assessment of the

direction and parameters of the incoming sound

signals can be used to control the movement of a

video camera that records the situation in the most

dangerous direction and submits the data to the

management centre.

The novelty of this paper is to use the adaptive

beamforming algorithm in order to locate, using a

microphone array, the direction of sound signals

coming from sensors or other sound sources.

Microphones arrays represent a set of microphones

arranged in some geometric configuration. They can

be realized as linear microphone arrays, where the

microphones are positioned in a straight line, or as

circular microphone arrays, where the microphones

are placed in a circle, or as rectangular microphone

arrays, where the microphones are arranged in the

shape of a rectangle plate (Benesty, 2008).

Microphone arrays have many advantages. Firstly,

the beamforming can be done digitally so as to

control all dangerous directions (door, windows,

cars) using only a single microphone array.

Otherwise, when using directional microphones of

other types, for example, parabolic microphones, a

lot of such microphones are required, because each

microphone can control only one direction.

Secondly, all noise signals coming from other

uncontrolled directions (speaking of people, banging

on the walls, etc.) are adaptively rejected by a

microphone array, which increases the detectability

of signals from sensors and improves the security of

the protected area. For comparison, when using a

Behar V., Kabakchiev H. and Garvanov I.

SOUND SOURCE LOCALIZATION IN A SECURITY SYSTEM USING A MICROPHONE ARRAY.

DOI: 10.5220/0004785700850094

In Proceedings of the Second International Conference on Telecommunications and Remote Sensing (ICTRS 2013), pages 85-94

ISBN: 978-989-8565-57-0

directional parabolic microphone, noise signals are

not removed and they interfere with the detection of

the signal. In third, a microphone array can

simultaneously generate several independent beam

patterns and collect the information from multiple

sound sources. In the fourth, the signal power at the

output of a microphone array is increased M times

(M - is the number of array microphones), which

allows to substantially increase the security of the

protected area. Moreover, a three-dimensional area

can be controlled using the rectangular or circular

microphone arrays, and, finally, microphone arrays

can be easy adapted to detect acoustic signals with

different frequency characteristics by change of the

distance between microphones in the array.

In this paper, we propose to use the Minimum

Variance Distortionless Response (MVDR)

beamforming algorithm for DOA estimation of

signals arrived from different sound sources at a

microphone array (Godara, 1997; Trees, 2002;

Vouras, 1996; Moelker, 1996). We consider the

case, when each sound source is located in the

array’s far-field, and the sounds generated by sound

sources propagate through the air. The DOA is

proposed to be estimated as a direction, in which the

signal power at the output of a microphone array

exceeds a previously predetermined threshold. The

paper is structured as follows. In the next second

section, the expressions for calculation of array

response vectors are derived for three types of

microphone arrays. The model of signals arrived at a

microphone array in a security system is described

in the third section. The MVDR algorithm for DOA

estimation is mathematically described in the forth

section.

The parallel version of the MVDR algorithm

tested in Blue Gene environment using the interface

MPI is described in the fifth section. The simulation

scenario, in which four sound sources located at

different points of the protected area generate

different sound signals (warning, alarm, emergency

and natural noise), is described in the sixth section.

The simulation scenario is used in order to verify the

algorithm for DOA estimation. The results obtained

show that the MVDR beamforming algorithm

applied to a microphone array can be successfully

used for accurate localization of all sound sources in

the observation area. The parallel version of the

described algorithm is tested in Blue Gene

environment using the interface MPI.

2 MICROPHONE ARRAYS

Microphone arrays are composed of many

microphones working jointly to establish a unique

beam pattern in the desire direction. The array

microphones are put together in a known geometry,

which is usually uniform - Uniform Linear Arrays

(ULA), Uniform Rectangular Arrays (URA) or

Uniform Circular Arrays (UCA) (Ioannidis, 2005).

Since the ULA beam pattern can be controlled only

in one dimension (azimuth), so in various sound

applications, URA and UCA configurations with

the elements extended in two dimensions must be

used in order to control the beam pattern in two

dimensions (azimuth and elevation).

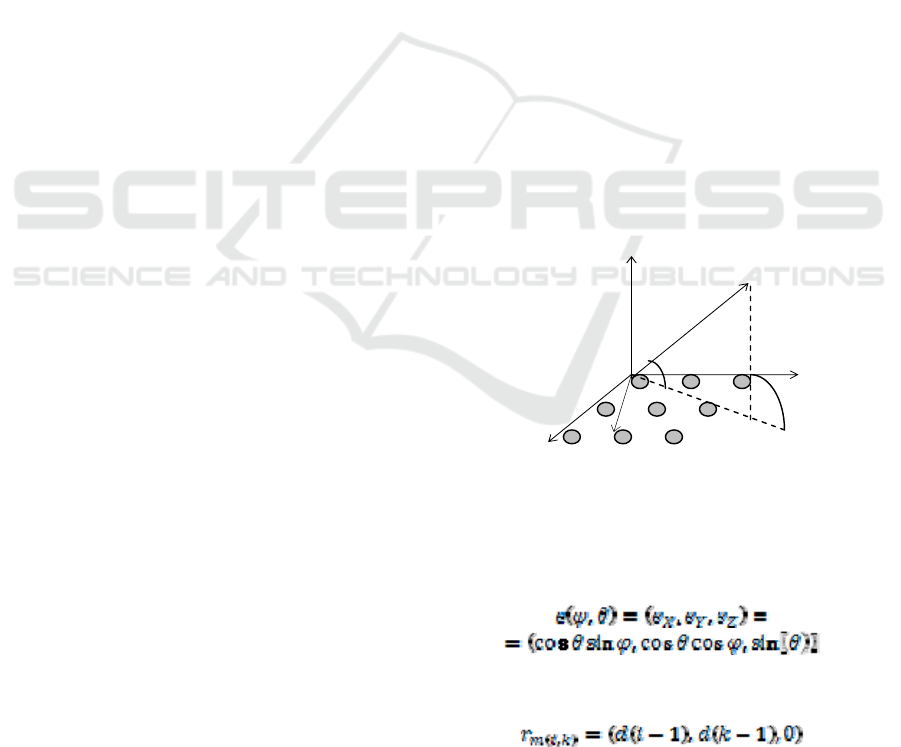
2.1 URA Configuration

In a URA array, all elements are extended in the x-y

plane. There are M

elements in the x-direction and

elements in the y-direction creating an array of

x M

) elements. All elements are uniformly

spaced d apart in both directions. Such a rectangular

array can be viewed as M

uniform linear arrays of

elements or M

uniform linear arrays of M

elements. Usually, the first array element is

considered as the origin of Cartesian coordinates as

shown in Fig.1.

Figure 1: URA configuration

The direction of a signal arriving from azimuth φ

and elevation θ can be described with a unit vector e

in Cartesian coordinates as:

(1)

The vector r

in the direction of the m(i,k) element

can be described in Cartesian coordinates as:

(2)

to a signal source

Second International Conference on Telecommunications and Remote Sensing

to a signal source

1 Y

In (2), i and k denote the element position along the

y- and the x-axis, respectively. The sequential

element number m(i,k) is defined as:

(3)

If the first element in the rectangular array is a

reference element, the path-length difference d

m(i,k)

for a signal incident at element m(i,k) can be defined

as the projection of the vector r

m(i,k)

on the signal

direction vector e:

(4)

Therefore, the URA array response vector a

takes the form:

(5)

In (5), the total number of elements in the

microphone array is:

(6)

2.2 ULA Configuration

The ULA array response vector a

is calculated by

(5) where M

=1.

2.3 UCA Configuration

In a UCA array, all elements are arranged along the

ring of radius r (Fig.2).

Figure 2: UCA configuration

The ring contains M array elements. Since these

elements are uniformly spaced within the ring, so

they have an interelement angular spacing Δφ=2π/M

and a linear interelement spacing d=2rπ/M. It is

usually assumed that the first antenna element is

located at the y-axis, and the ring center is the origin

of Cartesian coordinates. The vector in the direction

of the mth array element can be written in Cartesian

coordinates as:

(7)

In (7), the angle φ

is calculated as:

(8)

The unit vector e(φ,θ) in the direction of a signal

source is given by (1). If the ring center serves as a

reference point, the propagation path-length

difference d

for a signal incident at element m can

be defined as the projection of the vector r

on the

direction vector e:

(9)

Therefore, the UCA array response vector a

takes

the form:

(10)

where d

is calculated by (9) for m=1,2,..,M.

3 SIGNAL MODEL

The signal model is based on the scenario, according

to which one or several (L) sensor signals combined

with some sound noise arrive at the microphone

array with M microphones. The output signal of each

microphone is a sum of sound-source-generated

signals and thermal noise. The vector of complex

samples of the output signal of a microphone array

at time instant k can be mathematically described as:

(11)

In (1), x(k) is the (M x 1) complex data vector, s

(k)

is the complex signal generated by the lth sound

source, b

is the (M x 1) microphone array response

vector generated in the direction of the lth sound

source, n(k) is the (M x 1) complex noise vector and

L is the number of sound sources. The signal

received from the sound source l is given by:

Sound Source Localization in a Security System Using a Microphone Array

(12)

In (12), P

is the received signal power, A

(k) is the

modulating function, different for each sound source

and f

is the sound carrier frequency. The

microphone noise n(k) occupies the entire frequency

bandwidth of a microphone and can be represented

mathematically as band-limited white additive

Gaussian noise (AWGN).

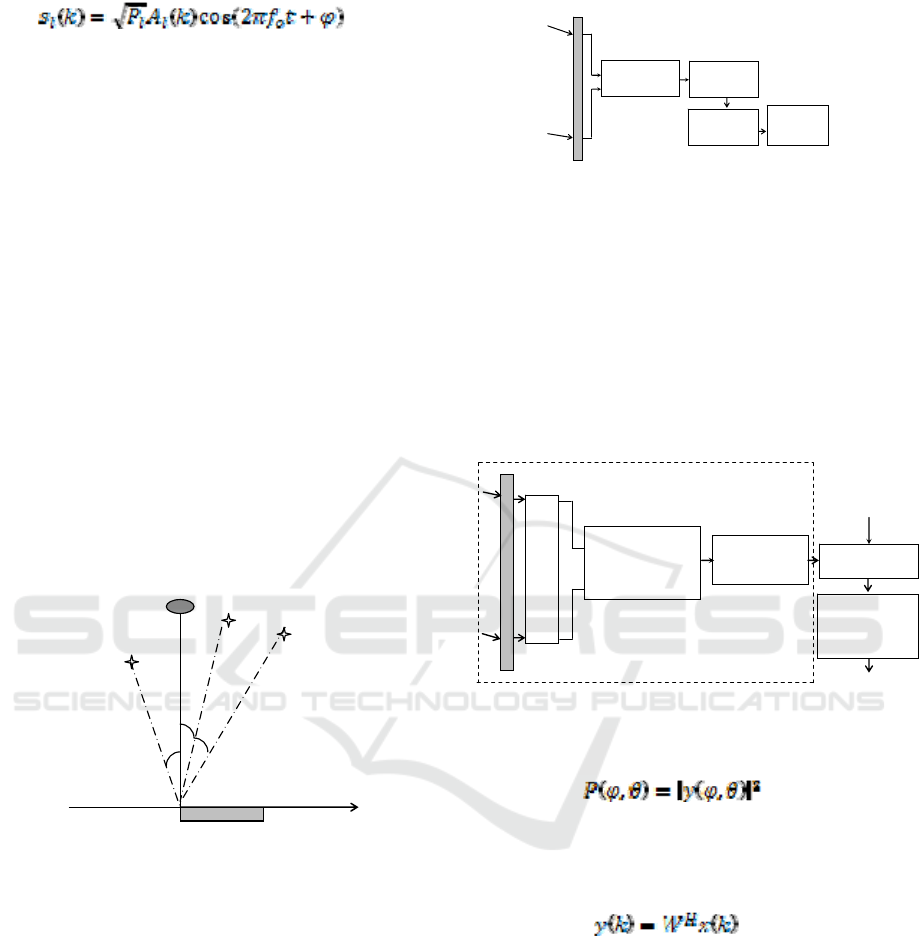
4 SIGNAL PROCESSING

Many sensors for fire detection or building

surveillance are equipped with sound alarm devices.

In case of alarm event (smoke, flame, intrusion,

glass breaking, and unauthorized car opening) the

alarm device generates powerful sound signal with

certain parameters and duration. For the sake of

simplicity, let’s assume that a set of sensors and one

microphone array are installed for the object

protection in the observation area and a video

camera is located above a microphone array as

shown in Fig.3.

Other sound

source Sensor B

Sensor C

Sensor A R

Microphone array (video camera)

Figure 3: The security system topology

In a security system, the sound source localization

could be used for pointing the additional video

surveillance devices (video cameras) in the needed

directions, which record the additional information

and send it to control center of a security system.

The priority direction for pointing of a video camera

is determined by analysis and identification of

signals received from the detected sound sources.

The analyzed signal parameters used for signal

identification are duration, frequency, modulation,

type (continuous, intermittent), and power. The

general block-scheme of a possible signal processing

in a security system is shown in Fig.4.

DOA

Estimation

Parameter

Estimation

Priority

Analysis

Camera

Control

Figure 4: Signal processing in a security system

We assume that the direction of-arrival (DOA) of

sound signals is referred to a Cartesian coordinate

system, the origin of which coincides with the first

element of a microphone array. In a security system,

in which each sensor is equipped with a sound

generator, a microphone array scans the protected

area of observation in an electronic way (Fig.5). In

the process of scanning, a microphone array with a

predetermined angular step directs its main beam in

a certain direction.

. . .

2D-Beam pattern calculation

Adaptive

Beamforming

(MVDR)

Power

Estimation

Angular

Coordinates

Estimation

Detection

Figure 5: The block-scheme of DOA estimation

At the output of a microphone array, the signal

power received from any direction is estimated as:

(13)

In (13), y and P are the output signal and the output

power of a microphone array steered in the (β,θ)-

direction (β - azimuth and θ - elevation). The output

of a microphone array with M elements is formed as:

(14)

where k is the time instant, and x(k) is the complex

vector of array observations, W=[w

,…w

]

is the

complex vector of the beamformer weights, T and H

denote transpose and conjugate transpose,

respectively. The conventional (delay-and-sum)

beamformer is the simplest, with all its weights of

equal magnitudes and the phases that are selected to

steer the array in particular direction, i.e. the

complex vector of weights W is equal to the array

response vector a

, which is defined by the array

configuration. The conventional non-adaptive

beamformer has unity response in each look

direction, that is, the mean output power of the

beamformer in the look direction is the same as the

Second International Conference on Telecommunications and Remote Sensing

received source power. In conditions of no

directional interferences, this beamformer provides

maximum SNR but it is not effective in the presence

of the other directional signals, intentional or

unintentional. The others beamformers such as a

Minimum Variance Distortionless Response

beamformer can overcome this problem by

suppressing unwanted signals from off-axis

directions (Tummonery, 1994; Vouras, 2008). To

suppress unwanted signals, this beamformer does

not require the a priori information about them. It

requires only the information for the direction-of-

arrival of expected signals. In this paper we propose

to form the signal y according to the adaptive

MVDR method. The MVDR-beamformer adaptively

calculates the vector of weights (W) providing the

maximum gain in the desired direction while

minimizing the power in the other directions.

According to this method, the optimal weight vector

(W) is chosen to maximize the signal to interference

plus noise ratio (SINR) in a certain direction

(15)

In (15), K is the “interference + noise”

covariance matrix of size (M x M), σS2 is the signal

power, and ac is the array response vector in the (,

θ) direction determined by an array configuration.

The solution is found by linear constrained

optimization. The criterion of optimization is

formulated as:

(1)

The solution of (16) gives the following weights:

Many practical applications of MVDR-

beamformers require online calculation of the

weights according to (17), and it means that the

covariance matrix K should be estimated and

inverted online. However, this operation is very

computationally expensive and it may be difficult to

estimate the sample covariance matrix in real time if

the number of samples is large. Furthermore, the

numerical calculation of the weights WMVDR using

the expression (17) may be very unstable if the

sample covariance matrix is ill-conditioned. A

numerical stable and computationally efficient

algorithm can be obtained by using QR

decomposition of the incoming signal matrix. This

matrix is decomposed as X=QR, where Q is the

unitary matrix and R is the upper triangular matrix.

Hence the QR-based algorithm for calculation of

beamformer weights includes the following three

stages:

The linear equation system

azR =

is solved

for

, and the solution is

aRz

)(

−

The linear equation system

zRz =

is solved

for

, and the solution is

zRz

−

The weight vector



is obtained as

)/(

zazW



In the process of scanning of the observation

area, the microphone array is digitally steered in

each angular direction (,θ). After adaptive

beamforming of a microphone array in the direction

(,θ), the signal power at the output of a

microphone array is stored, forming in this way the

beam pattern of a microphone array i.e. P(φ,θ). Next,

firstly the local maximums of the obtained beam

pattern must be found and after that they are

compared with a fixed predetermined threshold H. If

some local maximum of the beam pattern, i.e.

Pmax,i(φ*,θ*), corresponding to some angular

direction (φ *,θ*) exceeds the threshold H, then this

angular direction (φ *,θ*) is the estimate of the

DOA.

5 PARALLEL ALGORITHM

5.1 Algorithm Description

Parallel version of the algorithm for DOA estimation

is implemented as a program in Blue Gene

environment using the interface MPI. The parallel

program calculates the signal power at the output of

a microphone array simultaneously for all directions

of observation (Fig.5). The structure of the parallel

program uses the fact that the server loads one the

same copy of the program on all processors from 0

to (NumProc - 1) where NumProc is the number of

processors allocated to the program. The program

uses the current processor number iD, which is

defined by MPI-subroutine MPI_COMM_RANK, in

order to determine which of the two processes to be

performed (depending on that whether the processor

is a master processor, i.e. iD = 0 or slave processor,

i.e. iD> 0). The master processor (iD = 0) performs

initialization of parameters and prepares the data for

all processors. This processor performs simulation

Sound Source Localization in a Security System Using a Microphone Array

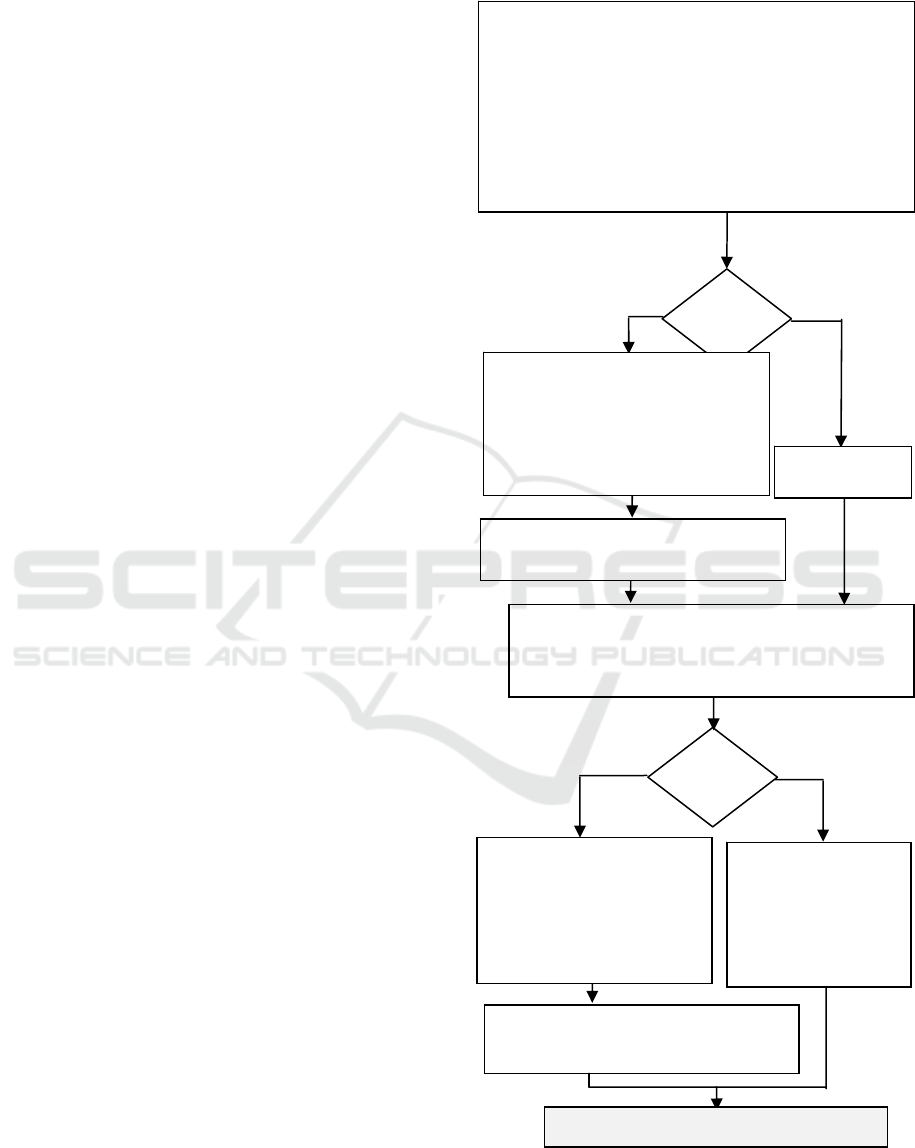
of signals (or, in practice, reading the signals from

the buffer), in result of which the signal matrix X is

formed. Moreover, for each slave processor, the

main processor calculates the angular direction

(FFI), for which the slave processor (iD = 1 ...

NumProc -1) calculates the signal power at the

output of an adaptive microphone array. The angular

direction (FFI), in which the microphone array is

steered, is sent from the master processor to each

slave processor using the loop organized by the

MPI-subroutine MPI_Send. The main processor also

prepares its data portion (FFI = -90 º and an array

FFI (i), i = 1 ... NumProc, which contains all angular

directions). Then all processors perform identical

calculations - each of them determines the signal

power at the output of a microphone array for

angular direction FFI, using the subroutine

DIAG_AZ_PAR. Once calculating the signal power

at the output of a microphone array, each slave

processor sends the resulting value to the master

processor via the MPI-subroutine MPI_Send.

The master processor via the MPI-function

MPI_Recv accepts the results from all slave

processors and forms the beam pattern of the

microphone array. After that the subroutine

FIND_AZIMUTH finds the angular positions of all

local maximums of the beam pattern, which exceed

the predetermined threshold H. The angular

positions of local maximums are the directions of

arrival of sound of signals. The number of

processors NumProc is equal to the number of

(,θ)- directions used in calculation of the beam

pattern of a

microphone array. At step 2º, the

number of processors is equal to NumProc = (180º

/2º +1) = 91.

5.2 Create and Run the Executable File

Firstly, in Blue Gene environment with the interface

MPI, the executable file, for example,

SOUND_F_PAR.exe, is created using the pre-

created file makesound_F_PAR.txt, which is started

with the command make:

> make-f makesound_F_PAR.txt

With this command all program modules of the

program package are translated and, as a result, the

executable file SOUND_F_PAR.exe is created. The

executable file SOUND_F_PAR.exe is run using

the control file SOUND_F_PAR.jcf (Job Control

File) with the following command:

> llsubmit SOUND_F_PAR.jcf

After the execution the system responds with a

message like:

llsubmit:

Figure 6: Parallel version of the algorithm

D=0

–

Master

ALL MPI

BCAST of

DO i=1, 2, …… NumProc-1

Calculation of FFI

MPI_Send of FFI

Form the data for the initial

direction

Receive FFI

Calculate the signal power P using

and FFI

CALL DIAG_AZ_PAR(…)

Receive the results

from each and every

one processor:

DO i=1…

umProc

Combine all results:

CALL FIND_AZIMUTH

()

Send the result

to the Master

processor

CALL

MPI

end

ALL MPI

Finalize(ierr)

No – Slave

D=0

–

Master

No – Slave

Initialization of MPI variables:

ALL MPI_INIT(ierr);

CALL

PI_COMM_SIZE(MPI_COMM_WORLD,

umProc,ierr);

CALL

PI COMM RANK

(

MPI COMM WORLD

Second International Conference on Telecommunications and Remote Sensing

The job "bgpfen.daits.government.bg. < task

number>" has been submitted.

The content of the control file

SOUND_F_PAR.jcf can be like that:

# @ job_name = SoundDetect

# @ comment = "SoundDetect :BlueGene"

# @ error = $(jobid).err

# @ output = $(jobid).out

# @ environment = COPY_ALL;

# @ wall_clock_limit = 01:00:00

# @ notification = error

# @ notify_user = never

# @ job_type = bluegene

# @ bg_size = 128

# @ class = n0128

# @ queue

/bgsys/drivers/ppcfloor/bin/mpirun

-exe SOUND_F_PAR.exe -verbose 1

-mode VN -np 91

The number of processors np in the file

SOUND_F_PAR.jcf given above, equals to the

number of angular (for example, azimuthal)

directions, which were used in the formation of the

beam pattern of a microphone array. At step 2º, the

number of processors is equal to np = 91

6 SIMULATION RESULTS

The computer simulation is performed to verify the

described algorithm for sound source localization.

As shown in Fig.3, the scenario of simulation

includes three sensors (A, B and C) located

respectively at 50m, 60m and 70m away from the

microphone array. In order to evaluate the

performance of the algorithm for DOA estimation

when using different types of sensors, the

parameters of the sensors produced by three well-

known companies (SONITRON, E2S and SYSTEM

SENSOR) are used in simulation.

Depending of the company of production, the

sirens of sensors generate sound signals at frequency

f0 with the power LW in range from 96dB to 103 dB

(Table 1). In simulation we assume that all sensors

in the protected area are produced by the same

company

According to the simulation scenario, the source

of natural noise is a car located in the perpendicular

direction relative to the microphone array.

The horn of this car generates a sound, whose

power is 110dB (Fig.3). The distance to the car is

90m.

Table 1: Sensor parameters

Company

Signal

power

LW [dB]

Sound

frequency

[Hz]

SONITRON 96 2500

E2S 100 1000

SYSTEM

SENSOR

103 2400

Figure 7: Microphone array WA 0807

Two microphone array configurations, the

uniform linear array (ULA) and the uniform

rectangular array (URA), are simulated for each

sensor type. The topology of a microphone array

WA 0807 of the company Brüel & Kjær is used in

simulation (Fig.7).

• The Brüel&Kjær microphone array

parameters are:

• Frequency, at which the controlled sensors

generate the sound (Hz);

• Array configuration (linear, rectangular,

square);

• Distance between array microphones (d),

which can be changed for each type of

sensors;

• Total number of microphones in the

microphone array.

The parameters of microphones of the type 4935

according to the catalogue of the company Brüel &

Kjær are used in simulation of the microphone array

(Fig.8).

Figure 8: Microphone 4935 (Brüel & Kjær)

Sound Source Localization in a Security System Using a Microphone Array

The noise level of such a microphone is 35dB in

the frequency range [100 - 5000] Hz. It is assumed

that all simulated microphone arrays (ULA and

URA) have the same overall dimension of 0.5m. The

interelement spacing of each microphone array and

as a consequence the corresponding number of

elements are determined according to the carrier

frequency of a signal generated by the sound source.

For each type of sensors, the interelement

distance in a microphone array is calculated as d = λ

/ 2, where λ is the wavelength of the sound

generated by a sensor. The sound wavelength

depends on the frequency of the generated sound,

i.e. λ = c/f0, where c = 344 m/s is the propagation

velocity of sound in air, and f0 is the frequency of

the acoustic signal (Table 1). The signal amplitude

(A) at the output of each microphone of a

microphone array is calculated as a function of the

sound pressure LP:

(18)

In (18), the sound pressure LP (in dB) depends

on the power of the sound LW, which is different for

each sensor (Table 1) and also depends on the

distance R to the sound source:

(19)

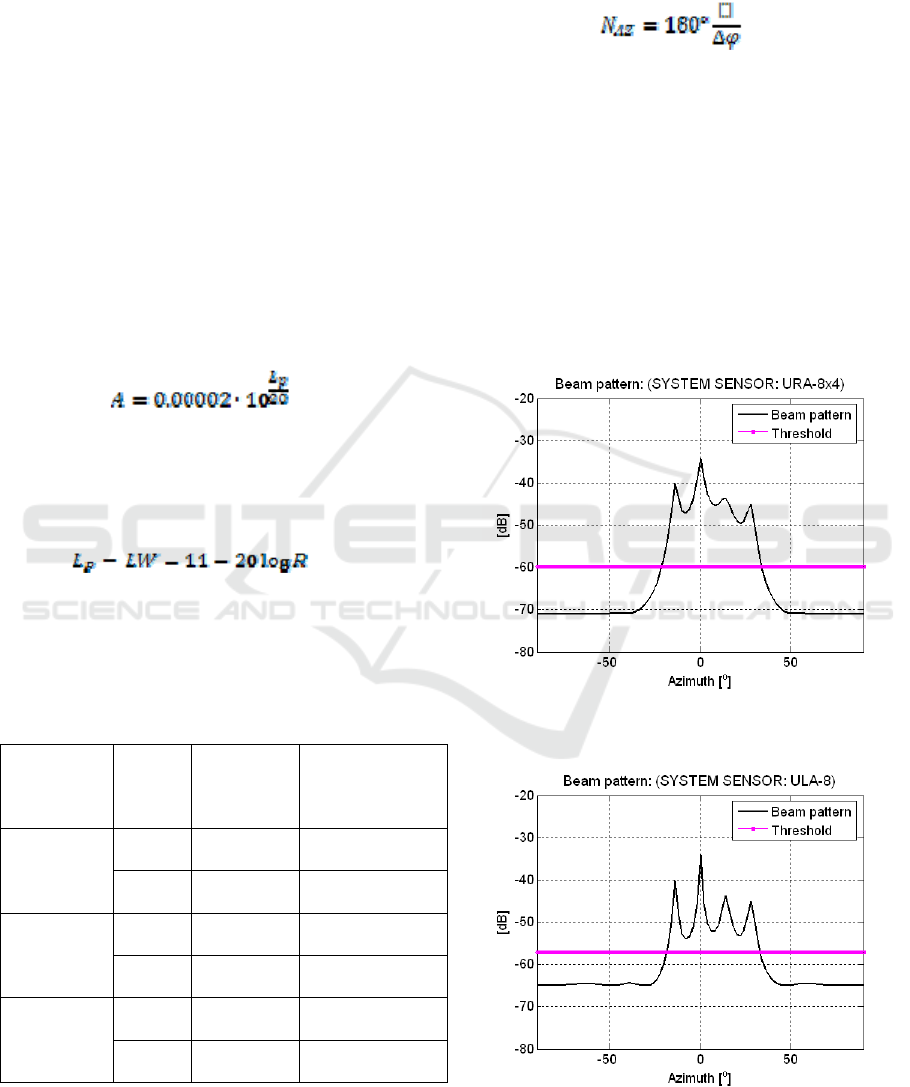
The real and estimated values of the DOA are

presented in Table 2 for each type of a microphone

array. The beam patterns of the microphone arrays

are presented respectively in Fig.9 … Fig.14.

Table 2: True and estimated azimuthal directions

SENSOR

TYPE

Array

Type

Source

Azimuth

[°]

Estimated

Azimuth [°]

ULA

(11x1)

-14;0;14;28 -14; 0;14; 28 SONITRON

URA

(11x4)

-14;0;14;28 -14; 0; 14; 28

ULA

(4x1)

-26; 0; 26 -26; 0; 26 E2S

URA

(4x4)

-26;0;26;52 -26; 0; 26; 52

ULA

(8x1)

-14;0;14;28 -14; 0;14; 28 SYSTEM

SENSOR

URA

(8x4)

-14;0;14;28 -14; 0;14; 28

The number of directions, for example, in

azimuth (NAZ), controlled by a microphone array

depends on the angular resolution of the microphone

array (Δ), which in its turn is determined by the

geometrical configuration of the microphone array

and the number of its elements:

(20)

The angular resolution Δφ is determined as the

width of the main lobe of the beam pattern created

by a microphone array. Comparing the plotted beam

pattern presented on Fig.9…Fig.14, it can be seen

that the best angular resolution in azimuth is

provided by using the microphone array ULA-11

(with 11 microphones) and opposite, the worst

angular resolution is provided by using the

microphone array ULA-4 (with 4 microphones).

Therefore, the ability of a microphone array to

separate

the signals from different sound

sources is improved with increasing the

number of microphones in the array.

Figure 9: Beam pattern of the URA-8x4 (Sensor

Type –SYSTEM SENSOR)

Figure 10: Beam pattern of the ULA-8x4 (Sensor Type –

SYSTEM SENSOR)

Second International Conference on Telecommunications and Remote Sensing

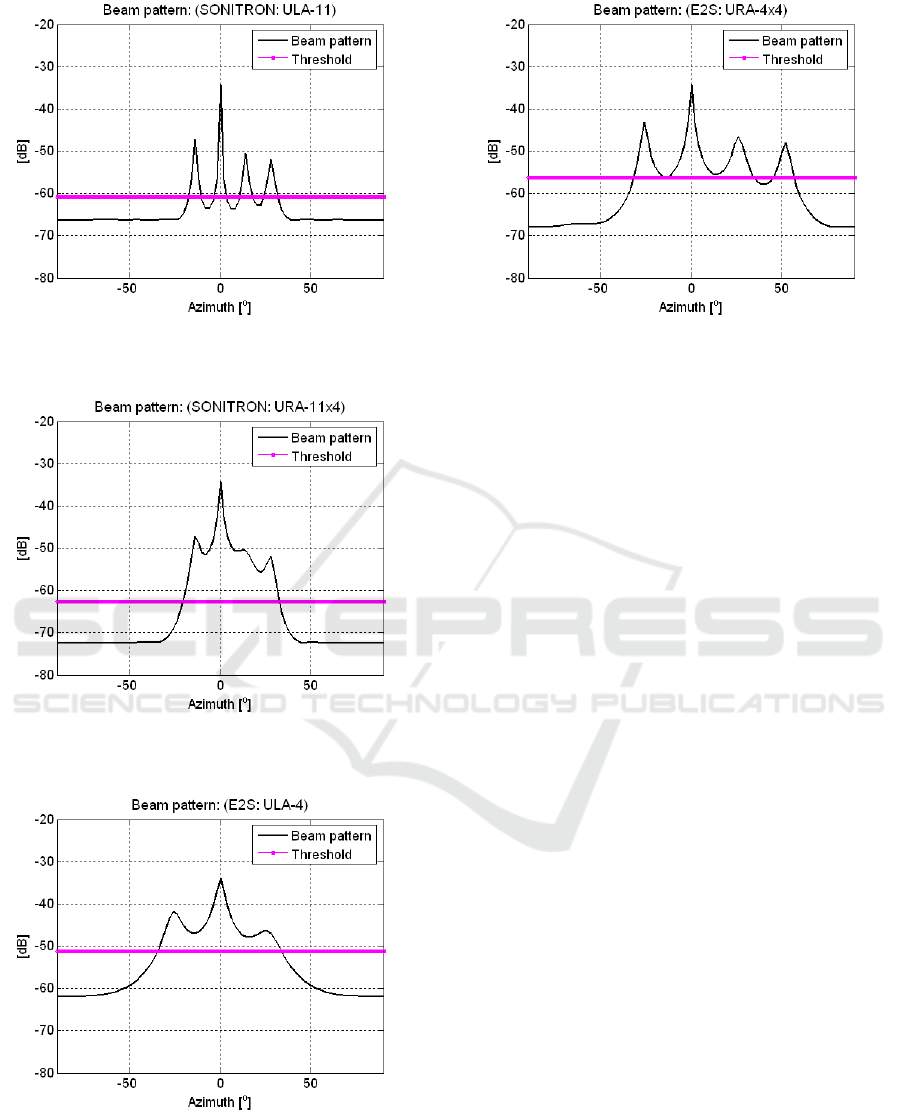
Figure 11: Beam pattern of the ULA-11 (Sensor

Type –SONITRON)

Figure 12: Beam pattern of the URA-11x4 (Sensor

Type –SONITRON)

Figure 13: Beam pattern of the ULA- 4x1 (Sensor

Type –E2S)

Figure 14: Beam pattern of the URA- 4x4 (Sensor

Type –E2S)

It is well known that the maximal number of signals

arrived from different directions, which can be

separated by a microphone array, equals (M-1),

where M is the number of array elements.

Therefore, the beam pattern plotted in Fig. 13 shows

that the microphone array ULA-4 can separate only

3 sound signals received from different directions

and generated by 3 E2S sensors. The graphical

results also show that linear microphone arrays

(ULA) should be used in cases where it is important

to control the movement of the video camera only in

azimuthal direction. However, when it is important

to control the movement of the video camera in 2D

space (azimuth and elevation), you must use

rectangular microphone arrays (URA). Comparison

analysis of the beam patterns plotted in Fig. 11 (for

ULA-11, SONITRON) and Fig.12 (for URA-11x4,

SONITRON) shows, that the use of a rectangular

microphone reduces the angular resolution in

azimuth

7 CONCLUSIONS

The results obtained show that the accurate

DOA estimates can be obtained using a

microphone array if the adaptive MVDR-

algorithm is used for beamforming. It is

also shown that the maximal number of

separated signals and also the effectiveness

of microphone arrays depend on the number

of array elements. Finally, the results

obtained can be successfully used for solving

different problems associated with noise source

localization and identification.

Sound Source Localization in a Security System Using a Microphone Array

ACKNOWLEDGEMENTS

The research work reported in the paper is partly

supported by the project AComIn "Advanced

Computing for Innovation", grant 316087, funded by

the FP7 Capacity Programme (Research Potential of

Convergence Regions).

REFERENCES

Benesty, J., Chen, J., Huang, Y., 2008. Microphone array

signal processing, Springer.

Godara, L., 1997. Application of antenna arrays to mobile

communications, part II: beam-forming and direction-

of-arrival considerations. In Proc. of the IEEE, vol.85,

No 8, pp.1195-1245.

Ioannides, P., Balanis, C., 2005. Uniform circular and

rectangular arrays for adaptive beamforming

applications. IEEE Trans. on Antenna. Wireless

Propagation. Letters, vol.4., pp. 351-354.

Trees, H., Van, L., 2002. Optimum Array Processing. Part

IV. Detection, Estimation, and Modulation Theory.

New York, JohnWiley and Sons, Inc..

Tummonery, L., Proudler, I., Farina, A., McWhirter, J.,

1994. QRD-based MVDR algorithm for adaptive

multi-pulse antenna array signal processing. In Proc.

Radar, Sonar, Navigation, vol.141, No 2, pp. 93-102.

Vouras, P., Freburger, B., 2008. Application of adaptive

beamforming techniques to HF radar. In Proc. IEEE

conf. RADAR’08, May, pp. 6.

Moelker, D.,VandePol, E., 1996. Adaptive Antenna Arrays

for Interference Cancellation in GPS and GLONASS

Receivers. In Proc. of the IEEE symp. on Position

Location and Navigation, April, pp.191-196.

http://sonitron.be/site/index.php,\

http://www.e2s.com/

http://www.systemsensor.com/

Second International Conference on Telecommunications and Remote Sensing